Some interior models of compact stars in $f(R)$ gravity

Abstract

This paper deals with the interior models of compact stars in the framework of modified $f(R)$ theory of gravity, which is the generalization of the Einstein’s gravity. In order to complete the study, we have involved solution of Krori and Barua to the static spacetime with fluid source in modified $f(R)$ theory of gravity. Further, we have matched the interior solution with the exterior solution to determine the constants of Krori and Barua solution. Finally, the constants have been formulated by using the observational data of various compact stars like 4U1820-30, Her X-1, SAX J1808-3658. Using the evaluated form of the solutions, we have discussed the regularity of matter components at the center as well as on the boundary, energy conditions, anisotropy, stability analysis and mass-radius relation of the compact stars 4U1820-30, Her X-1, SAX J1808-3658.

1 Introduction

In the weak field regime, General Relativity (GR) has succeeded to counter the observation tests whereas strong filed is yet to be explored. In fact the great success of GR has not stopped the alternatives being proposed and modifications begin to appear in very early days of this theory. Current investigations reveals the fact GR fails to explain the strong gravitational field effects which suggests that this theory may require modification. The presence of higher order term in Einstein-Hilbert (EH) action has motivated the researcher to modify this theory in strong field regime (Buchdahl 1970). In 1980, Starobinsky presented the idea of curvature driven inflationary scenario, where the action of GR is replaced by $f(R)=R+\lambda{R} ^{2}$ (Starobinsky 1980). In current years, numerous efforts have been made to get beyond the original Einstein theory, in order to explore the dark energy models in more scientific ways (Nojiri and Odintsov 2011; Sharif and Zubair 2013a, 2013b).

Exploring the exotic compact objects in modified gravity, would be a scientific tool to handle this problem. The study of strong gravitational field of compact objects clearly explain the significant differences between GR and its modification. The modeling of massive star in $f(R)$ gravity have added some additional proprieties to stars (Capozziello et al. 2011, 2012; Jamil et al. 2011; Azadi et al. 2008; Hendi and Momeni 2011; Momeni and Gholizade 2009; Farooq et al. 2013; Momeni et al. 2014; Houndjo et al. 2017). According to Psaltis (2008b) the strong gravitational fields could be considered as modified theories of gravity. One can consider the hydrostatic equilibrium of stars in $f(R)$ gravity as a test of the theory’s viability; there are several models of $f(R)$ gravity which exclude the existence of stable star and are considered unrealistic (Briscese et al. 2007). However, possible problems regarding the existence of these objects may be avoided due to scalar tensor theory (Tsujikawa et al. 2009). Recently, many people (Arapoglu et al. 2011; Alavirad and Weller 2013; Astashenok et al. 2014, 2015; Yazadjiev et al. 2014) have worked on existence of neutron star in $f(R)$.

During the last decades many researchers have derived the models of anisotropic compact stars. Egeland (2007) discussed the modeling of the mass-radius relation of Neutron star. Using spherical symmetry of compact stars, an exact solution of equation of was proposed by Mak and Harko (2004), which predicts the properties of strange stars. Rahaman et al. (2012) applied the Krori-Barua (1975) models to compact stars with Chaplygin gas EOS. Lobo (2006) investigated the models of the compact objects with a barotropic EOS. He also extended the Mazur-Mottola gravastar models by using the junction conditions between static spacetime and Schwarzschild vacuum solution. In the present study, we have investigated the formation of spherically symmetric anisotropic compact stars in $f(R)$ gravity that were initially suggested by Alcock et al. (1986) and Haensel et al. (1986). The anisotropic compact stars models with linear equation of state and variable cosmological constant have been formulated by Hossein et al. (2012). Further, Herrera and his collaborators (Herrera and Santos 1997; Herrera 2008; Herrera and Barreto 2013) have studied a class of anisotropic solutions for static and non static sources which have wide application in astrophysics and astronomy. Recently, Abbas and his collaborators (Abbas et al. 2014, 2015a, 2015b, 2015c, 2015d, 2015e; Zubair et al. 2016a, 2016c; Zubair and Abbas 2016b) have investigated the compact stars solutions in GR, $f(T)$ and $f(G)$ theories of gravity.

We study the formation of anisotropic compact stars with more generalized $f(R)$ model i.e., $f(R)=R+\lambda{R}^{2}$ (where $\lambda$ is constant) and conclude that $f(R)$ gravity can provide that existence the of anisotropic compact stars candidates. The objective of this paper is that if compact star solutions exist in $f(R)$, what are the constraints on $f(R)$ model and parameters of the theory? This paper is organized as follow. In the coming section, we formulate the equations of motion for anisotropic source and static metric in $f(R)$ gravity. In Sect. 3, we discuss the implementation of the solution to a class of compact stars and present the physical behavior of the constructed models. We summarize the findings of the paper in the last section.

2 Anisotropic matter configuration in $f(R)$ gravity

The action of $f(R)$ theory of gravity in the presence of matter is given by (Psaltis 2008a)

$$ \mathcal{\mathcal{I}}= \int{dx^{4}\sqrt{-g}\bigl[f(R)+\mathcal{L}_{(\mathit{matter})} \bigr]}, $$

(1)

where $8{\pi}G=1$, $R$ is the scalar curvature, $f(R)$ is an arbitrary function of $R$ as well as its higher powers and $\mathcal{L}_{(\mathit{matter})}$ denotes the Lagrangian density of matter part. Hence, we get the following form of field equations

$$ G_{{\mu}{\nu}}=R_{{\mu}{\nu}}-\frac{1}{2}Rg_{{\mu}{\nu}} =T_{ {\mu}{\nu}}^{(\mathit{curv})}+T_{{\mu}{\nu}}^{(\mathit{matter})}, $$

(2)

where $T_{{\mu}{\nu}}^{(\mathit{matter})}$ is the stress-energy tensor of the matter and $T_{{\mu}{\nu}}^{(\mathit{curv})}$ is curvature term, given by

$$\begin{aligned} T_{{\mu}{\nu}}^{(\mathit{curv})} =& \frac{1}{F(R)} \biggl[\frac{1}{2}g_{\mu\nu }\bigl(f(R)-RF(R)\bigr) \\ &{}+ F(R)^{;{\alpha}{\beta}}(g_{\mu\alpha}g_{\nu\beta}-g_{\mu\nu }g_{\alpha\beta})\biggr] , \end{aligned}$$

(3)

where $F(R)=f^{\prime}(R)$.

The general spherically symmetric metric is given by

$$ ds^{2}=-e^{\mu(r)}dt^{2}+e^{\nu(r)}dr^{2}+r^{2} \bigl(d\theta^{2}+\sin^{2} \theta{d\phi^{2}}\bigr), $$

(4)

where $\nu=Ar^{2}$, $\mu=Br^{2}+C$, $A$, $B$ and $C$ are constants (Krori and Barua 1975).

For the anisotropic fluid the stress energy tensor is defined by

$$ T^{m}_{\alpha\beta}=(\rho+p_{t})u_{\alpha}{u}_{\beta}-p_{t}g_{ \alpha\beta}+(p_{r}-p_{t})v_{\alpha}{v}_{\beta}, $$

(5)

where $u_{\alpha}=e^{\frac{\mu}{2}}\delta^{0}_{\alpha}$, $v_{\alpha}=e^{\frac{\nu}{2}}\delta^{0}_{\alpha}$, are four velocities, $\rho$ is energy density, $p_{r}$ and $p_{t}$ are radial and transverse pressures, respectively. In this case set of field equations is

$$\begin{aligned} \rho =& -e^{-\nu}F''+e^{-\nu}\biggl( \frac{\nu'}{2}-\frac{2}{r} \biggr) F' + \frac{e^{-\nu}}{r^{2}} \biggl( \frac{\mu''r^{2}}{2}+\frac{\mu ^{\prime\,2}r^{2}}{4} \\ &{}-\frac{\mu'\nu'r^{2}}{4}+\mu'r \biggr) F -\frac{1}{2}f, \end{aligned}$$

(6)

$$\begin{aligned} p_{r} =& e^{-\nu} \biggl( \frac{\mu'}{2}+\frac{2}{r} \biggr) F'-\frac {e^{-\nu}}{r^{2}} \biggl(\frac{\mu''r^{2}}{2}+\frac{\mu^{\prime\,2}r^{2}}{4} \\ &{}-\frac{\mu'\nu'r^{2}}{4} -\nu'r\biggr) F+\frac{1}{2}f, \end{aligned}$$

(7)

$$\begin{aligned} p_{t} =& -e^{-\nu}F''+e^{-\nu}\biggl( \frac{\mu'}{2}-\frac{\nu'}{2}+ \frac{1}{r} \biggr)F' \\ &{}-\frac{e^{-\nu}}{r^{2}} \biggl( \frac{\mu'r}{2}-\frac{\nu 'r}{2}-e^{\nu}+1 \biggr) F+\frac{1}{2}f. \end{aligned}$$

(8)

The Starobinsky model is (Starobinsky 1980)

$$ f(R)=R+\lambda{R}^{2}, $$

(9)

where $\lambda$ is an arbitrary constant. Here, we have considered the R-squared gravity ($R+\lambda{R}^{2}$) which introduces a new parameter $\lambda$. In modified gravitation theories the instability of models is tested through the Dolgov-Kawasaki instability criterion

$$ f_{R}(R)>0,\qquad f_{RR}(R)>0,\qquad R{\geq}R_{0}, $$

which restricts the Starobinsky’s parameter as $\lambda>0$. The parameter $\lambda$ has also been constrained under different consideration via neutron stars (Arapoglu et al. 2011; Orellana et al. 2013). The most important thing in existence of compact stars is the requirement of static configuration i.e., the EoS satisfies the condition $\rho-3p>0$. Therefor, in fixing $\lambda$, one needs to analyze this situation and avoid the existence of singularities. In this settings we find that the viable values of $\lambda$ lies in the range $0<\lambda<6$. One can choose suitable value of $\lambda$ according to this condition. Herein, we set $\lambda=2~\mbox{km}^{2}$, one value is presented keeping in mind the length of our work. However, other values can also be presented in similar fashion.

For this model (6)–(8) become

$$\begin{aligned} \rho =&\frac{e^{-2\nu}}{8r^{4}}\bigl\{ r^{4}\lambda \mu^{\prime\,4}-2r^{3} \lambda\mu^{\prime\,3} \bigl(-4+r \nu'\bigr) \\ &{} +r^{2}\lambda\mu^{\prime\,2}\bigl(16+8r\nu'-11r ^{2}\nu^{\prime\,2} +4r^{2}\mu''+8r^{2}\nu''\bigr) \\ &{} +4r^{2}\lambda\mu'\bigl(-16r\nu^{\prime\,2}+3r^{2} \nu^{\prime\,3}+ \nu'\bigl(-4+9r^{2} \mu'' \\ &{} -7r^{2}\nu''\bigr)+2r\bigl(-2\mu''+6\nu'' -2r\mu'''+r\nu'''\bigr)\bigr) \\ &{} +4\bigl(-2e^{\nu}{r}^{2}+2e^{2\nu}r^{2}-20 \lambda+24e^{\nu}\lambda-4e^{2\nu}\lambda \\ &{} +12r^{3}\lambda\nu^{\prime\,3}-3r^{4}\lambda\mu^{\prime\prime\,2}-r^{2}\lambda\nu^{\prime\,2}\bigl(12+11r^{2} \mu''\bigr) \\ &{} +8r^{2}\lambda\nu''+8r^{4} \lambda\mu'' \mu''-16 r^{3}\lambda\mu''' \\ &{} + 2r\nu'\bigl(e^{\nu}{r}^{2}-8\lambda+16r ^{2}\lambda\mu''-14r^{2}\lambda \nu''+6r^{3}\lambda\mu''' \bigr) \\ &{} + 8r ^{3}\lambda\nu'''-4r^{4}\lambda\mu^{(iv)}\bigr)\bigr\} , \end{aligned}$$

(10)

$$\begin{aligned} p_{r} =&\frac{e^{-2\nu}}{8r^{4}}\bigl\{ -r^{4}\lambda\mu^{\prime\,4}-2r^{4} \lambda\mu^{\prime\,3}\nu'+r^{3} \lambda\mu^{\prime\,2}\bigl(-24\nu' \\ &{} +3r\nu^{\prime\,2}+4r\bigl(\mu''-\nu''\bigr)\bigr)-4(-2e^{\nu}{r}^{2}+2e^{2\nu}r^{2} \\ &{} +28\lambda-24e^{\nu}\lambda-4e ^{2\nu}\lambda-12r^{2} \lambda\nu^{\prime\,2}-16r^{2}\lambda\mu'' \\ &{} +8r^{3}\lambda\nu'\mu''+r^{4}\lambda\mu^{\prime\prime\,2}+16r^{2}\lambda\nu''-8r^{3}\lambda\mu''' \\ &{} +8r\mu' \bigl(e^{\nu}{r}^{2}-8\lambda+3r ^{2}\lambda\nu^{\prime\,2}+6r^{2} \lambda\mu'' \\ &{} -r\lambda\nu'\bigl(8+r^{2}\mu''\bigr)-4r^{2}\lambda\nu''+r^{3}\lambda\mu'''\bigr)\bigr\} , \end{aligned}$$

(11)

$$\begin{aligned} p_{t} =&\frac{e^{-\nu}}{8r^{4}}\bigl\{ r^{4}\lambda\mu^{\prime\,4}+2r^{3}\lambda\mu^{\prime\,3}\bigl(2-3r\nu'\bigr)+ r^{2}\mu^{\prime\,2}\bigl(-32r\lambda \nu' \\ &{} +17r^{2}\lambda\nu^{\prime\,2}+2\bigl(e^{\nu}{r}^{2}-8\lambda+6r^{2} \lambda\mu''-6r^{2}\lambda\nu''\bigr)\bigr) \\ &{} -2r\mu'\bigl(-38r^{2}\lambda\nu^{\prime\,2}+6r^{3} \lambda \nu^{\prime\,3}+r\nu'\bigl(e^{\nu}{r}^{2}-24 \lambda \\ &{}+28r^{2}\lambda\mu''-14r^{2}\lambda\nu''\bigr)-2\bigl(e^{\nu}{r}^{2}-4\lambda+12e^{n}u\lambda \\ &{} +10r^{2}\lambda\mu''-14r^{2}\lambda\nu''+6r^{3}\lambda\mu'''-2r^{3}\lambda\nu'''\bigr)\bigr) \\ &{} -4\bigl(12r^{3} \lambda\nu^{\prime\,3}-11r^{4}\lambda \mu''\nu^{\prime\,2}-5r^{4}\lambda\mu ^{\prime\prime\,2} \\ &{} + \mu''\bigl(-e^{\nu}r^{4}+8r^{2}\lambda+8r^{4}\lambda \nu''\bigr)+r\nu\bigl(e^{\nu}{r}^{2}-28 \lambda \\ &{} +12e^{\nu}\lambda+28r^{2}\lambda\mu''-28r^{2} \lambda\nu''+12r^{3}\lambda\mu''' \bigr) \\ &{} +4\lambda\bigl(-7+6e^{\nu}+e^{2\nu}-3r^{3} \mu'''+2r^{3}\nu''' \\ &{} -r^{4}\mu^{(iv)} \bigr)\bigr)\bigr\} . \end{aligned}$$

(12)

We have five unknown functions $\rho$, $p_{r}$, $p_{t}$, $\mu$, $\nu$, and three equations (10)–(12). We have to chose any two functions, keeping in mind the regularity conditions of the compact stars, we chose $\mu$ and $\nu$ as after Eq. (4). As metric functions are exponential i.e., $e^{\mu(r)}$, $e^{\nu(r)}$, for $\nu=Ar^{2}$, $\mu=Br^{2}+C$, metric functions remain exponential as well as regular even at center of the star. Moreover, this choice satisfies the boundary conditions in the center of the star (Yazadjiev et al. 2014)

$$ \rho(0)=\rho_{c},\qquad\nu(0)=0, \qquad\frac{d\mu}{dr}(0)=0. $$

From the metric potential function, we have following results

$$\begin{aligned} \rho =&\frac{1}{r^{4}}e^{-2Ar^{2}}\bigl\{ e^{2Ar^{2}}\bigl(r^{2}-2\lambda\bigr)+2\bigl(-5-3B ^{2}r^{4}+6B^{3}r^{6} \\ &{} +B^{4}r^{8}+12A^{3}r^{6}\bigl(2+Br^{2}\bigr)-A^{2}r^{4} \bigl(40+68Br^{2} \\ &{} +11B^{2}r^{4}\bigr)+A\bigl(-4r^{2} +48Br ^{4}+26B^{2}r^{6} \\ &{} -2B^{3}r^{8}\bigr)\bigr)\lambda+e^{Ar^{2}}\bigl(-r^{2}+2Ar^{4}+12\lambda\bigr)\bigr\} , \end{aligned}$$

(13)

$$\begin{aligned} p_{r} =&\frac{1}{r^{4}}e^{-2Ar^{2}}\bigl\{ -e^{(}2Ar^{2}) \bigl(r^{2}-2\lambda\bigr) +2\bigl(-7+11B ^{2}r^{4} \\ &{} + 2B^{3}r^{6}-B^{4}r^{8}+3A^{2}r^{4}\bigl(2+Br^{2}\bigr)^{2} \\ &{} -2Ar^{2}\bigl(4+16Br^{2}+9B^{2}r^{4}+B^{3}r ^{6}\bigr)\bigr)\lambda \\ &{} +e^{Ar^{2}}\bigl(r^{2} +2Br^{4}+12\lambda\bigr)\bigr\} , \end{aligned}$$

(14)

$$\begin{aligned} p_{t} =&\frac{1}{r^{4}}e^{-2Ar^{2}}\bigl\{ -2\bigl(-7+6e^{Ar^{2}}+e^{2Ar^{2}}\bigr) \lambda+16B^{3}r^{6}\lambda \\ &{} +2B^{4}r^{8}\lambda-24A^{3}r^{6}\bigl(2+Br^{2}\bigr)\lambda \\ &{} +2A^{2}r^{4}\bigl(28+74Br^{2}+17B^{2}r^{4}\bigr)\lambda + B^{2}r^{4}\bigl(e^{Ar^{2}}r^{2} \\ &{} +22\lambda \bigr)+2Br^{2}\bigl(-6\lambda+e^{Ar^{2}}\bigl(r^{2}+6\lambda \bigr)\bigr) \\ &{} - Ar^{2}\bigl(4\bigl(-7+19Br ^{2}+25B^{2}r^{4}+3B^{3}r^{6} \bigr)\lambda \\ &{} + e^{Ar^{2}}\bigl(r^{2}+Br^{4}+12 \lambda\bigr)\bigr)\bigr\} . \end{aligned}$$

(15)

Here, we consider the following form of linear equation of state (EOS)

$$ p_{r}=w_{r}\rho, \quad\quad p_{t}=w_{t} \rho $$

(16)

The above equations lead to the following relations

$$\begin{aligned} \omega_{r} =&\bigl\{ -e^{2Ar^{2}}\bigl(r^{2}-2\lambda\bigr)+2\bigl(-7+11B^{2}r^{4}+2B^{3}r^{6} \\ &{} -B^{4}r^{8}+3A^{2}r^{4}\bigl(2+Br^{2}\bigr)^{2}-2Ar^{2}\bigl(4+16Br^{2} \\ &{} +9B^{2}r^{4}+B^{3}r^{6} \bigr)\bigr)\lambda+e^{A r^{2}}\bigl(r ^{2}+2Br^{4}+12 \lambda\bigr)\bigr\} \\ &{} /\bigl\{ e^{2Ar^{2}} \bigl(r^{2}-2\lambda\bigr)+2\bigl(-5-3B^{2}r^{4}+6B^{3}r^{6}+B^{4}r^{8} \\ &{} +12A^{3}r^{6}\bigl(2+Br^{2}\bigr)-A^{2}r^{4} \bigl(40+68Br^{2}+11B^{2}r^{4} \bigr) \\ &{} +A\bigl(-4r^{2} +48Br^{4}+26B^{2}r^{6}-2B^{3}r^{8}\bigr)\bigr)\lambda \\ &{} +e^{Ar^{2}}\bigl(-r^{2}+2Ar^{4}+12\lambda\bigr)\bigr\} , \end{aligned}$$

(17)

$$\begin{aligned} \omega_{t} =&\bigl\{ -2\bigl(-7+6e^{Ar^{2}}+e^{2Ar^{2}}\bigr)\lambda+16B^{3}r^{6} \lambda+2B^{4}r^{8}\lambda \\ &{} -24A^{3}r^{6}\bigl(2+Br^{2}\bigr)\lambda+2A^{2}r^{4}\bigl(28+74Br^{2} \\ &{} +17B^{2}r^{4}\bigr)\lambda+B^{2}r^{4}\bigl(e^{Ar^{2}}r ^{2}+22\lambda\bigr)+2Br^{2}\bigl(-6\lambda \\ &{} +e^{Ar^{2}}\bigl(r^{2}+6\lambda\bigr)\bigr)-Ar^{2}\bigl(4\bigl(-7+19Br^{2}+25B^{2}r^{4} \\ &{} +3B^{3}r^{6}\bigr)\lambda+e^{Ar^{2}}\bigl(r^{2}+Br^{4}+12\lambda\bigr)\bigr)\bigr\} \\ &{} /\bigl\{ e^{2Ar^{2}}\bigl(r^{2}-2\lambda\bigr)+2\bigl(-5-3B^{2}r^{4}+6B^{3}r^{6}+B^{4}r^{8} \\ &{} +12A^{3}r^{6}\bigl(2+Br^{2}\bigr)-A^{2}r^{4}\bigl(40+68Br^{2}+11B^{2}r^{4}\bigr) \\ &{} +A\bigl(-4r ^{2}+48Br^{4}+26B^{2}r^{6}-2B^{3}r^{8}\bigr)\bigr)\lambda \\ &{} +e^{Ar^{2}}\bigl(-r^{2}+2Ar^{4}+12\lambda\bigr)\bigr\} . \end{aligned}$$

(18)

3 Physical analysis

In this section, we discuss the following physical properties of the solutions.

3.1 Anisotropic constraints

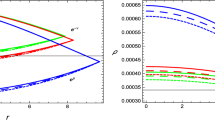
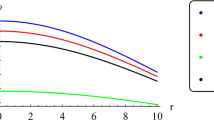
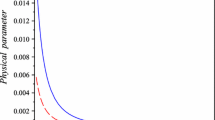
In the first place, we present the evolution of matter components as shown in Figs. 1–3 for different strange stars (see Table 1).

Fig. 1

Variation of energy density $\rho$ versus radial coordinate $r$ (km). Herein, we set $\lambda=2~\mbox{km}^{2}$

Fig. 2

Variation of radial pressure $p_{r}$ versus radial coordinate $r$ (km)

Fig. 3

Variation of transverse pressure $p_{t}$ versus radial coordinate $r$ (km)

Table 1 Values of $A$ and $B$

Taking derivatives of (13) and (14) with respect to radial coordinate, we have

$$\begin{aligned} \frac{d\rho}{dr} =&\frac{1}{r^{5}}2e^{-2Ar^{2}}\bigl\{ -e^{2Ar^{2}}\bigl(r^{2}-4 \lambda\bigr) -4\bigl(-5-3B^{3}r^{6} \\ &{} -B^{4}r^{8}+12A^{4}r^{8}\bigl(2+Br^{2}\bigr)-A^{3}r^{6}\bigl(52+80Br^{2} \\ &{} +11B^{2}r^{4}\bigr)+A^{2}r^{4}\bigl(-4 +82Br ^{2}+37B^{2}r^{4} \\ &{} -2B^{3}r^{6}\bigr)+Ar^{2}\bigl(-7-16B^{2}r^{4}+8B^{3}r^{6} \\ &{} +B^{4} r^{8}\bigr)\bigr) \lambda+e^{Ar^{2}}\bigl(Ar^{4}-2A^{2}r^{6}-24\lambda \\ &{} +r^{2}(1-12A\lambda)\bigr)\bigr\} , \end{aligned}$$

(19)

$$\begin{aligned} \frac{dp_{r}}{dr} =&\frac{1}{r^{5}}2e^{-2Ar^{2}}\bigl\{ e^{2Ar^{2}}\bigl(r^{2}-4 \lambda\bigr)-4\bigl(-7-B^{3}r^{6}+B^{4}r^{8} \\ &{} +3A^{3}r^{6}\bigl(2+Br^{2}\bigr)^{2}-A^{2}r^{4}\bigl(8+38Br^{2}+21B^{2}r^{4} \\ &{} +2B^{3}r^{6}\bigr)+Ar^{2}\bigl(-11 +20B ^{2}r^{4}+4B^{3}r^{6} \\ &{} -B^{4}r^{8}\bigr)\bigr)\lambda-e^{Ar^{2}}\bigl(Ar^{4}+2ABr^{6}+24\lambda \\ &{} +r^{2}(1+12A \lambda)\bigr)\bigr\} . \end{aligned}$$

(20)

The evolution of $\frac{d\rho}{dr}$ and $\frac{dp_{r}}{dr}$ is shown in Figs. 4 and 5. It can be seen that $\frac{d \rho}{dr}<0$ and $\frac{dp_{r}}{dr}<0$.

Fig. 4

Behavior of $\frac{d\rho}{dr}$ versus radial coordinate $r$ (km)

Fig. 5

Behavior of $\frac{p_{r}}{dr}$ versus radial coordinate $r$ (km)

We also examine the behavior of $\rho$ and $p_{r}$ at center of compact star at $r=0$ and it is found that

$$ \begin{aligned} &\frac{d\rho}{dr}=0, \qquad\frac{dp_{r}}{dr}=0, \\ &\frac{d^{2}\rho}{dr^{2}}< 0, \quad\quad\frac{d^{2}p_{r}}{dr^{2}}< 0. \end{aligned} $$

(21)

The behavior of above quantities is shown in Figs. 1–3. We present the evolution of EoS parameters $\omega_{r}$ and $\omega_{t}$ in Figs. 6 and 7. We call these parameters as effective since these involve the contribution from the additional terms in $f(R)$ gravity.

Fig. 6

Variation of EoS parameter $\omega_{r}$ versus radial coordinate $r$ (km)

Fig. 7

Variation of EoS parameter $\omega_{t}$ versus radial coordinate $r$ (km)

The anisotropy measurement $\Delta=\frac{2}{r}(p_{t}-p_{r})$ for this model is given by

$$\begin{aligned} \Delta =&\frac{1}{r^{5}}2e^{-2Ar^{2}}\bigl\{ e^{2Ar^{2}} \bigl(r^{2}-4\lambda\bigr)-4\bigl(-7+3Br ^{2}-3B^{3}r^{6} \\ &{} -B^{4}r^{8}+6A^{3}r^{6}\bigl(2+Br^{2}\bigr)-A^{2}r^{4}\bigl(8+31Br^{2} \\ &{} +7B^{2}r^{4}\bigr)+Ar^{2}\bigl(-11+3Br^{2}+16B ^{2}r^{4} +2B^{3} r^{6}\bigr)\bigr)\lambda \\ &{} -e^{Ar^{2}}\bigl(Ar^{4}+(A-B)Br^{6}+24\lambda+r ^{2}(1 +12A\lambda \\ &{} -12B\lambda)\bigr)\bigr\} . \end{aligned}$$

(22)

The measure of anisotropy is directed outward when $p_{t}> p_{r}$ which implies $\Delta>0$ whereas it is directed inward if $p_{t}< p_{r}$ resulting in $\Delta<0$. In this discussion we consider the fractional pressure anisotropy given by $\Delta{r}/p_{r}$. The evolution of fractional pressure anisotropy is shown in Fig. 8. It is obvious that $\Delta{r}/p_{r}$ remains positive and repulsive force exists which produces more massive configuration.

Fig. 8

Variation of anisotropy measurement

It is interesting to see that at center $r=0$, $p_{t}(0)=p_{r}(0)=p _{0}=34A^{2}\lambda+2B(1+11B\lambda)-A(1+64B\lambda)$.

3.2 Matching conditions

Cooney et al. (2010) studied the formation of compact objects like Neutron Star in $f(R)$ gravity theories with perturbation constraints. The Schwarzschild-de Sitter metric is considered as an exterior solution which is matched with the interior spherical symmetry using conditions analogous to that in GR. According to these authors (Goswami et al. 2014; Ganguly et al. 2014) Schwarzschild solution is the most suitable solution as exterior geometry of the star. Using this approach in $f(R)$ gravity, a lot of work has been done (Ifra and Zubair 2015; Sharif and Yousaf 2014a, 2014b; Ifra et al. 2015) by taking Schwarzschild or Vaidya metric to address the problems related to gravitational collapse. The Schwarzschild metric is given by

$$\begin{aligned} ds^{2} =& - \biggl( 1-\frac{2M}{r} \biggr)dt^{2}+ \biggl( 1- \frac{2M}{r} \biggr) ^{-1}dr^{2} \\ &{} +r^{2}d \theta^{2}+r^{2} \sin^{2}{\theta}d\varphi^{2}. \end{aligned}$$

(23)

The continuity of line elements yield,

$$\begin{aligned} g_{tt}^{-}=g_{tt}^{+},\quad \quad g_{rr}^{-}=g_{rr}^{+},\quad \quad \frac{\partial g_{tt}^{-}}{\partial r}=\frac{\partial g_{tt}^{+}}{ \partial r}, \end{aligned}$$

(24)

where − and +, are quantities for the inner and outer portion of star. Hence we get

$$\begin{aligned} A =&-\frac{1}{R^{2}}\ln \biggl( 1-\frac{2M}{R} \biggr) , \end{aligned}$$

(25)

$$\begin{aligned} B =&\frac{M}{R^{3}}{{ \biggl( 1-\frac{2M}{R} \biggr)}^{-1}}, \end{aligned}$$

(26)

$$\begin{aligned} C =&\ln \biggl( 1-\frac{2M}{R} \biggr) -\frac{M}{R}{{ \biggl( 1-\frac{2M}{R} \biggr) } ^{-1}}. \end{aligned}$$

(27)

Li et al. (1999) studied X-ray pulsar SAX J1808.4-3658 to compare its mass-radius relation with theoretical mass-radius relation of strange star and for neutron star candidates and shown the consistency of strange star model with SAX J1808.4-3658. They suggested that SAX J1808.4-3658 is a likely strange star candidate and calculated masses and radii of strange star as $1.44M_{\odot}$, $1.32M_{\odot}$ and $7.07~\mbox{km}$, $6.53~\mbox{km}$, respectively. Zhang et al. (1998) presented the mass measurement for the neutron star in 4U 1820-30 and reported mass of the order $\simeq2.2M\odot$. In Guver et al. (2010), mass and radius of neutron star in 4U 1820-30 are determined with $1\sigma$ error as $M =1.58\pm0.06M_{\odot}$ and a radius of $R=9.11\pm0.4~\mbox{km}$. However, upper bound limit in this measurement is consistent with that in Zhang et al. (1998). In fact there is a certain uncertainty in measurement of mass and radius of a compact stars. Abubekerov et al. (2008) estimated the mass of Her X-1 using more recent and physically justified techniques and found two different values of masses $m_{x}=0.85\pm0.15M_{\odot}$ and $m_{x}=1.8M_{\odot}$ through the radial-velocity curves. This uncertainty may be due to the tense X-ray heating in Her X-1. Using the observed values of $M$ and $R$ for various compact stars (Lattimer and Steiner 2014; Li et al. 1999), the values of $A$ and $B$ are given in the Table 1.

3.3 Energy conditions

The validity of these energy conditions is necessary for a physically reasonable energy-momentum tensor. The energy conditions for anisotropic fluid are following

$$\begin{aligned} \mathit{NEC}\colon\quad &\rho+p_{r}\geq0, \qquad\rho+p_{t}\geq0, \end{aligned}$$

(28)

$$\begin{aligned} \mathit{WEC}\colon\quad &\rho\geq0, \qquad\rho+p_{r}\geq0, \qquad\rho+p_{t} \geq0, \end{aligned}$$

(29)

$$\begin{aligned} \mathit{SEC}\colon\quad &\rho+p_{r}\geq0, \qquad\rho+p_{t}\geq0, \\ &\rho+p_{r}+2p_{t}\geq0, \end{aligned}$$

(30)

$$\begin{aligned} \mathit{DEC}\colon\quad &\rho>|p_{r}|, \qquad\rho>|p_{t}|. \end{aligned}$$

(31)

In Fig. 9 energy conditions are fulfilled for our model.

Fig. 9

Evolution of energy constraints for compact star Her X-1

3.4 TOV equation

In this case Tolman-Oppenheimer-Volkoff (TOV) is

$$ \frac{dp_{r}}{dr}+\frac{\nu'(\rho+p_{r})}{2}+ \frac{2(p_{r}-p_{t})}{r}=0 $$

(32)

Following Hossein et al. (2012), above equation can be written as

$$ \begin{aligned} &F_{g}+F_{h}+F_{a}=0,\qquad F_{g}=-Br(\rho+p_{r}), \\ &F_{h}=-\frac{dp_{r}}{dr}, \qquad F_{a}=\frac{2(p_{t}-p_{r})}{r} \end{aligned} $$

(33)

Using the effective $\rho$, $p_{r}$ and $p_{t}$ (10)–(12), for strange star Her X-1, we have plotted these values in Fig. 10.

Fig. 10

Variation of gravitating, hydrostatic and pressure anisotropic forces for compact star candidates

3.5 Stability analysis

People (Herrera 1992; Chan et al. 1993; Di Prisco et al. 1997) have discussed the appearance of cracking in spherical compact objects by using different approaches. Herrera (1992) introduced the concept of cracking to identify potentially unstable configuration. Now, by considering the sound speeds one can assess the potentially stable and unstable compact stars. The region for which $v^{2}_{sr}>v^{2}_{st}$ hold is potentially stable.

To complete this analysis, we calculate the radial and transverse speeds as

$$\begin{aligned} v^{2}_{sr} =&\bigl\{ -e^{2Ar^{2}}\bigl(r^{2}-4\lambda\bigr)+4\bigl(-7-B^{3}r^{6}+B^{4}r^{8} \\ &{} +3A^{3}r^{6}\bigl(2+Br^{2}\bigr)^{2} -A^{2}r^{4}\bigl(8+38Br^{2}+21B^{2}r^{4} \\ &{} +2B^{3}r^{6}\bigr)+Ar^{2}\bigl(-11+20B^{2}r ^{4}+4 B^{3}r^{6} \\ &{} -B^{4}r^{8}\bigr)\bigr)\lambda+e^{Ar^{2}}\bigl(Ar^{4}+2ABr^{6}+24\lambda \\ &{} +r^{2}(1+12A\lambda)\bigr)\bigr\} /\bigl\{ e^{2Ar^{2}}\bigl(r^{2}-4\lambda\bigr) \\ &{} +4\bigl(-5-3B^{3}r^{6}-B^{4}r^{8}+12A^{4}r^{8}\bigl(2+Br^{2}\bigr) \\ &{} -A ^{3}r^{6}\bigl(52+80Br^{2}+11B^{2}r^{4}\bigr) \\ &{} +A^{2}r^{4}\bigl(-4+82Br^{2}+37B^{2}r^{4}-2B^{3}r^{6}\bigr) \\ &{} +Ar ^{2}\bigl(-7-16B^{2}r^{4}+8B^{3}r^{6}+B^{4}r^{8}\bigr)\bigr)\lambda \\ &{} +e^{Ar^{2}}\bigl(-Ar^{4}+2A^{2}r^{6}+24\lambda \\ &{} +r^{2}(-1+12A\lambda)\bigr)\bigr\} , \end{aligned}$$

(34)

$$\begin{aligned} v^{2}_{st} =&\bigl\{ B^{2}e^{Ar^{2}}r^{6}+4\bigl(-7+6e^{Ar^{2}}+e^{2Ar^{2}}\bigr) \lambda \\ &{} -12B\bigl(-1+e^{Ar^{2}}\bigr)r^{2}\lambda+16B^{3}r^{6}\lambda+4B^{4}r^{8}\lambda \\ &{} +48A^{4}r^{8}\bigl(2+Br^{2}\bigr)\lambda-4A^{3}r^{6}\bigl(40+86Br ^{2} \\ &{} +17B^{2}r^{4}\bigr)\lambda+A^{2}r^{4}\bigl(4\bigl(-14+75Br^{2}+67B^{2}r^{4} \\ &{} +6B^{3}r^{6}\bigr)\lambda+e^{Ar^{2}}\bigl(r ^{2} +Br^{4}+12\lambda\bigr)\bigr) \\ &{} -Ar^{2}\bigl(-8\bigl(-7+3e^{Ar^{2}}\bigr)\lambda+56B^{3}r^{6}\lambda+4B^{4}r^{8} \lambda \\ &{} +B^{2}r^{4}\bigl(e^{Ar^{2}}r^{2}+144\lambda\bigr)+3Br^{2}\bigl(-8\lambda+e^{Ar^{2}}\bigl(r^{2} \\ &{} +4\lambda\bigr)\bigr)\bigr)\bigr\} /\bigl\{ -e^{2Ar^{2}}\bigl(r ^{2}-4\lambda\bigr)-4\bigl(-5-3B^{3}r^{6} \\ &{} -B^{4}r^{8}+12A^{4}r^{8}\bigl(2+Br^{2}\bigr)-A^{3}r^{6}\bigl(52 +80Br^{2} \\ &{} +11B^{2}r^{4}\bigr)+A^{2}r ^{4}\bigl(-4+82Br^{2}+37B^{2}r^{4} \\ &{} -2B^{3}r^{6}\bigr)+Ar^{2}\bigl(-7-16B^{2}r^{4}+8B^{3}r^{6}+B ^{4}r^{8}\bigr)\bigr)\lambda \\ &{} +e^{Ar^{2}}\bigl(Ar^{4}-2A^{2}r^{6}-24\lambda+r^{2}(1-12A\lambda)\bigr)\bigr\} . \end{aligned}$$

(35)

In Figs. 11 and 12 it is shown that $v^{2}_{sr}$ and $v^{2}_{st}$ satisfy the inequalities $0\leq{v}^{2}_{sr}\leq1$ and $0\leq{v}^{2}_{st}\leq1$ within the anisotropic matter configuration.

Fig. 11

Variation of $v^{2}_{sr}$ for compact star candidates

Fig. 12

Variation of $v^{2}_{st}$ for compact star candidates

The difference of $v^{2}_{sr}$ and $v^{2}_{st}$ can be obtained as

$$\begin{aligned} v^{2}_{st}-v^{2}_{sr} =&\bigl\{ e^{2Ar^{2}}\bigl(r^{2}-8\lambda\bigr)-4\bigl(-14+3Br^{2}+3B^{3}r^{6} \\ &{} + 2B^{4}r^{8}+12A^{4}r^{8}\bigl(2+Br^{2}\bigr)-2A^{3}r^{6}\bigl(14 \\ &{} +37Br^{2}+7B^{2}r^{4}\bigr)+A^{2}r^{4}\bigl(-22+37Br ^{2} \\ &{} +46B^{2}r^{4}+4B^{3}r^{6}\bigr)-Ar^{2}\bigl(25-6Br^{2} \\ &{} +16B^{2}r^{4}+10B^{3}r^{6}+2B^{4}r^{8}\bigr)\bigr)\lambda- e^{Ar^{2}}\bigl(\bigl(A^{2} \\ &{} -AB+B^{2}\bigr)r^{6}+A(A-B)Br^{8}+48 \lambda \\ &{} +Ar^{4}(1+12A\lambda-12B\lambda) +r^{2}(1+36A\lambda \\ &{} -12B\lambda)\bigr)\bigr\} /\bigl\{ e ^{2Ar^{2}}\bigl(r^{2}-4\lambda\bigr)+4\bigl(-5-3B^{3}r^{6} \\ &{} -B^{4}r^{8}+12A^{4}r^{8}\bigl(2+Br^{2}\bigr)-A^{3}r^{6}\bigl(52 \\ &{} +80Br^{2}+11B^{2}r^{4}\bigr)+A^{2}r^{4}\bigl(-4+82Br^{2} \\ &{} +37B^{2}r^{4}-2B^{3}r^{6}\bigr) +Ar ^{2}\bigl(-7-16B^{2}r^{4} \\ &{} +8B^{3}r^{6}+B^{4}r^{8}\bigr)\bigr)\lambda+e^{Ar^{2}}\bigl(-Ar^{4}+2A^{2}r^{6} \\ &{} +24\lambda+r^{2}(-1+12A\lambda)\bigr)\bigr\} . \end{aligned}$$

(36)

The $v^{2}_{st}-v^{2}_{sr}$ of different strange stars is shown in Fig. 13. Thus, our proposed model is stable.

Fig. 13

Variation of $v^{2}_{st}-v^{2}_{sr}$ for compact star candidates

3.6 Surface redshift

The Mass-radius relation is

$$\begin{aligned} u =& \frac{M(R)}{R} \\ =& \frac{{\pi}e^{-2AR^{2}}}{32A^{2}(AR^{2})^{3/2}}\bigl\{ -4\sqrt{A R^{2}}\bigl(15R^{2}B^{4}\lambda \\ &{} +192A^{5}R^{4}\bigl(2+R^{2}B\bigr)\lambda+2AR^{2}B^{3}\bigl(21+10R^{2}B\bigr)\lambda \\ &{} -16A^{4}R^{2}\bigl(22+53R^{2}B+11R^{4}B^{2}\bigr)\lambda \\ &{} +A^{2}R^{2}B^{2}\bigl(99+56R^{2}B+16R^{4}B^{2}\bigr)\lambda \\ &{} -4A^{3}\bigl(-49R^{4}B^{2}\lambda+8R^{6}B ^{3}\lambda+16\bigl(5-6e^{AR^{2}} \\ &{} +e^{2AR^{2}}\bigr)\lambda+R^{2}\bigl(-8e^{AR^{2}}+8e^{2AR^{2}}-33B\lambda\bigr)\bigr)\bigr) \\ &{} -1536A ^{4}R^{2}e^{2AR^{2}}Erf\bigl(\sqrt{AR^{2}}\bigr)\sqrt{\pi} {\lambda} +3R^{2}\bigl(224A^{4} \\ &{} +44A^{3}B+33A^{2}B^{2}+14AB^{3}+5B^{4}\bigr) \\ &{} \times e^{2AR^{2}}\sqrt{2\pi} {\lambda}Erf\bigl(\sqrt{2AR^{2}}\bigr)\bigr\} . \end{aligned}$$

(37)

The surface redshift ($Z_{s}$) is

$$\begin{aligned} 1+Z_{s} =& (1-2u)^{-1/2} \\ =& \biggl\{ 1-\frac{{\pi}e^{-2AR^{2}}}{16A^{2}(AR^{2})^{3/2}}\bigl\{ -4\sqrt{A R^{2}}\bigl(15R^{2}B^{4}\lambda \\ &{} +192A^{5}R^{4}\bigl(2+R^{2}B\bigr)\lambda+2AR^{2}B^{3}\bigl(21 \\ &{} +10R^{2}B\bigr)\lambda-16A^{4}R ^{2}\bigl(22+53R^{2}B \\ &{} +11R^{4}B^{2}\bigr)\lambda+A^{2}R^{2}B^{2}\bigl(99+56R^{2}B \\ &{} +16R^{4}B^{2}\bigr)\lambda-4A^{3}\bigl(-49R^{4}B^{2}\lambda+8R^{6}B^{3}\lambda \\ &{} +16\bigl(5-6e^{AR^{2}}e^{2AR^{2}}\bigr)\lambda+R^{2}\bigl(-8e^{AR^{2}} \\ &{} +8e^{2AR^{2}}-33B\lambda\bigr)\bigr)\bigr)-1536A^{4}R^{2}e^{2AR^{2}} \\ &{} \times Erf\bigl(\sqrt{AR^{2}}\bigr)\sqrt{\pi} {\lambda} +3R ^{2}\bigl(224A^{4}+44A^{3}B \\ &{} +33A^{2}B^{2}+14AB^{3}+5B^{4}\bigr)e^{2AR^{2}}\sqrt{2\pi} {\lambda} \\ &{} \times Erf\bigl(\sqrt{2AR^{2}}\bigr)\bigr\} \biggr\} ^{-1/2}. \end{aligned}$$

(38)

Figure 14 shows the plot of redshift of compact star Her X-1 of radius 7 km and the maximum redshift turns out to be $Z_{s}=0.845$.

Fig. 14

Surface redshift of Her X-1

4 Conclusion

The modified $f(R)$ theory of gravity providing the theoretical models of dark energy, has attracted the much attention of modern cosmologist. This theory has attained a particular interest since the $f(R)$ modifications to general theory of relativity appeared in a very natural way in the low-energy effective actions of the quantum theory of gravity and the quantization of underlying fields in curved spacetime. This theory is also conformally related to GR with some exotic scalar field (Barrow and Cotsakis 1988).

This paper is about the mathematical modeling of compact stars whose interior source is static anisotropic fluid. To complete the study, we have considered that in $f(R)$ gravity there may exists such compact stars that have anisotropy in their interiors. The interior geometry of the compact stars has been handled by metric assumption proposed by Krori and Barua (1975). Then we perform the junction conditions formalism for the interior metric with exterior Schwarzschild metric to determine the constants of interior metric in terms of masses and radii of the compact stars. These conditions yield the values of models constants that determine the nature of the compact stars. For these values of the constants, we found that the energy conditions hold for the proposed model. The results indicate that the EOS parameters are given by $0<\omega_{i}(r)<1$, ($i=r,t$). The matter energy density and pressure are regular and physical in the interior of stars.

It is interesting to note that $\Delta>0$ for the different strange stars as shown in Fig. 8. Hence, in this case repulsive force exists which allows more massive stellar configuration in $f(R)$ gravity. The subliminal velocity of sound is less than 1, i.e., $0 < v^{2}_{sr}$, $v^{2}_{st} < 1$ and $v^{2}_{sr} > v^{2}_{st}$. The variation of $v^{2}_{st}-v^{2}_{sr}$ for different strange stars is shown in Fig. 13, which satisfies the inequality $|v^{2}_{st}-v^{2}_{sr}|\leq1$. Thus, in the presence of $f(R)$ term the proposed models are stable. The range of surface redshift $Z_{s}$ for the class of the particular star is $0< Z_{s}\leq0.845$.