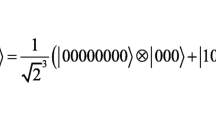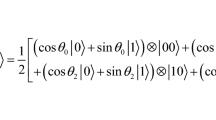Quantum image edge extraction based on classical Sobel operator for NEQR

Abstract

As the basic problem in image processing and computer vision, the purpose of edge detection is to identify the point where the brightness of the digital image changes obviously. It is an indispensable task in digital image processing that image edge detection significantly reduces the amount of data and eliminates information that can be considered irrelevant, preserving the important structural properties of the image. However, because of the sharp increase in the image data in the actual applications, real-time problem has become a limitation in classical image processing. In this paper, quantum image edge extraction for the novel enhanced quantum representation (NEQR) is designed based on classical Sobel operator. The quantum image model of NEQR utilizes the inherent entanglement and superposition properties of quantum mechanics to store all the pixels of an image in a superposition state, which can realize parallel computation for calculating the gradients of the image intensity of all the pixels simultaneously. Through constructing and analyzing the quantum circuit of realization image edge extraction, we demonstrate that our proposed scheme can extract edges in the computational complexity of $\mathrm{O}({n^2} + {2^{q + 4}})$ for a NEQR quantum image with a size of ${2^n} \times {2^n}$. Compared with all the classical edge extraction algorithms and some existing quantum edge extraction algorithms, our proposed scheme can reach a significant and exponential speedup. Hence, our proposed scheme would resolve the real-time problem of image edge extraction in practice image processing.

1 Introduction

As a young emerging sub-discipline, quantum image processing is focused on extending conventional image processing tasks and operations to the quantum computing framework, which primary work is devoted to utilizing quantum computing technologies to capture, manipulate, and recover quantum images in different formats and for different purposes [1, 2]. With the rapid development of quantum computation and quantum information, the quantum computer has demonstrated a bright prospect over the classic computer, particularly in Feynman’s computation model [3], Deutsch’s quantum parallelism assertion [4], Shor’s integer factoring algorithm [5], and Grover’s database searching algorithm [6].

In terms of applications, available literature on quantum image processing can be broadly classified into two groups: quantum-inspired image processing and classically-inspired quantum image processing [7, 8], respectively. Quantum computations and images recognition was closely followed by quantum imaging [9], quantum signal processing [10] and pattern recognition on a quantum computer [11].

The primary work for quantum image processing is how to represent images in quantum computer. The pioneering work is the quantum image model of qubit lattice [12], which using one qubit to hold one pixel. Following that, entangled images, in which geometric shapes are encoded in quantum states [13]; and Real Ket, where the images are quantum states having gray levels as coefficients of the states [14], were proposed by Venegas-Andraca and Latorre, respectively. More recently, Le et al. [15] proposed a flexible representation of quantum image (FRQI) using quantum superposition state to store the colors and the corresponding positions of an image. Years later, more quantum image representations were proposed which includes a novel enhance quantum representation (NEQR) [16] used q qubits encoding the grayscale values, which could perform the complex and elaborate color operations more conveniently than FRQI does. Quantum log-polar image [17] was proposed as a novel quantum image representation storing images sampled in log-polar coordinates. Color image representation utilized two sets of quantum states to store M colors and N coordinates, respectively [18]. A normal arbitrary quantum superposition state was used to represent a multi-dimensional image [19]. A simple quantum representation of infrared images is proposed based on the characteristic that infrared images reflect infrared radiation energy of objects [20]. Some novel quantum representations of color digital images were proposed [21, 22]. Then, based on these quantum image representation models, lots of quantum image processing algorithms are proposed which includes quantum image geometric transformation [23,24,25,26]; quantum image scaling [27,28,29]; quantum image scrambling [30,31,32]; quantum image watermarking [33,34,35,36,37]; quantum image steganography based on least significant bit (LSB) [38, 39]; quantum image edge detection [40,41,42]; quantum image feature point extraction [43]; quantum image matching [44].

In this paper, our proposed quantum edge extraction algorithm is based on NEQR model rather than FRQI model in Ref. [42]. Firstly, we elaborate that why we choose NEQR model to design the quantum edge extraction algorithm. Compared with FRQI model, NEQR utilizes q-qubit computational basis states to encode $2^q$ grayscale densities rather than 1-qubit superposition states in FRQI model. It is worth noting that since quantum image FRQI model encodes the color information in the state of one qubit by establishing a bijective relationship between the frequency of the monochromatic electromagnetic wave that determines the color and the angle parameter of a qubit [15], it has following three drawbacks that limit the applicability: (1) the original classical image cannot be accurately retrieved, i.e., the probability amplitudes of a quantum state cannot be accurately determined through using a finite number of measurements; (2) only simple color operations can be performed on the quantum image; (3) there are practical limitations on the number of colors that can be physically represented using the angle parameter of a qubit. Besides, Ref. [16] also has proven that the preparation circuit complexity of NEQR is lower than FRQI model, which achieves a quadratic speed up. Secondly, the quantum edge extraction algorithm proposed in [42] also not provides a integrate quantum circuit design for image edge extraction operation. Therein, the authors assume that there exists a quantum black box $U_{\varOmega }$ to calculate the Sobel gradients of all the pixels in the whole image and further store the classified results (i.e., edge points and non-edge points) into a single color qubit $\left| \varOmega (Y,X)\right\rangle$. However, because the pixels value is encoded via angle and stored in the coefficient of a single qubit’s superposition states, it is difficult to realize this special quantum oracle module $U_{\varOmega }$. Especially in this work involves a series of quantum numerical computations, which includes one or more of the operations of addition, subtraction, square, root square and comparison. Despite these disadvantages, this paper is the first paper to implement the quantum image edge extraction algorithm which utilizes the quantum parallel computation to speed up the classical image processing tasks than former researches. To conquer above-mentioned problems, in our proposed method, quantum image NEQR model is used to design quantum edge extraction algorithm through using Sobel operator, in which a series of quantum computations modules are introduced first (i.e., parallel add operation, parallel subtractor operation, cyclic shift transformation and other two quantum unitary operations). Then, based on these presented quantum models, we provide an integrated quantum circuit realization to implement quantum image edge extraction based on classical Sobel operator.

This paper is organized as follows. Section 2 briefly introduces the background on classical image, the novel enhanced quantum image representation (NEQR) and the principle of classical Sobel edge extraction. Section 3 designs a series of specific quantum circuit to realize a certain function for quantum Sobel image edge extraction. The circuit realization of quantum image edge extraction based on Sobel algorithm is constructed in Sect. 4. Section 5 analyses the computational complexity of our scheme and experimental results. The conclusions works are drawn in Sect. 6.

2 Preliminaries

In this section, we briefly introduce the conception of the classical image, the novel enhanced quantum image representation (NEQR) and the classical Sobel edge extraction algorithm.

2.1 Classical digital image

The classical monochromic N-by-N image is a matrix of real numbers [45, 46] as defined in Eq. (1)

$$\begin{aligned} F = \left[ {\begin{array}{llll} {{f_{00}}} &{}\quad {{f_{01}}} &{}\quad \cdots &{}\quad {{f_{0(N - 1)}}}\\ {{f_{01}}}&{}\quad {{f_{11}}}&{}\quad \cdots &{}\quad {{f_{1(N - 1)}}}\\ \vdots &{}\quad \vdots &{}\quad \cdots &{}\quad \vdots \\ {{f_{0(N - 1)}}} &{}\quad {{f_{1(N - 1)}}} &{}\quad \cdots &{}\quad {{f_{(N - 1)(N - 1)}}} \end{array}} \right] \end{aligned}$$

(1)

Each element of this matrix is called pixel where ${f_{ij}}$ is a gray-level value. Figure 1 illustrates the conception of digital image.

Fig. 1

An image with size $256 \times 256$ and the corresponding gray-level value on the right

2.2 The novel enhanced quantum representation (NEQR)

NEQR model [16] has improved the grayscale value of FRQI representation from 1 qubit to q qubits that makes lots of image operations perform more conveniently. Assume that the range of the grayscale value is from 0 to ${2^q} - 1$, the grayscale value ${C_{YX}}$ of the pixel coordinate (Y, X) is expressed by Eq. (2).

$$\begin{aligned} {C_{YX}} = {C_{YX}}^{q - 1}{C_{YX}}^{q - 2} \cdots {\mathrm{C}}_{\mathrm{YX}}^1{\mathrm{C}}_{\mathrm{YX}}^0,\quad {C_{YX}}^k \in \{ 0,1\} ,\quad {C_{YX}} \in [0,{2^q} - 1] \end{aligned}$$

(2)

Hence, NEQR for a ${2^n} \times {2^n}$ quantum image can be written as

$$\begin{aligned} \left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{C_{YX}}} \right\rangle \left| Y \right\rangle \left| X \right\rangle = } } \frac{1}{{{2^{n}}}}\sum \limits _{YX = 0}^{{2^{2n}} - 1} {\mathop \otimes \limits _{k = 0}^{q - 1} \left| {C_{YX}^k} \right\rangle } \otimes \left| {YX} \right\rangle \end{aligned}$$

(3)

Figure 2 shows an example of an $2 \times 2$ image, and the corresponding NEQR of which is on the right.

Fig. 2

An example of $2 \times 2$ image and its NEQR

2.3 Classical Sobel edge extraction algorithm

Image edge extraction is an important issue of digital image processing. The edge is caused by the discontinuities of an image’s color intensity, and the edges are the pixels at which the intensity changed fastest of the image [42]. Based on this property, there are many famous edge extraction algorithms such as Sobel [45], Prewitt [45], Kirsch [47] and Canny [48]. In order to find all the discontinuous pixels, all the classical algorithms need to analyze and calculate the gradient of the image intensity of every pixel. Thus, for an image with size of ${2^n} \times {2^n}$, any classical edge extraction algorithms will cost the computational complexity no less than $\mathrm{O}({2^{2n}})$. This is the main reason that the classical edge extraction algorithms will be low on real time with the sharp increase in the image data.

Sobel operator is mainly used for edge detection. Technically, it is a discrete differential operator that is used to calculate the image brightness function of the grayscale approximation. The operator consists of two sets of $3 \times 3$ mask, which are vertical as shown in Fig. 3b and horizontal as shown in Fig. 3c, respectively.

Fig. 3

(Figure adapted from [42])

a The pixel neighborhood window; b, c are two masks of Sobel algorithm

To obtain the difference between the horizontal and the vertical of the original image, suppose that using p represents the original image, ${G_x}$ and ${G_y}$ representing the image gradient value detected by the horizontal and vertical edges, respectively. Thus, the calculation of ${G_x}$ and ${G_y}$ is defined in Eq. (4).

$$\begin{aligned} {G_x} = \left[ {\begin{array}{lll} -\,1 &{}\quad 0&{}\quad 1\\ -\,2&{}\quad 0&{}\quad 2\\ -\,1&{}\quad 0&{}\quad 1 \end{array}} \right] *p,\quad {G_y} = \left[ {\begin{array}{lll} -\,1 &{}\quad -\,2 &{}\quad -\,1\\ 0&{}\quad 0&{}\quad 0\\ 1&{}\quad 2&{}\quad 1 \end{array}} \right] *p \end{aligned}$$

(4)

The specific calculation of Eq. (4) can be further expressed by Eq. (5).

$$\begin{aligned} {G_x}= & {} - 1 \times p(Y - 1,X - 1) + 0 \times p(Y - 1,X) + 1 \times p(Y - 1,X + 1)\nonumber \\&+\, (- 2) \times p(Y,X - 1) + 0 \times p(Y,X) + 2 \times p(Y,X + 1)\nonumber \\&+\, (- 1) \times p(Y + 1,X - 1) + 0 \times p(Y + 1,X)+ 1 \times p(Y + 1,X + 1)\nonumber \\= & {} p(Y - 1,X + 1) + 2p(Y,X + 1) + p(Y + 1,X + 1)\nonumber \\&-\,p(Y - 1,X - 1) - 2p(Y,X - 1) - p(Y + 1,X - 1)\nonumber \\ {G_y}= & {} - 1 \times p(Y - 1,X - 1) + (- 2) \times p(Y - 1,X) + (-1) \times p(Y - 1,X + 1)\nonumber \\&+\, 0 \times p(Y,X - 1) + 0 \times p(Y,X) + 0 \times p(Y,X + 1)\nonumber \\&+\, 1 \times p(Y + 1,X - 1) + 2 \times p(Y + 1,X) + 1 \times p(Y + 1,X + 1)\nonumber \\= & {} p(Y + 1,X - 1) + 2p(Y + 1,X) + p(Y + 1,X + 1)\nonumber \\&-\, p(Y - 1,X - 1) - 2p(Y - 1,X) - p(Y - 1,X + 1) \end{aligned}$$

(5)

The gradient of each pixel is calculated through its horizontal and vertical gradients values as defined in Eq. (6).

$$\begin{aligned} G = \sqrt{G_x^2 + G_y^2} \end{aligned}$$

(6)

Generally, in order to improve efficiency, we use the following calculation to substitute the gradient approximately.

$$\begin{aligned} G = \left| {{G_x}} \right| + \left| {{G_y}} \right| \end{aligned}$$

(7)

therein, || means 1st norm.

Through the above analysis, by comparing G with a gradient threshold T, the pixel will be considered as a part of edge if and only if $G \ge T$.

3 Quantum circuit design

In this section, a series of specific quantum circuit are designed to realize a certain function, which includes the parallel full adder (PA), the parallel full subtractor (PS), double operation (DO), X-Shift transformation $C(x\pm )$, Y-Shift transformation $C(y\pm )$, unitary operator ${U_S}$ and threshold operation ${U_T}$.

3.1 The parallel adder (PA) circuit

Islam et al. [49] proposed the reversible full adder based on the Peres Gate (PG). Here, the design of reversible half adder, reversible full adder and parallel adder are given.

• (a) Reversible half adder (RHA)

Figure 4a shows the PG working as a reversible half adder. Figure 4b, c is the quantum circuit realization of PG and it simplified diagram, respectively. Therein, $Q = A \oplus B$ represents the sum of $A + B$ and $R = AB$ represents the carry.

Fig. 4

The reversible half adder (RHA). a PG Gate working as half adder. b Quantum circuit implement of half adder. c The simplified diagram of RHA

• (b) Reversible full adder (RFA)

Based on the PG gates, we design the reversible full adder as shown in Fig. 5 where $R = A \oplus B \oplus C$ represents the sum of three bit $(A + {\mathrm{B}} + {\mathrm{C}})$ and $S = (A \oplus B)C \oplus AB$ represents the corresponding carry. The quantum circuit realization of RFA is shown in Fig. 5a, and its simplified diagram is shown in Fig. 5b.

Fig. 5

The reversible full adder (RFA). a Quantum implement of the reverse full adder. b The simplified diagram of RFA

• (c) Parallel adder (PA)

The parallel adder adding an n-bit $Y = {y_n}{y_{n - 1}} \cdots {y_1}{y_0}$ to an n-bit $X = {x_n}{x_{n - 1}} \cdots {x_1}{x_0}$ is designed by 1 RHA and $(n-1)$ RFA as shown in Fig. 6a. Therein, the output bit sequences ${S_n}{S_{n - 1}} \cdots {S_1}{S_0}$ represents the sum of $X + Y$ and other unremarked bits are the garbage outputs. The input bit 0 is the ancillary constant input. For convenience, the block diagram of PA omits the ancillary inputs and the garbage outputs as shown in Fig. 6b.

Fig. 6

The parallel adder (PA). a Quantum circuit realization of parallel adder (PA). b The block diagram of PA

3.2 The parallel subtractor (PS) circuit

Thapliyal and Ranganathan [50] designed subtractor using the TR gate and further realized optimization in terms of quantum cost and delay in [51]. Here, the concrete design of parallel subtractor circuit is given.

• (a) Reversible half subtractor (RHS)

As shown in Fig. 7a, the inputs of A and B are 1-bit binary number and the TR gate can work as a half subtractor performing $A - B$ operation, where the output $Q = A \oplus B$ produces the difference between A and B, the output $R = A'B$ generates the corresponding borrow bit. The quantum circuit of RHS is shown in Fig. 7b, and its simplified graph is shown in Fig. 7c.

Fig. 7

The reversible half subtractor (RHS). a TR Gate working as RHS. b Quantum circuit implement of RHS. c The simplified graph of RHS

• (b) Reversible full subtractor (RFS)

Based on the TR gate, we design the reversible full subtractor (RFS) as shown in Fig. 8a, which realizes the three bits operation of $A - B - C$. Therein, $Q = A \oplus B \oplus C$ represents the difference of $A - B - C$ and $S = C\overline{(A \oplus B)} \oplus \overline{A} B$ represents the borrow bit. The simplified diagram of RFS is shown in Fig. 8b.

Fig. 8

The reversible full subtractor (RFS). a The reversible full subtractor. b The simplified graph of RFS

• (c) Parallel subtractor (PS)

The parallel subtractor (PS) is used to compute the difference of two n-bit numbers X and Y, where $X = {x_{n - 1}} \cdots {x_0}$ and $Y = \mathrm{{ }}{y_{n - 1}} \cdots \mathrm{{ }}{y_0}$. The PS module can realize the function that subtracting an n-bit Y from n-bit X is designed by 1 RHS and $(n-1)$ RFS as shown in Fig. 9a. Therein, ${d_n}{d_{n - 1}} \cdots {d_1}{d_0}$ is the result of $X - Y$ and the input bit 0 is constant ancillary bit. For convenience, the block diagram of PS omits the constant ancillary bit 0 and the other unmarked garbage outputs as shown in Fig. 9b.

Fig. 9

The PS and its block diagram. a Quantum circuit realization of parallel subtractor (PS). b The block diagram of PS

It is should pay attention that the difference ${d_n}{d_{n - 1}} \cdots {d_1}{d_0}$ of ${d_n}{d_{n - 1}} \cdots {d_1}{d_0}$ is a complement code form in Fig. 9. Besides, the highest bit ${d_n}$ is the sign bit and other bit ${d_{n - 1}} \cdots {d_1}{d_0}$ is the numerical bit. That is to say, if ${d_n} = \;0$, it means that $X - Y \ge 0$; Otherwise, $X - Y < 0$.

To further calculate the absolute value of $X - Y$ ($\left| {X - Y} \right|$) of Fig. 9, a quantum black box ${U_R}$ was designed as shown in Fig. 10 which is divided into two parts.

Fig. 10

The quantum circuit realization of ${U_R}$ and its block diagram. a The process of $U_{R}$ calculating the absolute value of complement code. b The block diagram of $U_{R}$

As shown in Fig. 10a, first, n Control-NOT gate (CNOT) are acted on n qubit sequences ${d_n},{d_{n - 1}}, \cdots {d_1},{d_0}$ in part 1 when ${d_n} = 1$. Then, a series of multiple-Control-NOT gate are acted on n qubits sequences in part 2. Through these two parts, we can get the specific value of $X - Y$ as defined in Eq. (8).

$$\begin{aligned} X - Y = {d_n}{d'_{n - 1}}{d'_{n - 2}} \cdots {d'_1}{d'_0} \end{aligned}$$

(8)

Because of the highest bit ${d_n}$ of ${d_n}{d'_{n - 1}}{d'_{n - 2}} \cdots {d'_1}{d'_0}$ is a sign bit, the others bit ${d'_{n - 1}}{d'_{n - 2}} \cdots {d'_1}{d'_0}$ is numerical bit. Therefore, we can get the absolute value of $X - Y$ just omitting the highest bit ${d_n}$; the result value is the output as shown in Fig. 10a, which can be expressed by Eq. (9).

$$\begin{aligned} | {X - Y}| = {d'_{n - 1}}{d'_{n - 2}} \cdots {d'_1}{d'_0} \end{aligned}$$

(9)

An example as shown in Fig. 11 is used to describe the process of calculating the absolute value of $\left| {\;\left| A \right\rangle - \left| B \right\rangle \;} \right| = \left| {\;\left| B \right\rangle - \left| A \right\rangle \;} \right|$ more specifically.

Fig. 11

An example describes the process of calculating the absolute value

3.3 Double operation (DO)

Assume that $|{\mathrm{C}}\rangle = | {{c_{q -1}}{c_{q - 2}} \cdots {c_1}{c_0}}\rangle$, according to the characteristics of binary bits, if we move the binary bits one bit to the left in turn, we can obtain

$$\begin{aligned} |{2 \cdot {\mathrm{C}}}\rangle = |{{c_{q - 1}}{c_{q - 2}} \cdots {c_1}{c_0}0}\rangle \end{aligned}$$

(10)

To realize the function of Eq. (10), an auxiliary qubit $\left| 0 \right\rangle$ is needed, which is entangled with the q-qubit sequences as defined in Eq. (11)

$$\begin{aligned} |0\rangle \otimes |C\rangle = | {0{c_{q - 1}}{c_{q - 2}} \cdots {c_1}{c_0}}\rangle \end{aligned}$$

(11)

Figure 12a gives the quantum circuit realization of double operation (DO) and it simplified diagram. Therein, q swap gates are used to shift one bit to the left in turn. Figure 12b is the simplified diagram of DO which omits the ancillary qubit $|0\rangle$.

Fig. 12

Quantum circuit realization of double operation (DO) and its simplified diagram. a Quantum circuit realization of double operation (DO). b The simplified graph of DO

3.4 X-Shift and Y-Shift transformations

Le et al. [23] defined the cyclic shift transformation, which can be used to shift the whole image and every pixel will access the information of its neighborhood simultaneously. Here, based on the cyclic shift transformation, the X-Shift and Y-Shift transformations for a NEQR image with a size of ${2^n} \times {2^n}$ is discussed as follows.

Firstly, the two transformations are defined in Eq. (12)

$$\begin{aligned} \begin{array}{l} C(x\pm )\left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{C_{YX}}} \right\rangle \left| Y \right\rangle \left| {\left( {X \pm 1} \right) \bmod {2^n}} \right\rangle } } \\ C(y\pm )\left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{C_{YX}}} \right\rangle \left| {\left( {Y \pm 1} \right) \bmod {2^n}} \right\rangle \left| X \right\rangle } } \end{array} \end{aligned}$$

(12)

By using X to replace $X \pm 1$ and Y to replace $Y \pm 1$, we can obtain the relationship as Eq. (13)

$$\begin{aligned} \begin{array}{l} C(x \pm )\left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{C_{YX'}}} \right\rangle \left| Y \right\rangle \left| X \right\rangle } } \\ C(y \pm )\left| I \right\rangle = \frac{1}{{{2^{n}}}}\sum \limits _{Y = 0}^{{2^n} - 1} {\sum \limits _{X = 0}^{{2^n} - 1} {\left| {{C_{Y'X}}} \right\rangle \left| Y \right\rangle \left| X \right\rangle } } \end{array} \end{aligned}$$

(13)

where $X'{\mathrm{= (X}} \mp {\mathrm{1)mod}}{2^n}$ and ${\mathrm{Y' = (Y}} \mp {\mathrm{1)mod}}{2^n}$.

Figure 13 gives the concrete quantum circuit of the transformations $C(x + )$ and $C(y- )$ for an n-length qubits sequence. An example of the transformations $C(x + )$ and $C(y- )$ for an image with size of $4 \times 4$ also is shown in Fig. 14, where all pixels shift one unit rightwards and upwards, respectively. Therein, as an example shown in Fig. 14, (a) is the original image, (b) and (c) are the two resulted images after the transformations of $C(x + )$ and $C(y- )$, respectively. According to the discussion of the time complexity of shift operation in [23], we can conclude that the time complexity of the X-Shift and Y-Shift both is no more than $\mathrm{O}({n^2})$ for an n-length qubit sequence.

Fig. 13

Quantum circuit realizations of $C(x + )$ and $C(y- )$ for an n-length qubit sequence

Fig. 14

An example of the transformations $C(x + )$ and $C(y- )$ for an image with size of $4 \times 4$

3.5 Quantum unitary operator ${U_S}$

The quantum unitary operator as defined in Eq. (14) can copy the q-length qubit sequence information of $| C\rangle = | {{c_{q - 1}}{c_{q - 2}} \cdots {c_0}} \rangle$ into the q ancillary qubits ${|0\rangle ^{ \otimes q}}$. The quantum circuit realization of ${U_S}$ is shown in Fig. 15a, b gives the simplified graph of ${U_S}$. It is easy to conclude that the time complexity of the unitary operator ${U_S}$ is $\mathrm{O}(q)$.

$$\begin{aligned} {U_S}\left( {\left| C \right\rangle {{\left| 0 \right\rangle }^{ \otimes n}}} \right) = \left| {{C_{YX}}} \right\rangle \left| {{C_{YX}}} \right\rangle \end{aligned}$$

(14)

Fig. 15

Quantum unitary operator ${U_S}$. a Quantum circuit realization of $U_{S}$. b The simplified graph of $U_{S}$

3.6 Quantum unitary operator ${U_T}$

The function of quantum threshold operation ${U_T}$ makes the classification for the ($q+3$)-length qubit sequence. Via setting a threshold value T, all the ($q+3$)-length qubit sequence value less than T belong to one group and the left are in the other group. To store the result of the classification, an auxiliary qubit is needed, which is entangled with the ($q+3$)-length qubit sequence, and it will be set to $| 0\rangle$ in the initial state as defined in Eq. (15)

$$\begin{aligned} \left| {{C_{q{{ + 2}}}}{C_{q{{ + 1}}}} \cdots {C_1}{C_0}} \right\rangle \left| 0 \right\rangle \end{aligned}$$

(15)

The choice of the threshold is very important in this operation, which is relative to the quantum circuit and the time complexity. Generally speaking, when a threshold T is chosen, the auxiliary qubit $| 0 \rangle$ corresponding to all the ($q+3$)-length qubit sequence value no less than T should turn around. To be simple, the threshold T which is equal to powers of 2 is often chosen, and it is easy to design the quantum circuit.

An example as shown in Fig. 16, therein, the threshold is ${2^{q - 2}}$. Thus, the highest five qubits are needed to be the controllers. For the worst case, all the ($q+3$)-length qubit sequence are needed to be the controllers of the auxiliary qubit, which means that need ($q+3$)-CNOT quantum gates in the quantum circuit. According to the discussion of the time complexity of shift operation in [23], we can conclude that the time complexity of the threshold operation ${U_T}$ is no more than $\mathrm{O}({{{(q +3)}^2}})$.

Fig. 16

The quantum circuit realization of ${U_T}$ and its simplified graph. a The quantum circuit realization of $U_{T}$. b The simplified graph of $U_{T}$

4 Quantum image edge extraction based on classical Sobel algorithm

In this section, the whole workflow of our scheme, as well as the integrated quantum circuit realization, will be discussed. All of the detailed work will be introduced through the following three subsections.

4.1 Workflow of quantum image edge extraction

The flow chart is shown in Fig. 17, which is divided into 4 stages more specifically. The classical digital image is quantized into quantum image NEQR model first. Then, the X-Shift and Y-Shift transformations are used to obtain the shifted image set. Following that, very pixel’s gradient is further calculated according to Sobel mask using the shifted image set simultaneously. Finally, the edge of the original image is extracted through the threshold operation ${U_T}$.

Fig. 17

Workflow of quantum image edge extraction

4.2 Quantum circuit realization of Sobel mask computation

In this subsection, we will utilize the aforementioned shift transformations, PA module, PS module, quantum black box ${U_R}$, double operation (DO) and quantum unitary operator ${U_S}$ to calculate the intensity gradient of all the pixels in a quantum image according to the Sobel mask and the $3 \times 3$ neighborhood window simultaneously.

Figure 3b, c shows the Sobel mask on Y-direction and X-direction, respectively. In order to get the intensity gradient of every pixel, it needs to utilize the mask to calculate the approximately gradient according to Eq. (5). Through using the X-Shift and Y-Shift transformations and quantum unitary operator ${U_S}$ in a certain order, we can obtain the color information of every pixel of the $3 \times 3$ neighborhood window simultaneously. The computation prepared algorithm as shown in Algorithm 1 that can do this task.

In order to calculate the approximate gradient of image intensity of all the pixels based on Sobel operator, a quantum black box ${U_G}$ is designed, which utilizes the color qubits of the neighborhood pixels in algorithm 1. Figure 18 shows the function of the quantum black box ${U_G}$ calculating the image intensity $| G\rangle = | {\;| {{G_X}}\rangle }| +| {| {{G_Y}}\rangle }|$ as defined in Eq. (16). Figure 19 gives the concrete quantum circuit realization of the quantum black box ${U_G}$.

$$\begin{aligned} \begin{array}{l} |{| {{G_Y}}\rangle }| =\left| \begin{array}{l} ( {| {2{C_{Y + 1,X}}}\rangle + | {{C_{Y + 1,X + 1}}} \rangle + | {{C_{Y + 1,X - 1}}} \rangle } )\\ - ( {| {2{C_{Y - 1,X}}} \rangle + | {{C_{Y - 1,X + 1}}} \rangle + | {{C_{Y - 1,X - 1}}} \rangle } ) \end{array} \right| \\ | {| {{G_X}}\rangle } | = \left| \begin{array}{l} ( {| {2{C_{Y,X + 1}}}\rangle + | {{C_{Y - 1,X + 1}}} \rangle + | {{C_{Y + 1,X + 1}}} \rangle } )\\ -( {| {2{C_{Y,X - 1}}} \rangle + | {{C_{Y - 1,X - 1}}} \rangle + | {{C_{Y + 1,X - 1}}} \rangle } ) \end{array} \right| \\ | G\rangle = | {| {{G_Y}}\rangle } | + | {| {{G_X}}\rangle } | \end{array} \end{aligned}$$

(16)

Fig. 18

The quantum black box ${U_G}$

Fig. 19

Quantum circuit realization of the black box ${U_G}$

4.3 Circuit realization for quantum image edge extraction

In this subsection, the quantum circuit realization of quantum image edge extraction is constructed based on the X-Shift transformation, Y-Shift transformation, quantum unitary operation ${U_S}$, quantum black box ${U_G}$ and threshold operation ${U_T}$. As shown in Fig. 20, the concrete quantum circuit is divided into 4 stages, as an example, which realizes the edge extraction for a digital image with a size of ${2^n} \times {2^n}$.

Fig. 20

Four stages of circuit realization of Sobel edge extraction for quantum image

Stage 1: Firstly, the digital image should be quantized into a NEQR quantum image as Eq. (3). In order to store this quantum image, we need a $(2n+q)$-qubit quantum register. Meanwhile, 8 extra qubits for the next operations are needed to store the color information of the shifted pixels of all the pixels, which is defined in Eq. (17)

$$\begin{aligned} {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \otimes {\left| 0 \right\rangle ^{ \otimes q}} \end{aligned}$$

(17)

Stage 2: Perform computation prepared algorithm as defined in Algorithm 1. In the algorithm, after Steps 2–10, we can get the relative color qubits of the neighborhood pixels of the whole image and store them into the prepared extra qubits. The main operations in this step are X-Shift transformation, Y-Shift transformation and quantum unitary operator ${U_S}$. Thus, we can obtain the quantum image sets as defined in Eq. (18)

$$\begin{aligned} \left\{ \begin{array}{l} \left| {{C_{Y - 1X}}} \right\rangle ,\;\;\left| {{C_{Y - 1X + 1}}} \right\rangle ,\;\;\left| {{C_{YX + 1}}} \right\rangle ,\;\;\left| {{C_{Y + 1X + 1}}} \right\rangle ,\\ \left| {{C_{Y + 1X}}} \right\rangle ,\;\;\left| {{C_{Y + 1X - 1}}} \right\rangle ,\;\;\left| {{C_{YX - 1}}} \right\rangle ,\;\;\left| {{C_{Y - 1X - 1}}} \right\rangle ,\;\;\;\left| {{C_{YX}}} \right\rangle \; \end{array} \right\} \end{aligned}$$

(18)

Stage 3: Calculate the image intensity gradient using the relative images as defined in Eq. (18) through the quantum black box ${U_G}$. After the Stages 1–3, the calculated intensity gradient $\left| G \right\rangle \in [0,\;{2^{q + 3}} - 1]$ of the original image $\left| I \right\rangle$ in theory, which means ($q+3$) qubits are needed to store the qubit sequence.

Stage 4: Make the classification for the $\left| G \right\rangle$ through the threshold operation ${U_T}$ with a set threshold value T, all the qubits value less than the T belong to one group, and the others are in the other group as defined in Eq. (19)

$$\begin{aligned} {U_T}\left( {\sum \limits _{YX = 0}^{{2^{2n}} - 1} {\left| {{G_{YX}}} \right\rangle \left| 0 \right\rangle } } \right) = \sum \limits _{{G_{YX}} \ge T} {\left| {{G_{YX}}} \right\rangle \left| 1 \right\rangle + \sum \limits _{{G_{iYX}} < T} {\left| {{G_{iYX}}} \right\rangle \left| 0 \right\rangle } } \end{aligned}$$

(19)

From the above 4 stages analysis, the quantum image edge is extracted from the original quantum image $\left| I \right\rangle$ and stored in a binary quantum image as defined in Eq. (20)

$$\begin{aligned} \left| T \right\rangle = \frac{1}{{{2^n}}}\sum \limits _{i = 0}^{{2^{2n}} - 1} {\left| {{T_{YX}}} \right\rangle } \left| {YX} \right\rangle ,\quad {T_{YX}} \in \left\{ {0,\;1} \right\} \end{aligned}$$

(20)

when ${T_{YX}} = 1$, it means that the point is a edge point. Otherwise, it is not.

5 Circuit complexity and experiment analysis

In this section, the circuit complexity of quantum image edge detection of Fig. 20 is discussed firstly. Then, the differences in computational complexity performance between our scheme and other existing edge extraction algorithms are compared.

5.1 Circuit complexity analysis

Consider a digital image with a size of ${2^n} \times {2^n}$ as an example. Similarly, we will discuss the circuit computational complexity in 4 steps as shown in Fig. 20.

In step 1, the quantum circuit will make the construction of the NEQR quantum image $\left| I \right\rangle$. From the introduction of Ref. [16], it is known that the computational complexity of this stage is no more than $\mathrm{O}(qn{2^{2n}})$ because some operations will be done for every pixel one by one.

In step 2, we know that every shift transformation will cost $\mathrm{O}({n^2})$ for n-length qubit circuit according to Sect. 3.4 and every unitary operator ${U_S}$ cost $\mathrm{O}(q)$. Meanwhile, as shown in Fig. 20, there are totally 10 shift transformations and 8 quantum operations ${U_S}$. Thus, it is obvious that the computational complexity of step 2 is approximately $\mathrm{O}({n^2} + q)$.

In step 3, the quantum black box ${U_G}$ includes a series of PA module, PS module and quantum black box ${U_R}$ as shown Fig. 19. As shown in Fig. 19, there are 9 PA modules, 2 PS modules and 2 quantum black boxes ${U_R}$.

• (a) The computational complexity of PA

Therein, 8 PA perform the operation of ($q+1$) qubits plus ($q+1$) qubits, which needs 1 RHA and q RFA. A PA perform the operation of ($q+2$) qubits plus ($q+2$) qubits, which needs 1 RHA and ($q+1$) RFA. The quantum cost of RHA (see Fig. 4) is 4 and the quantum cost of RFA (see Fig. 5) is 8. Therefore, the quantum cost of 9 PA modules is

$$\begin{aligned} 8 \times ({8q} + 4) + 8(q + 1) + 4 = 72q + 44 \end{aligned}$$

• (b) The computational complexity of PS

Therein, 2 PS realizes the subtraction between two ($q+2$) qubits, which needs 1 RHS and ($q+1$) RFS. The quantum cost of RHS (see Fig. 7) is 4, and the quantum cost of RFS (see Fig. 8) is 6. Thus the quantum cost of 2 PS modules is

$$\begin{aligned} 2 \times \left[ 6(q + 1) + 4 \right] = 12q + 20 \end{aligned}$$

• (c) The computational complexity of ${U_R}$

Therein, 2 quantum black boxes ${U_R}$ act on ($q+3$) qubits. According to Lemmas 6.1 and 7.1 in [52] for any $2 \times 2$ unitary matrix U and any $n \ge 3$, a gate ${\varLambda _{n - 1}}(U)$ can be simulated by n qubits circuit consisting of $({2^{n - 1}} - 1)$ ${\varLambda _1}(V)$ gates, a ${\varLambda _1}({V^ + })$ gate and $({2^{n - 1}} - 2)$ ${\varLambda _1}({\sigma _x})$ gates, where V represents the unitary operator, ${V^ + }$ is the hermitian conjugate of V and ${\sigma _x}$ represents the NOT gate. Therefore, the quantum black box ${U_R}$ includes ($q+3$) CNOT and ($q+1$) multi-Control-Not gates of ${\varLambda _2}({\sigma _x}), \ldots , {\varLambda _{q + 1}}({\sigma _x}),{\varLambda _{{\mathrm{q + 2}}}}({\sigma _x})$. Therefore, the cost of 2 quantum black box ${U_R}$ is

$$\begin{aligned} 2 \times \left[ {(q + 3) + \sum \limits _{n = 3}^{q + 3} {({2^n} - 2)} } \right] = {2^{q + 4}} - 4 \end{aligned}$$

Therefore, the quantum cost in stage 3 is

$$\begin{aligned} ({72q + 44} ) +({12q + 20} ) + ({{2^{q + 4}} - 4} ) = {2^{q + 4}} + 84q + 60 \end{aligned}$$

In stage 4, the threshold operation ${U_T}$ will cost no more than $\mathrm{O}({{{(q + 3)}^2}})$ according to Sect. 3.6.

According to the above 4-stage analysis, we can conclude that the computational complexity of circuit realization of Sobel edge extraction for a ${2^n} \times {2^n}$ digital image in Fig. 20 is

$$\begin{aligned}&qn{2^{2n}}+ (10{n^2} + 8q) + ({2^{q + 4}} + 84q + 60) + (q + 2)^2\\&\quad = qn{2^{2n}} + 10{n^2} + {2^{q + 4}} + {{\mathrm{q}}^2} + 98q + 69\\&\quad = \mathrm{O}({qn{2^{2n}} + {n^2} + {2^{q + 4}}}) \end{aligned}$$

Note that the time cost of quantum image construction of NEQR is long; however, it is not considered as a part of the quantum image processing. Therefore, if the quantum image has been constructed, our proposed scheme can extract the edges for a NEQR quantum image in computational complexity of around $\mathrm{O}({n^2} + {2^{q + 4}})$. Table 1 demonstrates the performance comparisons between our proposed scheme and other three existing quantum edge extraction algorithms (Tseng [40], Fu [41] and Zhang [42] for a digital image with a size of ${2^n} \times {2^n}$. It is worth noting that the qubit lattice model uses the one qubit to store one pixel while FRQI and NEQR store the whole image information in a superposition state. Generally, the quantum image processing algorithm designed based on FRQI and NEQR model has a better performance than qubit lattice model. Also as described in Table 1, the classical image processing algorithm has to process the every pixel one-by-one, thus we can conclude that the computational complexity of the classical edge extraction algorithm is no less than $\mathrm{O}({2^{2n}})$. Therefore, our proposed quantum Sobel edge extraction algorithm has a lower computational complexity than the existing quantum edge extraction algorithms based on qubit lattice [40, 41], classical edge extraction algorithm, and near to [42].

Table 1 The performance comparisons between our scheme and other edge extraction algorithms for a digital image with a size of ${2^n} \times {2^n}$

5.2 Simulation analysis

In order to test our proposed scheme, all the experiments are simulated by MATLAB 2014 on the classical computer. Four common test images such as Lena, Peppers, Camera and Rice were chosen.

Table 2 Thresholds of algorithms when extracting edges for the test images

Through setting some certain thresholds as Table 2, all the edges of these test images extracted as shown in Fig. 21.

Fig. 21

a Four common and original test images. b The result images of quantum Sobel edge extraction. c The result images of classical Prewitt edge extraction. d The result images of classical Roberts edge extraction. All the thresholds used in edge extraction for different edge extraction methods are illustrated in Table 2

As illustrated in Fig. 21, under the same the threshold, our presented quantum Sobel edge extraction can extract more edge than classical Prewitt operator does. This is because the Sobel operator on the position of pixels is weighted, which can reduce the degree of edge ambiguity. Thus the actual effect of edge detection is better than Prewitt operator. Compared to the Sobel and Prewitt operators, the Roberts operator is an intersection gradient operator, which calculates the gradient in two diagonal directions. Thus, the simulation results shown in Fig. 21d demonstrate more diagonal edges rather than in vertical and horizontal directions.

6 Conclusion

Because of the sharp increase in the image data in the actual applications, real-time problem has become a limitation in classical image processing. In this paper, based on classical Sobel edge extraction algorithm, the quantum image edge extraction for NEQR model was proposed. NEQR utilizes the entanglement and superposition properties of quantum mechanics to store all the pixels of an image, which can process the information of all the pixels simultaneously.

Through the concrete quantum circuit realization of Fig. 20, it is reported that our constructed quantum circuit can extract edges with no more than $\mathrm{O}({n^2} + {2^{q + 4}})$ computational complexity for a NEQR quantum image with size of ${2^n} \times {2^n}$. The computational complexity compared with all the classical edge extraction algorithms can reach an exponential speedup than any classical edge extraction algorithm. Therefore, our proposed scheme can resolve the real-time problem of image edge extraction.