1 Introduction

The Kundu–Mukherjee–Naskar equation (KMNE) (Ekici et al. 2019; Wen 2017; Kundu et al. 2014; He and Yusry 2020; Yildirim 2019) is described by

$$\begin{aligned} i \phi _{t}+\alpha \phi _{xy}+i \mu \phi ( \phi \phi ^{*}_{x}-\phi ^{*}\phi _{x})=0, \end{aligned}$$
(1)

the first term represents the temporal evolution of pulses while the \(\phi (x, t, y)\) indicates the wave profile of the optical solitons. Besides, the dispersion term and the nonlinearity term are ensured by the coefficient of \(\alpha \), \(\mu \) respectively.

Nonlinear partial differential equations (NLPDEs) have great dominance because they play an indispensable role in the dynamics of many physical problems which are described in nonlinear sciences. Nonlinear science is one of the most fascinating and charming field for the research community in this cutting edge time of science. To seek the exact or analytical solutions has been the priority of researchers due to its elementary impact in the analysis of the actual feature of the systems (Gao et al. 2020; Seadawy et al. 2021a; Guo et al. 2018; Biswas et al. 2016; Bilal et al. 2021a; Guirao et al. 2020; Yokus et al. 2018; Sulaiman et al. 2019; Ali et al. 2019; Baskonus 2016) have been executed to explore the search for the new solutions to a different type of NLPDEs. This paper addresses the dynamics of optical soliton propagation through an optical fiber with the Kundu–Mukherjee–Naskar (KMN) model. The main feature of this governing model is that it has been given as a further extension of the nonlinear Schrödinger equation with the inclusion of different forms of nonlinearity for Kerr and nonlinearities of Kerr’s law to study soliton pulses in \( (2 + 1) \)-dimensions. Another important aspect of this model is that this model is used to deal with the propagation of optical waves through coherently excited resonant waveguides, especially in the phenomenon of diffraction of light rays (Ekici et al. 2019).

Moreover, solitons are also designated as special type of solitary waves, that are also solutions of various kinds of NLPDEs. Such particular kinds of solitary waves have various substantial usage in different zones as a result of its marvelous characteristic of stability. Precisely, mostly dispersive waves inelastically dissipated these waves and lose energy due to radiation phenomena, consequently these solitary waves fade, retaining their shape and speed after full nonlinear connection. Soliton theory has a significant contribution to narrate and express physical behavior and meaning of NLPDEs. Soliton hypothesis has pulled in extraordinary consideration in exploratory investigations for researchers since it is a functioning examination region in fields of media transmission, designing, numerical material science, mathematical physics, and diverse different parts of nonlinear sciences. In literature, a wide variety of exact solvers have been established to explore the nature of soliton solutions such that, new extended direct algebraic method (Mirhosseni-Alizamini et al. 2020; Nestor et al. 2020), unified method (Osman 2019), first integral method (Zhang et al. 2019), \(\tan (\frac{\phi }{2})\) approach (Ilhan et al. 2020), the extended Fan sub-equation method (Younis et al. 2020a, b), anstaz approach (Younis et al. 2017), the generalized exponential rational function scheme and modified Khater method (Ghanbari et al. 2020; Yue et al. 2020), Kudryashov method and its extended form (Ebaida et al. 2019; Ali et al. 2020), the exp-function method (Zulfiqar and Ahmad 2020), the novel Φ6-model expansion method (Zayed et al. 2018), the extended sinh-Gordon equation expansion method (Baskonus et al. 2019b), improved Bernoulli sub-equation function approach (Baskonus et al. 2019a), extended auxiliary equation mapping method (Seadawy et al. 2021b) and several other efficient methods (Rehman and Ahmad 2020; Aslan et al. 2017; Inc et al. 2017a, 2018a, c, d; Baleanu et al. 2017a, b; Miah et al. 2019; Seadawy et al. 2020a, b; Alam et al. 2020; Farah et al. 2020; Baskonus et al. 2018). On exploring the available literature it is observed that solutions of KMNE have not been recovered yet by a novel Φ6-model expansion method (Rehman et al. 2021). Therefore, we successfully implement the proposed method and extract optical soliton solutions to the nonlinear model in this manuscript. The proposed method is powerful, efficient, skilled to examine NLPDEs, consistent with computer algebra, and presents more general solutions.

The paper has the following sequence: an overview of the proposed method is summarized in Sect 2. The application of new Φ6-model expansion method is executed in Sect. 3. Modulation instability is analyzed is given in Sect. 4. Results and discussion are discussed in Sect. 5. The paper is summarized with conclusions in Sect. 6. In the following section, the novel Φ6-model expansion method is discussed.

2 Overview of a novel Φ 6-model expansion method

Here, we discuss a brief detail of the proposed method. Consider a NLPDE

$$\begin{aligned} \varGamma (\psi ,\psi _{t}, \psi _{x},\psi _{tt}, \psi _{xt},\psi _{xx}, \ldots )=0, \end{aligned}$$
(2)

where \(\varGamma \) is a polynomial in its arguments.

The essence of proposed method is summarized in the following steps.

Step 1 We introduce traveling wave transformation as

$$\begin{aligned} \psi (x,t)=\varPsi (\eta )\quad {\text{ and }}\quad \eta = \kappa (x- c t), \end{aligned}$$

where c is the velocity . After substituting this transformation into Eq. (2), we get nonlinear ODE in the following form.

$$\begin{aligned} \varUpsilon (\varPsi , \varPsi ^{\prime }, \varPsi ^{\prime \prime }, \varPsi ^{\prime \prime \prime }, \ldots )=0, \end{aligned}$$
(3)

where \(\varUpsilon \) is in general a polynomial function of its arguments and \(^\prime \) denotes the derivative w.r.t \(\eta \).

Step 2 Suppose that Eq. (3) has the solution as follows

$$\begin{aligned} \varPsi (\eta )=\sum _{j=0}^{2n}\delta _{j}\varphi ^{j}(\eta ), \end{aligned}$$
(4)

where constants \(\delta _{j}\) \((j=0,\ldots ,2n)\) are determined later, while \(\varphi (\eta )\) satisfies the following NODE

$$\begin{aligned} \varphi ^{\prime ^{2}}(\eta )=h_{0}+h_{2}\varphi ^{2}(\eta ) +h_{4}\varphi ^{4}(\eta )+h_{6}\varphi ^{6}(\eta ),\nonumber \\ \varphi ^{\prime \prime }(\eta )=h_{2}\varphi (\eta )+2h_{4} \varphi ^{3}(\eta )+3h_{6}\varphi ^{5}(\eta ).~~~~~~~ \end{aligned}$$
(5)

Step 3 The value of n in Eq. (4) will be evaluated by using homogeneous balance principle (Sirisubtawee and Koonprasert 2018). More precisely, if \(deg\big [\varPsi (\eta )\big ]=n\) then the degree of the other terms will be expressed as follows

$$\begin{aligned}&deg\bigg [\dfrac{d^{k}\varPsi }{d \eta ^{k}}\bigg ]=n+k,\nonumber \\&deg\bigg [(\varPsi (\eta ))^{p}\bigg (\dfrac{d^{k}\varPsi }{d \eta ^{k}}\bigg )^{s} \bigg ]=np+s(n+k). \end{aligned}$$
(6)

Step 4 It is well known that Eq. (5) has the solution

$$\begin{aligned} \varphi (\eta )=\frac{\varTheta (\eta )}{\sqrt{f\varTheta ^{2}(\eta )+g}}, \end{aligned}$$
(7)

where \((f\varTheta ^{2}(\eta )+g)>0\) and \(\varTheta (\eta )\) is the solution of the Jacobian elliptic equation

$$\begin{aligned} \varTheta ^{\prime ^{2}}(\eta )=l_{0}+l_{2}\varTheta ^{2}(\eta )+l_{4}\varTheta ^{4}(\eta ), \end{aligned}$$
(8)

and \(l_{k} (k=0,2,4)\) are real constant, while f and g are given by

$$\begin{aligned} f=\frac{h_{4}(l_{2}-h_{2})}{(l_{2}-h_{2})^{2}+3l_{0} l_{4}-2l_{2}(l_{2}-h_{2})},\\ g=\frac{3l_{0} h_{4}}{(l_{2}-h_{2})^{2}+3l_{0} l_{4}-2l_{2}(l_{2}-h_{2})}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2}(l_{2}-h_{2})[9l_{0} l_{4}-(l_{2}-h_{2})(2l_{2}+h_{2})]+ 3h_{6}\big [3 l_{0} l_{4}-\big (l_{2}^{2}-h_{2}^{2}\big )\big ]^{2}=0. \end{aligned}$$
(9)

Step 5 The solutions of Eq. (8) are expressed in the shape of Jacobi elliptic functions (JEFs) as in Rehman et al. (2021). Substituting (8) along with (7) into Eq. (4). A bunch of equations is retrieved through the comparison of specific terms which is further solved for required set of parameters which earns the solutions of Eq. (2).

3 Mathematical preliminaries

The complex wave transformation \( \phi (x, y, t)\) = \(\varPhi (\eta )e^{i\psi (x, y, t)} , \eta = x+y -\nu t\) and \(\psi =-\kappa _{1} x-\kappa _{2} y+\omega t+\theta _{0}\) . Here, \(\nu , \kappa _{1}\) and \(\kappa _{2}\) are the velocity of solitons, frequencies along the x and y plane directions respectively, \(\omega \) is the wave number and \(\theta _{0}\) is the phase constant, while \(\psi (x, y, t)\) denotes the phase component. Putting above solitary wave transformation into Eq. (1) and separating the imaginary and real parts, one can get

$$\begin{aligned} \nu = -\alpha (\kappa _{1}+\kappa _{2}), \end{aligned}$$
(10)

real part gives

$$\begin{aligned} \big (\alpha \kappa _{1} \kappa _{2}+\omega ^{2}\big )\varPhi + 2 \kappa _{1} \mu \varPhi ^{3} - \alpha \varPhi ''=0, \end{aligned}$$
(11)

by making balance between \(\varPhi ^{3}(\eta )\) and \(\varPhi ''(\eta )\) in Eq. (11) via using formula (6) as follows

$$\begin{aligned} deg\big [\varPhi ^{\prime \prime }\big ]=n+2=deg\big [\varPhi ^{3}\big ]=3n,~\implies n+2=3n, \end{aligned}$$
(12)

which leads to \(n= 1\). Thus, the solution of Eq. (11) takes the following form

$$\begin{aligned} \varPhi (\eta )=\delta _{0}+\delta _{1} \varphi +\delta _{2}\varphi ^{2}, \end{aligned}$$
(13)

where \(\delta _{0}, \delta _{1}, \delta _{2}\) are constants to be determined later. Placing Eq. (13) and its derivatives in Eq. (11) and collecting same power coefficients of \(\varphi ^{j}(\eta )\) \([\varphi ^{'}(\eta )]^{k}\), \((j=0,\ldots ,8)\) and \((k=0,1)\) to zero, the strategic equations are easily obtained. After solving the strategic equations by the assistance of Mathematica, we get the solutions sets as follows

Family-1

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta _{0}= 0,~\delta _{1}= \frac{\sqrt{\alpha } \sqrt{h_{4}}}{\sqrt{\kappa _{1}} \sqrt{\mu }},\delta _{2}= 0,\; h_{6}= 0,\; \omega = \sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}},\; h_{4}= h_{4},\; h_{2}= h_{2}. \end{array}\right. } \end{aligned}$$

The following solutions can be constructed for the given family and the JEFs are selected from Rehman et al. (2021). The resulting solutions of Eq. (1) are summarized as under.

1. If \(l_{0}=1\), \(l_{2}=-(1+m^{2})\), \(l_{4}=m^{2}\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{sn}}(\eta , m)\) or \(\varTheta (\eta )={\mathrm{cd}}(\eta , m)\), retrieve JEFs

$$\begin{aligned} \phi _{1}(x, y, t)=\left[\frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sn}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}+1\right) {\text{sn}}(\eta ,m)^{2}-3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}} \right]\times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(14)

or

$$\begin{aligned} \phi _{2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{cd}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}+1\right) {\text{cd}}(\eta ,m)^{2}-3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(15)

where

$$\begin{aligned} f=\frac{h_{4} \left( h_{2}+m^{2}+1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g=-\frac{3 h_{4}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (14), the dark soliton solution is formulated

$$\begin{aligned} \phi _{1,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \tanh (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( 3-\left( h_{2}+2\right) \tanh ^{2}(\eta )\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(16)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (14), the periodic wave solutions is attained

$$\begin{aligned} \phi _{1,2}(x, y, t)=\left[\frac{\sqrt{\alpha } \sqrt{h_{4}} \sin (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( h_{2} \sin ^{2}(\eta )+\sin ^{2}(\eta )-3\right) }{1-h_{2}^{2}}}}\right]\times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(17)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

2. If \(l_{0}=1-m^{2}\), \(l_{2}=2m^{2}-1\), \(l_{4}=-m^{2}\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{cn}}(\eta , m)\), gives JEFs

$$\begin{aligned} \phi _{3}(x, y, t)=\bigg [\frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{cn}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}-2 m^{2}+1\right) {\text{cn}}(\eta ,m)^{2}+3 \left( m^{2}-1\right) \right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\bigg ]\times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(18)

where

$$\begin{aligned} f=\frac{h_{4} \left( h_{2}-2 m^{2}+1\right) }{-\,h_{2}^{2}+m^{4}-m^{2}+1},\\ g=\frac{3 h_{4} \left( m^{2}-1\right) }{-\,h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (18), the bright soliton solution is calculated

$$\begin{aligned} \phi _{3,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sech}}(\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} {\text{sech}}^{2}(\eta )}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(19)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (18), the periodic wave solution is achieved

$$\begin{aligned} \phi _{3,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \cos (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( h_{2} \cos ^{2}(\eta )+\cos ^{2}(\eta )-3\right) }{1-h_{2}^{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(20)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

3. If \(l_{0}=m^{2}-1\), \(l_{2}=2-m^{2}\), \(l_{4}=-1\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{dn}}(\eta , m)\), gives JEFs

$$\begin{aligned} \phi _{4}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{dn}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}-2\right) {\text{dn}}(\eta ,m)^{2}-3 m^{2}+3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(21)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}+m^{2}-2\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=-\frac{3 h_{4} \left( m^{2}-1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (21), the solitary wave solution is achieved

$$\begin{aligned} \phi _{4,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sech}}(\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} {\text{sech}}^{2}(\eta )}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(22)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (21), the rational function solution is achieved

$$\begin{aligned} \phi _{4,2}(x, y, t)=\left[ -\frac{\sqrt{\alpha } \left( h_{2}-1\right) }{\sqrt{h_{4}} \sqrt{\kappa _{1}} \sqrt{\mu }}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(23)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

4. If \(l_{0}=m^{2}\), \(l_{2}=-(1+m^{2})\), \(l_{4}=1\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{ns}}(\eta , m)\) or \(\varTheta (\eta )={\mathrm{dc}}(\eta , m)\), retrieve JEFs

$$\begin{aligned} \phi _{5}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{ns}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}+1\right) {\text{ns}}(\eta ,m)^{2}-3 m^{2}\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(24)

or

$$\begin{aligned} \phi _{6}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{dc}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}+1\right) {\text{dc}}(\eta ,m)^{2}-3 m^{2}\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(25)

where

$$\begin{aligned} f=\frac{h_{4} \left( h_{2}+m^{2}+1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g=-\frac{3 h_{4} m^{2}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (24), the singular soliton solution is calculated

$$\begin{aligned} \phi _{5,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \coth (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+2\right) {\text{csch}}^{2}(\eta )+h_{2}-1\right) }{1-h_{2}^{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(26)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (24), the trigonometric solution is formulated

$$\begin{aligned} \phi _{5,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \csc (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \csc ^{2}(\eta )}{1-h_{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(27)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

5. If \(l_{0}=-m^{2}\), \(l_{2}=-1+2m^{2}\), \(l_{4}=1-m^{2}\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{nc}}(\eta , m)\), gives JEFs

$$\begin{aligned} \phi _{7}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{nc}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}-2 m^{2}+1\right) {\text{nc}}(\eta ,m)^{2}+3 m^{2}\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(28)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}-2 m^{2}+1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=\frac{3 h_{4} m^{2}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (28), the soliton solution is attained

$$\begin{aligned} \phi _{7,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \cosh (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -h_{2} \cosh ^{2}(\eta )+\cosh ^{2}(\eta )-3\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(29)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (28), the periodic wave solution is achieved.

$$\begin{aligned} \phi _{7,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \sec (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \sec ^{2}(\eta )}{1-h_{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(30)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

6. If \(l_{0}=-1\), \(l_{2}=2-m^{2}\), \(l_{4}=-(1-m^{2})\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{nd}}(\eta , m)\), retrieve JEFs

$$\begin{aligned} \phi _{8}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{nd}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}-2\right) {\text{nd}}(\eta ,m)^{2}+3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(31)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}+m^{2}-2\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=\frac{3 h_{4}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (31), the soliton solution is retrieved

$$\begin{aligned} \phi _{8,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \cosh (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -h_{2} \cosh ^{2}(\eta )+\cosh ^{2}(\eta )-3\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(32)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (31), the similar plane wave solution is retrieved as in Eq. (23).

7. If \(l_{0}=1\), \(l_{2}=2-m^{2}\), \(l_{4}=1-m^{2}\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{sc}}(\eta , m)\), retrieve JEFs

$$\begin{aligned} \phi _{9}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sc}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}-2\right) {\text{sc}}(\eta ,m)^{2}-3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(33)

where

$$\begin{aligned} f=\frac{h_{4} \left( h_{2}+m^{2}-2\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g=-\frac{3 h_{4}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (33), the hyperbolic solution is achieved

$$\begin{aligned} \phi _{9,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \sinh (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -h_{2} \sinh ^{2}(\eta )+\sinh ^{2}(\eta )+3\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(34)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (33), the periodic wave solution is attained

$$\begin{aligned} \phi _{9,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \tan (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( 3-\left( h_{2}-2\right) \tan ^{2}(\eta )\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(35)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

8. If \(l_{0}=1\), \(l_{2}=2m^{2}-1\), \(l_{4}=-m^{2}(1-m^{2})\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{sd}}(\eta , m)\),gives JEFs

$$\begin{aligned} \phi _{10}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sd}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}-2 m^{2}+1\right) {\text{sd}}(\eta ,m)^{2}-3\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(36)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}-2 m^{2}+1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=-\frac{3 h_{4}}{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (36), the soliton solution is achieved

$$\begin{aligned} \phi _{10,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \sinh (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -h_{2} \sinh ^{2}(\eta )+\sinh ^{2}(\eta )+3\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(37)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (36), the periodic wave solution is attained

$$\begin{aligned} \phi _{10,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \sin (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+1\right) \sin (\eta )^{2}-3\right) }{1-h_{2}^{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(38)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

9. If \(l_{0}=1-m^{2}\), \(l_{2}=2-m^{2}\), \(l_{4}=1\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{cs}}(\eta , m)\), gives JEFs

$$\begin{aligned} \phi _{11}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{cs}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}+m^{2}-2\right) {\text{cs}}(\eta ,m)^{2}+3 \left( m^{2}-1\right) \right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(39)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}+m^{2}-2\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=\frac{3 h_{4} \left( m^{2}-1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (39), the singular soliton solution is achieved

$$\begin{aligned} \phi _{11,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{csch}}(\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} {\text{csch}}^{2}(\eta )}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(40)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (39), the periodic wave solution is attained

$$\begin{aligned} \phi _{11,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \cot (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -h_{2} \cot ^{2}(\eta )+2 \cot ^{2}(\eta )+3\right) }{h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(41)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

10. If \(l_{0}=-m^{2}(1-m^{2})\), \(l_{2}=2m^{2}-1\), \(l_{4}=1\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{ds}}(\eta , m)\), gives JEFs

$$\begin{aligned} \phi _{12}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{ds}}(\eta ,m)}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( \left( h_{2}-2 m^{2}+1\right) {\text{ds}}(\eta ,m)^{2}-3 m^{4}+3 m^{2}\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(42)

where

$$\begin{aligned} f&=\frac{h_{4} \left( h_{2}-2 m^{2}+1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1},\\ g&=-\frac{3 h_{4} m^{2} \left( m^{2}-1\right) }{-h_{2}^{2}+m^{4}-m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} h_{4}^{2} \left( -h_{2}+2 m^{2}-1\right) \left( h_{2}+m^{2}-2\right) \left( h_{2}+m^{2}+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (42), the hyperbolic solution is achieved as

$$\begin{aligned} \phi _{12,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{csch}}(\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} {\text{csch}}^{2}(\eta )}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(43)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (42), the periodic wave solution is attained

$$\begin{aligned} \phi _{12,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \csc (\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \csc ^{2}(\eta )}{1-h_{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(44)

provided that

$$\begin{aligned} \left( h_{2}-2\right) \left( h_{2}+1\right) {}^{2} h_{4}^{2}=0. \end{aligned}$$

11. If \(l_{0}=\frac{1-m^{2}}{4}\), \(l_{2}=\frac{1+m^{2}}{2}\), \(l_{4}=\frac{1-m^{2}}{4}\), \(0<m<1\), then \(\varTheta (\eta )={\mathrm{nc}, m}(\eta , m)\pm {\mathrm{sc}}(\eta , m)\) or \(\varTheta (\eta )=\frac{{\mathrm{cn}}(\eta , m)}{1\,\pm \,{\mathrm{sn}}(\eta , m)}\), gives JEFs

$$\begin{aligned} \phi _{13}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} ({\text{nc}}(\eta ,m)\,\pm \, {\text{sc}}(\eta ,m))}{2 \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} \left( 2 \left( -2 h_{2}+m^{2}+1\right) ({\text{nc}}(\eta ,m)\,\pm \, {\text{sc}}(\eta ,m))^{2}-3 m^{2}+3\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(45)

or

$$\begin{aligned} \phi _{14}(x, y, t)&=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{cn}}(\eta ,m)}{2 \sqrt{\kappa _{1}} \sqrt{\mu } (1\,\pm \, {\text{sn}}(\eta ,m)) \sqrt{\frac{h_{4} \left( 3 \left( m^{2}-1\right) (1\,\pm \, {\text{sn}}(\eta ,m))^{2}-2 \left( -2 h_{2}+m^{2}+1\right) {\text{cn}}(\eta ,m)^{2}\right) }{\left( -16 h_{2}^{2}+m^{4}+14 m^{2}+1\right) (1\,\pm \, {\text{sn}}(\eta ,m))^{2}}}}\right] \nonumber \\&\qquad \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(46)

where

$$\begin{aligned} f=-\frac{8 h_{4} \left( -2 h_{2}+m^{2}+1\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1},\\ g=\frac{12 h_{4} \left( m^{2}-1\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} \frac{1}{32} h_{4}^{2} \left( -2 h_{2}+m^{2}+1\right) \left( 4 h_{2}+(m-6) m+1\right) \left( 4 h_{2}+m (m+6)+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (45), the combo soliton solution is achieved as

$$\begin{aligned} \phi _{13,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} (\sinh (\eta )+\cosh (\eta ))}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} (\sinh (2 \eta )+\cosh (2 \eta ))}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y \,+\,(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(47)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (45), the mixed periodic wave solution is attained

$$\begin{aligned} \phi _{13,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} (\tan (\eta )+\sec (\eta ))}{2 \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( 4 h_{2} (\sin (\eta )+1)+\sin (\eta )-5\right) }{\left( 16 h_{2}^{2}-1\right) (\sin (\eta )-1)}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(48)

provided that

$$\begin{aligned} \frac{1}{32} \left( -32 h_{2}^{3}+6 h_{2}+1\right) h_{4}^{2}=0. \end{aligned}$$

12. If \(l_{0}=\frac{-(1-m^{2})^{2}}{4}\), \(l_{2}=\frac{1+m^{2}}{2}\), \(l_{4}=-\frac{1}{4}\), \(0<m<1\), then \(\varTheta (\eta )=m\,{\mathrm{cn}}(\eta , m)\,\pm \,{\mathrm{dn}}(\eta , m)\), achieves JEFs

$$\begin{aligned} \phi _{15}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} (m {\text{cn}}(\eta ,m)\pm {\text{dn}}(\eta ,m))}{2 \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( 3 \left( m^{2}-1\right) ^{2}-2 \left( -2 h_{2}+m^{2}+1\right) (m {\text{cn}}(\eta ,m)\,\pm \, {\text{dn}}(\eta ,m))^{2}\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(49)

where

$$\begin{aligned} f=-\frac{8 h_{4} \left( -2 h_{2}+m^{2}+1\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1},\\ g=\frac{12 h_{4} \left( m^{2}-1\right) ^{2}}{-16 h_{2}^{2}+m^{4}+14 m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} \frac{1}{32} h_{4}^{2} \left( -2 h_{2}+m^{2}+1\right) \left( 4 h_{2}+(m-6) m+1\right) \left( 4 h_{2}+m (m+6)+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (49), the solitary wave solution is achieved as

$$\begin{aligned} \phi _{15,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sech}}(\eta )}{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{-\frac{h_{4} {\text{sech}}^{2}(\eta )}{h_{2}+1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(50)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (49), the plane wave solution is attained

$$\begin{aligned} \phi _{15,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \left( 1-4 h_{2}\right) }{4 \sqrt{h_{4}} \sqrt{\kappa _{1}} \sqrt{\mu }}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(51)

provided that

$$\begin{aligned} \frac{1}{32} \left( -32 h_{2}^{3}+6 h_{2}+1\right) h_{4}^{2}=0. \end{aligned}$$

13. If \(l_{0}=\frac{1}{4}\), \(l_{2}=\frac{1-2m^{2}}{2}\), \(l_{4}=\frac{1}{4}\), \(0<m<1\), then \(\varTheta (\eta )=\frac{{\mathrm{sn}}(\eta , m)}{1\,\pm \,{\mathrm{cn}}(\eta , m)}\), gives JEFs

$$\begin{aligned} \phi _{16}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sn}}(\eta ,m)}{2 \sqrt{\kappa _{1}} \sqrt{\mu } (1\pm {\text{cn}}(\eta ,m)) \sqrt{\frac{h_{4} \left( 2 \left( 2 h_{2}+2 m^{2}-1\right) {\text{sn}}(\eta ,m)^{2}-3 (1\pm {\text{cn}}(\eta ,m))^{2}\right) }{\left( -16 h_{2}^{2}+16 m^{4}-16 m^{2}+1\right) (1\pm {\text{cn}}(\eta ,m))^{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(52)

where

$$\begin{aligned} f=\frac{8 h_{4} \left( 2 h_{2}+2 m^{2}-1\right) }{-16 h_{2}^{2}+16 m^{4}-16 m^{2}+1},\\ g=-\frac{12 h_{4}}{-16 h_{2}^{2}+16 m^{4}-16 m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} \frac{1}{32} h_{4}^{2} \left( 2 h_{2}+2 m^{2}-1\right) \left( 8 h_{2} \left( -2 h_{2}+2 m^{2}-1\right) +32 m^{4}-32 m^{2}-1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (52), the combine soliton solution is retrieved

$$\begin{aligned} \phi _{16,1}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \tanh \left( \frac{\eta }{2}\right) }{\sqrt{2} \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} {\text{sech}}^{2}\left( \frac{\eta }{2}\right) \left( -4 h_{2} (\cosh (\eta )-1)+\cosh (\eta )+5\right) }{16 h_{2}^{2}-1}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(53)

provided that

$$\begin{aligned} \frac{1}{32} \left( 32 h_{2}^{3}-6 h_{2}+1\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (52), the periodic wave solution is achieved

$$\begin{aligned} \phi _{16,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \tan \left( \frac{\eta }{2}\right) }{2 \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \sec ^{2}\left( \frac{\eta }{2}\right) \left( 4 h_{2} (\cos (\eta )-1)+\cos (\eta )+5\right) }{32 h_{2}^{2}-2}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(54)

provided that

$$\begin{aligned} \frac{1}{32} \left( -32 h_{2}^{3}+6 h_{2}+1\right) h_{4}^{2}=0. \end{aligned}$$

14. If \(l_{0}=\frac{1}{4}\), \(l_{2}=\frac{1+m^{2}}{2}\), \(l_{4}=\frac{(1-m^{2})^{2}}{4}\), \(0<m<1\), then \(\varTheta (\eta )=\frac{{\mathrm{sn}}(\eta , m)}{{\mathrm{cn}}(\eta , m)\pm {\mathrm{dn}}(\eta , m)}\), gives JEFs

$$\begin{aligned} \phi _{17}(x, y, t)&=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} {\text{sn}}(\eta ,m)}{2 \sqrt{\kappa _{1}} \sqrt{\mu } ({\text{cn}}(\eta ,m)\pm {\text{dn}}(\eta ,m)) \sqrt{-\frac{h_{4} \left( 3 ({\text{cn}}(\eta ,m)\pm {\text{dn}}(\eta ,m))^{2}+2 \left( -2 h_{2}+m^{2}+1\right) {\text{sn}}(\eta ,m)^{2}\right) }{\left( -16 h_{2}^{2}+m^{4}+14 m^{2}+1\right) ({\text{cn}}(\eta ,m)\pm {\text{dn}}(\eta ,m))^{2}}}}\right] \nonumber \\&\qquad \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(55)

where

$$\begin{aligned} f&=-\frac{8 h_{4} \left( -2 h_{2}+m^{2}+1\right) }{-16 h_{2}^{2}+m^{4}+14 m^{2}+1},\\ g&=-\frac{12 h_{4}}{-16 h_{2}^{2}+m^{4}+14 m^{2}+1}, \end{aligned}$$

under the constraints condition

$$\begin{aligned} \frac{1}{32} h_{4}^{2} \left( -2 h_{2}+m^{2}+1\right) \left( 4 h_{2}+(m-6) m+1\right) \left( 4 h_{2}+m (m+6)+1\right) =0. \end{aligned}$$

Remark For \(m\rightarrow 1\) in Eq. (55), bright-dark soliton solution is retrieved

$$\begin{aligned} \phi _{17,1}(x, y, t)=\left[ \frac{2 \sqrt{\alpha } \sqrt{h_{4}} \tanh \left( \frac{\eta }{2}\right) }{\sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \left( -4 h_{2} \tanh ^{2}(\eta )+\tanh ^{2}(\eta )+6 {\text{sech}}(\eta )+6\right) }{\left( h_{2}^{2}-1\right) ({\text{sech}}(\eta )+1)^{2}}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(56)

provided that

$$\begin{aligned} \left( h_{2}-1\right) {}^{2} \left( h_{2}+2\right) h_{4}^{2}=0. \end{aligned}$$

Remark For \(m\rightarrow 0\) in Eq. (55), the periodic wave solution is achieved

$$\begin{aligned} \phi _{17,2}(x, y, t)=\left[ \frac{\sqrt{\alpha } \sqrt{h_{4}} \tan \left( \frac{\eta }{2}\right) }{2 \sqrt{\kappa _{1}} \sqrt{\mu } \sqrt{\frac{h_{4} \sec ^{2}\left( \frac{\eta }{2}\right) \left( 4 h_{2} (\cos (\eta )-1)+\cos (\eta )+5\right) }{32 h_{2}^{2}-2}}}\right] \times e^{i(\theta _{0}-\kappa _{1} x-\kappa _{2} y +(\sqrt{\alpha } \sqrt{h_{2}-\kappa _{1} \kappa _{2}}) t)}, \end{aligned}$$
(57)

provided that

$$\begin{aligned} \frac{1}{32} \left( -32 h_{2}^{3}+6 h_{2}+1\right) h_{4}^{2}=0. \end{aligned}$$

4 Modulation instability analysis

Many nonlinear phenomena exhibit instability which results in the modulation of the stationary state due to the coaction between the nonlinear and dispersive effects. In this case, we analyze the modulation instability (MI) of KMNE using the concept of linear stability (Inc et al. 2017b, 2018b; Bilal et al. 2021b).

Consider the steady-state solutions of the KMNE to be of the form

$$\begin{aligned} \phi (x,y,t)=(\sqrt{\mu }+P(x,y,t))e^{i \mu t}, \end{aligned}$$
(58)

where \(\mu \) represents the normalized optical power.

Placing Eq. (58) into Eqs. (1), after linearizing, we attain

$$\begin{aligned} \mu (P+P^{*})-i P_{t}-a P_{xy}=0, \end{aligned}$$
(59)

where \(*\) stands for the conjugate .

Suppose the solutions of Eq. (59) to be of the form

$$\begin{aligned} P(x, y, t)=f_{1}e^{i(l_{1}x+l_{2}y-\varpi t)} +f_{2}e^{-i(l_{1} x+l_{2}y-\varpi t)} \end{aligned}$$
(60)

where \(l_{1}\), \(l_{2}\) and \(\varpi \) denote the normalized wave numbers and frequency of perturbation, respectively.

Placing Eq. (60) into Eq. (59), splitting the coefficients of \(e^{i(l_{1} x+l_{2} y-\varpi t)}\) and \(e^{-i(l_{1} x+l_{2} y-\varpi t)}\), we attain the dispersion relation after solving the determinant of the coefficient matrix.

$$\begin{aligned} \begin{aligned} a^{2} l_{1}^{2} l_{2}^{2}+2 a \mu l_{1} l_{2}-\varpi ^{2}=0. \end{aligned} \end{aligned}$$
(61)

Calculating the dispersion relation (61) for \(\varpi \), grants

$$\begin{aligned} \varpi =\sqrt{a} \sqrt{l_{1}} \sqrt{l_{2}} \sqrt{a l_{1} l_{2}+2 \mu }. \end{aligned}$$
(62)

The obtained dispersion relation reveals the steady-state stability. If the wave number \(\varpi \) is an imaginary one then the steady-state solution turns to unstable since the perturbation grows exponentially. Besides, if the wavenumber \(\varpi \) has real part then steady-state turns to stable against small perturbation. Therefore, the steady-state solution is unstable if:

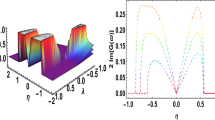
$$\begin{aligned} a l_{1} l_{2}+2 \mu <0. \end{aligned}$$

Finally, the MI gain spectrum \(G(\mu )\) is achieved as

$$\begin{aligned} G(\mu )=2Im(\varpi )=2Im \bigg (\sqrt{a} \sqrt{l_{1}} \sqrt{l_{2}} \sqrt{a l_{1} l_{2}+2 \mu }\bigg ). \end{aligned}$$
(63)
Fig. 1
figure 1

Gain spectrum of MI of Eq. (63), for distinct values \(a=\{1,1.4\}\), \(l_{2}=\{1.6,1\}\) and \(\mu =\{1.5,1.48\}\)

Full size image

5 Result and discussion

We have depicted the graphical view of some wave structures of the studied model in this manuscript. By implementing the proposed method, the wave structures (multiple-soliton solutions, trigonometric, rational function, periodic, and singular wave structures) are extracted and graphically depicted in 3-D, 2-D, and their contours with different parameters. The graphs show that these wave structures have different physical meanings. For example, hyperbolic functions such as the hyperbolic tangent appear in the calculation and rapidity of special relativity while the hyperbolic cotangent arises in the Langevin function for magnetic polarization. The modulation instability of the governing model is also examined. We observe that the retrieved solutions are new and to the best of our knowledge the applications of this technique to the (\(2+1\))-dimensional KMNE have not been reported in the literature beforehand and could be beneficial to understand the different physical behaviors.

Fig. 2
figure 2

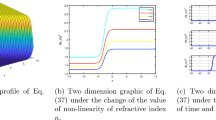
The letters a–c sequentially draw the physical 3-, 2-dimensional and their corresponding contour behavior of a dark soliton solution (16), for the values \(\omega =1.3\), \(h_{2}=0.5\), \(h_{4}=0.4\), \(\theta _{0}=0.03\), \(\kappa _{1}=1.6\), \(\kappa _{2}=0.8\), \(\alpha =1.4\), \(\mu =1.2\), \(\nu =1.1\) and \(y=1.7\)

Full size image
Fig. 3
figure 3

The letters a–c sequentially draw the physical 3-, 2-dimensional and their corresponding contour behavior of a singular wave solution (26), for the values \(\omega =1.5\), \(h_{2}=0.6\), \(h_{4}=0.7\), \(\theta _{0}=0.02\), \(\kappa _{1}=1.4\), \(\kappa _{2}=0.9\), \(\alpha =1.3\), \(\mu =1.1\), \(\nu =1.2\) and \(y=1.6\)

Full size image
Fig. 4
figure 4

The letters a–c sequentially draw the physical 3-, 2-dimensional and their corresponding contour behavior of a periodic wave solution (35), for the values \(\omega =0.5\), \(h_{2}=0.7\), \(h_{4}=0.6\), \(\theta _{0}=0\), \(\kappa _{1}=1.4\), \(\kappa _{2}=0.8\), \(\alpha =1.5\), \(\mu =0.9\), \(\nu =0.4\) and \(y=1.3\)

Full size image
Fig. 5
figure 5

The letters a–c sequentially draw the physical 3-, 2-dimensional and their corresponding contour behavior of a combine soliton solution (53), for the values \(\omega =1.2\), \(h_{2}=0.7\), \(h_{4}=1.6\), \(\theta _{0}=0.05\), \(\kappa _{1}=0.5\), \(\kappa _{2}=0.8\), \(\alpha =0.6\), \(\mu =1.1\), \(\nu =0.35\) and \(y=1.3\)

Full size image
Fig. 6
figure 6

The letters a–c sequentially draw the physical 3-, 2-dimensional and their corresponding contour behavior of a bright-dark soliton solution (56), for the values \(\omega =0.4\), \(h_{2}=1.7\), \(h_{4}=1.6\), \(\theta _{0}=0.04\), \(\kappa _{1}=1.5\), \(\kappa _{2}=1.8\), \(\alpha =1.2\), \(\mu =1.9\), \(\nu =3.8\) and \(y=1.3\)

Full size image

6 Conclusion

In this research, a novel Φ6-model expansion method has been effectively applied to a KMN model which is one of the most fascinating problems of modern optics. A series of optical soliton solutions such as single (dark, bright and singular), combo solitons, as well as a hyperbolic, plane wave, trigonometric and the families of Jacobi elliptic function solutions, have been successfully retrieved. For the limiting case, when \(m\rightarrow 1\) and \(m\rightarrow 0\), the hyperbolic functions and the periodic, as well as rational solutions, are observed respectively. The stability of the given model is studied by exercising the modulation instability analysis which confirms that the model is stable and guarantees that all extracted solutions are stable and exact. The main accomplishment of this strategy lies in the way that, we have succeeded in a single move to extract maximum solutions which can differ it from other techniques. The constraint conditions for valid exact solutions are also reported. The graphical depiction of the derived solutions are presented in Figs. 1, 2, 3, 4, 5 and 6. The results are new, interesting and have a great impact on the field of magneto-optic waveguides, optical fiber and useful in the telecommunication industry to enhance the performance capacity of transmission systems. Consequently, we have shown that the propagation dynamics of these solitons having more number of arbitrary parameters can find an added advantage over the solutions reported earlier in oceanic waves, nonlinear optical waves through coherently excited resonant waveguides, etc. As a further study, the present investigation can be extended to any other integrable systems.