1 Introduction

In the past two decades, investigations of the solutions to the various nonlinear evolution equations (NLEEs) have attracted the attention of many scientists from all over the world. Nonlinear evolution equations are used in modeling complex nonlinear aspects describing some of our real-life problems in the various fields of nonlinear sciences such as modeling the interaction between atmosphere and ocean influences, optic fibers, fluid mechanics, hydrodynamics, metrology and plasma physics. It is very important to investigate the behaviors of the models that arise in dynamics of the ocean because of the vital roles they play in our daily activities.

Various analytical and numerical techniques have been formulated for tackling these kinds of nonlinear models such as the improved tan\((\varphi /2)\)-expansion method [1], the sine-Gordon expansion method [2,3,4,5,6,7,8], the multivariate transformation technique [9], the homogeneous balance method [10], the Jacobi elliptic function method [11, 12], the extended homoclinic test function method [13], the local fractional Riccati differential equation method [14], the improved Bernoulli sub-equation function method [15], the Hirota’s bilinear method, homoclinic test approach and parameter perturbation technique [16], semi-inverse variational principle [17], the modified simple equation method [18], the ansatz and mapping methods [19], the lumped Galerkin approach [20], the Fourier pseudo-spectral method [21], the shooting method [22], the meshless kernel-based method of lines [23] and many other mathematical approaches [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54].

This study uses the modified exp \((-\varphi (\zeta ))\)-expansion function method (MEFM) [55,56,57,58] in constructing analytical solutions to the coupled Boussinesq equation [59]. We further utilize the finite forward difference scheme in obtaining the numerical and exact approximations to the coupled Boussinesq equation by taking one of the obtained analytical solutions into consideration.

The Boussinesq equations for variable water depth that are effective for shallow water and referred to as the standard Boussinesq equations were first developed by Peregrine [60, 61]. The Boussinesq-type equations are very popular nonlinear evolution equations formulated for describing the dynamics of water with small amplitude and long wave. Boussinesq-type equations are also the most important equations in the prediction of wave transformations in coastal areas. The Boussinesq equation is widely used in coastal and ocean engineering. Tsunami wave modeling and mathematical modeling of tidal oscillations show some of the applications of this equation in ocean engineering [60, 61].

The coupled Boussinesq equation is given by [59]

$$\begin{aligned} v_{t}+w_{x}+vv_{x} &= 0, \\ w_{t}+(wv)_{x}+v_{xxx} &= 0. \end{aligned}$$
(1)

Boussinesq equations are used to model the dynamics of shallow water waves that arise in different places like rivers, lakes and sea beaches [59, 60]. The coupled Boussinesq equation arises in the shallow water waves for two-layered fluid flow. This occurs whenever there is an accidental oil spill from a ship that results in a layer of oil floating above the layer of water [60, 61].

2 The MEFM

In this section, we present the general facts of the MEFM .

Consider the nonlinear partial differential equation of the form

$$\begin{aligned} F\left( v, v_{x}, v_{x}v^{2}, v_{xx}, v_{xxt}, \ldots \right) =0, \end{aligned}$$
(2)

where \(v=v(x, t)\) is an unknown function, and F is a polynomial in v(x, t) and its derivatives. The subscript indicates the partial derivatives of v with respect to x and t.

Step 1: Consider the following wave transformation:

$$\begin{aligned} v(x, t)=V(\zeta ),\;\;\; \zeta =x-kt. \end{aligned}$$
(3)

Substituting Eq. (3) into Eq. (2) yields the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} Q(V, V^{'}V^{2}, V^{'}, V^{''}, \ldots )=0, \end{aligned}$$
(4)

where Q is a polynomial of V and its derivatives.

Step 2: The solution of Eq. (4) is assumed to be of the form [55]

$$\begin{aligned} V(\zeta )= & {} \frac{\sum _{i=0}^{\delta }A_{i}\Big [e^{-\varphi (\zeta )}\Big ]^{i}}{\sum _{j=0}^{\sigma }B_{j}\Big [e^{-\varphi (\zeta )}\Big ]^{j}}\nonumber \\= & {} \frac{A_{0}+A_{1}e^{-\varphi }+\ldots +A_{\delta }e^{-\delta \varphi }}{B_{0} +B_{1}e^{-\varphi }+\ldots +B_{\sigma }e^{-\sigma \varphi }}, \end{aligned}$$
(5)

where \(A_{i}, B_{j}, (0\le i\le \delta , 0\le j\le \sigma )\) are constants to be obtained later, such that \(A_{\delta }\ne 0\), \(B_{\sigma }\ne 0.\)

The function \(\varphi =\varphi (\zeta )\) simplifies the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} \varphi ^{'}(\zeta )=e^{-\varphi (\zeta )}+\mu e^{\varphi (\zeta )}+\lambda . \end{aligned}$$
(6)

Equation (6) has the following family of solutions [55]:

Family 1: When \(\mu \ne 0\), \(\lambda ^{2}-4\mu >0\),

$$\begin{aligned} \varphi (\zeta ) & = ln\Bigg (\frac{-\sqrt{\lambda ^{2}-4\mu }}{2\mu }\nonumber \\&\times tanh\Big (\frac{\sqrt{\lambda ^{2}-4\mu }}{2}(\zeta +E)\Big )-\frac{\lambda }{2\mu }\Bigg ). \end{aligned}$$
(7)

Family 2: When \(\mu \ne 0\), \(\lambda ^{2}-4\mu <0\),

$$\begin{aligned} \varphi (\zeta ) & = ln\Bigg (\frac{\sqrt{-\lambda ^{2}+4\mu }}{2\mu }\nonumber \\&\times tan\Big (\frac{\sqrt{-\lambda ^{2}+4\mu }}{2}(\zeta +E)\Big )-\frac{\lambda }{2\mu }\Bigg ). \end{aligned}$$
(8)

Family 3: When \(\mu =0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\mu >0\),

$$\begin{aligned} \varphi (\zeta )=-ln\Bigg (\frac{\lambda }{e^{\lambda (\zeta +E)}-1}\Bigg ). \end{aligned}$$
(9)

Family 4: When \(\mu \ne 0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\mu =0\),

$$\begin{aligned} \varphi (\zeta )=ln\Bigg (-\frac{2\lambda (\zeta +E)+4}{\lambda ^{2}(\zeta +E)}\Bigg ). \end{aligned}$$
(10)

Family 5: When \(\mu =0\), \(\lambda =0\) and \(\lambda ^{2}-4\mu =0\),

$$\begin{aligned} \varphi (\zeta )=ln(\zeta +E). \end{aligned}$$
(11)

\(A_{i}, B_{j}, (0\le i\le \delta , 0\le j\le \sigma )\), \(E, \lambda , \mu \) are coefficients to be obtained, and \(\sigma \), \(\delta \) are positive integers that can be determined by using the homogeneous balancing principle.

Step 3: Substituting Eq. (5) with fixed value of \(\delta \) and \(\sigma \), its possible derivatives along with Eq. (6) into Eq. (4), we get a polynomial in powers of \(e^{-\varphi (\zeta )}\). We collect a set of algebraic equations from the polynomial by equating each summation of the coefficients of \(e^{-\varphi (\zeta )}\) with the same power to zero. To get the solutions of (2), we solve the set of equations with aid of symbolic software and get the values of the coefficients \(A_{i}, B_{j}, (0\le i\le \delta , 0\le j\le \sigma )\), \(E, \lambda , \mu \). Substituting the obtained values of the coefficients into Eq. (5) gives the solutions to (2).

3 The analysis of FDM

In this section, we give the analysis of the finite forward difference. To present this analysis, the following notations need to be given:

  1. 1.

    \(\Delta x\) is the spatial step

  2. 2.

    \(\Delta t\) is the time step

  3. 3.

    \(x_{i}=a+i\Delta x,\)\(i=0,1,2,...,N\) points are the coordinates of mesh and \( N=\frac{b-a}{\Delta x},\)\(t_{j}=j\Delta x,\)\(j=0,1,2,...,M\) and \(M=\frac{T}{ \Delta t}\).

  4. 4.

    The functions \(v\left( x,t\right) \) and \(w\left( x,t\right) \) represent the values of these solutions at these grid points; \(v\left( x_{i},t_{j}\right) \approx v_{i,j}\) and \(w\left( x_{i},t_{j}\right) \approx w_{ij}\), respectively.

  5. 5.

    \(v_{i,j}\) and \(w_{i,j}\) represent the numerical solutions of the exact values of \(v\left( x,t\right) \) and \(w\left( x,t\right) \) at the point \(\left( x_{i},t_{j}\right) \), respectively.

For v(x, t):

$$ H_{t}v_{i,j} = v_{i,j+1}-v_{i,j}, $$
(12)
$$ H_{x}v_{i,j} = v_{i+1,j}-v_{i,j}, $$
(13)
$$ H_{xxx}v_{i,j} = v_{i+2,j}-2v_{i+1,j}+2v_{i-1,j}-v_{i-2,j}. $$
(14)

For w(x, t):

$$ H_{t}w_{i,j} = w_{i,j+1}-w_{i,j}, $$
(15)
$$ H_{x}w_{i,j} = w_{i+1,j}-w_{i,j}. $$
(16)

Thus, one may approximate the partial derivatives into the finite difference operators as

For v(x, t):

$$ \left. \frac{\partial v}{\partial t}\right| _{i,j} = \frac{H_{t}v_{i,j}}{ \Delta t}+O((\Delta t)), $$
(17)
$$ \left. \frac{\partial v}{\partial x}\right| _{i,j} = \frac{H_{x}v_{i,j}}{ \Delta x}+O((\Delta x)), $$
(18)
$$ \left. \frac{\partial ^{3}v}{\partial x^{3}}\right| _{i,j} = \frac{ H_{xxx}v_{i,j}}{(\Delta x)^{3}}+O((\Delta x)^{2}). $$
(19)

For w(x, t):

$$ \left. \frac{\partial w}{\partial t}\right| _{i,j} = \frac{H_{t}w_{i,j}}{ \Delta t}+O((\Delta t)), $$
(20)
$$ \left. \frac{\partial w}{\partial x}\right| _{i,j} = \frac{H_{x}w_{i,j}}{ \Delta x}+O((\Delta x)). $$
(21)

One may rewrite Eq. (1) in the finite forward difference operator’s form as

$$\begin{aligned} \frac{H_{t}v_{i,j}}{ \Delta t}+\frac{H_{x}w_{i,j}}{ \Delta x}+v_{i,j}\frac{H_{x}v_{i,j}}{ \Delta x} &= 0, \\ \frac{H_{t}w_{i,j}}{ \Delta t}+w_{i,j}\frac{H_{x}v_{i,j}}{ \Delta x}+v_{i,j}\frac{H_{x}w_{i,j}}{ \Delta x}+\frac{ H_{xxx}v_{i,j}}{(\Delta x)^{3}} &= 0. \end{aligned}$$
(22)

We get the following indexed forms by substituting Eqs. (12–16) into Eq. (22):

$$\begin{aligned} v_{i+1, j}= & {} -\frac{1}{2(\Delta t)\Big (1+(\Delta x)^{2}v_{i,j}^{2}-(\Delta x)^{2}w_{i,j}\Big )}\Bigg ((\Delta t)v_{i-2,j}-2(\Delta t)v_{i-1,j}-2(\Delta x)^{3}v_{i,j}^{2}\nonumber \\&\quad -2(\Delta t)(\Delta x)^{2}v_{i,j}^{3}+2(\Delta x)^{3}v_{i,j}v_{i,j+1}-(\Delta t)v_{i+2,j}+2(\Delta x)^{3}w_{i,j}\nonumber \\&\quad +2(\Delta t)(\Delta x)^{2}v_{i,j}w_{i,j}-2(\Delta x)^{3}w_{i,j+1}\Bigg ), \end{aligned}$$
(23)
$$\begin{aligned} w_{i+1, j}= & {} -\frac{1}{2(\Delta t)\Big (1+(\Delta x)^{2}v_{i,j}^{2}-(\Delta x)^{2}w_{i,j}\Big )}\Bigg (-2(\Delta x)v_{i,j}-(\Delta t)v_{i-2,j}v_{i,j}\nonumber \\&\quad +2(\Delta t)v_{i-1,j}v_{i,j}-2(\Delta t)v_{i,j}^{2}+2(\Delta x)v_{i,j+1}+(\Delta t)v_{i,j}v_{i+2,j}-2(\Delta t)w_{i,j}\nonumber \\&\quad -2(\Delta t)(\Delta x)^{2}v_{i,j}^{2}w_{i,j}-2(\Delta x)^{3}v_{i,j+1}w_{i,j}+2(\Delta t)(\Delta x)^{2}w_{i,j}^{2}+2(\Delta x)^{3}v_{i+j}w_{i,j+1}\Bigg ), \end{aligned}$$
(24)

where the initial values \(u_{i,0}=u_{0}(x_{i})\) and \(v_{i,0}=v_{0}(x_{i})\).

4 Von Neumann stability analysis

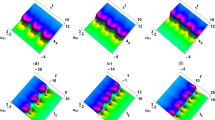
In this section, the stability of the numerical scheme with the coupled Boussinesq equation is analyzed by using the Fourier–Von Neumann stability analysis (Figs. 1, 2, 3, 4). We consider \(\zeta ^{n}\) as the amplification factor. The growth factor of a typical Fourier mode may be given as follows:

$$\begin{aligned} v_{m}^{n}=P\zeta ^{n}e^{i\beta },w_{m}^{n}=W\zeta ^{n}e^{i\beta }\text { }, \end{aligned}$$
(25)

where \(i=\sqrt{-1}\).

To check the stability of the numerical scheme, the nonlinear terms in the coupled Boussinesq equation \(vv_{x}, wv_{x}\) and \(vw_{x}\) must be linearized by making v and w local constants. Thus, the nonlinear terms \(vv_{x}, wv_{x}\) and \(vw_{x}\) become \(Av_{x}, Bv_{x}\) and \(Aw_{x},\) respectively.

The finite difference operator form of these linearized terms is given as

$$\begin{aligned} Av_{x}=A\frac{H_{x}v_{i,j}}{ \Delta x},\;\; Bv_{x}=B\frac{H_{x}v_{i,j}}{ \Delta x},\;\;Aw_{x}=A\frac{H_{x}w_{i,j}}{ \Delta x}, \end{aligned}$$
(26)

where \(A=v_{m}^{n}\) and \(B=w_{m}^{n}.\)

Implementing these changes on Eq. (22), one may obtain

$$\begin{aligned} \frac{H_{t}v_{i,j}}{ \Delta t}+\frac{H_{x}w_{i,j}}{ \Delta x}+A\frac{H_{x}v_{i,j}}{ \Delta x} &= 0, \\ \frac{H_{t}w_{i,j}}{ \Delta t}+B\frac{H_{x}v_{i,j}}{ \Delta x}+A\frac{H_{x}w_{i,j}}{ \Delta x}+\frac{ H_{xxx}v_{i,j}}{(\Delta x)^{3}} &= 0. \end{aligned}$$
(27)

Now, inserting Eq. (25) into Eq. (27) yields

$$\begin{aligned}&P\Bigg ( \frac{1}{(\Delta t)+( A^{2}-B) (\Delta t)(\Delta x)^{2}} (( -A^{2}+B) (\Delta t)(\Delta x)^{2}+A(\Delta x)^{3}( \zeta -1)\nonumber \\&\quad +( A^{2}-B) (\Delta t)(\Delta x)^{2}cos [\beta ]+i\Delta t( 2+( A^{2}-B) \Delta x^{2}\nonumber \\&\quad -2cos [\beta ]sin [\beta ]) )\nonumber \\&\quad -W\Big ( \frac{\Delta x^{3}( \zeta -1) }{\Delta t+( A^{2}-B) \Delta t\Delta x^{2}}\Big )\Bigg ) =0 \end{aligned}$$
(28)
$$\begin{aligned}&P\Big ( \Big (-A\Delta t-\Delta x( -1+B\Delta x^{2}) ( \zeta -1) +A\Delta t cos [\beta ]\nonumber \\&\quad -iA\Delta t sin [\beta ]+2iA\Delta t cos [\beta ]sin [\beta ]\Big )\nonumber \\&\quad \times (\Delta t+( A^{2}-B) \Delta t\Delta x^{2})^{-1}\Big ) + W\Big ( \Big (-A^{2}\Delta t\Delta x^{2}+\Delta t( 1-B\Delta x^{2}) +A\Delta x^{3}( \zeta -1) \nonumber \\&\quad +\Delta t cos [\beta ]+( A^{2}-B) \Delta t\Delta x^{2}cos [\beta ]\nonumber \\&\quad +i\Delta t sin [\beta ]+i( A^{2}-B) \Delta t\Delta x^{2}sin [\beta ]\Big )(\Delta t+( A^{2}-B) \Delta t\Delta x^{2})^{-1}\Big ) =0, \end{aligned}$$
(29)

where \(A=v_{m}^{n}, B=w_{m}^{n}\) Next, Let \(\zeta ^{n+1}=\zeta \zeta ^{n}\) and assume that \( \zeta \) is independent of time. Then, we easily obtain the following system of algebraic equations.

Therefore,

$$\begin{aligned} \zeta _{1}= & {} \frac{1}{\Delta x^{4}\cos \left[ \frac{\beta }{2}\right] -i\Delta x^{4}sin \left[ \frac{\beta }{2}\right] }\Big (\Delta x^{4}cos \left[ \frac{\beta }{2}\right] \nonumber \\&-2iA\Delta t\Delta x^{3}sin \left[ \frac{\beta }{2}\right] -i\Delta x^{4}sin \left[ \frac{\beta }{2}\right] \nonumber \\&-2\Big (\Big (\left( \Delta t^{2}\Delta x^{4}-B\Delta t^{2}\Delta x^{6}\right) cos \left[ \frac{\beta }{2} \right] ^{2}sin \left[ \frac{\beta }{2}\right] ^{2}\nonumber \\&-\Delta t^{2}\Delta x^{4}cos \left[ \frac{\beta }{ 2}\right] cos \left[ \frac{3\beta }{2}\right] sin \left[ \frac{\beta }{2}\right] ^{2} \nonumber \\&-i\Delta t^{2}\Delta x^{4}cos \left[ \frac{\beta }{2}\right] sin \left[ \frac{\beta }{2} \right] ^{3}+i\Delta t^{2}\Delta x^{4}cos \left[ \frac{3\beta }{2}\right] sin \left[ \frac{\beta }{2} \right] ^{3}\nonumber \\&-B\Delta t^{2}\Delta x^{6}sin \left[ \frac{\beta }{2}\right] ^{4} \Big )\Big )^{\frac{1}{2}}\Big ) \end{aligned}$$
(30)
$$\begin{aligned} \zeta _{2}= & {} \frac{1}{\Delta }x^{4}\cos \left[ \frac{\beta }{2}\right] \nonumber \\&-i\Delta x^{4}sin \left[ \frac{\beta }{2}\right] \Big ((\Delta x^{4}cos \left[ \frac{\beta }{2}\right] -2iA\Delta t\Delta x^{3}sin \left[ \frac{\beta }{2}\right] -i\Delta x^{4}sin \left[ \frac{\beta }{2}\right] \nonumber \\&+2\Big ((\left( \Delta t^{2}\Delta x^{4}-B\Delta t^{2}\Delta x^{6}\right) cos \left[ \frac{\beta }{2} \right] ^{2}sin \left[ \frac{\beta }{2}\right] ^{2}\nonumber \\&-\Delta t^{2}\Delta x^{4}cos \left[ \frac{\beta }{ 2}\right] cos \left[ \frac{3\beta }{2}\right] sin \left[ \frac{\beta }{2}\right] ^{2} \nonumber \\&-i\Delta t^{2}\Delta x^{4}cos \left[ \frac{\beta }{2}\right] sin \left[ \frac{\beta }{2} \right] ^{3}+i\Delta t^{2}\Delta x^{4}cos \left[ \frac{3\beta }{2}\right] sin \left[ \frac{\beta }{2} \right] ^{3}\nonumber \\&-B\Delta t^{2}\Delta x^{6}sin \left[ \frac{\beta }{2}\right] ^{4} \Big )^{\frac{1}{2}}\Big ). \end{aligned}$$
(31)

According to the Fourier stability, numerical scheme is unconditionally stable as \(\left| \zeta _{1}\right| \le 1,\)\(\left| \zeta _{1}\right| \le 1\).

5 L\(_{2}\) and L\(_{\infty }\) Error Norms

To show how close the exact and numerical solutions are, we use \(L_{2}\) and \(L_{\infty }\) error norms.

The \(L_{2}\) and \(L_{\infty }\) error norms are defined as [62]

$$\begin{aligned} L_{2}=\,& {} \left\| u^{exact}-u^{numeric}\right\| _{2}\nonumber \\=\,& {} \sqrt{h\sum \limits _{j=0}^{N}\left| u_{j}^{exact}-u_{j}^{numeric}\right| ^{2}}, \end{aligned}$$
(32)
$$\begin{aligned} L_{\infty }=\,& {} ||u^{exact}-u^{numeric}||_{\infty }\nonumber \\=\,& {} \;^{Max}_{\;\;j}|u^{exact}_{j}-u^{numeric}_{j}|. \end{aligned}$$
(33)

6 Theoretical calculations

In this section, we present the computational parts of the study.

6.1 Application of the MEFM to Eq. (1)

In this subsection, we present the application of the MEFM to the coupled Boussinesq equations.

Consider the coupled Boussinesq equations given in Eq. (1).

Using the wave transformation

$$\begin{aligned} v(x,t)=V(\zeta ),\;w=W(\zeta ),\;\zeta =x-kt, \end{aligned}$$
(34)

Eq. (1) is carried to the following single NODE:

$$\begin{aligned} 2V^{''}-V^{3}+3kV^{2}-2k^{2}V=0, \end{aligned}$$
(35)

where \(W=kV-\frac{V^{2}}{2}\).

Balancing the terms \(V^{''}\) and \(V^{3}\) in (35), we have the following relation between \(\sigma \) and \(\delta \):

$$\begin{aligned} \delta =\sigma +1, \end{aligned}$$
(36)

choosing \(\sigma =1\) implies that \(\delta =2\).

Using \(\sigma =1\), \(\delta =2\) along with Eq. (5), we get

$$\begin{aligned} V(\zeta )= \frac{A_{0}+A_{1}e^{-\varphi }+A_{2}e^{-2\varphi }}{B_{0}+B_{1}e^{-\varphi }}. \end{aligned}$$
(37)

Substituting Eq. (37) and its second derivative into Eq. (35), we get an equation in a polynomial of \(e^{-\varphi }\). We collect a group of the algebraic equation from this polynomial by equating the sum of the coefficients of \(e^{-\varphi }\) with the same power to zero. We solve the group of equations with the help of Wolfram Mathematica software and find the values of the coefficients. The values of the coefficients are obtained in various cases. For each case, to obtain the solutions of Eq. (1), we put the values of the coefficients into Eq. (37) along with one of (Family 1–5).

Case-1:

$$\begin{aligned} A_{0} & = B_{0}\Big (\sqrt{\lambda ^{2}-4\mu }-\lambda \Big ), A_{1}=B_{1}\Big (\sqrt{\lambda ^{2}-4\mu }-\lambda \Big )\\ \quad &-2B_{0}, A_{2}=-2B_{1}, k=\sqrt{\lambda ^{2}-4\mu }. \end{aligned}$$

Case-2:

$$\begin{aligned} A_{0} & = B_{0}\Big (\sqrt{k^{2}+4\mu }+k\Big ),A_{1}=B_{1}\Big (\sqrt{k^{2} +4\mu }+k\Big )\\ \quad &-2B_{0}, A_{2}=-2B_{1}, \lambda =\sqrt{k^{2}+4\mu }. \end{aligned}$$

With case-1, we obtained the following families of solutions:

solution-1:When \(\mu \ne 0\), \(\lambda ^{2}-4\mu >0\),

$$\begin{aligned} v_{1.1}(x,t) & = \sqrt{\lambda ^{2}-4\mu }-\lambda \nonumber \\ \quad &+\frac{4\mu }{\lambda +\sqrt{\lambda ^{2}-4\mu }\;tanh[\psi _{1.1}(x,t)]}, \end{aligned}$$
(38)
$$\begin{aligned} w_{1.1}(x,t) & = 2\mu (\lambda ^{2}-4\mu )\Big /\Big (\lambda cosh[\psi _{1.1}(x,t)]\nonumber \\ \quad &+\sqrt{\lambda ^{2}-4\mu }sinh[\psi _{1.1}(x,t)]\Big )^{2}, \end{aligned}$$
(39)

where

\(\psi _{1.1}(x,t)=\frac{1}{2}\Big (E+x-\sqrt{\lambda ^{2}-4\mu }\;t\Big ) \times \sqrt{\lambda ^{2}-4\mu }.\)

Fig. 1
figure 1

The (a) kink-type and (b) soliton surfaces of Eq. (38) and (39) under the values \(\mu =2\), \(\lambda =3\), \(E=2.5\) and \(t=2\) for the 2D graphics

Full size image

solution-2: When \(\mu =0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\mu >0\),

$$ v_{1.2}(x,t) = \lambda \Big (1-coth[\psi _{1.2}(x,t)]\Big ), $$
(40)
$$ w_{1.2}(x,t) = -\frac{\lambda ^{2}}{cosh[2\psi _{1.2}(x,t)]-1}, $$
(41)

where

\(\psi _{1.2}(x,t)=\frac{1}{2}\lambda (E+x-\lambda t).\)

Fig. 2
figure 2

The singular soliton surfaces of Eq. (40) and (41) under the values \(\lambda =1\), \(E=1\) and \(t=2\) for the 2D graphics

Full size image

With case-2, we obtained the following families of solutions:

solution-1:When \(\mu \ne 0\), \(\lambda ^{2}-4\mu >0\),

$$\begin{aligned} v_{2.1}(x,t) & = \sqrt{k^{2}+4\mu }+k\nonumber \\ \quad &-\frac{4\mu }{\sqrt{k^{2}+4\mu }-k\;tanh[\psi _{2.1}(x,t)]}, \end{aligned}$$
(42)
$$\begin{aligned} w_{2.1}(x,t) & = 2k^{2}\mu \Big / \Big (\sqrt{k^{2}+4\mu }\;cosh[\psi _{2.1}(x,t)]\nonumber \\ \quad &-k\;sinh[\psi _{2.1}(x,t)]\Big )^{2}, \end{aligned}$$
(43)

where

\(\psi _{2.1}(x,t)=\frac{1}{2}k\Big (E+x-kt\Big ).\)

Fig. 3
figure 3

The (a) kink-type and (b) soliton surfaces of Eq. (42) and (43) under the values \(\mu =0.7\), \(k=0.35\), \(E=1\) and \(t=2\) for the 2D graphics

Full size image

solution-2: When \(\mu =0\), \(\lambda \ne 0\) and \(\lambda ^{2}-4\mu >0\),

$$ v_{2.2}(x,t) = k(1-coth[\psi _{2.2}(x,t)]), $$
(44)
$$ w_{2.2}(x,t) = -\frac{k^{2}}{cosh[2\psi _{2.2}(x,t)]-1}, $$
(45)

where

\(\psi _{2.2}(x,t)=\frac{1}{2}k(E+x-k t).\)

Fig. 4
figure 4

The singular soliton surfaces of Eq. (44) and (45) under the values \(k=0.35\), \(E=1\) and \(t=2\) for the 2D graphics

Full size image

6.2 Exact and numerical approximations

In this subsection, we obtain the exact and numerical approximations of Eq. (1) using Eq. (38) and (39) and the datum \(k=1,\lambda = 3, \mu =2, E=2.5\). Substituting these values into Eqs. (38) and (39) gives the following special exact solutions for the approximations:

$$ v(x,t) = -2+\frac{8}{3+tanh\Big [\frac{1}{2}(2.5-t+x)\Big ]}, $$
(46)
$$ w(x,t) = 4\Big (3cosh\Big [\frac{1}{2}(2.5-t+x)\Big ]+sinh\Big [\frac{1}{2}(2.5-t+x) \Big ]\Big )^{-2}. $$
(47)

At \(t=0\), Eqs. (46) and (47) become

$$ v_{0}(x) = -2+\frac{8}{3+tanh\Big [\frac{1}{2}(2.5+x)\Big ]}, $$
(48)
$$ w_{0}(x) = 4\Big (3cosh\Big [\frac{1}{2}(2.5+x)\Big ]+sinh\Big [\frac{1}{2}(2.5+x) \Big ]\Big )^{-2}. $$
(49)

Inserting \((\Delta x)=(\Delta t)=0.01\) into Eq. (23) and (24) yields

$$\begin{aligned} v_{i+1,j} & = (9999.10+v_{i,j}^{2}-w_{i,j})^{-1}\Big (-4999.10v_{i-2,j}\nonumber \\ \quad &+9999.10v_{i-1,j}\nonumber \\ \quad &+v_{i,j}^{2}+v_{i,j}^{3}-v_{i,j}v_{i,j+1}\nonumber \\ \quad &+4999.10v_{i+2,j}-w_{i,j} -v_{i,j}w_{i,j}+w_{i,j+1}\Big ), \end{aligned}$$
(50)
$$\begin{aligned} w_{i+1,j} & = (9999.10+v_{i,j}^{2}-w_{i,j})^{-1}\Big (9999.10v_{i,j}\nonumber \\ \quad &+4999.10v_{i-2,j}v_{i,j}\nonumber \\&-9999.10v_{i-1,j}v_{i,j}+9999.10v_{i,j}^{2}\nonumber \\ \quad &-9999.10v_{i,j+1} -4999.10v_{i,j}v_{i+2,j}\nonumber \\ \quad &+9999.10w_{i,j}+v_{i,j}^{2}w_{i,j}+v_{i,j+1}w_{i,j}\nonumber \\ \quad &-w_{i,j}^{2} -v_{i,j}w_{i,j+1}\Big ), \end{aligned}$$
(51)

respectively.

Hence, we present the exact and numerical approximations of Eq. (1) in Tables 1 and 2 and \(L_{2}\) and \(L_{\infty }\) error norms in Table 3.

Table 1 Numerical and exact approximations of Eq. (1) and absolute errors under Eq. (38)
Full size table
Table 2 Numerical and exact approximations of Eq. (1) and absolute errors under Eq. (39)
Full size table
Table 3 \(L_{2}\) and \(L_{\infty }\) error norm under \(0\le h\le 1\) and \(0\le x\le 1\)
Full size table
Fig. 5
figure 5

Numerical and exact approximations graph of Eq. (1) under Eq. (38)

Full size image
Fig. 6
figure 6

Numerical and exact approximations graph of Eq. (1) under Eq. (39)

Full size image
Fig. 7
figure 7

Absolute error graph under Eq. (38)

Full size image
Fig. 8
figure 8

Absolute error graph under Eq. (39)

Full size image

7 Results and discussion

In this study, we successfully employed the modified exp \((-\varphi (\zeta ))\)-expansion function method to the coupled Boussinesq equation. Several wave solutions are constructed. Jawad et al. [59] constructed some exponential function and non-topological soliton solutions to the coupled Boussinesq equation. In this study, soliton, topological kink-type soliton and singular soliton solutions are reported. When we compare our results with the results presented in [59], we observed that the reported analytical solutions in this study are newly constructed. Furthermore, the well-known numerical scheme, namely the finite forward difference method, is used in obtaining the approximate exact and numerical solutions to the coupled Boussinesq equation. We observed that as \(\Delta x=\Delta t\) are getting smaller, the approximations are approaching zero (Figs. 5 and  6).

8 Conclusion

In this study, we use the modified exp \((-\varphi (\zeta ))\)-expansion function method in obtaining the analytical solutions to the coupled Boussinesq equation. Topological kink-type soliton, soliton and singular soliton solutions are successfully extracted. By choosing the suitable values of the parameters, the 2D and 3D of the reported solutions are also plotted. Via one of the obtained analytical solutions, the finite forward difference scheme is used in approximating the exact and numerical solutions to the studied nonlinear model. The stability of the numerical scheme is also checked. The \(L_{2}\) and \(L_{\infty }\) error norms are also computed (Figs. 7, 8). The numerical and exact approximations are compared, and the comparison is supported by graphical plots.

The modified exp \((-\varphi (\zeta ))\)-expansion function method is an efficient mathematical tool which provides good analytical solutions for numerical study, and finite forward difference method supplies good approximations when it is utilized on these analytical solutions.