1 Introduction

Nonlinear partial differential equations (NPDEs) arise in various areas of nonlinear science such as hydrodynamics, plasma physics, molecular biology, quantum mechanics, nonlinear optics, surface water waves etc. Various symbolic approaches have been employed to obtain different kind of travelling wave solutions to these type of equations. Saravanan and Dhamayanthi [1] obtained some exact solutions to a nonlinear Schrödinger equation with spin current. Ray [2] obtained some novel double periodic solutions to the coupled Schrödinger–Boussinesq equations. Xie et al. [3] investigated the solitons collisions in the higher-order nonlinear Schrödinger–Maxwell–Bloch system. Tariq and Younis [4] obtained dark and bright solitons to the NLSE with second order spatiotemporal dispersion. Zayed et al. [5] investigated the analytical solutions of the nonlinear Schrödinger equation with fourth-order dispersion and dual power law nonlinearity using five computational approaches. Mao et al. [6] investigated the existence and concentration of positive solutions in the Shrödinger–Poisson system. Kalogiratou et al. [7] investigated the numerical solutions of the two dimensional time-independent Shrödinger equation. In general, several studies have been conducted in this area [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59].

This study is aimed at investigating the Klein–Gordon–Zakharov equations [60, 61] by using the extended sinh-Gordon equation expansion method [62, 63].

The Klein–Gordon–Zakharov equations is given by [60]

$$\begin{aligned} \phi _{tt}-\phi _{xx}+\phi +\lambda \psi \phi & = 0, \\ \psi _{tt}-\psi _{xx}-\sigma (|\phi |^{2})_{xx} & = 0, \end{aligned}$$
(1)

where \(\phi \) is a complex-valued function which represents the fast time scale component of electric field raise by electrons, \(\psi \) is a real-valued function and it represents the deviation of ion density from its equilibrium, \(\lambda \) and \(\sigma \) are two nonzero real constants. The Klein–Gordon–Zakharov equations describe the interaction between the Langmuir wave and the ion acoustic wave in a high frequency plasma [64]. Recently, various computational approaches have been used to investigate the Klein–Gordon–Zakharov equations such as the solitary wave ansazt [64], the extended hyperbolic functions method [65], the the bifurcation method [66], the trial equation method [67], the He’s variational principle method [68], the simplest equation method [69], the sine–cosine method and the extended tanh method [70], the conservative finite difference scheme [71] and the complete discrimination system for polynomial method [72].

2 Analysis of the extended ShGEEM

Consider the sinh-Gordon equation given by [62]

$$\begin{aligned} \phi _{xt}=\alpha sinh(\phi ), \end{aligned}$$
(2)

where \(\alpha \) is a nonzero constant.

Substituting the travelling wave transformation

$$\begin{aligned} \phi (x,t)=\Psi (\zeta ),\quad \zeta =\mu (x-k t) \end{aligned}$$
(3)

into (2), we get the following nonlinear ordinary differential equation (NODE):

$$\begin{aligned} \Psi ^{\prime \prime }=-\frac{\alpha }{\mu ^{2}k}sinh(\Psi ), \end{aligned}$$
(4)

where \(\mu \) and k are nonzero constant and the wave velocity, respectively.

Integrating Eq. (4), we get

$$\begin{aligned} \left( \frac{\Psi ^{\prime }}{2}\right) ^{2}=-\frac{\alpha }{\mu ^{2}k}sinh^{2}\left( \frac{\Psi }{2}\right) +c, \end{aligned}$$
(5)

where c is the integration constant.

Setting \(-\frac{\alpha }{\mu ^{2}k}=b\) and \(\frac{\Psi }{2}=w\), Eq. (5) becomes

$$\begin{aligned} w^{\prime }=\sqrt{bsinh^{2}(w)+c}. \end{aligned}$$
(6)

For the different values of the parameters b and c, Eq. (6) has the following set of significant solutions:

Set-I When \(c=0\) and \(b=1\), Eq. (6) becomes

$$\begin{aligned} w^{\prime }=sinh(w). \end{aligned}$$
(7)

Simplifying Eq. (7), we get the following solutions:

$$\begin{aligned} sinh(w)=\pm csch(\zeta )\quad {\text{or}}\quad sinh(w)=\pm \;i\; sech(\zeta ) \end{aligned}$$
(8)

and

$$\begin{aligned} cosh(w)=\pm coth(\zeta )\quad {\text{or}}\quad cosh(w)=\pm \;\; tanh(\zeta ), \end{aligned}$$
(9)

where \(i=\sqrt{-1}\).

Set-II When \(c=1\), \(b=1\), Eq. (6) becomes

$$\begin{aligned} w^{\prime }=cosh(w). \end{aligned}$$
(10)

Simplifying Eq. (10), we get the following solutions:

$$\begin{aligned} sinh(w)=tan(\zeta )\quad {\text{or}}\quad sinh(w)=-cot(\zeta ) \end{aligned}$$
(11)

and

$$\begin{aligned} cosh(w)=\pm sec(\zeta )\quad {\text{or}}\quad cosh(w)=\pm \; csc(\zeta ). \end{aligned}$$
(12)

Consider the general nonlinear partial differential equation in the form

$$\begin{aligned} P(\phi ,\phi _{x}, \phi _{xt}, \phi ^{2}\phi _{t}, \ldots )=0, \end{aligned}$$
(13)

The given steps below are to be followed in obtaining the wave solutions to Eq. (13)

Step-1 We start by transforming Eq. (13) into the following nonlinear NODE by using Eq. (3):

$$\begin{aligned} Q(\Psi , \Psi ^{\prime }, \Psi ^{\prime \prime }, \Psi ^{2}\Psi ^{\prime }, \ldots )=0. \end{aligned}$$
(14)

Step-2 The solution to Eq. (14) is assumed to be of the form

$$\begin{aligned} \Psi (w)=\sum _{j=1}^{m}\left[ B_{j}sinh(w)+A_{j}cosh(w)\right] ^{j}+A_{0}, \end{aligned}$$
(15)

where w is a function of \(\zeta \) and it satisfies Eq. (6) and \(A_{0}, A_{j}, B_{j}\)\((j=1, 2,\ldots , m)\) are constants to be determine letter. To obtain the value of m, the homogeneous balance principle is used on the highest derivative and highest power nonlinear term in Eq. (14).

Step-3 We substitute Eq. (15) and it is possible derivative with fixed value of m along with Eq. (3) into Eq. (14) to obtain a polynomial equation in \(w^{\prime s}sinh^{i}(w)cosh^{j}(w)\)\((s=0,1\quad {\text{and}}\quad i, j=0, 1, 2, \ldots )\). We collect a set of over-determined nonlinear algebraic set of equations in \(A_{0}, A_{j}, B_{j}, k,\mu \) by setting the coefficients of \(w^{\prime s}sinh^{i}(w)cosh^{j}(w)\) to zero.

Step-4 The obtained set of over-determined nonlinear algebraic equations is then solved with aid of symbolic software to determine the values of the parameters \(A_{0}, A_{j}, B_{j}, k,\mu \).

Step-5 Using the results obtained in Eqs. (8), (9), (11) and (12), we secure the wave solutions to any given nonlinear partial differential equation in the forms

$$\begin{aligned} \Psi (\zeta )&= \sum _{j=1}^{m}\left[ \pm B_{j}\;i\;sech(\zeta )\pm A_{j}tanh(\zeta )\right] ^{j}+A_{0}, \end{aligned}$$
(16)
$$\begin{aligned} \Psi (\zeta )&= \sum _{j=1}^{m}\left[ \pm B_{j}\;csch(\zeta )\pm A_{j}coth(\zeta )\right] ^{j}+A_{0}, \end{aligned}$$
(17)
$$\begin{aligned} \Psi (\zeta )&= \sum _{j=1}^{m}\left[ \pm B_{j}sec+A_{j}tan(\zeta )\right] ^{j}+A_{0} \end{aligned}$$
(18)

and

$$\begin{aligned} \Psi (\zeta )=\sum _{j=1}^{m}\left[ \pm B_{j}csc(\zeta )-A_{j}\;cot(\zeta )\right] ^{j}+A_{0}. \end{aligned}$$
(19)

3 Theoretical calculations

In this section, the application of the extended sinh-Gordon equation expansion method to the Klein–Gordon–Zakharov equations is presented.

Consider the Klein–Gordon–Zakharov equations (Eq. (1)) given in Sect. 1.

Substituting the wave transformation

$$\begin{aligned} \phi =\Psi (\zeta )e^{i\varphi }, \psi =\Phi (\zeta ), \zeta =\mu (x-kt), \varphi =px+rt \end{aligned}$$
(20)

into Eq. (1), we obtain the following NODE:

$$\begin{aligned} (k^{2}-1)(1+p^{2}-r^{2})\Psi +\lambda \sigma \Psi ^{3}+\mu ^{2}(k^{2}-1)^{2}\Psi ^{\prime \prime }=0 \end{aligned}$$
(21)

from the real part, and the relation \(k=-\frac{p}{r}\) from the imaginary part.

Balancing \(\Psi ^{\prime \prime }\) and \(\Psi ^{3}\) in Eq. (21), gives \(m=1\).

With \(m=1\), Eqs. (15), (16), (17), (18) and (19) take the forms

$$\begin{aligned} \Psi (w)&= B_{1}sinh(w)+A_{1}cosh(w)+A_{0}, \end{aligned}$$
(22)
$$\begin{aligned} \Psi (\zeta )&= \pm B_{1}\;i\;sech(\zeta )\pm A_{1}tanh(\zeta )+A_{0}, \end{aligned}$$
(23)
$$\begin{aligned} \Psi (\zeta )&= \pm B_{1}\;csch(\zeta )\pm A_{1}coth(\zeta )+A_{0}, \end{aligned}$$
(24)
$$\begin{aligned} \Psi (\zeta )&= \pm B_{1}sec+A_{1}tan(\zeta )+A_{0}, \end{aligned}$$
(25)
$$\begin{aligned} \Psi (\zeta )&= \pm B_{1}csc(\zeta )-A_{1}\;cot(\zeta )+A_{0}, \end{aligned}$$
(26)

respectively.

Substituting Eq. (22) and it is second derivative into Eq. (21), yields a polynomial equation in the power hyperbolic functions. After making some hyperbolic identities substitutions into the polynomial equation, we collect a set of algebraic equations by equating each summation of the coefficients of the hyperbolic functions having the same power to zero. We simplify the set of algebraic equations to obtained the values of the parameters involved. To explicitly obtain the solutions of Eq. (1), we substitute the values of the parameters into each of Eqs. (23), (24), (25) and (26).

Case-1 When

$$\begin{aligned} A_{0}=0,\;A_{1}=-\frac{\mu }{(r^{2}-2\mu ^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\; B_{1}=0, \;p=\frac{r\sqrt{-(r^{2}-2\mu ^{2}-1)}}{\sqrt{2\mu ^{2}-r^{2}}}, \end{aligned}$$

we get

$$\begin{aligned} \phi _{1}(x,t)&= \pm \frac{\mu }{(r^{2}-2\mu ^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\;tanh\left[ \mu \left( x+\frac{p}{r}t\right) \right] e^{i(px+rt)}, \end{aligned}$$
(27)
$$\begin{aligned} \psi _{1}(x,t)&= \frac{2\mu ^{2}}{\lambda ((r^{2}-2\mu ^{2})^{2}+(1-r^{2}+2\mu ^{2}))}tanh^{2}\left[ \mu \left( x+\frac{p}{r}t\right) \right] , \end{aligned}$$
(28)
$$\begin{aligned} \phi _{2}(x,t)&= \pm \frac{\mu }{(r^{2}-2\mu ^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\;coth\left[ \mu \left( x+\frac{p}{r}t\right) \right] e^{i(px+rt)}, \end{aligned}$$
(29)
$$\begin{aligned} \psi _{2}(x,t)&= \frac{2\mu ^{2}}{\lambda ((r^{2}-2\mu ^{2})^{2}+(1-r^{2}+2\mu ^{2}))}coth^{2}\left[ \mu \left( x+\frac{p}{r}t\right) \right] , \end{aligned}$$
(30)

where \(\lambda \sigma <0\) and \((2\mu ^{2}-r^{2})(1-r^{2}+2\mu ^{2})<0\) for valid solutions.

Case-2 When

$$\begin{aligned} A_{0}=0,\;A_{1}=0,\; B_{1}=-\frac{\mu }{(r^{2}+\mu ^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\;, \;p=r\sqrt{\frac{r^{2}+\mu ^{2}-1}{r^{2}+\mu ^{2}}}, \end{aligned}$$

we get

$$\begin{aligned} \phi _{3}(x,t)&= \pm \frac{\mu }{(r^{2}+\mu ^{2})}\sqrt{\frac{2}{\lambda \sigma }} \;sech\left[ \mu \left( x+\frac{p}{r}t\right) \right] e^{i(px+rt)}, \end{aligned}$$
(31)
$$\begin{aligned} \psi _{3}(x,t)&= -\frac{2\mu ^{2}}{\lambda ((r^{2}+\mu ^{2})^{2}+(1-r^{2}-\mu ^{2})(r^{2}+\mu ^{2}))} sech^{2}\left[ \mu \left( x+\frac{p}{r}t\right) \right] , \end{aligned}$$
(32)
$$\begin{aligned} \phi _{4}(x,t)&= \pm \frac{\mu }{(r^{2}+\mu ^{2})}\sqrt{-\frac{2}{\lambda \sigma }} \;csch\left[ \mu \left( x+\frac{p}{r}t\right) \right] e^{i(px+rt)}, \end{aligned}$$
(33)
$$\begin{aligned} \psi _{4}(x,t)&= \frac{2\mu ^{2}}{\lambda ((r^{2}+\mu ^{2})^{2}+(1-r^{2}-\mu ^{2})(r^{2}+\mu ^{2}))} csch^{2}\left[ \mu \left( x+\frac{p}{r}t\right) \right] , \end{aligned}$$
(34)

where \(\lambda \sigma <0\) or \(\lambda \sigma >0\) and \((r^{2}+\mu ^{2}-1)(r^{2}+\mu ^{2})>0\) for valid solutions.

Case-3 When

$$\begin{aligned} A_{0}=0,\;A_{1}=-\frac{\mu }{(\mu ^{2}-2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }},\; B_{1}=A_{1}, \;p=r\sqrt{\frac{2+\mu ^{2}-2r^{2}}{\mu ^{2}-2r^{2}}}, \end{aligned}$$

we get

$$\begin{aligned} \phi _{5}(x,t)&= -\frac{\mu }{(\mu ^{2}-2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\left( \pm i\;sech\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right. \nonumber \\&\left. \pm tanh\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) e^{i(px+rt)}, \end{aligned}$$
(35)
$$\begin{aligned} \psi _{5}(x,t)&= -2\mu ^{2}(\lambda (\mu ^{2}-2r^{2})((2-2r^{2}+\mu ^{2})-(\mu ^{2}-2r^{2})))^{-1}\nonumber \\&\times \left( \pm i\;sech\left[ \mu \left( x+\frac{p}{r}t\right) \right] \pm tanh\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) ^{2}, \end{aligned}$$
(36)
$$\begin{aligned} \phi _{6}(x,t)&= \frac{\mu }{(\mu ^{2}-2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }}\left( \pm coth\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right. \nonumber \\&\left. \pm csch\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) e^{i(px+rt)}, \end{aligned}$$
(37)
$$\begin{aligned} \psi _{6}(x,t)&= -2\mu ^{2}(\lambda (\mu ^{2}-2r^{2})((2-2r^{2}+\mu ^{2})-(\mu ^{2}-2r^{2})))^{-1}\nonumber \\&\times \left( \pm coth\left[ \mu \left( x+\frac{p}{r}t\right) \right] \pm csch\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) ^{2}, \end{aligned}$$
(38)

where \(\lambda \sigma <0\) and \((2+\mu ^{2}-2r^{2})(\mu ^{2}-2r^{2})>0\) for valid solutions.

Case-4 When

$$\begin{aligned} A_{0}=0,\;A_{1}=-\frac{\mu }{(\mu ^{2}+2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }},\; B_{1}=-A_{1}, \;p=r\sqrt{\frac{2r^{2}-2+\mu ^{2}}{\mu ^{2}+2r^{2}}}, \end{aligned}$$

we get

$$\begin{aligned} \phi _{7}(x,t)&= -\frac{\mu }{(\mu ^{2}+2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }} \left( \pm sec\left[ \mu \left( x+\frac{p}{r}t\right) \right] \pm tan\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) e^{i(px+rt)}, \end{aligned}$$
(39)
$$\begin{aligned} \psi _{7}(x,t)&= \frac{\mu ^{2}}{\lambda (2r^{2}+\mu ^{2})}\left( \pm sec\left[ \mu \left( x+\frac{p}{r}t\right) \right] \pm tan\left[ \mu \left( x+\frac{p}{r}t\right) \right] \right) ^{2}, \end{aligned}$$
(40)
$$\begin{aligned} \phi _{8}(x,t)&= \pm \frac{\mu }{(\mu ^{2}+2r^{2})}\sqrt{-\frac{2}{\lambda \sigma }} tan\left[ \frac{1}{2}\mu \left( x+\frac{p}{r}t\right) \right] e^{i(px+rt)}, \end{aligned}$$
(41)
$$\begin{aligned} \psi _{8}(x,t)&= \frac{\mu ^{2}}{\lambda (2r^{2}+\mu ^{2})}tan^{2}\left[ \frac{1}{2}\mu \left( x+\frac{p}{r}t\right) \right] , \end{aligned}$$
(42)

where \(\lambda \sigma <0\) or \(\lambda \sigma >0\) and \((2r^{2}-2+\mu ^{2})(\mu ^{2}+2r^{2})>0\) for valid solutions.

4 Results and discussion

The extended sinh-Gordon equation expansion method is utilized to construct various solitary wave solutions to the Klein–Gordon–Zakharov equations. There are some results to the studied model that have been previously reported in the literature. Triki and Boucerredj [64] reported some bright and dark soliton to Eq. (1) by using the solitary wave ansazt. Shang et al. [65] obtained some bell-type, kink-type, compound bell-type and kink-type, singular and periodic travelling wave solutions to Eq. (1) by using the extended hyperbolic functions method. Zhang et al. [66] secured some hyperbolic and trigonometric to Eq. (1) by utilizing the bifurcation method. Akbari and Taghizadeh [68] acquired some exact solitary wave solutions with hyperbolic function structure to Eq. (1) by using He’s semi-inverse method. Kudryashov [69] utilized the simplest equation method in constructing soliton and singular periodic wave solutions to Eq. (1). Shi et al. [70] utilized the sine–cosine method and the extended tanh method to construct some solitons and periodic wave solutions. In this study, some topological, non-topological, compound topological and non-topological, singular soliton and singular periodic wave solutions are constructed. We observed that the reported results of this study have some features that explain some of their physical meanings, for instance; the hyperbolic tangent which arises in the calculation of magnetic moment and rapidity of special relativity, the hyperbolic cotangent which arises in the Langevin function for magnetic polarization and the hyperbolic secant which arises in the profile of a laminar jet [73] (Figs. 1, 2, 3, 4).

Fig. 1
figure 1

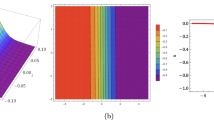
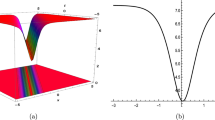
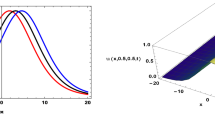
The (a) 3D, 2D, (b) contour graphs of Eq. (27) under the values \(r=0.075\), \(\mu =0.2\), \(\lambda =-2\), \(\sigma =5\), (\(-10\le x\le 10\), \(-10\le t\le 10\) for the 2D and 3D plots), (\(-20\le x\le 20\), \(-20\le t\le 20\) for the contour plot) and \(t=0.8\) for the 2D graph

Full size image
Fig. 2
figure 2

The (a) 3D, 2D, (b) contour graphs of Eq. (31) under the values \(r=0.5\), \(\mu =0.75\), \(\lambda =2\), \(\sigma =5\), (\(-10\le x\le 10\), \(-10\le t\le 10\) for the 2D and 3D plots), (\(-20\le x\le 20\), \(-20\le t\le 20\) for the contour plot) and \(t=0.8\) for the 2D graph

Full size image
Fig. 3
figure 3

The (a) 3D, 2D, (b) contour graphs of Eq. (33) under the values \(r=0.5\), \(\mu =0.75\), \(\lambda =-2\), \(\sigma =5\), \(-20\le x\le 20\), \(-20\le t\le 20\) and \(t=0.8\) for the 2D graph

Full size image
Fig. 4
figure 4

The (a) 3D, 2D, (b) contour graphs of Eq. (39) under the values \(r=2\), \(\mu =3\), \(\lambda =-2\), \(\sigma =5\), (\(-10\le x\le 10\), \(-10\le t\le 10\) for the 2D and 3D plots), (\(-20\le x\le 20\), \(-20\le t\le 20\) for the contour plot) and \(t=0.8\) for the 2D graph

Full size image

5 Conclusions

This study constructed family of solitary wave solutions to the Klein–Gordon–Zakharov equations by using the extended sinh-Gordon equation expansion method such as the topological, non-topological, compound topological and non-topological, singular soliton and singular periodic wave solutions. All the obtained solutions satisfied the Klein–Gordon–Zakharov equations. The 2D, 3D and the contour graphs to some of the obtained solutions are also plotted. We feel that the reported results may be useful in explaining the physical meaning of some nonlinear models arising in various fields of nonlinear sciences. From the results presented in this study, it can be seen that the extended sinh-Gordon equation expansion method is powerful and efficient mathematical tool which can be utilized to obtain varieties of solitary wave solutions to various complex nonlinear models.