Dark, bright and other optical solitons to the decoupled nonlinear Schrödinger equation arising in dual-core optical fibers

Abstract

The dynamical systems of soliton propagation through optical fibers for trans-continental and trans-oceanic distances is one of the most interesting areas of study. Optical solitons are restrained electromagnetic waves that stretch in nonlinear dispersive media and allow the intensity to remain unchanged due to the balance between dispersion and nonlinearity effects. In this study, we successfully acquire dark, bright, combined dark–bright, singular and combined singular soliton solutions to the decoupled nonlinear Schrödinger equation arising in dual-core optical fibers by using the extended sinh-Gordon equation expansion method. The constraint conditions for the existence of valid soliton solutions are given. We discuss how change in parameters affect the solitons transmission. We present the 2D, 3D and the contour graphs to some of the reported solutions.

1 Introduction

The theory of optical solitons is one of the interesting topics for the investigation of soliton propagation through nonlinear optical fibers (Younis et al. 2016a). Optical fibers can be utilized in data transmission or light exhibitor operations. Optical fibers utilized in light exhibitor applications transfer safe, no-heat light, which is optimal for medical, inspection, automotive, or display applications. A single optical fiber uses total internal reflection to transfer light, granting bends along its path. Minimal light loss at the transmission time grants optical fibers to transfer light or data quickly over long distances. When fastened, fiber optics can transfer large quantities of data for telecommunication operations (Liu et al. 2016; Chen and Zhu 2016; Ma et al. 2017; Martincek and Pudis 2014; Yang et al. 2004; Cap and Chmela 2003; Heng et al. 2017; Zhao et al. 2017; Zhang et al. 2014). It is therefore good to investigate the optical soliton solutions of the nonlinear models describing various complex physical aspects in the field of optical fibers. Optical solitons are restrained electromagnetic waves that stretch in nonlinear dispersive media and allow the intensity to remain unchanged due to the balance between dispersion and nonlinearity effects (Agrawal 2013). There are a lot of considerable number of researches in this context that have been submitted to the literature (Bulut et al. 2018a; Younis et al. 2016b; Seadawy 2015; Eslami and Rezazadeh 2016; Triki and Wazwaz 2016; Ali et al. 2017; Cattani 2003; Dai et al. 2017a, b; Liu et al. 2016, 2017; Zhang et al. 2017; Seadawy and Lu 2017; Bulut et al. 2018; Helal and Seadawy 2011; Baskonus 2016; Mirzazadeh et al. 2017; Kumar et al. 2012; Kumar and Chand 2013).

This study extracts some optical soliton solutions from the decoupled nonlinear Schrödinger equation with Kerr law nonlinearity arising in dual-core optical fibers (Arnous et al. 2017) by using the extended sinh-Gordon equation expansion method (Xian-Lin and Jia-Shi 2008; Baskonus et al. 2018; Sulaiman et al. 2017; Bulut et al. 2018c, d).

The decoupled nonlinear Schrödinger equation (Arnous et al. 2017) is given as

$$\begin{aligned} \begin{array}{ccl} i(u_{x}+\lambda _{1}q_{t})+\lambda _{2}u_{tt}+\lambda _{3}|u|^{2}u+\lambda _{4}q &{} = &{} 0, \\ i(q_{x}+\lambda _{1}u_{t})+\lambda _{2}q_{tt}+\lambda _{3}|q|^{2}q+\lambda _{4}u &{} = &{}0, \end{array} \end{aligned}$$

(1.1)

where u and q are field envelopes, x is the propagation co-ordinate, $\frac{1}{\lambda _{1}}$ is the group velocity mismatch, λ₂ is the group velocity dispersion, λ₄ is the linear coupling coefficient and λ₃ is defined as $\lambda _{3}=\frac{2\pi m_{2}}{\kappa B_{eff}}$, where m₂ is the nonlinear refractive index, $\kappa$ is the wavelength and B _eff is effective mode area of each wavelength (Younis et al. 2015a). There are considerable number of studies on various type of Eq. (1.1) (Younis et al. 2015b; Boumaza et al. 2009; Raju et al. 2005).

2 The extended ShGEEM

This sections discuses the analysis of the extended sinh-Gordon equation expansion method.

To apply the ShGEEM, we go by the following steps:

Step 1 Consider the following NPDE:

$$\begin{aligned} F(q_{x},\;q^{2}q_{xx},\;q_{t},\;q_{xt},\ldots )=0, \end{aligned}$$

(2.1)

where F is a polynomial in q, the subscripts indicate the partial derivative of q with respect to x or t.

Substituting the travelling wave transformation

$$\begin{aligned} q=\Phi (\eta ), \quad \eta =x-ct \end{aligned}$$

(2.2)

into Eq. (2.1), yields the following NODE:

$$\begin{aligned} Q(\Phi ,\;\Phi ^{'},\;\Phi ^{''},\;\Phi ^{2}\Phi ^{'},\ldots )=0, \end{aligned}$$

(2.3)

where Q is a polynomial in $\Phi$ and the superscripts indicate the ordinary derivative of $\Phi$ with respect to $\eta$.

Step 2 The trial solution to Eq. (2.3) is assumed to be of the form (Xian-Lin and Jia-Shi 2008)

$$\begin{aligned} \Phi (\theta )=\sum _{j=1}^{k}\left[ b_{j}sinh(\theta )+a_{j}cosh(\theta )\right] ^{j}+a_{0}, \end{aligned}$$

(2.4)

where a₀, a _j , b _j (j = 1, 2, …, k) are constants to be determine later and θ is a function of $\eta$ that satisfies the following ordinary differential equation:

$$\begin{aligned} \theta ^{'}=sinh(\theta ). \end{aligned}$$

(2.5)

To find the value of k, the homogeneous balance principle is applied on the highest derivatives and highest power nonlinear term in Eq. (2.3).

Equation (2.5) is obtained from sinh-Gordon equation (Xian-Lin and Jia-Shi 2008) given as

$$\begin{aligned} q_{xt}=\lambda sinh(q). \end{aligned}$$

(2.6)

Equation (2.5) posses the following solutions (Xian-Lin and Jia-Shi 2008):

$$\begin{aligned} sinh(\theta )=\pm csch(\eta )\;\;\;{\text{or}}\;\;\;sinh(\theta )=\pm \;i\; sech(\eta ) \end{aligned}$$

(2.7)

and

$$\begin{aligned} cosh(\theta )=\pm coth(\eta )\;\;\;{\text{or}}\;\;\;cosh(\theta )=\pm \;\; tanh(\eta ), \end{aligned}$$

(2.8)

where $i=\sqrt{-1}$.

Step 3 Inserting Eq. (2.4), its derivatives under fixed value of k along with Eq. (2.5) into Eq. (2.3), yields a polynomial equation in $\theta ^{'l}sinh^{i}(\theta )cosh^{j}(\theta )$ (l = 0, 1 and i, j = 0, 1, 2,…). We collect a group of over-determined nonlinear algebraic equations in $a_{0},\;a_{j},\;a_{j},\;c$ by setting the coefficients of $\theta ^{'l}sinh^{i}(\theta )cosh^{j}(\theta )$ to zero.

Step 4 The secured set of over-determined nonlinear algebraic equations is then solved with aid of symbolic software to determine the values of the parameters $a_{0},\;a_{j},\;b_{j},\;c$.

Step 5 Based on Eqs. (2.7) and (2.8), Eq. (2.1) posses the following forms of solutions:

$$\begin{aligned}&\Phi (\eta )=\sum _{j=1}^{k}\left[ \pm ib_{j}\;\;sech(\eta )\pm a_{j}tanh(\eta )\right] ^{j}+a_{0}, \end{aligned}$$

(2.9)

$$\begin{aligned}&\Phi (\eta )=\sum _{j=1}^{k}\left[ \pm b_{j}\;csch(\eta )\pm a_{j}coth(\eta )\right] ^{j}+a_{0}. \end{aligned}$$

(2.10)

3 Applications

In this section, the application of the extended ShGEEM to the decoupled nonlinear Schrödinger equation is presented.

Consider the decoupled nonlinear Schrödinger equation given in Eq. (1.1) and the following complex wave transformation:

$$\begin{aligned} u=\Phi (\eta )e^{i\Psi },\;q=\psi (\eta )e^{i\Psi },\;\eta =\vartheta (x-ct),\;\Psi =-\mu x+\omega t+p, \end{aligned}$$

(3.1)

where $\Psi$ is the soliton phase component, $\vartheta$ is a nonzero constant, $\mu$ is the frequency of the soliton, $\omega$ is the soliton wave number, p is the phase constant and c is the soliton velocity.

Putting Eq. (3.1) into Eq. (1.1), yields

$$\begin{aligned} \begin{array}{ccl} (\mu -\omega ^{2} \lambda _{2})\Phi +\lambda _{3}\Phi ^{3}+\lambda _{4}\psi -\lambda _{1}\omega \psi +c^{2}\vartheta ^{2}\lambda _{2}\Phi ^{''} &{} = &{} 0, \\ (\mu -\omega ^{2} \lambda _{2})\psi +\lambda _{3}\psi ^{3}+\lambda _{4}\Phi -\lambda _{1}\omega \Phi +c^{2}\vartheta ^{2}\lambda _{2}\psi ^{''} &{} = &{}0 \end{array} \end{aligned}$$

(3.2)

from the real part, and

$$\begin{aligned} \begin{array}{ccl} (2c\omega \lambda _{2}-1)\Phi ^{'}+\lambda _{1}c\psi ^{'} &{} = &{} 0, \\ (2c\omega \lambda _{2}-1)\psi ^{'}+\lambda _{1}c\Phi ^{'} &{} = &{}0 \end{array} \end{aligned}$$

(3.3)

from the imaginary part. Integrating Eq. (3.3) once, yields

$$\begin{aligned} \begin{array}{ccl} (2c\omega \lambda _{2}-1)\Phi +\lambda _{1}c\psi &{} = &{} 0, \\ (2c\omega \lambda _{2}-1)\psi +\lambda _{1}c\Phi &{} = &{}0. \end{array} \end{aligned}$$

(3.4)

As $\Phi$ and $\psi$ functions of $\eta$ satisfy both Eqs. (3.2), (3.3) and (3.4), we get the following relation from Eq. (3.4):

$$\begin{aligned} \frac{2c\omega \lambda _{2}-1}{\lambda _{1}c}=\frac{\lambda _{1}c}{2c\omega \lambda _{2}-1}. \end{aligned}$$

(3.5)

Simplifying Eq. (3.5) for c, yields

$$\begin{aligned} c=\frac{1}{2\omega \lambda _{2}-\lambda _{1}}. \end{aligned}$$

(3.6)

Balancing the terms $\Phi ^{3}$, $\Phi ^{''}$, $\psi ^{3}$ and $\psi ^{''}$ in Eq. (3.2), yields $k=1$.

With the value k = 1, Eqs. (2.4), (2.9) and (2.10) with respect to $\Phi$ and $\psi$ take the forms

$$\begin{aligned}&\Phi (\theta )=b_{1}sinh(\theta )+a_{1}cosh(\theta )+a_{0}, \end{aligned}$$

(3.7)

$$\begin{aligned}&\psi (\theta )=d_{1}sinh(\theta )+c_{1}cosh(\theta )+c_{0}, \end{aligned}$$

(3.8)

$$\begin{aligned}&\Phi (\eta )=\pm ib_{1}\;sech(\eta )\pm a_{1}tanh(\eta )+a_{0}, \end{aligned}$$

(3.9)

$$\begin{aligned}&\psi (\eta )=\pm id_{1}\;sech(\eta )\pm c_{1}tanh(\eta )+c_{0}, \end{aligned}$$

(3.10)

$$\begin{aligned}&\Phi (\eta )=\pm b_{1}\;csch(\eta )\pm a_{1}coth(\eta )+a_{0} \end{aligned}$$

(3.11)

and

$$\begin{aligned} \psi (\eta )=\pm d_{1}\;csch(\eta )\pm c_{1}coth(\eta )+c_{0}, \end{aligned}$$

(3.12)

respectively.

Substituting Eqs. (3.7), (3.8) and their second derivatives along with Eq. (2.5) into Eq. (3.2), produces a polynomial in powers of hyperbolic functions. Summing each coefficients of the hyperbolic functions of the same power and equating each summation to zero, produces a group of algebraic equations. The set of algebraic equations is simplified to obtain the values of the parameters involved. For each case, substituting the secured values of the parameters into Eqs. (3.9), (3.10), (3.11) and (3.12) and then into Eq. (3.1), yields the solutions to Eq. (1.1).

Case 1 When

$$\begin{aligned} a_{0}=0,\;a_{1}=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}},\;c_{1}=-a_{1},\;c_{0}=0,\;b_{1}=0,\;d_{1}=0, \end{aligned}$$

$\mu =\frac{2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})}{(\lambda _{1}-2\omega \lambda _{2})^{2}},$

we get the dark optical solitons

$$\begin{aligned}&u_{1}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}tanh[\vartheta (x-ct)]e^{i \left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.13)

$$\begin{aligned}&q_{1}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}tanh[\vartheta (x-ct)]e^{i\left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) } \end{aligned}$$

(3.14)

where $\lambda _{2}\lambda _{3}<0$ for valid solitons, and the singular solitons

$$\begin{aligned}&u_{2}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}coth[\vartheta (x-ct)]e^{i\left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.15)

$$\begin{aligned}&q_{2}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}coth[\vartheta (x-ct)]e^{i\left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.16)

where $\lambda _{2}\lambda _{3}<0$ for valid solitons.

Case 2 When

$$\begin{aligned} a_{0}=0,\;a_{1}=0,\;c_{1}=0,\;c_{0}=0,\;b_{1}=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}},\; d_{1}=-b_{1}, \end{aligned}$$

$\mu =\frac{(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2}}{(\lambda _{1}-2\omega \lambda _{2})^{2}},$

we get the bright optical solitons

$$\begin{aligned}&u_{3}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{\frac{2\lambda _{2}}{\lambda _{3}}}sech[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.17)

$$\begin{aligned}&q_{3}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{\frac{2\lambda _{2}}{\lambda _{3}}}sech[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) } \end{aligned}$$

(3.18)

where the solitons are valid for both $\lambda _{2}\lambda _{3}<0$ and $\lambda _{2}\lambda _{3}>0$, and the singular solitons

$$\begin{aligned}&u_{4}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}csch[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.19)

$$\begin{aligned}&q_{4}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{2\lambda _{2}}{\lambda _{3}}}csch[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(3.20)

where the solitons are valid for both $\lambda _{2}\lambda _{3}<0$ and $\lambda _{2}\lambda _{3}>0$.

Case 3 When

$$\begin{aligned} a_{0}=0,\;a_{1}=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{\lambda _{2}}{2\lambda _{3}}},\;c_{1}=-a_{1},\;c_{0}=0,\; b_{1}=a_{1},\; d_{1}=-a_{1}, \end{aligned}$$

$\mu =\frac{\vartheta ^{2}\lambda _{2}+2(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})}{2(\lambda _{1}-2\omega \lambda _{2})^{2}},$

we get the combined dark–bright optical solitons

$$\begin{aligned}&u_{5}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{\lambda _{2}}{2\lambda _{3}}} \left( i\;sech[\vartheta (x-ct)]+tanh[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.21)

$$\begin{aligned}&q_{5}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{\lambda _{2}}{2\lambda _{3}}} \left( i\;sech[\vartheta (x-ct)]+tanh[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.22)

where $\lambda _{2}\lambda _{3}>0$ for valid solitons, and the combined singular solitons

$$\begin{aligned}&u_{6}(x,t)=\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{\lambda _{2}}{2\lambda _{3}}} \left( coth[\vartheta (x-ct)]+csch[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.23)

$$\begin{aligned}&q_{6}(x,t)=-\frac{\vartheta }{\lambda _{1}-2\omega \lambda _{2}}\sqrt{-\frac{\lambda _{2}}{2\lambda _{3}}} \left( coth[\vartheta (x-ct)]+csch[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.24)

where the solitons are valid for both $\lambda _{2}\lambda _{3}>0$ and $\lambda _{2}\lambda _{3}<0$.

Case 4 When

$$\begin{aligned} a_{0}=0,\;a_{1}=-\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}},\;c_{1}=-a_{1},\;c_{0}=0,\;b_{1}=0,\; d_{1}=0, \end{aligned}$$

$\vartheta =(\lambda _{1}-2\omega \lambda _{2})\sqrt{\frac{\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4}}{2\lambda _{2}}},$

we get the dark optical solitons

$$\begin{aligned}&u_{7}(x,t)=-\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}tanh[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.25)

$$\begin{aligned}&q_{7}(x,t)=\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}tanh[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.26)

where $\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4}<0$, $\lambda _{2}<0$ and $\lambda _{3}>0$ for valid solitons, and the combined singular solitons

$$\begin{aligned}&u_{8}(x,t)=-\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}coth[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.27)

$$\begin{aligned}&q_{8}(x,t)=\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}coth[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.28)

where the solitons are valid for $\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4}<0$, $\lambda _{2}<0$, and for both $\lambda _{3}>0$, $\lambda _{3}<0$.

Case 5 When

$$\begin{aligned} a_{0}=0,\;a_{1}=0,\;c_{1}=0,\;c_{0}=0,\;b_{1}=-\sqrt{\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}},\; d_{1}=-b_{1}, \end{aligned}$$

$\vartheta =-(\lambda _{1}-2\omega \lambda _{2})\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{2}}},$

we get the bright optical solitons

$$\begin{aligned}&u_{9}(x,t)=-\sqrt{-\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}sech[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.29)

$$\begin{aligned}&q_{9}(x,t)=\sqrt{-\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}sech[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.30)

and the singular optical solitons

$$\begin{aligned}&u_{10}(x,t)=-\sqrt{\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}csch[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.31)

$$\begin{aligned}&q_{10}(x,t)=\sqrt{\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}csch[\vartheta (x-ct)]e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.32)

where $\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4}<0$, $\lambda _{2}>0$ and $\lambda _{3}>0$ or $\lambda _{3}<0$ for valid solitons.

Case 6 When

$$\begin{aligned} a_{0}=0,\;a_{1}=-\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}},\;c_{1}=-a_{1},\;c_{0}=0,\;b_{1}=a_{1},\; d_{1}=-a_{1}, \end{aligned}$$

$\vartheta =-(\lambda _{1}-2\omega \lambda _{2})\sqrt{\frac{2(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{2}}},$

we get the combined dark–bright optical solitons

$$\begin{aligned}&u_{11}(x,t)=\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}\left( i\;sech[\vartheta (x-ct)]+tanh[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.33)

$$\begin{aligned}&q_{11}(x,t)=-\sqrt{-\frac{(\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4})}{\lambda _{3}}}\left( i\;sech[\vartheta (x-ct)]+tanh[\vartheta (x-ct)]\right) e^{i(-\mu x+\omega t+p)}, \end{aligned}$$

(3.34)

where $\mu +\omega (\lambda _{1}-\omega \lambda _{2})-\lambda _{4}<0$, $\lambda _{2}<0$ and $\lambda _{3}>0$ for valid solitons.

4 Results and discussion

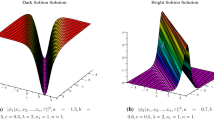
The extended sinh-Gordon equation expansion method is utilized to construct family of optical solitons to the decoupled nonlinear Schrödinger equation arising in dual-core optical fibers. Dark, bright, combined dark–bright, singular and combined singular optical solitons are successfully constructed. Dark soliton describes the solitary waves with lower intensity than the background, bright soliton describes the solitary waves whose peak intensity is larger than the background (Scott 2005) while the singular soliton solutions is a solitary wave with discontinuous derivatives; examples of such solitary waves are compactions, which have finite (compact) support, and peakons, whose peaks have a discontinuous first derivative (Rosenau 2005; Camassa and Holm 1993). These types of solitary waves are very important due to their flexibility in the long-distance optical communication.

It is to be noted that optical fibers are thin long strands of ultra-pure glass or plastic that can transmit light from one end to another without much attenuation or loss (Keiser 2008). To see how related parameters affect the transmission of solitons, the following analysis is carried out:

Considering $\vartheta$ to be a complex number that is $\vartheta \in {{\mathbb {C}}}$, solution (3.13), (3.15), (3.17) and (3.19) become the following singular periodic wave solutions:

$$\begin{aligned}&u_{1}(x,t)=\frac{\vartheta \sqrt{-2\lambda _{2}\lambda _{3}}}{\lambda _{3}(\lambda _{1}-2\omega \lambda _{2})}tan[\vartheta (x-ct)]e^{i\left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(4.1)

$$\begin{aligned}&u_{2}(x,t)=\frac{\vartheta \sqrt{-2\lambda _{2}\lambda _{3}}}{\lambda _{3}(\lambda _{1}-2\omega \lambda _{2})}cot[\vartheta (x-ct)]e^{i\left( -\frac{(2\vartheta ^{2}\lambda _{2}+(\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1}))}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(4.2)

$$\begin{aligned}&u_{3}(x,t)=\frac{\vartheta \sqrt{-2\lambda _{2}\lambda _{3}}}{\lambda _{3}(\lambda _{1}-2\omega \lambda _{2})}sec[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }, \end{aligned}$$

(4.3)

$$\begin{aligned}&u_{4}(x,t)=\frac{\vartheta \sqrt{-2\lambda _{2}\lambda _{3}}}{\lambda _{3}(\lambda _{1}-2\omega \lambda _{2})}csc[\vartheta (x-ct)]e^{i\left( -\frac{((\lambda _{1}-2\omega \lambda _{2})^{2}(\omega ^{2}\lambda _{2}+\lambda _{4}-\omega \lambda _{1})-\vartheta ^{2}\lambda _{2})}{(\lambda _{1}-2\omega \lambda _{2})^{2}}x +\omega t+p\right) }. \end{aligned}$$

(4.4)

Similarly, when we consider $\vartheta$ throughout the secured solutions in this study, they would all become singular periodic wave solutions.

We observe that when we take $\vartheta$ to be a complex value, the long distance light transmission through the optical materials is affected or may even get lost due to the low attenuation (see Fig. 4).

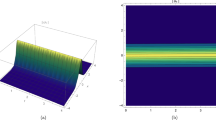
In order to have the clear meaning of the physical properties to the reported results, under the choice of suitable values of the parameters involved, the 2D, 3D and the contour graphics to some of the obtained solutions are plotted. The perspective view of the dark (Eq. 3.13), bright (Eq. 3.17), singular (Eq. 3.15) solitons and singular periodic wave (Eq. 4.1) solutions can be seen in the 3D from the (a) parts of Figs. 1, 2, 3 and 4, respectively. The propagation pattern of the wave along the x-axis for the dark (Eq. 3.13), bright (Eq. 3.17), singular (Eq. 3.15) solitons and singular periodic wave (Eq. 4.1) solutions is depicted in the 2D plots located at the right of the (a) parts of Figs. 1, 2, 3 and 4, respectively. The contour graphs is an alternative plot to the 3D plot which is placed at the (b) parts of each figure.

Fig. 1

The a 3D, 2D and b contour graphs of Eq. (3.13)

Fig. 2

The a 3D, 2D and b contour graphs of Eq. (3.15)

Fig. 3

The a 3D, 2D and b contour graphs of Eq. (3.17)

Fig. 4

The a 3D, 2D and b contour graphs of Eq. (4.1)

5 Conclusions

This study constructed dark, bright, combined dark–bright, singular and combined singular optical soliton solutions to the decoupled nonlinear Schrödinger equation by utilizing the extended sinh-Gordon equation expansion method. The constraint conditions for the existence of valid soliton solutions are stated. We plotted the 3D, 2D and contour graphs to some of the acquired results by choosing the convenient values of the parameters. The reported results may be useful in explaining the physical meaning of the studied model. The extended sinh-Gordon equation expansion method is an efficient computational scheme that can be used for studying various complex nonlinear models.