1 Introduction

Nonlinear partial differential equations (NLPDEs) are significant families of equation that are extensively used in the modeling and analysis of nonlinear evolutionary dynamical systems in engineering, fluid mechanics, geochemistry, hydrodynamics, solid state physics, water waves, plasma physics, chaos theory, solitary waves theory, cosmology and optical fibers, among other disciplines and some more (Yusuf et al. 2022; Younas et al. 2023; Tanwar and Wazwaz 2022). Soliton theory is very useful in many domains to comprehend these phenomena. Solitons are a type of wave that always has the same shape and never dissipates energy. Soliton is a very important concept in the disciplines of electromagnetism and communications because of these characteristics. The dynamics of the propagation of solitons has been worked by the aid of nonlinear Schrodinger’s equation (NLSE). This equation for optical solitons has produced a wide variety of results. In order to describe nonlinear physical events, one of the most crucial components is to obtain exact solutions to nonlinear fractional partial differential equations (NLFPDEs) (Abaid Ur Rehman et al. 2022). Due to their numerous uses in contemporary communication sectors, optical solitons are progressively assuming centre stage in nonlinear optics. Long-haul optical fibers are currently being investigated for trans-oceanic and trans-continental data transmission using optical communications. However, some aspects of optical communication remain unresolved, such as the well-known dispersive optical solitons, which hinder communication when they release soliton radiation due to the presence of higher-order dispersion factors.

Moreover, a variety of nonlinear Schrödinger equations (NLSE) are used to describe how soliton propagation changes over time in optical fibres. The Schrödinger–Hirota (SH) equation, in particular, is a significant class of the NLSE that was generated by the use of Lie’s transformation and has seen intense study in recent decades, utilising a variety of analytical and computational techniques (Biswas et al. 2012; Bernstein et al. 2015; Bakodah et al. 2019). Numerous methods have been used to obtain the exact solutions of the fractional Schrödinger–Hirota (FSH) equation, including Rezazadeh et al. Rezazadeh et al. (2018) attained several travelling wave solutions of the nonlinear conformable fractional Schrodinger-Hirota (NLCFSH) equation by employing new extended direct algebraic technique, Eslami et al. (2017) use the first integral method and the functional variable method and get the the bright and singular solutions, the NLCFSHE, which governs ocean wave propagation and optical fibres, a novel soliton solution is obtained by Zafar et al. (2022) via combining the Kudryashov technique and improved \(\left( \frac{G'}{G}\right)\)-expansion with a conformable truncated M-fractional operator, for the extraction of bright, dark, and other soliton solutions, Ray (2020) uses the extended auxiliary equation approach, Kilic and Inc Kilic and Inc (2017) used the Bäcklund transformation to solve the SH equation with power law nonlinearity for optical solitons and solitary wave solutions, Tang (2022) applied the complete discriminant system method to gain the hyperbolic function solutions, rational function solutions, and dispersive optical solitons in optical nanofibers of the NLSH equation with the constraint conditions by employing the \(tanh-coth\) integration algorithm (Sardar et al. 2016).

Conversely, analytical approximation techniques are preferred by scientists because they have deeper physical roots and are more deserving of parametric investigation. As a result, many academics promoted various tactics up until recently namely, Bilinear transformation (Jisha and Dubey 2022), Backland transformation (Zhao et al. 2022), Painleve analysis (Wazwaz et al. 2022), Hirota bilinear method (Bilal et al. 2022; Ismael et al. 2022; Kumar and Mohan 2022), Trilinear analysis (Manafian 2021), Lie point symmetries analysis (Adeyemo et al. 2022), improved generlized riccati mapping scheme (Islam et al. 2022), F-expansion method (Li et al. 2020; Akbulut et al. 2022), new Kudryashov technique (Samir et al. 2022), generlized Kudryashov method (Akbar et al. 2022; El-Sayed and Al-Nowehy 2016), Ansatz method (Akinyemi and Morazara 2022), \(\frac{G'}{G}\)-expansion method (Adeyemo and Khalique 2022), three integral schemes the generalized Kudryashov, the new extended FAN sub-equation approach (Fendzi-Donfack et al. 2023), generlized exponential rational function method (Rehman et al. 2022), extended ratioal sine-cosine/sinh-cosh method (Akbar et al. 2021), tanh method (Chukkol et al. 2017; Hu et al. 2020; Biazar and Ayati 2011), new extended direct algebric method (Gao et al. 2020; Mirhosseini-Alizamini et al. 2022; Hubert et al. 2018), extended sinh-Gordon equation expansion and \(\left( \frac{G'}{G^2}\right)\)-expansion function methods (Sulaiman et al. 2022; Bilal et al. 2022), first integral method (Aggarwal et al. 2018), variational iterative method (Anjum and He 2019; Nadeem and He 2021; Mungkasi 2021; Noeiaghdam et al. 2021), Adomian decomposition method (Cheng et al. 2021), q-homotopy analysis method (Hussain et al. 2022), residual power series method (Modanli et al. 2021; Qazza et al. 2022), improved Bernoulli sub-equation function method (Dusunceli et al. 2021). \(\left( \frac{G'}{G}\right)\)-expansion method (Zulfiqar and Ahmad 2021).

In each of these aforementioned works, a variety of approaches mentioned in Yao et al. (2021); Veeresha et al. (2021a, 2021b) have been proposed for securing soliton solutions of NLPDEs. The choice of an appropriate method is of great importance when using these analytical methods. Among those approaches, the proposed improved F-expansion method and the unified method are reliable and credible mechanisms to construct more general soliton solutions of NLPDEs in engineering and applied sciences. The foremost purpose of these methods are to express the soliton solutions of NLPDEs in terms of functions that satisfy the Riccati equation \(F'(\xi )= p+ F^2(\xi )\) and \(F'(\xi )=\Omega +(F(\chi ))^2\) for improved F-expansion function method and for the unified method, respectively. The main benefit of the improved F-expansion method over the existing other methods mentioned is that this scheme provide more abundant exact soliton solutions including some novel solutions with additional parameters in a simple and straight way. The exact soliton solutions have its great importance to know entirely the effect of the parameters in any circumstances. On the other hand, the advantages of the unified method, firstly it produces many more solutions than the other methods give. Namely, it gives not only the solutions of the other methods but also new exact solutions not obtained using other methods. Secondly, it unifies the merits of all the methods in one method without needing extra effort. Lastly, it has simple algorithm to apply on computer. Unlike the others, it reduces the process on computer as much as sometimes even calculated by hand. The unified method makes easier solving process at computer program. When using the unified method, it is not needed complex algorithm on computer programs. On the other hand, it is essential to use complex algorithm for some members of the \(\left( \frac{G'}{G}\right)\)-expansion method. To exhibit the productivity and dependability of these proposed methods, some higher order nonlinear dynamical models have been solved in which new results are found. It is vital to note that analysis of convergence and stability for the numerical methods is required, a distinct disadvantage when compared with analytical methods that do not require such an analysis. Apart from the physical relevance, soliton solutions of NLPDEs can assist the numerical solvers to measure up to the accuracy of their results and thus aid in the convergence analysis.

Over the past few decades, nonlinear fractional dynamical model research has been increasingly popular. Nonlinear fractional models have thus been utilized to mimic a variety of physical procedures. Compared to the conventionally used integer-order models, these more recent models are more suited and more flexible, because nonlinear models enable scientists to better define and characterise phenomena in everyday life. As a result, under some circumstances, these dynamical models can be used to accurately model genuine physical processes.

In this manuscript, the nonlinear conformable fractional Schrödinger–Hirota (NLCFSH) equation is considered as

$$\begin{aligned} iv_t^{(\beta )}+\frac{1}{2}v_{xx}+|v|^2 v+i \alpha v_{xxx}=0,t \ge 0, 0<\beta \le 1. \end{aligned}$$
(1)

Where v(x, t) signify the complex wave profile, \(\alpha\) represents the the coefficient of third order dispersion (3OD). \((.)_t^{(\beta )}\) is the conformable derivative operator.

This article is drafted as follows: The Sect. 3 explains the suggested methods for the NLCFSH equation. The applications of selected method are explained in the Sect. 4. The Sect. 5 discusses the stability study of the NLCFSH equation. The Sect. 6 covers concluding comments. The concluding remarks are included in the Sect. 7.

2 Conformable fractional derivative

Assume that \(D^\beta _\eta\) is a differential operator of any order, such as \(0 < \beta \le 1\). Then conformable fractional derivative of \(v(\eta )\) is given by

$$\begin{aligned} D^\beta _\eta (v(\eta ))=\lim \limits _{\epsilon \rightarrow 0}\frac{v(\eta +\epsilon \eta ^{1-\beta })-v(\eta )}{\epsilon },~\eta >0. \end{aligned}$$
(2)

Following are some characteristics of conformable fractional derivative:

Theorem 1

Suppose that function \(v(\eta )\) and \(w(\eta )\) are \(\beta -\)differentiable at \(\eta >0\) with \(\beta \in (0,1]\), therefore

$$\begin{aligned} \begin{aligned}&(i)~ D^\beta _\eta (\eta ^n)=n\eta ^{n-\beta }~\forall ~ n\in R..\\&(ii)~ D^\beta _\eta (c)=0,~where~ c ~is~ constant.\\&(iii) ~ D^\beta _\eta (dv(\eta )+ew(\eta ))= d D^\beta _\eta (v(\eta )) +eD^\beta _\eta (w(\eta ))~ \forall ~ d,~e \in R..\\&(iv)~ D^\beta _\eta (v(\eta )w(\eta ))=v(\eta )D^\beta _\eta (v(\eta ))+v(\eta )D^\beta _\eta (w(\eta )).\\&(v) ~ D^\beta _\eta (\frac{v(\eta )}{w(\eta )})=\frac{w(\eta )D^\beta _\eta (v(\eta ))-v(\eta )D^\beta _\eta (w(\eta ))}{w^2(\eta )}.\\&(vi)~ if~ v ~is~ differentiable,~ then~ D^\beta _\eta (v)(\eta )=\eta ^{1-\beta }~\frac{dv(\eta )}{d\eta }. \end{aligned} \end{aligned}$$

Theorem 2

Assume that \(v(\eta )\) is both differentiable and sigma-differentiable in the range \(\beta \in (0, 1]\). Furthermore, let \(v(\eta )\) be a differentiable function with the same range \(v(\eta )\),

$$\begin{aligned} D^\beta _\eta (v(\eta ).~w(\eta ))=\eta ^{1-\beta }v'(\eta )~w'(v(\eta )). \end{aligned}$$

3 Mathematical formulation of the methods

The solution of NLPDEs is often difficult and frequently necessitates advanced mathematical techniques. NLPDEs can be solved using a variety of strategies, including analytical, semi-analytical, and numerical techniques. Analytical approaches, such as variable separation and perturbation methods, are restricted to certain types of NLPDEs and idealised conditions. Semi-analytical methods, such as homotopy analysis and variational iteration, combine analytical and numerical techniques to generate approximate solutions. Numerical methods, such as finite difference, finite element, and spectral methods, are extensively exercised for solving NLPDEs as they can handle complex geometries and boundary conditions. However, numerical approaches necessitate high computational resources and may suffer from numerical errors. Moreover, selecting an suitable method for solving a particular NLPDE is often dependent on the nature of the problem, the complexity of the PDE, and the preferred accuracy of the solution. Therefore, choosing a proficient and accurate method is decisive for solving NLPDEs and advancing scientific research and technological innovation.

Take into account the nonlinear partial differential (NLPD) equation.

$$\begin{aligned} R(g,g_x,g_y,g_t,g_{xx},g_{yy},g_{tt},g_{xt},\ldots )=0, \end{aligned}$$
(3)

where the polynomial R in g(x, t) has partial derivatives that constitute its highest derivatives plus a nonlinear term and g(x, t) is an undefined function. The following phases tell the story of the improved F-expansion and the unified methods contexts.

The wave variables with the formula \(g(x,t)=v(\xi )\), where \(\xi =x - \frac{t^\beta }{\beta }c\) (where c denotes the speed of the traveling wave), are presumably acceptable for transformation into nonlinear form (3).

$$\begin{aligned} G(g,g',g'',\ldots )=0. \end{aligned}$$
(4)

3.1 The improved F-expansion method

The circumstances for the improved F-expansion method are described in the following phases.

Step-1: The solution of Eq. (4) is presumable in the form that follows the improved F-expansion method.

$$\begin{aligned} \phi (\xi ) =\sum _{i=0}^{N}\mu _i(n +F(\xi ))^i +\sum _{i=1}^{N}\rho _i(n+F(\xi ))^{-i}, \end{aligned}$$
(5)

where either \(\mu _i\) or \(\rho _i\) may be zero, but neither may be zero simultaneously. \(\rho _i (i=1,2,3,\ldots ,N)\) and n are fictitious factors that will eventually be chosen, along with \(\mu _i(i=0,1,2,\ldots ,N)\). We consider about popular Riccati equation.

$$\begin{aligned} F'(\xi )= p+ F^2(\xi ), \end{aligned}$$
(6)

where p represents the real part of the equation and the prime represents derivatives with respect to \(\xi\). The three general solutions of the Riccati equation Eq. (6) are follows as

Case-I: If\(p <0\), then the general solutions are

$$\begin{aligned} F_1= & {} -\sqrt{-p} \tanh (\sqrt{-p} \xi ),\end{aligned}$$
(7)
$$\begin{aligned} F_2= & {} -\sqrt{-p} \coth (\sqrt{-p} \xi ). \end{aligned}$$
(8)

Case-II: If \(p >0\), textitCasethen the general solutions are

$$\begin{aligned} F_3= & {} \sqrt{p} \tan (\sqrt{p} \xi ),\end{aligned}$$
(9)
$$\begin{aligned} F_4= & {} -\sqrt{p} \cot (\sqrt{p} \xi ). \end{aligned}$$
(10)

Case-III: If \(p=0\), then the general solution is

$$\begin{aligned} F_5 = -\frac{1}{\xi }. \end{aligned}$$
(11)

Step-2: The balancing principal is used to gain the value of N come out the solution of Eq. (4).

Step-3: With the help of equation Eq. (5) togather with Eq. (6) in Eq. (4), it is possible to calculate the polynomial in \(F(\xi )\). An algebraic system of equations is therefore produced when the same index of \(F(\xi )\) is equal to zero. By using Mathematica to solve these equations, we can get the values of the unknowns \(\mu _i, \rho _ i\), p, and n, which will be utilized to obtain the answer to equation Eq. (3).

3.2 The unified method

Step-1: The nonlinear equation (3) is considered to have a solution in the following form, in accordance with the unified framework.

$$\begin{aligned} v(\xi )=a_0+\sum _{i=0}^{N}[a_i F(\xi )^i+b_i F(\xi )^{-i}]. \end{aligned}$$
(12)

Here, the variables \(a_0\), \(a_ i\), and \(b_ i\) are unknowns that will be known later, but they cannot both zero simultaneously. Riccati equation is satisfied by F and its derivative.

$$\begin{aligned} F'(\xi )=\Omega +(F(\chi ))^2, \end{aligned}$$
(13)

where \(\Omega\) refers to a real component and prime stands for derivatives with regard to \(\xi .\) Case-I: If \(\Omega <0\), then the general solutions are

$$\begin{aligned} F_{1,2}= & {} \frac{\pm \sqrt{\Omega \left( -\left( d^2+e^2\right) \right) }-d \sqrt{-\Omega } \cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }{d \sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +e}. \end{aligned}$$
(14)
$$\begin{aligned} F_{3,4}= & {} \pm \sqrt{-\Omega }\pm \frac{2 d \sqrt{-\Omega }}{d-\sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +\cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }. \end{aligned}$$
(15)

Case-II: If \(\Omega >0\), then the general solutions are

$$\begin{aligned} F_{5,6}= & {} \pm \frac{\sqrt{\Omega \left( d^2-e^2\right) }-d \sqrt{-\Omega } \cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }{d \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +e}. \end{aligned}$$
(16)
$$\begin{aligned} F_{7,8}= & {} \pm i \sqrt{-\Omega }\pm \frac{2 i d \sqrt{-\Omega }}{d-i \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +\cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }. \end{aligned}$$
(17)

Case-III: If \(\Omega =0\), then the general solution is

$$\begin{aligned} F_{9,10}=-\frac{1}{f+\xi }. \end{aligned}$$
(18)

Where f is an arbitrary constant and d and e are real arbitrary constants.

Step-2 The balancing principal is used to gain the value of N come out the solution of Eq. (4).

Step-3 With the help of Eq. (13) and the solution Eq. (12), it is possible to calculate the polynomial in \(F(\chi )\). The same index of \(F(\xi )\) then equals zero, yielding an algebraic system of equations. By using Mathematica 13.0 to solve these equations, to get the values of the unknowns \(a_i, b_i, p,~ and~ c\), which will be used to get the solution of Eq. (3).

4 Extraction of solutions

This section demonstrates how well the improved F-expansion method and unified method to get the solitary wave solutions of Eq. (1). The wave transformation is defines as:

$$\begin{aligned} v(x,t)= V(\xi )\exp \left( i \left( \phi \right) \right) ,~~~\xi =x-\frac{2 \nu t^{\beta }}{\beta },~~\phi =\nu x+\frac{m t^{\beta }}{\beta }. \end{aligned}$$
(19)

Inserting Eqs. (19) and (6) into Eq. (1), then the real and imaginary components are Re : 

$$\begin{aligned} -2 m V(\xi )-6 \alpha \nu V''(\xi )+V''(\xi )+2 \alpha \nu ^3 V(\xi )-\nu ^2 V(\xi )+2 V(\xi )^3=0. \end{aligned}$$
(20)

Im : 

$$\begin{aligned} \left( 6 \alpha \nu ^2+2 \nu \right) V'(\xi )-2 \alpha V^{(3)}(\xi )=0. \end{aligned}$$
(21)

The imaginary part yielding the following result

$$\begin{aligned} \nu = \frac{-1}{3 \alpha }. \end{aligned}$$
(22)

Inserting Eq. (22) into Eq. (21), one can get the following form of ODE:

$$\begin{aligned} V^3+\frac{3 V''}{2}-V \left( \frac{5}{54 \alpha ^2}+m \right) =0. \end{aligned}$$
(23)

4.1 Application of improved F-expansion method

For the requirement of the improved F-expansion method, follow the balancing principal of terms \(V{''}\) and \(V^3\) in Eq. (23), we gain \(N=1\). Then from Eq. (5) we get,

$$\begin{aligned} V(\xi )=\mu _0+\mu _1 (F(\xi )+n)+\frac{\rho _1}{F(\xi )+n}, \end{aligned}$$
(24)

where \(\mu ,~\rho\) and n are constants. When Eq. (24) is plugged into Eq. (23), we get a system of algebraic equations correspond to coefficients of \(V(\xi )\) equating to zero. By simplifying these algebraic equations, novel clusters of solutions for Eq. (1) are gained.

Set-1

$$\begin{aligned} \mu _0=-i \sqrt{3} n,~\mu _1=0,~\rho _1=i \left( \sqrt{3} n^2+\sqrt{3} p\right) ,~m =\frac{162 \alpha ^2 p-5}{54 \alpha ^2}. \end{aligned}$$
(25)

When \(p<0\), the solutions are

Family 1:

$$\begin{aligned} v_{1,2}(x,t)=\frac{i \sqrt{3} e^{i \left( \frac{3 p t^{\beta }}{\beta }-\frac{5 t^{\beta }}{54 \alpha ^2 \beta }+\nu x\right) } \left( n \sqrt{-p} \tanh \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) +p\right) }{n-\sqrt{-p} \tanh \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(26)
Fig. 1
figure 1

3D, 2D graphs of Eq. (26)

Full size image

Family 2:

$$\begin{aligned} v_{3,4}(x,t)=\frac{i \sqrt{3} e^{i \left( \frac{3 p t^{\beta }}{\beta }-\frac{5 t^{\beta }}{54 \alpha ^2 \beta }+\nu x\right) } \left( n \sqrt{-p} \coth \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) +p\right) }{n-\sqrt{-p} \coth \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(27)

When \(p>0\), the solutions are

Family 3:

$$\begin{aligned} v_{5,6}(x,t)=\frac{i \sqrt{3} \sqrt{p} e^{i \left( \frac{3 p t^{\beta }}{\beta }-\frac{5 t^{\beta }}{54 \alpha ^2 \beta }+\nu x\right) } \left( \sqrt{p}-n \tan \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \right) }{n+\sqrt{p} \tan \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }. \end{aligned}$$
(28)

Family 4:

$$\begin{aligned} v_{7,8}(x,t)=-i \sqrt{3} e^{i \left( \frac{3 p t^{\beta }}{\beta }-\frac{5 t^{\beta }}{54 \alpha ^2 \beta }+\nu x\right) } \left( n-\frac{n^2+p}{n-\sqrt{p} \cot \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }\right) . \end{aligned}$$
(29)

When \(p=0\), the solutions are

Family 5:

$$\begin{aligned} v_{9,10}(x,t)=\frac{i \sqrt{3} \left( \beta n-2 \nu p t^{\beta }+\beta p x\right) e^{i \left( \frac{3 p t^{\beta }}{\beta }-\frac{5 t^{\beta }}{54 \alpha ^2 \beta }+\nu x\right) }}{\beta (n x-1)-2 \nu n t^{\beta }}. \end{aligned}$$
(30)
Fig. 2
figure 2

3D, 2D graphs of Eq. (29)

Full size image

Set-2

$$\begin{aligned} \mu _0=0,~\rho _1=-i \sqrt{3} p,~n=0,~\alpha =-\frac{1}{3} \sqrt{\frac{5}{6}} \sqrt{-\frac{1}{\nu +3 i \sqrt{3} \mu _1 p-3 p}}. \end{aligned}$$
(31)

When \(p<0\), the solutions are

Family 1:

$$\begin{aligned} v_{11,12}(x,t)=\frac{e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( \mu _1 p \tanh \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) +i \sqrt{3} p \coth \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \right) }{\sqrt{-p}}. \end{aligned}$$
(32)

Family 2:

$$\begin{aligned} v_{13,14}(x,t)=\frac{e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( \mu _1 p \coth \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) +i \sqrt{3} p \tanh \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \right) }{\sqrt{-p}}. \end{aligned}$$
(33)

When \(p>0\), the solutions are

Family 3:

$$\begin{aligned}{} & {} v_{15,16}(x,t)=\nonumber \\{} & {} \quad \sqrt{p} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \tan \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \left( \mu _1-i \sqrt{3} \cot ^2\left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \right) . \end{aligned}$$
(34)
Fig. 3
figure 3

3D, 2D graphs of Eq. (33)

Full size image

Family 4:

$$\begin{aligned}{} & {} v_{17,18}(x,t)\nonumber \\{} & {} \quad =\sqrt{p} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \tan \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) \left( -\mu _1 \cot ^2\left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) +i \sqrt{3}\right) . \end{aligned}$$
(35)

When \(p=0\), the solutions are

Family 5:

$$\begin{aligned} v_{19,20}(x,t)=e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( -\frac{\beta \mu _1}{\beta x-2 \nu t^{\beta }}+i \sqrt{3} p \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) . \end{aligned}$$
(36)

Set-3

$$\begin{aligned} \mu _0=-i \sqrt{3} n,~~\mu _1=0,~~\rho _1=i \sqrt{3} \left( n^2+p\right) ,~\alpha =-\frac{\sqrt{\frac{5}{6}}}{3 \sqrt{3 p-\nu }}. \end{aligned}$$
(37)

When \(p<0\), the solutions are

Family 1:

$$\begin{aligned} v_{21,22}(x,t)=-i \sqrt{3} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( n-\frac{n^2+p}{n-\sqrt{-p} \tanh \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }\right) . \end{aligned}$$
(38)

Family 2:

$$\begin{aligned} v_{23,24}(x,t)=i \sqrt{3} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( n-\frac{n^2+p}{n-\sqrt{-p} \coth \left( \sqrt{-p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }\right) . \end{aligned}$$
(39)

When \(p>0\), the solutions are

Family 3:

$$\begin{aligned} v_{25,26}(x,t)=-i \sqrt{3} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( n-\frac{n^2+p}{n+\sqrt{p} \tan \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }\right) . \end{aligned}$$
(40)
Fig. 4
figure 4

3D, 2D graphs of Eq. (38)

Full size image

Family 4:

$$\begin{aligned} v_{27,28}(x,t)=-i \sqrt{3} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( n-\frac{n^2+p}{n-\sqrt{p} \cot \left( \sqrt{p} \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }\right) . \end{aligned}$$
(41)

When \(p=0\), the solutions are

Family 5:

$$\begin{aligned} v_{29,30}(x,t)=\frac{i \sqrt{3} e^{i \left( \frac{m t^{\beta }}{\beta }+\nu x\right) } \left( n+p \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) \right) }{n \left( x-\frac{2 \nu t^{\beta }}{\beta }\right) -1}. \end{aligned}$$
(42)

4.2 Application of the unified method

For the requirement of the unified method, follow the balancing principal of terms \(V{''}\) and \(V^3\) in Eq. (23), we gain \(N=1\). Then from Eq. (12) we get,

$$\begin{aligned} V(\xi )=a_0+a_1 F(\xi )+\frac{b_1}{F(\xi )}, \end{aligned}$$
(43)

where \(a_0,~a_1\) and \(b_1\) are constants. When Eq. (43) is plugged into Eq. (23), we obtain a system of algebraic equations correspond to coefficients of \(V(\xi )\) equating to zero. By simplifying these algebraic equations, novel clusters of solutions for Eq. (1) are gained.

Set-1

$$\begin{aligned} a_0=0,~a_1=i \sqrt{3},~b_1=-i \sqrt{3} \Omega ,~~m =12 \Omega -\frac{5}{54 \alpha ^2}. \end{aligned}$$
(44)

When \(\Omega <0\), the solutions are

Family 1:

$$\begin{aligned} v_{1,2}(x,t)=\frac{i \sqrt{3} e^{i \phi } \left( \left( \sqrt{-\left( \Omega \left( d^2+e^2\right) \right) }-d \sqrt{-\Omega } \cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) \right) ^2-\Omega \left( d \sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +e\right) ^2\right) }{\left( d \sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +e\right) \left( \sqrt{-\left( \Omega \left( d^2+e^2\right) \right) }-d \sqrt{-\Omega } \cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) \right) }. \end{aligned}$$
(45)

Family 2:

$$\begin{aligned} v_{3,4}(x,t)=-\frac{i \sqrt{3} e^{i \phi } \left( \Omega \left( 1-\frac{2 d}{d-\sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +\cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }\right) ^2+\Omega \right) }{\sqrt{-\Omega } \left( 1-\frac{2 d}{d-\sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +\cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }\right) }. \end{aligned}$$
(46)

When \(\Omega >0\), the solutions are

Family 3:

$$\begin{aligned} v_{5,6}(x,t)=\frac{i \sqrt{3} e^{i \phi } \left( \left( \sqrt{\Omega \left( d^2-e^2\right) }-d \sqrt{\Omega } \cos \left( 2 \sqrt{\Omega } (f+\xi )\right) \right) ^2-\Omega \left( d \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +e\right) ^2\right) }{\left( d \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +e\right) \left( \sqrt{\Omega \left( d^2-e^2\right) }-d \sqrt{\Omega } \cos \left( 2 \sqrt{\Omega } (f+\xi )\right) \right) }. \end{aligned}$$
(47)

Family 4:

$$\begin{aligned} v_{7,8}(x,t)=\sqrt{3} e^{i \phi } \left( -\frac{\Omega }{\sqrt{\Omega }-\frac{2 d \sqrt{-\Omega }}{d-i \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +\cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }}+\frac{2 d \sqrt{-\Omega }}{d-i \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +\cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }-\sqrt{\Omega }\right) . \end{aligned}$$
(48)

When \(\Omega =0\), the solutions are

Family 5:

$$\begin{aligned} v_{9,10}(x,t)=\frac{i \sqrt{3} e^{i \phi } \left( f^2 \Omega +2 f \xi \Omega +\xi ^2 \Omega -1\right) }{f+\xi }. \end{aligned}$$
(49)

For set-1: \(\xi =x-\frac{2 \nu t^{\beta }}{\beta },~~\psi =\frac{\left( 12 \Omega -\frac{5}{54 \alpha ^2}\right) t^{\beta }}{\beta }+\nu x.\)

Set-2

$$\begin{aligned} a_1=\frac{i \left( 3 a_0 \Omega +2 a_0^3-3\right) }{3 \sqrt{3} a_0 \Omega },~b_1=-i \sqrt{3} \Omega ,~m =-\frac{5}{54 \alpha ^2}+5 a_0^2-\frac{3}{a_0}+6 \Omega . \end{aligned}$$
(50)

When \(\Omega <0\), the solutions are

Family 1:

$$\begin{aligned}{} & {} v_{11,12}(x,t)\nonumber \\{} & {} \quad =\frac{i e^{i \phi } \left( 3 a_0 \Omega +2 a_0^3-3\right) \left( \sqrt{-\left( \Omega \left( d^2+e^2\right) \right) }-d \sqrt{-\Omega } \cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) \right) }{3 \sqrt{3} a_0 \Omega \left( d \sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +e\right) }+a_0 \nonumber \\{} & {} \quad -\frac{i \sqrt{3} \Omega \left( d \sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +e\right) }{\sqrt{-\left( \Omega \left( d^2+e^2\right) \right) }-d \sqrt{-\Omega } \cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }. \end{aligned}$$
(51)
Fig. 5
figure 5

3D, 2D graphs of Eq. (46)

Full size image

Family 2:

$$\begin{aligned} v_{13,14}(x,t)= & {} -\frac{i e^{i \phi } \left( 3 a_0 \Omega +2 a_0^3-3\right) \left( 1-\frac{2 d}{d-\sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +\cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }\right) }{3 \sqrt{3} a_0 \sqrt{-\Omega }}\nonumber \\{} & {} \quad +a_0+\frac{i \sqrt{3} \sqrt{-\Omega }}{1-\frac{2 d}{d-\sinh \left( 2 \sqrt{-\Omega } (f+\xi )\right) +\cosh \left( 2 \sqrt{-\Omega } (f+\xi )\right) }}. \end{aligned}$$
(52)

When \(\Omega >0\), the solutions are

Family 3:

$$\begin{aligned} v_{15,16}(x,t)= & {} \frac{i e^{i \phi } \left( 3 a_0 \Omega +2 a_0^3-3\right) \left( \sqrt{\Omega \left( d^2-e^2\right) }-d \sqrt{\Omega } \cos \left( 2 \sqrt{\Omega } (f+\xi )\right) \right) }{3 \sqrt{3} a_0 \Omega \left( d \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +e\right) }+a_0\nonumber \\{} & {} \quad + \frac{i \sqrt{3} \Omega \left( d \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +e\right) }{d \sqrt{\Omega } \cos \left( 2 \sqrt{\Omega } (f+\xi )\right) -\sqrt{\Omega \left( d^2-e^2\right) }}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \end{aligned}$$
(53)
Fig. 6
figure 6

3D, 2D graphs of Eq. (41)

Full size image

Family 4:

$$\begin{aligned} v_{17,18}(x,t)= & {} \frac{e^{i \phi } \left( 3 a_0 \Omega +2 a_0^3-3\right) \left( \sqrt{\Omega }-\frac{2 d \sqrt{-\Omega }}{d+i \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +\cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }\right) }{3 \sqrt{3} a_0 \Omega }\nonumber \\{} & {} \quad +a_0+\frac{\sqrt{3} \Omega }{\sqrt{\Omega }-\frac{2 d \sqrt{-\Omega }}{d+i \sin \left( 2 \sqrt{\Omega } (f+\xi )\right) +\cos \left( 2 \sqrt{\Omega } (f+\xi )\right) }}. \end{aligned}$$
(54)

When \(\Omega =0\), the solutions are

Family 5:

$$\begin{aligned} v_{19,20}(x,t)=-\frac{i e^{i \phi } \left( 3 a_0 \Omega +2 a_0^3-3\right) }{3 \sqrt{3} a_0 \Omega (f+\xi )}+a_0+i \sqrt{3} \Omega (f+\xi ). \end{aligned}$$
(55)

For set-2: \(\xi =x-\frac{2 \nu t^{\beta }}{\beta },~~\psi =\frac{t^{\beta } \left( -\frac{5}{54 \alpha ^2}+5 a_0^2-\frac{3}{a_0}+6 \Omega \right) }{\beta }+\nu x.\)

5 Stability analysis

Numerous nonlinear processes exhibit an instability in the modulation of the steady-state as a result of the interaction of the nonlinear and dispersive effects. Examining the equation’s modulation instability (MI) (Shehata 2010; Rehman and Ahmad 2023; Houwe et al. 2021; Ismael et al. 2021; Yépez-Martínez et al. 2022; Ismael et al. 2023; Sylvere et al. 2023) through linear stability technique is the main goal of the study in this part.

Assuming the FSH equation has following steady-state solutions

$$\begin{aligned} v=e^{i \lambda \frac{t^{\alpha }}{\alpha }} \left( P(x,t)+\sqrt{\lambda }\right) , \end{aligned}$$
(56)

where \(\lambda\) signifies for normalized optical power.

Plugging Eq. (56) into Eqs. (1). We earn

$$\begin{aligned} 4 \lambda \left( P^*+P\right) +2 i \frac{\partial ^{\beta }P}{\partial t^{\beta }}+\frac{\partial ^{2} P}{\partial x^{2}}+2 i \alpha \frac{\partial ^{3} P}{\partial x^{3}}=0, \end{aligned}$$
(57)

where \(*\) stands for the conjugate.

Let Eq. (57) has solution of the form as

$$\begin{aligned} {\left\{ \begin{array}{ll} P(x,t)=p_1 e^{i (\eta x-\frac{t^{\beta }}{\beta } \varpi )}+p_2 e^{-i (\eta x-\frac{t^{\beta }}{\beta } \varpi )}, &{} \\ P^{*}(x,t)=p_1 e^{-i (\eta x-\frac{t^{\beta }}{\beta } \varpi )}+p_2 e^{i (\eta x-\frac{t^{\beta }}{\beta } \varpi )}, &{} \end{array}\right. } \end{aligned}$$
(58)

where \(p_{1}\) and \(p_{2}\) stands for the normalized wave number, while frequency of perturbation represented by \(\varpi\).

Embedding Eq. (58) into Eq. (57), separating the coefficients of \(e^{i(\eta x+\varpi \frac{t^{\beta }}{\beta })}\) and \(e^{-i(\eta x+\varpi \frac{t^{\beta }}{\beta })}\), and solving the determinant of the coefficient matrix, we get the following dispersion relation:

$$\begin{aligned} \begin{aligned} 4 \alpha ^2 \eta ^6+4 \alpha \eta ^5-16 \alpha \eta ^3 \lambda -4 \varpi ^{2}+\eta ^4-8 \eta ^2 \lambda =0. \end{aligned} \end{aligned}$$
(59)

Evaluating the dispersion relation (59) for \(\varpi\), imparts

$$\begin{aligned} \varpi =2^{-1/\beta } \sqrt{\left( \eta ^2 (2 \alpha \eta +1) \left( 2 \alpha \eta ^3+\eta ^2-8 \lambda \right) \right) ^{1/\beta }}. \end{aligned}$$
(60)

The stability of the steady state is shown by the dispersion relation that was attained. The steady state appears to be stable against tiny dispersion when the wave number \(\varpi\) has a real component. When the wave number is imaginary, the steady state becomes unstable and the perturbation increases exponentially. Under this condition, the growth rate is:

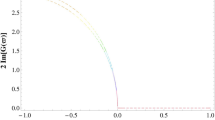
$$\begin{aligned} \eta ^2 (2 \alpha \eta +1) \left( 2 \alpha \eta ^3+\eta ^2-8 \lambda \right) <0. \end{aligned}$$

Lastly, the gain spectrum \(G(\lambda )\) is calculated as

$$\begin{aligned} G(\lambda )=2Im\bigg (\varpi \bigg )=2 Im\bigg (2^{-1/\beta } \sqrt{\left( \eta ^2 (2 \alpha \eta +1) \left( 2 \alpha \eta ^3+\eta ^2-8 \lambda \right) \right) ^{1/\beta }}\bigg ). \end{aligned}$$
(61)
Fig. 7
figure 7

Modulation Instability regions for distinct values of \(\alpha =\{0.2,0.4,0.6\},~\alpha =\{0.15,0.2,0.25\}\) from left to right, respectively

Full size image
Fig. 8
figure 8

Modulation Instability regions for distinct values of \(\alpha =\{0.1,0.2,0.3\},~\alpha =\{0.11,0.21,0.31\}\) from left to right, respectively

Full size image
Fig. 9
figure 9

Modulation Instability regions for distinct values of \(\alpha =\{0.2,0.4,0.6\},~\alpha =\{0.5,0.6,0.7\}\) from left to right, respectively

Full size image
Fig. 10
figure 10

Modulation Instability regions for distinct values of \(\alpha =\{0.2,0.4,0.6\},~\alpha =\{0.55,0.65,0.75\}\) from left to right, respectively

Full size image

6 Results and discussion

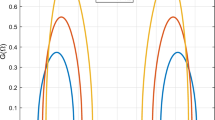
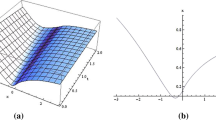
In this section, the originality and novelty of present work is demonstrated by a detailed comparison of the obtained solutions with the previous ones. Odabasi Koprulu constructed multi-solitons in the form of singular, dark, and bright by applying direct method and trial equation method (Odabasi Koprulu 2022). But in this study we have computed various solutions in the forms of dark, rational, singular, hyperbolic, trignometric and periodic wave solutions by manipulating two mathematical methods improved F-expansion method and the unified method. Several of our outcomes diverge from those mentioned in Odabasi Koprulu (2022) if we compare our achievements with their results. Even so, if we give various values to the components involved, we can obtain some similar outcomes. This present study differs from others in that it assessed the impact that parameters of the model have on the actions of solitons, despite the fact that the proposed techniques were applied for the first time on the model under investigation and several soliton were created. This study focuses on the influence of model parameters on solitons behavior. This study offers numerous innovative optical soliton solutions for the NLCFSH dynamical model. The soliton solutions are constructed via powerful analytical methods, which are the improved F-expansion method, the unified method and the effectiveness of the employed schemes demonstrates their strength and superiority over other applied analytical procedures. The physical implications of the extracted wave solutions for the specific values of the resultant parameters are illustrated graphically and the internal structure of the connected physical phenomena is analyzed in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. These kinds of solutions may be useful to explain some physical phenomena related to wave propagation in a nonlinear Schrödinger system supporting high-order nonlinear and dispersive effects. Here, we provide some 3-dimensional and 2-dimensional plots of the obtained solutions in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Figure 1 simulates the dark behavior Eq. (26) with arbitrary parameter values for \(p=-0.7,~n=2.1,~m=1.3,~\alpha =0.2\). The Fig. 2 represents the periodic behavior Eq. (29) by choosing the arbitrary parameter values for \(p=0.8,~n=0.5,~m=1.3,~\alpha =0.2,~\beta =0.1\). The Fig. 3 demonstrates the dark behavior of Eq. (33) with arbitrary parameter values for \(p=-0.6,~\mu _1=1.8,~\nu =0.9,~m=-0.7\). The Fig. 4 represents the dark behavior of Eq. (38) with arbitrary parameter values for \(p=-0.34,~\nu =0.84,~m=2,~n=1\). The Fig. 6 shows the periodic behavior Eq. (41) with arbitrary parameter values for \(p=2.5,~m=0.34,~n=0.2,~\nu =2.34\). The Fig. 5 illustrates the hyperbolic behavior Eq. 46 with arbitrary parameter values for \(\Omega =-0.01,~d=0.19,~e=1.4,~f=0.4,~c=1.07,~\alpha =0.2,~m=1.21\). The Fig. 11 shows the periodic behavior Eq. (53) with arbitrary parameter values for \(\Omega =0.6,~d=0.19,~e=0.4,~f=0.7,~c=1.07,~\alpha =-1.2,~m=1.1,~a_0=0.3\). The Fig. 12 represents the trigonometric behavior Eq. (54) with arbitrary parameter values for \(\Omega =0.5,~d=0.019,~e=-0.4,~f=0.07,~c=1.09,~\alpha =1.2,~m=-1.01,~a_0=0.6\). The wave profiles of the obtained solutions have been sketched for various values of \(\beta\) to demonstrate the effect of the fractional derivative on the dynamic behavior of the waves. From the figures, it is observed that the fractional order has a significant impact on the characteristics of the wave profiles via the memory effect phenomenon, which means that the signal takes into account its past evolution at any point; acting on this parameter allows having better and more complete information about the shape of a signal or a pulse. The soliton has the ability to keep its amplitude, velocity, and form constant throughout its propagation. These reported solutions have some physical meaning for instance dark soliton is a soliton whose intensity is lower than the background and which isn’t produced by a typical pulse but rather is basically devoid of energy in a continuous time beam. There are further types of solitary waves called singular solitons that have singularities, typically infinite discontinuities. Singular solitons might be linked to solitary waves when the location of the center of the solitary wave is imaginary. Therefore, discussing the topic of singular solitons is relevant. This type of solution contains spikes and therefore may recommend a description for the development of rogue waves. Periodic wave solution describes a wave with repeating continuous pattern, which determines its wavelength and frequency, while period defines as time required to complete cycle of waveform and frequency is a number of cycles per second of time. The regions of gain curves versus the angular frequency with the effect of the dispersion and fractional derivative order have been exemplified in figures 7, 8, 9 and 10. We observe that, when the fractional derivative order decreases, the MI band increases and the instability zones also increase.

Fig. 11
figure 11

3D, 2D graphs of Eq. (53)

Full size image
Fig. 12
figure 12

3D, 2D graphs of Eq. (54)

Full size image

7 Conclusion

In this article, we provided several new solutions for the fractional Schrödinger–Hirota (FSH) equation with conformable fractional derivative, which is well known for playing a crucial role in optical fiber communication between continents as well as the telecommunication industry. By using the improved F-expansion and unified method, we have successfully secured several new solitons of the Eq. (1). Several notable oceanic phenomena related to nonlinear shallow or deep water wave propagation have been elucidated in terms of soliton propagation. A number of significant optical solitons, including dark optical, singular optical, mixed singular optical, and periodic function solutions, have been recovered. It has been demonstrated that these techniques are quite successful in exposing the different soliton solutions of our selected model. To observe the internal structure of the solutions to nonlinear phenomena, researchers may use and develop many new approaches. In this way, you can find novel solutions to the dynamical models under consideration. Studying these innovative solution characteristics significantly enhances the physical realisation of wave phenomena in higher-dimensional fractional dynamical models in nonlinear optics and oceanography. The responses of the soliton solutions of the govering models can be evaluated in the future by adding the bifurcation and chaotic behaviors of FSH equation, and a new debate ground can be formed.