Alternating direction method of multipliers for truss topology optimization with limited number of nodes: a cardinality-constrained second-order cone programming approach

Abstract

This paper addresses the compliance minimization of a truss, where the number of available nodes is limited. It is shown that this optimization problem can be recast as a second-order cone programming with a cardinality constraint. We propose a simple heuristic based on the alternative direction method of multipliers. The efficiency of the proposed method is compared with a global optimization approach based on mixed-integer second-order cone programming. Numerical experiments demonstrate that the proposed method often finds a solution having a good objective value with small computational cost.

1 Introduction

It is common to use the ground structure method (Topping 1983; Kirsch 1989; Bendsøe et al. 1994) for truss topology optimization, where the cross-sectional areas of the truss members are treated as design variables to be optimized. Particularly, compliance minimization with continuous design variables is a convex problem (Bendsøe et al. 1994; Ohsaki 2011), and can be solved efficiently. An optimal solution of this problem often consists of too many members (including ones that are too thin) connected by many nodes¹ and, hence, is regarded as too complex a design from the viewpoint of practical manufacturability. Also, the fabrication cost of a truss usually increases as the number of nodes increases. To obtain a practically acceptable truss design, Asadpoure et al. (2015) proposed to minimize the weighted sum of the structural weight and the fabrication cost related to the number of members. In this method, the number of members is approximated by using a regularized Heaviside step function. Torii et al. (2016) used the same approach to take into account the number of nodes. In this paper, we consider the compliance minimization of a truss subject to an explicit upper bound constraint on the number of nodes.

The number of nodes in structural optimization has also been discussed in the layout optimization of trusses. In the classical layout optimization, we minimize the total weight of the members when the allowable stress is specified. When the potential locations of nodes of a truss are not limited, the optimal solution becomes a so-called truss-like continuum with infinitely many nodes (Hegemier and Prager 1969; Michell 1904). Prager (1978, 1977) showed that, by adding the weight of the nodes to the objective function, the problem has an optimal solution with a finite number of nodes. To avoid complex truss design, Parkes (1975) proposed to introduce modification of member lengths such that, at each node, a constant is added to the length of each member connected to the node. As a post-processing step for this method, He and Gilbert (2015) proposed to make use of geometry optimization. Similarly, Mazurek et al. (2011) defined a so-called performance index, by using member lengths and axial forces, to assess the cost of a structure; see also Mazurek (2012). The number of nodes in a truss is not specified explicitly in the methods in the literature (Asadpoure et al. 2015; Torii et al. 2016; Parkes 1975; He and Gilbert 2015; Mazurek 2012; Mazurek et al. 2011) cited above.

In this paper, based on the ground structure method we deal with the compliance minimization problem of a truss subjected to an upper bound constraint on the number of nodes (i.e., a cardinality constraint on the set of nodes). This design optimization problem essentially consists of two decisions: We first select a set of nodes, satisfying the cardinality constraint, among the candidate nodes in a ground structure, and then find the optimal cross-sectional areas of the members connected to the selected nodes. The first decision gives a combinatorial attribute to the design optimization problem. In this paper, we show that this optimization problem can be recast as a mixed-integer second-order cone programming (MISOCP) problem; see Sect. 3.2. Since an SOCP problem can be solved efficiently with a primal-dual interior-point method (Anjos and Lasserre 2012; Ben-Tal and Nemirovski 2001), we can compute a globally optimal solution of an MISOCP problem with, e.g., a branch-and-bound method. Several software packages are available for this purpose (Andersen et al. 2003; Gurobi Optimization, Inc. 2016). However, due to its large computational cost, the MISOCP approach can be applied only to small- to medium-size truss optimization problems. The reader may refer to Bertsimas and Shioda (2009) and Miyashiro and Takano (2015) for applications of MISOCP to variable selection in statistics, and to Kanno (2013, 2016a, b) and Kočvara (2017) for applications in structural optimization.

We refer to the number of nonzero components of a real vector as the $\ell _{0}$-norm of the vector.² We refer to an upper bound constraint on the $\ell _{0}$-norm of a vector, i.e., an $\ell _{0}$-norm constraint, as a cardinality constraint (i.e., an upper bound constraint on the cardinality of the support of the vector). Cardinality constraints, as well as $\ell _{0}$-norm minimization, frequently appear in diverse fields including variable selection in statistics, image processing, compressed sensing, and portfolio selection (Natarajan 1995; Chartrand 2007; Bruckstein et al. 2009; Candès et al. 2008; Gotoh et al. 2018; Le Thi et al. 2015; Zheng et al. 2014; Burdakov et al. 2016; Bertsimas and Shioda 2009; Cui et al. 2013). An application of $\ell _{0}$-minimization to structural design generating link mechanisms can be found in Ohsaki et al. (2014). In this paper, we show that truss topology optimization with a limited number of nodes can be formulated as cardinality-constrained SOCP; see Sect. 3.1.

The alternating direction method of multipliers (ADMM) is an algorithm for convex optimization (Boyd et al. 2010). For various nonconvex optimization problems, it is known that ADMM can often serve as a simple but powerful heuristic (Takapoui et al. 2018; Kanamori and Takeda 2014; Chartrand and Wohlberg 2013; Magnússon et al. 2016; Chartrand 2012; Diamond et al. 2018). This motivates us to develop a simple heuristic based on ADMM, to find approximate solutions to the problem of truss topology optimization with a limited number of nodes. The proposed method is expected to find a local optimal solution having a reasonable objective value with small computational cost. In control theory, ADMM has been used for various sparsity-promoting optimal control methods, including the design of sparse feedback gains (Lin et al. 2013), sparse output feedback (Arastoo et al. 2015), and sparse gain matrices for the extended Kalman filter (Masazade et al. 2012).

The paper is organized as follows: Sect. 2 provides an overview of necessary background for the ADMM. Sect. 3 formulates the truss topology optimization problem with a limited number of nodes as cardinality-constrained SOCP, and recasts it as MISOCP. Section 4 presents a heuristic based on ADMM to solve the cardinality-constrained SOCP formulation. Section 5 is devoted to a discussion on the treatment of overlapping members in a ground structure. Section 6 reports results of numerical experiments. Some conclusions are drawn in Sect. 7.

In our notation, ${}^{\top }$ denotes the transpose of a vector or a matrix. We use $\mathbf{1} = (1,1,\dots ,1)^{\top }$ to denote the all-ones vector. For vectors $\varvec{x} = (x_{i}) \in \mathbb {R}^{n}$ and $\varvec{y} = (y_{i}) \in \mathbb {R}^{n}$, we write $\varvec{x} \ge \varvec{y}$ if $x_{i} \ge y_{i}$ $(i=1,\dots ,n)$. We use $\Vert \varvec{x} \Vert$ to denote the Euclidean norm (or the $\ell _{2}$-norm) of $\varvec{x}$, i.e., $\Vert \varvec{x} \Vert = \sqrt{\varvec{x}^{\top } \varvec{x}}$. We denote by $\Vert \varvec{x} \Vert _{0}$ the number of nonzero components of $\varvec{x}$, which is the so-called $\ell _{0}$-norm of $\varvec{x}$. For a finite set T, let |T| denote the cardinality of T, i.e., the number of elements in T. If we define $\mathop {\mathrm {supp}}\nolimits (\varvec{x}) \subseteq \{ 1,\dots ,n \}$ by $\mathop {\mathrm {supp}}\nolimits (\varvec{x}) = \{ i \in \{ 1,\dots ,n \} \mid x_{i} \not = 0 \}$, then $\Vert \varvec{x} \Vert _{0} = | \mathop {\mathrm {supp}}\nolimits (\varvec{x}) |$. For a set $S \subseteq \mathbb {R}^{n}$, we denote by $\delta _{S} : \mathbb {R}^{n} \rightarrow \mathbb {R}\cup \{+\infty \}$ the indicator function of S, which is defined by

$$\begin{aligned} \delta _{S}({\varvec{x}}) = {\left\{ \begin{array}{ll} \ 0 \quad &{} {\text {if }}\quad {\varvec{x}} \in S, \\ +\infty \quad &{} {\text {if }} \quad{\varvec{x}} \not \in S. \\ \end{array}\right. } \end{aligned}$$

For a closed set $S \subseteq \mathbb {R}^{n}$, the projection of a point $\varvec{z} \in \mathbb {R}^{n}$ onto S, denoted $\Pi _{S}(\varvec{z}) \in \mathbb {R}^{n}$, is defined by

$$\begin{aligned} \Pi _{S}(\varvec{z}) \in S, \quad \Vert \varvec{z} - \Pi _{S}(\varvec{z}) \Vert = \min \{ \Vert \varvec{z} - \varvec{x} \Vert \mid \varvec{x} \in S \}. \end{aligned}$$

If S is closed and convex, then $\Pi _{S}(\varvec{z})$ exists uniquely for any point $\varvec{z} \in \mathbb {R}^{n}$. The n-dimensional second-order cone, denoted $\mathcal {L}^{n}$, is defined by

$$\begin{aligned} \mathcal {L}^{n} = \{ (s_{0},\varvec{s}_{1}) \in \mathbb {R}\times \mathbb {R}^{n-1} \mid \Vert \varvec{s}_{1} \Vert \le s_{0} \}. \end{aligned}$$

The n-dimensional rotated second-order cone, denoted $\mathcal {K}^{n}$, is defined by

$$\begin{aligned} \mathcal {K}^{n} = \{ (\varvec{x},y,z) \in \mathbb {R}^{n-2} \times \mathbb {R}\times \mathbb {R}\mid \varvec{x}^{\top } \varvec{x} \le y z, \ y \ge 0, \ z \ge 0 \}. \end{aligned}$$

We recall that $(\varvec{x},y,z) \in \mathcal {K}^{n}$ if and only if $(y+z, y-z, 2\;\varvec{x}) \in \mathcal {L}^{n}$. We use $\mathcal {U}(a,b)$ to denote the continuous uniform distribution on the interval $(a,b) \subset \mathbb {R}$.

2 Fundamentals of alternating direction method of multipliers

In this section, we briefly outline the alternating direction method of multipliers (ADMM) for solving convex optimization problems; see Boyd et al. (2010) for more accounts.

Let $f : \mathbb {R}^{n} \rightarrow \mathbb {R}\cup \{ +\infty \}$ and $g : \mathbb {R}^{m} \rightarrow \mathbb {R}\cup \{ +\infty \}$ be closed proper convex functions. Consider the following convex optimization problem in variables $\varvec{x} \in \mathbb {R}^{n}$ and $\varvec{z} \in \mathbb {R}^{m}$:

$$\begin{aligned}&\mathop {\mathop {\mathrm {Minimize}}}\limits _{\varvec{x},\varvec{z}} \quad f(\varvec{x}) + g(\varvec{z}) \end{aligned}$$

(1a)

$$\begin{aligned}&\mathop {\mathrm {subject}}\,{\mathrm {to}}\quad A \varvec{x} + B \varvec{z} = \varvec{c}. \end{aligned}$$

(1b)

Here, $A \in \mathbb {R}^{l \times n}$ and $B \in \mathbb {R}^{l \times m}$ are constant matrices, and $\varvec{c} \in \mathbb {R}^{l}$ is a constant vector.

The augmented Lagrangian of problem (1) is defined as

$$\begin{aligned} L_{\rho }(\varvec{x},\varvec{z},\varvec{y}) = f(\varvec{x}) + g(\varvec{z}) + \varvec{y}^{\top } (A \varvec{x} + B \varvec{z} - \varvec{c}) + \frac{\rho }{2} \Vert A \varvec{x} + B \varvec{z} - \varvec{c} \Vert ^{2}, \end{aligned}$$

(2)

where $\rho > 0$ is the penalty parameter, and $\varvec{y} \in \mathbb {R}^{l}$ is the Lagrange multiplier (also called the dual variable). At each iteration of ADMM, we update $\varvec{x}^{k}$, $\varvec{z}^{k}$, and $\varvec{y}^{k}$ as

$$\begin{aligned} \varvec{x}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{x}} L_{\rho }(\varvec{x},\varvec{z}^{k},\varvec{y}^{k}), \end{aligned}$$

(3)

$$\begin{aligned} \varvec{z}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{z}} L_{\rho }(\varvec{x}^{k+1},\varvec{z},\varvec{y}^{k}), \end{aligned}$$

(4)

$$\begin{aligned} \varvec{y}^{k+1}&:= \varvec{y}^{k} + \rho (A \varvec{x}^{k+1} + B \varvec{z}^{k+1} - \varvec{c}). \end{aligned}$$

(5)

The so-called scaled form of ADMM is defined below. Letting $\varvec{v} = \varvec{y} / \rho$, we see that (2) is reduced to

$$\begin{aligned} \tilde{L}_{\rho }(\varvec{x},\varvec{z},\varvec{v}) = f(\varvec{x}) + g(\varvec{z}) + \frac{\rho }{2} \Vert A \varvec{x} + B \varvec{z} - \varvec{c} + \varvec{v} \Vert ^{2} - \frac{\rho }{2} \Vert \varvec{v} \Vert ^{2}. \end{aligned}$$

(6)

By using $\tilde{L}_{\rho }$ in (6), the iteration of ADMM given by (3), (4), and (5) is written as

$$\begin{aligned} \varvec{x}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{x}} \tilde{L}_{\rho }(\varvec{x},\varvec{z}^{k},\varvec{v}^{k}), \end{aligned}$$

(7)

$$\begin{aligned} \varvec{z}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{z}} \tilde{L}_{\rho }(\varvec{x}^{k+1},\varvec{z},\varvec{v}^{k}), \end{aligned}$$

(8)

$$\begin{aligned} \varvec{v}^{k+1}&:= \varvec{v}^{k} + A \varvec{x}^{k+1} + B \varvec{z}^{k+1} - \varvec{c}. \end{aligned}$$

(9)

We refer to the form given in (7), (8), and (9) as the scaled form of ADMM, and we refer to $\varvec{v}$ as the scaled dual variable.

Primarily, ADMM is an algorithm for solving convex optimization problems. It is known that ADMM can often serve as an efficient heuristic for diverse nonconvex optimization problems; see, e.g., Takapoui et al. (2018), Kanamori and Takeda (2014), Chartrand and Wohlberg (2013), Magnússon et al. (2016), Chartrand (2012), and Boyd et al. (2010, Sect. 9). For nonconvex problems, ADMM does not necessarily converge. Also, when it converges, the obtained solution is not necessarily a global optimum. Furthermore, the obtained solution can depend on the penalty parameter and the initial point. Nevertheless, ADMM can be a simple algorithm, and can be efficient in the sense that it often converges to a solution with a good objective value.

3 Design optimization with limited number of nodes

In Sect. 3.1, we define truss topology optimization subject to an upper bound constraint on the number of nodes. In Sect. 3.2, we show that this problem can be recast as an MISOCP problem.

3.1 Problem setting

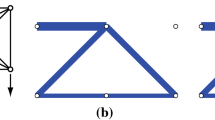
Following the ground structure approach, consider an initial truss consisting of many candidate members that are connected by nodes with given locations. The cross-sectional areas of the members are treated as the design variables to be optimized. It is worth noting that the ground structure may involve some overlapping members, an example is shown in Fig. 1. The necessity, as well as the treatment, of overlapping members in a ground structure is thoroughly discussed in Sect. 5. We use m, l, and d to denote the number of members, the number of nodes, and the number of degrees of freedom of the nodal displacements, respectively.

Fig. 1

An example of ground structure with overlapping members

Let $x_{i} \,(i=1,\dots ,m)$ denote the member cross-sectional areas. We use $K(\varvec{x}) \in \mathbb {R}^{d \times d}$ to denote the stiffness matrix, which can be written as

$$\begin{aligned} K(\varvec{x}) = \sum _{i=1}^{m} \frac{E}{c_{i}} x_{i} \varvec{b}_{i} \varvec{b}_{i}^{\top }. \end{aligned}$$

Here, $c_{i}$ is the undeformed member length, E is the Young modulus, and $\varvec{b}_{i} \in \mathbb {R}^{d}$ is a constant vector reflecting the member connectivity and the direction cosine of member i. For a given external load vector $\varvec{p} \in \mathbb {R}^{d}$, the compliance of the truss, denoted $\pi (\varvec{x})$, is defined by

$$\begin{aligned} \pi (\varvec{x}) = \sup \{ 2\varvec{p}^{\top } \varvec{u} - \varvec{u}^{\top } K(\varvec{x}) \varvec{u} \mid \varvec{u} \in \mathbb {R}^{d} \}. \end{aligned}$$

(10)

Let $V (>0)$ denote the specified upper bound on the structural volume. The conventional compliance minimization problem is formulated as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}_{\varvec{x}} {\quad } \pi (\varvec{x}) \end{aligned}$$

(11a)

$$\begin{aligned}&\mathop {\mathrm {subject}}\,{\mathrm {to}}\quad \varvec{x} \ge \mathbf{0}, \end{aligned}$$

(11b)

$$\begin{aligned}&\qquad \qquad \qquad \varvec{c}^{\top } \varvec{x} \le V. \end{aligned}$$

(11c)

This is a convex problem, and can be recast as follows (Ben-Tal and Nemirovski 2001, Sect. 3.4.3):

$$\begin{aligned}&\mathop {\mathrm {Minimize}}_{\varvec{x},\varvec{q},\varvec{w}} & {\quad } \sum _{i=1}^{m} w_{i} \end{aligned}$$

(12a)

$$\begin{aligned}\mathop {\mathrm {subject}}\,{\mathrm {to}} & \quad w_{i} x_{i} \ge \frac{c_{i}}{E} q_{i}^{2}, \quad i=1,\dots ,m, \end{aligned}$$

(12b)

$$\begin{aligned}& \varvec{x} \ge \mathbf{0}, \end{aligned}$$

(12c)

$$\begin{aligned}& \sum _{i=1}^{m} q_{i} \varvec{b}_{i} = \varvec{p}, \end{aligned}$$

(12d)

$$\begin{aligned} & \varvec{c}^{\top } \varvec{x} \le V. \end{aligned}$$

(12e)

Constraints (12b) and (12c) can be rewritten equivalently as the rotated second-order cone constraints

$$\begin{aligned} (\sqrt{c_{i}/E}q_{i}, w_{i}, x_{i}) \in \mathcal {K}^{3}, \quad i=1,\dots ,m. \end{aligned}$$

These constraints also can be rewritten equivalently as the second-order cone constraints

$$\begin{aligned} w_{i} + x_{i} \ge \left\| \left[\begin{array}{l} w_{i} - x_{i} \\ 2\sqrt{c_{i}/E} q_{i} \\ \end{array} \right] \right\|, \quad i=1,\dots ,m. \end{aligned}$$

Thus, the conventional compliance minimization, (12), can be recast as an SOCP problem (Ben-Tal and Nemirovski 2001, Sect. 3.4.3); see also Kanno (2016a) and Kočvara (2017).

We are now in a position to consider an upper bound constraint on the number of nodes in a truss design. Let n denote the specified upper bound. For the jth node $(j=1,\dots ,l)$, define $I(j) \subseteq \{ 1,\dots ,m\}$ as the set of indices of the members connected to node j. For example, in the case of Fig. 1, we have $I(j) = \{ 1,2,7,10,11 \}$. Defining $z_{j} \, (j=1,\dots ,l)$ by

$$\begin{aligned} z_{j} = \sum _{i \in I(j)} x_{i}, \end{aligned}$$

(13)

we see that the number of nodes is equal to $\Vert \varvec{z} \Vert _{0}$. For notational simplicity, we write (13) as

$$\begin{aligned} \varvec{z} = Z \varvec{x} \end{aligned}$$

with a constant matrix $Z \in \mathbb {R}^{l \times m}$. The upshot is that compliance minimization subject to an upper bound constraint on the number of existing nodes is formulated as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}_{\varvec{x},\varvec{z}} {\quad } \pi (\varvec{x}) \end{aligned}$$

(14a)

$$\begin{aligned}&\mathop {\mathrm {subject}}\,{\mathrm {to}}\quad \varvec{x} \ge {\mathbf{0}}, \end{aligned}$$

(14b)

$$\begin{aligned}&\qquad \qquad \qquad \varvec{c}^{\top } \varvec{x} \le V, \end{aligned}$$

(14c)

$$\begin{aligned}&\qquad \qquad \qquad \varvec{z} = Z \varvec{x}, \end{aligned}$$

(14d)

$$\begin{aligned}&\qquad \qquad \qquad \Vert \varvec{z} \Vert _{0} \le n. \end{aligned}$$

(14e)

As mentioned above, the conventional compliance minimization in (11) can be recast as an SOCP problem. Therefore, problem (14) can be reduced to a cardinality-constrained SOCP problem. In Sect. 3.2, we present its MISOCP reformulation.

3.2 MISOCP formulation

In this section, we show that problem (14) can be recast as an MISOCP problem.

For node j $(j=1,\dots ,l)$, we introduce a new variable, $s_{j} \in \{ 0,1 \}$, to indicate whether the node vanishes ($s_{j}=0$) or exists ($s_{j}=1$). The relationship between $s_{j}$ and $z_{j}$ can be given as

$$\begin{aligned} 0 \le z_{j} \le M s_{j}, \end{aligned}$$

where $M>0$ is a sufficiently large constant. The upper bound constraint on the number of existing nodes is written in terms of $s_{1},\dots ,s_{l}$ as

$$\begin{aligned} \sum _{j=1}^{l} s_{j} \le n. \end{aligned}$$

This observation, in conjunction with the SOCP reformulation of problem (11), allows us to conclude that problem (14) is reduced to the following MISOCP problem:

$$\begin{aligned}\mathop {\mathrm {Minimize}}_{\varvec{x}, \varvec{q}, \varvec{w}, \varvec{z}, \varvec{s}} & {\quad } \sum _{i=1}^{m} w_{i} \end{aligned}$$

(15a)

$$\begin{aligned}\mathop {\mathrm {subject}}\,{\mathrm {to}}& \quad w_{i} + x_{i} \ge \left\|\left[\begin{array} {l} w_{i} - x_{i} \\ 2\sqrt{c_{i} / E} q_{i} \\ \end{array} \right]\right\| , \quad i=1,\dots ,m, \end{aligned}$$

(15b)

$$\begin{aligned}& \sum _{i=1}^{m} q_{i} \varvec{b}_{i} = \varvec{p}, \end{aligned}$$

(15c)

$$\begin{aligned}& \varvec{c}^{\top } \varvec{x} \le V , \end{aligned}$$

(15d)

$$\begin{aligned}& \varvec{z} = Z \varvec{x}, \end{aligned}$$

(15e)

$$\begin{aligned}& \varvec{z} \le M \varvec{s}, \end{aligned}$$

(15f)

$$\begin{aligned}& \sum _{j=1}^{l} s_{j} \le n, \end{aligned}$$

(15g)

$$\begin{aligned}& \varvec{s} \in \{ 0,1 \}^{l}. \end{aligned}$$

(15h)

Here, the optimization variables are $\varvec{x} \in \mathbb {R}^{m}$, $\varvec{q}\in \mathbb {R}^{m}$, $\varvec{w} \in \mathbb {R}^{m}$, $\varvec{z} \in \mathbb {R}^{l}$, and $\varvec{s} \in \mathbb {R}^{l}$. Although problem (15) is a fairly straightforward extension of the existing SOCP formulation for problem (11), it cannot be found in literature to the best of the authors’ knowledge.

4 Simple heuristic based on alternating direction method of multipliers

In this section, we present an ADMM as a heuristic for solving problem (14).

For notational simplicity, define $F \subseteq \mathbb {R}^{m}$ and $G \subseteq \mathbb {R}^{l}$ by

$$\begin{aligned} F&= \{ \varvec{x} \in \mathbb {R}^{m} \mid \varvec{x} \ge {\mathbf{0}}, \ \varvec{c}^{\top } \varvec{x} \le V \}, \\ G&= \{ \varvec{z} \in \mathbb {R}^{l} \mid \Vert \varvec{z} \Vert _{0} \le n \}. \end{aligned}$$

We see that problem (14) can be written as follows:

$$\begin{aligned}\mathop {\mathrm {Minimize}}&\quad \pi (\varvec{x}) + \delta _{F}(\varvec{x}) + \delta _{G}(\varvec{z}) \end{aligned}$$

(16a)

$$\begin{aligned}\mathop {\mathrm {subject}}\,{\mathrm {to}}&\quad Z \varvec{x} - \varvec{z} = \varvec{0}. \end{aligned}$$

(16b)

The augmented Lagrangian for problem (16) is formulated as

$$\begin{aligned} L_{\rho }(\varvec{x},\varvec{z},\varvec{y}) = \pi (\varvec{x}) + \delta _{F}(\varvec{x}) + \delta _{G}(\varvec{z}) + \varvec{y}^{\top } (Z \varvec{x} - \varvec{z}) + \frac{\rho }{2} \Vert Z \varvec{x} - \varvec{z} \Vert ^{2}, \end{aligned}$$

(17)

where $\rho > 0$ is the penalty parameter, and $\varvec{y} \in \mathbb {R}^{l}$ is the Lagrange multiplier. Letting $\varvec{v}=\varvec{y}/\rho$, we see that (17) is reduced to

$$\begin{aligned} \tilde{L}_{\rho }(\varvec{x},\varvec{z},\varvec{v}) = \pi (\varvec{x}) + \delta _{F}(\varvec{x}) + \delta _{G}(\varvec{z}) + \frac{\rho }{2} \Vert Z \varvec{x} - \varvec{z} + \varvec{v} \Vert ^{2} - \frac{\rho }{2} \Vert \varvec{v} \Vert ^{2}. \end{aligned}$$

Using $\tilde{L}_{\rho }$, we can write the iterations of ADMM in scaled form as

$$\begin{aligned} \varvec{x}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{x}} \Bigl \{ \pi (\varvec{x}) + \delta _{F}(\varvec{x}) + \frac{\rho }{2} \Vert Z \varvec{x} - \varvec{z}^{k} + \varvec{v}^{k} \Vert ^{2} \Bigr \}, \end{aligned}$$

(18)

$$\begin{aligned} \varvec{z}^{k+1}&:= \mathop {{\text {arg min}}}\limits _{\varvec{z}} \Bigl \{ \delta _{G}(\varvec{z}) + \frac{\rho }{2} \Vert Z \varvec{x}^{k+1} - \varvec{z} + \varvec{v}^{k} \Vert ^{2} \Bigr \}, \end{aligned}$$

(19)

$$\begin{aligned} \varvec{v}^{k+1}&:= \varvec{v}^{k} + Z \varvec{x}^{k+1} - \varvec{z}^{k+1}. \end{aligned}$$

(20)

The first step of ADMM in (18) means that $\varvec{x}^{k+1}$ is an optimal solution of the following convex optimization problem:

$$\begin{aligned}\mathop {\mathrm {Minimize}}&{\quad } \pi (\varvec{x}) + \frac{\rho }{2} \Vert Z \varvec{x} - \varvec{z}^{k} + \varvec{v}^{k} \Vert ^{2} \end{aligned}$$

(21a)

$$\begin{aligned}\mathop {\mathrm {subject}}\,{\mathrm {to}}&\quad \varvec{x} \ge {\mathbf{0}}, \end{aligned}$$

(21b)

$$\begin{aligned} & \varvec{c}^{\top } \varvec{x} \le V. \end{aligned}$$

(21c)

This problem can be recast as an SOCP problem. To see this, using the SOCP formulation of problem (11), we rewrite problem (21) as follows:

$$\begin{aligned}\mathop {\mathrm {Minimize}}&{\quad } \sum _{i=1}^{m} w_{i} + \frac{\rho }{2} t \end{aligned}$$

(22a)

$$\begin{aligned}\mathop {\mathrm {subject}}\,{\mathrm {to}}&\quad t \ge \Vert Z \varvec{x} - \varvec{z}^{k} + \varvec{v}^{k} \Vert ^{2}, \end{aligned}$$

(22b)

$$\begin{aligned}& w_{i} + x_{i} \ge \left\|\left[\begin{array}{l} w_{i} - x_{i} \\ 2\sqrt{c_{i} / E} q_{i} \\ \end{array} \right]\right\| , \quad i=1,\dots ,m, \end{aligned}$$

(22c)

$$\begin{aligned}& \sum _{i=1}^{m} q_{i} \varvec{b}_{i} = \varvec{p}, \end{aligned}$$

(22d)

$$\begin{aligned}&\varvec{c}^{\top } \varvec{x} \le V, \end{aligned}$$

(22e)

where $t \in \mathbb {R}$ is an auxiliary variable. Since constraint (22b) is a rotated second-order cone constraint³

$$\begin{aligned} (Z \varvec{x} - \varvec{z}^{k} + \varvec{v}^{k}, t, 1) \in \mathcal {K}^{l+2}, \end{aligned}$$

problem (22) is an SOCP problem. We adopt a primal-dual interior-point method for solving this problem. Next, the second step of ADMM in (19) can be written as

$$\begin{aligned} \varvec{z}^{k+1} \in \Pi _{G}(Z \varvec{x}^{k+1} + \varvec{v}^{k}), \end{aligned}$$

(23)

where $\Pi _{G}$ is the projection onto G.⁴ We can compute (23) easily (Boyd et al. 2010, Chap. 9); for a point $\varvec{z} \in \mathbb {R}^{l}$, $\Pi _{G}(\varvec{z})$ keeps the n largest magnitude components of $\varvec{z}$ and zeros out the other components. In this way, each step of ADMM in (18), (19), and (20) can be carried out very easily.

5 On overlapping members

Unlike the conventional compliance minimization of a truss, overlapping members in a ground structure are not redundant for the optimization problem considered in this paper. This section explains the treatment of overlapping members.

Fig. 2

An example of truss topology optimization and hinge cancellation. a The problem setting; b the optimal solution; and c the final design after hinge cancellation

We begin by reviewing that overlapping members in a ground structure is redundant for the conventional compliance minimization problem of a truss. For example, consider the ground structure shown in Fig. 2a. Here, any two nodes are connected by a member, but overlapping of members is avoided by removing the longer member when two members overlap. The leftmost nodes are pin-supported. The vertical external force is applied to the bottom rightmost node. Figure 2b shows the optimal solution of the compliance minimization problem, i.e., problem (11). This solution has four horizontal consecutive members that are connected by nodes supported only in the direction of those members. A sequence of such members is sometimes called a chain (Achtziger 1999). In this example, without changing the objective value, we can remove three intermediate nodes to replace the chain with a single longer member. This procedure is called hinge cancellation (Achtziger 1999; Rozvany 1996). As a result of hinge cancellation, we obtain the final truss design shown in Fig. 2c. Thus, longer overlapping members, like the horizontal member in Fig. 2c, are unnecessary to a ground structure. In contrast, when we consider a constraint on a number of nodes, the optimal solution depends on the existence of overlapping members in a ground structure. For example, the truss in Fig. 2b has five free nodes, while the one in Fig. 2c has two free nodes. Thus, hinge cancellation can possibly change the feasibility of the cardinality constraint and, hence, overlapping members in a ground structure are not redundant.⁵

When we consider a ground structure with some overlapping members, the existence of overlapping members in an obtained solution is not allowed from a practical point of view. The method proposed in Sect. 4 does not consider explicitly the constraint prohibiting presence of overlapping members. Nevertheless, in practice, a solution obtained by the proposed method often has no overlapping members, as illustrated through numerical experiments in Sect. 6.

Within the framework of MISOCP, we can explicitly incorporate the constraints prohibiting the presence of mutually overlapping members in a truss design. To do this, besides $\varvec{s} \in \{0,1 \}^{l}$ in Sect. 3.2, we use additional binary variables $\varvec{t}\in \{ 0,1 \}^{m}$ to indicate whether each member vanishes or exists. Namely, $t_{i}=0$ means that member i is removed, while $t_{i}=1$ means that member i exists. The relationship between $t_{i}$ and $x_{i}$ is given by

$$\begin{aligned} 0 \le x_{i} \le M t_{i} \end{aligned}$$

where $M>0$ is a sufficiently large constant. Recall that I(j) denotes the set of indices of members connected to node j; see Sect. 4. The relationship between $t_{i}$ $(i \in I(j))$ and $s_{j}$ is given by

$$\begin{aligned} t_{i} \le s_{j}, \quad \forall i \in I(j). \end{aligned}$$

Let D denote the set of pairs of indices of members that mutually overlap. Namely, $(i_{1},i_{2}) \in D$ means that member $i_{1}$ and member $i_{2}$ cannot exist simultaneously. This constraint is written as

$$\begin{aligned} t_{i_{1}} + t_{i_{2}} \le 1, \quad \forall (i_{1},i_{2}) \in D. \end{aligned}$$

The upshot is that the truss topology optimization problem can be formulated as the following MISOCP problem:

$$\begin{aligned}\mathop {\mathrm {Minimize}}&{\quad } \sum _{i=1}^{m} w_{i} \end{aligned}$$

(24a)

$$\begin{aligned} \mathop {\mathrm {subject}}\,{\mathrm {to}}&\quad w_{i} + x_{i} \ge \left\|\left[\begin{array} {l} w_{i} - x_{i} \\ 2\sqrt{c_{i} / E} q_{i} \\ \end{array} \right]\right\| , \quad i=1,\dots ,m, \end{aligned}$$

(24b)

$$\begin{aligned}& \sum _{i=1}^{m} q_{i} \varvec{b}_{i} = \varvec{p}, \end{aligned}$$

(24c)

$$\begin{aligned}& \varvec{c}^{\top } \varvec{x} \le V , \end{aligned}$$

(24d)

$$\begin{aligned}& \varvec{x} \le M \varvec{t}, \end{aligned}$$

(24e)

$$\begin{aligned}& t_{i} \le s_{j} \ (\forall i \in I(j)), \quad j=1,\dots ,l, \end{aligned}$$

(24f)

$$\begin{aligned}& \mathbf{} \varvec{s} \ge {\mathbf{0}}, \end{aligned}$$

(24g)

$$\begin{aligned}& \sum _{j=1}^{l} s_{j} \le n, \end{aligned}$$

(24h)

$$\begin{aligned}& t_{i_{1}} + t_{i_{2}} \le 1, \quad \forall (i_{1},i_{2}) \in D, \end{aligned}$$

(24i)

$$\begin{aligned}& \varvec{t} \in \{ 0,1 \}^{m}. \end{aligned}$$

(24j)

It is worth noting that the binary constraints on $s_{1},\dots ,s_{k}$ can be omitted.

6 Numerical experiments

In this section, we report on numerical experiments on the method presented in Sect. 4. In Sect. 6.1, we describe implementation details of the algorithm and the problem settings of the numerical experiments. The computational results of the proposed ADMM approach, together with a comparison with the MISOCP approach, are presented in Sects. 6.2, 6.3, and 6.4. Empirical evidences of our stopping criterion and selection of initial points are presented in Sects. 6.5 and 6.6, respectively. Section 6.7 presents an application of the proposed method to robust truss optimization, which is recast as a mixed-integer semidefinite programming problem.

6.1 Implementation and problem settings

At each iteration of the proposed method, we solved problem (22) by using CVX ver. 2.1, a MATLAB package for specifying and solving convex optimization problems (Grant and Boyd 2008, 2016). As a solver, we used SDPT3 ver. 4.0 (Tütüncü et al. 2003) on MATLAB ver. 9.1.0. The cvx_precision of CVX is set to best, which means that the solver continues as long as it can make progress (Grant and Boyd 2016). For comparison, we solved the MISOCP problem in (15) with a global optimization approach. The value of M in constraint (15f) is set to $1.0\times 10^5$ in $\mathrm {m}$.⁶ We used PICOS ver. 1.1.2, a Python interface to diverse optimization solvers (Sagnol 2017). MOSEK ver. 8.0.1 (Andersen et al. 2003) was used as the solver. Computation was carried out on two $3.2\,\mathrm {GHz}$ Intel Xeon E5-2667 v4 processors with $256\,\mathrm {GB}$ RAM.

In practice, we slightly modify the original version of ADMM introduced in Sect. 2 so that the penalty parameter in the augmented Lagrangian is gradually increased. Specifically, $\rho$ in subproblem (22) is given by

$$\begin{aligned} \rho _{k+1}:= \min \{ \mu \rho _{k}, \rho _{\mathrm {max}} \}, \end{aligned}$$

where $\mu$ ($>1$) and $\rho _{\mathrm {max}}$ $(>\rho _{0})$ are constants. In the following, we set $\mu =1.5$, $\rho _{0}=1$, and $\rho _{\mathrm {max}}=10^{6}$. Define $J_{0}^{k} \subseteq \{ 1,\dots ,l \}$ by

$$\begin{aligned} J_{0}^{k} = \{ j \in \{ 1,\dots ,l \} \mid z_{j}^{k} \le \epsilon \} , \end{aligned}$$

where we set $\epsilon = 0.1\,\mathrm {mm^{2}}$. We terminate the ADMM when

$$\begin{aligned} l - |J_{0}^{k}| \le n \end{aligned}$$

is satisfied. Then we solve problem (11) with the additional constraints

$$\begin{aligned} \sum _{i \in I(j)} x_{i} = 0, \quad \forall j \in J_{0}^{k} \end{aligned}$$

to generate the final output. As for the initial point for the ADMM, we examine two cases:

• Initial point (A): $\varvec{z}^{0} := Z \varvec{x}^{{0}}$ and $\varvec{v}^{0} := {{\bf 0}}$, where $\varvec{x}^{{0}}$ is an optimal solution of problem (11).

• Initial point (B): $\varvec{z}^{0} := Z \varvec{x}^{0}$ and $\varvec{v}^{0} := {{\bf 0}}$ with $\varvec{x}^{0} := (V / \varvec{c}^{\top } {{\bf 1}}) {{\bf 1}}$.

It should be clear that only $\varvec{z}^{0}$ and $\varvec{v}^{0}$ are used as input data of the ADMM; $\varvec{x}^{0}$ is not required as input.

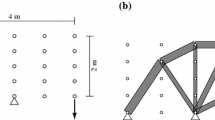
Consider the problem setting shown in Fig. 3. The nodes are aligned on a $1\,\mathrm {m} \times 1\,\mathrm {m}$ grid. We vary the values of $N_{X}$ and $N_{Y}$ to generate problem instances with diverse sizes. The number of free nodes in this ground structure is $N_{X}(N_{Y}+1)$. The members in a ground structure are generated as follows: We first consider all possible members such that any two nodes are connected by a member. Then, we remove members that are longer than a specified value, $5\,\mathrm {m}$ in Sects. 6.2 and 6.3 and $7\,\mathrm {m}$ in Sect. 6.4. It is worth noting that the ground structure retains overlapping members.

In the following examples, the Young modulus is $E=20\,\mathrm {GPa}$, and the specified upper bound for the structural volume is $V=2 N_{X} N_{Y} \times 10^{5}\,\mathrm {mm^{3}}$. As for $\varvec{p}$, the external vertical force of $100\,\mathrm {kN}$ is applied to the bottom rightmost node. Let n be the upper bound on the number of free nodes. In other words, the number of supports is not restricted in the following examples, and l in the previous sections denotes the number of free nodes of a ground structure.

6.2 Example (I)

Table 1 Characteristics of the problem instances for the numerical experiments

Table 2 Computational results of example (I)

Fig. 3

The problem setting for numerical experiments with $(N_{X},N_{Y})=(5,2)$

Fig. 4

Example (I). The optimal solutions of the compliance minimization problem (without the cardinality constraint). a $(N_{X},N_{Y})=(5,2)$; b $(N_{X},N_{Y})=(5,3)$; and c $(N_{X},N_{Y})=(5,4)$

Fig. 5

Example (I). The solutions obtained by the proposed method for the compliance minimization problem with the cardinality constraint ($n=4$). a $(N_{X},N_{Y})=(5,2)$; b $(N_{X},N_{Y})=(5,3)$; and c $(N_{X},N_{Y})=(5,4)$

Fig. 6

Example (II). The optimal solutions of the compliance minimization (without the cardinality constraint). a $(N_{X},N_{Y})=(8,2)$; b $(N_{X},N_{Y})=(9,2)$; c $(N_{X},N_{Y})=(8,4)$; d $(N_{X},N_{Y})=(9,4)$; e $(N_{X},N_{Y})=(8,6)$; and f $(N_{X},N_{Y})=(9,6)$

Fig. 7

Example (II). The solutions obtained by the ADMM for the compliance minimization problem with the cardinality constraint ($n=5$). a $(N_{X},N_{Y})=(8,2)$; b $(N_{X},N_{Y})=(9,2)$; c $(N_{X},N_{Y})=(8,4)$; d $(N_{X},N_{Y})=(9,4)$; e $(N_{X},N_{Y})=(8,6)$; and f $(N_{X},N_{Y})=(9,6)$

Fig. 8

Example (II). The optimal solutions obtained from the MISOCP formulation for the compliance minimization problem with the cardinality constraint ($n=5$). a $(N_{X},N_{Y})=(8,2)$; b $(N_{X},N_{Y})=(9,2)$; c $(N_{X},N_{Y})=(8,4)$; d $(N_{X},N_{Y})=(9,4)$; e $(N_{X},N_{Y})=(8,6)$; and f $(N_{X},N_{Y})=(9,6)$

In this section, we set the upper bound for the existing free nodes to $n=4$. As for problem instances, we consider $(N_{X},N_{Y})=(5,2)$, (5, 3), and (5, 4) in Fig. 3. Figure 4 shows the optimal solutions⁷ of the conventional compliance minimization without the constraint on the number of nodes, i.e., problem (11), where the width of each member is proportional to its cross-sectional area. Table 1 reports the optimal values, denoted $\hat{w}$, the number of members (m), and the number of degrees of freedom of the nodal displacements (d). As mentioned in Sect. 5, the intermediate nodes on a chain in Fig. 4 can be removed without changing the objective value. After this hinge cancellation procedure, the numbers of free nodes in Fig. 4a–c become 9, 7, and 5, respectively, as listed in Table 1.

Figure 5 shows the solutions obtained by the proposed ADMM for the problem with the limited number of free nodes. In Fig. 5b we see that the number of free nodes is 3 $(<n)$. It should be clear that $\varvec{x}^{0}$ used to generate initial point (A) for the ADMM is in general different from the one in Fig. 4, because $\varvec{x}^{0}$ is computed from the ground structure involving the overlapping members. Indeed, $\varvec{x}^{0}$ for $(N_{X},N_{Y})=(5,2)$, (5, 3), and (5, 4) have 12, 15, and 13 free nodes, respectively. Thus, the number of nodes is decreased successfully by the proposed method. It is observed that the solutions in Fig. 4a, b have too many members from a practical point of view. In contrast, we can see in Fig. 5a, b that the number of members is decreased as a result of optimization with the limitation of the number of nodes. The computational results of the ADMM are listed in Table 2, where $w^{*}$ is the objective value of the obtained solution, “#iter.” is the number of iterations required before convergence, and “time” is the computational time. As mentioned before, we examine two different values, denoted (A) and (B), for $\varvec{z}^{0}$ and $\varvec{v}^{0}$. The one which yields the better objective value is indicated by “$*$.” It is observed in Table 2 that, for every instance, the objective value of the solution obtained by the ADMM approach is identical to the optimal value of the problem without the limitation of the number of nodes (i.e., problem (11)). Since problem (11) can be regarded as a relaxation problem, the solutions obtained by the proposed ADMM are globally optimal. This also illustrates that, in general, the compliance minimization of a truss has more than one optimal solution, and the optimal solutions may have different numbers of nodes.

For comparison, we also solved the MISOCP problem (15) with a global optimization approach. Table 2 lists the obtained results,⁸ where $\bar{w}$ is the objective value. The solutions obtained by the MISOCP solver are identical to the ones obtained by the ADMM approach.

Table 3 Computational results of example (II)

6.3 Example (II)

As for instances with larger sizes, consider N _X , N _Y = (8,2), (9,2), (8,4), (9,4), (8,6), and (9, 6). In this section, we set the upper bound for the number of free nodes to $n=5$.

6.3.1 Results

Figure 6 collects the optimal solutions without limiting the number of nodes. The number of free nodes after applying hinge cancellation is reported in Table 1. Figure 7 shows the solutions obtained by the ADMM approach. The number of free nodes in Fig. 7e is 4 ($<n$). Two nodes can be removed from the solution in Fig. 7a, which results in a truss design with three free nodes. It is observed in Figs. 6 and 7 that the limitation of the number of nodes often yields a solution with fewer members. Also, very thin members are observed in Fig. 6, while such thin members do not appear in Fig. 7. These two features of the solutions in Fig. 7 are considered practically preferable. The initial design $\varvec{x}^{0}$ used for generating initial points (A) for the ADMM to solve $(N_{X},N_{Y})=(8,2)$, $(9,2),\dots ,(9,6)$ have 20, 18, 19, 20, 24, and 26 free nodes, respectively.

It is observed in Table 3 that the ADMM terminates after at most 20 iterations. The increase of the objective value over the optimal value of the problem without the cardinality constraint is quite small, i.e., the increase by at most about 10%. Particularly, for $(N_{X},N_{Y})=(8,4)$ and (9, 4) we have only about a 1% increase. Thus, it is often the case that the number of nodes can be reduced at the expense of only a small increase of the compliance.

The computational results of the MISOCP approach are listed in Table 3. Figure 8 collects the obtained solutions. For $(N_{X},N_{Y})=(8,4)$, the solution obtained by MISOCP is identical to the one obtained by the ADMM; i.e., the ADMM found a global optimal solution. For $(N_{X},N_{Y})=(9,4)$, it is observed in Table 3 that the objective values obtained by the two methods are almost the same, but the two solutions are slightly different as seen in Fig. 7d and 8d. The largest value of $w^{*}/\bar{w}$ is 1.072 in the case of $(N_{X},N_{Y})=(8,2)$. It is also worth noting that, for $(N_{X},N_{Y})=(8,6)$ and (9, 6), although the global optimal solutions in Fig. 8e, f involve very thin members, the solutions obtained by the ADMM shown in Fig. 7e, f do not have such a thin member.

It is observed from Table 3 that the proposed ADMM often converges more quickly than the MISOCP solver; exceptions are $(N_{X},N_{Y})=(8,4)$ and (9, 4). The computational time required by the MISOCP solver varies drastically depending on the problem instances. In contrast, the number of iterations required by the ADMM is almost independent of the problem instances. Since the computation time required for solving the SOCP subproblem of the ADMM depends on the problem size, it is possible to roughly estimate the total computational cost of the ADMM from the problem size. This might be considered one of advantages of ADMM over MISOCP.

As mentioned in Sect. 5, the proposed method does not incorporate a constraint prohibiting overlapping members. Nevertheless, for the problems with limitation of the number of nodes, all the solutions obtained in Sect. 6 do not involve overlapping members.

6.3.2 MISOCP with slenderness constraints

Constraints preventing the presence of very thin members observed in Fig. 8e, f can be handled within the framework of mixed-integer programming (MIP) (Kanno and Yamada 2017). Recall problem (24) in Sect. 5, where $t_{i}$ is a binary variable indicating whether member i exists or vanishes. Let $x_{\mathrm {min}} > 0$ denote the specified lower bound for the member cross-sectional area. The constraint avoiding the existence of too-thin members, which we refer to as slenderness constraints, can be formulated as

$$\begin{aligned} x_{\mathrm {min}} \varvec{t} \le \varvec{x} \le M \varvec{t}. \end{aligned}$$

(25)

In problem (24), we replace constraint (24e) with (25). The constraint avoiding the presence of overlapping members, (24i), is not considered. We solve this MISOCP problem for the instances $(N_{X},N_{Y})=(8,6)$ and (9, 6) with $x_{\mathrm {min}}=200\,\mathrm {mm^{2}}$. The obtained solutions are shown in Fig. 9. Both solutions have parallel consecutive members that are connected by nodes supported only in the direction of those members. The intermediate nodes can be removed without changing the optimal value. Hence, the number of free nodes of these solutions is essentially two. The objective value of the solution for $(N_{X},N_{Y})=(8,6)$ is 3168.97 J, which is slightly less than that for the case without the slenderness constraints in Table 3. This is due to computational error in computing the objective value via the finite element method. In the solution shown in Fig. 7e, i.e., in the solution obtained by the ADMM without the slenderness constraints, the cross-sectional area of the thinnest member is $75.4\,\mathrm {mm^{2}}$. Hence, this solution is not globally optimal under the slenderness constraint. The computational time required by MOSEK is 365.0 s. The objective value of the solution for $(N_{X},N_{Y})=(9,6)$ is 4028.94 J. This is larger than that for the case without the slenderness constraints as expected, and is less than that of the solution obtained by the ADMM. Since the cross-sectional area of the thinnest member of the solution shown in Fig. 7f is $146.7\,\mathrm {mm^{2}}$, Hence, the solution shown in Fig. 7f is not globally optimal under the slenderness constraints. The computational time required by MOSEK to find the solution in Fig. 9b was 1676.0 s, which is much larger than the computational time of the ADMM.

Fig. 9

The optimal solutions of example (II) with the constraints avoiding the presence of thin members. a $(N_{X},N_{Y})=(8,6)$; and b $(N_{X},N_{Y})=(9,6)$

6.4 Example (III)

Fig. 10

Example (III). The solutions obtained by ADMM for the compliance minimization problem with the cardinality constraint. a $(N_{X},N_{Y},n)=(12,6,6)$; b $(N_{X},N_{Y},n)=(13,6,6)$; and c $(N_{X},N_{Y},n)=(14,6,7)$,

Fig. 11

Example (III). The optimal solutions obtained by MISOCP for the compliance minimization problem with the cardinality constraint. a $(N_{X},N_{Y},n)=(12,6,6)$; b $(N_{X},N_{Y},n)=(13,6,6)$; and c $(N_{X},N_{Y},n)=(14,6,7)$

Consider problem instances $(N_{X},N_{Y},n)=(12,6,6), (13,6,6)$, and (14, 6, 7). The maximum member length in a ground structure is set to $7\,\mathrm {m}$.

Figure 10 shows the solutions obtained by the proposed ADMM approach. The ADMM terminates with a solution having n free nodes. One of these nodes vanishes in post-processing. The objective value as well as the computational cost is reported in Table 4.

Figure 11 collects the optimal solutions found by the MISOCP approach. These solutions use exactly n free nodes. It is observed from Table 4 that the objective value obtained by the ADMM for the largest instance, $(N_{X},N_{Y},n)=(14,6,7)$, is very close to the optimal value. In contrast, for $(N_{X},N_{Y},n)=(13,6,6)$ the objective value obtained by the ADMM is more than 20% larger than the optimal value. However, the computational cost of the ADMM is much less than the MISOCP approach (which requires more than four hours). Thus, the quality of the solution obtained by the ADMM approach can possibly be very good, although in general it depends on problem instances. As the problem size increases, the computational cost of the ADMM approach becomes much smaller compared with the MISOCP approach.

Table 4 Computational results of example (III)

6.5 On heuristic for stopping ADMM

Table 5 The computational results when the ADMM is run until convergence to evaluate effectiveness of the heuristic stopping criterion

As mentioned in Sect. 6.1, we use a heuristic criterion for stopping the ADMM. Namely, we stop the ADMM when the cardinality constraint is satisfied with $\epsilon$ tolerance. Then, as post-processing, we solve the compliance minimization problem, (11), specifying the set of vanishing nodes. This section presents some empirical justification for this procedure. Namely, it is illustrated through numerical experiments that with this heuristic procedure the number of subproblems to be solved is drastically reduced, without missing out solutions having better objective values. We use the problem instances in Sect. 6.3.

We performed the following experiment. The ADMM is run until it terminates with a small tolerance, namely, $\Vert \varvec{x}^{k+1} - \varvec{x}^{k} \Vert \le 10^{-1}$ (in $\mathrm {mm}^{2}$) is satisfied. This requires many more iterations than the procedure described above. In the iteration history, we select every iterate that satisfies the cardinality constraint, i.e., that satisfies $l-|J_{0}^{k}| \le n$. For every selected iterate, we run the post-processing, i.e., we solve problem (11), specifying the set of vanishing nodes.

The computational results are listed in Table 5, where $\tilde{K}$ and $\tilde{K}_{\mathrm {p}}$ are the number of iterations required before convergence and the number of iterates that approximately satisfy the cardinality constraint, respectively. For all the $\tilde{K}_{\mathrm {p}}$ iterates, the post-processing yields the same solution as the one reported in Table 3. In the case $(N_{X},N_{Y},n)=(9,2,5)$ with initial point (A), the ADMM does not converge after 100 iterations. In this iteration history, there exist 77 iterates satisfying the cardinality constraint approximately. From all of them, the post-processing generates the solution reported in Table 3. In a nutshell, the set of vanishing nodes does not change, even if the ADMM iterations are continued after the iterate at which our heuristic stopping criterion is satisfied.

For ease of comparison, the number of iterations reported in Table 3 is listed again as $K^{*}$ in Table 5. Our stopping criterion reduces the number of iterations from $\tilde{K}$ to $K^{*}$, without changing the final output. It is worth noting that the solutions found between the $(K^{*}+1)$th iteration and the $\tilde{K}$th iteration do not necessarily satisfy the cardinality constraint within an $\epsilon$-tolerance.

6.6 On choice of initial points

Table 6 Computational results of ADMM from randomly generated initial points

Since we apply an ADMM to a nonconvex problem, the obtained solution may depend on the choice of initial points. In Sect. 6.1, we suggested using two initial points, (A) and (B), and adopt the better solution as the final output. In this section, we perform comparison with the results obtained by using randomly generated initial points to empirically justify our selection. As for two representative instances for which initial points (A) and (B) lead to different solutions, we use $(N_{X},N_{Y},n)=(5,3,4)$ in Sect. 6.1 and $(N_{X},N_{Y},n)=(9,4,5)$ in Sect. 6.2 in the following numerical experiments.

As for randomly generated initial points, we examine two cases:

• Initial point (C): $\varvec{x}^{0} := (V / \varvec{c}^{\top } \varvec{\xi }) \varvec{\xi }$, $\varvec{z}^{0} := Z \varvec{x}^{0}$, and $\varvec{v}^{0} := Z \varvec{x}^{0} - \varvec{z}^{0} = \bf{0}$, where $\varvec{\xi }\in \mathbb {R}^{m}$ is a random vector with entries independently drawn from $\mathcal {U}(0,1)$.

• Initial point (D): $\varvec{x}^{0} := (V / \varvec{c}^{\top } \varvec{\xi }) \varvec{\xi }$, $\varvec{z}^{0} := Z \varvec{x}^{0}$, and $\varvec{v}^{0} := \max \{ z_{1}^{0},\dots ,z_{l}^{0} \} \varvec{\zeta }$, where $\varvec{\xi }\in \mathbb {R}^{m}$ and $\varvec{\zeta } \in \mathbb {R}^{l}$ are random vectors with entries independently drawn from $\mathcal {U}(0,1)$.

We generate 100 samples of each of these initial points, and run our ADMM approach from every sample. Table 6 reports the minimum value, maximum value, mean, and variance of the objective value.

For $(N_{X},N_{Y},n)=(5,3,4)$ with initial point (C), in all the cases the ADMM converges to the same solution. This solution is the one obtained by using initial point (B), as shown in Table 2. Therefore, using initial point (A) yielded a better solution (which is globally optimal) than using 100 samples of (C). In contrast, when initial point (D) was adopted, the global optimal solution is obtained from 7 sampled initial points, among 100 trials. From the other 93 samples, the ADMM converges to the solution obtained with initial point (B). The mean and the variance of the objective value are listed in Table 6. In this manner, it is demonstrated that the global optimal solution, easily obtained by carrying out our ADMM procedure with initial point (A), is rarely obtained from randomly generated initial points.

For $(N_{X},N_{Y},n)=(9,4,5)$ with initial point (C), the best solution is the same as the one obtained from initial point (B) in Table 3. This is not globally optimal. Among 100 trials, 67 sampled initial points yield this solution. In contrast, the objective value of the worst solution is larger than the one obtained from initial point (A). By using initial point (D), the variance of the objective value increased, but the global optimal solution was not obtained. Thus, the ADMM with randomly generated initial points could not find a solution better than the one obtained from initial point (B).

In short, for these two problem instances, using many randomly generated initial points does not yield a better solution. Therefore, using initial points (A) and (B) might be considered a reasonable selection.

6.7 Application to robust optimization against uncertainty in external load

Table 7 Computational results of the robust optimization problem with the cardinality constraint

The ADMM approach presented in this paper can easily be extended to the case in which the external load possesses uncertainty. The set of nodes at which the external forces can possibly be applied is supposed to be specified. Then we consider the robust optimization against the uncertainty, under the upper bound constraint on the number of nodes. In this section, we examine the efficiency of the ADMM applied to this problem, as an example of optimization problems that are not handled with current mainstream MIP solvers. The computation in this section was carried out on a 2.2 GHz Intel Core i5 processor with 8 GB RAM.

As a concrete instance, consider the problem setting shown in Fig. 3. The external force is applied at the bottom right node, but this time its direction and magnitude are assumed to be uncertain. Without loss of generality, let $p_{1}$ and $p_{2}$ denote the horizontal and vertical components, respectively, of this external force. The set of possible realizations of the external load is defined by

$$\begin{aligned} P = \{ (p_{1},p_{2},0,\dots ,0)^{\top } \mid p_{1} = p^{0}_{1} \psi _{1}, \ p_{2} = p^{0}_{2} \psi _{2}, \ \Vert (\psi _{1},\psi _{2}) \Vert \le 1 \}, \end{aligned}$$

where $p^{0}_{1}=30\,\mathrm {kN}$ and $p^{0}_{2}=100\,\mathrm {kN}$. With referring to (10), we see that the compliance in the worst case is given by

$$\begin{aligned} \hat{\pi }(\varvec{x}) = \sup \{ 2 \varvec{p}^{\top } \varvec{u} - \varvec{u}^{\top } K(\varvec{x}) \varvec{u} \mid \varvec{u} \in \mathbb {R}^{d}, \ \varvec{p} \in P \}. \end{aligned}$$

In the following, we consider the minimization problem of this function.

When the constraint on the number of nodes is not considered, it is known that this optimization problem can be recast as semidefinite programming (SDP) (Ben-Tal and Nemirovski 1997). Since the upper bound constraint on the number of nodes is treated as presented in Sect. 3.2, the optimization problem under this constraint can be recast as mixed-integer semidefinite programming (MISDP). For comparison, we solve this MISDP problem with YALMIP (Löfberg 2004), which finds a global optimal solution with a branch-and-bound method (Löfberg 2004). We used YALMIP with the default setting, in which SDP subproblems are solved with SeDuMi ver. 1.3 (Pólik 2005; Sturm 1999). Alternatively, consider the problem obtained by replacing the objective function of (14) by $\hat{\pi }$. It is fairly straightforward to apply the ADMM in Sect. 4 to this optimization problem. The subproblem solved to update the variable $\varvec{x}$ at each iteration is formulated as SDP.

Table 7 reports the computational results. For five instances, $(N_{X},N_{Y},n)=(5,2,4)$, (5, 3, 4), (5, 4, 4), (8, 4, 5), and (9, 4, 5), the ADMM approach found the global optimal solutions. In all these cases, the computational cost of the ADMM is smaller than that of YALMIP. The difference of computational cost increases as the problem size increases. For $(N_{X},N_{Y},n)=(9,6,5)$, YALMIP did not terminate after 300 iterations. The best solution is the same as the one found by the ADMM with initial point (A), but a better solution was found by the ADMM with initial point (B). For three instances, $(N_{X},N_{Y},n)=(8,2,5)$, (9, 2, 5), and (8, 6, 5), the solutions found by the ADMM are not optimal. The difference between the obtained objective value and the optimal value is 7% or less, like in the cases in Sect. 6.3. The computational time required by YALMIP is more than 10 times (in some cases, more than 100 times) larger than that of the ADMM. Figure 12 collects the solutions obtained by the ADMM. The global optimal solutions that could not be obtained by the ADMM are shown in Fig. 13. The set of nodes in Fig. 12d is much different from that in Fig. 13a. The solution in Fig. 12e has only one node that is not included in the solution in Fig. 13b. Similarly, the difference between the solutions in Figs. 12h and 13c is the location of one node.

Figure 14 shows the solutions obtained by the ADMM for problem instances with larger sizes. The computational results are listed in Table 8. A global optimization method, YALMIP, cannot solve these problems within a reasonable amount of time.

Fig. 12

The solutions obtained by the ADMM applied to the robust optimization problem. a $(N_{X},N_{Y},n)=(5,2,4)$; b $(N_{X},N_{Y},n)=(5,3,4)$; c $(N_{X},N_{Y},n)=(5,4,4)$; d $(N_{X},N_{Y},n)=(8,2,5)$; e $(N_{X},N_{Y},n)=(9,2,5)$; f $(N_{X},N_{Y},n)=(8,4,5)$; g $(N_{X},N_{Y},n)=(9,4,5)$; h $(N_{X},N_{Y},n)=(8,6,5)$; and i $(N_{X},N_{Y},n)=(9,6,5)$

Fig. 13

The optimal solutions of the robust optimization problem obtained by YALMIP. a $(N_{X},N_{Y},n)=(8,2,5)$; b $(N_{X},N_{Y},n)=(9,2,5)$; and c $(N_{X},N_{Y},n)=(8,6,5)$

Fig. 14

The solutions obtained by ADMM for the large-scale robust optimization problems. a $(N_{X},N_{Y},n)=(12,6,6)$; b $(N_{X},N_{Y},n)=(13,6,6)$; c $(N_{X},N_{Y},n)=(14,6,7)$;

Table 8 Computational results of the ADMM approach applied to the robust optimization problem with the cardinality constraint

7 Conclusions

In this paper, we have studied the compliance minimization of a truss with a limited number of nodes. It has been shown that this optimization problem can be formulated as a cardinality-constrained SOCP problem. We have proposed a simple and efficient heuristic based on an ADMM.

The problem considered in this paper can also be formulated as an MISOCP problem involving the so-called big-M. In the numerical experiments, we compared the proposed ADMM approach with a global optimization approach using this MISOCP formulation. For small-size problem instances, it has been confirmed that the ADMM can find a global optimal solution. For middle-size instances, the objective value of the solution obtained by the ADMM is often close to the optimal value. The number of iterations of the ADMM is almost the same for instances with different sizes. In contrast, the computational cost required by a standard MISOCP solver depends strongly on instances, even if the instances have similar sizes.

In the numerical experiments, it has also been illustrated that, for some problem instances, the compliance minimization problem of a truss has some different optimal solutions, and the number of nodes can be decreased without losing optimality. In most other cases, the number of nodes can be decreased at the expense of only a small increase of the compliance.