1 Introduction

In truss design, member strength and stability considerations form the basis of structural integrity. Members in compression are most likely to buckle before reaching their compression strength. Therefore, in optimization, member buckling should be included in the problem formulation.

Typically in truss optimization, cross-sectional areas of the members are taken as design variables. However, as the buckling strength of a member depends also on the shape of the cross-section, this information must be somehow provided. In particular, the second moment of area of the cross-section is needed in determining the buckling strength. For simple cross-sections such as circular or square, the second moment of area can be expressed exactly in terms of the cross-sectional area. In general, such a dependence cannot be derived. Then, the relation between the cross-sectional area and the second moment of area must be approximated, or more variables must be introduced to the problem in order to determine the correct buckling strength.

An elementary approach for taking member buckling into account is to set the allowable strength in compression to be some specified (constant) fraction of the tensile strength. This reduces the problem to one with unequal permissible stresses in tension and in compression, and no further modifications are needed for member buckling. However, choosing a constant lower bound for member stress is in general very difficult. Too tight a bound will lead to unnecessarily large members, and if the bound is too close to the tensile strength, compression members will most likely buckle in practice. Therefore, this approach does not provide a practical means for taking member buckling into account.

In truss topology optimization, incorporating buckling constraints in the problem induces severe difficulties, when the conventional ground structure approach (Dorn et al. 1964) using the nested analysis and design (NAND) formulation (Arora and Wang 2005) is employed. In the NAND formulation, the variables are the cross-sectional areas, and structural responses, such as displacements and stresses, are treated as implicit functions of the variables. They are evaluated by performing a structural analysis for given values of the variables.

The first observation on member buckling constraints is that they exhibit similar behaviour as stress constraints, that are known for making the feasible set non-convex and for inducing degenerated regions, where the optimum may lie (Cheng and Jiang 1992). For buckling constraints, the feasible set becomes even disjointed (Guo et al. 2001). These regions can be treated in the numerical solution process by the so-called 𝜖-relaxation approach (Guo et al. 2001), a technique adopted from similar idea for stress constraints (Cheng and Guo 1997). Even though the disjointness and degeneracy of the feasible set can be avoided, one still has to face the numerical difficulties related with non-convexity and choosing the parameter 𝜖. Furthermore, it has been shown for stress constraints, that this process may not be able to find the global optimum (Stople and Svanberg 2001).

Arguably the most severe difficulty related to member buckling constraints in topology optimization is the so-called jump in buckling length phenomenon, identified and illustrated by Zhou (1996). Optimum topologies often contain parallel and consecutive compression members that are connected by nodes supported only in the direction of the members. Such nodes are clearly kinematically unstable, i.e. the structure is actually a mechanism, even though it is in equilibrium with respect to the given loads. An intuitive approach is to remove the unstable nodes and to merge the members into a single longer member. This process is sometimes called hinge cancellation. However, the buckling strength of the resulting longer member is much lower than the buckling strengths of the shorter members. Consequently, the longer member is likely to violate the buckling constraint. In order to find kinematically stable solutions, Rozvany (1996) has proposed adding system stability constraints and imperfections to the problem, requiring that equilibrium is maintained if small displacements are introduced. As Rozvany points out, these techniques might not be sufficient for capturing the true optimum topology.

Achtziger (1999a) has proposed an elaborate formulation for buckling constraints, where so-called chains (consecutive members laying on a line) are employed to capture the correct buckling length of compression members. Separate constraints are written for ”simple” member buckling and topological buckling (buckling of a chain of members), the latter being more complicated than the former. Neglecting compatibility conditions, the formulation leads to a nearly linear problem that is solved by a sequential linear programming method (Achtziger 1999b) where the conditional topological buckling constraints are transformed into regular constraints by an approximation parameter. A numerical example shows that including topological stability leads to a different topology than the ”simple” buckling constraints.

Another approach for treating the jump in the buckling length phenomenon along with stability of solutions is proposed by Guo et al. (2005). Stability is enforced by exploiting the fact that an unstable truss has a zero critical load factor. By assigning a positive lower bound for the critical load factor, unstable topologies can be avoided. Evaluating this constraint requires the solution of the generalized eigenvalue problem of linear stability theory. The correct buckling length is captured by incorporating overlapping members in the ground structure. In several example problems, the proposed formulation is able to remove unnecessary overlapping members from the solution. However, there is no explicit mechanism for disallowing member overlapping, and in some of the example problems presented, member overlapping appears in the solution.

From the discussion above, it can be concluded that while the importance of buckling constraints has been acknowledged and they have been addressed by several researchers, there is still a need for more rigorous approach. In this study, the ideas of chains and overlapping members are employed and a new formulation for truss topology optimization with member buckling constraints is presented. It is assumed that the member cross-sections are selected from a finite set of discrete alternatives. The approach relies on a mixed variable problem formulation, where member forces and nodal displacements are the continuous state variables, whereas member and node existence as well as cross-section selection are handled by binary variables (Ghattas and Grossmann 1991; Grossmann et al. 1992; Ohsaki and Katoh 2005; Rasmussen and Stolpe 2008). Following the principles of the simultaneous analysis and design (SAND) approach (Arora and Wang 2005), the equations of structural analysis are written as constraints. Within this formulation, member buckling constraints become simple linear constraints. The correct buckling length is captured by identifying chains of members, adding overlapping members between each pair of nodes that belong to a chain, and writing buckling constraints for all added members. Linear constraints are written for the binary variables controlling member existence to disallow impractical topologies.

The formulation is also employed for sizing of the so-called stiffening members, i.e. members that are used to reduce the buckling length of compression members. Typically, the stiffening members do not carry any applied load, so they can be assigned with the smallest available profile. However, as noted by Rozvany (1996), in practice, the smallest profile would lead to too slender stiffening members that would fail to support the compression member. A simplified approach is proposed for this issue.

The formulation leads to a mixed-integer linear programming (MILP) problem, which can be solved by any general-purpose software. As there are no singularities and only linear expressions are used, the formulation does not suffer from any difficulties related to vanishing members, and no special solution techniques are needed. Furthermore, due to linearity of the formulation, moderate-sized discrete truss topology optimization problems can be solved to global optimum using deterministicmethods.

A further benefit that increases the practicality of the proposed formulation is that not only the conventional Euler buckling constraints, but also more complicated buckling constraints derived from design codes can be incorporated in the problem. In this paper, buckling constraints for steel trusses according to Eurocode 3 (EN 1993–1–1 2005) are presented in detail.

The paper is organized as follows. In Section 2, the framework for mixed variable formulation is presented. Then, the notation and constraints related to chains are introduced in Section 3. Member buckling constraints are written in Section 4. The approach is demonstrated on example problems in Section 5. Finally, the paper is summarized in Section 6.

2 Mixed variable formulation

The proposed approach employs binary variables that control the existence of ground structure members and nodes. A suitable problem formulation, based on the SAND approach, for these variables has been introduced by Ghattas and Grossmann (1991), see also Grossmann et al. (1992). The idea is to include the equations of structural analysis as constraints in the problem, and to use member forces and nodal displacements as state variables. The stiffness equation is disaggregated such that the compatibility conditions and Hooke’s law are written for each member separately, and member forces are coupled by nodal equilibrium equations. The main benefit of this formulation is that vanishing members cause no singularities or degenerate regions to the feasible set. For continuous member areas, the approach leads to a mixed-integer nonlinear problem (Stolpe 2004; Ohsaki and Katoh 2005), but for discrete cross-sections, a mixed-integer linear problem is obtained (Rasmussen and Stolpe 2008). In the present study, the latter formulation is employed.

In the following, the mixed variable framework for truss topology optimization is briefly presented. The details can be found, for example, in Rasmussen and Stolpe (2008).

2.1 Basic formulation

Suppose the member cross-sections are to be chosen from a discrete set of n S alternatives. The cross-sectional area of alternative j is denoted \(\hat {A}_{j}\). Denote the index set of members of the ground structure \(\mathcal {M} = \{1, 2, \ldots , n_{E}\}\). The set of ground structure nodes is \(\mathcal {N} = \{1, 2, \ldots , n_{N}\}\). The set of loading conditions is \(\mathcal {L} = \{1, 2, \ldots , n_{L}\}\), and the set of available profiles is \(\mathcal {P} = \{1, 2, \ldots , n_{S}\}\).

Member cross-section is selected by the binary variable y i j , which takes the value 1, if profile j is chosen for member i and 0 otherwise. Binary variables y i , \(i\in \mathcal {M}\) control member existence: y i = 1 if member i is present and y i = 0 otherwise. Finally, binary variables z ℓ , \(\ell \in \mathcal {N}\) control the existence of nodes: if z ℓ = 1, then node ℓ is present in the truss and z ℓ = 0 otherwise.

The continuous state variables are member normal forces, \(N_{ij}^{k}\), and nodal displacements, u k, \(i\in \mathcal {M}\), \(j\in \mathcal {P}\), \(k \in \mathcal {L}\). The variable \(N_{ij}^{k}\) is the normal force of member i in load case k for profile j and u k is the vector of nodal displacements in load case k.

With these variables, the minimum weight problem with member strength constraints can be written as

$$\begin{array}{@{}rcl@{}} &\min \sum\limits_{i=1}^{n_{E}}\sum\limits_{j=1}^{n_{S}}\rho L_{i} \hat{A}_{j}y_{ij}\notag\\ & \text{such that} \qquad y_{i} = \sum\limits_{j=1}^{n_{S}} y_{ij} \quad \forall i\notag\\ & y_{i} \leq z_{\ell} \quad \forall\, \ell,\, i\ \in\mathcal{M}_\ell\notag\\ & {\underline{u}}_{r}z_{\ell} \leq u _{r}^{k} \leq {\overline{u}}_{r}z_{\ell} \quad \forall\, \ell,\,k\,,r\ \in\mathcal{D}_{\ell} \notag\\ & \frac{E_{i}}{L_{i}}\hat{A}_{j}\mathbf{b}^{T}_{i}\mathbf{u}^{k} - N_{ij}^{k} \leq (1-y_{ij}){\overline{N}}_{ij}^{k}\quad \forall\, i,\, j,\,k \notag\\ & \frac{E_{i}}{L_{i}}\hat{A}_{j}\mathbf{b}^{T}_{i}\mathbf{u}^{k} - N_{ij}^{k} \geq (1-y_{ij}){\underline{N}}_{ij}^{k}\quad \forall\, i,\, j,\,k\notag\\ & \hat{\mathbf{B}}\hat{\textbf{N}}^{k} = \mathbf{p}^{k} \quad \forall\, k\notag\\ & \min\left\{{\overline{N}}_{ij}^{k}, {\overline{\sigma}}\hat{A}_{j}\right\}y_{ij} \geq N_{ij}^{k} \quad \forall\, i,\, j,\,k\notag\\ & \max\left\{{\underline{N}}_{ij}^{k},-{\underline{\sigma}}\hat{A}_{j}\right\}y_{ij} \leq N_{ij}^{k}\quad \forall\, i ,\, j,\,k\notag\\ & y_{i}, y_{ij}, z_{\ell} \in \{0,1\} \end{array} $$
(P)

Unless otherwise stated, in all constraints, i ∈ ℳ, j ∈ 𝓟, and k ∈ 𝓛. The sets ℳℓ and 𝒟ℓ denote the members connected to the node ℓ and the global degrees of freedom of node ℓ, respectively.

In the above, ρ is the density of the material (assumed same for all members), L i , and E i are the length and Young’s modulus of member i, respectively, and b i is the i th column of the statics matrix of the ground structure. Furthermore, \(\textit {u}_{\ell }^{k}\) is the r th global nodal displacement in load case k. The displacement bounds u̲ r and u̅ r are used to compute the bounds for the force variables, \(\underline {N}_{ij}^{k}\) and \(\overline {N}_{ij}^{k}\):

$$ \underline{N}_{ij}^{k} = \frac{E_{i}\hat{A}_{j}}{L_{i}}\left(\sum\limits_{r: b_{ir}>0} b_{ir} \underline{u}_{r} + \sum\limits_{r: b_{ir}<0} b_{ir} \overline{u}_{r} \right) $$
(1)
$$ \overline{N}_{ij}^{k} = \frac{E_{i}\hat{A}_{j}}{L_{i}}\left(\sum\limits_{r: b_{ir}>0} b_{ir} \overline{u}_{r} + \sum\limits_{r: b_{ir}<0} b_{ir} \underline{u}_{r} \right) $$
(2)

where b i r are the components of the vector b i . The global load vector of loading condition k is p k, and \(\hat {\mathbf {B}}\) and \(\hat {\mathbf {N}}^{k}\) are the extended statics matrix and force variable vector, respectively. For the derivation of these bounds and the formulation above, see Rasmussen and Stolpe (2008).

Problem P differs from the formulation proposed byRasmussen and Stolpe (2008) in binary variables. Rasmussen and Stolpe (2008) use only the variables y i j , whereas here, also variables y i and z ℓ are employed. Consequently, the first three constraints of Problem P are different from similar constraints by Rasmussen and Stolpe (2008). The first constraint guarantees a unique profile for each member. Note that if y i = 0, then by this constraint, y i j = 0 for all \(j\in \mathcal {P}\). The second constraint states that if node ℓ is removed, then all members connected to that node must also vanish. The third constraint relates the displacements of node ℓ to its binary variable z ℓ : if z ℓ = 0, then the corresponding nodal displacements must be zero as well.

Problem P is a mixed-integer linear programming (MILP) problem. Several commercial and freely available computer programs are available for solving MILP problems. The most successful solution approach implemented in most programs is the branch-and-cut method, where cutting planes and valid inequalities are added to the well-known branch-and-bound framework (Wolsey 1998). In the following, Problem P is appended by various constraints. From the computational point of view it is crucial that the problem formulation remains linear. Fortunately, all the subsequent constraints are linear.

2.2 Kinematic stability

A common problem in truss topology optimization is that the optimum solution in equilibrium with respect to the given loads, but is kinematically unstable, i.e. a mechanism. Using the binary variables of the mixed variable formulation, constraints preventing kinematically unstable structures can be written.

The necessary condition for kinematic stability can be stated as

$$ N_{y} + N_{R} \geq N_{D}N_{c} $$
(3)

where N y , N R , and N c are the number of members, support reactions, and nodes, respectively. Furthermore, N D is the dimension of the truss (N D = 2 or N D = 3). In terms of the binary variables, this condition can be written as

$$ \sum\limits_{i=1}^{n_{E}} y_{i} + \sum\limits_{s \in \mathcal{N}_{S}} R_{s}z_{s} \geq N_{D}\sum\limits_{\ell=1}^{n}z_{\ell} $$
(4)

where \(\mathcal {N}_{S}\subseteq \mathcal {N}\) is the set of supported nodes and R s is the number of support reactions at the supported node s.

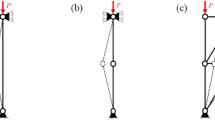
The necessary condition does not guarantee that the solution is kinematically stable, but it will disallow a large number of topologies that are mechanisms. In order to ensure kinematic stability, a method resembling the approach proposed by Faustino et al. (2006) (see also Kanno and Guo 2010) is employed in the present study. The idea is to include an additional loading condition in the problem, where all unsupported nodes of the ground structure are loaded by small predefined loads (Fig. 1a), and to require that the structure is in equilibrium with respect to these loads. The nodal variables z ℓ are used to control the presence of these auxiliary loads in the equilibrium equations of the supplementary loading condition, and the member forces in this loading condition are introduced as continuous variables to the problem. Compatibility conditions of the auxiliary loading condition are neglected.

Fig. 1
figure 1

Auxiliary loads. The truss must be in equilibrium with respect to the forces \(\tilde {p}_{ij}\). If a node is removed, the corresponding loads vanish as well

Full size image

Denote by 𝒟 ℓ . Then, the auxiliary loads for this node are

$$ \tilde{p}_{j} = \tilde{p}_{j\ell}z_{\ell} \quad j \in \mathcal{D}{\ell} $$
(5)

where \(\tilde {p}_{j\ell } > 0\) are predefined values for the loads. Essentially, any values can be given to the \(\tilde {p}_{j\ell }\), but they should be small enough such that neither strength nor buckling constraints of any member become active. In order to minimize the possibility that the structure is a mechanism but in equilibrium with respect to the auxiliary loads, the resultant force of the load components at a node should not be parallel to any of the members connected to that node, and all \(\tilde {p}_{j\ell }\) are chosen to be positive.

The auxiliary loads can be assembled to a load vector. This is denoted by

$$ \tilde{\mathbf{p}} = \mathbf{P}\mathbf{z} \in \mathbb{R}^{n_{d}} $$
(6)

where \(\mathbf {P} \in \mathbb {R}^ {n_{d}}{n_{N}}\). The elements of P are \(P_{ij} = \tilde {p}_{ij}\), when \(i\in \mathcal {D}_{j}\) and P i j = 0 otherwise. The nodal equilibrium is then expressed in matrix form as

$$ \mathbf{B}\tilde{\mathbf{N}} = \tilde{\mathbf{p}} = \mathbf{P}\mathbf{z} $$
(7)

where B is the statics matrix of the ground structure and \(\tilde {\mathbf {N}}\) is the vector of auxiliary member forces.

The role of the strength constraints is to ensure that the auxiliary force variables of vanishing members are set to zero, and they are written (for all \(i\in \mathcal {M}\)) as

$$ -\underline{\sigma}\sum\limits_{j=1}^{n_{S}}\hat{A}_{j}y_{ij} \leq \tilde{N}_{i} \leq \overline{\sigma}\sum\limits_{j=1}^{n_{S}}\hat{A}_{j}y_{ij} $$
(8)

Alternatively, if it assumed that the normal force \(\tilde {N}_{i}\) does not reach the strength of any cross-section, the following form of strength constraints can be employed:

$$ -\underline{\sigma}\min_{j=1,2,\ldots,n_{S}}{\{\hat{A}_{j}\}}y_{i} \leq \tilde{N}_{i} \leq \overline{\sigma}\min_{j=1,2,\ldots,n_{S}}{\{\hat{A}_{j}\}}y_{i} $$
(9)

When buckling constraints are included in the problem, the left-hand side of (8) (or (9)) can be replaced by the corresponding value of the buckling constraint (see (31) in Section 4).

The auxiliary loading condition is illustrated in Fig. 1. All the free nodes are loaded (Fig. 1a). A kinematically unstable topology, shown in Fig. 1b, cannot attain equilibrium, i.e. it cannot satisfy the constraints of (7). If the unstable nodes 3 and 6 are removed, their auxiliary loads vanish from the equilibrium equations, and a stable topology is found (Fig. 1c), assuming that in the ground structure, members between nodes 5 and 7, and 2 and 4 are included.

Remark 1

Formally, the above idea can be justified as follows. The member strains and nodal displacements are related by the matrix B T. A truss is a mechanism, only if there are no deformations in the members exactly when the displacements vanish. This is equivalent of saying that B T u = 0 ⇒ u = 0 (Rajasekaran and Sankarasubramanian 2001, pp.18–19). This happens, when rank (B)=n d , assuming that n d ≤n E , which is true for all trusses satisfying (3).

Suppose then that the rows and columns corresponding to degrees of freedom of vanishing nodes and vanishing members, respectively, have been eliminated from B and \(\tilde {\mathbf {p}}\), and denote their reduced counterparts by B 0 and \(\tilde {\mathbf {p}}^{0}\). Suppose the number of degrees of freedom of the reduced structure is \(n_{d}^{\prime }\). By linear algebra, if rank\(({\mathbf {B}^{0}}) = n_{d}^{\prime }\) (i.e. B 0 has full rank), then (7) has a solution for any \(\tilde {\mathbf {p}}^{0}\), which means that the structure is kinematically stable. On the other hand, if rank\(({\mathbf {B}^{0}}) < n_{d}^{\prime }\), which corresponds to a mechanism, then \(\tilde {\mathbf {p}}^{0}\) should be such that (7) does not have a solution. This is true, if and only if \(\tilde {\mathbf {p}}^{0} \notin \mathcal {R}(\mathbf {B}^{0})\), where \(\mathcal {R}(\mathbf {B}^{0})\) is the range of B 0. The author is not aware of a \(\tilde {\mathbf {p}}\) that would satisfy this for all possible mechanisms included in B, i.e. for all possible \(\tilde {\mathbf {p}}^{0}\) related to B 0 that corresponds to a mechanism. Nevertheless, in all computations the author has carried out, the proposed method has succeeded in preventing mechanisms from appearing in the optimum topologies.

Remark 2

The proposed approach is similar with the idea of adding a ”system stability constraint” to the problem, as suggested by Rozvany (1996). Rozvany formulates the system stability constraint as equilibrium of forces induced by prescribed small nodal displacements. In the present work, prescribed forces are considered instead of displacements, but the rationale is identical: an unstable topology cannot attain equilibrium when ”arbitrarily” loaded. Without the binary nodal variables, z ℓ , implementing this idea as constraints is not straightforward, because it is difficult to know a priori, which nodes should be loaded.

3 Chains

From the previous section it can be seen that overlapping members are needed in the ground structure in order to eliminate unstable nodes. In Section 4 it will be shown that these members are also used to capture the correct buckling length of compression members. To avoid impractical topologies related to overlapping members in the ground structure, a series of constraints is added to the problem. The constraints are written for groups of members called chains. In this section the definition of chains and the corresponding constraints are presented.

When the ground structure is created, nodes laying on a line are identified (see nodes 1 to 4 in Fig. 2). Each such a sequence of nodes forms the basis for a chain. Conventionally, only two consecutive nodes of a sequence are connected by a member. In this study, a member is added to the ground structure between each pair of nodes in the sequence. As a result, some of the members are overlapping. The union of the original and the added overlapping members is called chain. For example, in Fig. 2, members 4, 5, and 6 form a chain together with members 1, 2, and 3, which connect the sequence of nodes {1,2,3,4}. Formal definition of chains is as follows.

Fig. 2
figure 2

Idea of chains. Members 1 to 3 form the basis of the chain. Members 4 to 6 are added to the ground structure. Constraints related to the chain include also members 7 to 12

Full size image

A ground structure member e i , \(i \in \mathcal {M}\), can be identified with its nodes by denoting e i = {s i 1, s i 2}, \(s_{i_{1}},\,s_{i_{2}}\in \mathcal {N}\). A chain is a sequence of K≥2 pair-wise distinct members, denoted by \(c = (e_{i_{1}},\ldots ,e_{i_{K}})\), such that each member shares a node with another member, i.e. for all k = 1, 2, ‣, K, there exists an ℓ such that \(e_{i_{k}}\cap e_{i_{\ell }} \neq \emptyset \). Also, each chain member is parallel to every other member of the chain. This definition has been proposed by Achtziger (1999a), but without overlapping members, which is a crucial feature in the present study. The set of chains is denoted by \(\mathcal {C}\). For each chain \(c\in \mathcal {C}\), the sets of members and nodes are denoted by \(\mathcal {E}_{c}\) and \(\mathcal {V}_{c}\), respectively.

Every chain has two nodes that are connected to only one chain member. The set of interior nodes of chain c, denoted by \(\mathcal {J}_{c}\), is obtained by removing these two nodes from \(\mathcal {V}_{c}\). Then, denote by \(\mathcal {M}_{c}(s)\) the set of members of the chain connected to the interior node \(s\in \mathcal {J}_{c}\). Similarly, \(\mathcal {N}_{c}(s)\) is the set of members of the ground structure connected to s but not belonging to the chain. Mathematically, these two sets can be expressed as

$$ \mathcal{M}_{c}(s) = \{i\;|\; i \in \mathcal{E}_{c} \;\text{and}\;e_{i} \cap \{s\} \neq \emptyset, s\in\mathcal{J}_{c}\} $$
(10)
$$ \mathcal{N}_{c}(s) = \{i\;|\; i \notin \mathcal{E}_{c} \;\text{and}\;e_{i} \cap \{s\} \neq \emptyset, s\in\mathcal{J}_{c}\} $$
(11)

For the chain in Fig. 2, the set of interior points is \(\mathcal {J}_{c} = \{2,3\}\), and the sets \(\mathcal {M}_{c}(s)\) and \(\mathcal {N}_{c}(s)\) of node 2 are \(\mathcal {M}_{c}(2) = \{1,2,5\}\), and \(\mathcal {N}_{c}(2) = \{7,8,11\}\).

Three sets of constraints are added to the problem in order to disallow topologies that display impractical behaviour.

Firstly, overlapping of members is prevented. This condition is expressed by the constraint

$$ \sum\limits_{i\in\mathcal{E}_{c}(s)} y_{i} \leq 1 \quad \forall\;s\in\mathcal{V}_{c} $$
(12)

where \(\mathcal {E}_{c}(s)\subseteq \mathcal {E}_{c}\) is the set of chain members partly or fully belonging to the line segment between the nodes s and s+1. A constraint of (12) is included for each line segment between two consecutive nodes of every chain.

For the truss in Fig. 2, the overlapping constraints are

$$ y_{1}+y_{4}+y_{6} \leq 1\qquad \qquad (\mathcal{E}_{c}{(1)}= \{1,4,6\}) \\ $$
(13)
$$ y_{2}+y_{4}+y_{5}+y_{6}\leq 1\qquad (\mathcal{E}_{c}{2}= \{2,4,5,6\})\\ $$
(14)
$$ y_{3}+y_{5}+y_{6}\leq 1 \qquad\qquad (\mathcal{E}_{c}{3}= \{3,5,6\}) $$
(15)

Secondly, unstable nodes that are supported only in the direction of the chain are prohibited. In other words, if all ground structure members connected to an interior node but not belonging to a chain vanish, then the chain members connected to that node must also vanish. A constraint for this condition is

$$ \sum\limits_{i\in \mathcal{M}_{c}(s)} y_{i} \leq |\mathcal{M}_{c}(s)|\sum\limits_{r\in\mathcal{N}_{c}(s)}y_{r} \quad \forall\, s\in\mathcal{J}_{c} $$
(16)

where \(|\mathcal {M}_{c}(s)|\) is the number of members of the chain connected to the node s.

Now if any y r = 1, \(r \in \mathcal {N}_{c}(s)\), which means that a member not belonging to the chain but connected to the node is present in the design, then any member of the chain connected to node s is allowed to be present. On the other hand, if all y r = 0, \(r \in \mathcal {N}_{c}(s)\), then also all chain members connected to that node must vanish.

The constraint of (16) can be modified to computationally more appealing form by replacing it with the following set of constraints:

$$ y_{i} \leq \sum\limits_{r\in\mathcal{N}_{c}(s)}y_{r} \quad \forall\, s\in\mathcal{J}_{c},\, i\in \mathcal{M}_{c}(s) $$
(17)

Consider node 2 of the chain in Fig. 2. As \(\mathcal {M}_{c}(2) = \{1,2,5\}\), and \(\mathcal {N}_{c}(2) = \{7,8,11\}\), constraint (16) for node 2 is

$$ y_{1}+y_{2}+y_{5} \leq 3(y_{7}+y_{8} + y_{11}) $$
(18)

Alternatively, using (17)

$$ y_{1} \leq y_{7}+y_{8}+ y_{11} $$
(19)
$$ y_{2} \leq y_{7}+y_{8}+ y_{11} $$
(20)
$$ y_{5} \leq y_{7}+y_{8}+ y_{11} $$
(21)

Finally, the situation is prohibited, where both an interior node and a member overlapping it are present. This condition prevents interior nodes of the chain to be supported by non-chain members only while simultaneously being overlapped by a member of the chain. The following constraint implements this statement:

$$ y_{i} +z_{s} \leq 1 \quad \forall\, i \in \mathcal{E}^{o}_{c}(s), \in\mathcal{J}_{c} $$
(22)

where \(\mathcal {E}^{o}_{c}(s)\) is the set of chain members overlapping the node s.

For the node 2 of the chain in Fig. 2, \(\mathcal {E}^{o}_{c}(2) = \{4,6\}\), and the constraints of (22) are

$$ y_{4}+z_{2} \leq 1 $$
(23)
$$ y_{6}+z_{2} \leq 1 $$
(24)

4 Member buckling constraints

4.1 General form

If member buckling constraints are expressed in terms of member forces, they can be written in general as

$$ N \geq -f_{B}(\mathbf{x},\mathbf{q}) $$
(25)

where N is the axial force of the member and f B is a function depending on the properties of the cross-section, gathered into the vector x, and some additional parameters q. The value f B (x, q) is the buckling strength of the member. Note that due to the minus sign, members in tension (i.e. with N>0) satisfy the buckling constraint automatically. The expression of f B and the contents of q depend on the rule according to which the buckling strength is evaluated. For example, the typically used buckling strength according to Euler’s theory is

$$ f_{B}(\mathbf{x},\mathbf{q}) = \pi^{2}\frac{EI}{{L_{n}^{2}}} $$
(26)

where E is the Young’s modulus, L n is the buckling length (L n = L in pin-jointed trusses) and I is the second moment of area which depends on the design variables. Consequently, x = {I} and q = {E L} in Euler buckling.

In practical truss design, the buckling strength should be evaluated according to applicable design codes such as the Eurocodes or the specifications of AISC. The design codes take into account initial crookedness of the members and residual stresses that remain in the member after the manufacturing process. From experimental data, analytical expressions have been developed for buckling strength. For example, in Eurocode 3 (EN 1993–1–1 2005) which concerns steel structures, the following expression is given

$$ f_{B}(\mathbf{x},\mathbf{q}) = \chi(\mathbf{x},\mathbf{q})A\frac{\ensuremath{f_{\text{y}}}}{\ensuremath{\gamma_{\text{M1}}}} $$
(27)

where

$$ \chi(\mathbf{x},\mathbf{q}) = \min\left\{1.0,\;\frac{1}{\Phi(\mathbf{x},\mathbf{q}) + \sqrt{\Phi(\mathbf{x},\mathbf{q})^{2}-\ensuremath{\bar{\lambda}}(\mathbf{x},\mathbf{q})^{2}}}\right\} $$
(28)

is the reduction factor,

$$ \Phi(\mathbf{x},\mathbf{q}) = 0.5\left[1+\alpha(\ensuremath{\bar{\lambda}}(\mathbf{x},\mathbf{q})-0.2)+\ensuremath{\bar{\lambda}}(\mathbf{x},\mathbf{q})^{2} \right] $$
(29)

and

$$ \ensuremath{\bar{\lambda}}(\mathbf{x},\mathbf{q}) = \sqrt{\frac{A\ensuremath{f_{\text{y}}}}{\ensuremath{N_{\text{cr}}}(\mathbf{x},\mathbf{q})}} $$
(30)

is the non-dimensional slenderness. The critical force N cr is the buckling force according to Euler’s theory, as in (26). In (29), the parameter α is the imperfection factor that depends on the manufacturing method of the member. Also, in (27), f y is the yield strength of the material, and γ M1 is the partial safety factor, whose value depends on the country. For example, in Finland, γ M1 = 1.0 is used. Consequently, for buckling according to Eurocode 3, x = {A I} and q = {γ M1 f y α E L}.

As can be seen from the above, the expression of the buckling strength, f B , can be highly nonlinear in terms of the cross-sectional properties, which typically correspond to the design variables. However, when discrete cross-sections are considered, member buckling constraints can be written conveniently in the following linear form

$$ N_{ij}^{k} \geq -f_{B}(\mathbf{x}_{j},\mathbf{q}_{ij})y_{ij} \quad \forall\, i \in \mathcal{M},\; j \in \mathcal{P}, \; k \in \mathcal{L} $$
(31)

where x j and q i j contain the cross-sectional properties of alternative j and the additional parameters of member i for alternative j, respectively. Thus, the buckling strength, f B (x j , q i j ), becomes a constant in the constraint. For Euler buckling, the constraint (31) takes the form

$$ N_{ij}^{k} \geq -\pi^{2}\frac{E\hat{I}_{j}}{L_{ni}^{2}}y_{ij} $$
(32)

where \(\hat {I}_{j}\) is the second moment of area of the j th profile alternative.

If member i is present in the solution with profile r, then y i r = 1, and y i j = 0 and \(N_{ij}^{k} = 0\) for j ≠ r. Then, for the profiles not selected for member i, (31) is automatically satisfied. For the selected profile, (31) becomes simply \(N_{ir}^{k} \geq -f_{B}(\mathbf {x}_{r},\mathbf {q}_{ir})\) which means that the axial compressive force in member i must not exceed the buckling strength of profile r in any load case.

Buckling constraints of (31) can be included in Problem P by modifying the last constraint to the form

$$ N_{ij}^{k} \geq \max\left\{\underline{N}_{ij}^{k},-\underline{\sigma}\hat{A}_{j},-f_{B}(\mathbf{x}_{j},\mathbf{q}_{ij})\right\}y_{ij} \quad \forall\, i ,\; j, \; k $$
(33)

Consequently, the number of constraints is not increased. Using this procedure, any design rule following the shape of (25) can be incorporated in the problem formulation as linear constraints of (33). For example, in addition to Euler buckling and buckling according to Eurocode 3, the design rules of AISC (2010) for member buckling are suitable for the proposed formulation.

4.2 Stiffening members

An obvious strategy for enabling more slender cross-sections for compression members is to support them by additional transversal members. These stiffening members split the compression member to two or more shorter members, which are sized against buckling using their own length as buckling length. This leads to smaller cross-sections for members in compression. Often the stiffening members do not carry any applied load, so they can be assigned the smallest available profile. If this profile is too small, the stiffening member may not be able to provide the necessary support for the compression member in practice (Rozvany 1996).

The mixed variable framework allows to employ the following strategy for sizing of the stiffening members. The idea is derived from (EN 1993–1–1 2005, Clause 5.3.3 (4) and (5)), where it is stated that the ”stiffening system” (including the stiffening members and the members supporting them) must be able to withstand a load whose magnitude is a given fraction of the axial force in the compression member being stiffened. Here, a simplified approach is proposed, where each stiffening member is sized against a compressive axial force of magnitude a N, where 0 < a < 1 is some prescribed fraction and N is the normal force of the stiffened member. This approach can be included in the optimization problem as a further set of linear constraints as follows.

First note that the stiffening members are always related to chains. The verbal statement is: if a chain member i connected to interior node s is in compression and if node s is connected by two chain members, then the non-chain members connected to that node must support a load of magnitude a N i in compression, where 0 < a < 1 is some prescribed fraction. This statement can be written as the following constraint:

$$\begin{array}{@{}rcl@{}} a\sum\limits_{j=1}^{n_{S}}N_{ij}^{k} \geq &-&\sum\limits_{j=1}^{n_{S}} f_{B}(\mathbf{x}_{j},\mathbf{q}_{rj}) y_{rj} - a\underline{N}_{i}^{k}(1-y_{r}) \notag\\ &-&a\underline{N}_{i}^{k}\left(2-\sum\limits_{t\in \mathcal{M}_{c}(s)}y_{t}\right) \quad \forall\,i\in \mathcal{M}_{c}(s),\,r \in \mathcal{N}_{c}(s)\notag\\ \end{array} $$
(34)

This constraint is written for all chain members that are connected to an interior node and for every potential stiffening member (\(\forall \,r \in \mathcal {N}_{c}(s)\)). The first term on the right-hand side of (34) is the buckling strength of the stiffening member r. The second term states that if the stiffening member is not present (y r = 0), then the constraint is automatically satisfied. The third term corresponds to the condition that if only one chain member is connected to the interior node (\(2-\sum _{t\in \mathcal {M}_{c}(s)}y_{t} = 1\)), then the node is actually an end node in the current topology, and constraint (34) should be automatically satisfied. Note that if member i is in tension or if it vanishes, i.e. if \(N_{ij}^{k} \geq 0\) for all j, then (34) is immediately satisfied.

5 Numerical examples

The proposed approach for buckling constraints is demonstrated on two examples. In both problems, the members are made of steel with Young’s modulus E = 210 GPa, density ρ = 7850 kg/m 3, and yield strength f y = 355 MPa. The yield strength is used as the maximum allowable stress in tension and in compression. Member profiles are square hollow sections (SHS) taken from the catalogue of a Finnish steel manufacturer (Ruukki 2011). The profile data is given in Appendix. For Eurocode 3 buckling constraints, the imperfection factor α = 0.49, which is the value for cold-formed hollow sections. Furthermore, the partial safety factor γ M1 = 1.0.

The mixed variable truss topology optimization problems are solved by the software Gurobi 5.6 (Gurobi Optimization, Inc. 2012). The relative optimality gap is set to 0.1 %. This is the relative difference between the best known solution and the lower bound obtained from the relaxations. Thus, the solutions obtained are global optima within the stated numerical accuracy.

In addition to the constraints related to kinematic stability, chains, and buckling, the following constraints prohibiting crossing members are introduced:

$$ y_{i} + y_{j} \leq 1 $$
(35)

for all pairs of members i and j of the ground structure that are crossing each other. It is assumed that crossing members would cause severe difficulties in the manufacturing, and therefore the constraints of (35) are employed. The constraints of (34) are not included in the problem unless otherwise stated.

In addition to the optimum member profiles, the utilization ratios of strength and buckling constraints of the members are reported. The utilization ratio for constraint X is defined as

$$ \ensuremath{U_{t},_{X}} = \frac{|N|}{N_{\text{Rd, }X}} $$
(36)

where N is the axial force and N Rd,X is the resistance of the member against the corresponding phenomenon. For example, N Rd,N is the member strength and N Rd,e u is the Euler buckling strength. If U t , X ≤1 then the member satisfies the constraint related to X.

5.1 Truss tower

Consider a truss tower with the ground structure shown in Fig. 3a. The height of the tower is h = 6.2 m, and the distance of the supports is L = 2 m. The diagonal lines from the loaded node to the supports have been divided into 10 segments of equal length. Every node is connected to every other node by a member, with the exception that the supported nodes are not connected to each other. The ground structure consists of 209 members and 21 nodes with two chains each having 55 members. The magnitude of the load is F = 400 kN. Altogether 20 SHS cross-section alternatives are available, see Appendix A. The displacement bounds are \(\overline {u} = -\underline {u} = 100\) mm.

Fig. 3
figure 3

Truss tower: a Ground structure, and b Optimum solution without buckling constraints

Full size image

The minimum weight Problem (P) is solved without buckling constraints, with Euler buckling and with buckling constraints according to Eurocode 3.

The optimum solution without buckling constraints is shown in Fig. 3b. The weight of the truss is W 0 = 65.17 kg. The cross-section of both members is 60 × 3, and their normal forces are N = 202.58 kN. The utilization ratio of strength constraints is U t , N = 0.86 for both members. The buckling strength of the members is N Rd,e u = 18.46 kN for Euler buckling, and N Rd,e c = 16.20 kN for Eurocode 3 buckling. Thus, both types of buckling constraints are violated.

If the design is resized for Euler buckling constraints, keeping the topology fixed, no feasible solution can be found for the available cross-sections. Using a larger set of alternatives, the minimum weight W 0,e u = 178.96 kg is obtained by the cross-section 120 × 4. The utilization ratios are U t,N = 0.31, U t,eu = 0.96, and U t,ec = 1.27. Thus, the Eurocode 3 buckling constraint is violated.

Resizing the solution for Eurocode 3 buckling constraints, the minimum weight of W 0,e c = 259.90 kg is obtained. The optimum cross-section is 140 × 5. The utilization ratios are U t,N = 0.22, U t,eu = 0.49, and U t,ec = 0.69.

When Problem (P) is solved with Euler and Eurocode 3 buckling constraints, the topologies shown in Fig. 4a and b, respectively, are obtained. In both cases, braces have been added to the truss in order to reduce the buckling length of the main diagonals. None of the braces carry any load, so they are assigned the smallest available profile (30 × 3).

Fig. 4
figure 4

Optimum solutions with buckling constraints: a Euler buckling, W e u = 84.46 kg; b Eurocode 3 buckling, W e c = 100.93 kg

Full size image

The minimum weight for Euler buckling constraints is W e u = 84.46 kg, which is 2.1 times smaller than W 0,e u . For Eurocode 3 buckling constraints, the minimum weight is W e c = 100.93 kg, being 2.6 times smaller than the corresponding resized minimum weight W 0,e c . On the other hand, W e c is 19.5 % greater than W e u . This means that the Eurocode 3 buckling constraints are more stringent than those derived from Euler’s theory, leading to larger profiles. This can also be seen from Table 1, where the dimensions and utilization ratios of the members are shown. Most members of the solution for Euler buckling violate the Eurocode 3 buckling constraints.

Table 1 Truss tower member dimensions and utilization ratios for buckling constraints
Full size table

It can be observed that the optimum topology depends on the buckling constraint type. It is therefore important to incorporate the correct buckling constraints required by the prevailing design codes in the problem in order to capture the true optimum topology.

As the loading scenario and the ground structure are symmetric, it can be seen that the optimum solutions are not unique; by mirroring the trusses with respect to the vertical axis, the same minimum weights can be obtained by different designs.

5.2 L-shaped truss

Consider the well-known ”L-shaped” truss with the ground structure shown in Fig. 5. It consists of 21 nodes and 146 members, including the overlapping members, constituting 23 chains. The nodes are evenly distributed both in the vertical and in the horizontal direction. The dimensions are L = 6 m and h = 3 m. The vertical load is F = 400 kN. Altogether 21 SHS profile alternatives are included in the problem (see Appendix). The displacement bounds are \(\overline {u} = -\underline {u} = 60\) mm.

Fig. 5
figure 5

L-shaped ground structure with 146 members and 21 nodes

Full size image

The optimum topology without buckling constraints is shown in Fig. 6, and the optimum design is given in Table 2. From the table, it can be seen that members 1, 2, 5, and 10 are in compression and the others are in tension. None of the compression members satisfy buckling constraints of Eurocode 3, and member 1 violates also Euler buckling constraints. Member 6 does not carry any load, and it is included in the solution only to provide sufficient kinematic stability. The weight of the truss is W 0 = 259.74 kg.

Fig. 6
figure 6

Optimum solution without buckling constraints. W 0=259.74 kg

Full size image
Table 2 Optimum design of the L-shaped truss without buckling constraints
Full size table

When buckling constraints are added to the problem, the optimum topology changes to those shown in Fig. 7 (Euler) and Fig. 8 (Eurocode 3). The optimum topology depends on the buckling constraint type. The optimum designs are given in Tables 3 and 4. The solution for Euler buckling constraints is nearly identical to the design without buckling constraints. The only difference is that the stiffening member 5 (Fig. 7) has been added in order to reduce the buckling length of the long member in compression. More stiffening members and resizing of compression members are needed for the optimum solution with Eurocode 3 buckling constraints. The long vertical compression member is divided into three segments by the stiffening members 6 and 8 (Fig. 8), and member 11 is introduced for the horizontal compression member (members 9 and 12).

Fig. 7
figure 7

Optimum solution with Euler buckling constraints. W e u = 264.75 kg

Full size image
Fig. 8
figure 8

Optimum solution for Eurocode 3 buckling constraints. W e c = 311.56kg

Full size image
Table 3 Optimum design of the L-shaped truss with Euler buckling constraints
Full size table
Table 4 Optimum design of the L-shaped truss with Eurocode 3 buckling constraints
Full size table

The minimum weight for Euler buckling constraints is W e u = 264.75 kg, which corresponds to a 1.9 % increase to W 0. For Eurocode 3 buckling, the minimum weight is W e c = 311.56 kg, which is 20.0 % greater than W 0 and 17.7 % greater than W e u . The latter difference is due to the fact that all compression members of the solution for Euler buckling violate the buckling constraints of Eurocode 3, for which larger profiles are required.

Finally, consider the solution for Eurocode 3 buckling constraints. The stiffening members 5, 6, and 11 are assigned the smallest available profile (30 × 3). The normal force in the chain defined by members 1, 4, and 7 is −400 kN. Suppose the a in (34) is a = 0.02, which means that the stiffening members must be able to withstand a compressive force with magnitude of 2 % of the force in the chain, i.e. 0.02 ⋅400 kN = 8 kN. This force is greater than the buckling strength of members 5 and 6 (5.75 kN, and 7.09 kN, respectively). Similar consideration applies for member 11. When the constraints (34) are added to the problem with a = 0.02, the optimum topology shown in Fig. 9 is obtained. Member 6 has been replaced by shorter stiffening members, and members 10 and 17 have been added for stiffening member 11. The optimum design and the utilization ratios are given in Table 5. This example shows that, in general, the optimum topology is susceptible to the sizing of the stiffening members.

Fig. 9
figure 9

Optimum solution for buckling constraints according to Eurocode 3 and with strength requirement for stiffening members. W e c = 315.26 kg

Full size image
Table 5 Optimum design of the L-shaped truss with Eurocode 3 buckling constraints and strength requirement for stiffening members
Full size table

6 Conclusions

The numerical examples considered above verify that the mixed variable approach forms a suitable platform for incorporating member buckling constraints in truss topology optimization. The formulation is able to capture the correct buckling length of compression members, and it also provides kinematically stable designs. Both of these issues have been plaguing the conventional formulations. Furthermore, buckling constraints derived from design codes can be included in the problem in addition to commonly used Euler buckling, making the mixed variable approach more suitable to structural designers. As the examples demonstrated, the optimum topology depends on the buckling constraint type, highlighting the importance of formulating buckling constraints based on the applicable design codes.

The mixed variable formulation is also able to handle the sizing of members that are used to reduce the buckling length of compression members. The L-shaped truss showed that appropriate sizing of these stiffening members can affect the optimum topology. The solution proposed in this study is simple yet applicable. However, a more involved approach might be needed for correct sizing of the entire ”stiffening system” (i.e. stiffening members and the members supporting them) in addition to the stiffening members.

The mixed variable formulation is mostly applicable to truss topology optimization with discrete cross-sections, which leads to a linear problem formulation. Linearity is essential for treating problems with practical ground structures, and it allows verifying the global optimality of the obtained solution. On the other hand, finding and verifying the globally optimal design poses certain limitations regarding the size of the ground structure and the number of available profiles. If global optimality is not required, as is often the case in practice, these limitations can be alleviated. As the mixed variable formulation does not suffer from issues related to vanishing members, further research efforts can be directed at improving the numerical solution methods.