1 Introduction

Numerical layout optimization provides an efficient means of identifying (near-)optimal truss layouts. The ‘ground structure’ layout optimization procedure was first proposed by Dorn et al. (1964) and more recently was made more efficient for single and multiple load case problems respectively by Gilbert and Tyas (2003) and Pritchard et al. (2005). In the latter contributions an adaptive ‘member adding’ algorithm was proposed which meant that much larger scale layout optimization problems could be solved; this and similar techniques are helping to provide new insights on a wide range of problems (e.g. Darwich et al 2010; Sokół and Rozvany 2012; Pichugin et al 2012). However, whilst fine numerical discretizations are needed in order to obtain highly accurate numerical solutions, the associated truss bar layouts can become very complex. Therefore identifying means of rationalizing such layouts is potentially of significant interest. Various rationalization approaches are possible, for example: (i) the problem formulation can be modified to ensure solution complexity is addressed directly from the outset; or (ii) a standard layout optimization solution can be subsequently modified in a post-processing step.

In the case of (i), directly addressing complexity within the formulation, a range of optimization methods can be applied (e.g. mixed integer linear programming, MILP, or non-classical optimization methods such as genetic algorithms); the downside of such procedures is that they are generally comparatively computationally expensive, so that only relatively small problems can be tackled. However, simple formulations are also available, and here the efficacy of the simple ‘joint length’ method proposed by Parkes (1975) will be explored. A key benefit of this method is that the linear character of the standard linear programming (LP) based layout optimization formulation is retained.

In the case (ii), addressing complexity via a post-processing step, it can be observed that the solutions obtained from the layout optimization procedure will generally comprise far fewer bars than are present in the initial ‘ground structure’. This is significant as it means that any post-processing step need only deal with a comparatively small number of bars.

One option is to use the truss layout derived from the layout optimization process as the starting point for a geometry optimization post-processing step. Integrating layout optimization with geometry optimization has been examined before (e.g. Bendsøe et al 1994; Bendsøe and Sigmund 2003, who pose the problem as one of non-smooth optimization). Gil and Andreu (2001) combined size and geometry optimization, obtaining solutions to small-scale problems by using optimality criteria and conjugate gradient methods in succession. Martínez et al. (2007) proposed a ‘growth’ method, in which geometry optimization was carried out in conjunction with a heuristic ‘node adding’ algorithm, allowing an increasingly complex truss structure to evolve from a relatively simple initial layout. Although not of specific interest in the present study, their ‘growth’ method allowed a limit to be placed on the number of joints in the resulting optimized truss to be controlled, thereby ensuring that the resulting optimized trusses could be rationalized as desired. (Limiting the number of joints was also of specific interest to Prager 1978 and, more recently, Mazurek et al. 2011; Mazurek 2012.) However, the focus of most work in this field has been on single load case problems, and most of the aforementioned methods cannot easily be extended to treat multiple load cases. An exception is the combined topology/layout and geometry optimization procedure put forward by Achtziger (2007), which was recently extended by Descamps and Filomeno Coelho (2013) to allow small-scale multiple load case problems to be considered. However, in general, geometry optimization requires the starting layout to quite closely resemble the true optimal solution in order to work effectively. Furthermore, the geometry optimization process can be computationally expensive. Here the efficacy of a geometry optimization post-processing step will be explored, which involves starting with a layout optimization solution comprising a reduced number of nodes and bars, and then using a highly efficient interior point method to solve the resulting non-linear optimization problem. This approach is general, and can be applied to a wide variety of problems, including those involving multiple load cases and self-weight.

The format of the paper is as follows: firstly the general layout optimization problem is considered and then revised to incorporate ‘joint lengths’; secondly, the geometry optimization problem is mathematically defined and extensions and implementation issues discussed; finally a number of numerical examples are solved to demonstrate the efficacy of the rationalization methods considered, and conclusions are drawn.

2 Rationalization of layout optimization solutions using joint lengths

The first rationalization technique considered is one proposed by Parkes (1975). According to his formulation, a notional joint length, s, is added to the length of each bar. Thus, the computed volume of the truss structure under consideration becomes: \(V=\tilde {\mathbf {l}}^{\mathrm {T}}\mathbf {a}\), where V is the total computed volume of the truss structure; \(\tilde {\mathbf {l}}\) is a vector containing modified truss bar lengths (i.e. {l 1+s,l 2+s,...,l m +s}, for a problem involving m bars), and a is a vector containing the bar cross-sectional areas.

Note that though this can simplify the truss layout, the calculated structural volume will clearly always increase because of the inclusion of additional joint lengths. However, after the optimization has been completed, the ‘standard’ volume can be calculated by summing up the volumes of all bars, excluding the joint lengths from this calculation (all volumes reported herein were calculated in this way).

The updated layout optimization problem, now including joint lengths, can therefore be stated as:

$$\begin{array}{@{}rcl@{}} &\min\limits_{a,q} & V=\tilde{\mathbf{l}}^{\mathrm{T}}\mathbf{a}\\ &\text{s.t.} \end{array} $$
(1a)
$$\begin{array}{@{}rcl@{}} &&\qquad\left. \begin{array}{lc} \mathbf{Bq}^{\alpha} + \mathbf{Wa} = \mathbf{f}^{\alpha}\\ -\mathbf{\sigma^{-}a}\le\mathbf{q}^{\alpha}\le\mathbf{\sigma^{+}a} \end{array} \right\}\text{for all }\alpha \in \mathbb{F} \end{array} $$
(1b)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{a}\ge\mathbf{0} \end{array} $$
(1c)

where W contains self-weight coefficients, here assuming self-weight to be lumped at the nodes; B is an equilibrium matrix comprising direction cosines; q is a vector containing the internal bar forces and f is a vector containing the external forces. Also σ + and σ − are limiting tensile and compressive stresses respectively, \(\mathbb {F}=\{1,2,...,p\}\) is a load case set, where α is the load case identifier and p represents the total number of load cases.

The optimization variables are the cross-sectional areas in a and the internal forces in q. It can be observed that the coefficient matrices are determined by the positions of the nodes and the connectivity of the truss bars; therefore the optimization formulation (1) is an LP problem.

3 Post-processing rationalization using geometry optimization

The second technique considered involves the use of geometry optimization as a post-processing step to rationalize solutions obtained using layout optimization. Initially the geometry optimization process will be considered in isolation; subsequently practical issues related to combining geometry optimization with layout optimization will be considered.

3.1 Basic geometry optimization formulation

Initially consider an unbounded 2D design domain, where the x,y positions of the nodes in a truss are considered as optimization variables. (For sake of simplicity, formulae for 3D trusses are not explicitly provided in the paper; however, the relevant formulae can be derived similarly.)

Considering first a problem involving a single load case, without self-weight, gives:

$$\begin{array}{@{}rcl@{}} &\min\limits_{x,y,a,q} & V=\mathbf{l(x,y)}^{\mathrm{T}}\mathbf{a} \end{array} $$
(2a)
$$\begin{array}{@{}rcl@{}} &~~~\textrm{s.t.} ~~& \mathbf{B(x,y)q}=\mathbf{f} \end{array} $$
(2b)
$$\begin{array}{@{}rcl@{}} ~~~~~~~~~&&-\mathbf{\sigma^{-}a}\le\mathbf{q}^{\alpha}\le\mathbf{\sigma^{+}a} \end{array} $$
(2c)
$$\begin{array}{@{}rcl@{}} ~~~~~~~~~&& \mathbf{a}\ge\mathbf{0} \end{array} $$
(2d)

where l is a vector containing the lengths of the truss bars. The optimization variables in this case are x, y, a and q; it is evident that the objective function (2a) and equality constraint (2b) are both now non-linear. Without loss of generality, problem (2) can be categorized as a non-linear, non-convex optimization problem.

Also, although problem (2) can be considered as a combined layout and geometry problem, similar to the approach put forward by Achtziger (2007), and developed further by Descamps and Filomeno Coelho (2013), in this paper geometry optimization is considered as a separate process, which is carried out only after an initial layout optimization solution has been performed, and active bars in the optimum truss have been identified. Advantages of this approach stem from the fact that the layout optimization formulation: (i) allows a globally optimal solution to be obtained for a given ground structure, typically very close to the true optimal solution; (ii) can be be solved extremely rapidly. Thus the layout optimization solution provides an excellent starting point for a subsequent geometry optimization, which, although capable of rationalizing the structure, is fundamentally non-convex and may be computationally expensive.

Figure 1 illustrates the non-convex nature of a simple four-bar truss problem. Suppose that the truss shown in Fig. 1 has only one free (movable) node C, whose position can be optimized in the x-y plane. In this case there exists two zones Ω1 and Ω2 in which node C can potentially become trapped, leading to different optimum solutions. In fact node C must be positioned in zone Ω2, at (1.00, 0.25), in order to obtain the globally optimal solution.

Fig. 1
figure 1

Four-bar truss illustrating non-convex nature of geometry optimization. The optimum position of node C is sought; contours show the variation of the structural volume for differing positions of node C

Full size image

Assuming that a truss layout is available, various methods of improving the solution via geometry optimization techniques are possible, though some methods appear to have inherent limitations. For example, the geometry optimization step in the ‘growth’ method proposed by Martínez et al. (2007) requires that the truss under consideration is statically determinate. With this stipulation, the state variable q can be eliminated by taking q=B −1 f, simplifying the underlying optimization problem. However, for problems with multiple load cases, this stipulation cannot be imposed. As both single and multiple load case problems are considered here, a more general approach is required, with statically indeterminate truss structures allowed. To solve the resulting non-linear problem efficiently, first and second derivatives of the objective function and constraints in (2) with respect to optimization variables are obtained analytically.

Note that the entire geometry optimization formulation for a truss structure can be assembled using locally derived formulae for each truss bar. Also, the derivatives can be assembled similarly. In the following section local formulae for a single bar are introduced, permitting the problem for the whole structure to be constructed.

3.1.1 Mathematical expressions for a single truss bar

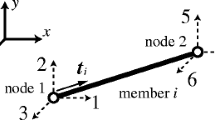
For the truss bar connecting nodes A(x A ,y A ) and B(x B ,y B ) shown in Fig. 2, let X=x B−x A and Y=y B−y A. The length of this bar is \(l=\sqrt {X^{2}+Y^{2}}\) and volume V AB=l a.

Fig. 2
figure 2

Notation used for a truss bar

Full size image

The contribution to the equilibrium matrix of this single bar can be stated as:

$$ \mathbf{B}^{\text{AB}}= \left[-\cos\theta\quad -\sin\theta\quad\cos\theta\quad\sin\theta\right]^{\mathrm{T}} $$
(3)

Assuming the optimization variables are defined as \(\left [x_{\mathrm {A}}, y_{\mathrm {A}}, x_{\mathrm {B}}, y_{\mathrm {B}}, a, q\right ]\), the gradient of the objective function is written as:

$$ \triangledown V^{\text{AB}}= \left[-\frac{Xa}{l} \quad -\frac{Ya}{l} \quad \frac{Xa}{l} \quad \frac{Ya}{l} \quad l \quad 0 \right]^{\mathrm{T}} $$
(4)

The Jacobian matrix of the equality constraint (2b) can be derived as:

$$ \mathbf{J}_{Bq}^{\text{AB}}=\left[ \begin{array}{llllll} \frac{q\, Y^{2}}{l^{3}} & -\frac{q\, XY}{l^{3}} & -\frac{q\, Y^{2}}{l^{3}} & \frac{q\, XY}{l^{3}} & 0 & -\frac{X}{l}\\\\ -\frac{q\, XY}{l^{3}} & \frac{q\, X^{2}}{l^{3}} & \frac{q\, XY}{l^{3}} & -\frac{q\, X^{2}}{l^{3}} & 0 & -\frac{Y}{l}\\\\ -\frac{q\, Y^{2}}{l^{3}} & \frac{q\, XY}{l^{3}} & \frac{q\, Y^{2}}{l^{3}} & -\frac{q\, XY}{l^{3}} & 0 & \frac{X}{l}\\\\ \frac{q\, XY}{l^{3}} & -\frac{q\, X^{2}}{l^{3}} & -\frac{q\, XY}{l^{3}} & \frac{q\, X^{2}}{l^{3}} & 0 & \frac{Y}{l} \end{array}\right] $$
(5)

The stress inequality constraint (2c) is linear; therefore the coefficients directly form the Jacobian matrix.

For a single truss bar, first derivatives of the objective function and associated constraints can also be obtained. To ensure rapid convergence of the non-linear optimization process, second-order terms are also derived analytically; the Hessian matrix of the objective function, V AB=l a can be derived as:

$$ \triangledown^{2}V^{\text{AB}}= \left[\begin{array}{lllllll} \frac{aY^{2}}{l^{3}} & -\frac{aXY}{l^{3}} & -\frac{aY^{2}}{l^{3}} & \frac{aXY}{l^{3}} & -\frac{X}{l} & 0\\\\ -\frac{aXY}{l^{3}} & \frac{aX^{2}}{l^{3}} & \frac{aXY}{l^{3}} & -\frac{aX^{2}}{l^{3}} & -\frac{Y}{l} & 0\\\\ -\frac{aY^{2}}{l^{3}} & \frac{aXY}{l^{3}} & \frac{aY^{2}}{l^{3}} & -\frac{aXY}{l^{3}} & \frac{X}{l} & 0\\\\ \frac{aXY}{l^{3}} & -\frac{aX^{2}}{l^{3}} & -\frac{aXY}{l^{3}} & \frac{aX^{2}}{l^{3}} & \frac{Y}{l} & 0\\\\ -\frac{X}{l} & -\frac{Y}{l} & \frac{X}{l} & \frac{Y}{l} & 0 & 0\\\\ 0 & 0 & 0 & 0 & 0 & 0\\ \end{array}\right] $$
(6)

For equality constraint B AB q−f AB=0, note that this comprises four constraints: \(-q\cos \theta - f_{x_{\mathrm {A}}} = 0\), \(-q\sin \theta - f_{y_{\mathrm {A}}} = 0\), \(q\cos \theta - f_{x_{\mathrm {B}}} = 0\) and \(q\sin \theta - f_{y_{\mathrm {B}}} = 0\), where \(f_{x_{\mathrm {A}}}\), \(f_{y_{\mathrm {A}}}\), \(f_{x_{\mathrm {B}}}\) and \(f_{y_{\mathrm {B}}}\) are external loads applied at nodes A and B. Also note that the magnitude of external loads are assumed not to change during the optimization process, so that \(\triangledown ^{2}f_{x_{\mathrm {A}}}=\triangledown ^{2}f_{y_{\mathrm {A}}}=\triangledown ^{2}f_{x_{\mathrm {B}}}=\triangledown ^{2}f_{y_{\mathrm {B}}}=\mathbf {0}\). The Hessian matrix of each of the constraints can readily be derived. For instance, \(\triangledown ^{2}(q\cos \theta )\) is shown in (7), and the mathematical expression for \(\triangledown ^{2}(q\sin \theta )\) can be obtained in a similar manner. Also, as the inequality constraint (2c) is linear, its second-order derivative term is zero.

$$ \triangledown^{2}(q\cos\theta)= \left[\begin{array}{llllllllll} -\frac{3qXY^{2}}{l^{5}} & -\frac{qY(-2X^{2}+Y^{2})}{l^{5}} & \frac{3qXY^{2}}{l^{5}} & \frac{qY(-2X^{2}+Y^{2})}{l^{5}} & 0 & -\frac{Y^{2}}{l^{3}} \\ -\frac{qY(-2X^{2}+Y^{2})}{l^{5}} & \frac{qX(-X^{2}+2Y^{2})}{l^{5}} & \frac{qY(-2X^{2}+Y^{2})}{l^{5}} & -\frac{qX(-X^{2}+2Y^{2})}{l^{5}} & 0 & \frac{XY}{l^{3}}\\ \frac{3qXY^{2}}{l^{5}} & \frac{qY(-2X^{2}+Y^{2})}{l^{5}} & -\frac{3qXY^{2}}{l^{5}} & -\frac{qY(-2X^{2}+Y^{2})}{l^{5}} & 0 & \frac{Y^{2}}{l^{3}}\\ \frac{qY(-2X^{2}+Y^{2})}{l^{5}} & -\frac{qX(-X^{2}+2Y^{2})}{l^{5}} & -\frac{qY(-2X^{2}+Y^{2})}{l^{5}} & \frac{qX(-X^{2}+2Y^{2})}{l^{5}} & 0 & -\frac{XY}{l^{3}} \\ 0 & 0 & 0 & 0 & 0 & ~~0\\ -\frac{Y}{l^{3}} & \frac{XY}{l^{3}} & \frac{Y^{2}}{l^{3}} & -\frac{XY}{l^{3}} & 0 & ~~0 \end{array}\right] $$
(7)

3.2 Geometry optimization formulation with self-weight

The basic formulation can be extended to account for self-weight. For a single truss bar AB, the corresponding self-weight coefficient matrix W AB is given as:

$$ \mathbf{W}^{\text{AB}}= \frac{\rho gl}{2}\left[\begin{array}{lllll}0 & 1 & 0 & 1 \end{array}\right]^{\mathrm{T}} $$
(8)

In which ρ and g are respectively the material density and acceleration due to gravity. The Jacobian matrix \(\mathbf {J}_{Wa}^{\text {AB}}\) can be derived as:

$$ \mathbf{J}_{Wa}^{\text{AB}}=\frac{\rho g}{2}\left[ \begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0\\\\ -\frac{aX}{l} & -\frac{aY}{l} & \frac{aX}{l} & \frac{aY}{l} & l & 0\\\\ 0 & 0 & 0 & 0 & 0 & 0\\\\ -\frac{aX}{l} & -\frac{aY}{l} & \frac{aX}{l} & \frac{aY}{l} & l & 0 \end{array}\right] $$
(9)

Also, the Hessian matrix can be obtained by considering only the second and fourth (i.e. non-zero) terms of W AB. Note that the relevant terms in both cases are:

$$ \triangledown^{2}(\frac{\rho g}{2}ql)= \frac{\rho g}{2}\left[\begin{array}{lllllll} \frac{qY^{2}}{l^{3}} & -\frac{qXY}{l^{3}} & -\frac{qY^{2}}{l^{3}} & \frac{qXY}{l^{3}} & 0 & -\frac{X}{l}\\\\ -\frac{qXY}{l^{3}} & \frac{qX^{2}}{l^{3}} & \frac{qXY}{l^{3}} & -\frac{qX^{2}}{l^{3}} & 0 & -\frac{Y}{l}\\\\ -\frac{qY^{2}}{l^{3}} & \frac{qXY}{l^{3}} & \frac{qY^{2}}{l^{3}} & -\frac{qXY}{l^{3}} & 0 & \frac{X}{l} \\\\ \frac{qXY}{l^{3}} & -\frac{qX^{2}}{l^{3}} & -\frac{qXY}{l^{3}} & \frac{qX^{2}}{l^{3}} & 0 & \frac{Y}{l} \\\\ 0 & 0 & 0 & 0 & 0 & 0\\ -\frac{X}{l} & -\frac{Y}{l} & \frac{X}{l} & \frac{Y}{l} & 0 & 0\\\\ \end{array}\right] $$
(10)

With respect to the geometry optimization problem (2), analytical expressions for the first and second derivatives have been derived. Thus simple problems (e.g. the problem in Fig. 1) can now be optimized without difficulty (though without any certainty of obtaining the global optimum). However, when dealing with structures involving large numbers of nodes, various practical issues might prevent the process obtaining a satisfactory solution; these issues are considered in the next section.

3.3 Practical issues

A number of practical issues which must be considered in order to develop a robust and flexible geometry optimization procedure are now considered.

3.3.1 Node move limits

It has been shown that geometry optimization will in general lead to a non-convex mathematical optimization problem, which can cause issues when applying convex optimization methods. To try to avoid such issues it is convenient to impose upper and lower limits on nodal positions x and y. However, it is worth pointing out that imposing such limits will mean that only locally optimal solutions will be found. Considering the evolving nature of the geometry of the structure during the optimization process, rules can be applied which ensure that the structure always remains similar in form to the initial structure. Hence the starting point, or initial condition, for the problem is crucial as it directly determines which local optimum zone the solution lies in. For instance, considering the structure shown in Fig. 1, as node C lies on the edge of zone Ω2, it is likely that imposed move limits will eliminate the possibility of this node being moved to zone Ω1. However, whether node C is restricted to lie within zone Ω1 or Ω2 depends upon the initial position of C, and upon the imposed move limits.

To describe node move limits concisely, coordinates of a given node in a 2D truss are written in column vector form: \(\boldsymbol {\nu }=\left [x,y,1\right ]^{\mathrm {T}}\) in \(\mathbb {R}^{3}\). (Note that although nodal positions lie in \(\mathbb {R}^{2}\), the redundant ‘1’ in ν is used solely to condense the mathematical expression.)

Now consider the node move limits. Suppose that each node is allowed to move within a circular zone, determined according to the distance from a given node to adjacent nodes. Figure 3 shows adjacent nodes A and B, which are originally located at \(\boldsymbol {\nu }_{\mathrm {A}}^{0}\) and \(\boldsymbol {\nu }_{\mathrm {B}}^{0}\) respectively. Two circular zones ΩA and ΩB, with radius \({r_{\text {AB}}}=\frac {1}{2}\left \|\boldsymbol {\nu }_{\mathrm {B}}^{0}-\boldsymbol {\nu }_{\mathrm {A}}^{0} \right \|_{2}\), are defined to restrict nodal movements. Let ν A and ν B represent the positions of node A and B respectively. When ν A=ν B, a zero length bar may be implied. To prevent this occurring, a gap of length 𝜖 is created between zones, such that the restriction for node A becomes: \( \left \|\boldsymbol {\nu }_{\mathrm {A}}-\boldsymbol {\nu }_{\mathrm {A}}^{0}\right \|_{2}^{2} \leq (r_{\text {AB}}-\epsilon )^{2}\). This is an extra constraint compared with those in the standard formulation (2a2). Its Jacobian matrix J A and Hessian matrix H A can be obtained as:

$$\begin{array}{@{}rcl@{}} &&\mathbf{J}^{\mathrm{A}}= 2\left[ x_{\mathrm{A}}-{x_{\mathrm{A}}^{0}}, y_{\mathrm{A}}-{y_{\mathrm{A}}^{0}} \right] \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} &&\mathbf{H}^{\mathrm{A}}= \left[\begin{array}{lllll} 2 & 0\\ 0 & 2 \end{array}\right] \end{array} $$
(12)
Fig. 3
figure 3

Node move limit zone: shaded circular zones indicate node move limits

Full size image

Although the restriction shown in Fig. 3 is normally sufficient to assure the non-linear, non-convex, optimization process is stable, in some cases additional restrictions need to be imposed. Thus, a program parameter r s is introduced which defines the maximum node move limit for all nodes; in this case the above restriction is modified to:

$$ \left\|\boldsymbol{\nu}_{\mathrm{A}}-\boldsymbol{\nu}_{\mathrm{A}}^{0}\right\|_{2}^{2} \leq (r^{*})^{2} $$
(13)

where \(r^{*}=\min \{r_{\mathrm {s}}, r_{\text {AB}}\}-\epsilon \) is the modified node move limit. In this paper r s is taken as the x- or y-distance between the nodes used in the original layout optimization process. When the non-linear optimization fails to converge rapidly, this parameter can be reduced with a view to stabilizing the non-linear problem. Also, from a computational point of view it is useful to impose relatively tight bounds on the variables x A and y A representing movements of a given node A, for simplicity applying these limits in the Cartesian directions:

$$ \begin{array}{l} {x_{\mathrm{A}}^{0}}-r^{*} \le x_{\mathrm{A}} \le {x_{\mathrm{A}}^{0}}+r^{*}\\ {y_{\mathrm{A}}^{0}}-r^{*} \le y_{\mathrm{A}} \le {y_{\mathrm{A}}^{0}}+r^{*} \end{array} $$
(14)

However, restricting nodal movements means that the final solution will normally not be obtained in a single step, and an iterative solution scheme is therefore required. In this scheme all nodes are moved to optimum positions within the prescribed move limit zones; these zones are then updated based on the new nodal positions. The optimization process proceeds iteratively, until all nodes are stationary (to within a specified tolerance).

Note that the aforementioned constraints are defined using the nodal distances between adjacent nodes. Therefore when a node is quite close to another, each node is restricted from moving a significant distance. This might affect convergence speed, especially when particular nodes lie in an extremely small region, with a radius r not significantly larger than 𝜖. As a consequence these nodes can become effectively locked, and cannot be moved further.

Additionally, various design limitations may need to be taken into account. The first is the line constraint, which restricts certain nodes (e.g. nodes on supported boundaries) to move only along given line paths. The second of these is the design domain constraint, which restricts all nodes to lie within the specified design domain. It is only necessary to apply this constraint to nodes which have the potential to move outside the domain (this can conveniently be determined by taking account of the move limit for each node). For sake of simplicity, polygonal design domains and straight line supports are considered in this paper, so that only linear constraints need to be formulated for these two types of design constraint.

A line in \(\mathbb {R}^{2}\) can be written as: T x x+T y y+T c=0, where T x, T y and T c are coefficients of the line; its vector form is then written as: T ν=0, in which, \(\mathbf {T} = \left [T^{x}, T^{y}, T^{c}\right ]\). Thus the line constraint for a given node A can be written as:

$$ \mathbf{T}^{\mathrm{L}}_{\mathrm{A}} \boldsymbol{\nu}_{\mathrm{A}} = 0 $$
(15)

where \(\mathbf {T}^{\mathrm {L}}_{\mathrm {A}}\) is the coefficient vector for the line node A is prescribed to lie on. Also, the domain constraint can be written as:

$$ \mathbf{T}^{\mathrm{D}}_{\mathrm{A}} \boldsymbol{\nu}_{\mathrm{A}} \geq \mathbf{0} $$
(16)

where \(\mathbf {T}^{\mathrm {D}}_{\mathrm {A}}\) contains coefficients of all domain boundary lines close to node A (each row in \(\mathbf {T}^{\mathrm {D}}_{\mathrm {A}}\) comprises coefficients of a single boundary line):

$$ \mathbf{T}^{\mathrm{D}}_{\mathrm{A}}= \left[\begin{array}{llll} \mathbf{T}_{1}\\ \mathbf{T}_{2}\\ \vdots \end{array}\right] = \left[\begin{array}{lllll} {T^{x}_{1}} & {T^{y}_{1}} & {T^{c}_{1}}\\ {T^{x}_{2}} & {T^{y}_{2}} & {T^{c}_{2}}\\ {\vdots} & {\vdots} & \vdots \end{array}\right] $$
(17)

Note that for a domain boundary line, its normal direction (i.e. the sign of T) matters as it determines which side of the line is ‘inward’ facing.

3.3.2 Modified formulation

Consider a truss comprising \(\mathbb {N}=\{1,2,...,n\}\) nodes, with subsets of nodes \(\mathbb {N}^{\mathrm {L}}\) and \(\mathbb {N}^{\mathrm {D}}\) denoting nodes lying on lines or close to domain boundaries respectively. The full optimization problem, taking account of node move limits and self-weight, can now be written as:

$$\begin{array}{@{}rcl@{}} &\min\limits_{x,y,a,q^{\alpha}} & V=\mathbf{l}^{\mathrm{T}}\mathbf{a}\\ &\text{s.t.} \end{array} $$
(18a)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\left. \begin{array}{lll} \mathbf{Bq}^{\alpha} + \mathbf{Wa}=\mathbf{f}^{\alpha}\\ \mathbf{\sigma^{-}a}\le\mathbf{q}^{\alpha}\le\mathbf{\sigma^{+}a} \end{array}\right\} \textrm{for all } \alpha \in \mathbb{F} \end{array} $$
(18b)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\left\|\boldsymbol{\nu}_{j}-\boldsymbol{\nu}_{j}^{0}\right\|_{2}^{2} \leq (r^{*})^{2} \,\,\, \textrm{for all } j \in \mathbb{N} \end{array} $$
(18c)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{T}^{\mathrm{L}}_{j_{\mathrm{L}}} \boldsymbol{\nu}_{j_{\mathrm{L}}} = 0 \quad \textrm{for all } {j_{\mathrm{L}}} \in \mathbb{N}^{\mathrm{L}} \end{array} $$
(18d)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{T}^{\mathrm{D}}_{j_{\mathrm{D}}} \boldsymbol{\nu}_{j_{\mathrm{D}}} \geq \mathbf{0} \quad \textrm{for all } {j_{\mathrm{D}}} \in \mathbb{N}^{\mathrm{D}} \end{array} $$
(18e)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{a}\ge\mathbf{0} \end{array} $$
(18f)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{x}^{\text{lb}}\le\mathbf{x}\le\mathbf{x}^{\text{ub}} \end{array} $$
(18g)
$$\begin{array}{@{}rcl@{}} &&\qquad~~\mathbf{y}^{\text{lb}}\le\mathbf{y}\le\mathbf{y}^{\text{ub}} \end{array} $$
(18h)

The new constraints (18d) and (18e) are linear, so coefficient matrices T D and T L directly form the Jacobian matrices. (The Hessian matrices are zero matrices in this case.)

3.3.3 Merging nodes

During the geometry optimization process some nodes may migrate towards one another (this phenomenon was also observed by Achtziger (2007), who addressed this by adding the possibility for nodes to ‘melt’ (i.e. merge together) in his proposed procedure). In this paper, it can be observed that the gap 𝜖 included in constraint (13) will prevent nodes from taking up the same position, and hence merging. Therefore an approach is needed to merge nodes into a concentrated node; here this involves two major steps.

In the first step, nodes to be merged are identified and grouped, based on a program parameter, the node merge radius r M. A node merge group contains candidate nodes to be merged. For a given node, adjacent nodes lying within radius r M are added to the same group; an example is shown in Fig. 4. When r M is greater than the distance between nodes A and C (Fig. 4a), a single group containing all three nodes is created, and then merged to a single node. When r M is greater than the distance between nodes A and B, but is less than the distance between A and C (Fig. 4b), one group is created, and the two nodes in this group are then merged.

Fig. 4
figure 4

Merging a group of nodes: a a large merge radius results in a group containing the three nodes, A, B and C, which can then be merged into a single node; b a small merge radius results in a group consisting of nodes A and B, which can then be merged, whilst node C remains as-is

Full size image

In the second step, all nodes in a given node merge group are merged to the centroid of the nodes in the group. Due to its heuristic nature, the validity of this process needs to be numerically validated; the merging process is deemed to be successful if the resulting structure has the same computed volume as before (within a prescribed error tolerance).

All steps in process to merge nodes are listed below:

Node merge algorithm

1.

Select an initial prescribed node merge radius, r M .

2.

Create node merge groups.

3.

For every group, check whether a valid merge can be undertaken.

4.

If a valid merge can be carried out for all groups go to 6, else 5.

5.

If invalid group can be split, reduce r M and go to 2, else 6.

6.

End of node merge process.

3.3.4 Considering crossovers

In a truss layout derived from layout optimization, bars will very often intersect / crossover one another. However, crossover points do not normally coincide with nodes. A crossover creation process can be carried out to create nodes at these points, thereby splitting the intersecting bars. With these newly created nodes, there is scope to further reduce structural volume. However, creating new nodes also leads to a growth in problem size, which becomes significant in the first few iterations, when a large number of crossover points are typically observed. To avoid significantly increasing problem size, the crossover creation process is therefore not carried out initially. This is achieved by using inner and outer loops in the main procedure as follows: (i) inner loop: the optimization is progressed without creating crossover nodes; this loop terminates when a prescribed termination criterion has been met; (ii) outer loop: this carries out the process of creating crossover nodes when the inner loop ends. The outer loop terminates when no more crossover nodes need to be created, also terminating the entire optimization procedure.

This approach is based on the assumption that, whenever an inner loop terminates, the form of an optimized layout has been identified, and the number of crossover points has been significantly reduced. Note that when considering 3D structures, bars are less likely to intersect one another, since for this to occur both bars must lie on the same plane. However, often a bar in a 3D structure can pass very close to one or more other bars. This indicates that crossovers should be identified approximately, using a tolerance which is progressively increased from zero to a prescribed value.

3.3.5 Extracting nodes and bars from the layout optimization solution

A viable structural layout, obtained using layout optimization, is the starting point of the geometry optimization-based rationalization process described here. However, ensuring a viable layout is obtained requires various steps to be taken, as described in this section.

Conventionally, when using an interior point-based linear programming solver, an optimum truss layout is ‘extracted’ by identifying bars which have an area above a given filter threshold. Though this typically provides a qualitatively reasonable layout, it can mean that one or more small but structurally important bars are filtered out. To ensure this does not happen, the ‘extracted’ structure can be used as the basis of a new layout optimization, and the volume compared with that obtained originally; if these are not within a prescribed tolerance then the filter threshold should be reduced and the process repeated until a viable layout is obtained.

Finally, chains of in-line bars should be merged into single bars to avoid intermediate nodes from moving freely along their axis without improving the solution (though this is not required in cases when intermediate nodes are either loaded or supported, or when self-weight is being considered).

3.3.6 Dealing with structures which are in unstable equilibrium with the applied loads

Layout optimization may identify structures which are in unstable equilibrium with the applied loads. When dealing with such structures in the geometry optimization rationalization technique, it will normally be observed that the calculated structural volume is very sensitive to the position of certain nodes. This can cause numerical issues in the non-linear optimization solution process. To address this, virtual supports are added and connected with all unsupported nodes by connections which incorporate large joint length penalties to ensure they are not present in the final optimized structure. (In the case of 2D trusses two virtual pinned supports are required to ensure that every node is adequately constrained, whilst in the case of 3D trusses three virtual supports are required.)

3.4 Overall procedure

The overall procedure is shown in Fig. 5. As indicated in the figure, initially the geometry optimization steps are performed within an inner loop, starting with the layout derived from layout optimization. Within this loop the form of the structure will gradually change, due to moving and merging of nodes; crossover points, if present, are completely ignored in this loop. The maximum movement of any node is used as the termination criterion (taken as 1×10−4 in this paper). Thereafter, crossover points are considered in the outer loop. The process then continues as indicated until no crossover points are identified, with the entire optimization process then terminating.

Fig. 5
figure 5

Flow chart of the ‘two phase’ geometry optimization procedure

Full size image

It is worth pointing out that, when merging nodes, the coordinates of the new merged nodes will be obtained approximately. As a consequence the calculated volume may in some cases be very slightly higher than in the previous step.

4 Numerical examples

The efficacy of the two rationalization techniques considered in this paper, i.e. (i) introduction of ‘joint lengths’ and, (ii) application of geometry optimization, are now demonstrated through application to a range of example problems. Unless stated otherwise, a reference length L is used to define the size of a given problem, a load P is applied, and the limiting material stresses are taken as: σ +=σ −=σ. Also, in cases where advantage is taken of symmetry (or anti-symmetry), the volume quoted is that of the full structure. With respect to the optimization solvers employed, all LP layout optimization problems were solved using MOSEK (2011) and the non-linear geometry optimization problems solved using IPOPT 3.11.0 (Vigerske and Wachter 2013), with default settings except for the maximum iteration number which was set to 500. All calculations were carried out using MATLAB2013a running on an Intel i5-2310 powered desktop PC with 6G RAM, and running Windows 7 (64bit).

For many of the problems considered a known analytical solution is available. In these cases the errors in the numerical solutions can be quantified, and are denoted ξ L, ξ J and ξ G for the percentage errors of the layout optimization, joint length and geometry optimization rationalized solutions respectively. Also, ξ M denotes the percentage error in the solution obtained using the software described by Martínez et al. (2007). Also, as the geometry optimization procedure will generally improve on the layout optimization solution, it is also useful to quantify this improvement, here denoted \(\eta = \frac {(\xi _{\mathrm {L}} - \xi _{\mathrm {G}})}{\xi _{\mathrm {L}}}\times 100~\%\).

4.1 Hemp cantilever

The first example is a cantilever truss considered by Hemp (1974). The problem involves application of a point load at mid-height between two pinned supports, as illustrated in Fig. 6a. (Note that only half of the domain needs to be considered if anti-symmetry is taken into account.) Hemp (1974) quoted the analytical volume to be 4.34P L/σ, but Lewiński (2005) repeated the calculations using greater precision to obtain a more accurate solution, 4.32168P L/σ.

Fig. 6
figure 6

Hemp cantilever: a problem definition and layout optimization solution obtained using 30×15 nodal divisions, V=4.3541P L/σ (ξ L=0.75 %); b rationalized solution obtained using joint length s=0.006L, V=4.3863P L/σ (ξ J=1.49 %); c rationalized solution obtained using geometry optimization, V=4.3318P L/σ (ξ G=0.23 %)

Full size image

A sample layout optimization solution and corresponding rationalized solutions are also shown in Fig. 6. It is evident that both rationalization techniques allow simplified solutions to be obtained. However, whereas the volume associated with the solution obtained using joint length rationalization is 1.49 % above the exact value, the solution obtained using geometry optimization rationalization is only 0.23 % above the exact value, a significant improvement on the original layout optimization error of 0.75 % (η=69 % in this case).

4.1.1 Factors affecting the joint length rationalization technique

With the joint length rationalization technique, adding an additional length s to the real length of each bar has the effect of modifying the solution by effectively penalizing short bars. For the Hemp cantilever shown in Fig. 6a, the influence of the value of s on the layout and corresponding volume is illustrated in Fig. 7. It is evident that the volume tends to increase as the joint length is increased, and also that the form of the solution is generally simpler when an increased joint length is used. Note that the CPU times were similar for all joint length cases considered.

Fig. 7
figure 7

Hemp cantilever: influence of joint length on numerical solution and layout (using 30×15 nodal divisions)

Full size image

4.1.2 Factors affecting the geometry optimization rationalization technique

The geometry optimization rationalization technique is affected by several factors, two of which are now considered: (i) influence of starting structural layout; (ii) influence of node merge radius.

(i) Influence of starting structural layout

Geometry optimization is here viewed as a post-processing technique and a better starting layout, obtained using a finer numerical discretization, will naturally be likely to result in an improved solution, at least in terms of volume. Figure 8 shows a fine resolution starting layout (obtained using a layout optimization involving 150×75 nodal divisions) and the corresponding rationalized solution obtained using geometry optimization, demonstrating that this rationalization technique can be applied to relatively large-scale problems. However, as indicated on Table 1, the computational cost associated with the non-linear optimizations employed in the geometry optimization process does increase markedly with problem size (number of nodes). Also, it is evident that the structure shown in Fig. 8b is still quite complex compared with that shown in Fig. 6c, suggesting that more practically useful solutions will often be obtained when using coarse nodal discretizations.

Fig. 8
figure 8

Hemp cantilever: a layout optimization solution obtained using 150×75 nodal divisions, V=4.3258P L/σ (ξ L=0.09 %) ; b rationalized solution obtained using geometry optimization, V=4.3228P L/σ (ξ G=0.03 %)

Full size image
Table 1 Hemp cantilever: solution and non-linear optimization CPU cost for varying layout optimization nodal densities
Full size table

(ii) Influence of node merge radius

Using a smaller node merge radius r M can be expected to allow more detail from the original layout optimization solution to be retained, implying also that a better quality solution can be expected to be obtained in this case. However, disabling the merging of nodes altogether can lead to problems (for example some nodes can become effectively locked in position when the node move limits are applied). Table 2 shows the influence of the choice of node merge radius for the Hemp cantilever problem shown in Fig. 6a. It is clear that the choice of node merge radius has a significant influence on the CPU time, and also does affect the solution slightly (and, for the reason outlined previously, the use of a zero node radius does not lead to the best solution). Thus in this paper a merge radius r M which equals half the x- or y-distance between the nodes used in the original layout optimization process is pragmatically utilized unless specified otherwise.

Table 2 Hemp cantilever: solution and non-linear optimization CPU cost for varying nodal merging radii (30×15 nodal divisions)
Full size table

Finally, in Fig. 9 the progress of the entire iterative solution procedure is shown for the Hemp cantilever example shown in Fig. 6a. The optimization process stays in the inner loop (see Fig. 5) until the end of the 7th iteration. Crossover nodes are then created and the inner loop is entered for a second time. The layout of the structure evolves further, until the termination criterion is met.

Fig. 9
figure 9

Hemp cantilever: geometry optimization solutions obtained during the iterative solution procedure

Full size image

4.2 Centrally loaded Michell beam

The problem shown in Fig. 10 is similar to the problem originally considered by Michell (1904), though here the inclination of the midspan point load is allowed to vary. For comparative purposes numerical solutions obtained using the ‘growth’ method described by Martínez et al. (2007) are also provided (using software downloaded using the link given in the paper).

Fig. 10
figure 10

Centrally loaded Michell beam: problem definition

Full size image

Numerical solutions are shown in Table 3. Note that in order to ensure that the geometry optimization rationalization technique produced forms which were anti-symmetric about the line of load application, similar to those obtained when using layout optimization, it was necessary to prescribe that the horizontal reaction forces at the two pinned supports were equal in magnitude; this was achieved by replacing one of the supported degrees of freedom with an equivalent reaction force, of magnitude \(\frac {P\cos (\phi )}{2}\). (However, this approach did not allow sensible solutions to be obtained using the method proposed by Martínez et al. (2007), because Martínez’s method appears to ‘grow’ either the top or the bottom part of the structure, but not both simultaneously.) Also, to avoid nodes being merged in the geometry optimization phase in the vicinity of the singularities at the supports and load position, the node merge radius r M used was taken as half the standard value (being a quarter of the x- or y-distance between the nodes used in the original layout optimization process).

Table 3 Centrally loaded Michell beam: volumes (×P L/σ) and layouts obtained using various methods vs. inclined load angle ϕ. Minimum volume shown in boldface
Full size table

It is apparent from Table 3 that for this problem the geometry optimization rationalization technique provides the best all-round solutions, successfully simplifying the standard layout optimization layouts. Also, although the ‘growth’ method proposed by Martínez et al. (2007) produces the most accurate solution for the ϕ=90∘ case, in most other cases it fails to capture important detail present in the (near-) optimal layouts, leading to less accurate solutions and to higher computed volumes.

4.3 Hemp arch with distributed load

Details of the arch problem investigated by Hemp (1974) are provided in Fig. 11a. Hemp proposed an analytical solution but found that this was in fact non-optimal. However, what is likely to be a very close estimate of the volume of the exact layout (\(V=3.15163\frac {wL^{2}}{\sigma }\)) was recently put forward by Pichugin et al. (2012). This was obtained using the ‘Type III’ uniformly distributed loading pattern proposed by Darwich et al. (2010), which is also used here. Additionally, due to the sensitivity of the computed volume to the position of particular nodes, virtual supports are utilized in the geometry optimization rationalization technique. Also, to avoid nodes being merged in the geometry optimization phase in the vicinity of the singularity at the support, the node merge radius r M used was half the standard value (being a quarter of the x- or y-distance between the nodes used in the original layout optimization process).

Fig. 11
figure 11

Hemp arch with distributed load: a problem definition and layout optimization solution obtained using 40×40 nodal divisions, V=3.1679w L 2/σ (ξ L=0.51 %); b method by Martínez et al. (2007), using 20 nodal divs as software failed to yield reasonable results when 40 nodal divs were employed, V=3.2736w L 2/σ (ξ M=3.86 %); c rationalized solution obtained using joint length s=0.01L, V=3.2044w L 2/σ (ξ J=1.66 %); d rationalized solution obtained using geometry optimization, V=3.1550w L 2/σ (ξ G=0.10 %)

Full size image

Considering the layouts shown in Fig. 11, it is clear that only the geometry optimization rationalization technique is capable of simplifying the layout whilst maintaining key features of the original form. The geometry optimization rationalization step also reduces the error from 0.51 % in the original layout optimization solution to 0.10 % (η= 81 %).

4.4 Hemp cantilever with self-weight

The Hemp cantilever shown in Fig. 6a is revisited, though now taking account of self-weight, with ρ×g=1.5σ/L. The solutions are shown in Fig. 12.

Fig. 12
figure 12

Hemp cantilever with self-weight: a problem definition and layout optimization solution using 30×30 nodal divisions, V=35.894P L/σ; b rationalized solution obtained using joint length s=0.06L, V=38.150P L/σ; c rationalized solution obtained using geometry optimization, V=34.608P L/σ

Full size image

Although a relatively large joint length has been used in an attempt to derive a suitably simplified structure, it is evident that the resulting layout is significantly more complex than the equivalent layout obtained using the geometry optimization technique.

4.5 Chan cantilever with two load cases

The problem shown in Fig. 13a is a variation on the cantilever truss considered by Chan (1962), though now involving two load cases (and two forces, P and Q, which are each active in only one of the load cases). Considering the case when P=Q, the exact solution can readily be calculated using superposition principles (e.g. see Nagtegaal and Prager 1973; Spillers and Lev 1971): in this case the ‘sum’ problem clearly gives a volume of 0.5P L/σ, and the ‘difference’ problem takes the form of a ‘Michell’ truss (Lewiński et al. 1994), whose volume is given by Graczykowski and Lewiński (2010) as 4.729085649P L/σ. Therefore the exact solution can be calculated to be (4.729085649+0.5)P L/σ.

Fig. 13
figure 13

Chan cantilever with two load cases: a problem definition (Q=P) and layout optimization solution obtained using 30×20 nodal divisions, V=5.2450P L/σ (ξ L=0.30 %); b rationalized solution obtained using joint length s=0.015L, V=5.2712P L/σ (ξ J=0.80 %); c rationalized solution obtained using geometry optimization, V=5.2344P L/σ (ξ G=0.10 %)

Full size image

It can be observed from Fig. 13 that both rationalization techniques described here successfully simplify the layout, with the geometry optimization rationalization technique also reducing the error in the computed volume, from 0.30 % to 0.10 % (error reduction η=66.7 %).

4.6 Flower truss with two load cases

To further demonstrate the capability of the rationalization techniques, another problem involving two load cases will be considered; details of the problem are shown in Fig. 14a. The analytical solution for this problem can again be derived using superposition principles. Thus with given dimension R=0.5L, the optimal volume can be calculated to be: V=(46.052+10.000)P L/σ (refer to Fig. 15 for further details).

Fig. 14
figure 14

Flower truss with two load cases: a problem definition (P=Q), circular support modelled using 18 nodes; b layout optimization solution obtained using 50×50 nodal divisions, V=57.387P L/σ (ξ L=2.38 %); c rationalized solution obtained using using joint length s=0.05L, V=57.801P L/σ (ξ J=3.12 %); d rationalized solution obtained using geometry optimization, V=56.324P L/σ (ξ G=0.49 %)

Full size image
Fig. 15
figure 15

Flower truss with two load cases: equivalent single load case problems using superposition principle a ‘sum’ problem \(V=\frac {1}{2}\times 5 \log \left (\frac {5}{0.5} \right ) \times 2\times 4 {PL/\sigma }= 46.052{PL/\sigma }\) (Michell 1904); b ‘difference’ problem \(V= \frac {1}{2}\sin ^{2} \left (\frac {\pi }{4} \right ) \times 5\times 4 {PL/\sigma }= 10.000{PL/\sigma }\)

Full size image

Due to the relatively coarse nodal discretization employed in this case, comparatively little rationalization of the initial layout optimization solution is required. However, the geometry optimization rationalization clearly simplifies the layout and also reduces the error (η=80 %) in this case. (Also note that for this problem ξ L and ξ G are both relatively high, partly because the circular support is modelled with only 18 nodes and, in this paper, these are non-movable in the geometry optimization phase. i.e. a curved nodal movement path is beyond the scope of the present paper).

4.7 Michell sphere

The Michell sphere is the minimum volume 3D structure to support a pair of axial torques (Michell 1904). Though the exact solution to this problem has been derived theoretically (e.g. Michell 1904; Hemp 1973; Lewiński 2004), existing numerical solutions are not satisfactory. For example in (Czarnecki 2003) the difference between the quoted computed and exact volumes was found to be 40.6 % (Lewiński 2004). Here, using anti-symmetric boundary conditions, the problem can be modelled using a reduced domain; in this case one eighth of a cube was used, as shown in Fig. 16a. The torque on one side is modelled by applying point loads to 20 circumferentially positioned nodes in the full problem (i.e. to 20/4 + 1 = 6 nodes in the reduced problem). The analytical solution is \(V = \frac {4T}{\sigma }\log {\cot {\frac {\phi }{2}}}\) (after Hemp 1973; Lewiński 2004). For the given dimensions (R=50L, ϕ=18∘ and T=100P L), the exact volume is therefore 737.09P L/σ.

Fig. 16
figure 16

Michell sphere: a problem definition (R=50L, T=100P L,ϕ=18∘), torsional load modelled using 20 nodes in the full problem; b layout optimization solution obtained using 10×10×10 nodal divisions, V=768.34P L/σ (ξ L=4.24 %) (showing half of the full structure); c rationalized solution obtained using geometry optimization, V=740.26P L/σ (ξ G=0.43 %) (showing half of the full structure); d alternative view of solution shown in c (showing full structure)

Full size image

The results of the geometry optimization rationalization technique are shown in Fig. 16c, d. It is clear that the rationalization technique does an excellent job of simplifying the complex initial layout optimization solution shown in Fig. 16b, also reducing the error in the volume in this case from 4.24 % to 0.43 % (error reduction η=90 %).

5 Conclusions

Numerical layout optimization provides an efficient means of identifying (near-)optimal truss topologies for a variety of problem types. However, the solutions obtained are often complex in form, and effective means of rationalizing the output are often needed. In this paper two rationalization techniques are explored:

  • Rationalization by including joint lengths in the layout optimization problem is computationally efficient since it simply requires minor modification of the underlying linear programming (LP) problem. The solutions obtained are often simplified effectively, according to the joint length utilized. However, the solutions are normally lessefficient (i.e. have a higher structural volume) than solutions obtained using the standard layout optimization procedure. Also, in some cases this method fails to simplify the truss topology effectively.

  • Rationalization by performing geometry optimization is a post-processing step which involves the solution of a non-linear optimization problem. This approach has been found to be effective in simplifying the solution obtained via layout optimization for a wide variety of problem types, including those involving distributed loads, self-weight, multiple load-cases and 3D geometries. Starting with a layout optimization solution, which typically comprises relatively few bars, means that the subsequent geometry optimization phase is relatively computationally inexpensive (cf. the integrated layout and geometry optimization strategies proposed by others). Also, the solutions are normally more efficient (i.e. have a lower structural volume) than the original layout optimization solutions. However, the non-linear, non-convex, nature of the geometry optimization formulation means that there can be no guarantee as to the proximity of the solution obtained to the global optimum; thus its use primarily as a rationalization technique, as proposed in this paper, appears appropriate.