Robust truss topology optimization via semidefinite programming with complementarity constraints: a difference-of-convex programming approach

Abstract

The robust truss topology optimization against the uncertain static external load can be formulated as mixed-integer semidefinite programming. Although a global optimal solution can be computed with a branch-and-bound method, it is very time-consuming. This paper presents an alternative formulation, semidefinite programming with complementarity constraints, and proposes an efficient heuristic. The proposed method is based upon the concave–convex procedure for difference-of-convex programming. It is shown that the method can often find a practically reasonable truss design within the computational cost of solving some dozen of convex optimization subproblems.

1 Introduction

Many studies have been done on robust optimization of structures against uncertainty in external loads. A possibilistic (or bounded-but-unknown) model of uncertainty, assuming only the set of values that the input data can possibly take, might be useful when reliable statistical property of uncertainty, which is required for a probabilistic model of uncertainty, is unavailable or imprecise. With a possibilistic model of uncertainty, design optimization considering structural robustness against the uncertainty is treated within the framework of robust optimization [5].

Attention of this paper is focused on robust topology optimization of truss structures against uncertainty in the static nodal external load.¹ Namely, we attempt to find a truss design that minimizes the worst-case compliance, i.e., the maximal value of the compliance among the specified set of external loads.² The seminal work of Ben-Tal and Nemirovski [7] shows that, based on the conventional ground structure method, this optimization problem can be formulated as semidefinite programming (SDP).³ SDP is a class of convex optimization, and can be solved efficiently with a primal-dual interior-point method [3, 60]. Closely related formulations of continuum-based robust structural optimization can be found in Cherkaev and Cherkaev [12, 13], Calafiore and Dabbene [11], de Gournay et al. [16], Takezawa et al. [57], Brittain et al. [10], Hashimoto and Kanno [25] and Thore [58]. Furthermore, nonlinear SDP approaches to robust structural optimization have been proposed in Guo et al. [22, 24], Kanno and Takewaki [33], and Holmberg et al. [26]. This paper discusses and deals with intrinsic difficulty in robust truss topology optimization.

Suppose that uncertain external forces can possibly be applied at any nodes, and that no external force is applied at an intermediate point of a truss member. If the set of exiting nodes is specified, then the robust truss optimization problem can be recast as SDP [7]. In this approach, all the nodes in the specified set remain in the obtained solution. Also, the obtained solution can possibly have some nodes other than the specified ones, but at such extra nodes no uncertain external force is considered. Thus, it is difficult to predict in advance the set of existing nodes in the robust optimal truss. In other words, the uncertainty model of external forces should be treated as a design-dependent model [32]. This design dependency can be addressed by introducing 0–1 variables to represent the set of existing members in a truss design [61]. The robust truss topology optimization problem is then formulated as mixed-integer semidefinite programming problem (MISDP), which can be solved globally with a branch-and-bound method [61]. Unfortunately, due to large computational cost, this MISDP approach can be applied only to small-scale problem instances [61].

Another issue that has not been considered in literature on robust truss topology optimization [7, 32, 61] is the treatment of parallel consecutive members in the ground structure method. Specifically, in robust truss topology optimization with uncertain external load, overlapping members in the ground structure are not redundant.⁴ Such non-redundancy of overlapping members has also been recognized in truss topology optimization considering the self-weight load [8, 34] and the member buckling constraints [23, 41]. Consider the conventional truss topology optimization. It is often that the optimal solution has parallel consecutive members that are connected by nodes supported only in the direction of those members. A sequence of such members is sometimes called a chain [1]. If only the compliance is considered as the structural performance, one can remove the intermediate nodes and replace the chain with a single longer member. This procedure is called the hinge cancellation [1, 49]. Since the hinge cancellation does not change the compliance, overlapping of members in a ground structure can be removed in advance by deleting the longer member when two members overlap. In contrast, in robust truss optimization under load uncertainties, a solution having a chain is infeasible,⁵ while the one stabilized by hinge cancellation can be feasible. This means that, in general, a global optimal truss topology cannot be captured without incorporating overlapping members in a ground structure. However, on the other hand, presence of overlapping members in a final truss design is not allowed from a practical point of view. Therefore, a special treatment is required in a robust optimization method to prohibit the presence of overlapping members.

This paper addresses the two difficulties in robust truss optimization explained above: the design dependency of the uncertainty model of the external load and the necessity of incorporating overlapping members in a ground structure. Both can be dealt with by introducing, for each member, a 0–1 design variable indicating whether the member vanishes or exists. Therefore, the robust truss topology optimization can be formulated as MISDP; see Sect. 4.2. However, as mentioned before, this approach is applicable only to problems of small size. In contrast, in this paper we attempt to propose a heuristic that can often find a feasible solution with a reasonable objective value. Through the numerical experiments with problem instances having up to about 700 members, it is shown that the proposed method usually converges after solving only a few dozen of convex optimization subproblems, and that it finds a practically reasonable solution.

This paper is partially inspired by papers of Jara-Moroni et al. [30] and Lipp and Boyd [39]. Jara-Moroni et al. [30] present a DC (difference-of-convex) programming approach to finding a stationary point of linear programming with complementarity constraints; see also Le Thi and Pham Dinh [38] and Muu et al. [43] for DC programming approaches to complementarity constraints. A function is said to be a DC (difference-of-convex) function if it can be represented as a difference of two convex functions. A DC programming problem is a minimization problem of a DC function under some inequality constraints, where all the constraint functions are DC functions. One of well-known heuristics for finding a local optimal solution of DC programming is the concave–convex procedure⁶ [14, 18, 44, 50, 64]. Lipp and Boyd [39] show that an extension of the concave–convex procedure can serve as an efficient heuristic for diverse nonconvex optimization problems. For more account on the DC programming and the concave–convex procedure, see Sect. 3.1 and the references therein. In this paper, we first formulate the robust truss topology optimization as semidefinite programming with complementarity constraints (SDPCC). Following an idea found in Jara-Moroni et al. [30], we recast this problem as a DC programming problem. A variant of the concave–convex procedure, which is similar to the one in Lipp and Boyd [39], is then applied to this DC programming formulation. Each iteration of the proposed method consists of solving an SDP problem.

The paper is organized as follows. In Sect. 2 we explain intrinsic difficulties in robust truss topology optimization by using some illustrative examples. Section 3 provides an overview of the necessary background of the DC programming and the concave–convex procedure, and presents the general framework of the algorithm used in this paper. Section 4 briefly reviews the existing MISDP formulation for robust truss topology optimization, and extends it to the problem setting with a ground structure incorporating overlapping members. Section 5 presents a new formulation, as well as a solution method, of robust truss topology optimization. Section 6 reports the results of numerical experiments. Conclusions are drawn in Sect. 7.

In our notation, we use $\varvec{x}^{\top }$ and $X^{\top }$ to denote the transposes of vector $\varvec{x} \in \mathbb {R}^{n}$ and matrix $X \in \mathbb {R}^{m \times n}$, respectively. For vectors $\varvec{x} = (x_{i}) \in \mathbb {R}^{n}$ and $\varvec{y} = (y_{i}) \in \mathbb {R}^{n}$, we write $\varvec{x} \ge \varvec{y}$ if $x_{i} \ge y_{i}$ $(i=1,\dots ,n)$. Particularly, $\varvec{x} \ge \varvec{0}$ means $x_{i} \ge 0$ $(i=1,\dots ,n)$. The Euclidean norm of $\varvec{x}$ is denoted by $\Vert \varvec{x} \Vert = \sqrt{\varvec{x}^{\top } \varvec{x}}$. We use $\varvec{1} = (1,1,\dots ,1)^{\top }$ to denote the all-ones vector. Let $\mathcal {S}^{n}$ denote the set of $n \times n$ real symmetric matrices. We write $X \succeq 0$ if $X \in \mathcal {S}^{n}$ is positive semidefinite. We use $\mathop {\mathrm {diag}}\nolimits (\varvec{x})$ to denote a diagonal matrix, the vector of diagonal entries of which is $\varvec{x}$. For a finite set T, we use |T| to denote the cardinality of T, i.e., the number of elements in T.

2 Motivation

In this section, we explain intrinsic difficulties in robust truss topology optimization, which motivate us to develop the method proposed in this paper. Details of the examples in this section appear in Sect. 6.1.

Suppose that uncertain static external forces are possibly applied at all the nodes. The robust truss topology optimization is to find a truss design that minimizes the worst-case compliance, i.e., the maximum value of the compliance among possible realizations of the external load, under the upper bound constraint on the structural volume.

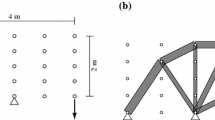
With reference to the examples in Figs. 1 and  2, we explain that incorporating overlapping members into a ground structure is necessary for the robust truss topology optimization. We begin with the conventional compliance minimization, without considering uncertainties. Figure 1a shows a ground structure, which consists of 12 members and has no overlapping members. The ground structure is an initial setting for truss topology optimization. The members consisting of a ground structure are called the candidate members, and their cross-sectional areas are design variables to be optimized. It is worth noting that the locations of the nodes are not treated as design variables. If the cross-sectional area of a member becomes equal to zero as a result of optimization, then the member is removed from the truss. Thus, the connectivity of members, called the topology in this research area, usually changes from the ground structure. Suppose that a vertical external load is applied at the rightmost bottom node, as shown in Fig. 1a. The optimal solution is shown in Fig. 1b, where the width of each member is proportional to its cross-sectional area. This solution has a chain consisting of two members. The hinge cancellation yields the final truss design shown in Fig. 1c. It should be clear that the objective value, i.e., the compliance, of the solution in Fig. 1c is same as the one in Fig. 1b. We next consider the robust optimization. Since uncertain external force is supposed to be applied also at the intermediate node of the chain, the solution in Fig. 1b becomes infeasible. As a result, the optimal solution has one additional member to stabilize that node, as shown in Fig. 2a. Alternatively, consider a ground structure in Fig. 2b, which consists of 14 members. The newly added two members, depicted as slightly curved lines, are in fact straight bars. Therefore, each of them overlaps with two shorter members, and is called an overlapping members. Moreover, the middle node is exactly located on a line forming an overlapping member. Therefore, we say that the overlapping member lies on the middle node. The robust optimal solution obtained from this ground structure is shown in Fig. 2c.⁷ Namely, at the global optimal solution, the longer member is selected instead of the chain and the intermediate node of the chain is removed. Thus, overlapping members do not mean redundancy, because connection of two members via an intermediate node introduces an extra uncertain load applied to that node. Similar non-redundancy of overlapping members in a ground structure can be observed also in, e.g., the compliance minimization of trusses under the self-weight loads [8, 34].

Fig. 1

An example of the conventional compliance minimization. a The ground structure (with 12 members); b the optimal solution; and c the final truss design after hinge cancellation

Fig. 2

The robust optimization corresponding to the example in Fig. 1. a The optimal solution obtained from the ground structure in Fig. 1a; b the ground structure including overlapping members (14 members in total); and c the global optimal solution

Fig. 3

Difficulties in the robust truss topology optimization. a The ground structure and the nominal external load; b the optimal solution for the nominal load; c a solution obtained for a design-independent uncertainty model of the external load; d the robust optimal solution for the design-dependent uncertainty model and the ground structure without overlapping members (the objective value is $3259.115\,\mathrm {J}$); and e the robust optimal solution for the design-dependent uncertainty model and the ground structure with overlapping members (the objective value is $2442.708\,\mathrm {J}$)

A key in this robust optimization is selecting the set of nodes which the optimal solution has. This is because the uncertainty in external loads depends on the set of existing nodes, in a manner that uncertain external forces are supposed to be applied to all the existing nodes. Moreover, a node lying on an existing member should be removed. The next example illustrates that exploring an optimal set of nodes in a heuristic manner is indeed difficult.

Consider the problem setting shown in Fig. 3a. Figure 3b shows the optimal solution of the nominal (i.e., not robust) optimization problem. A simple heuristic to predict a set of existing nodes in a robust optimal solution is to adopt the set of nodes that the nominal optimal solution has. Suppose that uncertain external forces are applied only to the five free nodes that the solution in Fig. 3b has. The optimal solution of this robust optimization problem is shown in Fig. 3c. This solution has two extra nodes that the solution in Fig. 3b does not have. Therefore, the solution in Fig. 3c assumes that external forces are not applied to these two nodes (in this sense, this solution is not truly robust). On the other hand, Fig. 3d shows the optimal solution of the robust topology optimization with a ground structure which does not include overlapping members. It is observed that one of the nodes in Fig. 3c is missing in the solution in Fig. 3d. Furthermore, Fig. 3e shows the optimal solution of the robust topology optimization with a ground structure including overlapping members. It is observed that the three intermediate nodes in Fig. 3b are removed and the two chains are replaced by longer members. As a result, the objective value of the solution in Fig. 3d is more than 1.33 times larger than that of the solution in Fig. 3e. Thus, it is crucial to design an optimization process so as to allow vanishment of intermediate nodes on chains.

It is also possible that a node which is not lying on a chain vanishes as a result of robust optimization. Consider the problem setting in Fig. 4a. The optimal solution of the nominal optimization problem is shown in Fig. 4b. If we suppose that uncertain external forces are applied to the eight free nodes in Fig. 4b, then the solution in Fig. 4c becomes optimal. Unlike the example in Fig. 3c, uncertain external forces are supposed to be applied to all the nodes that the solution in Fig. 4c has. In this sense, the solution in Fig. 4c is a local optimal solution of the robust topology optimization. In contrast, the global optimal solution of the robust topology optimization is shown in Fig. 4d.⁸ It is observed that three nodes in Fig. 4c are missing in Fig. 4d. The objective value of the solution in Fig. 4c is more than 1.25 times larger than that of the solution in Fig. 4d. Thus, it is crucial to design an optimization algorithm that can deal with the design-dependent uncertainty model of the external load.

Fig. 4

A node which is not on a chain can also vanish as a result of the robust topology optimization. a The ground structure and the nominal external load; b the optimal solution for the nominal load; c the robust solution obtained for a design-independent uncertainty model of the external load (the objective value is $13934.896\,\mathrm {J}$); d the robust optimal solution for the design-dependent uncertainty model (the objective value is $11093.750\,\mathrm {J}$)

In Sects. 4 and  5, we propose a formulation and an algorithm for overcoming the difficulties discussed in this section.

3 Algorithmic framework

As preliminaries, Sect. 3.1 briefly introduces the notion of DC programming and the concave–convex procedure for solving it. In Sect. 3.2, we introduce the optimization problem that we consider in this paper, and present an extension of the concave–convex procedure.

3.1 Fundamentals: DC programming and concave–convex procedure

Let $f_{i}$, $g_{i} : \mathbb {R}^{n} \rightarrow \mathbb {R}$ $(i=0,1,\dots ,m)$ be convex. The optimization problem having the following form is called a DC programming problem:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } f_{0}(\varvec{x}) - g_{0}(\varvec{x}) \end{aligned}$$

(1a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad f_{i}(\varvec{x}) - g_{i}(\varvec{x}) \le 0 , \quad i=1,\dots ,m . \end{aligned}$$

(1b)

For simplicity, we assume that $g_{0}$, $g_{1},\dots ,g_{m}$ are differentiable.

The concave–convex procedure is known as a heuristic for finding a local optimal solution of problem (1). Let $\varvec{x}^{(k)} \in \mathbb {R}^{n}$ denote the incumbent value of $\varvec{x}$ at the kth iteration. Define $\hat{g}_{i}(\,\cdot \, ; \varvec{x}^{(k)}) : \mathbb {R}^{n} \rightarrow \mathbb {R}$ $(i=0,1,\dots ,m)$ by

$$\begin{aligned} \hat{g}_{i}(\varvec{x}; \varvec{x}^{(k)}) = g_{i}(\varvec{x}^{(k)}) + \nabla g_{i}(\varvec{x}^{(k)})^{\top } (\varvec{x} - \varvec{x}^{(k)}) . \end{aligned}$$

(2)

The concave–convex procedure updates the solution by letting $\varvec{x}^{(k+1)}$ be the optimal solution of the following optimization problem:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } f_{0}(\varvec{x}) - \hat{g}_{0}(\varvec{x}; \varvec{x}^{(k)}) \end{aligned}$$

(3a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad f_{i}(\varvec{x}) - \hat{g}_{i}(\varvec{x}; \varvec{x}^{(k)}) \le 0 , \quad i=1,\dots ,m . \end{aligned}$$

(3b)

It is worth noting that this subproblem is convex.

For the sequence, $\{ \varvec{x}^{(k)} \}$, generated by the concave–convex procedure, it is known that the objective value of (1), i.e., $\{ f_{0}(\varvec{x}^{(k)}) - g_{0}(\varvec{x}^{(k)}) \}$, converges. However, $\{ \varvec{x}^{(k)} \}$ does not necessarily converges to a local optimal solution; see, e.g., Lipp and Boyd [39, Sect. 1.3]. Applications of the concave–convex procedure include transductive support vector machines (transductive SVMs) [14, 18], feature selection in SVMs [44], sparse learning [19], etc.

The concave–convex procedure can be considered as a version of DCA (difference of convex algorithm) [45, 47]; see Lipp and Boyd [39] and Sriperumbudur and Lanckriet [50] for accounts of this fact. For DCA and its applications we direct the reader to Le Thi and Pham Dinh [37] and Pham Dinh and Le Thi [46]; an application of DCA in structural engineering can be found in Stavroulakis and Polyakova [52]. As shown in Sriperumbudur and Lanckriet [50], the concave–convex procedure can also be viewed as a variant of MM algorithms (majorization-minimization algorithms) [28, 36].⁹ The MM algorithm is a generalization of the well-known EM algorithm (expectation-maximization algorithm) [15]. The MM algorithms have been frequently employed in machine learning and image processing as seen in, e.g, Hunter and Li [29], Hunter and Lange [27], Figueiredo et al. [17], Sriperumbudur et al. [51], and Sun et al. [54].

MMA (the method of moving asymptotes) [55, 56, 65], which is frequently used for continuum-based topology optimization [9], also solves a sequence of convex optimization approximations of the original problem. MMA approximates the objective function and the constraint functions by convex linear fractional functions by using the function values and gradients as well as some parameters controlling the vertical asymptotes of the generated functions. Also, sequential parametric convex approximation methods with application to truss optimization can be found in Beck et al. [4] and Ben-Tal et al. [6].

3.2 Heuristic for convex optimization with complementarity constraints

In this paper we attempt to solve problems having the following form:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } f(\varvec{\xi },\varvec{y},\varvec{z}) \end{aligned}$$

(4a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{\xi }, \varvec{y}, \varvec{z}) \in \varOmega , \end{aligned}$$

(4b)

$$\begin{aligned}&\varvec{y} \ge \varvec{0} , \end{aligned}$$

(4c)

$$\begin{aligned}&\varvec{z} \ge \varvec{0} , \end{aligned}$$

(4d)

$$\begin{aligned}&\varvec{y}^{\top } \varvec{z} = 0 . \end{aligned}$$

(4e)

Here, $f : \mathbb {R}^{l} \times \mathbb {R}^{n} \times \mathbb {R}^{n} \rightarrow \mathbb {R}$ is convex, $\varOmega \subseteq \mathbb {R}^{l} \times \mathbb {R}^{n} \times \mathbb {R}^{n}$ is closed and convex, and the optimization variables are $\varvec{\xi } \in \mathbb {R}^{l}$, $\varvec{y} \in \mathbb {R}^{n}$, and $\varvec{z} \in \mathbb {R}^{n}$. Problem (4) is convex optimization with complementarity constraints.

Following the idea in Jara-Moroni et al. [30], we can reduce problem (4) to a DC programming problem as follows. Consider a differentiable function $\phi : \mathbb {R}^{n} \times \mathbb {R}^{n} \rightarrow \mathbb {R}$ satisfying

$$\begin{aligned} \phi (\varvec{y}, \varvec{z}) = 0&\quad \Leftrightarrow \quad \varvec{y}^{\top } \varvec{z} = 0 , \\ \phi (\varvec{y}, \varvec{z}) \ge 0&\quad \Leftarrow \quad \varvec{y} \ge \varvec{0} , \ \varvec{z} \ge \varvec{0} . \end{aligned}$$

The complementarity constraints, (4e), can be replaced by a penalization term as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } f(\varvec{\xi },\varvec{y},\varvec{z}) + \rho \phi (\varvec{y},\varvec{z}) \end{aligned}$$

(5a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{\xi }, \varvec{y}, \varvec{z}) \in \varOmega , \end{aligned}$$

(5b)

$$\begin{aligned}&\varvec{y} \ge \varvec{0} , \end{aligned}$$

(5c)

$$\begin{aligned}&\varvec{z} \ge \varvec{0} . \end{aligned}$$

(5d)

Here, $\rho > 0$ is a penalty parameter. For sufficiently large $\rho$, problem (5) is equivalent to problem (4). We next assume that $\phi$ can be decomposed as

$$\begin{aligned} \phi (\varvec{y},\varvec{z}) = \phi _{+}(\varvec{y},\varvec{z}) - \phi _{-}(\varvec{y},\varvec{z}) , \end{aligned}$$

where $\phi _{+}$ and $\phi _{-}$ are convex. Then problem (5) is reduced to the following form:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } (f(\varvec{\xi },\varvec{y},\varvec{z}) + \rho \phi _{+}(\varvec{y},\varvec{z}) ) - \rho \phi _{-}(\varvec{y},\varvec{z}) \end{aligned}$$

(6a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{\xi }, \varvec{y}, \varvec{z}) \in \varOmega , \end{aligned}$$

(6b)

$$\begin{aligned}&\varvec{y} \ge \varvec{0} , \end{aligned}$$

(6c)

$$\begin{aligned}&\varvec{z} \ge \varvec{0} . \end{aligned}$$

(6d)

This is a DC programming problem, because $f(\varvec{\xi },\varvec{y},\varvec{z}) + \rho \phi _{+}(\varvec{y},\varvec{z})$ and $\rho \phi _{-}(\varvec{y},\varvec{z})$ are convex. There exist several different choices for $\phi$, $\phi _{+}$, and $\phi _{-}$ [30, 38]. In this paper we adopt

$$\begin{aligned} \phi (\varvec{y},\varvec{z})&= \Vert \varvec{y} + \varvec{z} \Vert ^{2} - \Vert \varvec{y} - \varvec{z} \Vert ^{2} , \end{aligned}$$

(7)

$$\begin{aligned} \phi _{+}(\varvec{y},\varvec{z})&= \Vert \varvec{y} + \varvec{z} \Vert ^{2} , \end{aligned}$$

(8)

$$\begin{aligned} \phi _{-}(\varvec{y},\varvec{z})&= \Vert \varvec{y} - \varvec{z} \Vert ^{2} . \end{aligned}$$

(9)

To solve problem (5), we apply the concave–convex procedure to problem (6) with gradually increasing the penalty parameter, $\rho$. For point $(\varvec{y}^{(k)},\varvec{z}^{(k)}) \in \mathbb {R}^{n} \times \mathbb {R}^{n}$, define $\hat{\phi }_{-}(\,\cdot \,; \varvec{y}^{(k)},\varvec{z}^{(k)}) : \mathbb {R}^{n} \times \mathbb {R}^{n} \rightarrow \mathbb {R}$ by

$$\begin{aligned}&\hat{\phi }_{-}(\varvec{y},\varvec{z}; \varvec{y}^{(k)},\varvec{z}^{(k)}) = \phi _{-}(\varvec{y}^{(k)},\varvec{z}^{(k)}) \nonumber \\&\qquad + \nabla _{\varvec{y}}\phi _{-}(\varvec{y}^{(k)},\varvec{z}^{(k)})^{\top }(\varvec{y} - \varvec{y}^{k}) + \nabla _{\varvec{z}}\phi _{-}(\varvec{y}^{(k)},\varvec{z}^{(k)})^{\top }(\varvec{z} - \varvec{z}^{k}). \end{aligned}$$

(10)

The proposed algorithm updates the solution by letting $(\varvec{\xi }^{(k+1)},\varvec{y}^{(k+1)},\varvec{z}^{(k+1)})$ be an optimal solution of the following convex optimization problem:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } f(\varvec{\xi },\varvec{y},\varvec{z}) + \rho _{k} \phi _{+}(\varvec{y},\varvec{z}) - \rho _{k} \hat{\phi }_{-}(\varvec{y},\varvec{z}; \varvec{y}^{(k)},\varvec{z}^{(k)}) \end{aligned}$$

(11a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{\xi }, \varvec{y}, \varvec{z}) \in \varOmega , \end{aligned}$$

(11b)

$$\begin{aligned}&\varvec{y} \ge \varvec{0} , \end{aligned}$$

(11c)

$$\begin{aligned}&\varvec{z} \ge \varvec{0} . \end{aligned}$$

(11d)

A reasonable stopping criterion is that the residual of the complementarity constraints is small enough, i.e.,

$$\begin{aligned} \phi (\varvec{y}^{(k+1)}, \varvec{z}^{(k+1)}) \le \epsilon _{1} , \end{aligned}$$

(12)

and the update of the incumbent solution is small enough, i.e.,

$$\begin{aligned} \Vert (\varvec{\xi }^{(k+1)},\varvec{y}^{(k+1)},\varvec{z}^{(k+1)}) - (\varvec{\xi }^{(k)},\varvec{y}^{(k)},\varvec{z}^{(k)}) \Vert \le \epsilon _{2} , \end{aligned}$$

(13)

where $\epsilon _{1}$, $\epsilon _{2} > 0$ are thresholds. The algorithm is formally stated in Algorithm 1.¹⁰.

Remark 1

Algorithm 1 is designed essentially based on the algorithm proposed by Lipp and Boyd [39] for solving problem (1). In their algorithm, the following subproblem is solved to update $\varvec{x}^{(k)}$:

$$\begin{aligned} \begin{array}{ll} \mathop {\mathrm {Minimize}}&{} \quad f_{0}(\varvec{x}) - \hat{g}_{0}(\varvec{x}; \varvec{x}^{(k)}) + \rho _{k} \sum _{i=1}^{m} s_{i} \\ \mathop {\mathrm {subject~to}}&{}\quad f_{i}(\varvec{x}) - \hat{g}_{i}(\varvec{x}; \varvec{x}^{(k)}) \le s_{i} , \quad i=1,\dots ,m , \\ &{} \quad s_{i} \ge 0 , \quad i=1,\dots ,m . \end{array} \end{aligned}$$

Thus, penalization terms for all the constraints are added to the objective function by using the $\ell _{1}$-exact penalty function. In contrast, in Algorithm 1 only the complementarity constraints are penalized, and the other constraints of the original optimization problem are satisfied at a solution of the subproblem. $\square$

4 Mixed-integer semidefinite programming formulation for robust truss topology optimization

In Sect. 4.1, we recall the existing MISDP formulation for robust truss topology optimization, without considering overlapping members in a ground structure. Section 4.2 presents treatment of overlapping members within the framework of MISDP.

4.1 Review of existing formulation

In this section we briefly review an MISDP formulation of the robust truss topology optimization under the load uncertainty [61]; see also Ben-Tal and Nemirovski [7].

Following the ground structure method, consider a truss consisting of candidate members connected by nodes. Let m and d denote the number of the members and the number of degrees of freedom of the nodal displacements,¹¹ respectively. We use $x_{i}$ $(i=1,\dots ,m)$ to denote the member cross-sectional areas, which are design variables to be optimized. Throughout the paper, we assume small deformation and linear elasticity.

Let $t_{i} \in \{ 0,1 \}$ be a variable that serves as an indicator of existence of member i such that $t_{i}=1$ means that member i exists and $t_{i}=0$ means that it vanishes. We use $\overline{x} > 0$ and $\underline{x} \in [0, \overline{x}]$ to denote the specified upper and lower bounds for the cross-sectional area of an existing member, i.e., $x_{i}$ should satisfy $x_{i} \in \{ 0 \} \cup [\underline{x}, \overline{x}]$. This constraint can be written by using $t_{i}$ as

$$\begin{aligned} \underline{x} t_{i}&\le x_{i} \le \overline{x} t_{i} . \end{aligned}$$

(14)

We next introduce $s_{j} \in \{ 0,1 \}$ $(j=1,\dots ,d)$ to represent the existence of the jth degree of freedom of the nodal displacements. A node in a ground structure is removed if and only if all the members connected to the nodes vanish. Let $s_{j}=1$ mean that the node having the jth degree of freedom exists, and $s_{j}=0$ mean that it vanishes. We use $I(j) \subseteq \{ 1,\dots ,m \}$ to denote the set of indices of the members connected to the node having the jth degree of freedom. Then $s_{j}$ is related to $t_{1},\dots ,t_{m}$ as follows:

$$\begin{aligned} t_{i}&\le s_{j} , \quad \forall i \in I(j) . \end{aligned}$$

(15)

Let $K(\varvec{x}) \in \mathbb {R}^{d \times d}$ denote the stiffness matrix of a truss, which is a (matrix-valued) linear function of $\varvec{x}$. For a given external load, denoted $\varvec{p} \in \mathbb {R}^{d}$, the compliance of the truss is defined by

$$\begin{aligned} \pi (\varvec{x};\varvec{p}) = \sup \{ 2\varvec{p}^{\top } \varvec{u} - \varvec{u}^{\top } K(\varvec{x}) \varvec{u} \mid \varvec{u} \in \mathbb {R}^{d} \} . \end{aligned}$$

(16)

The conventional compliance minimization problem is formulated in variable $\varvec{x}$ as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}\quad \pi (\varvec{x};\varvec{p}) \end{aligned}$$

(17a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad \varvec{x} \ge \varvec{0}, \end{aligned}$$

(17b)

$$\begin{aligned}&\,\,\varvec{c}^{\top } \varvec{x} \le \overline{c} . \end{aligned}$$

(17c)

Here, $c_{i}$ is the undeformed length of member i, $\varvec{c} = (c_{1},\dots ,c_{m})^{\top }$, and $\overline{c} > 0$ is the specified upper bound for the structural volume.

The uncertainty model of the external load is defined as follows: Let $\tilde{\varvec{p}} \in \mathbb {R}^{d}$ denote the nominal value (or the best estimate) of the external load. Define a constant matrix $Q \in \mathbb {R}^{d \times d}$ by

$$\begin{aligned} Q = \left[ \begin{array}{@{}c|c|c|c@{}} &{} &{} &{} \\ \tilde{\varvec{p}} &{} \alpha \varvec{q}_{1} &{} \cdots &{} \alpha \varvec{q}_{d-1} \\ &{} &{} &{} \\ \end{array} \right] , \end{aligned}$$

where $\varvec{q}_{1},\dots ,\varvec{q}_{d-1} \in \mathbb {R}^{d}$ are the orthonormal basis vectors of the orthogonal complement of $\tilde{\varvec{p}}$, and $\alpha > 0$ is a constant representing the level (or the magnitude) of uncertainty. Then the uncertainty set of the external load, i.e., the set of all possible realizations of the external load, is defined by

$$\begin{aligned} P(\varvec{s}) = \{ \mathop {\mathrm {diag}}\nolimits (\varvec{s}) Q \varvec{e} \mid \Vert \varvec{e} \Vert \le 1 \} . \end{aligned}$$

(18)

For example, suppose that $\tilde{\varvec{p}}$ has only one nonzero entry. Then, without loss of generality we can assume $\tilde{p}_{1} \not = 0$, and we have

$$\begin{aligned} \tilde{\varvec{p}} = \begin{bmatrix} \tilde{p}_{1} \\ 0 \\ 0 \\ \vdots \\ 0 \\ \end{bmatrix} , \quad Q = \begin{bmatrix} \tilde{p}_{1}&0&0&\cdots&0 \\ 0&\alpha&0&\cdots&0 \\ 0&0&\alpha&\cdots&0 \\ \vdots&\vdots&\vdots&\ddots&\vdots \\ 0&0&0&\cdots&\alpha \\ \end{bmatrix} . \end{aligned}$$

(19)

Let $J_{\mathrm {f}} \subseteq \{ 1,\dots ,d \}$ denote the set of indices of nonzero entries of $\tilde{\varvec{p}}$, i.e.,

$$\begin{aligned} J_{\mathrm {f}} = \{ j \in \{ 1,\dots ,d \} \mid \tilde{p}_{j} \not = 0 \} . \end{aligned}$$

The nodes to which the nominal external load, $\tilde{\varvec{p}}$, is applied should not be removed in the course of optimization. Therefore, we impose the following constraint:

$$\begin{aligned} s_{j} = 1 , \quad \forall j \in J_{\mathrm {f}} . \end{aligned}$$

(20)

In robust optimization, we attempt to find a truss design that minimizes the maximal compliance (i.e., the worst-case compliance) when the external load can take any value in $P(\varvec{s})$. With reference to (14), (15), (17), (18), and (20), we can see that this optimization problem can be formulated as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } \sup \{ \pi (\varvec{x};\varvec{p}) \mid \varvec{p} \in P(\varvec{s}) \} \end{aligned}$$

(21a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad s_{j} = 1 , \quad \forall j \in J_{\mathrm {f}} , \end{aligned}$$

(21b)

$$\begin{aligned}&t_{i} \le s_{j} , \quad \forall i \in I(j); \ j=1,\dots ,d , \end{aligned}$$

(21c)

$$\begin{aligned}&\underline{x} \varvec{t} \le \varvec{x} \le \overline{x} \varvec{t} , \end{aligned}$$

(21d)

$$\begin{aligned}&\varvec{c}^{\top } \varvec{x} \le \overline{c} , \end{aligned}$$

(21e)

$$\begin{aligned}&\varvec{s} \in \{ 0,1 \}^{d} , \end{aligned}$$

(21f)

$$\begin{aligned}&\varvec{t} \in \{ 0,1 \}^{m} . \end{aligned}$$

(21g)

For $\varvec{x} \in \mathbb {R}^{m}$ $(\varvec{x} \ge \varvec{0})$, $\varvec{s} \in \{ 0,1 \}^{d}$, and $w \in \mathbb {R}$, define $W(\varvec{x},\varvec{s},w) \in \mathcal {S}^{d+1}$ by

$$\begin{aligned} W(\varvec{x},\varvec{s},w) = \begin{bmatrix} w I&(\mathop {\mathrm {diag}}\nolimits (\varvec{s}) Q)^{\top } \\ \mathop {\mathrm {diag}}\nolimits (\varvec{s}) Q&K(\varvec{x}) \\ \end{bmatrix} . \end{aligned}$$

It is shown in Ben-Tal and Nemirovski [7, Lemma 2.2] that $w \in \mathbb {R}$ satisfies

$$\begin{aligned} w \ge \sup \{ \pi (\varvec{x};\varvec{p}) \mid \varvec{p} \in P(\varvec{s}) \} \end{aligned}$$

if and only if

$$\begin{aligned} \begin{bmatrix} w I&(\mathop {\mathrm {diag}}\nolimits (\varvec{s}) Q)^{\top } \\ \mathop {\mathrm {diag}}\nolimits (\varvec{s}) Q&K(\varvec{x}) \\ \end{bmatrix} \succeq 0 \end{aligned}$$

(22)

holds. Consequently, problem (21) is equivalently rewritten as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } w \end{aligned}$$

(23a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad W(\varvec{x},\varvec{s},w) \succeq 0 , \end{aligned}$$

(23b)

$$\begin{aligned}&s_{j} = 1 , \quad \forall j \in J_{\mathrm {f}} , \end{aligned}$$

(23c)

$$\begin{aligned}&t_{i} \le s_{j} , \quad \forall i \in I(j); \ j=1,\dots ,d , \end{aligned}$$

(23d)

$$\begin{aligned}&\underline{x} \varvec{t} \le \varvec{x} \le \overline{x} \varvec{t} , \end{aligned}$$

(23e)

$$\begin{aligned}&\varvec{c}^{\top } \varvec{x} \le \overline{c} , \end{aligned}$$

(23f)

$$\begin{aligned}&\varvec{s} \in \{ 0,1 \}^{d} , \end{aligned}$$

(23g)

$$\begin{aligned}&\varvec{t} \in \{ 0,1 \}^{m} . \end{aligned}$$

(23h)

Problem (23) is an MISDP problem. By relaxing the 0–1 constraints into linear inequality constraints, we obtain an SDP relaxation. Since SDP can be solved efficiently with a primal-dual interior-point method, we can find a global optimal solution of problem (23) with a branch-and-bound method [61].

4.2 Treatment of members lying on a line

As explained in Sect. 2, for the robust truss topology optimization it is necessary to incorporate overlapping members to a ground structure. Since the existence of overlapping members in a final truss design is not accepted, it is required to incorporate the constraints prohibiting the presence of overlapping members in a truss design. To the best of the author’s knowledge, such a consideration cannot be found in literature on robust truss topology optimization.

Fig. 5

A ground structure consisting of 18 members

Recall that, for each $j=1,\dots ,d$, $s_{j}=1$ means that the node having the jth degree of freedom exists, and $s_{j}=0$ means that it vanishes. Also, $t_{i}=1$ means that member i exists and $t_{i}=0$ means that it vanishes. Let $L(j) \subseteq \{ 1,\dots ,m \}$ denote the set of indices of the members lying on the node having the jth degree of freedom. Figure 5 shows an example of ground structure with overlapping members. It has $m=18$ members and $d=12$ degrees of freedom of the nodal displacements. In this example, we have $L(j)=\{ 16,18 \}$ and $I(j)=\{ 1,4,13,14,17 \}$. If $s_{j}=1$, then all the members in L(j) cannot exist, i.e., $t_{i}=0$ $(\forall i \in L(J))$. Also, if there exists an $i \in L(j)$ such that $t_{i}=1$, then the corresponding node cannot exist, i.e., $s_{j}=0$. These two conditions can be formulated as

$$\begin{aligned} s_{j} \le 1-t_{i} , \quad \forall i \in L(j) . \end{aligned}$$

(24)

In the following, we add (24) to problem (23).

It is worth noting that a truss design involving a chain is infeasible for the presented robust optimization problem, because it is unstable and cannot be in equilibrium with uncertain forces applied at an intermediate node of the chain. Therefore, a solution obtained by the proposed method does not involve a member that is longer than the maximum member length of the ground structure. This might be considered an advantage of the robust topology optimization, because in a conventional truss topology optimization an optimal solution may possibly have a long chain and special treatment, such as the local buckling constraints [23, 41], is necessary for avoiding presence of a too long member.

5 Simple heuristic for robust truss topology optimization

The MISDP approach presented in Sect. 4 is only applicable to small-scale problem instances. Alternatively, in this section we present a heuristic having small computational cost. In Sect. 5.1, we reformulate our robust truss topology optimization as SDPCC. A concave–convex procedure is then applied to this formulation in Sect. 5.2.

5.1 Formulation as semidefinite programming with complementarity constraints

In this section, we reformulate problem (23) with constraint (24) as SDPCC, which is well suited for applying the concave–convex procedure.

We begin with constraints (23d) and (23e), which describe the relation between $s_{j}$ and $\varvec{x}$. Let $r_{j}$ $(j=1,\dots ,d)$ denote the sum of the cross-sectional areas of the members that are connected to the node having the jth degree of freedom, i.e.,

$$\begin{aligned} r_{j} = \sum _{i \in I(j)} x_{i} . \end{aligned}$$

(25)

Observe that $r_{j}>0$ implies $s_{j}=1$, because at least one member connected to the corresponding node exists and, hence, the node should exist. Also, $s_{j}=0$ implies that the corresponding node vanishes, and hence $r_{j}=0$, i.e., all the members connected to the node should vanish. These two assertions can be written as

$$\begin{aligned} (1 - s_{j}) r_{j} = 0 . \end{aligned}$$

(26)

Namely, constraint (23d) can be replaced with (26). For notational simplicity, in the following we write (25) as

$$\begin{aligned} \varvec{r} = R \varvec{x} \end{aligned}$$

with a constant matrix $R \in \mathbb {R}^{d \times m}$.

We next consider constraints (23e) and (24), which describe the relation between $s_{j}$ and $\varvec{x}$. Let $v_{j}$ $(j=1,\dots ,d)$ denote the sum of the cross-sectional areas of the members that lying across the node with the jth degree of freedom, i.e.,

$$\begin{aligned} v_{j} = \sum _{i \in L(j)} x_{i} . \end{aligned}$$

(27)

Observe that $v_{j}>0$ implies $s_{j}=0$, because at least one member lying across the corresponding node exists and, thence, the node should vanish. Also, $s_{j}=1$ implies that the corresponding node exists, and hence all the members lying across the node should vanish, i.e., $v_{j}=0$. These two assertions can be written as

$$\begin{aligned} s_{j} v_{j} = 0 . \end{aligned}$$

(28)

Namely, constraint (24) can be replaced with (28), For notational simplicity, we write (27) as

$$\begin{aligned} \varvec{v} = V \varvec{x} \end{aligned}$$

by using a constant matrix $V \in \mathbb {R}^{d \times m}$.

Finally, consider constraint (23e). For each $i=1,\dots ,m$, we introduce a new variable $z_{i} \in \mathbb {R}$ so that $\underline{x}-z_{i}$ corresponds to the lower bound for the cross-sectional area of member i. If $x_{i}>0$, then member i exists and the lower bound should be $\underline{x}$, which means $z_{i}=0$. Also, when the lower bound becomes smaller than $\underline{x}$ (i.e., $z_{i}>0$), then member i should vanish (i.e., $x_{i}=0$), and hence we set $z_{i}=\underline{x}$. These relations can be written as follows:

$$\begin{aligned} \underline{x} - z_{i}&\le x_{i} \le \overline{x} , \end{aligned}$$

(29)

$$\begin{aligned} 0&\le z_{i} \le \underline{x} , \end{aligned}$$

(30)

$$\begin{aligned} x_{i} z_{i}&= 0 . \end{aligned}$$

(31)

Consequently, constraints (23e) and (23h) can be replaced with (29), (30), and (31).

The upshot is that problem (23) incorporating constraint (24) is equivalently rewritten as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } w \end{aligned}$$

(32a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad W(\varvec{x},\varvec{s},w) \succeq 0 , \end{aligned}$$

(32b)

$$\begin{aligned}&s_{j} = 1 , \quad \forall j \in J_{\mathrm {f}} , \end{aligned}$$

(32c)

$$\begin{aligned}&\varvec{r} = R \varvec{x} , \end{aligned}$$

(32d)

$$\begin{aligned}&\varvec{v} = V \varvec{x} , \end{aligned}$$

(32e)

$$\begin{aligned}&\varvec{0} \le \varvec{s} \le \varvec{1} , \end{aligned}$$

(32f)

$$\begin{aligned}&\underline{x} \varvec{1} - \varvec{z} \le \varvec{x} \le \overline{x} \varvec{1} , \end{aligned}$$

(32g)

$$\begin{aligned}&\varvec{0} \le \varvec{z} \le \underline{x} \varvec{1} , \end{aligned}$$

(32h)

$$\begin{aligned}&\varvec{c}^{\top } \varvec{x} \le \overline{c} , \end{aligned}$$

(32i)

$$\begin{aligned}&(1 - s_{j}) r_{j} = 0 ,&j=1,\dots ,d , \end{aligned}$$

(32j)

$$\begin{aligned}&s_{j} v_{j} = 0 ,&j=1,\dots ,d , \end{aligned}$$

(32k)

$$\begin{aligned}&x_{i} z_{i} = 0 ,&i=1,\dots ,m . \end{aligned}$$

(32l)

Here, $\varvec{x}$, $\varvec{z}$, $\varvec{s}$, $\varvec{r}$, $\varvec{v}$, and w are variables to be optimized. Observe that any feasible solution of problem (32) satisfies $1-s_{j} \ge 0$, $r_{j} \ge 0$, $s_{j} \ge 0$, $v_{j} \ge 0$, $x_{i} \ge 0$, and $z_{i} \ge 0$. Therefore, constraints (32j), (32k), and (32l) are complementarity constraints. Constraint (32b) is a linear matrix inequality constraint in terms of $\varvec{x}$, $\varvec{s}$, and w. Thus, problem (32) has the form of SDPCC.

Remark 2

Since the algorithm presented in this paper consists of sequential approximation, adding some linear inequalities may possibly limit the search space and enhance the convergence. In the following, we consider linear valid inequalities, which naturally stem from the complementarity constraints and can be handled effectively in the numerical solution. Suppose that two variables, $\alpha$, $\beta \in \mathbb {R}$, are subjected to the complementarity constraint and their upper bounds are given, i.e.,

$$\begin{aligned} 0&\le \alpha \le \bar{\alpha } , \end{aligned}$$

(33)

$$\begin{aligned} 0&\le \beta \le \bar{\beta } , \end{aligned}$$

(34)

$$\begin{aligned} \alpha \beta&= 0 , \end{aligned}$$

(35)

where $\bar{\alpha }$ and $\bar{\beta }$ are positive constants. It is known that the inequality

$$\begin{aligned} \bar{\beta } \alpha + \bar{\alpha } \beta \le \bar{\alpha } \bar{\beta } \end{aligned}$$

serves as a valid constraint for (33), (34), and (35) [42, 63]. In the same manner, we can construct valid constraints for problem (32). Concerning (32j), observe that we obtain

$$\begin{aligned} 1 - s_{j}&\le 1 , \\ r_{j}&\le \overline{x} |I(j)| \end{aligned}$$

from (32f) and (25), respectively. Therefore, the constraints

$$\begin{aligned} {-}\overline{x} |I(j)| s_{j} + r_{j}&\le 0 , \quad j=1,\dots ,d \end{aligned}$$

(36)

are valid for (32j). Similarly, inequalities

$$\begin{aligned} \overline{x} |L(j)| s_{j} + v_{j}&\le \overline{x} |L(j)| , {\quad } j=1,\dots ,d, \end{aligned}$$

(37)

$$\begin{aligned} \underline{x} x_{i} + \overline{x} z_{i}&\le \underline{x} \overline{x}, {\quad }\qquad \,\,\, i=1,\dots ,m \end{aligned}$$

(38)

are valid constraints for (32k) and (32l), respectively. In the following, we add constraints (36), (37), and (38) to problem (32). $\square$

5.2 Penalty concave–convex procedure for robust truss topology optimization

Problem (32) has the form of problem (4) studied in Sect. 3.2. To see this, it is convenient to rewrite problem (32) as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } w \end{aligned}$$

(39a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{x},\varvec{z},\varvec{s},\varvec{r},\varvec{v},w) \in F , \end{aligned}$$

(39b)

$$\begin{aligned}&\varvec{1}-\varvec{s} \ge \varvec{0} , \quad \varvec{r} \ge \varvec{0} , \quad (\varvec{1}-\varvec{s})^{\top } \varvec{r} = 0 , \end{aligned}$$

(39c)

$$\begin{aligned}&\varvec{s} \ge \varvec{0} , \quad \varvec{v} \ge \varvec{0} , \quad \varvec{s}^{\top } \varvec{v} = 0 , \end{aligned}$$

(39d)

$$\begin{aligned}&\varvec{x} \ge \varvec{0} , \quad \varvec{z} \ge \varvec{0} , \quad \varvec{x}^{\top } \varvec{z} = 0 . \end{aligned}$$

(39e)

Here, F is defined by

$$\begin{aligned} F = \{ (\varvec{x},\varvec{z},\varvec{s},\varvec{r},\varvec{v},w) \mid \,&W(\varvec{x},\varvec{s},w) \succeq 0 , \ \varvec{r} = R \varvec{x} , \ \varvec{v} = V \varvec{x} , \nonumber \\&\varvec{0} \le \varvec{s} \le \varvec{1} , \ s_{j} = 1 \ (\forall j \in J_{\mathrm {f}}) , \nonumber \\&\underline{x} \varvec{1} - \varvec{z} \le \varvec{x} \le \overline{x} \varvec{1} , \ \varvec{0} \le \varvec{z} \le \underline{x} \varvec{1} , \ \varvec{c}^{\top } \varvec{x} \le \overline{c} , \nonumber \\&{-}\overline{x} |I(j)| s_{j} + r_{j} \le 0 \ (j=1,\dots ,d), \nonumber \\&\overline{x} |L(j)| s_{j} + v_{j} \le \overline{x} |L(j)| \ (j=1,\dots ,d), \nonumber \\&\underline{x} \varvec{x} + \overline{x} \varvec{z} \le \underline{x} \overline{x} \varvec{1} \} , \end{aligned}$$

which is a convex set. The complementarity constraints in (39c), (39d), and (39e) can be replaced with penalization terms added to the objective function as follows:

$$\begin{aligned}&\mathop {\mathrm {Minimize}}{\quad } w + \rho \phi (\varvec{1}-\varvec{s}, \varvec{r}) + \rho \phi (\varvec{s}, \varvec{v}) + \rho \phi (\varvec{x}, \varvec{z}) \end{aligned}$$

(40a)

$$\begin{aligned}&\mathop {\mathrm {subject~to}}\quad (\varvec{x},\varvec{z},\varvec{s},\varvec{r},\varvec{v},w) \in F . \end{aligned}$$

(40b)

Here, $\rho > 0$ is a sufficiently large penality parameter, and $\phi$ has been defined by (7). Problem (40) has the same form as problem (5).

We are now in position to apply Algorithm 1 to problem (40). Algorithm 1 solves the subproblem in (11), which is explicitly written as follows:

$$\begin{aligned}&\begin{array}{ll} \mathop {\mathrm {Minimize}}&{} w + \rho _{k} \phi _{+}(\varvec{1}-\varvec{s}, \varvec{r}) + \rho _{k} \phi _{+}(\varvec{s}, \varvec{v}) + \rho _{k} \phi _{+}(\varvec{x}, \varvec{z}) \\ &{} \quad - \rho _{k} \hat{\phi }_{-}(\varvec{1}-\varvec{s},\varvec{r}; \varvec{1}-\varvec{s}^{(k)},\varvec{r}^{(k)}) - \rho _{k} \hat{\phi }_{-}(\varvec{s},\varvec{v}; \varvec{s}^{(k)},\varvec{v}^{(k)})\\ &{} \quad - \rho _{k} \hat{\phi }_{-}(\varvec{x},\varvec{z}; \varvec{x}^{(k)},\varvec{z}^{(k)}) \end{array} \end{aligned}$$

(41a)

$$\begin{aligned}&\begin{array}{ll} \mathop {\mathrm {subject~to}}&\quad (\varvec{x},\varvec{z},\varvec{s},\varvec{r},\varvec{v},w) \in F . \end{array} \end{aligned}$$

(41b)

Here, $\phi _{+}$ and $\hat{\phi }_{-}$ are defined by (8) and (10), respectively. Since the constant terms in the objective function can be neglected, problem (41) can be reduced to the following problem:

$$\begin{aligned}&\begin{array}{ll} \mathop {\mathrm {Minimize}}&{} \quad w + \rho _{k} ( \Vert \varvec{x} + \varvec{z} \Vert ^{2} + \Vert \varvec{1} - \varvec{s} + \varvec{r} \Vert ^{2} + \Vert \varvec{s} + \varvec{v} \Vert ^{2}) \\ &{} \quad -2\rho _{k} (\varvec{x}^{(k)} - \varvec{z}^{(k)})^{\top } \varvec{x} -2\rho _{k} (\varvec{z}^{(k)} - \varvec{x}^{(k)})^{\top } \varvec{z}\\ &{} \quad - 2\rho _{k} (2 \varvec{s}^{(k)} + \varvec{r}^{(k)} - \varvec{v}^{(k)} - \varvec{1})^{\top } \varvec{s} \\ &{} \quad - 2\rho _{k} (\varvec{s}^{(k)} + \varvec{r}^{(k)} -\varvec{1})^{\top } \varvec{r} - 2\rho _{k} (\varvec{v}^{(k)} - \varvec{s}^{(k)})^{\top } \varvec{v} \end{array}\end{aligned}$$

(42a)

$$\begin{aligned}&\begin{array}{ll} \mathop {\mathrm {subject~to}}&\quad (\varvec{x},\varvec{z},\varvec{s},\varvec{r},\varvec{v},w) \in F . \end{array} \end{aligned}$$

(42b)

Problem (42) is a minimization problem of a convex quadratic function under a linear matrix inequality constraint. Hence, this problem can be recast as SDP. Thus, at each iteration of Algorithm 1 we solve an SDP problem.

As mentioned in Sect. 3.2, a reasonable stopping criterion is that (12) and (13) are satisfied. In practice, however, we might use a relaxed criterion, which may save some iterations before convergence. Specifically, we terminate the algorithm when either (12) or

$$\begin{aligned} \Vert \varvec{x}^{(k+1)} - \varvec{x}^{(k)} \Vert \le \epsilon _{2} \end{aligned}$$

(43)

is satisfied. Then, by using the obtained solution we can fix the set of existing members and the set of existing nodes. Fixing these sets means that one variable in all the complementarity constraints in problem (32) is fixed. Therefore, the problem now becomes SDP, which is to be solved as the post process. The solutions presented in Sect. 6 are obtained in this manner.

6 Numerical experiments

This section reports three numerical experiments.

The proposed algorithm was implemented in MATLAB ver. 9.0. At each iteration we solved an SDP problem in (42) by using CVX, a MATLAB package for specifying and solving convex optimization problems [20, 21]. SDPT3 ver. 4.0 [59] was used as a solver. Computation was carried out on a $2.2\,\mathrm {GHz}$ Intel Core i5 processor with $8\,\mathrm {GB}$ RAM. The Young modulus of the trusses in the following numerical examples is $20\,\mathrm {GPa}$.

The initial point for Algorithm 1 is chosen as follows. We first solve problem (17) for the nominal external load $\tilde{\varvec{p}}$, i.e., the compliance minimization without considering uncertainties,¹² and let $\varvec{x}^{(0)}$ be the obtained optimal solution. The initial values for the other variables are given by $\varvec{z}^{(0)}=\varvec{0}$, $\varvec{s}^{(0)}=\varvec{1}/2$, $\varvec{r}^{(0)}=R \varvec{x}^{(0)}$, and $\varvec{v}^{(0)}=V \varvec{x}^{(0)}$. The parameters of Algorithm 1 are $\rho _{0}=10^{-2}$, $\rho _{\mathrm {max}}=10^{6}$, and $\mu =1.5$. We terminate Algorithm 1 if either (12) or (43) is satisfied, where $\epsilon _{1}=2m\times 10^{-2} \,\mathrm {mm}^{2}$ and $\epsilon _{2}=10^{-2}\,\mathrm {mm}^{2}$. Then, as explained in Sect. 5.2, we fix one variable in all the complementarity constraints in problem (32), and solve the resulting SDP problem to obtain the final solution. The settings of the initial point and the parameters explained above were determined by preliminary numerical experiments. In Sect. 6.1, we consider three problem instances that could be solved with a global optimization method. Cantilever truss examples with two different loading conditions, which are frequently solved in structural optimization, are considered in Sects. 6.2 and 6.3.

6.1 Example (I): Comparison with global optimization

In this section, we consider the small-scale instances presented in Sect. 2. For comparison, the MISDP formulation, i.e., problem (23) with constraint (24), is solved with YALMIP [40]. YALMIP finds a global optimal solution of an MISDP problem with a branch-and-bound method, at each iteration of which an SDP problem is solved. We used YALMIP with the default setting, where SDP subproblems are solved with SeDuMi ver. 1.3 [48, 53].

Consider the problem settings in Figs. 2, 3, and 4. Table 1 lists the number of members (m), the number of degrees of freedom of displacements (d), and the upper bound for the structural volume ($\overline{c}$). In Figs. 2b and 3a, the nodes are aligned on a $1\,\mathrm {m} \times 1\,\mathrm {m}$ grid. In Fig. 4a, we use a $1\,\mathrm {m} \times 0.5\,\mathrm {m}$ grid. In Fig. 3a, the ground structure has all possible members connecting two nodes but are no longer than $3\,\mathrm {m}$. The nominal external load, $\tilde{\varvec{p}}$, is applied as shown in Figs. 2b, 3a and  4a. The uncertainty model of the external load is defined by using (19) with $\tilde{p}_{1}=100\,\mathrm {kN}$, $\alpha = 0.75 \tilde{p}_{1}$ for Figs. 2 and  3, and $\alpha = 0.5\tilde{p}_{1}$ for Fig. 4. The lower and upper bounds for the member cross-sectional areas are $\underline{x}=1\,\mathrm {mm^{2}}$ and $\overline{x}=700\,\mathrm {mm^{2}}$, respectively. In Table 1, “rob. opt.” reports the optimal value, obtained by YALMIP, of the robust optimization problem. The obtained solutions are shown in Figs. 2c, 3e and 4d. For reference, the optimal solutions of the (not robust) compliance minimization with the nominal external load, $\tilde{\varvec{p}}$, are shown in Figs. 1b, 3b and 4b.¹³ The optimal values are listed in “nom. opt.” of Table 1.

It is remarkable that, for every problem instance, the solution obtained by the proposed algorithm coincides with the global optimal solution (obtained by YALMIP). Table 2 reports the computational costs of the two methods, where “#iter.” is the number of iterations, and “time” is the required computational time. Note that the computational cost of the proposed method does not include the ones for generation of an initial point and for the post-processing. It is also worth noting that the problem size of SDP solved at each iteration of the proposed method is larger than that of YALMIP, and hence the computational time per an iteration required by the proposed method is larger than that of YALMIP. For every instance, the number of SDP problems solved by the proposed method is smaller than that of YALMIP.

In the experiments in this section, it has been observed that the proposed method converges to a global optimal solution for a small-scale problem instance. In Sects. 6.2 and 6.3, we examine large-scale instances that cannot be solved with a global optimization method within realistic computational time.

6.2 Example (II)

Table 1 Characteristics of the problem instances in example (I)

Table 2 Computational costs for example (I)

Fig. 6

Example (II). The problem setting for $(N_{X},N_{Y})=(6,2)$

Consider the ground structures shown in Fig. 6. The nodes are aligned on a $1\,\mathrm {m} \times 1\,\mathrm {m}$ grid, and the number of the nodes is $(N_{X}+1)(N_{Y}+1)$. The leftmost nodes are pin-supported. The candidate members are defined as follows. We first generate all possible members such that any two nodes are connected by a member. Then we remove members that are longer than $3\,\mathrm {m}$. It should be clear that the ground structure retains overlapping members.

As for the nominal external load, $\tilde{\varvec{p}}$, a vertical force is applied to the bottom rightmost node as shown in Fig. 6. The uncertainty model of the external load is given as explained in (19), where $\tilde{p}_{1}=100\,\mathrm {kN}$ and $\alpha = 0.5 \tilde{p}_{1}$. The lower and upper bounds for the member cross-sectional areas are $\underline{x}=50\,\mathrm {mm^{2}}$ and $\overline{x}=700\,\mathrm {mm^{2}}$. The upper bound for the structural volume is $\overline{c}=2N_{X}N_{Y} \times 10^{5}\,\mathrm {mm}^{3}$.

As for problem sizes, we consider six cases, $(N_{X},N_{Y})=(3,7)$, (4, 6), (5, 5), (6, 4), (7, 3), and (8, 2). Table 3 lists the number of members, the number of degrees of freedom of the nodal displacements, and the upper bound for the structural volume. Figure 7 collects the optimal solutions of the conventional (i.e., not robust) compliance minimization in (17) for the nominal external load, $\tilde{\varvec{p}}$. For the robust optimization, the solutions obtained by the proposed method are shown in Fig. 8. It is observed in Fig. 8a that the three chains in Fig. 7a are replaced with longer single members and four intermediate nodes are removed. The length of the bottom horizontal chain in Fig. 7c is $5\,\mathrm {m}$. This chain is replaced with two members in Fig. 8c, because the maximum member length in the ground structure is $3\,\mathrm {m}$. Similar observation can be made also in Fig. 8d, e. The nominal optimal solution in Fig. 7f has many thin members as well as many nodes. In contrast, the robust solution in Fig. 8f has simple topology, which may be considered practically preferable. In all the solutions in Fig. 8, the longest member is not longer than the maximum member length in the ground structure, as explained in Sect. 4.1.

The computational results are listed in Table 4. Here, “obj.” reports the objective value of the solution obtained by the proposed method, and $\tilde{w}$ is the compliance of this solution for the nominal external load, $\tilde{\varvec{p}}$. The optimal value of problem (17) for $\tilde{\varvec{p}}$ is listed as “nom. opt.” Therefore, $\tilde{w}$ is no smaller than the value of “nom. opt.” It is observed in Table 4 that these two values are very close. Namely, in these examples, robustness can be achieved with compensation of only very small increase of the nominal compliance.

Fig. 7

Example (II). The optimal solutions of the compliance minimization for the nominal external load. a $(N_{X},N_{Y})=(3,7)$; b (4, 6); c (5, 5); d (6, 4); e (7, 3); and f (8, 2)

Fig. 8

Example (II). The solutions obtained by the proposed method for the robust optimization under the load uncertainty. a $(N_{X},N_{Y}) = (3,7)$; b (4, 6); c (5, 5); d (6, 4); e (7, 3); and f (8, 2)

Table 3 Characteristics of the problem instances in example (II)

Table 4 Computational results of example (II)

Fig. 9

The optimal solution of problem (44), where $\bar{\varvec{s}}$ is defined from the solutions in Fig. 7

As explained in Sect. 2, one of difficulties of the robust truss topology optimization is that the uncertainty model of the external load depends on the existing nodes, i.e., on $\varvec{s}$. For comparison, we fix $\varvec{s}$ to obtain a robust solution. As a simple heuristic, we construct an estimate of $\varvec{s}$, denoted $\bar{\varvec{s}}$, from the existing nodes of a solution in Fig. 7. Then we solve the following robust optimization problem:

$$\begin{aligned} \begin{array}{ll} \mathop {\mathrm {Minimize}}&{} \quad w \\ \mathop {\mathrm {subject~to}}&{} \quad \sup \{ \pi (\varvec{x};\varvec{p}) \mid \varvec{p} \in P(\bar{\varvec{s}}) \} \\ &{} \quad \varvec{x} \ge \varvec{0} , \\ &{} \quad \varvec{c}^{\top } \varvec{x} \le \overline{c} . \end{array} \end{aligned}$$

This problem can be recast as SDP. For simplicity, the lower bound constraints on the cross-sectional areas of the existing members are omitted. The obtained solutions are shown in Fig. 9. The optimal value is reported in “fixed $\varvec{s}$” of Table 4. It should be clear that, at each solution in Fig. 9, uncertain external forces are applied only to the nodes that the corresponding solution in Fig. 7 has. Nevertheless, the objective value of a solution in Fig. 9 is much larger than that of the corresponding solution in Fig. 8. In other words, the solution obtained by the proposed method has quite high quality.

6.3 Example (III)

Fig. 10

Example (III). The problem setting for $(N_{X},N_{Y})=(6,2)$

Fig. 11

Example (III)-1. The optimal solutions of the compliance minimization for the nominal external load. a $(N_{X},N_{Y})=(5,2)$; b (6, 2); c (7, 2); d (8, 2); and e (9, 2)

Fig. 12

Example (III)-1. The solutions obtained by the proposed method for the robust optimization under the load uncertainty. a $(N_{X},N_{Y})=(5,2)$; b (6, 2); c (7, 2); d (8, 2); and e (9, 2)

Table 5 Characteristics of the problem instances in example (III)

Table 6 Computational results of example (III)

Fig. 13

Example (III)-2. The optimal solutions of the compliance minimization for the nominal external load. a $(N_{X},N_{Y})=(5,4)$; b (6, 4); c (7, 4); d (8, 4); and e (9, 4)

Fig. 14

Example (III)-2. The solutions obtained by the proposed method for the robust optimization under the load uncertainty. a (5, 4); b (6, 4); c (7, 4); d (8, 4); and e (9, 4)

Fig. 15

Example (III)-3. The optimal solutions of the compliance minimization for the nominal external load. a (5, 6); b (6, 6); c (7, 6); d (8, 6); and e (9, 6)

Fig. 16

Example (III)-3. The solutions obtained by the proposed method for the robust optimization under the load uncertainty. a (5, 6); b (6, 6); c (7, 6); d (8, 6); and e (9, 6)

Consider the problem setting shown in Fig. 10. Ground structures are generated in the manner explained in Sect. 6.2. The maximum length of the members in a ground structure is $3\,\mathrm {m}$. The uncertainty model of the external load is defined by using (19) with $\tilde{p}_{1}=100\,\mathrm {kN}$ and $\alpha =0.75\tilde{p}_{1}$. The lower and upper bounds for the member cross-sectional areas are $\underline{x}=50\,\mathrm {mm^{2}}$ and $\overline{x}=500\,\mathrm {mm^{2}}$, respectively. The upper bound for the structural volume is $\overline{c}=4N_{X}N_{Y} \times 10^{5}\,\mathrm {mm}^{3}$.

For problem instances with $(N_{X},N_{Y})=(5,2)$, $(6,2),\dots ,(9,2)$, Fig. 11 shows the optimal solutions of the compliance minimization for the nominal external load. For the robust optimization, the solutions obtained by the proposed method are collected in Fig. 12. The problem sizes are listed in Table 5. The computational results are listed in Table 6. It is observed in Fig. 12a, d that the intermediate nodes on chains in Fig. 11a, d are removed as a result of robust optimization. Although the nominal optimal solutions in Fig. 11b, c, e have very complicated forms, the robust solutions in Fig. 12b, c, e are simple and practically preferable. Thus, it is often that robustness against uncertain loads and the minimal cross-sectional area constraints for the existing members yield simple truss topology.

The solutions obtained for the instances with $(N_{X},N_{Y})=(5,4)$, $(6,4),\dots ,(9,4)$ are collected in Figs. 13 and  14. The robust optimal solution obtained by the proposed method has a form similar to the corresponding nominal optimal solution, but many chains in the nominal optimal solution are replaced with single members.

The solutions obtained for the instances with $(N_{X},N_{Y})=(5,6)$, $(6,6),\dots ,(9,6)$ are collected in Figs. 15 and  16. It is observed that the nominal optimal solutions in Fig. 15c, e have so many thin members. In contrast, the robust solutions in Fig. 16c, e have fewer members. The layout of thick members in Fig. 16b is different from that in Fig. 15b. Also, the layout of thick members in Fig. 16d is different from that in Fig. 15d.

It is observed in Table 6 that the proposed method converged mostly within 40 iterations. The computational time for the instance with about 600 members is about 10 min. Thus, the proposed method finds a reasonable feasible solution with relatively small computational cost.

7 Conclusions

In this paper, we have presented a new formulation and algorithm for robust truss topology optimization considering uncertainty in the external load. Specifically, combinatorial aspects of the problem have been dealt with in the framework of the complementarity constraints. As for the uncertainty model of the external load, we have supposed that uncertain external forces can be applied to all the nodes of a truss. This model depends on the set of existing nodes, and hence on the set of existing members, while the member cross-sectional areas are the design variables to be optimized. Thus, the robust optimization problem involves design-dependent constraints. Also, it has been explained that overlapping members should be incorporated to a ground structure. In the final truss design, however, presence of overlapping members is not allowed from a practical point of view. In this paper, the set of existing nodes, the selection among overlapping members, and the lower bound constraints for the cross-sectional areas of the existing members are treated by using the complementarity constraints.

In the conventional truss topology optimization, it is often that an optimal solution has a sequence of parallel consecutive members, called a chain. To stabilize a truss, a chain is replaced with a longer single member. Special consideration, such as the local buckling constraints, is needed to avoid presence of a too long member converted from a chain. In contrast, the solution obtained with the proposed method does not have a member which is longer than the maximum member length of the ground structure, because a truss design including a chain is infeasible for the presented robust optimization problem.

This paper has presented an SDPCC (semidefinite programming with complementarity constraints) formulation of a structural optimization problem. Then, its DC programming reformulation has been solved with a convex-concave procedure. This algorithm is a version of MM algorithms and EM algorithms, which are widely used in machine learning, image processing, etc. It has been shown through the numerical experiments that the proposed heuristic can converge to a high-quality solution within relatively small computational cost. The method can certainly handle complementarity constraints other than the ones presented in this paper. An example is a set of constraints that prohibits the presence of mutually crossing members in a truss design.