Topology optimization of truss-like structures with bidirectional non-orthogonal materials based on mathematical programming

Abstract

Topology optimization of structures composed of truss-like members has been shown to produce results that are very close to the theoretical solution. However, solving complex optimization problems based on the traditional orthogonal truss-like material model remains a challenge. This article proposes a unified framework for solving topology optimization problems based on a non-orthogonal truss-like material model. The framework first establishes a new non-orthogonal truss-like material model that considers the stiffness singularity problem. Several strategies for dynamically changing shear stiffness are studied comparatively. Then, a globally convergent moving asymptote method is employed in three numerical examples, including minimum compliance problems under single and multiple load cases, as well as a stress-constrained problem for an L-shaped design domain. Finally, optimal truss-like structures are obtained with the help of a simple post-processing method. Numerical examples demonstrate that the optimization results for the multiple load cases are better than those obtained using traditional methods for minimum compliance problems. The framework can efficiently solve different types of optimization problems in a unified form, which confirms the effectiveness and advantages of the proposed method.

1 Introduction

Topology optimization is a computational design method that automates the process of generating an optimal structural layout based on a set of design requirements. In contrast to size and shape optimization, topology optimization is not constrained by the initial topological configuration of the structure. As a result, the structures generated by topology optimization outperform those designed using engineers' intuition and manual experience. Consequently, topology optimization has gained significant momentum and is now widely applied in various fields such as aerospace structures (Zhu et al. 2016), architecture (Beghini et al. 2014), 3D printing (Rosen 2016; Zhu et al. 2021), and more, owing to its substantial benefits.

Over the past few decades, various numerical optimization methods have been developed for topology optimization. These methods can be primarily categorized into two groups based on the material field description: density-based methods and geometry-based methods. Density-based methods, such as the pioneering homogenization method (Bendsøe and Kikuchi 1988) introduced by Bendsøe and Kikuchi, use material-related parameters as design variables, with optimization results represented as the detailed material distribution at each point within the design domain. Additional density-based methods include the solid isotropic material with penalization (SIMP) method (Bendsøe 1989; Rozvany and Zhou 1991), evolutionary structural optimization (ESO) method (Xie and Steven 1993, 1994), multi-scale topology optimization (MTO) method (Sigmund 1994, 2000; Sigmund and Torquato 1997), de-homogenization method (Groen and Sigmund 2018; Groen et al. 2020, 2019), free material optimization (FMO) method (Ben-Tal et al. 2000; Bendsoe et al. 1994; Zowe et al. 1997) and others. In contrast, the level set method (Sethian and Wiegmann 2000; Wang et al. 2003; Zhu et al. 2015) introduced by Osher and Sethian (Osher and Sethian 1988) defines the structural boundary through the level set, where the function's value is zero. The optimal topology is found by evolving the implicit level set equation. Moving morphable components (MMC) (Guo et al. 2016, 2014; Zhang et al. 2020) or moving morphable voids (MMV) (Coniglio et al. 2020; Hoang and Jang 2017; Norato et al. 2015) methods and related methods treat structural topology as a combination of a finite number of moving morphable components and indirectly realize the topological change of the material distribution field by manipulating geometric features.

The Michell-truss analytical solution (Lewiński and Rozvany 2007; Michell 1904; Rozvany 1998) has always been the standard for comparing numerical optimization results. It's a fine mesh based on beam elements or truss-like rod elements (Cheng 1981), forming a continuum structure. However, Sigmund (Sigmund et al. 2016) points out that interpreting the Michell-truss analytical solution as a discrete frame structure is inaccurate. This is because limiting the structure's topology to frame-like structures is a severe design limitation that results in structures that are far from optimal in terms of stiffness. Optimized truss structures, topology optimization based on homogenization of rank-n laminates (Bendsøe 1989), and even generalized shapes of perforated plates can become Michell-like (Bendsøe and Haber 1993; Rozvany et al. 1987). Thus, the variable-thickness plate-shell structure or the variable-thickness anisotropic plate-shell structure (Sigmund et al. 2016) is the real optimal structure.

Density-based optimization methods, such as homogenization, MTO, and FMO, can obtain optimal topological structures that reflect more details of material distribution than geometry-based topology optimization methods. The de-homogenization method (Groen and Sigmund 2018; Groen et al. 2019) has produced well-connected mono-scale designs from a spatially varying multi-scale design. It provides a solution that is easier to manufacture and closer to the theoretical solution. Due to exceptional properties, lattice structure is highly appealing as a material for various design applications. Some topology optimization methods, such as the geometry projection technique (Kazemi et al. 2020), isogeometric TO (ITO) scheme (Wang et al. 2017), Approximation of Reduced Substructure with Penalization (ARSP) model (Wu et al. 2019), have been successfully extended to lattice structure design. Wu et al. (2021) presented a method to design conforming lattice structures by extending homogenization-based topology optimization and field-aligned parameterization. From the manufacturability point of view, the researchers also proposed some lattice structure design strategies (Panesar et al. 2018; Wang et al. 2018, 2023) applicable to additive manufacturing technology. However, density-based optimization methods face significant challenges in dealing with material homogenization (Guedes and Kikuchi 1990; Hassani and Hinton 1998a, b), connectivity between microstructures, and high computational costs.

In order to avoid the above problems, a simple and efficient anisotropic material model (Zhou and Li 2005) with fewer degrees of freedom (DOFs) can be employed. The anisotropic material has a Poisson's ratio of zero, a variable shear modulus, and its density is proportional to the sum of the directional stiffnesses. During the topology optimization, the material properties at each finite element (FE) node are used as design variables. The previous research work is mainly based on the orthogonal truss-like material model and the criterion method. The generality and solution efficiency of traditional methods are low or even impossible when facing complex loading cases. In this article, a new unified solution framework based on a non-orthogonal truss-like material model is proposed. It firstly addresses the problem of stiffness matrix singularity by introducing a set of base materials and builds a general non-orthogonal truss-like material model. Based on this model, we derive the optimization problem formulation considering the minimum compliance and stress constraints and the gradient-based sensitivity formulation, respectively, and propose several shear stiffness update strategies. Finally, three numerical examples are solved using a globally convergent moving asymptote method (Svanberg 1987, 2001), which verifies the effectiveness of the method in this article.

The rest of this article is organized as follows. Section 2 briefly reviews the orthogonal truss-like material model. Section 3 develops a new non-orthogonal truss-like material model, proposes several strategies for updating the shear stiffness, and derives the optimization problem formulation and the gradient-based sensitivity formulation respectively. Numerical examples are presented in Sect. 4 to illustrate the validity and effectiveness of the proposed method. The conclusions of this study are presented in Sect. 5.

2 Orthogonal truss-like material model

In the plane stress state, Michell truss-like can be treated as a continuum constructed of 2D materials with special properties (Sigmund et al. 2016):

• (a) Structures made of materials with stiffness in only two orthogonal directions (corresponding to the principal strain directions).

• (b) The direction density is proportional to the absolute value of the corresponding principal stress.

• (c) The total density is equal to the sum of the directional densities.

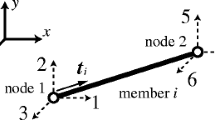
The truss-like material model is a fundamental model derived from the aforementioned properties. As depicted in Fig. 1a, a microelement, denoted as ${\text{d}}V$, represents a localized portion within a thin plate. It comprises two distinct components: the base material and the reinforced material. The reinforced material consists of a dense configuration of embedded members oriented along a specific direction within the weaker base material. In the microelement, the total cross-sectional area comprising both the members and the base material is denoted as ${\text{d}}A_{t}$. Additionally, the sum of the areas of the reinforced members is represented by ${\text{d}}A_{1}$. Define the average stress in the two parts of the material as $\sigma$ and the true stress in the members as $\sigma^{\prime}$. According to the equilibrium relationship we have

$$\sigma {\text{d}}A_{t} = \sigma^{\prime}{\text{d}}A_{1} .$$

(1)

Fig. 1

Truss-like material model: a density model of truss-like members; b orthogonal truss-like members

The density of truss-like members in a microelement can be defined as

$$t = \frac{{{\text{d}}A_{1} }}{{{\text{d}}A_{t} }}.$$

(2)

Assuming that there are two groups of orthogonal members distributed at any point in the design domain. As shown in Fig. 1b, two sets of orthogonal member directions are defined as the material principal axes. The material densities of these two material principal axes are denoted as $t_{1} ,t_{2}$, respectively. All members are made of the same material, and Young's modulus is denoted as $E$. At the macroscopic level, the relationship between stress and strain along the two material principal axes is given by

$$\left[ \begin{gathered} \sigma_{1} \hfill \\ \sigma_{2} \hfill \\ \tau_{12} \hfill \\ \end{gathered} \right] = E \cdot {\text{diag}}\left( {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {\frac{{\left( {t_{1} + t_{2} } \right)}}{4}} \\ \end{array} } \right)\left[ \begin{gathered} \varepsilon_{1} \hfill \\ \varepsilon_{2} \hfill \\ \gamma_{12} \hfill \\ \end{gathered} \right] = \overline{\varvec{D}}_{0} \left[ \begin{gathered} \varepsilon_{1} \hfill \\ \varepsilon_{2} \hfill \\ \gamma_{12} \hfill \\ \end{gathered} \right],$$

(3)

where $\sigma_{1} ,\sigma_{2} ,\tau_{12}$ and $\varepsilon_{1} ,\varepsilon_{2} ,\gamma_{12}$ represent the stress and strain components along the material principal axes, respectively. The elastic matrix in the direction of the principal axis of the material is $\overline{\varvec{D}}_{0} = E \cdot {\text{diag}}\left( {\begin{array}{*{20}c} {t_{1} } & {t_{2} } & {\frac{{\left( {t_{1} + t_{2} } \right)}}{4}} \\ \end{array} } \right)$.

Define the coordinate transformation matrix as ${\varvec{T}}$. The angle between the material principal axis and the Cartesian coordinate system is $\alpha$. The constitutive equation at any point is

$$\left[ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{y} \hfill \\ \tau_{xy} \hfill \\ \end{gathered} \right] = {\varvec{T}}^{{\text{T}}} (\alpha )\left[ \begin{gathered} \sigma_{1} \hfill \\ \sigma_{2} \hfill \\ \tau_{12} \hfill \\ \end{gathered} \right] = {\varvec{T}}^{{\text{T}}} (\alpha )\overline{\varvec{D}}_{0} \left[ \begin{gathered} \varepsilon_{1} \hfill \\ \varepsilon_{2} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right] = {\varvec{T}}^{{\text{T}}} (\alpha )\overline{\varvec{D}}_{0} {\varvec{T}}(\alpha )\left[ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{y} \hfill \\ \gamma_{xy} \hfill \\ \end{gathered} \right],$$

(4)

where $\sigma_{x} ,\sigma_{y} ,\tau_{xy}$ and $\varepsilon_{x} ,\varepsilon_{y} ,\gamma_{xy}$ represent the stress and strain components along the coordinate axes, respectively. The coordinate transformation matrix ${\varvec{T}}$ is

$${\varvec{T}}(\alpha ) = \left[ {\begin{array}{*{20}c} {\cos^{2} \alpha } & {\sin^{2} \alpha } & {0.5\sin 2\alpha } \\ {\sin^{2} \alpha } & {\cos^{2} \alpha } & { - 0.5\sin 2\alpha } \\ { - \sin 2\alpha } & {\sin 2\alpha } & {\cos 2\alpha } \\ \end{array} } \right].$$

(5)

From formula (4), the elastic matrix ${\varvec{D}}\left( {t_{1} ,t_{2} ,\alpha } \right)$ based on the orthogonal truss-like material model is

$${\varvec{D}}\left( {t_{1} ,t_{2} ,\alpha } \right) = {\varvec{T}}^{{\text{T}}} (\alpha )\overline{\varvec{D}}_{0} {\varvec{T}}(\alpha ).$$

(6)

3 Topology optimization with non-orthogonal truss-like materials

3.1 Bidirectional non-orthogonal truss-like material model

Two bidirectional nonorthogonal truss-like material models with variable shear stiffness are investigated as shown in Fig. 2. It is assumed that there are two sets of non-orthogonal members. The density and orientation angles of the members are $t_{1} ,t_{2}$ and $\alpha_{1} ,\alpha_{2}$ respectively. The elastic matrices $\overline{\varvec{D}}_{1} ,\overline{\varvec{D}}_{2}$ along the two member directions are

$$\begin{gathered} \overline{\varvec{D}}_{1} = E \cdot {\text{diag[}}\begin{array}{*{20}c} {t_{1} } & 0 & {{{(1 - R_{G} )} \mathord{\left/ {\vphantom {{(1 - R_{G} )} 4}} \right. \kern-0pt} 4}} \\ \end{array} {],} \\ \overline{\varvec{D}}_{2} = E \cdot {\text{diag[}}\begin{array}{*{20}c} {t_{2} } & 0 & {{{(1 - R_{G} )} \mathord{\left/ {\vphantom {{(1 - R_{G} )} 4}} \right. \kern-0pt} 4}} \\ \end{array} {],} \\ \end{gathered}$$

(7)

where $R_{G}$ is defined as the shear ratio. The shear stiffness of the material cannot be zero. According to formulas (6) and (7), the elastic matrix ${\varvec{D}}\left( {t_{1} ,t_{2} ,\alpha_{1} ,\alpha_{2} } \right)$ based on the bidirectional non-orthogonal truss-like material model is

$${\varvec{D}}\left( {t_{1} ,t_{2} ,\alpha_{1} ,\alpha_{2} } \right) = {\varvec{T}}^{{\text{T}}} (\alpha_{1} )\overline{\varvec{D}}_{1} {\varvec{T}}(\alpha_{1} ) + {\varvec{T}}^{{\text{T}}} (\alpha_{2} )\overline{\varvec{D}}_{2} {\varvec{T}}(\alpha_{2} ).$$

(8)

Fig. 2

Two groups of non-orthogonal truss members

Equation (8) can also be written as

$${\varvec{D}}\left( {t_{1} ,t_{2} ,\alpha_{1} ,\alpha_{2} } \right) = E\sum\limits_{b = 1}^{2} {t_{b} \sum\limits_{r = 1}^{6} {g_{r} (\alpha_{b} ){\varvec{A}}_{r} } } ,$$

(9)

where $g_{r}$ is the $r{\text{ - th}}$ element in matrix ${\varvec{g}}\left( \alpha \right)$,

$${\varvec{g}}(\alpha ) = \left[ {\begin{array}{*{20}c} {R_{G} \cos 4\alpha } & {R_{G} \sin 4\alpha } & {\cos 2\alpha } & {\sin 2\alpha } & {R_{G} } & 1 \\ \end{array} } \right].$$

(10)

The constant matrix ${\varvec{A}}_{r}$ is

$$\begin{aligned} & {\varvec{A}}_{1} = \frac{1}{8}\left[ {\begin{array}{*{20}c} 1 & { - 1} & 0 \\ { - 1} & 1 & 0 \\ 0 & 0 & 0 \\ \end{array} } \right],\quad {\varvec{A}}_{2} = \frac{1}{8}\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ 0 & 0 & { - 1} \\ 1 & { - 1} & 0 \\ \end{array} } \right],\quad {\varvec{A}}_{3} = \frac{1}{2}{\text{diag}}\left( {\begin{array}{*{20}c} 1 & { - 1} & 0 \\ \end{array} } \right) \\ & {\varvec{A}}_{4} = \frac{1}{4}\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \\ \end{array} } \right],\quad {\varvec{A}}_{5} = \frac{1}{8}\left[ {\begin{array}{*{20}c} 0 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \\ \end{array} } \right],\quad \, {\varvec{A}}_{6} = \frac{1}{2}{\text{diag}}\left( {\begin{array}{*{20}c} 1 & 1 & {{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}} \\ \end{array} } \right). \\ \end{aligned}$$

(11)

3.2 The singularity problem with the stiffness of materials

The method proposed in this article is based on a bidirectional nonorthogonal truss-like material model. The densities and orientation angles of the non-orthogonal truss-like members at the four nodes of the finite element are denoted as $t_{bj}$ and $\alpha_{bj}$ respectively. As shown in Fig. 3b, the member density $t_{bj}$ and the angle $\alpha_{bj}$ are selected as the design variables. Where $j = 1,2,3,...,n_{nd}$ represents the node index number, and $n_{nd}$ represents the total number of nodes. $b = 1,2$ refers to the number of the two member directions. Combined with formula (9), the elastic matrix ${\varvec{D}}_{1}$ at any point inside the finite element is

$${\varvec{D}}_{1} = E\sum\limits_{{j \in S_{e} }} {N_{j} (\xi ,\eta )\sum\limits_{b = 1}^{2} {t_{bj} \sum\limits_{r = 1}^{6} {g_{r} (\alpha_{bj} ){\varvec{A}}_{r} } } } ,$$

(12)

where $e$ is the finite element number, $N_{j} (\xi ,\eta )$ is the shape function, $\xi ,\eta$ is the local coordinate, $S_{e}$ is the set of nodes in the finite element $e$.

Fig. 3

Meshing in Finite Element Method (FEM): a elements and nodes; b interpolation of truss-like member properties within element

In contrast to orthogonal truss-like members, the orientation angles of the two members in the non-orthogonal truss-like material model are independent of each other. This means that the overlap of the members leads to stiffness matrix singularities.

As shown in Fig. 4a, two groups of dense truss-like members with the same density are distributed in a micro-element. Define the angles of the two groups of members as $\alpha_{1} ,\alpha_{2}$ respectively, the included angle of the members as $\Delta \alpha$, and the uniformly distributed stress in the horizontal direction as $\sigma_{x}$. If the included angle remains constant, both sets of members rotate in a circular motion. The resulting strain in the horizontal direction can be plotted as a closed curve in a polar coordinate system. As shown in Fig. 4b, the hoop coordinate of the polar coordinate system is the member’s angle, and the radial coordinate represents the normalized horizontal strain. Since the stress $\sigma_{x}$ is constant, the strain profile reflects the distribution of material stiffness along different directions. When the value of the included angle $\Delta \alpha$ is ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$, the strain profile is a standard circle. The stiffness of the material is consistent in all directions. However, as the included angle between the members gradually decreases, the difference in material stiffness between different directions becomes more pronounced. When the two members align perfectly, the stiffness along their normal direction approaches zero, resulting in a singular stiffness matrix in the finite element method.

Fig. 4

Influence of angles on directional stiffness: a micro-element of a non-orthogonal truss-like material; b horizontal strains corresponding to different member angles

To prevent the singularity of the stiffness matrix in this study, a set of weak-density orthogonal members was incorporated into the bi-directional non-orthogonal material model. The corresponding elastic matrix is denoted as

$${\varvec{D}}_{0} = E \cdot {\text{diag[}}\begin{array}{*{20}c} {t_{0} } & {t_{0} } & {{{t_{0} } \mathord{\left/ {\vphantom {{t_{0} } 2}} \right. \kern-0pt} 2}} \\ \end{array} {],}$$

(13)

where $t_{0}$ is the member density as the base material. According to Eqs. (12) and (13), the elastic matrix of the bidirectional nonorthogonal material model at any point in the finite element is

$${\varvec{D}}_{e} = {\varvec{D}}_{0} + {\varvec{D}}_{1} .$$

(14)

The equilibrium equation of the finite element method is

$${\varvec{K}}(t_{bj} ,\alpha_{bj} ){\varvec{u}}_{l} = {\varvec{F}}_{l} ,$$

(15)

where ${\varvec{K}}(t_{bj} ,\alpha_{bj} )$ is the global stiffness matrix, and ${\varvec{u}}_{l} ,{\varvec{F}}_{l}$ are the global nodal displacement vector and the known external load vector in the $l{\text{ - th}}$ load case, respectively. The global stiffness matrix of the structure is

$${\varvec{K}}(t_{bj} ,\alpha_{bj} ) = \sum\limits_{e = 1}^{{n_{e} }} {{\varvec{k}}_{e} } ,$$

(16)

where $n_{e}$ is the total number of finite elements. The element stiffness matrix is

$${\varvec{k}}_{e} = \int_{{\Omega_{e} }} {{\varvec{B}}^{{\text{T}}} {\varvec{D}}_{e} {\varvec{B}}h{\text{d}}A} ,$$

(17)

where $h$ is the thickness of the integration domain. ${\varvec{B}}$ is the geometric matrix. $\Omega_{e}$ is the $e{\text{ - th}}$ finite element field. According to formulas (12), (13), (16) and (17), the following equation can be determined.

$${\varvec{K}} = {\varvec{K}}_{0} + {\varvec{K}}_{1} .$$

(18)

The stiffness matrices corresponding to the elastic matrices ${\varvec{D}}_{0} ,{\varvec{D}}_{1}$ are ${\varvec{K}}_{0} ,{\varvec{K}}_{1}$, respectively.

$${\varvec{K}}_{0} = \sum\limits_{e = 1}^{{n_{e} }} {\int_{{\Omega_{e} }} {{\varvec{B}}^{{\text{T}}} {\varvec{D}}_{0} {\varvec{B}}h{\text{d}}A} } ,$$

(19)

$$\begin{aligned} {\varvec{K}}_{1} & = \sum\limits_{e = 1}^{{n_{e} }} {\sum\limits_{{j \in S_{e} }} {\sum\limits_{b = 1}^{2} {t_{bj} \sum\limits_{r}^{6} {g_{r} (\alpha_{bj} ){\varvec{H}}_{ejr} } } } } \\ & = \sum\limits_{j = 1}^{{n_{nd} }} {\sum\limits_{{e \in S_{j} }} {\sum\limits_{b = 1}^{2} {t_{bj} \sum\limits_{r}^{6} {g_{r} (\alpha_{bj} ){\varvec{H}}_{ejr} } } } } , \\ \end{aligned}$$

(20)

where $n_{e}$ is the total number of elements, $S_{j}$ is the set of elements around the $j{\text{ - th}}$ node, the matrix ${\varvec{H}}_{ejr}$ is

$${\varvec{H}}_{ejr} = E\int\limits_{{\Omega_{e} }} {N_{j} {\varvec{B}}^{{\text{T}}} {\varvec{A}}_{r} {\varvec{B}}h{\text{d}}A} .$$

(21)

Deriving formula (18) separately for each design variable, the sensitivity formula of the stiffness matrix can be expressed as:

$$\frac{{\partial {\varvec{K}}}}{{\partial t_{bj} }} = \frac{{\partial {\varvec{K}}_{1} }}{{\partial t_{bj} }} = \sum\limits_{{e \in S_{j} }} {\sum\limits_{r}^{6} {g_{r} (\alpha_{bj} ){\varvec{H}}_{ejr} } } ,$$

(22)

$$\frac{{\partial {\varvec{K}}}}{{\partial \alpha_{bj} }} = \frac{{\partial {\varvec{K}}_{1} }}{{\partial \alpha_{bj} }} = \sum\limits_{{e \in S_{j} }} {t_{bj} \sum\limits_{r}^{6} {g^{\prime}_{r} (\alpha_{bj} ){\varvec{H}}_{ejr} } }$$

(23)

where $g^{\prime}_{r} (\alpha_{bj} )$ represents the derivative of $g_{r} (\alpha_{bj} )$ with respect to variable $\alpha_{bj}$.

3.3 Strategies for variation of shear stiffness

This section primarily focuses on the update strategy of shear stiffness in the non-orthogonal material model during the optimization process. From the point of view of the analytical solution, the optimal Michell-truss is a structure that does not assume shear action. However, the absence of shear stiffness in the material can cause singularity issues in the stiffness matrix during finite element numerical calculations. To obtain a structure closer to the analytical solution, it may be feasible to dynamically adjust the shear stiffness throughout the optimization process.

In formula (7), we control the shear stiffness of the material by adjusting the parameter $R_{G}$, where $R_{G} \in [0,1]$. When the parameter $R_{G}$ takes different values, the normalized strain distribution along different directions of the material model is shown in Fig. 5. The strain in various directions can also indicate the stiffness of a material. Generally, a larger strain value under the same load indicates a smaller stiffness. Combining Figs. 4 and 5, it is evident that an increase in parameter $R_{G}$ results in a gradual irregularity of the stiffness distribution outer contour of non-orthogonal materials. Especially as shown in Fig. 5c, the extremely irregular material strain outer profile undoubtedly increases the difficulty of the topology optimization process.

Fig. 5

Strain along different directions of the material for different $R_{G}$ values

In this article, two common functional forms are used to dynamically update the parameter $R_{G}$.

$$R_{G} = \left\{ \begin{aligned} &{\text{case}}(1):\quad f_{1} (\ell_{5} ) = \left( {1 - \ell_{5} } \right)^{q} \hfill \\ &{\text{case(2)}}:\quad f_{2} (\ell_{5} ) = - \frac{1}{n}\lg \left( {\ell_{5} } \right) \hfill \\ \end{aligned} \right..$$

(24)

where $\ell_{5}$ is the average rate of change of the last five times of the objective function, $\ell_{\min } = 10^{ - n}$ is the lower limit of the average rate of change, and $q$ is the penalty factor. Define

$$\ell_{5} = \max \{ \min \{ \ell_{5} ,1\} ,\ell_{\min } \} .$$

(25)

In the power function form, five different values of $q$ are taken to study the influence of different update strategies on the optimization process. The variation trend of parameter $R_{G}$ with $\ell_{5}$ is shown in Fig. 6.

Fig. 6

Variation trend of parameter $R_{G}$ with different cases

Based on the analysis of the results in Sect. 4.2.3, in the optimization problem, it is a better choice to choose the shear stiffness update strategy in the form of a power function or a relatively large value of $q \ge 10$.

3.4 Minimum compliance problem with multi-load cases

3.4.1 Problem statement

For a compliance problem, in this study, the structural compliance minimization problem under volume constraints in a two-dimensional plane is investigated. As shown in Fig. 7, the displacement and force boundary conditions in the design domain $\Omega$ are defined as $\Gamma_{u} ,\Gamma_{f}$, respectively. The known load vector for case $l$ is ${\varvec{F}}_{l}$, ${\varvec{u}}_{l}$ is the corresponding structural displacement. The formulation of a volume-constrained compliance minimization optimization problem with multiple load cases is

$$({\mathbb{P}}_{1} )\left\{ {\begin{array}{*{20}l} {{\text{find}}\quad {\varvec{x}}_{bj} \quad (b = 1,2;j = 1,2,3,...,n_{nd} )} \hfill \\ {\min \quad c = \sum\limits_{l} {w_{l} {\varvec{F}}_{l}^{{\text{T}}} {\varvec{u}}_{l} ({\varvec{x}}_{bj} )} } \hfill \\ {{\text{s}}.{\text{t}}{.}\quad {\varvec{K}}({\varvec{x}}_{bj} ){\varvec{u}}_{l} ({\varvec{x}}_{bj} ) = {\varvec{F}}_{l} } \hfill \\ {\quad \quad \quad {0} \le t_{bj} \le t_{\max } \, } \hfill \\ {\quad \quad \quad V \le V_{0} } \hfill \\ \end{array} ,} \right.$$

where ${\varvec{x}}_{bj} = \left[ {\begin{array}{*{20}c} {t_{bj} } & {\alpha_{bj} } \\ \end{array} } \right]$ is a vector of design variables, ${\varvec{K}}({\varvec{x}}_{bj} )$ is the global stiffness matrix, $c$ is the total structural compliance for multiple load cases. $t_{\max }$ is the upper limit of material density. $w_{l}$ is the weighting factor corresponding to the structural compliance of each load case. $V$ is the total volume of the structure and $V_{0}$ is the upper volume limit.

Fig. 7

Minimum compliance problem under multiple load cases

The total volume of the structure is calculated as

$$V = \sum\limits_{e = 1}^{{n_{e} }} {\sum\limits_{{j \in S_{e} }} {\int_{{\Omega_{e} }} {N_{j} h{\text{d}}A} \sum\limits_{b = 1}^{2} {t_{bj} } } = \sum\limits_{j = 1}^{{n_{nd} }} {z_{j} \sum\limits_{b = 1}^{2} {t_{bj} } } } ,$$

(26)

where $z_{j}$ is defined as

$$z_{j} = \sum\limits_{{e \in S_{j} }} {\int_{{\Omega_{e} }} {N_{j} h{\text{d}}A} } .$$

(27)

3.4.2 Sensitivity analysis

In gradient-based optimization algorithms, sensitivity analysis of objective functions and constraint functions are necessary. The sensitivity of the equilibrium Eq. (15) to the design variables in the finite element method is

$$\frac{{\partial {\varvec{K}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}{\varvec{u}}({\varvec{x}}_{bj} ) + {\varvec{K}}({\varvec{x}}_{bj} )\frac{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} = 0,$$

(28)

From Formula (28), the derivation of the displacement vector ${\varvec{u}}({\varvec{x}}_{bj} )$ to the design variable ${\varvec{x}}_{bj}$ is

$$\frac{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} = - {\varvec{K}}^{ - 1} ({\varvec{x}}_{bj} )\frac{{\partial {\varvec{K}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}{\varvec{u}}({\varvec{x}}_{bj} ).$$

(29)

The derivation of the compliance objective function with respect to the design variable $t_{bj}$ is

$$\frac{\partial c}{{\partial t_{bj} }} = \sum\limits_{l} {w_{l} {\varvec{F}}_{l}^{{\text{T}}} \frac{{\partial {\varvec{u}}_{l} }}{{\partial t_{bj} }}} .$$

(30)

Substituting formula (29) into formula (30), it can be rewritten as

$$\frac{\partial c}{{\partial t_{bj} }} = - \sum\limits_{l} {w_{l} {\varvec{u}}_{l}^{{\text{T}}} \frac{{\partial {\varvec{K}}}}{{\partial t_{bj} }}} {\varvec{u}}_{l} .$$

(31)

Substituting formula (22) into formula (31), then

$$\frac{\partial c}{{\partial t_{bj} }} = - \sum\limits_{l} {w_{l} \sum\limits_{{e \in S_{j} }} {\sum\limits_{r = 1}^{6} {g_{r} (\alpha_{bj} ){\varvec{u}}_{el}^{{\text{T}}} {\varvec{H}}_{ejr} {\varvec{u}}_{el} } } } .$$

(32)

where ${\varvec{u}}_{el}$ is displacement vector of $e{\text{ - th}}$ element in $l{\text{ - th}}$ load case. Using the same method, the objective function is derived with respect to the design variable $\alpha_{bj}$ as

$$\frac{\partial c}{{\partial \alpha_{bj} }} = - t_{bj} \sum\limits_{l} {w_{l} \sum\limits_{{e \in S_{j} }} {\sum\limits_{r = 1}^{6} {g^{\prime}_{r} (\alpha_{bj} ){\varvec{u}}_{el}^{{\text{T}}} {\varvec{H}}_{ejr} {\varvec{u}}_{el} } } } .$$

(33)

Since the volume of a material is only related to the density of the material, Eq. (26) can be derived with respect to the density variable. The derivative of volume with respect to the density variable is

$$\frac{\partial V}{{\partial t_{bj} }} = \sum\limits_{j = 1}^{{n_{nd} }} {z_{j} } .$$

(34)

3.5 Stress constraint problem

3.5.1 Problem statement

The topology-optimized strength design of continuum structures is one of the important engineering design problems. In the stress constraint problem, the minimization of the structural volume under stress constraint is studied. For truss-like materials, member density $t_{bj}$ and member orientation $\alpha_{bj}$ at finite element nodes are used as design variables. In the local stress constraint strategy, the formula for the stress-constrained topology optimization problem can be written as

$$({\mathbb{P}}_{2} )\left\{ {\begin{array}{*{20}l} {{\text{find}}\quad {\varvec{x}}_{bj} \quad (b = 1,2;j = 1,2,3,...,n_{nd} )} \hfill \\ {\min \quad V = \sum\limits_{j = 1}^{{n_{nd} }} {z_{j} \sum\limits_{b = 1}^{2} {t_{bj} } } } \hfill \\ {{\text{s}}.{\text{t}}{.}\quad \frac{{\left| {\sigma_{i} } \right|}}{{\sigma_{{\text{p}}} }} - 1 \le 0{ (}i = 1,2,3,...,n_{\sigma } {)}} \hfill \\ {\quad \quad\quad {\varvec{K}}({\varvec{x}}_{bj} ){\varvec{u}}({\varvec{x}}_{bj} ) = {\varvec{F}}} \hfill \\ {\quad \quad\quad {0} \le t_{bj} \le t_{\max } \, } \hfill \\ \end{array} } \right.,$$

where ${\varvec{x}}_{bj} = \left[ {t_{bj} ,\alpha_{bj} } \right]$ represents the design variables vector, ${\varvec{K}}({\varvec{x}}_{bj} )$ is the global stiffness matrix, ${\varvec{u}}({\varvec{x}}_{bj} )$ is the global displacement vector and ${\varvec{F}}$ is the global load vector. $t_{\max }$ denotes the upper bound for node density. $V$ is the total volume of the structure, and $\sigma_{{\text{p}}}$ is the allowable stress of the truss-like member material. $\sigma_{i}$ is the stress at $i{\text{ - th}}$ sample point. $n_{\sigma }$ is the total number of stress constraints. The optimization problem $({\mathbb{P}}_{2} )$ involves a significant number of stress constraints in the discretized mode, leading to a challenging numerical solution process. An alternative approach to the local constraint formula is to substitute all stress constraints with their maximum values, yielding a single global stress constraint formula, represented by:

$$\frac{{\max \left\{ {{\varvec{\sigma}}_{eq} } \right\}}}{{\sigma_{{\text{p}}} }} - 1 \le 0,$$

(35)

where $\max \left\{ {{\varvec{\sigma}}_{eq} } \right\} = \max \left\{ {\left| {\sigma_{i} } \right|,i = 1,2,3,...,n_{\sigma } } \right\}$.

3.5.2 Global stress-constrained formulation

From a numerical solution perspective, replacing numerous local stress constraints with a single maximum stress constraint is a cost-effective approach. This is because adjoint analysis can efficiently compute the gradient of a single constraint as opposed to the gradient of each local constraint individually. However, using the maximization operator in this process renders the constraint function non-differentiable, making it unsuitable for standard gradient algorithms to solve the optimization problem. A simple and efficient way to solve this problem is to replace the maximization operator with a smooth approximation function. Duysinx and Sigmund presented the p-norm and p-mean aggregation functions as valid alternatives. The author discusses the balance between accuracy and numerical stability: the greater the value of p, the more accurate the maximum stress value of the approximate function; When the value of p is small enough, the nonlinear degree of the approximate function is smaller, and the stability of the numerical solution process is better. Based on the seminal work of Duysinx and Sigmund (Duysinx and Sigmund 1998), many alternative aggregation functions and solutions have been adopted to solve the stress constraint problem (Da Silva et al. 2021; Holmberg et al. 2013; Le et al. 2009), most popular ones being the p-norm/p-mean and upper/lower bound KS functions.

Verbart (Verbart et al. 2016) comprehensively discussed the lower and upper bound aggregation functions of stress-constrained topology design. The author found that in the stress-constrained topology design, using the lower bound aggregation function to approximate the maximum operator can avoid using the constraint relaxation technique to overcome the stress singularity, because the lower bound function naturally provides the combination effect of aggregation and relaxation in the design domain.

In this work, the p-mean function is employed to smooth the maximum operator of Eq. (35). In the finite element calculation of the bidirectional non-orthogonal member-like truss structure, the stress constraint is defined as that the principal stress of the structure cannot exceed the permissible stress. The global stress-constrained problem with the p-mean aggregation function is written as

$$({\mathbb{P}}_{3} )\left\{ {\begin{array}{*{20}l} {{\text{find}}\quad {\varvec{x}}_{bj} \quad (b = 1,2;j = 1,2,3,...,n_{nd} )} \hfill \\ {\min \quad V = \sum\limits_{j = 1}^{{n_{nd} }} {z_{j} \sum\limits_{b = 1}^{2} {t_{bj} } } } \hfill \\ {{\text{s}}.{\text{t}}{. }\quad \, \left[ {\frac{1}{{2n_{nd} }}\sum\limits_{{b_{0} = 1}}^{2} {\sum\limits_{{j_{0} = 1}}^{{n_{nd} }} {\left( {\left( {\frac{{E\varepsilon_{{b_{0} j_{0} }} }}{{\sigma_{{\text{p}}} }}} \right)^{2} } \right)} }^{p} } \right]^{{\frac{1}{p}}} - 1 \le 0 \, } \hfill \\ {\quad \quad \quad {\varvec{K}}({\varvec{x}}_{bj} ){\varvec{u}}({\varvec{x}}_{bj} ) = {\varvec{F}}} \hfill \\ {\quad \quad \quad {0} \le t_{bj} \le t_{\max } \, } \hfill \\ \end{array} } \right.,$$

where p is the penalty factor of the aggregation function, and $\varepsilon_{{b_{0} j_{0} }}$ is the two maximum principal strains of the finite element node. According to Hooke's Law, the square term $\left( {{{E\varepsilon_{{b_{0} j_{0} }} } \mathord{\left/ {\vphantom {{E\varepsilon_{{b_{0} j_{0} }} } {\sigma_{{\text{p}}} }}} \right. \kern-0pt} {\sigma_{{\text{p}}} }}} \right)^{2}$ can be simplified as $\left( {{{\varepsilon_{{b_{0} j_{0} }} } \mathord{\left/ {\vphantom {{\varepsilon_{{b_{0} j_{0} }} } {\varepsilon_{{\text{p}}} }}} \right. \kern-0pt} {\varepsilon_{{\text{p}}} }}} \right)^{2}$, where $\varepsilon_{{\text{p}}}$ is the allowable strain of each node. It is well known that the p-mean function will underestimate the actual maximum value of the general value of p, but it will gradually approach the maximum value as the value of p increases. When the value of p is relatively small, there is an error between the optimization problem $({\mathbb{P}}_{3} )$ described by the aggregation function and the original problem. A common strategy is to use the adaptive constraint normalization scheme (Le et al. 2009) associated with moderate values of p. The global stress constraint formula can be written as

$$\tilde{\sigma }_{{{\text{pm}}}} - 1 \le 0,$$

(36)

where $\tilde{\sigma }_{{{\text{pm}}}} = c_{{{\text{pm}}}} \sigma_{{{\text{pm}}}}$, and $\sigma_{{{\text{pm}}}} = \left[ {\frac{1}{{2n_{nd} }}\sum\nolimits_{{b_{0} = 1}}^{2} {\sum\nolimits_{{j_{0} = 1}}^{{n_{nd} }} {\left( {\left( {\frac{{\varepsilon_{{b_{0} j_{0} }} }}{{\varepsilon_{{\text{p}}} }}} \right)^{2} } \right)} }^{p} } \right]^{{\frac{1}{p}}}$, The parameter values $c_{{{\text{pm}}}}$ in each iteration are updated by the following rules:

$$c_{{{\text{pm}}}}^{\left( I \right)} = \alpha \frac{{\sigma_{\max }^{{\left( {I - 1} \right)}} }}{{\sigma_{{{\text{pm}}}}^{{\left( {I - 1} \right)}} }} + \left( {1 - \alpha } \right)c_{{{\text{pm}}}}^{{\left( {I - 1} \right)}} ,$$

(37)

where $\alpha \in \left[ {0,1} \right]$ is the control factor. In this work, $\alpha = 0.5$ and $c_{{{\text{pm}}}}^{\left( 0 \right)} = 1$. The changes of $c_{{{\text{pm}}}}^{\left( I \right)}$ in the optimization process are discontinuous, which leads to slight problems in each step of optimization. However, as the optimization converges the changes between successive design iterations diminish and hence $c_{{{\text{pm}}}}^{\left( I \right)}$ converges, thereby reducing impact of corrections to constraint functions.

From the equilibrium equation formula (15) in the finite element method, the node displacement of the finite element is

$${\varvec{u}}({\varvec{x}}_{bj} ) = {\varvec{K}}^{ - 1} ({\varvec{x}}_{bj} ){\varvec{F}}\varvec{.}$$

(38)

Define the strain component vector of the $j_{0} {\text{ - th}}$ element node along the coordinate axis as $\overline{\varvec{\varepsilon }}_{{j_{0} }}$, then

$$\overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} ) = \left[ {\begin{array}{*{20}c} {\varepsilon_{{j_{0} }}^{x} } & {\varepsilon_{{j_{0} }}^{y} } & {\gamma_{{j_{0} }}^{xy} } \\ \end{array} } \right] = \frac{1}{{n_{{j_{0} }} }}\sum\limits_{{e \in S_{{j_{0} }} }} {{\varvec{B}}_{e} {\varvec{u}}_{e} ({\varvec{x}}_{bj} )} .$$

(39)

Here, the strain at a finite element node is the average of the strain values at the node of all surrounding elements. ${\varvec{B}}_{e} ,{\varvec{u}}_{e}$ are the displacement–strain matrix and displacement vector of the $e{\text{ - th}}$ element, respectively. $n_{{j_{0} }}$ is the number of finite elements around the $j_{0} {\text{ - th}}$ node. Further, the two principal strains $\varepsilon_{{b_{0} j_{0} }}$ of $j_{0} {\text{ - th}}$ node can be obtained as follows,

$$\varepsilon_{{b_{0} j_{0} }} = \frac{{\varepsilon_{{j_{0} }}^{x} + \varepsilon_{{j_{0} }}^{y} }}{2} - \left( { - 1} \right)^{{b_{0} }} \sqrt {\left( {\frac{{\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} }}{2}} \right)^{2} + \left( {\gamma_{{j_{0} }}^{xy} } \right)^{2} } ,$$

(40)

The principal strain number is $b_{0} = 1,2$, and the node number is $j_{0} = 1,2,3,...,n_{nd}$.

3.5.3 Sensitivity analysis

In the optimization problem formulation $({\mathbb{P}}_{3} )$, the calculation of the total volume of the structure is the same as that as shown in Eq. (26). The sensitivity expression of the objective function to the design variables is the same as that shown in formula (34). Next, the sensitivity of the strain constraints to design variables can be calculated. Define the single global stress constraint expression as function $f({\varvec{x}}_{bj} )$, and

$$f({\varvec{x}}_{bj} ) = \left[ {\frac{1}{{2n_{nd} }}\sum\limits_{{b_{0} = 1}}^{2} {\sum\limits_{{j_{0} = 1}}^{{n_{nd} }} {\left( {\left( {\frac{{\varepsilon_{{b_{0} j_{0} }} }}{{\varepsilon_{{\text{p}}} }}} \right)^{2} } \right)} }^{p} } \right]^{{\frac{1}{p}}} - 1 \le 0.$$

(41)

where $\left( {\frac{{\varepsilon_{{b_{0} j_{0} }} }}{{\varepsilon_{{\text{p}}} }}} \right)^{2}$ can be denoted as $f_{{b_{0} j_{0} }}$, then the sensitivity of constraint expression (41) to design variables is

$$\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} = \sum\limits_{{b_{0} ,j_{0} }} {\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial f_{{b_{0} j_{0} }} }}\frac{{\partial f_{{b_{0} j_{0} }} }}{{\partial \varepsilon_{{b_{0} j_{0} }} }}\frac{{\partial \varepsilon_{{b_{0} j_{0} }} }}{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}\frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}} .$$

(42)

where

$$\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial f_{{b_{0} j_{0} }} }} = \frac{1}{p}\left[ {\frac{1}{{2n_{nd} }}\sum\limits_{b = 1}^{2} {\sum\limits_{j = 1}^{{n_{nd} }} {\left( {f_{{b_{0} j_{0} }} } \right)} }^{p} } \right]^{{\left( {\frac{1}{p} - 1} \right)}} \cdot \frac{p}{{2n_{nd} }}\left( {f_{{b_{0} j_{0} }} } \right)^{p - 1} ,$$

(43)

$$\frac{{\partial f_{{b_{0} j_{0} }} }}{{\partial \varepsilon_{{b_{0} j_{0} }} }} = \frac{{2\varepsilon_{{b_{0} j_{0} }} }}{{\left( {\varepsilon_{{\text{p}}} } \right)^{2} }}.$$

(44)

From formulas (39), (40), the sensitivity of principal strain to the strain component vector can be obtained as

$$\frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \varepsilon_{{j_{0} }}^{x} }}} & {\frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \varepsilon_{{j_{0} }}^{y} }}} & {\frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \gamma_{{j_{0} }}^{xy} }}} \\ \end{array} } \right],$$

(45)

where

$$\begin{aligned} & \frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \varepsilon_{{j_{0} }}^{x} }} = \frac{1}{2} - \frac{{\left( { - 1} \right)^{{b_{0} }} }}{4}\left[ {\left( {\frac{{\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} }}{2}} \right)^{2} + \left( {\gamma_{{j_{0} }}^{xy} } \right)^{2} } \right]^{ - 0.5} \left( {\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} } \right) \\ & \frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \varepsilon_{{j_{0} }}^{y} }} = \frac{1}{2} + \frac{{\left( { - 1} \right)^{{b_{0} }} }}{4}\left[ {\left( {\frac{{\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} }}{2}} \right)^{2} + \left( {\gamma_{{j_{0} }}^{xy} } \right)^{2} } \right]^{ - 0.5} \left( {\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} } \right) \\ & \frac{{\partial \varepsilon_{{b_{0} j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial \gamma_{{j_{0} }}^{xy} }} = \left( { - 1} \right)^{{b_{0} + 1}} \left[ {\left( {\frac{{\varepsilon_{{j_{0} }}^{x} - \varepsilon_{{j_{0} }}^{y} }}{2}} \right)^{2} + \left( {\gamma_{{j_{0} }}^{xy} } \right)^{2} } \right]^{ - 0.5} \gamma_{{j_{0} }}^{xy} . \\ \end{aligned}$$

(46)

From formula (29) and (39), the sensitivity of the strain component of the $j_{0} {\text{ - th}}$ node to the global displacement vector can be obtained as

$$\begin{aligned} \frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} & = \frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}\frac{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} \\ & = \left[ {\begin{array}{*{20}c} {\frac{{\partial \varepsilon_{{j_{0} }}^{x} }}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}} & {\frac{{\partial \varepsilon_{{j_{0} }}^{y} }}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}} & {\frac{{\partial \gamma_{{j_{0} }}^{xy} }}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}} \\ \end{array} } \right]\frac{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}. \\ \end{aligned}$$

(47)

In most cases, the number of design variables ${\varvec{x}}_{bj}$ will be large and the number of constraints can be kept moderate. Here, the term ${{\partial {\varvec{u}}({\varvec{x}}_{bj} )} \mathord{\left/ {\vphantom {{\partial {\varvec{u}}({\varvec{x}}_{bj} )} {\partial {\varvec{x}}_{bj} }}} \right. \kern-0pt} {\partial {\varvec{x}}_{bj} }}$ in (47) is calculated from Eq. (29). Substituting (29), (47) into (42) gives

$$\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} = \sum\limits_{{b_{0} ,j_{0} }} {\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial f_{{b_{0} j_{0} }} }}\frac{{\partial f_{{b_{0} j_{0} }} }}{{\partial \varepsilon_{{b_{0} j_{0} }} }}\frac{{\partial \varepsilon_{{b_{0} j_{0} }} }}{{\overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}\frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}\left( { - {\varvec{K}}^{ - 1} ({\varvec{x}}_{bj} )\frac{{\partial {\varvec{K}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}{\varvec{u}}({\varvec{x}}_{bj} )} \right)} .$$

(48)

An adjoint variable is now defined by

$${\varvec{\psi}} = {\varvec{K}}^{ - 1} ({\varvec{x}}_{bj} )\sum\limits_{{b_{0} ,j_{0} }} {\left( {\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial f_{{b_{0} j_{0} }} }}\frac{{\partial f_{{b_{0} j_{0} }} }}{{\partial \varepsilon_{{b_{0} j_{0} }} }}\frac{{\partial \varepsilon_{{b_{0} j_{0} }} }}{{\overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}\frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}} \right)}^{{\text{T}}} ,$$

(49)

which means that it can be calculated from the adjoint equation

$${\varvec{K}}({\varvec{x}}_{bj} ){\varvec{\psi}} = \sum\limits_{{b_{0} ,j_{0} }} {\left( {\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial f_{{b_{0} j_{0} }} }}\frac{{\partial f_{{b_{0} j_{0} }} }}{{\partial \varepsilon_{{b_{0} j_{0} }} }}\frac{{\partial \varepsilon_{{b_{0} j_{0} }} }}{{\overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}\frac{{\partial \overline{\varvec{\varepsilon }}_{{j_{0} }} ({\varvec{x}}_{bj} )}}{{\partial {\varvec{u}}({\varvec{x}}_{bj} )}}} \right)}^{{\text{T}}} .$$

(50)

The adjoint variable is now inserted into (48) which finally gives the gradient as

$$\frac{{\partial f({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }} = - {\varvec{\psi}}^{{\text{T}}} \left( {\frac{{\partial {\varvec{K}}({\varvec{x}}_{bj} )}}{{\partial {\varvec{x}}_{bj} }}{\varvec{u}}({\varvec{x}}_{bj} )} \right),$$

(51)

where $b = 1,2$ and $j = {1,2,}...{,}n_{nd}$ are the number of design variable.

3.6 Post-processing of truss-like structure

It can be seen from formula (13) that a group of orthogonal members can be uniformly set as the base material in the design domain. Therefore, the lowest material density in the optimal material distribution field in this article will not be zero. In fact, the purpose of introducing a base material is primarily to prevent singularity in the stiffness matrix during finite element calculations. The density of the base material, denoted as $t_{0}$, is usually assigned a very small value to disregard its influence on load transfer effects.

In this part, by setting an appropriate density threshold, the contour of the density threshold on the density distribution surface can be drawn. Areas with a material density less than this threshold are considered material free. In this way, a variable stiffness truss-like topology with well-defined boundaries can be generated. The threshold value of the minimum density is denoted as $\overline{t}$, then the boundary curve expression of the truss-like structure is as follows:

$$\sum\limits_{b = 1,2} {t_{b} } = \overline{t},$$

(52)

where $t_{b}$ is the material density at any point in the design domain, and $b = 1,2$ is the member number.

4 Numerical example

In this part, the effectiveness and advantages of the proposed topology optimization method with bidirectional non-orthogonal materials are verified by solving three numerical examples. In these examples, bilinear rectangular elements are used to discretize the finite elements in the design domain. The optimization problem only involves linear elastic deformation. The material properties in all examples are as follows. The thickness of the design domain is $h = 0.01{\text{m}}$, the Young's modulus of the material is $E = 2.1 \times 10^{11} {\text{Pa}}$, and the Poisson's ratio is zero. The material volume fraction constraint is 0.4 and $R_{G}$ is generally taken as 0.5. All examples in this article use the globally convergent moving asymptote method (GCMMA) from Krister Svanberg (Svanberg 1987, 2001) as the optimizer.

The optimization iteration is terminated when one of the following two conditions is satisfied. (1) the average rate of change of the objective function every 5 steps is less than 0.01%; (2) the current number of loop steps exceeds the given maximum number of iterations, which is set to 100 in this article.

4.1 Minimum compliance problem under a single load case

4.1.1 Solution of the single load case example

In this section, the minimum compliance problem for a rectangular design domain under a single load case is solved using the presented in this article. The analytical solution of the Michell truss-like (Graczykowski and Lewiński 2007) can be used as a benchmark for comparison of the numerical topology optimization results from the approach presented in this article. As shown in Fig. 8, the width to height ratio of the rectangular design domain is 1.6, and the height is $L = 10\,{\text{m}}$. The left end of the cantilever member is fixed, and there is a vertical downward concentrated load $F = 1 \times 10^{6} \,{\text{N}}$ applied in the middle of the right end. The finite element mesh size is $10 \times 16$, and the two member densities and angles at each node are used as design variables. As shown in Fig. 9a, the initial value of the member density at any point is $t_{bj} = 0.4$, the base material density is $t_{0} = 1 \times 10^{ - 3}$, and the initial value of the member direction angle is $\alpha_{bj} = ( - 1)^{b} \times {\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}$, where the subscript $b = 1,2$,$j = 1,2,3,...,n_{nd}$.

Fig. 8

Minimum compliance problem in single load case

Fig. 9

Example of the minimum compliance problem: a initial material distribution field; b optimized material distribution field

The optimal material distribution field is shown in Fig. 9b and the objective function value is ${9}{\text{.5930}} \times {10}^{3} \,{\text{J}}$. The two segment directions on each node in the figure represent the two member directions. The length of the line segment represents the relative value of the member density. To enhance the clarity of member density display, excessively long line segments have been scaled accordingly.

Next, we investigate the effect of mesh size on the optimization results. While keeping other conditions constant, we also consider two additional finite element mesh sizes ($6 \times 10$ and $20 \times 32$). Figure 10 shows the corresponding optimal material distribution fields when different mesh sizes are implemented. The corresponding values when the objective function converges are ${9}{\text{.7504}} \times {10}^{3} \,{\text{J}}$ and ${9}{\text{.4148}} \times {10}^{3} \,{\text{J}}$, respectively. From the optimization results for three different grid sizes shown in Figs. 9b and 10, it can be found that there is no significant difference in the convergence values of the objective function. Sparse meshing involves fewer design variables, which results in a less robust ability to represent the material distribution field. As a result, the compliance objective function is slightly larger.

Fig. 10

Topology optimization results under different mesh sizes: a 6 × 10; b 20 × 32

4.1.2 The effect of initial values

Next, we explore how the selection of initial values for the design variables affects the optimization solution process. Table 1. lists four sets of different initial values and their corresponding optimization results. The average error for the four optimization results is 2.53%.

Table 1 Four groups of initial values and optimization results with 20 × 32 elements

The iterative history for the minimum compliance problem corresponding to the four initial values of the design variables is shown in Fig. 11. It can be seen that the compliance objective function and the volume fraction constraint function can quickly converge to the optimal solution from different initial states. The maximum difference ratio of the four objective function values is 0.14%. This indicates that the final solution of the minimum compliance problem is less affected by the initial value, and the optimization solution process has high robustness.

Fig. 11

Convergence process of minimum compliance problem with different initial values

4.1.3 Error analysis of optimization results

In order to investigate the accuracy of the optimization results from the proposed approach, the results shown in Fig. 10b were compared with the analytical solution given by Lewinski.

In Fig. 12a, the tension and compression members in the analytical solution are represented by two clusters of red lines. The blue line segment in the background depicts the numerical optimization result obtained by the method presented in this article, which describes a continuous and dense distribution field of truss-like members through interpolation.

Fig. 12

Comparison of member angle: a analytical solution (red) and numerical solution (blue) of the direction distribution of the member; b error distribution of the member angle. (Color figure online)

It can be seen that the distribution direction of the members at each finite element node of the numerical results is basically the same as the analytical solution. It is worth mentioning that the material distribution field obtained by the finite element interpolation method tends to slightly exceed the outer contour of the analytical solution area. However, this error is caused by the discrete characteristics of finite elements, which is acceptable in numerical methods. In addition, in the analytical solution, there is a situation where multiple members converge at one point as shown in Fig. 12a at the upper and lower corners of the left end of the design domain. These members convergence points are often accompanied by stress concentration, and the angle errors of the members in these special positions are acceptable. Except for the above two special cases, the error between the numerical solution and the analytical solution of the member angle and the cloud diagram of the member angle error distribution are shown in Fig. 12b. It can be seen from the figure that the directional deviation of the members in most areas of the domain is less than 0.15 rad. The average direction angle error of the sample points in the whole area is 0.0167 rad, indicating that the numerical optimization result is very close to the analytical solution.

The accuracy of the density distribution results of truss-like members is also analyzed. In the analytical solution, the current case is called the Prager-Hill cantilever beam. Its analytical solution of the plan view of distribution field of truss-like members is shown in Fig. 13a, in which there are dense truss-like members distributed in the regions of RAB, NAC, and ABDC. Two bold curves RBD and NCD are reinforced members. The dimensionless material density function surface of the distributed member area is shown in Fig. 13b. Reinforced member diagrams with infinite material density are not shown.

Fig. 13

Analytical solution of Prager-Hill cantilever beam: a plan view of distribution field of truss-like members; b surface of material density function

Since the material density cannot describe the reinforced member in the numerical method, it is difficult to uniformly compare the absolute error between the numerical solution and the analytical solution. The numerical optimal solution of the actual truss-like member density distribution is shown in Fig. 14. It can be seen from Fig. 14 that the material density near the three points R, N and D in the figure is very large, which conforms to the characteristic that the density of the members at the stress concentration tends to be infinite. The material densities stand out and agree well with the curves RBD and NCD depicted in Fig. 13a, indicating that the optimization results of the member density are mostly accurate.

Fig. 14

Prager-Hill cantilever beam numerical solution: a material density surface; b material density contour

In addition, as shown in Fig. 13a, select a set of sample point density $t_{i}^{{{\text{NO}}}} ,i = 1,2,3...n_{no}$ along the member curve NO. The total number of sample points is $n_{no} = 80$. The density ratio between the numerical solution and the analytical solution for each sample point position is shown in Fig. 15. The blue curve represents the ratio curve, while the red line is the horizontal line of constant 1. We can see that since there are reinforced members at the O point on the right end, the error near this point is relatively larger. But in other intervals, the ratio curve fluctuates around the constant line, and the numerical solution is very close to the analytical solution.

Fig. 15

Material density ratio at sample point location

4.1.4 Comparison and post-processing of optimization results

Next, we use the traditional orthogonal material approach to solve the single load case example. The initial member density and angle are $t_{bj} = 0.9$,$\alpha_{j} = \frac{\pi }{4}$, and other parameters are consistent with the ones in non-orthogonal material approach. Figure 16a shows the optimization results for two material distribution fields, where the red line segments correspond to the orthogonal material approach and the black ones to the non-orthogonal material approach. It is clear that the optimal material distribution fields obtained by the two methods are generally consistent, and only some of the members in the stress concentration region have a relatively large difference in orientation. The above errors are acceptable due to the limited accuracy of the finite element meshing. Figure 16b shows the iteration history of the objection and constraint function values for the two methods, where the iteration process of the two constraint functions is very close to each other, but the convergence of the objective function of the method in this paper is slightly faster.

Fig. 16

Comparison of iteration process and results: a truss-like member distribution field; b iteration history

As shown in Table 2, for the single load case example, the non-orthogonal material approach requires fewer iterations than the orthogonal material approach, but the objective and constraint function values at convergence are very close to each other. This example shows that the non-orthogonal material approach, for the single load case, can completely replace the traditional orthogonal approach and yield optimization results with the same level of accuracy.

Table 2 Comparison of optimization results based on different material methods

After setting the density threshold to a specific value and performing some straightforward post-processing on the optimization results, as shown in Fig. 10b, the optimal truss-like structure is obtained for the minimum compliance problem under a single load case. This structure is illustrated in Fig. 17a, where the black line segments represent the distribution of truss-like members at the finite element nodes. The grey area represents the material distribution field of non-uniform anisotropic truss-like materials, which is a continuum consisting of dense truss-like members. In order to obtain a structure suitable for engineering applications, the continuous material field can also be discretized (Shi and Zhou 2021) into the fine discrete topology shown in Fig. 17b. The structure is an approximation of the optimization result, which can be discretized into truss-like structures with different accuracies by adjusting the parameters.

Fig. 17

Post-processing of optimization result: a truss-like continuum; b discretized truss-like structure

4.2 Minimum compliance problem under multiple load cases

4.2.1 Solution of multiple load cases example

In this section, a minimum structural compliance problem under multiple load cases is investigated. As shown in Fig. 18, the width and height ratio of the rectangular design domain is 1.6, and the length is $L = 10{\text{m}}$. There are two hinge support constraints at the bottom of the design domain. Two vertically downward concentrated loads are applied at points A and B on the bottom boundary respectively. The index number of the load case is $l = 1,2$, and the corresponding weights are $w_{1} = w_{2} = 0.5$. The size of the finite element mesh is $20 \times 32$. The density of the base material is $t_{0} = 1 \times 10^{ - 3}$.The initial values of member density and angle are $t_{bj} = 0.4$ and $\alpha_{bj} = ( - 1)^{b} {\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}$, respectively, where $b = 1,2$ and $j = 1,2,3,...,n_{nd}$.

Fig. 18

Minimum compliance problem under multiple load cases

First, Fig. 19 displays the topology optimization results of the two load cases, which are symmetric about the vertical axis of symmetry. The problem converges in 47 and 49 steps, respectively. Then, Fig. 20a depicts the initial state of the material distribution field, while Fig. 20f presents the optimized truss-like material distribution field achieved in the 49th step. At this step, the convergence condition is met, and the value of the compliance objective function is 26.850J.

Fig. 19

Topology optimization results for each load case individually: a the load applied only at point A; b the load applied only at point B

Fig. 20

Optimization process of minimum compliance problem under multiple load cases

Figure 21 shows the structural compliance and the volume fraction convergence procedure. It can be seen that structural compliance and volume fraction can quickly stabilize in the early stage of optimization and converge at the 47-th step. The proposed approach has a good convergence when dealing with the minimum compliance problem for multiple load cases.

Fig. 21

Iteration history of the minimum compliance problem for multiple load cases

4.2.2 Comparison of optimization results

Further comparison on the optimization results of the problem using the proposed approach with it based on orthogonal truss-like material model is made and shown in Fig. 22. In the multiple load cases compliance minimization problem, the optimal material distribution field can be considered as the composite of the two single-case optimization results in Fig. 19. However, the composite effect is not a simple superposition of the optimization results. There is also an interaction between the two load cases. Therefore, the optimal material distribution under multiple load cases will become more complicated, which means that the two member directions at any point tend to be non-orthogonal. Figure 22a shows the topology optimization results based on the orthogonal truss-like material model. According to the symmetry principle, the optimal material distribution field of this example should be symmetric. However, since the orthogonal material model cannot describe the non-orthogonal members, the distribution of member orientations in the optimization results is obviously asymmetric and fluctuating. In the topology optimization results shown in Fig. 22b obtained by using the non-orthogonal material model in this article, the distribution of members has good symmetry and less fluctuation. In addition, the number of iterations for the two optimization results shown in Fig. 22 are 47 and 61, respectively, and the objective function values at convergence are 26.850J and 27.192J, respectively. It can be concluded that the non-orthogonal material model adopted in this article is more efficient than the traditional orthogonal material model. The objective function accuracy is improved by 1.3%. The advantages of the non-orthogonal material model are more pronounced under more complex load cases.

Fig. 22

Topology optimization results of the minimum compliance problem for multiple load cases: a orthogonal truss-like material models; b non-orthogonal truss-like material models

In addition, we increase the number of load cases in the above example to four, as shown in Fig. 23, The vertical downward load is denoted as $F$, and the four load cases are applied at equal intervals at the bottom edge of the simply supported beam design domain. The dimensions of the design domain are shown in the figure, where $L = 10$, the initial density of the members is $t_{bj} = 0.4$, the angle is $\alpha_{bj} = ( - 1)^{b} {\raise0.5ex\hbox{$\scriptstyle \pi $} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 4$}}$, the number of finite element meshes is $40 \times 80$, and the other parameters are selected to be consistent with the two load cases example.

Fig. 23

Numerical example of the four load cases

Optimization solutions for the four load cases were performed based on orthogonal and non-orthogonal material models respectively. The results of the two optimizations are shown in Fig. 24. In complex multi-load cases, due to the cross-effects between different load cases, the optimal member distribution in some areas is often non-orthogonal, rather than the orthogonal distribution of all members in single load case. Therefore, the traditional orthogonal material method can only yield an approximate optimal solution. As can be seen from Fig. 24, in the local areas of the material distribution field obtained using the orthogonal material method, there are issues with periodic fluctuations in material distribution, resulting in poor smoothness of material density distribution. In the corresponding areas, the continuity of the optimal member distribution of the non-orthogonal material method is significantly better.

Fig. 24

Optimization results of four load cases example: a orthogonal material model; b non-orthogonal material model

The approximate structures obtained by discretizing the above two optimization results are shown in Fig. 25. It can be seen that the discretized structure obtained based on the non-orthogonal material model has better continuity and smoothness than the orthogonal one. Therefore, the non-orthogonal material approach has better generalization than the orthogonal material approach for the multiple load cases problem, and the distribution of the members in the discretized structure is more reasonable.

Fig. 25

Discretized truss-like structures: a orthogonal member structure; b non-orthogonal member structure

4.2.3 Dynamic variable stiffness optimization strategy

In this section, the variable shear stiffness strategy in Sect. 3.3 is applied to the minimum compliance problem under multiple load cases, and the optimization results are shown in Table 3.

Table 3 Topology optimization results under different update strategies

In the update strategy of logarithmic function, the objective function quickly reaches the convergence condition at the 59th iteration, but the shear stiffness of the material does not approach zero. The update strategy in the form of a power function can make the parameter $R_{G} > 0.99$, which means that the optimization result is closer to the optimal Michell truss. In addition, among these power functions, when $q = 10$, the number of iterations is the least, and the objective function value is also better. The convergence process of the objective function corresponding to each update strategy is shown in Fig. 26. It can be seen from the figure that in the update strategy of logarithmic function, the convergence of the objective function is obviously worse. In several optimization strategies based on the form of power function, the objective function can converge well and tend to be stable. Among them, when $q = 10$, the volatility of the objective function value is smaller. Therefore, in the optimization problem, it is a better choice to choose the shear stiffness update strategy in the form of a power function and a relatively large value of $q$.

Fig. 26

Iteration of objective function based on dynamic shear stiffness

4.2.4 Post-processing of optimization results

When the density threshold is set to be $\overline{t} = 0.1$ and after post-processing on the final optimization results, the optimal truss-like structure for minimum compliance problem under multiple load cases can be determined and is shown in Fig. 27a. The corresponding approximate discretized truss-like structure that satisfies the engineering application is shown in Fig. 27b.

Fig. 27

Post-processing of optimization result: a truss-like continuum; b discretized truss-like structure

4.3 Stress constraint problem

4.3.1 Solution of the stress constraint problem

In order to further investigate the performance of the proposed approach for the topology optimization of a more general case, in this section, a stress-constrained minimum volume problem for an L-shaped design domain under a single load case is investigated. As shown in Fig. 28, a vertical downward external load acts at the top corner point at the right end of the design domain. The load value is $F = 1 \times 10^{5} {\text{N}}$. The length of the design domain is $L = 4{\text{m}}$. The design domain is divided into 1024 finite elements. The density of the base material is $t_{0} = 1 \times 10^{ - 3}$, the initial value of the member density is $t_{bj} = 0.9$, and the allowable stress of each node is taken as $\sigma_{{\text{p}}} { = }160{\text{MPa}}$. The corresponding permissible strain is $\varepsilon_{{\text{p}}} = {{16} \mathord{\left/ {\vphantom {{16} {21}}} \right. \kern-0pt} {21}} \times 10^{ - 3}$. The initial value of the direction angle of the member is $\alpha_{bj} = \pm {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4}$, where $b = 1,2$ and $j = 1,2,3,...,n_{nd}$. In this work, the initial value of the penalty factor p is 2, which increases every 20 iterations, and the maximum value is 100. In this example, the total number of iterations is 500. After the 50th iteration, the approximate function value is adjusted according to formula (37) in each iteration.

Fig. 28

Stress constraints in L-shaped design domains

4.3.2 Analysis of the optimization process

Figure 29 shows the iterative process of the density and angle of truss-like members in the L-shaped domain at different steps as a stress-constrained minimum volume problem. Compared with the minimum compliance problem, due to the nonlinear enhancement of the constraint function, the stress constraint problem needs more iterations to achieve convergence. Figure 30 shows the iterative process for maximum stress surfaces at each element node within the domain at different time steps, where the colored surface is the distribution surface of the absolute value of the maximum stress. The color change of the surface corresponds to the allowable stress range. At each iteration, the gray translucent plane represents the allowable stress plane. During the optimization process, the stress distribution surface gradually approaches the allowable stress surface. At the same time, the distribution state of the material field is gradually approaching the optimum. The error between the real maximum stress of the structure and the allowable stress is $\frac{{\sigma_{\max } }}{{\sigma_{{\text{p}}} }} - 1$, and its value is 0.01% when it converges, where $\sigma_{\max }$ is the real maximum stress of the structure.

Fig. 29

Optimization process of distribution field of truss-like members

Fig. 30

Iterative process for maximum stress (Pa) surfaces

Figure 31 shows the convergence process of the objective function and the maximum stress in the stress-constrained minimum volume problem. During the optimization solution process, the structure volume and the maximum stress quickly converge to their optimal values. After satisfying the given convergence conditions, the objective function and the maximum stress keep stable until the 500-th iteration.

Fig. 31

Convergence history for stress constraint problems

4.3.3 Comparison of optimization results and discretization

The topological distribution of the analytical solution to the L-shaped design domain stress constraint minimum volume problem (Lewiński et al. 2013) is shown in Fig. 32a. Taking the density threshold $\overline{t} = 0.1$ and after post-processing on the optimization results shown in Fig. 29i, the optimal truss-like structure for the stress constraint problem is determined and shown in Fig. 32b. As shown in Fig. 32b, the optimal structural topology obtained in this article is basically consistent with the analytical solution. Due to the discrete characteristics of finite elements, the uniformity of material density near points ${\text{P}}$ and ${\text{G}}_{1}$ is slightly uneven, which is acceptable.

Fig. 32

The optimal topology of the stress constraint problem: a analytical solution; b numerical solution

Further approximate discretization of the continuous truss-like material distribution field leads to the approximate topology shown in Fig. 33.

Fig. 33

Discretized truss-like structure for stress-constrained problem

5 Concluding remarks

In this article, a new framework for solving topology optimization problems of truss-like structures based on mathematical programming method is proposed and numerically validated with three different numerical models. The major conclusions can be made as follows.

• 1. The framework adopts a bidirectional non-orthogonal truss-like material model, which can describe the distribution fields of various non-orthogonal members. This model introduces a set of orthogonal members as the base material, which avoids the singular problem of stiffness matrix that may be caused by the overlapping member directions in the traditional non-orthogonal material model. In addition, the non-orthogonal truss-like material model has greater design freedom and stronger description ability. Compared with the orthogonal truss-like material model, the accuracy of the topology optimization results is improved by 1.3% under the two load cases. Optimization problem is solved more efficiently, and the fluctuation of material distribution is smaller.

• 2. The three numerical examples demonstrate the high efficiency of the proposed solution framework when tackling diverse optimization problems. In fact, the results obtained are remarkably close to the theoretically optimal solutions. Specifically, for the minimum compliance problem with a single load and a grid size of 20 × 32, the average percentage error of the optimization results is only 2.53%. These findings underscore the effectiveness of the solution framework in addressing various optimization challenges.

• 3. Furthermore, when utilizing mathematical programming methods for optimization problems, it’s more advantageous to select a shear stiffness update strategy in the form of a power function with a relatively high $q$ value. This approach has been proven to be more effective in achieving the desired outcomes.

The framework proposed in this article inherits high-efficiency characteristics as a density-based topology optimization method. However, the density-based method still suffers from the difficulties when handling optimization problem for structures with large number of variables. In contrast, boundary description-based topology optimization methods have been developed to reduce the number of optimization variables while increasing the nonlinearity between the design variables and the objective function (Guo et al. 2016, 2014). Nevertheless, incorporating such methods in complex optimization problems could potentially exacerbate the difficulty of the optimization process. Therefore, investigating the combination of density-based and boundary description-based methods in the future could be a valuable avenue of research.