General high-order solitons and breathers with a periodic wave background in the nonlocal Hirota–Maccari equation

Abstract

Soliton and breather solutions to the nonlocal Hirota–Maccari equation with a periodic wave background are constructed via the KP hierarchy reduction approach. By constraining tau functions of bilinear equations in the KP hierarchy, we obtain general 2N-line solitons and N-breather solutions with a periodic wave background. What needs to be emphasized are the two-soliton can be divided into non-degenerate and degenerate soliton according to the asymptotic analysis. Meanwhile, one- and two-breather solutions in a periodic wave and constant background are investigated.

1 Introduction

The study of the dynamical behavior of physical systems has been, and continues to be, a major source of mathematical inspiration. In nonlinear physics, PT-symmetry can be used to describe energy transfer and wave behavior [1,2,3,4,5]. Due to the potential application in nonlinear optics, a new class of integrable systems known as nonlocal models has just recently been proposed. The first PT-symmetric nonlocal integrable equation was introduced by Ablowitz and Musslimani [6]. In the past few years, some research on PT-symmetric equations has achieved new results in both theory and applications [7,8,9,10,11,12].

Nonlinear integrable equations can be solved in a variety of methods, such as the Darboux transformation [13], the Riemann–Hilbert approach [14], the Kadomtsev–Petviashvili (KP) hierarchy reduction method [15,16,17], and so on. Among them, the KP hierarchy reduction method is a powerful tool because it can bypass the spectral problem and the Lax pair of the equation and directly obtain the exact solution in a concise form.

In our recent work [18], inspired by Yang [19], a nonlocal Hirota–Maccari (HM) equation was proposed

$$\begin{aligned}&u_t-iu_{xy}{+}\beta u_{xxx}{+}ur+\beta uu^*(-x,y,-t)u_x{=}0,\nonumber \\&3ir_x-(uu^*(-x,y,-t))_y=0, \end{aligned}$$

(1)

where u stands for the long wave, r is short wave and $\beta$ is real parameter. By replacing $x\rightarrow ix, t\rightarrow -it, y\rightarrow -y$, the nonlocal HM equation reduces to the local Hirota–Maccari equation:

$$\begin{aligned} \begin{aligned}&iu_t+u_{xy}+i\beta u_{xxx}+ur-i\beta |u|^2u_x=0,\\&3r_x+(|u|^2)_y=0, \end{aligned} \end{aligned}$$

(2)

which comes from a higher-dimensional generalization of the Hirota equation [20,21,22]. Notably, compared to the local Eq. (2), this solution of the nonlocal Eq. (1) at position (x, t) relies on both the local solution at (x, t) and the nonlocal solution at $(-x,-t)$. Meanwhile, the nonlocal HM equation admits some interesting physical phenomenon for its new time- or space-coupling, which could lead to new physical consequences and encourage new practical applications [23]. From our work, we derived degenerate and non-degenerate solitons and examined the dynamical behavior of rational and lump-soliton solutions. Indeed, it is clearly richer than the variety of exact solutions in the local HM equation [24,25,26].

Furthermore, regarding soliton solutions studied on a periodic wave background also attracts attention. Tian and his group have discussed N-soliton solutions on the nonzero background in the Korteweg–de Vries–Calogero–Bogoyavlenskii–Schif equation [27]. Rao and his collaborators have studied various kinds of solutions on a periodic background to the Dave–Stewartson I equation [28]. Zha et al. have investigated breathers and rogue waves on a double-periodic wave background in the Gerdjikov–Ivanov equation [29]. It should be noted that the local HM equation don’t have the soliton solutions with a periodic wave background. Thus, a natural motivation is to use the KP hierarchy reduction method to study the dynamical behavior of a periodic wave background in the nonlocal HM equation.

The structure is as follows. The characteristics of line solitons in Eq. (1) are described and examined in Sect. 2. In Sect. 3, we are committed to investigating the breather solutions on both a constant and periodic background. In Sect. 4, we discuss the solutions in detail. Section 5 is the conclusion.

2 High-order solitons with a periodic background

General soliton solutions of Eq. (1) with a periodic wave background are examined in the part. To demonstrate the general 2N-soliton solutions of (1) on the periodic background, we first give the following Theorem. And the appendix includes relevant proofs.

Theorem 2.1

The nonlocal (1) with a periodic wave background has soliton solutions

$$\begin{aligned} u=\frac{g}{f}, \qquad r=-2i(\ln f)_{xy}, \end{aligned}$$

(3)

with f and g shown by determinants

Fig. 1

Periodic wave solution with $\beta =2, b_1=\frac{1}{4}, p_1=i, \chi _{0,1}=\pi$

$$\begin{aligned} \begin{aligned}&f = \begin{pmatrix} c_i\delta _{ij}e^{-\chi _i}+\frac{1}{p_i+p_j^*}&{}\frac{1}{p_i-p_j^*}&{}\frac{1}{p_i-p_{2N+1}^*}\\ -\frac{1}{p_i-p_j^*}&{}-c_i^*\delta _{ij}e^{-\chi _i^*(-x,y,-t)-\frac{1}{p_i+p_j^*}}&{}-\frac{1}{p_i+p_{2N+1}^*}\\ \frac{1}{p_{2N+1}+p_j^*}&{}\frac{1}{p_{2N+1}-p_j^*}&{}ic_{2N+1}e^{-\chi _{2N+1}}+\frac{1}{p_{2N+1}-p_{2N+1^*}} \end{pmatrix}_{0\le i,j\le N},\\&g = \begin{pmatrix} c_i\delta _{ij}e^{-\chi _i}-\frac{p_i}{p_j^*}\frac{1}{p_i+p_j^*}&{}\frac{p_i}{p_j^*}\frac{1}{p_i-p_j^*}&{}\frac{p_i}{p_j^*}\frac{1}{p_i-p_{2N+1}^*}\\ -\frac{p_i}{p_j^*}\frac{1}{p_i-p_j^*}&{}-c_i^*\delta _{ij}e^{-\chi _i^*(-x,y,-t)+\frac{p_i}{p_j^*}\frac{1}{p_i+p_j^*}}&{}\frac{p_i}{p_{2N+1}^*}\frac{1}{p_i+p_{2N+1}^*}\\ -\frac{p_{2N+1}}{p_j^*}\frac{1}{p_{2N+1}+p_j^*}&{}\frac{p_{2N+1}}{p_j^*}\frac{1}{p_{2N+1}-p_j^*}&{}ic_{2N+1}e^{-\chi _{2N+1}}+\frac{p_{2N+1}}{p_{2N+1}^*}\frac{1}{p_{2N+1}-p_{2N+1^*}} \end{pmatrix}_{0\le i,j\le N}, \end{aligned} \end{aligned}$$

(4)

and

$$\begin{aligned} \chi _i= & {} \frac{2p_{iR}x}{\sqrt{6}}-2p_{iR}p_{iI}y\nonumber \\{} & {} -\frac{\sqrt{6}}{9}(\beta t+x)(2p_{iR}^3-6p_{iR}p_{iI}^2)+\chi _{0,i},\nonumber \\ \chi _{2N+1}= & {} \frac{2ip_{2N+1,I}x}{\sqrt{6}}-2p_{2N+1,R}p_{2N+1,I}y\nonumber \\{} & {} -\frac{\sqrt{6}}{9}(\beta t+x)(6ip_{2N+1,R}^2p_{2N+1,I}\nonumber \\{} & {} -2ip_{2N+1,I}^3)+\chi _{0,2N+1}, \end{aligned}$$

(5)

where $\delta _{ij}$ is the Kronecker symbol, $c_i,p_i$ are complex, $\chi _{0,i}$ are real for $i=0,1,\ldots ,N$, and $p_{2N+1}$ is imaginary number.

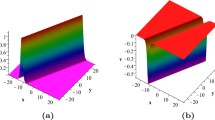
To better understand the actions of the line solitons with a periodic wave background, we take $N=0$ in Theorem (2.1), then f, g could be denoted as

$$\begin{aligned} \begin{aligned}&f=ic_1e^{l-\chi _{0,1}}+\frac{1}{2ip_{1I}},\\&g=ic_1e^{l-\chi _{0,1}}+\frac{1}{2ip_{1I}}\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}},\\ \end{aligned} \end{aligned}$$

(6)

where $l=-\frac{2p_{1R}x}{\sqrt{6}}+2p_{1R}p_{1I}y+\frac{\sqrt{6}}{9}(\beta t+x)(2p_{1R}^3-6p_{1R}p_{1I}^2).$

As discussed in Ref. [30], in order to avoid the solution being singular, we take $p_{1R}=0$. Then the solution is independent of y. It is important to emphasize that $\chi _{0,1}$ controls the amplitude of periodic wave. Fig. 1 shows the periodic wave.

Further, the two-soliton solution with a periodic wave background is derived when setting $N=1$ and the expressions for $f_1,g_1$ are given

$$\begin{aligned} \begin{aligned} f_1&= \begin{pmatrix} c_1e^{-\chi _1}+\frac{1}{p_1+p_1^*}&{}\frac{1}{p_1-p_1^*}&{}\frac{1}{p_1-p_3^*}\\ -\frac{1}{p_1-p_1^*}&{}-c_1^*e^{-\chi _1^*(-x,y,-t)-\frac{1}{p_1+p_1^*}}&{}-\frac{1}{p_1+p_3^*}\\ \frac{1}{p_3+p_1^*}&{}\frac{1}{p_3-p_1^*}&{}ic_3e^{-\chi _3}+\frac{1}{p_3-p_3^*} \end{pmatrix},\\ g_1&=\begin{pmatrix} c_1e^{-\chi _1}-\frac{p_1}{p_1^*}\frac{1}{p_1+p_1^*}&{}\frac{p_1}{p_1^*}\frac{1}{p_1-p_1^*}&{}\frac{p_1}{p_3^*}\frac{1}{p_1-p_3^*}\\ -\frac{p_1}{p_1^*}\frac{1}{p_1-p_1^*}&{}-c_1^*e^{-\chi _1^*(-x,y,-t)+\frac{p_1}{p_1^*}\frac{1}{p_1+p_1^*}}&{}\frac{p_1}{p_3^*}\frac{1}{p_1+p_3^*}\\ -\frac{p_3}{p_1^*}\frac{1}{p_3+p_1^*}&{}\frac{p_3}{p_1^*}\frac{1}{p_3-p_1^*}&{}ic_3e^{-\chi _3}+\frac{p_3}{p_3^*}\frac{1}{p_3-p_3^*} \end{pmatrix}, \end{aligned} \end{aligned}$$

(7)

where $f_1$, $g_1$ both are $3\times 3$ determinants and

$$\begin{aligned} \chi _1&=\frac{2p_{1R}x}{\sqrt{6}}-2p_{1R}p_{1I}y-\frac{\sqrt{6}}{9}(\beta t+x)(2p_{1R}^3\nonumber \\&\quad -6p_{1R}p_{1I}^2)+\chi _{0,1},\nonumber \\ \chi _3&=\frac{2ip_{3I}x}{\sqrt{6}}{-}2p_{3R}p_{3I}y{-}\frac{\sqrt{6}}{9}(\beta t+x)(6ip_{3R}^2p_{3I}\nonumber \\&\quad -2ip_{3I}^3)+\chi _{0,3}. \end{aligned}$$

(8)

The patterns of the two-soliton solution with a periodic wave background are the same as those with a constant background due to the soliton interacts elastically with the periodic line waves.

Fig. 2

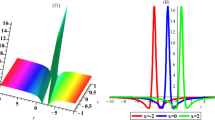
Five types of the two line-soliton solutions at $t=5$ with $p_1=-1-i, p_3=-3i, c_3=\frac{i}{4}, \chi _{0,1}=0, \chi _{0,3}=\pi$. a, b Two antidark-soliton solution with $c_1=1+i$. c, d A antidark-dark-soliton solution with $c_1=1+\frac{i}{2}$. e, f Two dark-soliton solution with $c_1=-1-2i$. g, h Degenerate dark-soliton solution with $c_1=1-i$. i, j Degenerate antidark-soliton solution with $c_1=1+i$

In what follows, by removing the third row and third column of the determinant (7), we explore the asymptotic results for two soliton. The asymptotic soliton along the two lines $\frac{2p_{1R}x}{\sqrt{6}}-2p_{1R}p_{1I}y-\frac{\sqrt{6}}{9}(\beta t+x)(2p_{1R}^3-6p_{1R}p_{1I}^2)+\chi _{0,1}$ and $-\frac{2p_{1R}x}{\sqrt{6}}-2p_{1R}p_{1I}y+\frac{\sqrt{6}}{9}(\beta t+x)(2p_{1R}^3-6p_{1R}p_{1I}^2)+\chi _{0,1}$, which have some different results:

(i) Before collision ($x\rightarrow -\infty$)

Soliton 1 ($\chi _1\approx 0, \chi _1^*(-x,y,-t)\rightarrow +\infty$):

$$\begin{aligned} u_1^-\simeq \frac{c_1e^{-\chi _1}-\frac{1}{p_1+p_1^*}\frac{p_1}{p_1^*}}{c_1e^{-\chi _1}+\frac{1}{p_1+p_1^*}}, \end{aligned}$$

(9)

Soliton 2 ($\chi _1^*(-x,y,-t)\approx 0, \chi _1\rightarrow -\infty$):

$$\begin{aligned} u_2^-\simeq -\frac{p_1}{p_1^*}\frac{c_1^*e^{-\chi _1^*(-x,y,-t)+\theta }-\frac{1}{p_1+p_1^*}\frac{p_1}{p_1^*}}{c_1^*e^{-\chi _1^*(-x,y,-t)+\theta }+\frac{1}{p_1+p_1^*}}, \end{aligned}$$

(10)

where $e^\theta =-\frac{(p_1-p_1^*)^2}{4p_1p_1^*}$.

(ii) After collision ($x\rightarrow +\infty$)

Soliton 1 ($\chi _1\approx 0, \chi _1^*(-x,y,-t)\rightarrow -\infty$):

$$\begin{aligned} u_1^+\simeq -\frac{p_1}{p_1^*}\frac{c_1e^{-\chi _1+\theta }-\frac{1}{p_1+p_1^*}\frac{p_1}{p_1^*}}{c_1e^{-\chi _1+\theta }+\frac{1}{p_1+p_1^*}}, \end{aligned}$$

(11)

Soliton 2 ($\chi _1^*(-x,y,-t)\approx 0, \chi _1\rightarrow +\infty$):

$$\begin{aligned} u_2^+\simeq \frac{c_1^*e^{-\chi _1^*(-x,y,-t)}-\frac{1}{p_1+p_1^*}\frac{p_1}{p_1^*}}{c_1^*e^{-\chi _1^*(-x,y,-t)}+\frac{1}{p_1+p_1^*}}, \end{aligned}$$

(12)

Since $u_1^+(\chi _1)=(-\frac{p_1}{p_1^*})u_1^-(\chi _1-\theta )$ and $|-\frac{p_1}{p_1^*}|=1$, thus these properties imply that the amplitude and velocity of the two-soliton are the same before and after collision. Meanwhile, $|u_j|$ has a maximum value expressed as $|u_j|_{max}$ along the line $\chi _j-\frac{1}{2}\ln (4p_{1,R}^2(c_{1,R}^2+c_{1I}^2))=0$ for $j=1,2$. According to the above analysis, Fig. 2 displays all forms of the two-soliton, namely, two-antidark-antidark-soliton (see Fig. 2a, b), two-dark-antidark-soliton (see Fig. 2c, d), two-dark-dark-soliton (see Fig. 2e, f), degenerate two-antidark soliton (see Fig. 2g, h), degenerate two-dark soliton (see Fig. 2i, j).

We could also gain the higher-order line solitons with a periodic wave background. When $N=2$, there are several patterns of the non-degenerate four-soliton solutions, and three of them are shown in the Fig. 3.

Fig. 3

The four-soliton solution at $t=0$. a, b Non-degenerate four-antidark-soliton solution with $p_1=-\frac{1}{2}-\frac{i}{2}, p_2=-1-\frac{4i}{5}, p_5=-3i, c_1=1+\frac{i}{2}, c_2=1+\frac{2i}{5}, c_5=-\frac{i}{4}, \chi _{0,1}=0, \chi _{0,2}=0, \chi _{0,5}=-\pi$. c, d Non-degenerate three-antidark-one-dark-soliton solution with $p_1=-\frac{1}{2}-i, p_2=-1-i, p_5=-i, c_1=1+2i, c_2=1+\frac{i}{2}, c_5=-i, \chi _{0,1}=3\pi , \chi _{0,2}=-3\pi , \chi _{0,5}=-\frac{\pi }{2}$. e, f Non-degenerate one-antidark-three-dark-soliton solution with $p_1=-\frac{1}{2}-i, p_2=1-i, p_5=-i, c_1=1+2i, c_2=1+\frac{i}{2}, c_5=-i, \chi _{0,1}=3\pi , \chi _{0,2}=-3\pi , \chi _{0,5}=-\frac{\pi }{2}$

3 Breathers with a consant and periodic background

Breather solutions are studied from two distinct backgrounds, namely the constant background and the periodic wave background in this part. We express these solutions in terms of determinants in the following theorem.

Theorem 3.1

The nonlocal HM Eq. (1) has breather solutions

$$\begin{aligned} u=\frac{g}{f},\qquad r=-2i(\ln f)_{xy}, \end{aligned}$$

(13)

with f and g are:

$$\begin{aligned} \begin{aligned}&f=\Lambda |\frac{\delta _{ij}}{\omega _ie^{\chi _i}}+\frac{1}{\frac{1}{2}(\omega _i+\omega _j)+i(\lambda _i-\lambda _j)}|_{1\le i,j\le N},\\&g=\Lambda |\frac{\delta _{ij}}{\omega _ie^{\chi _i}}-\frac{\omega _i+2i\lambda _i}{\omega _j-2i\lambda _j}\frac{1}{\frac{1}{2}(\omega _i+\omega _j)+i(\lambda _i-\lambda _j)}|_{1\le i,j\le N},\\ \end{aligned}\nonumber \\ \end{aligned}$$

(14)

and

$$\begin{aligned}{} & {} \zeta _i=\frac{1}{\sqrt{6}}i\omega _ix+\beta \omega _i\lambda _iy-\frac{\sqrt{6}}{9}i\nonumber \\{} & {} \quad \left( \frac{\omega _i^3}{4}-3\omega _i\lambda _i^2\right) (\beta t+x)+\chi _{0,i}, \end{aligned}$$

(15)

where $\Lambda =\Pi _{i=1}^{N}\omega _ie^{\chi _i}$, and $\omega _i, \lambda _i, \chi _{0,i}$ are real-valued parameters.

Remark 3.1

Depending on the parameter constraints, periodic waves have two dynamical behaviors:

$\bullet$ When $N=2K, \omega _{K+j}=-\omega _j, \lambda _{K+j}=-\lambda _j, \chi _{0,K+i}=\chi _{0,i}$, the breather with a constant background can be obtained.

$\bullet$ When $N=2K+1, \omega _{K+j}=-\omega _j, \lambda _{K+j}=-\lambda _j, \chi _{0,K+i}=\chi _{0,i}, \lambda _{2K+1}=0$, we yield the breather with a periodic wave background.

In what follows, we construct the breather in the constant background. To this end, by choosing

$$\begin{aligned} N=2,\qquad \omega _2=-\omega _1,\qquad \lambda _2=-\lambda _1,\qquad \zeta _{0,2}=\zeta _{0,1},\nonumber \\ \end{aligned}$$

(16)

Fig. 4

One-breather at $t=0$ with $\lambda _1=2, \omega _1=2, \beta =1, \zeta _{0,1}=0$

and the resulting breather read

$$\begin{aligned} u=\frac{g}{f},\qquad r=-2i(\ln f)_{xy}, \end{aligned}$$

(17)

with

$$\begin{aligned} f&=\left| \begin{array}{clr} \frac{1}{\omega _1e^{\zeta _1}}+\frac{1}{\omega _1}&{}\frac{1}{2i\lambda _1}\\ \frac{1}{-2i\lambda _1}&{}\frac{1}{-\omega _1e^{\zeta _1^*}}-\frac{1}{\omega _1} \end{array}\right| ,\\ g&=\left| \begin{array}{clr} \frac{1}{\omega _1e^{\zeta _1}}-\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1}&{}\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{2i\lambda _1}\\ -\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{2i\lambda _1}&{}-\frac{1}{\omega _1e^{\zeta _1^*}}+\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1} \end{array}\right| . \end{aligned}$$

After a simple algebraic calculation, the final form of the breather solution reads

$$\begin{aligned} u= & {} \frac{(-16\lambda _1^4+16i\lambda _1^3\omega _1+4i\lambda _1\omega _1^3+\omega _1^4)e^{2c_{1R}}+ 16((-\frac{\omega _1^2}{4}-\lambda _1^3)e^{c_1^*}+\left( \frac{\omega _1^2}{4}+\lambda _1^2\right) e^{c_1}+i\omega _1\lambda _1- \frac{\omega _1^2}{4}+\lambda _1^2)\lambda _1^2}{\nonumber }\\{} & {} {(4(i\lambda _1-\frac{\omega _1}{2})^2((4\lambda _1^2+\omega _1^2)e^{2c_{1R}}+4\lambda _1^2(e^{c_1}+e^{c_1^*}+1))},\nonumber \\ r= & {} -2i\ln \left( -\left( \frac{1}{\omega _1^2}+\frac{1}{4\lambda _1^2}+\frac{1}{\omega _1^2e^{c_1}}\right. \right. \left. \left. +\frac{1}{\omega _1^2e^{c_1^*}}+\frac{1}{\omega _1^2e^{2c_{1R}}}\right) \right) _{xy}. \end{aligned}$$

(18)

The above solution contains trigonometric functions, thus the solution is periodic as $c_1=c_{1R}+ic_{1I}$. Notably, the periodic solution does not progress in the y direction. Fig. 4 illustrates one breather for two independent variables.

With a larger K, the N-breathers with the constant background could be given. In this case, we take $K=2$, the corresponding solution has two individual breathers, and possesses interesting involution patterns. In order to observe the more interesting phenomenon of the two breathers, we fix the value of $\chi _{0,1}$ and take different values of $\chi _{0,2}$. Hence, we take the following parameters choices:

$$\begin{aligned} \begin{aligned}&\lambda _1=2,\qquad \lambda _2=2,\qquad \lambda _3=-2,\qquad \lambda _4=-2,\qquad \\&\omega _1=2,\qquad \omega _2=\frac{1}{2},\\&\omega _3=-2,\qquad \omega _4=-\frac{1}{2},\qquad \beta =1,\qquad \chi _{0,1}=0.\\ \end{aligned} \end{aligned}$$

(19)

With the parameter choices described above, Fig. 5 shows the evolutionary patterns of the two breathers. One can directly find that $\chi _{0,1}$ controls breather-1 and $\chi _{0,2}$ controls breather-2. When $\chi _{0,2}\ll 0$, there is a large distance between the two breathers. When $\chi _{0,2}\rightarrow 0$, two breathers are in close proximity and start interacting. When $\chi _{0,2}\gg 0$, two breathers will first form a single breather, after which the two breathers will separate from each other. We find the collision between two breathers is an elastic collision.

Fig. 5

The two-breather solution on a constant background with parameters: a $\chi _{0,2}=-2\pi$; b $\chi _{0,2}=-\frac{\pi }{2}$; c $\chi _{0,2}=0$; d $\chi _{0,2}=2\pi$

In order to examine the moving features of breathers with a periodic wave background, by taking $K=1$ and the parameters are satisfying

$$\begin{aligned}{} & {} \omega _2=-\omega _1,\qquad \lambda _2=-\lambda _1,\nonumber \\{} & {} \qquad \lambda _3=0,\qquad \chi _{0,2}=\chi _{0,1}, \end{aligned}$$

(20)

then we obtain one breather with a periodic wave background

$$\begin{aligned} u=\frac{g_2}{f_2}, \end{aligned}$$

(21)

where f and g are

$$\begin{aligned} \begin{aligned} f_2&= \begin{pmatrix} \frac{1}{\omega _1e^{\chi _1}}+\frac{1}{\omega _1}&{}\frac{1}{2i\lambda _1}&{}\frac{1}{\frac{1}{2}(\omega _1+\omega _3)+i\lambda _1}\\ \frac{1}{-2i\lambda _1}&{}\frac{1}{-\omega _1e^{\chi _1^*}}-\frac{1}{\omega _1}&{}\frac{1}{\frac{1}{2}(\omega _2+\omega _3)+i\lambda _2}\\ \frac{1}{\frac{1}{2}(\omega _3+\omega _1)-i\lambda _1}&{}\frac{1}{\frac{1}{2}(\omega _3+\omega _2)-i\lambda _2}&{} \frac{1}{\omega _3e^{\chi _3}}+\frac{1}{\omega _3} \end{pmatrix},\\ g_2&=\begin{pmatrix} \frac{1}{\omega _1e^{\chi _1}}-\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1}&{}\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{2i\lambda _1}&{}-\frac{\omega _1+2i\lambda _1}{\omega _3}\frac{1}{\frac{1}{2}(\omega _1+\omega _3)+i\lambda _1}\\ -\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{-2i\lambda _1}&{}\frac{1}{-\omega _1e^{\chi _1^*}}+\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1}&{}-\frac{\omega _2+2i\lambda _2}{\omega _3}\frac{1}{\frac{1}{2}(\omega _2+\omega _3)+i\lambda _2}\\ -\frac{\omega _3}{\omega _1-2i\lambda _1}\frac{1}{\frac{1}{2}(\omega _3+\omega _1)-i\lambda _1}&{}-\frac{\omega _3}{\omega _2-2i\lambda _2}\frac{1}{\frac{1}{2}(\omega _3+\omega _2)-i\lambda _2}&{} \frac{1}{\omega _3e^{\chi _3}}-\frac{1}{\omega _3} \end{pmatrix}, \end{aligned} \end{aligned}$$

(22)

and

$$\begin{aligned}{} & {} \chi _1=\frac{1}{\sqrt{6}}i\omega _1x+\lambda _1\omega _1y-\frac{\sqrt{6}i}{9}\nonumber \\{} & {} \left( \frac{\omega _1^3}{4}-3\lambda _1^2\omega _1\right) (x+t)+\chi _{0,1},\nonumber \\{} & {} \chi _3=\frac{i}{\sqrt{6}}\omega _3x-\frac{\sqrt{6}i}{9}\frac{\omega _1^3}{4}(t+x)+\chi _{0,3}. \end{aligned}$$

(23)

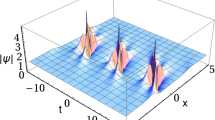
Based on the analysis of the solution, we thus conclude that the breather remains periodic in the (x, t) plane and localizes along y. The location of one breather is determined by $\chi _{0,3}$. Figure 6 illustrates different dynamics of the one-breather with distinct $\chi _{0,3}$.

Fig. 6

One-breather with a periodic wave background at $t=1$ with: a $\chi _{0,2}=-2\pi$; b $\chi _{0,2}=0$; c $\chi _{0,2}=2\pi$

Similarly, high order breathers with a periodic wave background are obtained from the Theorem (3.1). For example, we take $K=2$ and

$$\begin{aligned}{} & {} \lambda _5=0,\qquad \lambda _3=-\lambda _1,\qquad \lambda _4=-\lambda _2,\nonumber \\{} & {} \qquad \omega _3=-\omega _1,\qquad \omega _4=-\omega _2 \end{aligned}$$

(24)

the two breathers with a periodic wave background would be derived. According to the different values of $\chi _{0,1}$, the two breathers will be displayed in Fig. 7.

Fig. 7

Two-breather solution with a periodic wave background at $t=1$ with $\lambda _1=2, \lambda _2=2, \omega _1=1, \omega _2=\frac{1}{2}, \omega _5=1, \chi _{0,3}=0, \chi _{0,5}=\frac{4\pi }{5}$: a $\chi _{0,1}=-10\pi$; b $\chi _{0,1}=-\frac{\pi }{2}$; c $\chi _{0,1}=10\pi$

4 Discussion on solutions

In this section, we mainly discuss the influence of parameters on the solutions. By substituting two independent variables in the $\tau$ function, soliton solutions and breather solutions can be constructed respectively. For line solitons on the periodic wave background, when $N=0$, the periodic wave is shown in Fig. 1. If $N=1$, through asymptotic analysis, we conclude that $u_1^+(\chi _1)=(-\frac{p_1}{p_1^*})u_1^-(\chi _1-\theta )$ and $|-\frac{p_1}{p_1^*}|=1$. The elastic collision of two-soliton occurs at this time, including degenerate soliton and non-degenerate soliton. With respect to general two-soliton, |u| component possesses five dynamical patterns with a periodic wave background (see Fig. 2), while |r| component only appears the two-antidark-antidark-soliton. Meanwhile, the high-order line soliton solutions with a periodic wave background are demonstrated (see Fig. 3).

In the case of introducing parameters $p_i=\frac{\omega _i}{2}+i\lambda _i$, $q_i=\frac{\omega _i}{2}-i\lambda _i$, we derive the breather solutions. To manipulate the breathers in both constant and periodic wave background, our careful adjustment involves dividing the determinant’s order in Eq. (41). When $N=2K, \omega _{K+j}=-\omega _j, \lambda _{K+j}=-\lambda _j, \chi _{0,K+i}=\chi _{0,i}$, the breather with a constant background can be obtained, as shown in Fig. 4-5. When we fix $\chi _{0,1}$ and take different values for $\chi _{0,2}$, the two breathers will interact. It’s fascinating that two breathers will exhibit a triangular pattern in the case of $\chi _{0,2}$ is close to $\chi _{0,1}$. Conversely, if $N=2K+1, \omega _{K+j}=-\omega _j, \lambda _{K+j}=-\lambda _j, \chi _{0,K+i}=\chi _{0,i}, \lambda _{2K+1}=0$, we acquire the breathers within the periodic wave background (see Fig. 6-7). As for the rational solutions obtained by taking the long wave limit on the periodic solutions, we have studied it in Ref. [18].

5 Conclusion

In this paper, we mainly utilize the KP reduction method to construct the solitons and breathers with a periodic wave background in Eq. (1). Taking different parameter constraints on the tau functions, the 2N solitons and the N breather solutions with a periodic wave background could be expressed. Within the background of a periodic wave, line solitons exhibit a classification of five distinct wave types. The breathers on both the constant background and the periodic wave background can be formed when the order of the determinant (41) is either odd or even. Elastic collisions between two breathers are observed through an analysis of their dynamic behavior on a constant background. It is apparent that when the order of the determinant increases, the period of the periodic wave also strengthens. Besides, the form of these solutions that we obtain is more concise and meaningful for the research of nonlinear mathematical physical models.

Appendix A

In this part, we will prove the Theorem (2.1) and Theorem (3.1). Firstly, we utilize the variable transformations

$$\begin{aligned} u=\frac{g}{f}, \quad u^*(-x,y,-t)=\frac{h}{f},\quad r=-2i(\ln f)_{xy},\nonumber \\ \end{aligned}$$

(25)

to convert the Eq. (2) into the bilinear equation

$$\begin{aligned} \begin{aligned}&(D_t-iD_xD_y+\beta D_x^3+\beta D_x)g\cdot f=0,\\&(3D_x^2+1)f\cdot f=gh. \end{aligned} \end{aligned}$$

(26)

Taking reduction condition

$$\begin{aligned} (\partial _x-\partial _s)f=cf, \end{aligned}$$

(27)

the $(3 + 1)$ dimensional system of Eq. (1) can be obtained

$$\begin{aligned} \begin{aligned}&(D_t-iD_xD_y+\beta D_x^3+\beta D_x)g\cdot f=0,\\&(3D_xD_s+1)f\cdot f=gh, \end{aligned} \end{aligned}$$

(28)

under the nonlocal condition

$$\begin{aligned} f(x,y,t)g^*(-x,y,-t)=f^*(-x,y,-t)h(x,y,t),\nonumber \\ \end{aligned}$$

(29)

where c is constant, g, h are complex-valued functions, and f is a real-valued function.

Based on the Sato theory [31, 32], the bilinear equations in the KP hierarchy

$$\begin{aligned} \begin{aligned}&(D_{x_1}^3+3D_{x_1}D_{x_2}-4D_{x_3})\tau _{n+1}\tau _n=0,\\&(D_{x_1}D_{x_{-1}}-2)\tau _n\tau _n=-2\tau _{n+1}\tau _{n-1}, \end{aligned} \end{aligned}$$

(30)

exist the determinant

$$\begin{aligned} \tau _n=\mathop {det}\limits _{1\le i,j\le N}(m_{ij}^{(n)}), \end{aligned}$$

(31)

where

$$\begin{aligned} \begin{aligned}&m_{ij}^{(n)}=\widetilde{c_i}\delta _{ij}+\frac{p_i+s_i}{p_i+q_j}\left( \frac{-p_i}{q_j}\right) ^ne^{\xi _i+\eta _j},\\&\xi _i=\frac{1}{p_i}x_{-1}+p_ix_1+p_i^2x_2+p_i^3x_3+\xi _{0,i},\\&\eta _j=\frac{1}{q_j}x_{-1}+q_jx_1-q_j^2x_2+q_j^3x_3+\eta _{0,j}. \end{aligned} \end{aligned}$$

(32)

In order to obtain periodic solutions, we employ the independent variables $x_1=\frac{1}{\sqrt{6}}x$, $x_2=\frac{1}{2}i\beta y$, $x_3=-\frac{\sqrt{6}}{9}\beta t-\frac{\sqrt{6}}{9}x$, then the Eq. (31) can rewrite

$$\begin{aligned} \tau _n=\prod _{i=1}^{N}(p_i+s_i)e^{\zeta _i}\mathop {det}\limits _{1\le i,j\le N}(\widehat{m_{ij}^{(n)}}), \end{aligned}$$

(33)

where

$$\begin{aligned} \widehat{m_{ij}^{(n)}}=\widetilde{c_i}\delta _{ij}e^{-\zeta _i}\frac{1}{p_i+s_i}+\frac{1}{p_i+q_j}(-\frac{p_i}{q_j})^n, \end{aligned}$$

(34)

with

$$\begin{aligned} \begin{aligned} \zeta _i&=\xi _i+\eta _i\\&=\frac{1}{\sqrt{6}}(p_i+q_j)x+\frac{i}{2}\beta (p_i^2-q_j^2)y\\ {}&\quad -\frac{\sqrt{6}}{9}(\beta t+x)(p_i^3+q_j^3)+\chi _{0,i}. \end{aligned} \end{aligned}$$

(35)

To yield soliton solutions, we consider $M=2N+1$ in Eq. (31) and restrict the parameters obeying the following conditions

$$\begin{aligned} \begin{aligned}&s_j=-p_j+1,\quad p_{M+i}=-p_i,\quad q_{M+i}=-q_i,\quad q_i=p_i^*,\\&q_{2M+1}\!=\!-p_{2M+1}^*,\quad \widetilde{c_j}\!=\!b_j,\quad c_{M+i}\!=\!-c_i^*,\quad \widetilde{c_{2M+1}}\!=\!ic_{2M+1}, \end{aligned}\nonumber \\ \end{aligned}$$

(36)

then one can obtain

$$\begin{aligned} \begin{aligned} \chi _{2M+1}^*(-x,y,-t)&=\chi _{2M+1}(x,y,t),\\ \chi _{M+i}^*(-x,y,-t)&=\chi _i(x,y,t), \end{aligned} \end{aligned}$$

(37)

and derive

$$\begin{aligned} \begin{aligned} \widehat{m_{M+i,j}^{*(n)}}(-x,y,-t)&=-c_i^*\delta _{M+i,j}e^{-\chi _i}\\&\quad -\frac{1}{p_i^*+p_{M+j}} \left( -\frac{p_{M+j}}{p_i^*}\right) ^{-n}\\&=-\widehat{m_{i,M+j}}^{(-n)}(x,y,t), \end{aligned}\nonumber \\ \end{aligned}$$

(38)

which implies

$$\begin{aligned} \tau _n^*(-x,y,-t)=(-1)^{3N}\tau _{-n}(x,y,t). \end{aligned}$$

(39)

As a result, Eq. (30) can be reduced to the bilinear Eqs. (28) with $f=\tau _0, g=\tau _1, h=\tau _{-1}$.

To generate breathers to Eq. (1), we select several variable transformations

$$\begin{aligned}{} & {} x_{-1}=-\frac{1}{\sqrt{6}}is, \qquad x_1=\frac{1}{\sqrt{6}}ix, \qquad x_2=-\frac{1}{2}i\beta y, \nonumber \\{} & {} \qquad x_3=-i\frac{\sqrt{6}}{9}\beta t-i\frac{\sqrt{6}}{9}x, \end{aligned}$$

(40)

then the tau function becomes

$$\begin{aligned} \tau _n=\prod _{i=1}^{N}(p_i+s_i)e^{\chi _i}\mathop {det}\limits _{1\le i,j\le N}(\overline{m_{i,j}^{(n)}}), \end{aligned}$$

(41)

where $\overline{m_{i,j}^{(n)}}$ is given by

$$\begin{aligned}{} & {} \overline{m_{ij}^{(n)}}=\frac{\widetilde{c_i}\delta _{ij}}{(p_i+s_i)e^{\xi _i+\eta _j}}\nonumber \\{} & {} \quad +\frac{1}{p_i+q_j}\left( -\frac{p_i}{q_j}\right) ^n,\nonumber \\{} & {} \chi _i=\xi _i+\eta _i=\frac{1}{\sqrt{6}}(p_i+p_i^*)ix-\frac{1}{2}i\beta (p_i^2-p_i^{*2})y\nonumber \\{} & {} \quad -\frac{\sqrt{6}}{9}i(p_i^3+p_i^{*3})(\beta t+x)+\chi _i^0. \end{aligned}$$

(42)

When the parameters satisfy $\widetilde{c_{i,j}}=1, s_j=q_j, q_j=p_j^*$, one could conclude that $\chi _i^*(-x,y,-t)=\chi _i(x,y,t)$. In this case, we further derive

$$\begin{aligned} \overline{m_{j,i}^{*(-n)}}(x,y,t)= & {} \overline{m_{i,j}^{*(n)}}(-x,y,-t),\nonumber \\{} & {} \tau _n^*(-x,y,-t)=\tau _{-n}(x,y,t). \end{aligned}$$

(43)

Additionally, determining $f=\tau _0, g=\tau _1, h=\tau _{-1}$ and letting

$$\begin{aligned} p_i=\frac{\omega _i}{2}+i\lambda _i,\qquad q_i=\frac{\omega _i}{2}-i\lambda _i, \end{aligned}$$

(44)

solutions for the breather are discovered.