Broken and unbroken $\varvec{\mathcal {PT}}$-symmetric solutions of semi-discrete nonlocal nonlinear Schrödinger equation

Abstract

In this letter, we obtain multi-soliton solutions in terms of ratio of ordinary determinants for semi-discrete nonlocal nonlinear Schrödinger (sd-NNLS) equation by employing the Darboux transformation. We construct explicit expressions of single and double soliton solutions in zero background. We obtain symmetry-broken and symmetry-unbroken soliton solutions of sd-NNLS equation by using appropriate eigenfunctions. We notice that for symmetry non-preserving case, the potential term exhibits stable structure whereas individual fields display instability. We also obtain blowup or oscillating singular-type soliton solutions for symmetry-preserving case.

1 Introduction

In recent past, Ablowitz and Musslimani introduced a scalar $\mathcal {PT}$-symmetric nonlocal nonlinear Schrödinger (NNLS) equation [1]:

$$\begin{aligned} iq_{t}(x,t)=q_{xx}(x,t)\pm 2q^{2}(x,t)q^{*}(-x,t). \end{aligned}$$

(1)

The NNLS equation is said to be integrable as it admits Lax pair and an infinite number of conservation laws. NNLS equation (1) has attracted a great deal of attraction due to remarkable new features in contrast with classical standard NLS equation. Ablowitz and Musslimani [1] obtained oscillating singular-type of NNLS equation by using the inverse scattering transform (IST) mathod. Sarma et al. [2] illustrate that it can exhibit both bright and dark soliton solutions simultaneously. Hamiltonian formalism is developed in [3], periodic and hyperbolic soliton solutions [4], rational solutions [5] are derived and recently symmetry-preserving and symmetry-broken soliton solutions have also been studied [6].

Equation (1) is $\mathcal {PT}$-symmetric because the nonlinear term $V\left( x,t\right) =q(x,t)q^{*}(-x,t)$ is invariant under the action of $\mathcal {PT}$-symmetry, that is, $V\left( x,t\right) =V^{*}\left( -x,t\right)$. Moreover, this equation is invariant under the combined transformation $x\rightarrow -x$, $t\rightarrow -t$, $q\rightarrow q^{*}.$$\mathcal {PT}$-symmetry invariance is unique because the local solution state at x is directly coupled with the nonlocal solution at distant location $-x$, like quantum entanglement between pairs of particles. The initial interest in such systems was motivated by quantum mechanics. In [7], firstly it was pointed out that $\mathcal {PT}$-symmetric quantum systems with non-Hermitian Hamiltonians possess real eigenvalues. Since then, the pseudo-Hermitian systems have been studied extensively due to wide range of applications in nonlinear optics [8], complex crystals [9], quantum chromodynamics [10], Bose–Einstein condensates [11] etc.

Even more interestingly, $\mathcal {PT}$-symmetric system can also display a spontaneous symmetry breaking transitions. Such a phase transition takes place at an exceptional point in the parameter space. Once a pseudo-Hermitian parameter exceeds a certain threshold value; the spectrum of $\mathcal {PT}$-operator ceases to be entirely real instead becomes partially or completely imaginary. Further, as the $\mathcal {PT}$-operator is not linear, and thus the Hamiltonian and $\mathcal {PT}$-operator may or may not have the same set of eigenstates even though they still commute. As a consequence, the associated eigenvalues of the system change from real to complex that signifies the broken $\mathcal {PT}$-symmetry [12,13,14,15,16,17,18,19]. These observations are so much remarkable that they will revolutionize the optical physics by synthesizing integrated $\mathcal {PT}$ photonic devices and also extension of these ideas will be fruitful in other directions of research.

Integrable semi-discrete NLS (sd-NLS) equation was first proposed by Ablowitz and Ladik [20]:

$$\begin{aligned} i\frac{\mathrm{d}}{\mathrm{d}t}q_{n}{=}\frac{1}{\delta ^{2}}\left( q_{n+1}{-}2q_{n}+q_{n-1}\right) \pm \left| q_{n}\right| ^{2}\left( q_{n+1}+q_{n-1}\right) \end{aligned}$$

(2)

and showed that it is solvable, has soliton solution, admits an infinite number of conserved quantities and a Hamiltonian structure. There exists a wide range of physical and biological phenomena that are governed by this model, e.g., it describes biophysical systems [21], molecular crystals [22], selftraping on a dimer [23], Heisenberg spin chain [24] and so on. The nonlocal reductions are particularly important due to its applications in $\mathcal {PT}$-symmetric optics, especially in developing of theory of electromagnetic waves in artificial heterogenic media [25,26,27]. The nonlocal version of Ablowitz and Ladik equation was presented in [28, 29]:

$$\begin{aligned}&i\frac{\mathrm{d}Q_{n}}{\mathrm{d}\tau }=Q_{n+1}-2Q_{n}+Q_{n-1}\nonumber \\&\quad \pm Q_{n}Q_{-n}^{*}\left( Q_{n+1}+Q_{n-1}\right) , \end{aligned}$$

(3)

which is an integrable Hamiltonian model. $Q_{n}$ is complex valued function, n is an integer. Equation (3) is also a $\mathcal {PT}$-symmetric for the reason that the so-called nonlinear self-induced potential $V_{n}=Q_{n}Q_{-n}^{*}$ remains invariant under the joint action of $\mathcal {PT}$-symmetry [30]. Ablowitz and Musslimani [28] investigated it by using IST scheme and derived singularity formation. In [31], the authors constructed N-soliton solution for focusing case and get periodic and singular solutions using Hirota’s method.

In this letter, we focus on a semi-discrete coupled NLS (sd-CNLS) equations

$$\begin{aligned}&i\frac{\mathrm{d}Q_{n}}{\mathrm{d}\tau } =Q_{n+1}-2Q_{n}+Q_{n-1}\nonumber \\&\quad \quad \quad \quad -\,Q_{n}R_{n}\left( Q_{n+1}+Q_{n-1}\right) \nonumber \\&-i\frac{\mathrm{d}R_{n}}{\mathrm{d}\tau } =R_{n+1}-2R_{n}+R_{n-1}\nonumber \\&\quad \quad \quad \quad -\,Q_{n}R_{n}\left( R_{n+1}+R_{n-1}\right) . \end{aligned}$$

(4)

Coupled in the sense that authors have evaluated more general soliton solutions by solving system (4) simultaneously. And nonlocality has been investigated independently for $\mathcal {PT}$-symmetry-broken and $\mathcal {PT}$-symmetry-preserving cases. In the first case, $Q_{n}$ and $R_{n}$ are behaved as two independent functions and their evolution is governed by two different equations. In this case, $Q_{n}$ is evaluated at n and $R_{n}$ is evaluated at $-n$ simultaneously but solutions are not identical that means $R_{n}$ is not a parity transformed complex conjugate function of $Q_{n}.$ And illustrate that each function in the pair spontaneously breaks $\mathcal {PT}$-symmetry; one exhibits amplification and the other dissipation, but get stable soliton propagation for $\left| Q_{n}R_{n}\right|$. In the second case function $R_{n}$ is related to $Q_{n}$ and can be directly obtained from $Q_{n}$ by simply taking the parity conjugate. To get better understanding, it is very much essential to treat $Q_{n}$ and $R_{n}$ as two separate functions. This procedure is distinctive and not globally applied but give universal solutions.

Our work is organized as follows. In Sect. 2, sd-NNLS equations and associated Ablowitz–Ladik scheme are presented. In Sect. 3, a Darboux transformation is applied to the Lax pair system and obtain multi-soliton solutions in terms of ratio of ordinary determinants. In Sect. 4, explicit solutions are calculated and finally we illustrated our results by plotting the obtained solution for different values of spectral parameters. We discuss our results in Sect. 5 followed by a conclusion in Sect. 6.

2 Ablowitz–Ladik scheme

The sd-CNLS equation (4) can be presented as a consistency condition of linear difference-differential system

$$\begin{aligned} \varPsi _{n+1} =L_{n}\varPsi _{n}, \quad \frac{\mathrm{d}}{\mathrm{d}\tau }\varPsi _{n} =M_{n}\varPsi _{n}, \end{aligned}$$

(5)

where

$$\begin{aligned} L_{n}= & {} \left( \begin{array}{ll} z &{}\quad Q_{n} \\ R_{n} &{}\quad z^{-1} \end{array} \right) , \nonumber \\ M_{n}= & {} \left( \begin{array}{ll} iQ_{n}R_{n-1}-\frac{i}{2}\left( z-z^{-1}\right) ^{2} &{}\quad -\,i\left( zQ_{n}-z^{-1}Q_{n-1}\right) \\ i\left( z^{-1}R_{n}-zR_{n-1}\right) &{}\quad -\,iR_{n}Q_{n-1}+\frac{i}{2}\left( z-z^{-1}\right) ^{2} \end{array} \right) , \end{aligned}$$

where $\varPsi _{n}=\left( X_{n},Y_{n}\right) ^\mathrm{T}$ is a eigenvector and z be the associated eigenvalue. The linear system of difference-differential equations is also known as Ablowitz–Ladik (AL) scattering problem [32]. The AL Scheme (5) may be regarded as semi-discrete analogue of the Lax pair. The integrability condition of AL Scheme (5) becomes a semi-discrete analogue zero-curvature condition (namely, $\frac{\mathrm{d}}{\mathrm{d}t}L_{n}+L_{n}M_{n}-M_{n+1}L_{n}=0$) which yields the coupled system of Eq. (4).

In order to get the integrable a sd-NLS equation (2) from Eq. (4), we transform variable as follows:

$$\begin{aligned} Q_{n}\rightarrow \delta q_{n},\quad R_{n}\rightarrow \delta r_{n}, \quad \tau \rightarrow \delta ^{-2}t. \end{aligned}$$

(6)

Then the system (4) becomes

$$\begin{aligned} i\frac{\mathrm{d}q_{n}}{\mathrm{d}t}= & {} \frac{1}{\delta ^{2}}\left( q_{n+1}-2q_{n}+q_{n-1}\right) \nonumber \\&-q_{n}r_{n}\left( q_{n+1}+q_{n-1}\right) , \nonumber \\ -i\frac{\mathrm{d}r_{n}}{\mathrm{d}t}= & {} \frac{1}{\delta ^{2}}\left( r_{n+1}-2r_{n}+r_{n-1}\right) \nonumber \\&-\,q_{n}r_{n}\left( r_{n+1}+r_{n-1}\right) , \end{aligned}$$

(7)

which reduces to the integrable sd-NLS equation (2) by taking $r_{n}=\mp q_{n}^{*}$. On the other hand, Eq. (3) is obtained from the system (4) using the nonlocal symmetry reduction, i.e., $R_{n}=\mp Q_{-n}^{*}$. In addition to this, if we take continuum limit, that is $\delta \rightarrow 0$, the system (7) leads to continuous NLS equations,

$$\begin{aligned} iq_{t}=q_{xx}-2rq^{2},\quad -\,ir_{t}=r_{xx}-2qr^{2}. \end{aligned}$$

(8)

Similarly, if we replace $z=\exp \left( -i\lambda \delta \right)$ into the AL Scheme (5) reduces

$$\begin{aligned}&\frac{\varPsi _{n+1}-\varPsi _{n}}{\delta } =\left( \begin{array}{ll} -\,i\lambda &{}\quad q_{n} \\ r_{n} &{}\quad i\lambda \end{array} \right) \varPsi _{n}+O(\delta ^2), \nonumber \\&\frac{\mathrm{d}}{\mathrm{d}t }\varPsi _{n} =\left( \begin{array}{ll} iq_{n}r_{n-1}+2i\lambda ^2 &{} \quad -\,\lambda \left( q_{n}+q_{n-1}\right) -i\left( \frac{q_{n}-q_{n-1}}{\delta }\right) \\ -\lambda \left( r_{n}+r_{n-1}\right) +i\left( \frac{r_{n}-r_{n-1}}{\delta }\right) &{} \quad -\,ir_{n}q_{n-1}-2i\lambda ^2 \end{array} \right) \varPsi _{n}+O(\delta ^2), \end{aligned}$$

(9)

under the continuum limit take (that is, $x=n\delta , t=\delta ^2\tau$ and $\delta \rightarrow 0$), we obtain Lax pair for continuous NLS equation (8).

3 Darboux transformation for coupled semi-discrete NLS equations

Darboux transformation (DT) is a gauge transformation used to generate a family of infinitely many non-trivial solutions of a linear equations (differential, difference and differential-difference) from a known trivial solution. The DT can also be used to compute multiple solutions of a nonlinear integrable evolution equations (differential, difference and differential-difference equations) [33]. In order to calculate multi-soliton solutions of nonlinear evolution equation, we apply DT on the known solution of associated linear spectral problem. The covariance of the linear spectral problem generates non-trivial solutions of a given nonlinear evolution equation. In this section, we shall apply DT on the matrix-valued of AL scheme (5) and the covariance of the AL scheme generates the new solutions of sd-CNLS system (4).

The DT for AL Scheme (5) can be defined as

$$\begin{aligned} \varPsi _{n}[1]\equiv & {} T_{n,1}\varPsi _{n}\nonumber \\= & {} \left( \begin{array}{ll} -\,z+z^{-1}a_{n,1} &{}\quad b_{n,1} \\ c_{n,1}&{}\quad z^{-1}+zd_{n,1} \end{array} \right) \varPsi _{n}, \end{aligned}$$

(10)

where $T_{n,1}$ is the onefold Darboux matrix. Here $a_{n,1},$$b_{n,1},$$c_{n,1}$ and $d_{n,1}$ are some functions to be determined. The transformed solution $\varPsi _{n}[1]$ given by (10) also satisfies AL Scheme (5), that is,

$$\begin{aligned} \varPsi _{n+1}[1]=L_{n}[1]\varPsi _{n}[1], \quad \frac{\mathrm{d}}{\mathrm{d}t}\varPsi _{n}[1]= & {} M_{n}[1]\varPsi _{n}[1],\nonumber \\ \end{aligned}$$

(11)

where the transformed matrices $L_{n}[1]$ and $M_{n}[1]$ are obtained by replacing $Q_{n},R_{n}$ by $Q_{n}[1],R_{n}[1]$ in $L_{n}$ and $M_{n}$. On substitution of (10) in (11) and using (5), we obtain

$$\begin{aligned} Q_{n}[1]=-\frac{Q_{n}-b_{n,1}}{d_{n,1}}, \quad R_{n}[1]= & {} \frac{R_{n}-c_{n,1}}{a_{n,1}}. \end{aligned}$$

(12)

The unknown functions $a_{n,1}$$b_{n,1},$$c_{n,1}$ and $d_{n,1}$ can be determined by using the following constraint conditions

$$\begin{aligned} T_{n,1}\varPsi _{n}\mid _{ z=z_{k} }=0,\quad k=1,2. \end{aligned}$$

(13)

The above conditions (13) lead to following coupled system of linear algebraic equations

$$\begin{aligned} z_{k}^{-1}a_{n,1}X_{n,k}+b_{n,1}Y_{n,k}= & {} z_{k}X_{n,k},\nonumber \\ c_{n,1}X_{n,k}+z_{k}d_{n,1}Y_{n,k}= & {} -z_{k}^{-1}Y_{n,k}. \end{aligned}$$

(14)

The solution of linear system (14) of algebraic equations allows us to write

$$\begin{aligned} a_{n,1}= & {} \frac{\left| \begin{array}{ll} z_{2}X_{n,2} &{}\quad Y_{n,2}\\ z_{1}X_{n,1}&{}\quad Y_{n,1} \end{array} \right| }{\left| \begin{array}{ll} z_{2}^{-1}X_{n,2} &{}\quad Y_{n,2}\\ z_{1}^{-1}X_{n,1} &{}\quad Y_{n,1} \end{array} \right| },\quad b_{n,1}=\frac{\left| \begin{array}{ll} z_{2}^{-1}X_{n,2} &{}\quad z_{2}X_{n,2}\\ z_{1}^{-1}X_{n,1} &{}\quad z_{1}X_{n,1} \end{array} \right| }{\left| \begin{array}{ll} z_{2}^{-1}X_{n,2}&{}\quad Y_{n,2}\\ z_{1}^{-1}X_{n,1}&{}\quad Y_{n,1} \end{array} \right| }, \nonumber \\ c_{n,1}= & {} -\frac{\left| \begin{array}{ll} z_{2}^{-1}Y_{n,2} &{}\quad z_{2}Y_{n,2}\\ z_{1}^{-1}Y_{n,1}&{}\quad z_{1}Y_{n,1} \end{array} \right| }{\left| \begin{array}{ll} X_{n,2} &{}\quad z_{2}Y_{n,2}\\ X_{n,1} &{}\quad z_{1}Y_{n,1}\\ \end{array} \right| },\quad d_{n,1}=-\frac{\left| \begin{array}{ll} X_{n,2} &{}\quad z_{2}^{-1}Y_{n,2}\\ X_{n,1}&{}\quad z_{1}^{-1}Y_{n,1} \end{array} \right| }{\left| \begin{array}{ll} X_{n,2} &{}\quad z_{2}Y_{n,2}\\ X_{n,1}&{}\quad z_{1}Y_{n,1} \end{array} \right| }. \nonumber \\ \end{aligned}$$

(15)

Again under the continuum limit, the DT (10) for AL scheme (5) reduces to the standard DT for classical NLS equation [33]. For this purpose, take $x=n\delta , t=\delta ^2\tau$ and $\delta \rightarrow 0$, we have

$$\begin{aligned} \varPsi (x,t)[1]= & {} \lim _{\delta \rightarrow 0}\frac{\varPsi _{n}[1]}{2\text{ i }\delta }=\left( \lambda I_{2}-S_{1}\right) \varPsi , \end{aligned}$$

(16)

where $I_{2}$ is the identity matrix and

$$\begin{aligned} S_{1}= & {} \frac{1}{X_{1}Y_{2}-X_{2}Y_{1}}\nonumber \\&\left( \begin{array}{ll} \lambda _{1}X_{1}Y_{2}-\lambda _{2}X_{2}Y_{1}&{}\quad -\,\left( \lambda _{1}-\lambda _{2}\right) X_{1}X_{2} \\ \left( \lambda _{1}-\lambda _{2}\right) Y_{1}Y_{2} &{}\quad \lambda _{2}X_{1}Y_{2}-\lambda _{1}X_{2}Y_{1} \end{array} \right) \varPsi .\nonumber \\ \end{aligned}$$

(17)

Moreover, under continuum limits Eq. (12) reduces to

$$\begin{aligned} q[1]= & {} q+2i\frac{\left( \lambda _{1}-\lambda _{2}\right) X_{1}X_{2}}{X_{1}Y_{2}-X_{2}Y_{1}}, \nonumber \\ r[1]= & {} r-2i\frac{\left( \lambda _{1}-\lambda _{2}\right) Y_{1}Y_{2}}{X_{1}Y_{2}-X_{2}Y_{1}}, \end{aligned}$$

(18)

which agrees with the onefold transformation obtained in the literature for the classical NLS equation (see for example [33]). Similarly, one can define twofold DT on $\varPsi _{n}$

$$\begin{aligned}&\varPsi _{n}[2] \equiv T_{n,2}[1]\varPsi _{n}[1]=T_{n,2}[1]T_{n,1}\varPsi _{n},\nonumber \\&\quad =\left( \begin{array}{ll} z^{2}+A_{n}^{\left( 1\right) }+z^{-2}A_{n}^{\left( 2\right) }&{} zB_{n}^{\left( 1\right) }+z^{-1}B_{n}^{\left( 2\right) } \\ zC_{n}^{\left( 1\right) }+z^{-1}C_{n}^{\left( 2\right) } &{} z^{-2}+z^{2}D_{n}^{\left( 1\right) }+D_{n}^{\left( 2\right) } \end{array} \right) \varPsi _{n},\nonumber \\ \end{aligned}$$

(19)

where $A_{n}^{\left( 1\right) }=-a_{n,1}-a_{n,2}[1]+b_{n,2}[1]c_{n,1},A_{n}^{\left( 2\right) }=a_{n,1}a_{n,2}[1],\,B_{n}^{\left( 1\right) }=-b_{n,1}+b_{n,2}[1]d_{n,1},\,B_{n}^{\left( 2\right) }=b_{n,2}[1]+a_{n,2}[1]b_{n,1}, C_{n}^{\left( 1\right) }=-c_{n,2}[1]+c_{n,1}d_{n,2}[1],C_{n}^{\left( 2\right) }=c_{n,1}+a_{n,1}c_{n,2}[1], D_{n}^{\left( 1\right) }=d_{n,1}d_{n,2}[1]$ and $D_{n}^{\left( 2\right) }=d_{n,1}+d_{n,2}[1]+c_{n,2}[1]b_{n,1}$. The unknown functions $A_{n}^{\left( j\right) },$$B_{n}^{\left( j\right) },$$C_{n}^{\left( j\right) }$ and $D_{n}^{\left( j\right) }$ can be computed by using following conditions

$$\begin{aligned}&\left( \begin{array}{ll} z^{2}+A_{n}^{\left( 1\right) }+z^{-2}A_{n}^{\left( 2\right) }&{}\quad zB_{n}^{\left( 1\right) }+z^{-1}B_{n}^{\left( 2\right) } \\ zC_{n}^{\left( 1\right) }+z^{-1}C_{n}^{\left( 2\right) } &{}\quad z^{-2}+z^{2}D_{n}^{\left( 1\right) }+D_{n}^{\left( 2\right) } \end{array} \right) \nonumber \\&\left. \left( \begin{array}{ll} X_{n,k}\\ Y_{n,k} \end{array}\right) \right| _{z=z_{k}}=0, \end{aligned}$$

(20)

implies

$$\begin{aligned} \sum \limits _{j=1}^{2}A_{n}^{\left( j\right) }z_{k}^{2-2j} X_{n,k}+\sum \limits _{j=1}^{2}B_{n}^{\left( j\right) }z_{k}^{3-2j}Y_{n,k}= & {} -z_{k}^{2}X_{n,k}, \nonumber \\ \sum \limits _{j=1}^{2}C_{n}^{\left( j\right) }z_{k}^{3-2j}X_{n,k}+\sum \limits _{j=1}^{2}D_{n}^{\left( j\right) } z^{4-2j}Y_{n,k}= & {} -z_{k}^{-2}Y_{n,k}, \nonumber \\ \end{aligned}$$

(21)

for $k=1, 2, 3, 4.$ Twofold transformation (19) leads to following transformations

$$\begin{aligned}&Q_{n}[2] =(-1)^2\frac{Q_{n}-B_{n}^{(1)}}{D_{n}^{(1)}}, \quad R_{n}[2] =\frac{R_{n}-C_{n}^{(2)}}{A_{n}^{(2)}}.\nonumber \\ \end{aligned}$$

(22)

where

$$\begin{aligned} A_{n}^{\left( 2\right) }[2]= & {} \frac{\varDelta _{a}[2]}{\varDelta _{1}[2]},\quad \quad B_{n}^{\left( 1\right) }[2]=\frac{\varDelta _{b}[2]}{\varDelta _{1}[2]}, \nonumber \\ C_{n}^{\left( 2\right) }[2]= & {} \frac{\varDelta _{c}[2]}{\varDelta _{2}[2]},\quad \quad D_{n}^{\left( 1\right) }[2]=\frac{\varDelta _{d}[2]}{\varDelta _{2}[2]}, \end{aligned}$$

(23)

with

$$\begin{aligned} \varDelta _{1}[2]= & {} \det \left( \begin{array}{llll} X_{n,k}&\quad z_{k}^{-2}X_{n,k}&\quad z_{k}Y_{n,k}&\quad z_{k}^{-1}Y_{n,k} \end{array} \right) , \nonumber \\ \varDelta _{2}[2]= & {} \det \left( \begin{array}{llll} z_{k}X_{n,k}&\quad z_{k}^{-1}X_{n,k}&\quad z_{k}^{2}Y_{n,k}&\quad Y_{n,k} \end{array} \right) ,\nonumber \\ \varDelta _{a}[2]= & {} - \det \left( \begin{array}{llll} X_{n,k}&\quad z_{k}^{2}X_{n,k}&\quad z_{k}Y_{n,k}&\quad z_{k}^{-1}Y_{n,k} \end{array} \right) , \nonumber \\ \varDelta _{b}[2]= & {} -\det \left( \begin{array}{llll} X_{n,k}&\quad z_{k}^{-2}X_{n,k}&\quad z_{k}^{2}X_{n,k}&\quad z_{k}^{-1}Y_{n,k} \end{array} \right) ,\nonumber \\ \varDelta _{c}[2]= & {} -\det \left( \begin{array}{llll} z_{k}X_{n,k}&\quad z_{k}^{-2}Y_{n,k}&\quad z_{k}^{2}Y_{n,k}&\quad Y_{n,k} \end{array} \right) , \nonumber \\ \varDelta _{d}[2]= & {} -\det \left( \begin{array}{llll} z_{k}X_{n,k}&\quad z_{k}^{-1}X_{n,k}&\quad z_{k}^{-2}Y_{n,k}&\quad Y_{n,k} \end{array} \right) .\nonumber \\ \end{aligned}$$

(24)

If we repeat these steps N-times, we obtain N-fold DT on $\varPsi _{n}$:

$$\begin{aligned} \varPsi _{n}[N]= & {} T_{n,N}[N-1]\varPsi _{n}[N-1]\nonumber \\= & {} \prod _{j=1}^{N}T_{n,N-j+1}[N-j]\varPsi _{n}, \nonumber \\ T_{n,1}[0]= & {} T_{n,1}, \end{aligned}$$

(25)

with

$$\begin{aligned}&\prod _{j=1}^{N}T_{n,N-j+1}[N-j]\nonumber \\&=\left( \begin{array}{ll} (-z)^{N}+\sum \limits _{j=1}^{N}A_{n}^{\left( j\right) }z^{N-2j} &{}\quad \sum \limits _{j=1}^{N}B_{n}^{\left( j\right) }z^{N+1-2j} \\ \sum \limits _{j=1}^{N}C_{n}^{\left( j\right) }z^{N+1-2j} &{}\quad z^{-N}+\sum \limits _{j=1}^{N}D_{n}^{\left( j\right) }z^{N+2-2j} \end{array} \right) .\nonumber \\ \end{aligned}$$

(26)

The scalar potentials $Q_{n}$ and $R_{n}$ transform as

$$\begin{aligned} Q_{n}[N]=(-1)^{N}\frac{Q_{n}-B_{n}^{\left( 1\right) }}{D_{n}^{\left( 1\right) }},\quad R_{n}[N]= & {} \frac{R_{n}-C_{n}^{\left( N\right) }}{A_{n}^{\left( N\right) }} .\nonumber \\ \end{aligned}$$

(27)

Similarly, $A_{n}^{\left( j\right) },$$B_{n}^{\left( j\right) },$$C_{n}^{\left( j\right) }$ and $D_{n}^{\left( j\right) }$$\left( 1\le j\le N\right)$ can be uniquely calculated by requiring

$$\begin{aligned} \left. T_{n}[N]\varPsi _{n}^{\left( k\right) }\right| _{z=z_{k}}=0, \end{aligned}$$

(28)

which yields

$$\begin{aligned}&\sum \limits _{j=1}^{N}A_{n}^{\left( j\right) }z_{k}^{N-2j} X_{n,k}+\sum \limits _{j=1}^{N}B_{n}^{\left( j\right) }z_{k}^{N+1-2j}Y_{n,k} =-(-z_{k})^{N}X_{n,k}, \nonumber \\&\sum \limits _{j=1}^{N}C_{n}^{\left( j\right) }z_{k}^{N+1-2j}X_{n,k}+\sum \limits _{j=1}^{N}D_{n}^{\left( j\right) } z^{N+2-2j}Y_{n,k}=-z_{k}^{-N}Y_{n,k}, \nonumber \\ \end{aligned}$$

(29)

where $z_{k}\left( k=1,2,\ldots ,2N\right)$ be arbitrary parameters. The linear system (21) can be solved for the unknowns $A_{n}^{\left( j\right) },$$B_{n}^{\left( j\right) },$$C_{n}^{\left( j\right) }$ and $D_{n}^{\left( j\right) }$, we obtain the following results

$$\begin{aligned} A_{n}^{\left( N\right) }[N]= & {} \frac{\varDelta _{a}[N]}{\varDelta _{1}[N]},\quad B_{n}^{\left( 1\right) }[N]=\frac{\varDelta _{b}[N]}{\varDelta _{1}[N]}, \nonumber \\ C_{n}^{\left( N\right) }[N]= & {} \frac{\varDelta _{c}[N]}{\varDelta _{2}[N]},\quad D_{n}^{\left( 1\right) }[N]=\frac{\varDelta _{d}[N]}{\varDelta _{2}[N]}, \end{aligned}$$

(30)

with

$$\begin{aligned}&\varDelta _{1} [N]=\det \left( \begin{array}{cccccccc} z_{k}^{N-2}X_{n,k}&z_{k}^{N-4}X_{n,k}&\cdots&z_{k}^{-N}X_{n,k}&z_{k}^{N-1}Y_{n,k}&z_{k}^{N-3}Y_{n,k}&\cdots&z_{k}^{-N+1}Y_{n,k} \end{array} \right) ,\\&\varDelta _{2}[N] =\det \left( \begin{array}{cccccccc} z_{k}^{N-1}X_{n,k}&z_{k}^{N-3}X_{n,k}&\cdots&z_{k}^{-N+1}X_{n,k}&z_{k}^{N}Y_{n,k}&z_{k}^{N-2}Y_{n,k}&\cdots&z_{k}^{-N+2}Y_{n,k} \end{array} \right) ,\\&\varDelta _{a}[N] =\left( -1\right) ^{N+1} \det \left( \begin{array}{cccccccc} z_{k}^{N-2}X_{n,k}&z_{k}^{N-4}X_{n,k}&\cdots&z_{k}^{N}X_{n,k}&z_{k}^{N-1}Y_{n,k}&z_{k}^{N-3}Y_{n,k}&\cdots&z_{k}^{-N+1}Y_{n,k} \end{array} \right) ,\\&\varDelta _{b}[N] =\left( -1\right) ^{N+1}\det \left( \begin{array}{cccccccc} z_{k}^{N-2}X_{n,k}&z_{k}^{N-4}X_{n,k}&\cdots&z_{k}^{-N}X_{n,k}&z_{k}^{N}X_{n,k}&z_{k}^{N-3}Y_{n,k}&\cdots&z_{k}^{-N+1}Y_{n,k} \end{array} \right) ,\\&\varDelta _{c}[N] =-\det \left( \begin{array}{cccccccc} z_{k}^{N-1}X_{n,k}&z_{k}^{N-3}X_{n,k}&\cdots&z_{k}^{-N}Y_{n,k}&z_{k}^{N}Y_{n,k}&z_{k}^{N-2}Y_{n,k}&\cdots&z_{k}^{-N+2}Y_{n,k} \end{array} \right) ,\\&\varDelta _{d}[N] =-\det \left( \begin{array}{llllllll} z_{k}^{N-1}X_{n,k}&\quad z_{k}^{N-3}X_{n,k}&\quad \cdots&\quad z_{k}^{-N+1}X_{n,k}&\quad z_{k}^{-N}Y_{n,k}&\quad z_{k}^{N-2}Y_{n,k}&\quad \cdots&\quad z_{k}^{-N+2}Y_{n,k} \end{array} \right) . \end{aligned}$$

Equation (30) can be used to compute multi-soliton solutions of sd-NNLS equation. It is important to mention that under the continuum limit all results for N-fold transformation (25)–(30) for sd-CNLS equation (4) reduce to the results obtained in [33] for the classical NLS equation.

4 Explicit solution of coupled sd-NLS equations

In this section, we construct exact expressions of single and double soliton solutions of coupled sd-CNLS equation (4) in zero background. First, starting from the trivial solutions $Q_{n}=0$ and $R_{n}=0,$ we can present the solution of Lax pair (5) with $z=z_{k}$$\left( k=1,2,\ldots ,2N\right)$ as follows:

$$\begin{aligned} \varPsi _{n,k}=\left( \begin{array}{l} X_{n,k}\\ Y_{n,k} \end{array} \right) =\left( \begin{array}{l} \alpha _{k}z_{k}^{n}\exp \left( i\omega _{k}\tau \right) \\ \beta _{k}z_{k}^{-n}\exp \left( -i\omega _{k}\tau \right) \end{array} \right) , \end{aligned}$$

(31)

with

$$\begin{aligned} \omega _{k}=-\frac{1}{2}\left( z_{k}-z_{k}^{-1}\right) ^{2}, \end{aligned}$$

(32)

and $\alpha _{k}$ and $\beta _{k}$ are constants of integration. Under the continuum limits (31) reduces to the matrix-valued solution to the Lax pair (9) for classical NLS equation (8).

4.1 One-soliton solutions

In order to obtain explicit expressions of one-soliton solutions of coupled sd-NLS equation, we use values of $X_{n,k}$ and $Y_{n,k}$ from (31) into (12) along with (15), we obtain explicit expressions of onefold transformed scalar potentials as

$$\begin{aligned} Q _{n}(\tau )[1]= & {} \frac{\alpha _{1}\alpha _{2}(z_2^2-z_1^2) z_1^{2 n+1} z_2^{2 n+1} e^{2 i \tau \left( \omega _1+\omega _2\right) }}{\alpha _{1}\beta _{2}z_1^{2 n+1} e^{2 i \tau \omega _1}-\alpha _{2}\beta _{1}z_2^{2 n+1} e^{2 i \tau \omega _2}},\nonumber \\ R_{n}(\tau )[1]= & {} \frac{\beta _{1}\beta _{2}(z_1^2-z_2^2)}{\alpha _{1}\beta _{2}z_2^2 z_1^{2 n+3} e^{2 i \tau \omega _1}{-}\alpha _{2}\beta _{1}z_1^2 z_2^{2 n+3} e^{2 i \tau \omega _2}}.\nonumber \\ \end{aligned}$$

(33)

Equation (33) represents a more general expression of one-soliton solution of coupled system (4). If we take $\alpha _{1}=\alpha _{2}=1$ and $\beta _{1}=e^{i\theta _{1}}, \beta _{2}=-e^{-i\theta _{2}}$ in expression (33), we obtain

$$\begin{aligned} Q _{n}(\tau )[1]= & {} \frac{\left( z_1^2-z_2^2\right) e^{i\theta _{2}} z_2^{2 n+1} e^{2 i\omega _2\tau }}{1+e^{i\left( \theta _{1}+\theta _{2}\right) }e^{2i\tau \left( \omega _2-\omega _{1}\right) }z_2^{2n+1}z_1^{-2n-1}},\nonumber \\ \end{aligned}$$

(34)

which coincides with the results obtained in reference [29] but slightly different from expression (27) given in reference [28]. However, the one-soliton solution (34) under continuum limit $\delta \rightarrow 0$ with $Q_{n}(\tau )=\delta q_{n}, x=n\delta , t=\delta ^2\tau , z_{k}=e^{-i\lambda _{k}\delta }$ becomes

$$\begin{aligned} q(x,t)[1]= & {} \frac{2i\left( \lambda _1-\lambda _2\right) e^{i\theta _{2}} e^{4i\lambda _{2}^2t}e^{-2i\lambda _{2}x}}{1+e^{i\left( \theta _{1}+\theta _{2}\right) }e^{4it\left( \lambda _{2}^2-\lambda _{1}^2\right) }e^{2ix\left( \lambda _1-\lambda _2\right) }},\nonumber \\ \end{aligned}$$

(35)

which reduces to Eq. (22) of reference [1] for $\theta _2=\bar{\theta _{1}}, \lambda _{1}=i\eta _{1}$ and $\lambda _{2}=-i\bar{\eta _{1}}$.

Fig. 1

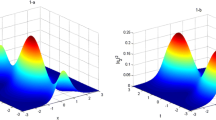
Stationary one-soliton solution of sd-NNLS equation (3)

Fig. 2

Traveling one-soliton solution of sd-NNLS equation (3)

Fig. 3

Singular-type one-soliton solution of sd-NNLS equation (3)

Fig. 4

Symmetry-broken decaying one-soliton solution of equation (4)

Fig. 5

Symmetry-broken growing one-soliton solution of equation (4)

Fig. 6

Symmetry-broken stable one-soliton solution of equation (4)

Now we would like to illustrate our results graphically by plotting (33) for different choices of parameters. First of all, we obtain stable one-soliton solution from (33) for sd-NNLS equation (3) at so-called exceptional points (EPs), namely $z_{2k}=\left( z_{2k-1}^{*}\right) ^{-1}$. For sd-NNLS equation at EPs eigenvalues no longer independent and eigenvectors become parallel; moreover, the system behaves like classical system as illustrated in Figs. 1 and 2. Figure 1 presents stationary soliton for the parameters $z_{1}=0.5, z_{2}=2$, $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$ whereas Fig. 2 represents the traveling soliton for parameters $z_{1}=0.5+0.1\text{ i }, z_{2}=1.923+0.385\text{ i }$, $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$. Secondly, we obtain symmetry-preserving singular-type solution for sd-NNLS equation (3) from (33). The absolute value of $Q _{n}(\tau )[1]$ is plotted in Fig. 3 for the parameters $z_{1}=0.7, z_{2}=2$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1.$ The family of solutions (33) oscillate in time $\tau$ and eventually blows up in finite time $\tau =\tau _{s}$ at $n=-1/2$; with $\tau _{s}=\frac{(2m+1)\pi }{2\left( \omega _2-\omega _1\right) },$$m\in \mathbb {Z}.$ Finally, we obtain symmetry-broken soliton solution from the explicit expressions of one-soliton solutions (33). The expressions (33) are plotted in Figs. 4, 5 and 6 for $z_{1}=0.5+0.05\text{ i }, z_{2}=2+0.05\text{ i }$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1.$ We obtain an unstable one-soliton solution for sd-NNLS equation below EP as shown in Figs. 4 and 5 which shows that amplitude of $|Q_{n}(\tau )|$ decays in the $-n$ direction as $\tau \rightarrow \infty$ while the amplitude of $|R_{n}(\tau )|$ grows in the $-n$ direction as $\tau \rightarrow \infty$ contrary to the dynamics of $|Q_{n}(\tau )|$ and we obtain a stable structure for the $|Q_{n}(\tau )R_{n}(\tau )|$ as shown in Fig. 6. It is worthwhile to mention that above EPs the dynamical variables $Q_{n}(\tau )$ and $R_{n}(\tau )$ switch their behavior as described in [19].

4.2 Two-soliton solutions

In zero background expression of two-soliton solution (22) becomes

$$\begin{aligned}&Q_{n}[2] =-\frac{\left| \begin{array}{llll} X_{n,4}&{}\quad z^{-2}_{4}X_{n,4}&{}\quad z^{2}_{4}X_{n,4} &{}\quad z^{-1}_{4}Y_{n,4}\\ X_{n,3}&{}\quad z^{-2}_{3}X_{n,3}&{}\quad z^{2}_{3}X_{n,3} &{}\quad z^{-1}_{3}Y_{n,3}\\ X_{n,2}&{}\quad z^{-2}_{2}X_{n,2}&{}\quad z^{2}_{2}X_{n,2} &{}\quad z^{-1}_{2}Y_{n,2}\\ X_{n,1}&{}\quad z^{-2}_{1}X_{n,1}&{}\quad z^{2}_{1}X_{n,1} &{}\quad z^{-1}_{1}Y_{n,1} \end{array} \right| \left| \begin{array}{llll} z_{4}X_{n,4}&{}\quad z^{-1}_{4}X_{n,4}&{}\quad z^{2}_{4}Y_{n,4} &{}\quad Y_{n,4}\\ z_{3}X_{n,3}&{}\quad z^{-1}_{3}X_{n,3}&{}\quad z^{2}_{3}Y_{n,3} &{}\quad Y_{n,3}\\ z_{2}X_{n,2}&{}\quad z^{-1}_{2}X_{n,2}&{}\quad z^{2}_{2}Y_{n,2} &{}\quad Y_{n,2}\\ z_{1}X_{n,1}&{}\quad z^{-1}_{1}X_{n,1}&{}\quad z^{2}_{1}Y_{n,1} &{}\quad Y_{n,1} \end{array} \right| }{\left| \begin{array}{llll} X_{n,4}&{}\quad z^{-2}_{4}X_{n,4}&{}\quad z_{4}Y_{n,4} &{}\quad z^{-1}_{4}Y_{n,4}\\ X_{n,3}&{}\quad z^{-2}_{3}X_{n,3}&{}\quad z_{3}Y_{n,3} &{}\quad z^{-1}_{3}Y_{n,3}\\ X_{n,2}&{}\quad z^{-2}_{2}X_{n,2}&{}\quad z_{2}Y_{n,2} &{}\quad z^{-1}_{2}Y_{n,2}\\ X_{n,1}&{}\quad z^{-2}_{1}X_{n,1}&{}\quad z_{1}Y_{n,1} &{}\quad z^{-1}_{1}Y_{n,1} \end{array} \right| \left| \begin{array}{llll} z_{4}X_{n,4}&{}\quad z^{-1}_{4}X_{n,4}&{}\quad z^{-2}_{4}Y_{n,4} &{}\quad Y_{n,4}\\ z_{3}X_{n,3}&{}\quad z^{-1}_{3}X_{n,3}&{}\quad z^{-2}_{3}Y_{n,3} &{}\quad Y_{n,3}\\ z_{2}X_{n,2}&{}\quad z^{-1}_{2}X_{n,2}&{}\quad z^{-2}_{2}Y_{n,2} &{}\quad Y_{n,2}\\ z_{1}X_{n,1}&{}\quad z^{-1}_{1}X_{n,1}&{}\quad z^{-2}_{1}Y_{n,1} &{}\quad Y_{n,1} \end{array} \right| },\nonumber \\&R_{n}[2] =-\frac{\left| \begin{array}{llll} z_{4}X_{n,4}&{}\quad z^{-2}_{4}Y_{n,4}&{}\quad z^{2}_{4}Y_{n,4} &{}\quad Y_{n,4}\\ z_{3}X_{n,3}&{}\quad z^{-2}_{3}Y_{n,3}&{}\quad z^{2}_{3}Y_{n,3} &{}\quad Y_{n,3}\\ z_{2}X_{n,2}&{}\quad z^{-2}_{2}Y_{n,2}&{}\quad z^{2}_{2}Y_{n,2} &{}\quad Y_{n,2}\\ z_{1}X_{n,1}&{}\quad z^{-2}_{1}Y_{n,1}&{}\quad z^{2}_{1}Y_{n,1} &{}\quad Y_{n,1} \end{array} \right| \left| \begin{array}{llll} X_{n,4}&{}\quad z^{-2}_{4}X_{n,4}&{}\quad z_{4}Y_{n,4} &{}\quad z^{-1}_{4}Y_{n,4}\\ X_{n,3}&{}\quad z^{-2}_{3}X_{n,3}&{}\quad z_{3}Y_{n,3} &{}\quad z^{-1}_{3}Y_{n,3}\\ X_{n,2}&{}\quad z^{-2}_{2}X_{n,2}&{}\quad z_{2}Y_{n,2} &{}\quad z^{-1}_{2}Y_{n,2}\\ X_{n,1}&{}\quad z^{-2}_{1}X_{n,1}&{}\quad z_{1}Y_{n,1} &{}\quad z^{-1}_{1}Y_{n,1} \end{array} \right| }{\left| \begin{array}{llll} z_{4}X_{n,4}&{}\quad z^{-1}_{4}X_{n,4}&{}\quad z^{2}_{4}Y_{n,4} &{}\quad Y_{n,4}\\ z_{3}X_{n,3}&{}\quad z^{-1}_{3}X_{n,3}&{}\quad z^{2}_{3}Y_{n,3} &{}\quad Y_{n,3}\\ z_{2}X_{n,2}&{}\quad z^{-1}_{2}X_{n,2}&{}\quad z^{2}_{2}Y_{n,2} &{}\quad Y_{n,2}\\ z_{1}X_{n,1}&{}\quad z^{-1}_{1}X_{n,1}&{}\quad z^{2}_{1}Y_{n,1} &{}\quad Y_{n,1} \end{array} \right| \left| \begin{array}{llll} X_{n,4}&{}\quad z^{2}_{4}X_{n,4}&{}\quad z_{4}Y_{n,4} &{}\quad z^{-1}_{4}Y_{n,4}\\ X_{n,3}&{}\quad z^{2}_{3}X_{n,3}&{}\quad z_{3}Y_{n,3} &{}\quad z^{-1}_{3}Y_{n,3}\\ X_{n,2}&{}\quad z^{2}_{2}X_{n,2}&{}\quad z_{2}Y_{n,2} &{}\quad z^{-1}_{2}Y_{n,2}\\ X_{n,1}&{}\quad z^{2}_{1}X_{n,1}&{}\quad z_{1}Y_{n,1} &{}\quad z^{-1}_{1}Y_{n,1} \end{array} \right| }, \end{aligned}$$

(36)

Fig. 7

Stationary two-soliton solution of sd-NNLS equation (3)

Fig. 8

Bound solitons solution of sd-NNLS equation (3)

where $X_{n,k}$ and $Y_{n,k}$ are given by (31) along with (32). The dynamics of two-soliton solutions of sd-NNLS equation at EPs is plotted in Figs. 7, 8 and 9 for various values of parameters as for Fig. 7 ($z_{1}=2,z_{2}=0.5,z_{3}=2.01,z_{4}=0.4975$), Fig. 8 ($z_{1}=2,z_{2}=0.5,z_{3}=3,z_{4}=0.333$) and Fig. 9 ($z_{1}=0.5+0.5\text{ i },z_{2}=1+\text{ i },z_{3}=0.40-0.4\text{ i },z_{4}=1.25-1.25\text{ i }$). Again we obtain stable structure at EPs. Figure 7 portrays propagation of slowly moving degenerate-type two-soliton solution whereas Fig. 8 displays propagation of bound solitons. The bound soliton solution occurs due to mutual attraction and repulsion between two solitons along their own trajectories, where they interact amplitude of solitons increase instantly after that they repel each other and got separated. For bound solitons, this process will repeat periodically; however, for degenerate case, interaction takes place once only. Figure 9 illustrates the interaction of two traveling solitons.

In order to obtain the interaction of symmetry-preserving singular-type solutions, we substitute values of $X_{n,k}$ and $Y_{n,k}$ from (31) and plotted absolute value of $Q_{n}[2]$ for parameters $z_{1}=0.5,z_{2}=1.6,z_{3}=0.53,z_{4}=1.57$ and $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha _{4}=1, \beta _{1}=-\beta _{2}=\beta _{3}=-\beta _{4}=1$ as shown in Fig. 10. Moreover, above and below the EPs we obtain unstable soliton solutions. Here we only study the interaction of two-soliton solutions below the EPs. We also obtain interaction of symmetry-broken two-soliton solutions (36) as illustrated in Figs. 11, 12 and 13 for $z_{1}=0.5+0.05\text{ i },z_{2}=2-0.05\text{ i },z_{3}=0.6+0.05\text{ i },z_{4}=1.9-0.05\text{ i }$ and $\alpha _{1}=\alpha _{2}=\alpha _{3}=\alpha _{4}=1, \beta _{1}=-\beta _{2}=\beta _{3}=-\beta _{4}=1.$ One can observed that we obtain stable two-soliton solution only for $|Q _{n}(\tau )[2]R _{n}(\tau )[2]|$ as shown in Fig. 13 whereas we obtain unstable two-soliton solution, see Figs. 11 and 12. It is interesting to note that all solutions obtained here for sd-CNLS equation (4) reduce to the results obtained for coupled NLS equation (8).

Fig. 9

Traveling two-soliton solution of sd-NNLS equation (3)

Fig. 10

Singular-type two-soliton solution of sd-NNLS equation (3)

Fig. 11

Symmetry-broken decaying two-soliton solution of equation (4)

Fig. 12

Symmetry-broken growing two-soliton solution of equation (4)

Fig. 13

Symmetry-broken stable two-soliton solution of equation (4)

5 Results and discussion

The complex eigenvalue $z=a+ib$ plays a fundamental role to obtain different kinds of solutions. All types of structural and dynamical properties from local reduction to nonlocality and from unbroken $\mathcal {PT}$ symmetry to spontaneously $\mathcal {PT}$ symmetry breaking are governed by this eigenvalue. Real part a of spectral parameter z introduces amplitude while imaginary part b is responsible for the velocity (both phase and group). The group velocity is zero for $b=0$ and phase part solely depends upon n which give us stationary soliton. However, for $z=a+ib$ we have traveling soliton whose speed is defined by b.

Fig. 14

Symmetry-preserving oscillating solution of sd-NNLS equation (3). For $z_{1}=1,z_{2}=2$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$

Fig. 15

Symmetry-preserving oscillating solution of sd-NNLS equation (3). For $n=-1/2$, $z_{1}=1,z_{2}=2$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$

Fig. 16

Profile of dynamical potential in broken $\mathcal {PT}$ symmetric regime. For $z_{1}=0.5+0.1\text{ i },z_{2}=2+0.1\text{ i }$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$

Fig. 17

Unstable features of one-soliton solution of sd-NNLS equation (4) near EP. For $z_{1}=0.5+0.1\text{ i },z_{2}=2+0.1\text{ i }$ and $\alpha _{1}=\alpha _{2}=\beta _{1}=-\beta _{2}=1$

Nonlocal $\mathcal {PT}$-symmetry continuous NLS equation [1] and discrete NLS system [28] are primarily presented by Ablowitz and Musslimani. But in both settings, they have only considered stationary solitons by taking $\lambda$ (purely imaginary) and z (real) for continuous and discrete systems, respectively. They obtained singular-type or blowup-type solutions in nonlocal $\mathcal {PT}$-symmetry regime. Such singular solutions are due to non-conservation of power $P=\sum _{n=-\infty }^{\infty }|Q_{n}(\tau )|^2$ which oscillate in time (also known as Rabi oscillations) with period $\frac{\pi }{\omega _{2}-\omega _{1}}$ as shown in Fig. 14 for various values of n, as observed in reference [12]. While at $n=-1/2$ amplitude of these oscillations abruptly enhance that ultimately generate singularities as shown in Figs. 3 and 15. Furthermore, it is important to note that the solutions $Q_{n}(\tau )$ and $R_{n}(\tau )=Q_{-n}^{*} (\tau )$ of Eq. (4) are related and so-called self-induced potential $V_{n}(\tau )=Q_{n}(\tau ) Q_{-n}^{*} (\tau )$ exhibit completely real spectrum for such nonlocal transitions. In other words, we can say that $\mathcal {PT}$-symmetry remains unbroken in this case.

In contrast to this, in case of traveling solitons, the solutions $Q_{n}(\tau )$ retain their shape during evolution in time as long as it remains centered around EP of $\mathcal {PT}$ symmetry. For any shift from this point, the nonlinearity in potential $V_{n}(\tau )=Q_{n}(\tau ) Q_{-n}^{*} (\tau )$ breaks its $\mathcal {PT}$ symmetry in spite of the fact it always obey the necessary condition of $\mathcal {PT}$ symmetry, i.e., $V_{n}(\tau )=V^{*}_{-n}(\tau )$ [2]. This spontaneous breaking of symmetry could be explained as follows: as discussed earlier, the traveling soliton is realized by the choice of complex eigenvalue, i.e., $z=a+ib$, the imaginary part of this is responsible for evolution in time. At EPs $(z_{2k}=(z_{2k-1}^{*})^{-1})$, the dynamical potential is completely real $V_{n}(\tau )=|Q_{n}(\tau )|^2$ and system retain stability as depicted in Figs. 1, 2 and 7, 8, 9. But when $z_{2k}$ and $z_{2k-1}$ are no more related and nonlocally disturbed slightly by producing variation in imaginary parts (velocity factor) the dynamical potential admits a complex spectrum, see in Fig. 16. Accordingly $Q_{n}(\tau )$ and $R_{n}(\tau )$ become independent and shifted from the center of the symmetry triggering instability as shown in Fig. 17. As a consequence $\mathcal {PT}$ symmetry is nonlinearly broken and solution $Q_{n}(\tau )$ and $R_{n}(\tau )$ shows exponential growth and decay, respectively, due to this instability as illustrated in Figs. 4, 5, 6 and 11, 12, 13. In short, $\mathcal {PT}$ symmetry spontaneously breaks may be due to asymmetric speed distribution of waveguide at different positions in a physical systems. Such phenomena have been observed in $\mathcal {PT}$ symmetric linear systems but how this could be realized practically in nonlinear regime is still a challenge.

6 Conclusion

In this paper, we have investigated multi-soliton solutions of sd-NNLS equation by employing Darboux transformation to the solution of the associated AL scheme. We have expressed multi-soliton solutions in terms of ratio of determinants and constructed symmetry-broken and symmetry-unbroken one- and two-soliton solutions for different values of parameters. Our results may be step forward to understand non-Hermitian photonics and other nonlinear $\mathcal {PT}$ symmetric systems effectively. The results obtained in this letter can be further extended in various directions, for example, one can explore soliton solution of sd-NNLS equation in nonzero background, study degenerate solutions of sd-NNLS equation, rogue wave of sd-NNLS equation and so on. We will address these problems in future as a separate work.