Bright and dark soliton solutions to the partial reverse space–time nonlocal Mel’nikov equation

Abstract

General bright and dark soliton solutions to the partial reverse space–time nonlocal Mel’nikov equation with parity–time symmetry are constructed by the Hirota bilinear method with KP hierarchy reduction method. These solutions of arbitrary order are given in forms of Gram-type determinants. The properties of propagation and collision of analytical solution including both bright and dark solitons are discussed in details. In the end, we provide a simple variable transformation to convert the nonlocal Mel’nikov equation to a local Mel’nikov equation.

1 Introduction

Very recently, Ablowitz and Musslimani [1] considered a new reduction

$$\begin{aligned} \begin{aligned} r(x,t)=\pm \, q^{*}(-x,t), \end{aligned} \end{aligned}$$

(1)

for the coupled nonlinear Schrödinger (NLS) equation

$$\begin{aligned} \begin{aligned}&iq_t(x,t)=\frac{1}{2}q_{xx}(x,t)-q^2(x,t)r(x,t),\\&ir_t(x,t)=-\frac{1}{2}r_{xx}(x,t)+r^2(x,t)q(x,t), \end{aligned} \end{aligned}$$

(2)

where q(x, t) and r(x, t) are complex dynamical variables, and proposed the following reverse space nonlocal NLS equation

$$\begin{aligned} \begin{aligned} iq_t(x,t)=\frac{1}{2}q_{xx}(x,t)\pm q^2(x,t)q^*(-x,t). \end{aligned} \end{aligned}$$

(3)

This newly proposed equation is obviously distinctive from the local NLS equation [2]

$$\begin{aligned} \begin{aligned} iq_t(x,t)=\frac{1}{2}q_{xx}(x,t)\pm q^2(x,t)q^*(x,t), \end{aligned} \end{aligned}$$

(4)

which can also be reduced from the coupled NLS equation (2) by letting

$$\begin{aligned} \begin{aligned} r(x,t)=\pm \,q^*(x,t). \end{aligned} \end{aligned}$$

(5)

The equations which possess such new symmetries (1) have important applications in nonlinear optics [3, 4]; various nonlocal NLS equations have been proposed and studied [5,6,7,8]. The reverse space–time nonlocal NLS:

$$\begin{aligned} \begin{aligned} iq_t(x,t)=\frac{1}{2}q_{xx}(x,t)\pm q^2(x,t)q(-x,-t), \end{aligned} \end{aligned}$$

(6)

and the reverse time nonlocal NLS:

$$\begin{aligned} \begin{aligned} iq_t(x,t)=\frac{1}{2}q_{xx}(x,t)\pm q^2(x,t)q(x,-t), \end{aligned} \end{aligned}$$

(7)

are such examples. The reverse space–time nonlocal NLS (6) is reduced from the coupled NLS equation (2) by taking

$$\begin{aligned} r(x,t)=\pm \,q(-x,-t), \end{aligned}$$

(8)

while the reverse time nonlocal NLS (7) is obtained via letting

$$\begin{aligned} \begin{aligned} r(x,t)=\pm \,q(x,-t). \end{aligned} \end{aligned}$$

(9)

Yang [9] discussed general N-solitons in the three nonlocal NLS equations (3), (6) and (7) by employing the Riemann–Hilbert method and observed the solitons in these three nonlocal NLS equations would blow up in a finite time. Before the work of Yang, Ablowitz and Musslimani [1] also found such singular behaviours in the one soliton of the reverse space nonlocal NLS equation (3). Recently, Feng et.al. [10] constructed all possible soliton solutions for the reverse space nonlocal NLS equation (3) via using the Hirota’s bilinear method combined with the Kadomtsev–Petviashvili (KP) hierarchy reduction method, including the singular and nonsingular bright solitons with zero boundary condition and the dark and antidark solitons with nonzero boundary condition. Besides, the singular and nonsingular localized waves such as rogue waves in the nonlocal NLS equations have also been investigated by different methods [11,12,13,14,15,16,17].

In addition to the nonlocal NLS equations, Ablowitz and Musslimani [8] also proposed a series of other nonlocal equations, such as the nonlocal Davey–Stewartson (DS) equation, nonlocal modified Kortweg–de Vries equation, and nonlocal sine-Gordon equation. We note that Fokas also introduced the nonlocal DS equations as multidimensional versions of the nonlocal NLS equation [18]. Before the work of Ablowitz and Musslimani [1], integrable equations which possess such symmetries did not attract attention, which leads to such nonlocal equations mathematically interesting. There are increasing works of investigating integrable nonlocal equations with such symmetries and their properties [19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].

In this paper, the main focus is on the partial reverse space–time nonlocal Mel’nikov equation [34]

$$\begin{aligned} \begin{aligned}&3u_{yy}(x,y,t)-u_{xt}(x,y,t)-[3u^2+u_{xx}\\&\qquad +\kappa {\varPsi }(x,y,t){\varPsi }^{*}(-x,y,-t)]_{xx}=0,\\&\quad \mathbf{i }{\varPsi }_{y}(x,y,t)=u(x,y,t){\varPsi }(x,y,t)+{\varPsi }_{xx}(x,y,t), \end{aligned} \end{aligned}$$

(10)

where u and ${\varPsi }$ are functions of x, y, t, $\kappa =\pm 1$. The nonlocal Mel’nikov equation can be regarded as a special reduction of the following coupled system

$$\begin{aligned} \begin{aligned}&3u_{yy}(x,y,t)-u_{xt}(x,y,t)-[3u^2+u_{xx}\\&\qquad -\kappa {\varPsi }(x,y,t){\varPhi }(x,y,t)]_{xx}=0,\\&\quad \mathbf{i }{\varPsi }_{y}(x,y,t)=u(x,y,t){\varPsi }(x,y,t)+{\varPsi }_{xx}(x,y,t),\\&\quad \mathbf{i }{\varPhi }_{y}(x,y,t)=-u(x,y,t){\varPhi }(x,y,t){-}{\varPhi }_{xx}(x,y,t). \end{aligned} \end{aligned}$$

(11)

Indeed, the nonlocal Mel’nikov equation (10) is obtained by taking the reduction in (11)

$$\begin{aligned} \begin{aligned} {\varPhi }(x,y,t)=-{\varPsi }^*(-x,y,-t). \end{aligned} \end{aligned}$$

(12)

Besides, the local (usual) Mel’nikov equation [35,36,37,38]

$$\begin{aligned} \begin{aligned}&3u_{yy}(x,y,t)-u_{xt}(x,y,t)-[3u^2+u_{xx}\\&\qquad +\kappa |{\varPsi }(x,y,t)|^2)]_{xx}=0,\\&\quad \mathbf{i }{\varPsi }_{y}(x,y,t)=u(x,y,t){\varPsi }(x,y,t)+{\varPsi }_{xx}(x,y,t), \end{aligned} \end{aligned}$$

(13)

can be obtained by taking the following standard (local) reduction in (11)

$$\begin{aligned} \begin{aligned} {\varPhi }(x,y,t)=-{\varPsi }^*(x,y,t). \end{aligned} \end{aligned}$$

(14)

The Mel’nikov equation (13) can be used to describe the long waves interacting with short wave packets [35,36,37,38]. In the mathematical version, this equation could be considered either as a generalization of the Kadomtsev–Petviashvili (KP) equation with the addition of a complex scalar field or as a generalization of the nonlinear Schrödinger (NLS) equation with a real scalar field [39,40,41]. All possible solitary wave solutions and localized wave solutions of the Mel’nikov equation (13) have been discussed in Ref. [39,40,41,42].

The rational solutions termed lumps and semi-rational solutions illustrating lumps on a background of periodic line wave for the nonlocal Mel’nikov equation (10) have been discussed in Ref. [34]. However, soliton solutions of the nonlocal Mel’nikov equation (10) have not been reported before. In Ref. [43], Yang found the transformations between many nonlocal and local integrable equations. A natural motivation is to search a transformation between the nonlocal and local Mel’nikov equation. The main purposes of this paper are to construct bright solitons with zero boundary condition and dark solitons with nonzero boundary condition of the nonlocal Mel’nikov equation (10) and to construct the transformation of the nonlocal Mel’nikov equation to the local Mel’nikov equation. In this work, we focus on the following aspects:

• (i) The general bright and dark soliton solutions of the nonlocal Mel’nikov equation (10) are generated and presented in forms of Gram-type determinants, and the dynamical properties of propagation and collision of the bright and dark solitons are demonstrated in details.

• (ii) The variable transformation between the nonlocal Melnikov equation (10) and a local Melnikov equation is provided, which converts the obtained soliton solutions of the nonlocal Melnikov equation (10) to solutions of a local Melnikov equation.

The structure of this article is as follows. In Sect. 2, we discuss general bright soliton solutions to the nonlocal Mel’nikov equation (10) with zero boundary condition. In Sect. 3, we focus on the dynamical features of general dark and antidark soliton solutions to the nonlocal Mel’nikov equation with nonzero boundary condition. In Sect. 4, we provide a transformation between the nonlocal and local Mel’nikov equation, and some conclusions are discussed.

2 The bright N-soliton solution

In this section, we consider general bright N-soliton solutions to the partial reverse space–time nonlocal Mel’nikov equation (10) with zero boundary condition:

$$\begin{aligned} ({\varPsi },u)\rightarrow (0,0),\quad \mathrm {as}\ x,y,t\rightarrow \pm \infty . \end{aligned}$$

We first transform the nonlocal Mel’nikov equation (10) into the following bilinear equations

$$\begin{aligned} \left\{ \begin{array}{llll} &{}(D_{x}^{2}-\mathbf{i }D_{y})g(x,y,t) \cdot f(x,y,t) =0,\\ &{}(D^{4}_{x}+D_xD_t-3D^2_{y})f(x,y,t) \cdot f(x,y,t)\\ &{} \quad =-2\kappa g(x,y,t)g^{*}(-x,y,-t), \end{array}\right. \end{aligned}$$

(15)

by introducing the dependent variable transformations

$$\begin{aligned} \begin{aligned} {\varPsi }=\sqrt{2}\frac{g(x,y,t)}{f(x,y,t)},u=2( \mathrm{log} f(x,y,t))_{xx}. \end{aligned} \end{aligned}$$

(16)

Here the function f meets the condition

$$\begin{aligned} f^*(-x,y,-t)=f(x,y,t), \end{aligned}$$

and the operator D is the Hirota’s bilinear differential operator [44, 45] defined by

$$\begin{aligned} \begin{aligned}&P(D_{x},D_{y},D_{t}, )F(x,y,t\ldots )\cdot G(x,y,t,\ldots )\\&\quad \!=P(\partial _{x}-\partial _{x^{'}},\partial _{y}-\partial _{y^{'}}, \partial _{t}-\partial _{t^{'}},\ldots )F(x,y,t,\ldots )\\&\qquad \quad G(x^{'},y^{'},t^{'},\ldots )|_{x^{'}=x,y^{'}=y,t^{'}=t}, \end{aligned} \end{aligned}$$

where P is a polynomial of $D_{x}$,$D_{y}$,$D_{t},\ldots$. Obviously, ${\varPsi }=0, u=0$ are a set of solutions of the equation (10).

The obtained bilinear equations (15) can be reduced from the bilinear equations of the two-component KP hierarchy. Furthermore, by constraining tau functions of the two-component KP hierarchy, solutions of the bilinear equations (15) could be constructed. Thus, general bright N-soliton solutions (16) to the nonlocal Mel’nikov equation (10) can be presented in the following theorem. The proof procedure of the theorem is in “Appendix A.”

Theorem 1

General bright N-soliton solutions to the nonlocal Mel’nikov equation (10) are

$$\begin{aligned} \begin{aligned} {\varPsi }=\sqrt{2}\frac{g}{f},\quad u=( {2 \mathrm log} f)_{xx}, \end{aligned} \end{aligned}$$

(17)

where

$$\begin{aligned} \begin{aligned}&f=\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j} \mathrm{e}^{(p_i+{\overline{p}}_j)x-i({p}_i^2-{\overline{p}}_j^2)y-4(p_i^3+{\overline{p}}_j^3)t}+\frac{1}{q_i+{\overline{q}}_j}\mathrm{e}^{\kappa ( {q}_i+{\overline{q}}_j)t+\eta _{i0}+{\overline{\eta }}_{j0}}) \end{vmatrix}_{1\le i,j\le N},\\&g=\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j} \mathrm{e}^{(p_i+{\overline{p}}_j)x-i({p}_i^2-{\overline{p}}_j^2)y-4(p_i^3+{\overline{p}}_j^3)t}+\frac{1}{q_i+{\overline{q}}_j}\mathrm{e}^{\kappa ( {q}_i+{\overline{q}}_j)t+\eta _{i0}+{\overline{\eta }}_{j0})} \mathrm{e}^{p_ix-i{p}_i^2y-4p_i^3t} \\&-\mathrm{e}^{\kappa {\overline{q}}_jt+{\overline{\eta }}_{j0}} 0 \end{vmatrix}_{1\le i,j\le N}, \end{aligned} \end{aligned}$$

(18)

where $p_i,{\overline{p}}_i,\eta _{i0}$ and ${\overline{\eta }}_{i0}$ are parameters which satisfy $p_i+{\overline{p}}_j=q_i+{\overline{q}}_j\,(i,j=1,2,\ldots ,N)$ and one of the following two parametric conditions : (i) $p_i,{\overline{p}}_j\,q_i,{\overline{q}}_j$ are real and $\eta _{i0},{\overline{\eta }}_{i0}$ are purely imaginary; (ii) the subset $(p_j,q_j,\eta _{j0})$ or $({\overline{p}}_j,{\overline{q}}_j,{\overline{\eta }}_{j0})$ occurs in pair such that $p_k=p_{k^{'}}^*,q_k=q_{k^{'}}^*,\eta _{k0}=\eta _{k^{'}0}^*$ or ${\overline{p}}_k={\overline{p}}_{k^{'}}^*,{\overline{q}}_k={\overline{q}}_{k^{'}}^*,{\overline{\eta }}_{k0}={\overline{\eta }}_{k^{'}0}^*$.

Below, we examine the dynamical properties of the one- and two-bright-soliton solutions:

The bright one-soliton solution By taking $N=1$ in equation (18), the tau functions f(x, y, t), g(x, y, t) of the one-bright-soliton solutions (17) can be yielded from Theorem 1 as

$$\begin{aligned} f(x,y,t)= & {} \frac{1}{p_1+{\overline{p}}_1} \mathrm{e}^{(p_1+{\overline{p}}_1)x-i({p}_1^2-{\overline{p}}_1^2)y-4(p_1^3+{\overline{p}}_1^3)t}\nonumber \\&+\frac{1}{q_1+{\overline{q}}_1}\mathrm{e}^{\kappa ( {q}_1+{\overline{q}}_1)t+\eta _{10}+{\overline{\eta }}_{10}}),\nonumber \\ g(x,y,t)= & {} \mathrm{e}^{p_1x-i{p}_1^2y-4p_1^3t+\kappa {\overline{q}}_1t+{\overline{\eta }}_{10}}. \end{aligned}$$

(19)

Then, the explicit expression of the one-bright-soliton solutions is

$$\begin{aligned} \begin{aligned}&{\varPsi }(x,y,t)=\sqrt{2}\frac{g(x,y,t)}{f(x,y,t)} =\sqrt{2}\frac{(p_1+{\overline{p}}_1)\mathrm{e}^{p_1x-ip_1^2y-(4p_1^3+kq_1)t-i\theta _1}}{1+\mathrm{e}^{(p_1+{\overline{p}}_1)x-i(p_1^2-{\overline{p}}_1^2)y-(4(p_1^3+{\overline{p}}_1^3)-k(q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}},\\&u(x,y,t)=({2 \mathrm log} f(x,y,t))_{xx}, =\frac{2(p_1+{\overline{p}}_1)\mathrm{e}^{(p_1+{\overline{p}}_1)x-i(p_1^2-{\overline{p}}_1^2)y-(4(p_1^3+{\overline{p}}_1^3)-k(q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}}{(1+\mathrm{e}^{(p_1+{\overline{p}}_1)x-i(p_1^2-{\overline{p}}_1^2)y-(4(p_1^3+{\overline{p}}_1^3)-k(q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)})^2}. \end{aligned} \end{aligned}$$

(20)

Here we have taken $\eta _{10}=i\theta _1,{\overline{\eta }}_{10}=i{\overline{\theta }}_1$, and $p_1,{\overline{p}}_1,q_1,{\overline{q}}_1,\theta _1$ and ${\overline{\theta }}_1$ are real and satisfy $p_1+{\overline{p}}_1=q_1+{\overline{q}}_1$. Specially, when one takes $p_1={\overline{p}}_1$, the one-bright soliton solutions $|{\varPsi }|$ and u are independent of y. In this case, the one-bright-soliton solutions are given as

$$\begin{aligned} {\varPsi }(x,y,t)= & {} \sqrt{2}\mathrm{e}^{-ip_1^2y}\frac{2p_1\mathrm{e}^{p_1x-(4p_1^3+\kappa q_1)t-i\theta _1}}{1+\mathrm{e}^{2p_1x-(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}},\nonumber \\ u(x,y,t)= & {} \frac{4p_1\mathrm{e}^{2p_1x-(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}}{(1+\mathrm{e}^{2p_1x-(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)})^2}. \end{aligned}$$

(21)

Thus, the corresponding solutions $|{\varPsi }|$ and |u| describe a line soliton only propagating along the x-directions and localized along the y-direction. As the two components share similar dynamical properties, namely bright solitons in the short-wave component ${\varPsi }$ and the long-wave component u, so we only investigate the properties of the ${\varPsi }$ component in the following context.

The bright two-soliton solution By taking $N=2$ in equation (18), the tau functions f(x, y, t), g(x, y, t) for the two-bright-soliton solution (17) can be obtained from Theorem 1, which are given as

$$\begin{aligned} \begin{aligned} f(x,y,t)=&\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}, \\ g(x,y,t)=&\begin{vmatrix}a_{11}&a_{12}&\mathrm{e}^{p_1x-i{p}_1^2y-4p_1^3t} \\ a_{21}&a_{22}&\mathrm{e}^{p_2x-i{p}_2^2y-4p_2^3t} \\ -\mathrm{e}^{\kappa {\overline{p}}_1t+{\overline{\eta }}_{10}}&-\mathrm{e}^{\kappa {\overline{p}}_2t+{\overline{\eta }}_{20}}&0 \end{vmatrix}, \end{aligned} \end{aligned}$$

(22)

where

$$\begin{aligned} \begin{aligned} a_{ij}&=\frac{1}{p_i+{\overline{p}}_j}\mathrm{e}^{(p_i+{\overline{p}}_j)x-\mathbf{i }(p_i^2-{\overline{p}}_j^2)y-4(p_i^3+{\overline{p}}_j^3)t}\\&\quad +\frac{1}{q_i+{\overline{q}}_j}\mathrm{e}^{\kappa ( {q}_i+{\overline{q}}_j)t+\eta _{i0}+{\overline{\eta }}_{j0}}, \end{aligned} \end{aligned}$$

(23)

and $i,j=1,2$, and the parameters $p_j,q_j,{\overline{p}}_j,{\overline{q}}_j$ have the relation $p_i+{\overline{p}}_j=q_i+{\overline{q}}_j$. Here, the parameters $p_j,q_j,{\overline{p}}_j,{\overline{q}}_j$ and $\eta _{j0},{\overline{\eta }}_{j0}$ satisfy the following four cases.

Fig. 1

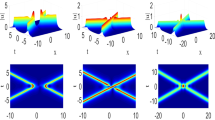
(Colour online) The time evolution of the two-bright-soliton solution $|{\varPsi }|$ (25)

Fig. 2

(Colour online) The time evolution of the two-bright-soliton solution (17) with functions f(x, y, t) and g(x, y, t) given by (22) with parameters (26)

Case i $p_j,q_j,{\overline{p}}_j,{\overline{q}}_j$ are real, and $\eta _{j0},{\overline{\eta }}_{j0}$ are all purely imaginary. In this case, the two bright solitons are two parallel line waves propagating along the x-direction and still keep localized along the y-direction. For illustrative purposes, we take parameter choices

$$\begin{aligned} p_1= & {} 1,\ {\overline{p}}_1=1,\ p_2=\frac{3}{2},\ {\overline{p}}_2=\frac{3}{2},\nonumber \\ q_1= & {} \frac{1}{2},\ {\overline{q}}_1=\frac{3}{2},\ q_2=1,\ {\overline{q}}_2=2,\nonumber \\ \kappa= & {} 1,\ \eta _{10}=0,\ {\overline{\eta }}_{10}=0,\ \eta _{20}=0,\ {\overline{\eta }}_{20}=0.\nonumber \\ \end{aligned}$$

(24)

The explicit expression of the two-bright-soliton solution ${\varPsi }$ is

$$\begin{aligned} \begin{aligned}&{\varPsi }=5\sqrt{2}\frac{2\,{\mathrm{e}^{-{\frac{ 59\,t}{2}}-iy+4\,x}}-3\,{\mathrm{e}^{-\frac{19}{2}t-\frac{9}{4}iy+\frac{3}{2}x}}-3\,{ \mathrm{e}^{-{\frac{39\,t}{2}}- \frac{9}{4}iy+\frac{7}{2}x}}+2\,{\mathrm{e}^{\frac{t}{2}-iy+x}}}{48\,{\mathrm{e}^{-15t+\frac{5}{2}x}}\cos \left( \frac{5}{4}\,y \right) -{\mathrm{e}^{-35\,t+5\,x}}-25\,{\mathrm{e}^{-5\,t+2\,x}}-25\,{ \mathrm{e}^{-25\,t+3\,x}}-{\mathrm{e}^{5\,t}}}. \end{aligned} \end{aligned}$$

(25)

The time evolution of this two-bright-soliton solution $|{\varPsi }|$ is plotted in Fig. 1. As can be seen that, at the initial sate of the evolution, the solution $|{\varPsi }|$ describes two parallel line solitons moving along the same direction on the zero background; the left line soliton moves at a higher speed than the right one (see the panels at $t=-2,-1$) and possesses higher amplitude than the right one. In the intermediate time, the left line soliton meets with the right line soliton and then interacts with each other. The interaction leads to wavefronts of the solution that are breather-type periodic wave, see the panel at $t=0$. At larger time, these two-line solitons would separate from each other, and the wavefronts of the solution return to line waves again, see the panel at $t=2$. We note that the line waves only propagate along the x-direction and not along the y-direction in the (x, y)-plane at the whole process of the evolution.

Case ii $p_1,p_2,{\overline{p}}_1,{\overline{p}}_2, \eta _{10},\eta _{20},{\overline{\eta }}_{10},{\overline{\eta }}_{20}$ are all complex and satisfy $p_1=p_2^*,q_1=q_2^*,{\overline{p}}_1={\overline{p}}_2^*,{\overline{q}}_1={\overline{q}}_2^*, \eta _{10}=- \eta _{20}^*,{\overline{\eta }}_{10}={\overline{\eta }}_{20}^*$. In this case, the solution describes two crossed line solitons interacting with each other. To show properties of this two bright solitons, we take parameter choices in Eq. (22)

$$\begin{aligned} p_1= & {} \frac{1}{2}+i,p_2=\frac{1}{2}-i,{\overline{p}}_1=\frac{1}{2}+i,\nonumber \\ {\overline{p}}_2= & {} \frac{1}{2}-i,q_1=\frac{1}{3}+i,q_2=\frac{1}{3}+i,\nonumber \\ {\overline{q}}_1= & {} \frac{2}{3}+i,{\overline{q}}_2=\frac{2}{3}-i,\kappa =1,\\ \eta _{j0}= & {} 0,{\overline{\eta }}_{j0}=0,j=1,2.\nonumber \end{aligned}$$

(26)

The corresponding solution $|{\varPsi }|$ is illustrated in Fig. 2. It is straightforward to see that, during the process of the evolution, these two crossed solitons pass through each other without any change in shape, amplitude and velocity. That feature indicates that there is no energy exchange between the two bright solitons after collision of these two bright solitons.

Case iii $p_1,p_2,q_1,q_2,\eta _{10},\eta _{20}$ are complex parameters, $p_1=p_2^{*},q_1=q_2^{*},\eta _{10}=-\eta _{20}^{*}$; ${\overline{p}}_1,{\overline{p}}_2,{\overline{q}}_1,{\overline{q}}_2$ are real, and ${\overline{\eta }}_{10},{\overline{\eta }}_{20}$ are purely imaginary.

Case iv ${\overline{p}}_1,{\overline{p}}_2,{\overline{q}}_1,{\overline{q}}_2,{\overline{\eta }}_{10},{\overline{\eta }}_{20}$ are complex parameters, ${\overline{p}}_1={\overline{p}}_2^{*},{\overline{q}}_1={\overline{q}}_2^{*},{\overline{\eta }}_{10}={\overline{\eta }}_{20}^{*}$; ${p}_1,{p}_2,{q}_1,{q}_2$ are real, and ${\eta }_{10}, {\eta }_{20}$ are purely imaginary.

Since the solutions of case iii and case iv exhibit similar behaviours as the case i and case ii, we would not shown them again. For larger N, high-order bright soliton solutions for the nonlocal Mel’nikov equation (10) could be constructed by Theorem 1, which demonstrate N parallel line waves only propagating along the x-direction as the two solitons shown in Fig. 1, or N crossed bright line solitons interacting with each other all the time as the two bright solitons illustrated in Fig. 2.

3 The dark N-soliton solution

In this section, we consider general N-dark soliton solutions to the nonlocal Mel’nikov equation (10) with nonzero boundary condition:

$$\begin{aligned} ({\varPsi },u)\rightarrow (\sqrt{2},\epsilon ),\qquad \mathrm {as} \qquad x,y,t\rightarrow \pm \infty . \end{aligned}$$

To construct dark solitons to the nonlocal Mel’nikov equation (10), we apply the following dependent variable transformations different from the transformations (16)

$$\begin{aligned} \begin{aligned} {\varPsi }=\sqrt{2}\mathrm{e}^{-\mathbf{i }\epsilon y}\frac{g(x,y,t)}{f(x,y,t)},u=\epsilon \!+\!2( \mathrm{log} f(x,y,t))_{xx}, \end{aligned} \end{aligned}$$

(27)

which transform the nonlocal Mel’nikov equation (10) into the following bilinear equations

$$\begin{aligned} \left\{ \begin{array}{lll} &{}(D_{x}^{2}-\mathbf{i }D_{y})g(x,y,t) \cdot f(x,y,t) =0,\\ &{}(D^{4}_{x}+D_xD_t-3D^2_{y})f(x,y,t) \cdot f(x,y,t)\\ &{}\quad =2\kappa [f^2(x,y,t)-gg^{*}(-x,y,-t)]. \end{array}\right. \end{aligned}$$

(28)

It is apparent that the bilinear form (28) is different from the bilinear form (15), see the right sides of the second bilinear equation in (15) and (28).

We present general dark N-soliton solutions (27) to the nonlocal Mel’nikov equation (10) by the following Theorem. The derivation of these solutions is given in “Appendix B.”

Theorem 2

The general dark soliton solutions to the nonlocal Mel’nikov equation (10) are

$$\begin{aligned} \begin{aligned} {\varPhi }(x,y,t)&=\sqrt{2}\mathrm{e}^{-\mathbf{i }\epsilon y}\frac{g_M(x,y,t)}{f_M(x,y,t)}\,,\\ u&=\epsilon +( {2 \mathrm log} f_M(x,y,t))_{xx}, \end{aligned} \end{aligned}$$

(29)

where

$$\begin{aligned} \begin{aligned}&f_M(x,y,t)=\begin{vmatrix} b_i\delta _{ij}\mathrm{e}^{-(\xi _i+\xi _j^*)}+{\frac{1}{p_i+p_j^*}}\end{vmatrix}_{1\le i,j\le 2M}, \\&g_M(x,y,t)=\begin{vmatrix} b_i\delta _{ij}\mathrm{e}^{-(\xi _i+\xi _j^*)}+{\frac{1}{p_i+p_j^*}\left( -\frac{p_i}{p_j^*}\right) }\end{vmatrix}_{1\le i,j\le 2M}, \\ \end{aligned} \end{aligned}$$

(30)

with

$$\begin{aligned} \xi _i=p_ix-\mathbf{i }p_i^2y+\left( \frac{\kappa }{p_i}-4p_i^3\right) t+\xi _{i0}, \end{aligned}$$

and $b_{M+i}=-b_i^*,p_{M+i}=-p_i,\xi _{M+i0}=\xi _{i0},i=1,2,\ldots M$, where $b_i,p_i$ are complex constants.

Below, we first present the explicit form of the two-soliton solution and detail analysis. By setting $M=1$, Theorem 2 would yield the following two-soliton solutions

$$\begin{aligned} \begin{aligned} {\varPsi }=\sqrt{2}\mathrm{e}^{-\mathbf{i }\epsilon y}\frac{g_1}{f_1}\,,u=\epsilon +( {2 \mathrm log} f_1)_{xx}, \end{aligned} \end{aligned}$$

(31)

Fig. 3

(Colour online) Three types of two-soliton solution $|{\varPsi }|$ (31) of the nonlocal Mel’nikov equation (10) at the time $t=0$: a two-dark–dark-soliton solution $|{\varPsi }|$ (31) with parameters $p_1=1+\mathbf{i },b_1=1+\frac{\mathbf{i }}{3},\kappa =1$; b two-dark–antidark-soliton solution $|{\varPsi }|$ (31) with parameters $p_1=1+\mathbf{i },b_1=\frac{1}{3}+2\mathbf{i },\kappa =1$; c two-antidark–antidark-soliton solution $|{\varPsi }|$ (31) with parameters $p_1=1+\mathbf{i },b_1=\frac{1}{3}-\frac{\mathbf{i }}{6},\kappa =1$

where

$$\begin{aligned} f_1= & {} \begin{vmatrix} b_1\mathrm{e}^{-\left( \xi _1+\xi _1^*\right) }+{\frac{1}{p_1+p_1^*}}&\frac{1}{p_1+p_2^*}\\ \frac{1}{p_2+p_1^*}&-b_1^*\mathrm{e}^{-\left( \xi _2+\xi _2^*\right) }+{\frac{1}{p_2+p_2^*}}\end{vmatrix} \nonumber \\= & {} -|b_1|^2\mathrm{e}^{-\left( \xi _1+\xi _1^*+\xi _2+\xi _2^*\right) }-\frac{b_{1}^{*}\mathrm{e}^{\xi _2+\xi _2^*}}{p_1+p_1^*}+\frac{b_{1}\mathrm{e}^{\xi _1+\xi _1^*}}{p_2+p_2^*}\nonumber \\&+\frac{\left( p_1-p_2\right) \left( p_1^*-p_2^*\right) }{\left( p_1+p_1^*\right) \left( p_2+p_2^*\right) \left( p_1+p_2^*\right) \left( p_1^*+p_2\right) }\nonumber \\= & {} -|b_1|^2\mathrm{e}^{2i\left( p_1^2-p_1^{*2}\right) y-4\xi _{10}}-\frac{b_{1}\mathrm{e}^{\xi _1+\xi _1^*}+b_{1}^{*}\mathrm{e}^{\xi _2+\xi _2^*}}{p_1+p_1^*}\nonumber \\&+\frac{4p_1p_1^*}{\left( p_1+p_1^*\right) ^2\left( p_1-p_1^*\right) ^2},\nonumber \\ g_1= & {} \begin{vmatrix} b_1\mathrm{e}^{-\left( \xi _1+\xi _1^*\right) }+{\frac{1}{p_1+p_1^*}\left( -\frac{p_1}{p_1^*} \right) }&\frac{1}{p_1+p_2^*}\left( -\frac{p_1}{p_2^*}\right) \\ \frac{1}{p_2+p_1^*}\left( -\frac{p_2}{p_1^*}\right)&-b_1^*\mathrm{e}^{-\left( \xi _2+\xi _2^*\right) }+{\frac{1}{p_2+p_2^*}\left( -\frac{p_2}{p_2^*}\right) }\end{vmatrix}, \nonumber \\= & {} -|b_1|^2\mathrm{e}^{-\left( \xi _1+\xi _1^*+\xi _2+\xi _2^*\right) }+\frac{b_{1}^{*}\mathrm{e}^{\xi _2+\xi _2^*}}{p_1+p_1^*}\frac{p_1}{p_1^*}-\frac{b_{1}\mathrm{e}^{\xi _1+\xi _1^*}}{p_2+p_2^*}\frac{p_2}{p_2^*}\nonumber \\&+\frac{\left( p_1-p_2\right) \left( p_1^*-p_2^*\right) }{\left( p_1+p_1^*\right) \left( p_2+p_2^*\right) \left( p_1+p_2^*\right) \left( p_1^*+p_2\right) }\frac{p_1p_2}{p_1^*p_2^*}\nonumber \\= & {} -|b_1|^2\mathrm{e}^{2i\left( p_1^2-p_1^{*2}\right) y-4\xi _{10}}+\frac{b_{1}\mathrm{e}^{\xi _1+\xi _1^*}+b_{1}^{*}\mathrm{e}^{\xi _2+\xi _2^*}}{p_1+p_1^*}\frac{p_1}{p_1^*}\nonumber \\&+\frac{4p_1^3}{p_1^*\left( p_1+p_1^*\right) ^2\left( p_1-p_1^*\right) ^2}, \end{aligned}$$

(32)

and

$$\begin{aligned} \xi _1+\xi _1^*= & {} -(p_1+p_1^*)x+\mathbf{i }(p_1^2-{p_1^*}^2)y\nonumber \\&+\left[ \frac{\kappa }{p_1}+\frac{\kappa }{p_1^*}-4(p_1^3+{p_1^*}^3)\right] t +\xi _{10}+\xi _{10}^*,\nonumber \\ \xi _2+\xi _2^*= & {} (p_1+p_1^*)x+\mathbf{i }(p_1^2-{p_1^*}^2)y\nonumber \\&-\left[ \frac{\kappa }{p_1}+\frac{\kappa }{p_1^*}-4(p_1^3+{p_1^*}^3)\right] t +\xi _{10}+\xi _{10}^*, \nonumber \\= & {} -(\xi _1+\xi _1^*)+2\mathbf{i }(p_1^2-{p_1^*}^2)y. \end{aligned}$$

(33)

The form of the two-soliton solution is determined by the parameters $p_1$ and $b_{1}$. For a given parameter $p_1$, the form of two-soliton solution alters from two dark–dark solitons to two dark–antidark solitons or to two antidark–antidark solitons by changing the parameter $b_1$. For example, with $p_1=1+\mathbf{i }$ and three different choices of $b_1=1+\frac{\mathbf{i }}{3},-\frac{1}{2}+2\mathbf{i },-\frac{1}{2}+\frac{\mathbf{i }}{6}$, the corresponding solutions are two dark–dark solitons, two dark–antidark solitons and two antidark–antidark solitons. These three types of two solitons are plotted in Fig. 3a–c, respectively. It is seen that after collision, the two solitons only pass through each other without any change in velocity and shape, which indicates energy exchange does not exist during the interaction between these two solitons. Here, we would like to emphasize that the two-soliton solutions demonstrated in Figs. 2, 3c have the similar wave structures, namely two crossed line waves. However, the two bright solitons shown in Fig. 2 are in the zero background, while the two-antidark–antidark solitons illustrated in Fig. 3c are in the nonzero background.

The higher-order dark soliton solutions can also be yielded from Theorem 2 with larger M in equation (31), which illustrate the collision of 2M line soliton. The forms of the solitons are still determined by the parameters $p_j,b_j,(j=1,2\ldots M)$. For example, with $M=2$ and fixed choice of parameters $p_1,p_2$ in (30), the status of the four-soliton solution is different for different parameter choices of $b_1,b_2$. Figure 4 displays two types of four solitons with the same parameters $p_1,p_2$ and different choices of parameters $b_1,b_2$. Figure 4a, b shows four dark solitons and four antidark solitons, respectively. On the other hand, with $M=2$ and the same choice of parameters $b_1,b_2$, the status of the four solitons is determined by the parameters $p_1,p_2$. Figure 5a, b shows the four antidark solitons and two antidark–two dark solitons respectively, which are generated by the same parameters $b_1,b_2$ and different choices of $p_1,p_2$.

Fig. 4

(Colour online) The four-soliton solution $|{\varPsi }|$ (29) with parameters $M=2,p_1=1+i,p_2=2+i,\xi _{10}=0,\xi _{20}=0,\kappa =1$ at time $t=0$: a four dark solitons with parameters $b_1=1+\frac{i}{3},b_2=1+\frac{i}{3}$; b four antidark solitons with parameter $b_1=-\frac{1}{2}-2i,b_2=-\frac{1}{2}-2i$

Fig. 5

(Colour online) The four-soliton solution $|{\varPsi }|$ (29) with parameters $M=2,\kappa =1,b_1=-\frac{1}{2}- \frac{i}{6},b_2=-\frac{1}{2}- \frac{i}{6},\xi _{10}=0,\xi _{20}=0$ at time $t=0$: a four antidark solitons with parameters $p_1=1+i,p_2=1+i$; b two antidark–two dark solitons with parameter $p_1=1-i,p_2=-1+\frac{i}{2}$

4 Summary and discussion

In the present paper, we present a thorough investigation for the partial reverse space–time nonlocal Mel’nikov equation (10). We construct the N-bright and N-dark soliton solutions expressed in terms of Gramian determinants for the nonlocal Mel’nikov equation. The bright N-soliton solutions are obtained by reducing the tau functions of two-component KP hierarchy, and the dark N-soliton solutions are generated by constraining the tau functions of single-component KP hierarchy. The bright solitons are illustrated in the zero background, while the dark solitons are demonstrated in the nonzero background. The properties of soliton propagation and collision are investigated in details, see Figs. 1, 2, 3, 4 and 5. In the future, we will try to analyze the orbit stability [46,47,48,49] of the above soliton solutions.

As discussed in Ref. [43], the nonlocal and local equations can be converted to each other via variable transformations. Here, we provide a simple variable transformation for translating the nonlocal Mel’nikov equation (10) to a local Mel’nikov equation. Under the variable transformation

$$\begin{aligned} \begin{aligned} x\rightarrow ix, y\rightarrow -y,t\rightarrow it, u\rightarrow -u, \end{aligned} \end{aligned}$$

(34)

the reverse space–time nonlocal Mel’nikov equation (10) would be converted into the following local (usual) Mel’nikov equation

$$\begin{aligned} \begin{aligned}&3u_{yy}(x,y,t)+u_{xt}(x,y,t)-[3u^2(x,y,t)\\&\qquad +u_{xx}(x,y,t)+\kappa {\varPsi }(x,y,t){\varPsi }^*(x,y,t)]_{xx}=0,\\&\mathbf{i }{\varPsi }_{y}(x,y,t)=u(x,y,t){\varPsi }(x,y,t)+{\varPsi }_{xx}(x,y,t). \end{aligned} \end{aligned}$$

(35)

It is obvious that the sign of nonlinearity k is not switched after the nonlocal-to-local conversion. That is different from the nonlocal-to-local transformation of the PT symmetric Davey–Stewartson equations. The sign of nonlinearity is switched after the nonlocal-to-local conversion in the PT symmetric Davey–Stewartson equations. Under the variable transformation (34), the solutions given in Theorems 1 and 2 would reduce solutions of the local Mel’nikov equation (35). For example, by taking the variable transformation (34), the bright one-soliton solution of the nonlocal Mel’nikov equation (10) given by Eq. (21) reduces to soliton-type solution of the local Mel’nikov equation (35), which reads as

$$\begin{aligned} \begin{aligned} {\varPsi }(x,y,t) =&\sqrt{2}\mathrm{e}^{ip_1^2y}\frac{2p_1\mathrm{e}^{ip_1x-i(4p_1^3+\kappa q_1)t-i\theta _1}}{1+\mathrm{e}^{2ip_1x-i(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}},\\ u(x,y,t) =&-\frac{4p_1\mathrm{e}^{2ip_1x-i(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)}}{(1+\mathrm{e}^{2ip_1x-i(8p_1^3-\kappa (q_1+{\overline{q}}_1))t-i(\theta _1+{\overline{\theta }}_1)})^2}. \end{aligned} \end{aligned}$$

(36)

The combination of the Hirota’s bilinear method and the KP hierarchy reduction method is a powerful method to construct solutions to the local and nonlocal integrable systems. We expect to use other methods to derive solutions of the nonlocal equations, such as the Darboux transformation [50, 51], the inverse scattering method [2] and the direct method [52,53,54].

Appendices

Appendix A

In this Appendix, we will provide the proof for Theorem 1 in Sect. (2). Let us first review Gramian determinant expression for the tau functions of the two-component KP hierarchy [55, 56].

Lemma 1

The following bilinear equations in the two-component KP hierarchy

$$\begin{aligned} \begin{aligned}&(D^2_{x_1}-D_{x_2})\tau _{1} \cdot \tau _0=0,\\&D_{x_1}D_{y_{1}}\tau _0 \cdot \tau _0+2\tau _{1}\tau _{-1}=0,\\&(D_{x_1}^4-3D_{x_{1}}D_{x_3}+4D_{x_{2}}^2)\tau _0 \cdot \tau _0=0, \end{aligned} \end{aligned}$$

(37)

have the following Gramian determinant tau functions

$$\begin{aligned} \begin{aligned}&\tau _0=|A|,\\&\tau _1=\begin{vmatrix}A&B^T \\ - \overline{C}&0 \end{vmatrix}, \tau _{-1}=\begin{vmatrix}A&C^T \\ - \overline{B}&0 \end{vmatrix}, \\ \end{aligned} \end{aligned}$$

(38)

where the elements of matrix A are

$$\begin{aligned} \begin{aligned} a_{ij}=\frac{1}{p_i+{\overline{p}}_j}\mathrm{e}^{\xi _i+{\overline{\xi }}_j}+\frac{1}{q_i+{\overline{q}}_j}\mathrm{e}^{\eta _i+{\overline{\eta }}_j}, \end{aligned} \end{aligned}$$

(39)

with

$$\begin{aligned}&\xi _i=p_ix_1+p_i^2x_2+p_i^3x_3,{\overline{\xi }}_i={\overline{p}}_ix_1-{\overline{p}}_i^2x_2+{\overline{p}}_i^3x_3,\nonumber \\&\eta _i=q_iy_{1}+\eta _{i0},{\overline{\eta }}_i={\overline{q}}_iy_{1}+{\overline{\eta }}_{i0}, \end{aligned}$$

(40)

and $B,{\overline{B}},C,{\overline{C}}$ are row vectors given by

$$\begin{aligned}&B=(\mathrm{e}^{\xi _1},\ldots ,\mathrm{e}^{\xi _N}),C=(\mathrm{e}^{\eta _1},\ldots ,\mathrm{e}^{\eta _N}),\nonumber \\&{\overline{B}}=(\mathrm{e}^{{\overline{\xi }}_1},\ldots ,\mathrm{e}^{{\overline{\xi }}_N}),{\overline{C}}=(\mathrm{e}^{{\overline{\eta }}_1},\ldots ,\mathrm{e}^{{\overline{\eta }}_N}). \end{aligned}$$

(41)

This lemma can be proved by the same method as for Gramian determinant solution to the nonlocal NLS equation in Ref. [10]; thus, the proof for this lemma is omitted here.

Taking variable transformation $y_1=\kappa t, x_1=x, x_2=-\mathbf{i }y, x_3=-4t$ in (40), it is easy to find that the tau functions satisfy

$$\begin{aligned} \begin{aligned}&\tau ^*_0(-x,y,-t)=c\tau _0(x,y,t),\tau _1(x,y,t)\\&\quad =c\tau ^*_{-1}(-x,y,-t),\\&c=c_1c_2,c_1=\prod \limits _{j=1}^{N}\mathrm{e}^{\xi _j+{\overline{\xi }}_j},c_2=\prod \limits _{j=1}^{N}\mathrm{e}^{\eta _j+{\overline{\eta }}_j}, \end{aligned} \end{aligned}$$

(42)

when the parameters $p_i,{\overline{p}}_j,q_i,{\overline{q}}_j$ meet the parametric condition $p_i+{\overline{p}}_j=q_i+{\overline{q}}_j\,(1\le i,j\le N)$ and one of the following two conditions: (i) $p_i,{\overline{p}}_j,q_i,{\overline{q}}_j$ are real, $\eta _i,{\overline{\eta }}_j$ are purely imaginary; (ii) the subsets $(p_i,q_i,\eta _{i0})$ or $({\overline{p}}_j,{\overline{q}}_j,{\overline{\eta }}_{j0})$ occur in pairs such that $p_k=p_{k^{'}}^*,q_k=q_{k^{'}}^*,\eta _{k0}=\eta _{k^{'}0}^*$, or ${\overline{p}}_k={\overline{p}}_{k^{'}}^*,{\overline{q}}_k={\overline{q}}_{k^{'}}^*,{\overline{\eta }}_{k0}={\overline{\eta }}_{k^{'}0}^*$.

In what follows, we give a short proof for condition (42). In the case, when $p_i,{\overline{p}}_j,q_i,{\overline{q}}_j$ are real and $\eta _{i0},{\overline{\eta }}_{j0}$ are purely imaginary, one can obtain

$$\begin{aligned}&\xi _i=p_i x-\mathbf{i }p_i^2y-4p_i^3t, \overline{\xi _j}={\overline{p}}_j x+i{\overline{p}}_j^2y-4{\overline{p}}_j^3t,\nonumber \\&\eta _i=\kappa p_i t+\mathbf{i }\theta _i,{\overline{\eta }}_j=\kappa {\overline{p}}_jt+\mathbf{i } {\overline{\theta }}_j \end{aligned}$$

(43)

and

$$\begin{aligned} \begin{aligned} \xi _i^*(-x,y,-t)&=-\xi _i(x,y,t),{\overline{\xi }}_j^*(-x,y,-t)\\&=-{\overline{\xi }}_j(x,y,t),\\ \eta _i^*(-x,y,-t)&=-\eta _i(x,y,t),{\overline{\eta }}_j^*(-x,y,-t)\\&=-{\overline{\eta }}_j(x,y,t). \end{aligned} \end{aligned}$$

(44)

Here, we have chosen $\eta _{i0}=i\theta _i,{\overline{\eta }}_{j0}=i{\overline{\theta }}_j$, and $\theta _i,{\overline{\theta }}_j$ are all real. It then follows

$$\begin{aligned}&\tau _0(x,y,t)=\prod _{j=1}^N\mathrm{e}^{\eta _i+\overline{\eta _j}}\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j}\mathrm{e}^{(p_i+{\overline{p}}_j) x-\mathbf{i }(p_i^2-{\overline{p}}_j^2)y-4(p_i^3+{\overline{p}}_j^3)t-\kappa ( {p}_i+{\overline{p}}_j)t-\mathbf{i }(\theta _{i}+{\overline{\theta }}_{j})}+\frac{1}{q_i+{\overline{q}}_j}\end{vmatrix}\nonumber \\&\quad \qquad \qquad =\prod _{j=1}^N\mathrm{e}^{\xi _i+\overline{\xi _j}}\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j}+\frac{1}{q_i+{\overline{q}}_j}\mathrm{e}^{-(p_i+{\overline{p}}_j) x+\mathbf{i }(p_i^2-{\overline{p}}_j^2)y+4(p_i^3+{\overline{p}}_j^3)t+\kappa ( {p}_i+{\overline{p}}_j)t+\mathbf{i }(\theta _{i}+{\overline{\theta }}_{j})}\end{vmatrix}. \end{aligned}$$

(45)

and

$$\begin{aligned}&\tau ^{*}_0(-x,y,-t) =\prod _{j=1}^N\mathrm{e}^{-\eta _i-\overline{\eta _j}}\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j}\mathrm{e}^{-(p_i+{\overline{p}}_j) x+\mathbf{i }(p_i^2-{\overline{p}}_j^2)y+4(p_i^3+{\overline{p}}_j^3)t+\kappa ( {p}_i+{\overline{p}}_j)t+\mathbf{i }(\theta _{i}+{\overline{\theta }}_{j})}+\frac{1}{q_i+{\overline{q}}_j}\end{vmatrix}. \end{aligned}$$

(46)

Since the parameters $p_i,{\overline{p}}_j,q_i$ and ${\overline{q}}_j$ meet the parametric condition

$$\begin{aligned} p_i+{\overline{p}}_j=q_i+{\overline{q}}_j, \end{aligned}$$

thus

$$\begin{aligned}&\tau ^{*}_0(-x,y,-t) =\prod _{j=1}^N\mathrm{e}^{-\eta _i-\overline{\eta _j}}\begin{vmatrix}\frac{1}{p_i+{\overline{p}}_j}+\frac{1}{q_i+{\overline{q}}_j} \mathrm{e}^{-(p_i+{\overline{p}}_j) x+\mathbf{i }(p_i^2-{\overline{p}}_j^2)y+4(p_i^3+{\overline{p}}_j^3)t+\kappa ( {p}_i+{\overline{p}}_j)t+\mathbf{i }(\theta _{i}+{\overline{\theta }}_{j})}\end{vmatrix}, \end{aligned}$$

(47)

which indicates that

$$\begin{aligned} \tau _0^*(-x,y,-t)=c\tau _0(x,y,t). \end{aligned}$$

Besides,

$$\begin{aligned} \begin{aligned} \tau _1(x,y,t) =&\begin{vmatrix} \frac{\mathrm{e}^{\xi _i+{\overline{\xi }}_j}}{p_i+{\overline{p}}_j}+\frac{\mathrm{e}^{\eta _i+{\overline{\eta }}_j}}{q_i+{\overline{q}}_j}&\mathrm{e}^{\xi _i} \\ -\mathrm{e}^{{\overline{\eta }}_j}&0 \end{vmatrix}\\ =&\prod _{j=1}^{N}\!\mathrm{e}^{\eta _i+{\overline{\eta }}_j}\!\begin{vmatrix} \frac{\mathrm{e}^{\xi _i+{\overline{\xi }}_j-\eta _i-{\overline{\eta }}_j}}{p_i+{\overline{p}}_j}+\frac{1}{q_i+{\overline{q}}_j}&\mathrm{e}^{-\eta _i+\xi _i}\\ -1&0 \end{vmatrix}\!, \end{aligned} \end{aligned}$$

(48)

and

$$\begin{aligned} \tau _{-1}(x,y,t)= & {} \begin{vmatrix} \frac{\mathrm{e}^{\xi _i+{\overline{\xi }}_j}}{p_i+{\overline{p}}_j}+\frac{\mathrm{e}^{\eta _i+{\overline{\eta }}_j}}{q_i+{\overline{q}}_j}&\mathrm{e}^{\eta _i} \\ -\mathrm{e}^{{\overline{\xi }}_j}&0 \end{vmatrix}\nonumber \\= & {} \prod _{j=1}^{N}\mathrm{e}^{\xi _i+{\overline{\xi }}_j}\begin{vmatrix} \frac{1}{p_i+{\overline{p}}_j}+\frac{\mathrm{e}^{-\xi _i-{\overline{\xi }}_j+\eta _i+{\overline{\eta }}_j}}{q_i+{\overline{q}}_j}&\mathrm{e}^{\eta _i-\xi _i}\\ -1&0 \end{vmatrix}.\nonumber \\ \end{aligned}$$

(49)

On the other hand,

$$\begin{aligned} \begin{aligned}&\tau _{1}^{*}(-x,y,-t) =\prod _{j=1}^{N}\mathrm{e}^{-\eta _i-{\overline{\eta }}_j}\\&\quad \begin{vmatrix} \frac{1}{p_i+{\overline{p}}_j}+\frac{\mathrm{e}^{-\xi _i-{\overline{\xi }}_j+\eta _i+{\overline{\eta }}_j}}{q_i+{\overline{q}}_j}&\mathrm{e}^{\eta _i-\xi _i}\\ -1&0 \end{vmatrix}, \end{aligned} \end{aligned}$$

(50)

thus one can obtain

$$\begin{aligned} \tau _{1}^{*}(-x,y,-t)=c\tau _{-1}(x,y,t). \end{aligned}$$

Therefore, condition (42) is satisfied in the case when $p_i$ and ${\overline{p}}_j$ are real and $\eta _{i0},{\overline{\eta }}_{j0}$ are purely imaginary. For the case, when the subset $(p_j,q_j,\eta _{j0})$ or $({\overline{p}}_j,{\overline{q}}_j,{\overline{\eta }}_{j0})$ occurs in pair such that $p_k=p_{k^{'}}^*,q_k=q_{k^{'}}^*,\eta _{k0}=\eta _{k^{'}0}^*$ or ${\overline{p}}_k={\overline{p}}_{k^{'}}^*,{\overline{q}}_k={\overline{q}}_{k^{'}}^*,{\overline{\eta }}_{k0}={\overline{\eta }}_{k^{'}0}^*$, condition (42) can be proved by a similar way, we omit its proof here.

Furthermore, under variable transformation

$$\begin{aligned} y_1=\kappa t, x_1=x, x_2=-\mathbf{i }y, x_3=-\,4\,t, \end{aligned}$$

namely

$$\begin{aligned} D_{y_1}=\frac{1}{\kappa }D_t, D_{x_1}=D_x, D_{x_2}=\mathbf{i }D_y, D_{x_3}=-\frac{1}{4}D_t, \end{aligned}$$

the bilinear equations of the two-component KP hierarchy (37) reduce to bilinear equations of the nonlocal Mel’nikov equation (15) for taking

$$\begin{aligned} f(x,y,t)= & {} \tau _0(x,y,t),g(x,y,t)\\= & {} \tau _1(x,y,t),g^{*}(-x,y,-t)=\tau _{-1}(x,y,t). \end{aligned}$$

Thus, general bright soliton solutions to the nonlocal Mel’nikov equation (10) presented in Theorem 1 are generated.

Appendix B

In this appendix, we prove Theorem 2 by reducing tau functions for the bilinear equations (28) from tau functions of single-component KP hierarchy [55,56,57,58].

Lemma 2

The following bilinear equations in the KP hierarchy

$$\begin{aligned} \begin{aligned}&(D^2_{x_1}-D_{x_2})\tau _{n+1} \cdot \tau _n=0,\\&(D_{x_1}D_{x_{-1}}-2)\tau _n \cdot \tau _n+2\tau _{n+1}\tau _{n-1}=0,\\&(D_{x_1}^4-3D_{x_{1}}D_{x_3}+4D_{x_{2}}^2)\tau _n \cdot \tau _n=0, \end{aligned} \end{aligned}$$

(51)

have the following Gramian determinant tau functions

$$\begin{aligned} \begin{aligned} \tau _{n}=\det \limits _{1\le i,j\le N} (m_{ij}^{(n)}), \end{aligned} \end{aligned}$$

(52)

where

$$\begin{aligned}&m_{ij}^{(n)}=b_{i}\delta _{ij}+\frac{1}{p+q}\left( -\frac{p}{q}\right) ^{(n)}\mathrm{e}^{\xi _i+\eta _j},\nonumber \\&\xi _i= \frac{1}{p_1}x_{-1}+p_ix_1+p_i^2x_2+p_i^3x_3+\xi _{i0},\\&\eta _j=\frac{1}{q_{j}}x_{-1}+q_jx_1-q_j^2x_2+q_j^3x_3+\eta _{j0},\nonumber \end{aligned}$$

(53)

and $p_i,q_j,b_{i},\xi _{i0}$ and $\eta _{j0}$ are arbitrary complex constants, $\delta _{ij}=1$ when $i=j$ and $\delta _{ij}=0$ elsewhere.

This lemma can be proved directly by using the Gramian technique [44, 45]; we omit the proof of this lemma here. By introducing the variable transformation

$$\begin{aligned} y_1=\kappa t,\ x_1=x,\ x_2=-\mathbf{i }y\ x_3=-4t,\ \end{aligned}$$

namely

$$\begin{aligned} D_{y_1}=\frac{1}{\kappa }D_t,\ D_{x_1}=D_x,\ D_{x_2}=\mathbf{i }D_y,\ D_{x_3}=-\frac{1}{4}D_t, \end{aligned}$$

the bilinear equations (51) become

$$\begin{aligned} \begin{aligned}&(D^2_{x}-\mathbf{i }D_{y})\tau _{n+1} \cdot \tau _n=0,\\&(D^{4}_{x}+D_xD_t-3D^2_{y})\tau _n \cdot \tau _n =2\kappa (\tau _n^2-\tau _{n+1}\tau _{n-1}). \end{aligned} \end{aligned}$$

(54)

If further taking

$$\begin{aligned} \begin{aligned} \tau _0(x,y,t)&=f(x,y,t),\tau _1(x,y,t)\\&=g(x,y,t),\tau _{-1}(x,y,t)={\overline{g}}(x,y,t), \end{aligned} \end{aligned}$$

(55)

then the bilinear equations (54) would be transformed into bilinear equations

$$\begin{aligned} \begin{aligned}&(D^2_{x}-\mathbf{i }D_{y})g(x,y,t) \cdot f(x,y,t)=0,\\&\quad (D^{4}_{x}+D_xD_t-3D^2_{y})f(x,y,t) \cdot f(x,y,t) \\&\qquad =2\kappa (f^2(x,y,t)-g(x,y,t){\overline{g}}(x,y,t)). \end{aligned} \end{aligned}$$

(56)

Furthermore, the bilinear equations (56) reduce to the bilinear equations of the nonlocal Mel’nikov equation (28) if functions $f(x,y,t),\ g(x,y,t)$ and ${\overline{g}}(x,y,t)$ satisfy

$$\begin{aligned} f(x,y,t)= & {} f^*(-x,y,-t),g^*(-x,y,-t)\nonumber \\= & {} {\overline{g}}(x,y,t). \end{aligned}$$

(57)

In what follows, we constrain functions $f(x,y,t), g(x,y,t)$ and ${\overline{g}}(x,y,t)$ satisfying condition (57) by taking particular parametric constraints

$$\begin{aligned} \begin{aligned}&N=2M,b_{M+i}=-b_{i}^*,q_j=p_j^*,\\&\eta _{j0}=\xi _{j0},p_{M+i}=-p_i,\\&\xi _{M+i0}=\xi _{i0},1\le j\le 2M, 1\le i\le M, \end{aligned} \end{aligned}$$

(58)

where $\eta _{j0}$ are real, $p_j,b_{j}$ are complex. In this case,

$$\begin{aligned} \begin{aligned} \xi _i\left( x,y,t\right)&=p_ix-\mathbf{i }p_i^2y+\left( \frac{\kappa }{p_i}-4p_i^3\right) t+\xi _{i0},\\ \eta _i\left( x,y,t\right)&=p_i^*x+\mathbf{i }p_i^{*2}y+\left( \frac{\kappa }{p_i^*}-4p_i^{*3}\right) t+\xi _{i0}. \end{aligned} \end{aligned}$$

(59)

Since

$$\begin{aligned}&(\xi _{N+i}+\xi _{N+i}^{*})(x,y,t)\nonumber \\&\quad =(p_{N+i}+p_{N+i}^*)x-\mathbf{i }(p_{N+i}^2-p_{N+i}^{*2})y\nonumber \\&\qquad +\left( \frac{\kappa }{p_{N+i}}+\frac{\kappa }{p_{N+i}^*}-4p_{N+i}^3-4p_{N+i}^{*3}\right) \nonumber \\&\qquad t+2\xi _{N+i0}\nonumber \\&\quad =-(p_{i}+p_{i}^*)x-\mathbf{i }(p_{i}^2-p_{i}^{*2})y\nonumber \\&\qquad -\left( \frac{\kappa }{p_{i}}+\frac{\kappa }{p_{i}^*}-4p_{i}^3-4p_{i}^{*3}\right) t+2\xi _{i0}, \end{aligned}$$

(60)

thus one can obtain

$$\begin{aligned} \begin{aligned}&(\xi _{N+i}+\xi _{N+i}^{*})^*(-x,y,-t)=(\xi _{i}+\xi _{i}^{*})(x,y,t),\\&\quad (\xi _{i}+\xi _{i}^{*})^*(-x,y,-t)=(\xi _{N+i}+\xi _{N+i}^{*})(x,y,t). \end{aligned} \end{aligned}$$

(61)

Besides, the tau function can be rewritten as

$$\begin{aligned} \begin{aligned}&\tau _n\left( x,y,t\right) =\prod \limits _{j=1}^{2M}\mathrm{e}^{\xi _j+\xi _j^*} \begin{vmatrix} b_i\delta _{ij}\mathrm{e}^{-\left( \xi _i+\xi _j^*\right) }+\frac{1}{p_i+p_{j}^*}\left( -\frac{p_i}{q_j^*}\right) ^n&\frac{1}{p_i+p_{M+j}^*}\left( -\frac{p_i}{q_{M+j}^*}\right) ^n \\ \frac{1}{p_{M+i}+p_{j}^*}\left( -\frac{p_{M+i}}{q_j^*}\right) ^n&b_{M+i}\delta _{M+i,M+j}\mathrm{e}^{-\left( \xi _{M+i}+\xi _{M+j}^*\right) }+\frac{1}{p_{M+i}+p_{M+j}^*} \left( -\frac{p_{M+i}}{q_{M+j}^*}\right) ^n\end{vmatrix}\\&=\prod \limits _{j=1}^{2M}\mathrm{e}^{\xi _j+\xi _j^*} \begin{vmatrix} b_{M+i}\delta _{M+i,M+j}\mathrm{e}^{-\left( \xi _{M+i}+\xi _{M+j}^*\right) }+\frac{1}{p_{M+i}+p_{M+j}^*} \left( -\frac{p_{M+i}}{q_{M+j}^*}\right) ^n&\frac{1}{p_{M+i}+p_{j}^*}\left( -\frac{p_{M+i}}{q_j^*}\right) ^n\\ \frac{1}{p_i+p_{M+j}^*}\left( -\frac{p_i}{q_{M+j}^*}\right) ^n&b_i\delta _{ij}\mathrm{e}^{-\left( \xi _i+\xi _j^*\right) }+\frac{1}{p_i+p_{j}^*}\left( -\frac{p_i}{q_j^*}\right) ^n\end{vmatrix}\\&=\prod \limits _{j=1}^{2M}\mathrm{e}^{\xi _j+\xi _j^*} \begin{vmatrix} -b_{i}^*\delta _{M+i,M+j}\mathrm{e}^{-\left( \xi _{M+i}+\xi _{M+j}^*\right) }-\frac{1}{p_{i}+p_{j}^*} \left( -\frac{p_{i}}{q_{j}^*}\right) ^n&-\frac{1}{p_{i}+p_{M+j}^*}\left( -\frac{p_{i}}{q_{M+j}^*}\right) ^n\\ -\frac{1}{p_{M+i}+p_{j}^*}\left( -\frac{p_{M+i}}{q_{j}^*}\right) ^n&-b_{M+i}^{*}\delta _{ij}\mathrm{e}^{-\left( \xi _i+\xi _j^*\right) }-\frac{1}{p_{M+i}+p_{M+j}^*}\left( -\frac{p_{M+i}}{q_{M+j}^*}\right) ^n\end{vmatrix}, \end{aligned} \end{aligned}$$

which implies

$$\begin{aligned} \begin{aligned}&\tau _{n}^{*}\left( -x,y,-t\right) =\prod \limits _{j=1}^{2M}\mathrm{e}^{\left( \xi _j+\xi _j^*\right) ^*\left( -x,y,-t\right) }\\&\qquad \begin{vmatrix} -b_{i}^*\delta _{M+i,M+j}\mathrm{e}^{-\left( \xi _{M+i}+\xi _{M+j}^*\right) ^*\left( -x,y,-t\right) }-\frac{1}{p_{i}+p_{j}^*} \left( -\frac{p_{i}}{q_{j}^*}\right) ^n&-\frac{1}{p_{i}+p_{M+j}^*}\left( -\frac{p_{i}}{q_{M+j}^*}\right) ^n\\ -\frac{1}{p_{M+i}+p_{j}^*}\left( -\frac{p_{M+i}}{q_{j}^*}\right) ^n&-b_{M+i}^{*}\delta _{ij}\mathrm{e}^{-\left( \xi _i+\xi _j^*\right) ^*\left( -x,y,-t\right) }-\frac{1}{p_{M+i}+p_{M+j}^*}\left( -\frac{p_{M+i}}{q_{M+j}^*}\right) ^n\end{vmatrix},\\&\quad =\prod \limits _{j=1}^{2M}\mathrm{e}^{\xi _j+\xi _j^*} \begin{vmatrix} b_{i}^*\delta _{i,j}\mathrm{e}^{-\left( \xi _{i}+\xi _{j}^*\right) }+\frac{1}{p_{i}+p_{j}^*} \left( -\frac{p_{i}}{q_{j}^*}\right) ^n&\frac{1}{p_{i}+p_{M+j}^*}\left( -\frac{p_{i}}{q_{M+j}^*}\right) ^n\\ \frac{1}{p_{M+i}+p_{j}^*}\left( -\frac{p_{M+i}}{q_{j}^*}\right) ^n&b_{M+i}^{*}\delta _{M+i,M+j}\mathrm{e}^{-\left( \xi _{M+i}+\xi _{M+j}^*\right) }+\frac{1}{p_{M+i}+p_{M+j}^*}\left( -\frac{p_{M+i}}{q_{M+j}^*}\right) ^n\end{vmatrix}. \end{aligned} \end{aligned}$$

Therefore, $\tau _n^{*}(-x,y,-t)=\tau _{-n}(x,y,t)$. With parametric constraints (58), functions $f(x,y,t),\ g(x,y,t),{\overline{g}}(x,y,t)$ satisfy the conjugate condition (57). By taking the gauge freedom of functions $f(x,y,t),\ g(x,y,t)$ in (16), we have Theorem 2 regarding the general soliton solutions to the nonlocal Mel’nikov equation (10) with nonzero boundary condition. That ends the proof for Theorem 2.