1 Introduction

The existence of various soliton solutions, such as breathers, solitons and rogue waves, is one of the most important characters in most of the integrable systems [1,2,3,4,5]. These soliton solutions can be well used to illustrate elastic or inelastic interaction between various types of nonlinear waves. Very recently, a new kind of integrable systems termed as nonlocal systems was proposed due to their potential application in nonlinear optics [6, 7]. The first one example of such integrable systems is the parity-time (PT)–symmetric nonlocal nonlinear schödinger (NLS) equation [8]:

$$\begin{aligned} \begin{aligned} iq_t(x,t)=q_{xx}(x,t)+2\delta q(x,t)q^*(-x,t)q(x,t). \end{aligned} \end{aligned}$$
(1)

This newly proposed nonlocal NLS equation was derived from the coupled NSL equations

$$\begin{aligned} \begin{aligned} iq_t(x,t)&=q_{xx}(x,t)+2 q(x,t)^2r(x,t),\\ -ir_t(x,t)&=r_{xx}(x,t)+2 r(x,t)^2q(x,t), \end{aligned} \end{aligned}$$
(2)

under the following reductions

$$\begin{aligned} \begin{aligned} r(x,t)=\delta q^*(-x,t). \end{aligned} \end{aligned}$$
(3)

Similar to the classical NLS equation, the nonlocal NLS equation (1) also admits solitons, breathers and rogue waves, and some other mixed solutions [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32]. Considering other types of reductions for the coupled NSL equations (2), some other nonlocal NLS equations possessing different PT-symmetries have also been introduced and discussed [10]. Taking the following reduction

$$\begin{aligned} \begin{aligned} r(x,t)=\delta q(x,-t) \end{aligned} \end{aligned}$$
(4)

the coupled system (2) leads to the reverse time nonlocal NLS:

$$\begin{aligned} \begin{aligned} iq_t(x,t)=q_{xx}(x,t)+2\delta q(x,t)^2q(x,-t). \end{aligned} \end{aligned}$$
(5)

Considering another reduction, namely

$$\begin{aligned} \begin{aligned} r(x,t)=\delta q(-x,-t) \end{aligned} \end{aligned}$$
(6)

the coupled system (2) leads to the following reverse space-time nonlocal NLS:

$$\begin{aligned} \begin{aligned} iq_t(x,t)=q_{xx}(x,t)+2\delta q(x,t)^2q(-x,-t). \end{aligned} \end{aligned}$$
(7)

In addition to these nonlocal NLS equations given by (1), (5) and (7), families of other integrable systems possessing different kinds of PT-symmetries have been proposed [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52]; examples of these newly proposed evolution equations include the nonlocal modified Kortweg-de Vries equation, the nonlocal sine-Gordon equation, the nonlocal derivative NLS equation. Usually, compared to the \((1+1)\)-dimensional nonlocal systems, the \((2+1)\)-dimensional integrable nonlocal systems correspond to more PT-symmetric versions. For example, the local Davey–Stewartson (DS) equation:

$$\begin{aligned} \begin{aligned} iA_{t}&=A_{xx}+\delta A_{yy}+(\epsilon AA^{*}-2Q)A,\\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA^{*})_{xx},\,\epsilon =\pm 1,\delta =\pm 1,\\ \end{aligned} \end{aligned}$$
(8)

corresponds to the following nonlocal DS equations:

  • The fully PT-symmetric nonlocal DS equations

    $$\begin{aligned} iA_{t}&=A_{xx}+\delta A_{yy}+(\epsilon AA^{*}(-x,-y,t)-2Q)A,\nonumber \\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA^{*}(-x,-y,t))_{xx}, \end{aligned}$$
    (9)

  • The partially PT-symmetric nonlocal DS equations

    $$\begin{aligned} iA_{t}&=A_{xx}+\delta A_{yy}+(\epsilon AA^{*}(-x,-y,t)-2Q)A,\nonumber \\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA^{*}(-x,-y,t))_{xx}, \end{aligned}$$
    (10)

  • The reverse space-time nonlocal DS:

    $$\begin{aligned} iA_{t}&=A_{xx}{+}\delta A_{yy}{+}(\epsilon AA(-x,-y,-t)-2Q)A,\nonumber \\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA(-x,-y,-t))_{xx}, \end{aligned}$$
    (11)

  • The partial reverse space-time nonlocal DS:

    $$\begin{aligned} iA_{t}&=A_{xx}+\delta A_{yy}+(\epsilon AA(-x,y,-t)-2Q)A,\nonumber \\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA(-x,y,-t))_{xx}, \end{aligned}$$
    (12)

  • The reverse time nonlocal DS:

    $$\begin{aligned} iA_{t}&=A_{xx}+\delta A_{yy}+(\epsilon AA(x,y,-t)-2Q)A,\nonumber \\ Q_{xx}&-\delta Q_{yy}=(\epsilon AA(x,y,-t))_{xx}. \end{aligned}$$
    (13)

Families of soliton solutions, including line solitons, breathers, lumps and rogue waves on a periodic line waves (PLWs) or a nonzero constant background, have been reported for these nonlocal DS equation [30, 39, 40, 53, 54].

In this paper, we mainly investigate another (\(2+1\))-dimensional nonlocal Mel’nikov (MK) equation [51, 52]

$$\begin{aligned} \begin{aligned}&u_{xt}+u_{xxxx}+3(u^{2})_{xx}-3u_{yy}\\&\quad +\kappa (\Phi \Phi ^*(-x,y,-t))_{xx}=0,\\&\quad i\Phi _{y}=u\Phi +\Phi _{xx}. \end{aligned} \end{aligned}$$
(14)

The associated local equation of this nonlocal equation is the MK equation [55,56,57]

$$\begin{aligned} \begin{aligned}&u_{xt}+u_{xxxx}+3(u^{2})_{xx}-3u_{yy}\\&\quad +\kappa (\Phi \Phi ^*(x,y,t))_{xx}=0,\\&\quad i\Phi _{y}=u\Phi +\Phi _{xx}, \end{aligned} \end{aligned}$$
(15)

where \(\kappa \) is a real constant and u and \(\Phi \) are a real long-wave (LW) field and a complex short-wave (SW) one, respectively. The local MK equation (15) was first proposed to describe the interaction of LW and SW packets by Mel’nikov [55,56,57]. This equation is integrable and admits solitons solutions [59,60,61,62,63,64] as other \((2+1)\)-dimensional integrable systems, such as bright and dark soliton, breather and rational localized solutions. Some soliton solutions in the nonlocal MK equation (14) have been reported, including bright solitons under zero boundary condition, dark solitons under nonzero boundary condition [52], breathers on a nonzero constant or PLWs background, lumps on a nonzero constant background or a PLWs background, and solutions showing the superposition of lumps and breathers on a nonzero constant or PLWs background [51]. However, there are some open issues about the nonlocal MK equation (14) that have not been well investigated. A typical example is that the solitons on a PLWs background have not been reported. Besides, Liu et.al. [52] derived breathers and semi-rational solutions comprised of lumps and breathers on a constant or PLWs background to the nonlocal MK equation (14); these solutions are not expressed by determinants. In the present work, we would investigate the following arguments to the nonlocal MK system defined in (14):

  • The general line solitons on a PLWs background in the nonlocal MK equation (14).

  • The mixed solutions describing breathers on a nonzero constant or PLWs background in the nonlocal MK equation defined in (14) expressed by determinants.

The structure of the paper is organized as follows. In Sect. 2, dynamics of line solitons on a PLWs background in the nonlocal MK equation (14) are analyzed in detail. In Sect. 3, dynamical features of general periodic solutions expressed via Gram-type determinants, which contain PLWs background, breathers on a nonzero constant or PLWs background, are investigated. The conclusions for this paper are discussed in Sect. 4.

2 General line solitons on a PLWs background

In this section, we would comprehensively analyze the dynamics of general line solitons on a PLWs background for the nonlocal MK equation (14). To this end, we combine the general line solitons on a nonzero constant background with the PLWs, and the corresponding solutions are expressed by \((2N+1)\times (2N+1)\) determinants. We note that Liu et al. constructed general line solitons on a constant background [52], and the corresponding soliton solutions are given by \(2N\times 2N\) determinants. Below, we present the general line solitons on a background of PLWs to the nonlocal MK equation (14) by the following theorem, whose proof procedure would be given in the Appendix in detail.

Theorem 1

The nonlocal MK equation (14) has the following solitons sitting on a PLWs background

$$\begin{aligned} \begin{aligned} \Phi =\sqrt{2}\frac{g}{f}, u=({2 \log } f)_{xx} \end{aligned} \end{aligned}$$
(16)

with functions f and g given by the following \((2N+1)\times (2N+1)\) determinants

$$\begin{aligned} \begin{aligned} f(x,t)=&\begin{vmatrix} b_s\delta _{sj}e^{-\zeta _s}+\frac{1}{p_s+p_j^*}&\frac{1}{p_s-p_{j}^*}&\frac{1}{p_s-p_{2N+1}^*}\\ -\frac{1}{p_{s}-p_{j}^*}&-b_s^*\delta _{sj}e^{-\zeta _{s}^*(-x,y,-t)} -\frac{1}{p_{s}+p_{j}^*}&-\frac{1}{p_{s}+p_{2N+1}^*}\\ \frac{1}{p_{2N+1}+p_j^*}&\frac{1}{p_{2N+1}-p_{j}^*}&ib_{2N+1} e^{-\zeta _{2N+1}}+\frac{1}{p_{2N+1}-p_{2N+1}^*} \end{vmatrix}_{0\le s,j\le N},\\ g(x,t)=&\begin{vmatrix} b_s\delta _{sj}e^{-\zeta _s}-\frac{p_s}{p_j^*}\frac{1}{p_s+p_j^*}&\frac{p_s}{p_{j^*}}\frac{1}{p_s-p_{j}^*}&\frac{p_s}{p_{j}^*} \frac{1}{p_s-p_{2N+1}^*}\\ -\frac{p_{s}}{p_j^*}\frac{1}{p_{s}-p_{j}^*}&-b_s^*\delta _{sj} e^{-\zeta _{s}^*(-x,y,-t)}+\frac{p_{s}}{q_{j}^*}\frac{1}{p_{s} +p_{j}^*}&\frac{p_{s}}{p_{2N+1}^*}\frac{1}{p_{s}+p_{2N+1}^*}\\ -\frac{p_{2N+1}}{p_j^*}\frac{1}{p_{2N+1}+p_j^*}&\frac{p_{2N+1}}{p_j^*}\frac{1}{p_{2N+1}-p_{j}^*}&ib_{2N+1}e^{-\zeta _{2N+1}} +\frac{p_{2N+1}}{p_{2N+1}^*}\frac{1}{p_{2N+1}-p_{2N+1}^*} \end{vmatrix}_{0\le s,j\le N}, \end{aligned} \end{aligned}$$
(17)

and

$$\begin{aligned} \begin{aligned} \zeta _s=&2p_{sR}x+4p_{sR}p_{sI}y-2p_{sR}\left[ 4(p_{sR}^2-3p_{sI}^2)\right. \\&\left. +\frac{\kappa }{p_{sR}^2+p_{sI}^2}\right] t+\zeta _{0,s},\\ \zeta _{2N+1}=&2ip_{2N+1,I}x+2p_{2N+1,R}p_{2N+1,I}y\\&+2ip_{2N+1,I} \left[ 4\left( 3p_{2N+1,R}^2-p_{2N+1,I}^2\right) \right. \\&\left. +\frac{\kappa }{p_{2N+1,R}^2+p_{2N+1,I}^2}\right] t+\zeta _{0,2N+1}, \end{aligned}\end{aligned}$$
(18)

where \(b_s,p_s\) are complex and \(\zeta _{0,s}\) are real for \(s=0,1,\ldots N\), the real part of \(p_{2N+1}\) are zero (i.e., \(p_{2N+1,R}=0\)), and \(b_{2N+1}\) is real.

To examine dynamics of the two line solitons on a PLWs background in the nonlocal MK equation (14), we have to consider a periodic solution, which can illustrate a PLWs background. By taking \(N=0\) in formula (17), a PLW solution could be yielded, and functions f and g read as

$$\begin{aligned} f= & {} ib_1e^{-2ip_{1I}x-2p_{1R}p_{1I}y-2ip_{1I}[4(3p_{1R}^2-p_{1I}^2) +\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t-\zeta _{0,1}}\nonumber \\&+\frac{1}{2ip_{1I}}\nonumber \\= & {} -b_1\sin \chi e^{-2p_{1R}p_{1I}y-\zeta _{0,1}}-\frac{1}{2p_{1I}}\nonumber \\&+ib_1\cos \chi e^{-2p_{1R}p_{1I}y-\zeta _{0,1}},\nonumber \\ g= & {} ib_1e^{-2ip_{1I}x-2p_{1R}p_{1I}y-2ip_{1I}\left[ 4\left( 3p_{1R}^2-p_{1I}^2\right) +\frac{\kappa }{p_{1R}^2+p_{1I}^2}\right] t-\zeta _{0,1}}\nonumber \\&-\frac{1}{2ip_{1I}} \frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}, \end{aligned}$$
(19)

where \(\chi =-2p_{1I}x-2p_{1I}[4(3p_{1R}^2-p_{1I}^2)+\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t\), and \(b_1,p_{1R},p_{1I},\zeta _{0,1}\) are arbitrary real parameters.

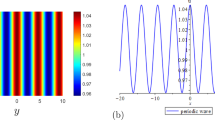
As discussed in earlier works of the literature [30], this type of periodic solutions also exists in the nonlocal DS equation, which provides a PLWs background. It can be directly obtained that this solution always possesses a series of singular points when \(p_{1R}\ne 0\). Hence, we take \(p_{1R}=0\) to avoid the singular solutions, and these corresponding solutions are independent of y. Besides, the real part of the function f denoted as \(f_r\) satisfies \(f_{r}\ne 0\) when \(|\frac{e^{\zeta _{01}}}{2b_1p_{1I}}|>1\). In this case, these periodic solutions are regular, and this character also holds for the mixed solutions demonstrating line solitons on a PLWs background, which will be discussed in the following context. The maximum amplitudes of the PLWs solutions \(|\Phi |\) and |u| are

$$\begin{aligned} \begin{aligned}&|\Phi |_{\max }=\sqrt{2}\left| \frac{2b_1p_{1I}e^{-\zeta _{0,1}} +1}{2b_1p_{1I}e^{-\zeta _{0,1}}-1}\right| ,\\&|u|_{\max }=\frac{16b_1p_{1I}^3e^{-\zeta _{0,1}}}{(2b_1p_{1I}e^{-\zeta _{0,1}}-1)^2}. \end{aligned} \end{aligned}$$
(20)

It is noteworthy that the shift parameter \(\zeta _{0,1}\) can also determine the maximum amplitudes of the PLWs, which is different from the local MK equation. Figure 1 shows the PLWs background.

Fig. 1
figure 1

The first-order periodic line wave solution (16) with functions f and g given by (19) with parameters \(\kappa =1, b_1=\frac{1}{4},p_{1R}=0,p_{1I}=1,\zeta _{1}^0=\pi \). The right panel is a section diagram along \(y=0\) of the left panel (Colour online)

Full size image

In what follows, we show the line solitons on a PLWs background, which are demonstrated by the solutions (16) in Theorem  1 with \(N\ge 1\). We first examine \(N=1\) in Theorem  1, i.e., the simplest solutions in Theorem 1. The solutions \(\Phi \) and u to the nonlocal MK equation (14) are generated from formula (16):

$$\begin{aligned} \begin{aligned} \Phi =\sqrt{2}\frac{g_1}{f_1}, u=({2 \log } f_1)_{xx} \end{aligned} \end{aligned}$$
(21)

where \(f_1\) and \(g_1\) are given by the following \(3\times 3\) determinants

$$\begin{aligned} \begin{aligned} f_1(x,t)=&\begin{vmatrix} b_1e^{-\zeta _1}+\frac{1}{p_1+p_1^*}&\frac{1}{p_1-p_{1}^*}&\frac{1}{p_1-p_{3}^*}\\ -\frac{1}{p_{1}-p_{1}^*}&-b_1^*e^{-\zeta _{1}^*(-x,y,-t)}-\frac{1}{p_{1} +p_{1}^*}&-\frac{1}{p_{1}+p_{3}^*}\\ \frac{1}{p_{3}+p_1^*}&\frac{1}{p_{3}-p_{1}^*}&ib_{3}e^{-\zeta _{3}} +\frac{1}{p_{3}-p_{3}^*} \end{vmatrix},\\ g_1(x,t)=&\begin{vmatrix} b_1e^{-\zeta _1}-\frac{p_1}{p_1^*}\frac{1}{p_1+p_1^*}&\frac{p_1}{p_{1^*}}\frac{1}{p_1-p_{1}^*}&\frac{p_1}{p_{3}^*}\frac{1}{p_1-p_{3}^*}\\ -\frac{p_{1}}{p_1^*}\frac{1}{p_{1}-p_{1}^*}&-b_1^*e^{-\zeta _{1}^*(-x,y,-t)} +\frac{p_{1}}{q_{1}^*}\frac{1}{p_{1}+p_{1}^*}&\frac{p_{1}}{p_{3}^*}\frac{1}{p_{1}+p_{3}^*}\\ -\frac{p_{3}}{p_1^*}\frac{1}{p_{3}+p_1^*}&\frac{p_{3}}{p_1^*}\frac{1}{p_{3} -p_{1}^*}&ib_{3}e^{-\zeta _{3}}+\frac{p_{3}}{p_{3}^*}\frac{1}{p_{3}-p_{3}^*} \end{vmatrix}, \end{aligned} \end{aligned}$$
(22)

and

$$\begin{aligned} \begin{aligned} \zeta _1=&2p_{1R}x+4p_{1R}p_{1I}y-2p_{1R}\\&\left[ 4\left( p_{1R}^2-3p_{1I}^2\right) +\frac{\kappa }{p_{1R}^2+p_{1I}^2}\right] t+\zeta _{0,1},\\ \zeta _3=&2ip_{3I}x+2ip_{3I}\left[ -4p_{3I}^2+\frac{\kappa }{p_{3I}^2}\right] t +\zeta _{0,3}, \end{aligned} \end{aligned}$$
(23)

where \(p_{1}=p_{1R}+ip_{1I},p_3=ip_{3I}\), \(b_1\) is a freely complex parameter, and \(\zeta _{0,1},\zeta _{0,3},b_{3}\) are real.

This solution demonstrates two line solitons moving on a PLWs background; the line orientations of the two line solitons are in the \((p_{1I},1)\) direction and \((p_{1I},-1)\) direction. Hence, only the parameter \(p_{1I}\) controls the direction of the two line solitons. As discussed in Ref. [30], the patterns of the two line solitons are the same in PLWs background and constant background under same parametric condition. Below, we analyze the asymptotic behaviors of the two line soliton solutions on a constant background, which are obtained by deleting the third column and the third row of determinant expression of functions f and g (22):

$$\begin{aligned} f= & {} -|b_1|^2e^{-(\zeta _1+\zeta _{1}^*(-x,y,-t))}\nonumber \\&-\frac{b_1e^{-\xi _1}+b_1^*e^{-\xi _1^*(-x,y,-t)}}{2p_{1R}} -\frac{p_{1R}^2+p_{1I}^2}{4p_{1R}^2p_{1I}^2},\nonumber \\ g= & {} -|b_1|^2e^{-(\zeta _1+\zeta _{1}^*(-x,y,-t))}\nonumber \\&-\frac{b_1e^{-\xi _1} +b_1^*e^{-\xi _1^*(-x,y,-t)}}{2p_{1R}}\left( -\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}\right) \nonumber \\&-\frac{p_{1R}^2+p_{1I}^2}{4p_{1R}^2p_{1I}^2}\left( \frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}\right) ^2. \end{aligned}$$
(24)

We assume \(p_{1R}>0\) and define the solitons along lines \(2p_{1R}x+4p_{1R}p_{1I}y-2p_{1R}[4(p_{1R}^2-3p_{1I}^2)+\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t+\zeta _{0,1}\) and \(-2p_{1R}x+4p_{1R}p_{1I}y+2p_{1R}[4(p_{1R}^2-3p_{1I}^2)+\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t+\zeta _{0,1}\) as soliton 1 and soliton 2, respectively, which lead to the following asymptotic forms:

(i) Before collision (\(x\rightarrow -\infty \))

Soliton 1 (\(\zeta _1\approx 0,\zeta _1^*(-x,y,-t)\rightarrow +\infty \)):

$$\begin{aligned} \begin{aligned} \Phi _{1}^{-}\simeq&\sqrt{2}\frac{b_1e^{-\zeta _1}+\frac{1}{2p_{1R}} (-\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}})}{b_1e^{-\zeta _1}+\frac{1}{2p_{1R}}}, \end{aligned} \end{aligned}$$
(25)

Soliton 2 (\(\zeta _1^*(-x,y,-t)\approx 0,\zeta _1\rightarrow -\infty \)):

$$\begin{aligned} \begin{aligned} \Phi _{2}^{-}\simeq&\sqrt{2}\left( -\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}\right) \\&\frac{b_1^*e^{-\left( \zeta _1^*(-x,y,-t)+\Delta \right) }+\frac{1}{2p_{1R}} \left( -\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}\right) }{b_1^*e^{-(\zeta _1^*(-x,y,-t) +\Delta )}+\frac{1}{2p_{1R}}}, \end{aligned} \end{aligned}$$
(26)

where \(e^{-\Delta }=\frac{p_{1I}^2}{p_{1R}^2+p_{1I}^2}\).

(ii) After collision (\(x\rightarrow +\infty \)) Soliton 1 (\(\zeta _1\approx 0,\zeta _1^*(-x,y,-t)\rightarrow -\infty \)):

$$\begin{aligned} \begin{aligned} \Phi _{1}^{-}\simeq&\sqrt{2}\left( -\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}\right) \\&\frac{b_1e^{-(\zeta _1+\Delta )}+\frac{1}{2p_{1R}}\left( -\frac{p_{1R} +ip_{1I}}{p_{1R}-ip_{1I}}\right) }{b_1e^{-\left( \zeta _1+\Delta \right) }+\frac{1}{2p_{1R}}}, \end{aligned} \end{aligned}$$
(27)

Soliton 2 (\(\zeta _1^*(-x,y,-t)\approx 0,\zeta _1\rightarrow +\infty \)):

$$\begin{aligned} \begin{aligned} \Phi _{2}^{+}\simeq&\sqrt{2}\frac{b_1^*e^{-\zeta _1^*(-x,y,-t)} +\frac{1}{2p_{1R}}(-\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}})}{b_1^*e^{-\zeta _1^*(-x,y,-t)}+\frac{1}{2p_{1R}}}. \end{aligned} \end{aligned}$$
(28)

Here \(\Phi _j^+\) and \(\Phi _j^-\) represent the asymptotic form of the jth soliton before and after interaction for \(j=1,2\). Then, we obtain \(\Phi _1^{+}(\zeta _1)=(-\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}})\Phi _1^{-} (\zeta _1+\Delta )\), \(\Phi _2^{+}(\zeta _1^*(-x,y,-t))=(-\frac{p_{1R}-ip_{1I}}{p_{1R}+ip_{1I}}) \Phi _2^{+}(\zeta _1^*(-x,y,-t)-\Delta )\). Since \(|-\frac{p_{1R}+ip_{1I}}{p_{1R}-ip_{1I}}|=1\), \(|\Phi _j^{-}|=|\Phi _j^{+}|\). These identities indicate the amplitude, shape and velocities of the jth are consistent before and after collision. Below, we classify the patterns of the two line soliton. Along the two lines \(2p_{1R}x+4p_{1R}p_{1I}y-2p_{1R}[4(p_{1R}^2-3p_{1I}^2) +\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t+\zeta _{0,1} +\frac{1}{2}\ln (4(b_{1R}^2+b_{1I}^2)^2p_{1R}^2)\) and \(-2p_{1R}x+4p_{1R}p_{1I}y+2p_{1R}[4(p_{1R}^2-3p_{1I}^2) +\frac{\kappa }{p_{1R}^2+p_{1I}^2}]t+\zeta _{0,1} +\frac{1}{2}\ln (4(b_{1R}^2+b_{1I}^2)^2p_{1R}^2)\), the asymptotic line solitons attain the max amplitudes denoted as \(|\Phi _1|_{\max }\) and \(|\Phi _2|_{\max }\):

$$\begin{aligned} \begin{aligned}&|\Phi _1|_{\max }\\&\quad =\sqrt{2}\sqrt{1-\frac{4\left( b_{1R}p_{1R} -b_{1I}p_{1I}\right) p_{1R}^2\sqrt{\left( b_{1R}^2+b_{1I}^2\right) p_{1R}^2}}{\Gamma }},\\&|\Phi _1|_{\max }\\&\quad =\sqrt{2}\sqrt{1-\frac{4\left( b_{1R}p_{1R} +b_{1I}p_{1I}\right) p_{1R}^2\sqrt{\left( b_{1R}^2+b_{1I}^2\right) p_{1R}^2}}{\Gamma }}, \end{aligned} \end{aligned}$$
(29)

where

$$\begin{aligned} \Gamma= & {} \left( b_{1R}p_{1R}p_{1I}{+}b_{1I}p_{1R}^2{+}\sqrt{(b_{1R}^2 +b_{1I}^2)p_{1R}^2}p_{1I}\right) ^2\\&+p_{1R}^2\left( b_{1R}p_{1R} {-}b_{1I}p_{1I}{-}\sqrt{(b_{1R}^2+b_{1I}^2)p_{1R}^2}\right) ^2, \end{aligned}$$

According the above analysis, the patterns of the two-line soliton solution \(\Phi \) are listed as follows:

  • Two-dark soliton if \(b_{1R}p_{1R}-b_{1I}p_{1I}>0,b_{1R}p_{1R}+b_{1I}p_{1I}>0,\);

  • Two-antidark soliton if \(b_{1R}p_{1R}-b_{1I}p_{1I}<0, b_{1R}p_{1R}+b_{1I}p_{1I}<0\);

  • One-antidark soliton and one-dark soliton if \((b_{1R}p_{1R}-b_{1I}p_{1I})(b_{1R}p_{1R}+b_{1I}p_{1I})<0\);

  • A degenerate two-line soliton if \((b_{1R}p_{1R}-b_{1I}p_{1I})(b_{1R}p_{1R}+b_{1I}p_{1I})=0\);

It should be note that here we analysis the asymptotic behaviors of the two-line soliton as \(x\rightarrow \pm \infty \), which were analyzed as \(t\rightarrow \pm \infty \) in [52]. Besides, we classify the patterns of the two-line soliton in the (x, y)-plane under different parametric conditions according to the asymptotic analysis that were not given in Ref. [52].

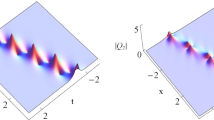
By doing similar analysis of the solution of the long wave component u, solution u only possesses two-antidark-soliton. Five different types of two-line-soliton solution \(\Phi \) on a background of PLWs are shown in Fig. 2: two-antidark-soliton (Fig. 2a), one-antidark-soliton and one-dark-soliton (Fig. 2b), two-dark-soliton (Fig. 2c), a degenerate two-dark-soliton (Fig. 2d) and a degenerate two-antidark-soliton (Fig. 2e). Figure 2f illustrates the two-antidark-soliton solution of the long wave component u. We note that the classification of the patterns of two-line-soliton on a constant background was not given in [52].

Fig. 2
figure 2

Several different types of two line solitons on a PLWs background given by (22) in the nonlocal MK equation (14) at the time \(t=0\): a Two-antidark-soliton on a PLWs background in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-1-i,p_3=-3i,b_1=1+i,b_3=-\frac{i}{4},\zeta _{0,1}=0,\zeta _{0,3}=\pi \); b One-antidark-soliton and one-dark-soliton on a PLWs background in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-1-i,p_3=-3i,b_1=1+\frac{i}{2},b_3=-\frac{i}{4},\zeta _{0,1}=0,\zeta _{0,3}=\pi \); c Two-dark-soliton on a PLWs background in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-1-i,p_3=-3i,b_1=-1-2i,b_3=-\frac{i}{4},\zeta _{0,1}=0,\zeta _{0,3}=\pi \); d A degenerated two-dark-soliton on a PLWs background in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-1+i,p_3=-3i,b_1=1-i,b_3=-\frac{i}{4},\zeta _{0,1}=0,\zeta _{0,3}=\pi \); e A degenerated two-antidark-soliton on a PLWs background in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=1+i,p_3=-3i,b_1=1-i,b_3=-\frac{i}{4},\zeta _{0,1}=0,\zeta _{0,3}=\pi \); and f Two-antidark-soliton in the LW component |u| with parameters \(\kappa =1,p_1=-1-i,p_3=-3i,b_1=1+\frac{i}{2},b_3=-\frac{i}{4}, \zeta _{0,1}=0,\zeta _{0,3}=\pi \) (Colour online)

Full size image

The higher-order line solitons on a PLWs background can be yielded from Theorem 1 with larger N. In addition to the degenerated 2N-line soliton, the SW component \(|\Phi |\) possesses \(2N+1\) different patterns: \(N^{'}\)-antidark-soliton and \(2N-N^{'}\)-dark-soliton (\(0\le N^{'}\le 2N\)) on a PLWs background. The LW component |u| only has one patterns: 2N-antidark-soliton on the PLWs background. For instance, with \(N=2\) and different parameters in Theorem 1, the corresponding solutions illustrate four-line solitons on a PLWs background. Figure 3a–e shows five different patterns of four-line-soliton solution on a background of PLWs in the SW component \(|\Phi |\), namely four-antidark-soliton (see Fig. 3a), three-antidark-soliton and one-dark-soliton (see Fig. 3b), two-antidark-soliton and two-dark-soliton (see Fig. 3c), one-antidark-soliton and three-dark-soliton (see Fig. 3d) and four-dark-soliton (see Fig. 3e). Figure 3f demonstrates the four-antidark-soliton in the LW component |u|. For larger N, these higher-order mixed solutions can be directly obtained. However, these high-order mixed solution do not have qualitatively different behaviors, but more line solitons interacting with each other on a PLWs background, and the interaction may give rise to more line wave patterns.

Fig. 3
figure 3

Five different types of four-line-soliton solution on a PLWs background in the SW component \(|\Phi |\), and one type of four-line-soliton solution on a background of PLWs in the LW component |u|, given by (22) to the nonlocal MK equation (14) at the time \(t=0\): a Four-antidark-soliton in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-\frac{1}{2}-\frac{1}{2}i,p_2=-1-\frac{4}{5}i,p_5=-3i,b_1=1+\frac{i}{2},b_2=1+\frac{2}{5}i,b_5=-\frac{1}{4}i,\zeta _{0,1}=0,\zeta _{0,2}=0,\zeta _{0,5}=-\pi \); b Three-antidark-soliton and one-dark-soliton in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-\frac{1}{2}-i,p_2=-1-i,p_5=-i,b_1=1+2i,b_2=1+\frac{1}{2}i,b_5=-i,\zeta _{0,1}=3\pi ,\zeta _{0,2}=-3\pi ,\zeta _{0,5}=-\frac{1}{2}\pi \); c Two-antidark-soliton and two-dark-soliton in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=-1-i,p_2=-1-\frac{4}{5}i,p_5=-3i,=-1-\frac{4}{5}i,b_1=1+\frac{1}{2}i,b_2=1+\frac{2}{5}i,b_5=-\frac{4}{5}i,\zeta _{0,1}=0,\zeta _{0,2}=0,\zeta _{0,5}=\pi \); d One-antidark-soliton and three-dark-soliton in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=1-i,p_2=-\frac{1}{2}-2i,p_5=-i,b_1=1,b_2=1-\frac{1}{2}i,b_5=-i,\zeta _{0,1}=0,\zeta _{0,1}=-4\pi ,\zeta _{0,2}=4\pi ,\zeta _{0,5}=0\); e Four-dark-soliton in the SW component \(|\Phi |\) with parameters \(\kappa =1,p_1=1-i,p_2=-2-i,p_5=-i,b_1=1,b_2=1,b_5=-i,\zeta _{0,1}=5\pi ,\zeta _{0,2}=-5\pi ,\zeta _{0,5}=-\frac{3}{2}\pi \); and f Four-antidark-soliton in the LW component |u| with parameters \(\kappa =1,p_1=1-i,p_2=-2-i,p_5=-i,b_1=1,b_2=1,b_5=-i,\zeta _{0,1}=5\pi ,\zeta _{0,2}=-5\pi ,\zeta _{0,5}=-\frac{3}{2}\pi \) (Colour online)

Full size image

3 General breathers on a background of constant and PLWs

In this section, we would comprehensively focus on the features of the breathers on two types of background in the nonlocal MK equation (14), namely the constant background and the PLWs background. These solutions are presented via determinant forms in the present paper, which are different from the results in Ref. [51], in which the solutions are given by complicate algebraic formula. As discussed in earlier works in the literature [51], breather solution is a type of periodic solutions. Furthermore, the PLWs background is also described by a periodic solution; thus, breathers on a constant or PLWs background are a kind of periodic solutions. Below, we would first give a general type of periodic solutions to the nonlocal MK equation (14) in the following theorem, whose proof procedure for the theorem would be provided in Appendix in detail.

Theorem 2

The nonlocal MK equation (14) has periodic solutions

$$\begin{aligned} \begin{aligned} \Phi =\sqrt{2}\frac{g}{f}, u=({2 \log } f)_{xx} \end{aligned} \end{aligned}$$
(30)

with functions f and g given by the following \(N\times N\) determinants

$$\begin{aligned} \begin{aligned} f(x,t)=&\Gamma _0\begin{vmatrix} \frac{\delta _{sj}}{\omega _se^{\zeta _s}}+\frac{1}{\frac{1}{2}(\omega _s +\omega _j)+i(\lambda _s-\lambda _j)} \end{vmatrix}_{1\le s,j\le N},\\ g(x,t)=&\Gamma _0\begin{vmatrix} \frac{\delta _{sj}}{\omega _se^{\zeta _s}}-\frac{\omega _s+2i\lambda _s}{\omega _j-2i\lambda _j}\frac{1}{\frac{1}{2}(\omega _s+\omega _j)+i(\lambda _s-\lambda _j)} \end{vmatrix}_{1\le s,j\le N}, \end{aligned} \end{aligned}$$
(31)

and

$$\begin{aligned} \begin{aligned} \zeta _s&=i\omega _s x-2\lambda _s\omega _sy+i\omega _s\left[ \left( 12\lambda _s^2-\omega _s^2\right) \right. \\&\quad \, \left. +\frac{4\kappa }{4\lambda _s^2+\omega _s^2}\right] t+\zeta _{0,s},\\ \end{aligned} \end{aligned}$$
(32)

where \(\Gamma _0=\prod \nolimits _{s=1}^{N}\omega _se^{\zeta _s}\), and \(\omega _s,\lambda _s,\zeta _{0,s}\) are real parameters.

Remark 1

With different parametric conditions, these periodic solutions have the following three different behaviors:

  • Breathers on a nonzero constant background when the parameters fulfill the following parametric constraints:

    $$\begin{aligned} \begin{aligned} N&=2M, \omega _{M+j}=-\omega _j, \lambda _{M+j}\\&=-\lambda _j, \zeta _{0,M+s}=\zeta _{0,s}, j=1,2,\ldots . \end{aligned} \end{aligned}$$
    (33)

  • Breathers on a PLWs background when the parameters fulfill the following parametric constraints:

    $$\begin{aligned} \begin{aligned} N&=2M+1, \omega _{M+j}=-\omega _j, \lambda _{M+j}\\&=-\lambda _j, \zeta _{0,M+s}=\zeta _{0,s}, \lambda _{2M+1}=0, j=1,2,\ldots . \end{aligned} \end{aligned}$$
    (34)

  • Periodic line waves when the parameters do not satisfy the parametric conditions given by (33) and (34).

In what follows, we consider the dynamics of the breathers on a background of constant and PLWs, respectively.

3.1 Breathers on a constant background

The first-order breather on a constant background is generated by taking the following parameters in Theorem 2

$$\begin{aligned} \begin{aligned} N=2,\omega _2=-\omega _1,\lambda _2=-\lambda _1,\zeta _{0,2}=\zeta _{0,1}, \end{aligned} \end{aligned}$$
(35)

and the functions f and g of solutions (30) read as

$$\begin{aligned} \begin{aligned} f=&\begin{vmatrix} \frac{1}{\omega _1e^{\zeta _1}}+\frac{1}{\omega _1}&\frac{1}{2i\lambda _1}\\ \frac{1}{-2i\lambda _1}&\frac{1}{-\omega _1e^{\zeta _1^*}}-\frac{1}{\omega _1} \end{vmatrix},\\ g=&\begin{vmatrix} \frac{1}{\omega _1e^{\zeta _1}}-\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1}&\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{ 2i\lambda _1}\\ -\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{2i\lambda _1}&-\frac{1}{\omega _1e^{\zeta _1^*}}+\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\frac{1}{\omega _1} \end{vmatrix},\\ \end{aligned} \end{aligned}$$
(36)

After simple algebra, the final expression for the first-order breather solution reads

$$\begin{aligned} \begin{aligned} \Phi =&\sqrt{2}e^{\delta _1+i\delta _2}\frac{\cos {\widetilde{\eta }} +\sqrt{\delta _0}\cosh ({\widetilde{\xi }}+{\widetilde{\Delta }} -\delta _1-i\delta _2)}{\cos {\widetilde{\eta }}+\sqrt{\delta _0} \cosh ({\widetilde{\xi }}+{\widetilde{\Delta }})} \\ u=&\frac{2\omega _1^2\sqrt{\delta _0}(\sqrt{\delta _0}+\cos {\widetilde{\eta }} \cosh ({\widetilde{\xi }}+{\widetilde{\Delta }}))}{(\cos {\widetilde{\eta }} +\sqrt{\delta _0}\cosh ({\widetilde{\xi }}+{\widetilde{\Delta }}))^2} \end{aligned} \end{aligned}$$
(37)

with

$$\begin{aligned} \begin{aligned} {\widetilde{\eta }}&=\omega _1 x+\omega _1[(12\lambda _1^2-\omega _1^2) +\frac{4\kappa }{4\lambda _1^2+\omega _1^2}]t,\\ {\widetilde{\xi }}&=-2\lambda _1\omega _1y+\zeta _{0,1},\\ \end{aligned} \end{aligned}$$
(38)

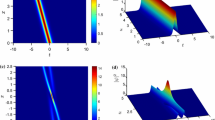
where \(\delta _0=1+\frac{\omega _1^2}{4\lambda _1^2},{\widetilde{\Delta }}=\ln (\frac{1}{\sqrt{\delta _0}}), \delta _1=|\frac{2i\lambda _1+\omega _1}{2i\lambda _1-\omega _1}|,\delta _2=\arg \frac{2i\lambda _1+\omega _1}{2i\lambda _1-\omega _1}\). From the above expression, one can clearly get that \((|\Phi |,u)\rightarrow (\sqrt{2},0)\) when \({\widetilde{\xi }}\rightarrow \pm \infty \). The periodic feature of the one-breather is controlled by \({\widetilde{\eta }}\), and the localized feature of the one-breather is controlled by \({\widetilde{\eta }}\). Hence, it is clear that, in the (x, y)-plane, this one-breather solution is only periodic along x and t, whose corresponding periods are \(\frac{2\pi }{\omega _1}\) and \(\frac{2\pi }{\omega [(12\lambda _1^2-\omega _1^2)+\frac{4\kappa }{4\lambda _1^2+\omega _1^2}]}\), respectively. It should be emphasized that the one breather does not move along y direction as time t propagates. Figure 4 shows an example of that one-breather solution at \(t=0\).

Fig. 4
figure 4

The one-breather solution for the nonlocal Mel’nikov equation (14) at the time \(t=0\) with parameters \(\lambda _1=1,\omega _1=1,\kappa =1,\zeta _{0,1}=0\) (Colour online)

Full size image

The high-order breathers on the constant background could be yielded from Theorem 2 by taking larger \(N=2M\), and other parameters meeting the parametric condition defined in (33). The corresponding solutions consist of M individual breathers, and the M individual breathers interact with each other and would generate interesting curvy wave patterns. For example, with \(M=2\) (i.e., \(N=4\)), the two-breather solution could be derived from Theorem 2:

$$\begin{aligned} \begin{aligned} \Phi =\sqrt{2}\frac{{\overline{g}}_2}{{\overline{f}}_2}, u=({2 \log } {\overline{f}}_2)_{xx}, \end{aligned} \end{aligned}$$
(39)

where functions f and g are

$$\begin{aligned} \begin{aligned}&\overline{f_2}=\begin{vmatrix} \frac{1}{\omega _1e^{\zeta _1}}+\frac{1}{\frac{1}{2}(\omega _1+\omega _1) +i(\lambda _1-\lambda _1)}&\frac{1}{\frac{1}{2}(\omega _1+\omega _2)+i(\lambda _1-\lambda _2)}&\frac{1}{\frac{1}{2}(\omega _1+\omega _3)+i(\lambda _1-\lambda _3)}&\frac{1}{\frac{1}{2}(\omega _1+\omega _4)+i(\lambda _1-\lambda _4)} \\ \frac{1}{\frac{1}{2}(\omega _2+\omega _1)+i(\lambda _2-\lambda _1)}&\frac{1}{\omega _2e^{\zeta _2}}+\frac{1}{\omega _2}&\frac{1}{\frac{1}{2}(\omega _2+\omega _3)+i(\lambda _2-\lambda _3)}&\frac{1}{\frac{1}{2}(\omega _2+\omega _4)+i(\lambda _2-\lambda _4)} \\ \frac{1}{\frac{1}{2}(\omega _3+\omega _1)+i(\lambda _3-\lambda _1)}&\frac{1}{\frac{1}{2}(\omega _3+\omega _2)+i(\lambda _3-\lambda _2)}&\frac{1}{\omega _3e^{\zeta _3}}+\frac{1}{2\omega _3}&\frac{1}{\frac{1}{2}(\omega _3+\omega _4)+i(\lambda _3-\lambda _4)}&\\ \frac{1}{\frac{1}{2}(\omega _4+\omega _1)+i(\lambda _4-\lambda _1)}&\frac{1}{\frac{1}{2}(\omega _4+\omega _2)+i(\lambda _4-\lambda _2)}&\frac{1}{\frac{1}{2}(\omega _4+\omega _3)+i(\lambda _4-\lambda _3)}&\frac{1}{\omega _4e^{\zeta _4}}+\frac{1}{\omega _4}&\end{vmatrix},\\&\overline{g_2}=\begin{vmatrix} \frac{1}{\omega _1e^{\zeta _1}}+{\overline{\omega }}_{11}\frac{1}{\frac{1}{2}(\omega _1 +\omega _1)+i(\lambda _1-\lambda _1)}&{\overline{\omega }}_{12}\frac{1}{\frac{1}{2}(\omega _1+\omega _2)+i(\lambda _1-\lambda _2)}&{\overline{\omega }}_{13}\frac{1}{\frac{1}{2}(\omega _1+\omega _3) +i(\lambda _1-\lambda _3)}&{\overline{\omega }}_{14}\frac{1}{\frac{1}{2}(\omega _1+\omega _4) +i(\lambda _1-\lambda _4)} \\ {\overline{\omega }}_{21}\frac{1}{\frac{1}{2}(\omega _2+\omega _1) +i(\lambda _2-\lambda _1)}&\frac{1}{\omega _2e^{\zeta _2}}+{\overline{\omega }}_{22}\frac{1}{\omega _2}&{\overline{\omega }}_{23}\frac{1}{\frac{1}{2}(\omega _2+\omega _3) +i(\lambda _2-\lambda _3)}&{\overline{\omega }}_{24}\frac{1}{\frac{1}{2}(\omega _2 +\omega _4)+i(\lambda _2-\lambda _4)} \\ {\overline{\omega }}_{31}\frac{1}{\frac{1}{2}(\omega _3+\omega _1) +i(\lambda _3-\lambda _1)}&{\overline{\omega }}_{32}\frac{1}{\frac{1}{2}(\omega _3+\omega _2) +i(\lambda _3-\lambda _2)}&\frac{1}{\omega _3e^{\zeta _3}}+{\overline{\omega }}_{33}\frac{1}{2\omega _3}&{\overline{\omega }}_{34}\frac{1}{\frac{1}{2}(\omega _3+\omega _4) +i(\lambda _3-\lambda _4)}&\\ {\overline{\omega }}_{41}\frac{1}{\frac{1}{2}(\omega _4+\omega _1) +i(\lambda _4-\lambda _1)}&{\overline{\omega }}_{42}\frac{1}{\frac{1}{2}(\omega _4+\omega _2) +i(\lambda _4-\lambda _2)}&{\overline{\omega }}_{43}\frac{1}{\frac{1}{2}(\omega _4+\omega _3) +i(\lambda _4-\lambda _3)}&\frac{1}{\omega _4e^{\zeta _4}}+{\overline{\omega }}_{44}\frac{1}{\omega _4} \end{vmatrix},\\ \end{aligned} \end{aligned}$$
(40)

with

$$\begin{aligned} \zeta _s=&i\omega _s x-2\lambda _s\omega _sy+i\omega _s\left[ \left( 12\lambda _s^2-\omega _s^2\right) \right. \nonumber \\&\left. +\frac{4\kappa }{4\lambda _s^2+\omega _s^2}\right] t+\zeta _{0,s},\nonumber \\ {\overline{\omega }}_{sj}=&-\frac{\omega _s+2i\lambda _s}{\omega _j-2i\lambda _j}, \end{aligned}$$
(41)

for \(s,j=1,2,3,4\), and parameters satisfy

$$\begin{aligned} \begin{aligned} \lambda _3&=-\lambda _1,\lambda _4=-\lambda _2,\omega _3=-\omega _1,\\ \omega _4&=-\omega _2, \zeta _{0,3}=\zeta _{0,1},\zeta _{0,4}=\zeta _{0,2}. \end{aligned} \end{aligned}$$
(42)

According to the analysis for the one-breather solution given by (47), these two breathers do not move along y on the (x, y)-plane as time t alters. To observe the different wave patterns generated from the interaction of the two breathers, we take a fixed value of the parameter \(\zeta _{0,2}\) and different values of \(\zeta _{0,1}\), which give rise to the location of one breather is fixed, and the other breather alters. Hence, one breather moves to the fixed breather and then interacts with each other. In this evolution, different wave patterns could be observed. To clearly observe the interaction wave patterns, we take the following parameter choices

$$\begin{aligned}&\lambda _1{=}1,\lambda _2{=}1,\lambda _3{=}-1,\lambda _4=-1,\omega _1=1,\omega _2=\frac{1}{2}, \nonumber \\&\omega _3=-1,\omega _4=-\frac{1}{2},\kappa =1,\zeta _{0,2}=0. \end{aligned}$$
(43)

We denote the breather determined by \(\zeta _1\) as breather-1 and the other one determined by \(\zeta _2\) as breather-2. Under parameter choices given by (43), the period of breather-2 is two times of the breather-1. Evolution of the interaction between of the two breathers is illustrated in Fig. 5 with different \(\zeta _{0,1}\). When \(\zeta _{0,1}>>0\), the two breathers are far from each other and out of interaction. When \(\zeta _{0,1}\rightarrow 0\), the two breathers are close to each other and begin to interact with each other. Due to the interaction, the period of the breather-2 changes, and the wave structures become periodic triangle patterns (see Fig. 5b). In the intermediate sate of the evolution, the two breathers merge into one breather and form periodic fundamental patterns (see Fig. 5c). At the final state of the evolution, the two breathers separate with each other completely, and the two breathers are out of interaction again (see Fig. 5d).

Fig. 5
figure 5

The two-breather on a constant background for the nonlocal Me’nikov equation (14) with parameters given by (43) and different choices of parameter \(\zeta _{0,2}\): a\(\zeta _{0,1}=-\frac{\pi }{2}\); b\(\zeta _{0,1}=0\); c\(\zeta _{0,1}=0.0174\pi \) and d\(\zeta _{0,1}=\pi \) (Colour online)

Full size image

3.2 Breathers on a PLWs background

To consider the dynamical behaviors of breathers on a PLWs background, we have to give the first-order PLWs solution, which is used to provide the PLWs background. By taking \(N=1\) in formula (31), the first-order periodic line wave solution could be yielded, and the functions f and g read as

$$\begin{aligned} \begin{aligned} f&=1+e^{i\omega _1 x-2\lambda _1\omega _1y+i\omega _1[(12\lambda _1^2-\omega _1^2) +\frac{4\kappa }{4\lambda _1^2+\omega _1^2}]t+\zeta _{0,1}}\\&=1+e^{\zeta _{0,1}-2\lambda _1\omega _1y}\cos \chi -i\sin \chi ,\\ g&=1-\frac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}e^{i\omega _1 x-2\lambda _1\omega _1y+i\omega _1\left[ \left( 12\lambda _1^2-\omega _1^2\right) +\frac{4\kappa }{4\lambda _1^2+\omega _1^2}\right] t+\zeta _{0,1}}, \end{aligned} \end{aligned}$$
(44)

where \(\chi =\omega _1 x+\omega _1[(12\lambda _1^2-\omega _1^2) +\frac{4\kappa }{4\lambda _1^2+\omega _1^2}]t\), and \(c_1,\omega _1,\lambda _1,\zeta _{0,1}\) are arbitrary real parameters. The periodic solution given by (44) is equivalent to the periodic solution defined in (19), and it is singular when \(\lambda _1=0,1>e^{\zeta _{1,0}}\) or \(\lambda _1=0, e^{\zeta _{1,0}}<-1\).

By taking \(N=3\) and the following parameter choices in Theorem  2

$$\begin{aligned} \begin{aligned} \omega _2=-\omega _1,\lambda _2=-\lambda _1,\lambda _3=0, \zeta _{0,2}=\zeta _{0,1}, \end{aligned} \end{aligned}$$
(45)

the one-breather on a PLWs background is obtained

$$\begin{aligned} \begin{aligned} \Phi =\sqrt{2}\frac{g_2}{f_2}, u=({2 \log } f_2)_{xx}, \end{aligned} \end{aligned}$$
(46)

where functions \(f_2\) and \(g_2\) are

$$\begin{aligned} \begin{aligned} \displaystyle f_2=&\begin{vmatrix} \dfrac{1}{\omega _1e^{\zeta _1}}+\dfrac{1}{\omega _1}&\quad \dfrac{1}{2i\lambda _1}&\quad \dfrac{1}{\frac{1}{2}(\omega _1+\omega _3)+i\lambda _1} \\ \dfrac{1}{-2i\lambda _1}&\quad \dfrac{1}{-\omega _1e^{\zeta _1^*}}-\dfrac{1}{\omega _1}&\quad \dfrac{1}{\frac{1}{2}(\omega _2+\omega _3)+i\lambda _2} \\ \dfrac{1}{\frac{1}{2}(\omega _3+\omega _1)-i\lambda _1}&\quad \dfrac{1}{\frac{1}{2}(\omega _3+\omega _2)-i\lambda _2}&\quad \dfrac{1}{\omega _3e^{\zeta _3}}+\dfrac{1}{\omega _3} \end{vmatrix},\\ \displaystyle g_2=&\begin{vmatrix} \dfrac{1}{\omega _1e^{\zeta _1}}-\dfrac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\dfrac{1}{\omega _1}&\dfrac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\dfrac{1}{ 2i\lambda _1}&-\dfrac{\omega _1+2i\lambda _1}{\omega _3}\dfrac{1}{\frac{1}{2}(\omega _1 +\omega _3)+i\lambda _1} \\ -\dfrac{\omega _1+2i\lambda _1}{\omega _1-2i\lambda _1}\dfrac{1}{2i\lambda _1}&-\dfrac{1}{\omega _1e^{\zeta _1^*}}+\dfrac{\omega _1+2i\lambda _1}{\omega _1 -2i\lambda _1}\dfrac{1}{\omega _1}&-\dfrac{\omega _2+2i\lambda _2}{\omega _3}\dfrac{1}{\frac{1}{2}(\omega _2+\omega _3) +i\lambda _2}&\\ -\dfrac{\omega _3}{\omega _1-2i\lambda _1}\dfrac{1}{\frac{1}{2}(\omega _3+\omega _1) -i\lambda _1}&-\dfrac{\omega _3}{\omega _2-2i\lambda _2}\dfrac{1}{\frac{1}{2}(\omega _3+\omega _2) -i\lambda _2}&\dfrac{1}{\omega _3e^{\zeta _3}}-\frac{1}{\omega _3} \end{vmatrix}, \end{aligned} \end{aligned}$$
(47)

and

$$\begin{aligned} \begin{aligned} \zeta _1=&i\omega _1 x-2\lambda _1\omega _1y+i\omega _1\left[ \left( 12\lambda _1^2-\omega _1^2\right) \right. \\&\left. +\frac{4\kappa }{4\lambda _1^2+\omega _1^2}\right] t+\zeta _{0,1},\\ \zeta _3=&i\omega _3 x+i\omega _3\left( -\omega _3^2+\frac{4\kappa }{ \omega _3^2}\right) t +\zeta _{0,3}. \end{aligned} \end{aligned}$$
(48)

This solution is a combination of the one-breather solution in (47) and the first-order PLWs solution in (44). According to the analysis for these two solutions, the solution given by (46) still keeps periodic along x and t, and localized along y. Besides, since these two periodic solutions are also periodic along time t, the breather would be fixed on the PLWs background as time changes in the (x, y)-plane. However, the location of the breather can be controlled by the parameter \(\zeta _{0,3}\). Figure 6 shows the dynamics of the one-breather on the PLWs background with different values of \(\zeta _{0,3}\). It is directly to obtain that the shape, velocity and amplitude of the one breather do not alter when its location changes; hence, the collision between the one-breather and the PLWs is elastic collision.

Fig. 6
figure 6

The one-breather on a PLWs background in the nonlocal MK equation (14) at the time \(t=0\) with \(\lambda _1=1,\lambda _3=0,\omega _1=1,\omega _3=2, \kappa =1,\zeta _{0,3}=-\frac{\pi }{2}\): a\(\zeta _{0,1}=-\pi \); b\(\zeta _{0,1}=0\); and c\(\zeta _{0,1}=\pi \) (Colour online)

Full size image
Fig. 7
figure 7

The two-breather on a PLWs background for the nonlocal Me’nikov equation (14) at the time \(t=0\) with parameters \(\lambda _1=1,\lambda _2=1,\lambda _3=-1,\lambda _4=-1,\lambda _=0,\omega _1=1,\omega _2=\frac{1}{2}, \omega _3=-1,\omega _4=-\frac{1}{2},\omega _5=1,\kappa =1,\zeta _{0,2}=\zeta _{0,1},\zeta _{0,3}=0,\zeta _{0,4}=0,\zeta _{0,5}=-\frac{4}{5}\pi \), and different values of parameter \(\zeta _{0,1}\): a\(\zeta _{0,1}=-5\pi \); b\(\zeta _{0,1}=-3\pi \); c\(\zeta _{0,1}=-\pi \); d\(\zeta _{0,1}=\frac{\pi }{2}\); e\(\zeta _{0,1}=\pi \) and f\(\zeta _{0,1}=3\pi \) (Colour online)

Full size image

In what follows, we consider the high-order breathers on a PLWs background. The M-breather on a PLWs background can be generated from Theorem 2 with \(N=2M+1\) and other parameters satisfying the parameters condition (34). For instance, with \(N=5\) and

$$\begin{aligned} \begin{aligned} \lambda _3&=-\lambda _1,\lambda _4=-\lambda _2,\lambda _5=0, \omega _3=-\omega _1,\omega _4\\&=-\omega _2, \zeta _{0,3}=\zeta _{0,1},\zeta _{0,4}=\zeta _{0,2}, \end{aligned} \end{aligned}$$
(49)

the two breathers on a PLWs background would be generated, and Fig. 7 shows the dynamical features of that mixed solutions. In order to compare the two-breather on the PLWs background with the two-breather on the constant background shown in Fig. 5, we take the same parameter choices in Fig. 7 as the parameter choices in Fig. 5 except the value of \(\zeta _{0,1}\). Here, the parameter \(\zeta _{0,1}\) is used to control the distance between the two breathers. As can be seen from Fig. 7, when the breather moves toward to the fixed breather, the wave patterns of the two breathers range from two usual breathers (see Fig. 7a) to triangular patterns (see Fig. 7b, c), then to fundamental patterns (see Fig. 7d), and to triangular patterns again (see Fig. 7e), and finally to two usual breathers (see Fig. 7f).

4 Summary and discussion

In this paper, we mainly consider dynamics of line solitons and breathers on a PLWs background in the nonlocal MK equation (14). These dynamical behaviors are described by two families of mixed solutions: one consists of line solitons and PLWs, and the other one comprises breathers and PLWs. These two families of mixed solutions are derived by constraining two different parametric conditions of tau functions of the KP hierarchy. For the general line solitons on a PLWs background, the SW component \(|\Phi |\) possesses five different wave patterns in the simplest (first-order) solutions: two-antidark-soliton on a PLWs background, one-antidark-soliton and one-dark-soliton on a PLWs background, two-dark-soliton on the PLWs background, a degenerated two-dark-soliton, a degenerated two-antidark-soliton (see Fig. 2a–e), while the LW component |u| only displays the two-antidark-soliton on a PLWs background (see Fig. 2f). The high-order mixed solutions demonstrate more line solitons on the PLWs background, which shows the features of superposition of several individual first-order mixed solutions (see Fig. 3). For the breathers on a PLWs background, both of SW component \(|\Phi |\) and LW component |u| only display one type of breather on a PLWs background, namely bright breather on a PLWs background. Besides, the breathers on a constant background can also be reduced from the breathers on a PLWs background under particular parametric conditions.

By comparing with the solutions containing line solitons and breathers to the nonlocal MK equation (14) discussed in Refs. [51, 52], the solutions investigated in the present paper can be summarized as follows:

  • The line solitons on PLWs background to the nonlocal MK equation (14) and their dynamical features are investigated in detail in this paper, while under investigation in Ref. [52] is the line solitons on a constant background. Besides, the patterns of the two-line-soliton are classified according to the asymptotic analysis.

  • The breathers on a constant or PLWs background were also reported in Ref. [51]. However, we construct these solutions by employing the KP hierarchy reduction method in the present paper, and these solutions are presented by Gram-type determinants. In Ref. [51], these solutions were constructed by employing the Hirota’s direct method with perturbation expansion, and these solutions are expressed by complicated algebraic formulae.

  • We have constructed more periodic solutions to the nonlocal MK equation, which have not been reported before.

Since rational and semi-rational solutions can be derived from periodic solutions by using the long wave limit technique, a natural extension of the present work could be constructed rational and semi-rational solutions for the nonlocal MK equation (14) by taking a long wave limit of the periodic solutions given in Theorem 2. The rational solutions would demonstrate lumps on a background of PLWs or constant, and the semi-rational solutions show a mixture of lumps, breathers and line solitons on a PLWs or constant background. We would continue to explore this interesting topic for the MK equation (14).