1 Introduction

The nonlinear Schrödinger equation [1, 2] (NLSE) has various applications in describing ocean waves [3,4,5], pulses in optical fibres [6,7,8], Bose–Einstein condensates [9,10,11,12], waves in the atmosphere [13], plasma [14] and many other physical systems [15,16,17,18,19]. Various extensions of the NLSE have been considered [20,21,22,23,24] that increase the accuracy of the description of nonlinear wave phenomena in these systems by incorporating higher-order effects [25,26,27,28]. Higher-order terms in these extensions are responsible for linear dispersion, as well as nonlinear effects such as self-phase modulation, pulse self-steepening and the Raman effect [7, 29]. These higher-order terms are important in nonlinear optics [30, 31], ocean wave dynamics [32,33,34] and especially in modelling high-amplitude rogue wave phenomena [35,36,37]. Two comprehensive reviews in the area of rogue waves and other nonlinear wave structures can be found in [38, 39].

Adding higher-order terms generally results in the loss of integrability of the resulting equation. This means that exact solutions cannot be written in analytical form, making the treatment more complicated. However, a special choice of the higher-order operators in these extensions allows us to keep the integrability. The power of using these operators consists in the possibility of applying arbitrary real coefficients to each of these operators, thus significantly extending the range of physical problems that can be solved in exact form. It was found that the NLSE can be extended to arbitrarily high orders of these operators [40,41,42], and these operators have been explicitly presented up to eighth order [41]. Using their recurrence relations, they can be calculated to any order, although the explicit form quickly becomes cumbersome. Nevertheless, there are no conceptual difficulties in construction of these equations. Moreover, infinitely many terms can be considered when finding solutions of these equations.

Presently, there are two sets of these operators that can be used for infinite-order extensions of the NLSE. We call them the class I [40,41,42] and class II [43, 44] infinite extensions of the NLSE [45]. The presence of two independent extensions enables the more accurate description of physical problems with greater flexibility. Here, we deal exclusively with the class I extension. The class II extension is more involved and will be left beyond the scope of the present work.

In this paper, we find 2-breather solutions of the class I infinitely extended NLSE equation. These are multi-parameter solutions that involve both the free parameters of the equation and free parameters of the solution, which together control the features of the two breather components, such as their localisation, propagation, and their relative position and frequencies. The presence of an infinite number of free parameters allows us to consider many particular cases, such as breather-to-soliton conversion, which is exclusive to higher-order extensions of the basic equation.

We also derive several limiting cases, the most important one of which is the general second-order rogue wave solution, a particular case of the 2-breather collision. However, only a limited number of special cases can be given in the frame of a single manuscript. We leave others for future work in this direction.

2 The class I infinitely extended NLSE

First, we give a brief exposition of the class I infinitely extended nonlinear Schrödinger equation. It is the integrable equation written in general form [40, 41]

$$\begin{aligned} i\psi _x+F(\psi ,\psi ^*)=0, \end{aligned}$$
(1)

where the operator \(F(\psi ,\psi ^*)\) is defined through

$$\begin{aligned} F=\sum _{n=1}^{\infty }(\alpha _{2n}K_{2n}-i\alpha _{2n+1}K_{2n+1}), \end{aligned}$$
(2)

with the operators \(K_n\) defined recursively by the integrals of the nonlinear Schrödinger equation [40], and where each coefficient \(\alpha _n\) is an arbitrary real number; that is,

$$\begin{aligned} K_n(\psi ,\psi ^*)=(-1)^n\frac{\delta }{\delta \psi ^*}\int p_{n+1}\mathrm{d}t, \end{aligned}$$

where \(p_n\) is the nth integral of the basic nonlinear Schrödinger equation and \(p_{n+1}\) can be defined recursively as

$$\begin{aligned} p_{n+1}=\psi \frac{\partial }{\partial t}\left( \frac{p_n}{\psi }\right) +\sum _{r=1}^{n}p_{n-r}p_r,~p_1=|\psi |^2. \end{aligned}$$

The four lowest-order operators \(K_n\)\((n=2,3,4,5)\) derived in this way are:

$$\begin{aligned} K_2(\psi ,\psi ^*)= & {} \psi _{tt}+2|\psi |^2\psi , \nonumber \\ K_3(\psi ,\psi ^*)= & {} \psi _{ttt}+6|\psi |^2\psi _t , \nonumber \\ K_4(\psi ,\psi ^*)= & {} \psi _{tttt}+8|\psi |^2\psi _{tt}+6|\psi |^4\psi \nonumber \\&+\,4\psi |\psi _t|^2+6\psi _t^2\psi ^*+2\psi ^2\psi ^*_{tt}. \nonumber \\ K_5(\psi ,\psi ^*)= & {} \psi _{ttttt} +10|\psi |^2 \psi _{ttt}+10(\psi \,|\psi _{t}|^2)_t \nonumber \\&+\,20 \psi ^* \psi _t \psi _{tt}+30|\psi |^4\psi _t. \end{aligned}$$
(3)

A few others can be found in [42]. The operators \(K_n\) involve linear terms with derivatives of order n,  and nonlinear terms involving t-derivatives of the function \(\psi \) and its complex conjugate \(\psi ^*\).

As already mentioned, the numbers \(\alpha _n\) can take any values whatsoever and do not need to be viewed as representing small perturbations for Eq. (1) to be completely integrable. This allows us to find solutions for which any order of dispersion can be taken into account without the need for approximation or numerical techniques. This extension substantially widens the range of applicability of the NLSE for solving nonlinear wave evolution problems.

When only \(\alpha _2\ne 0,\) we have the fundamental, or ‘basic’ nonlinear Schrödinger equation:

$$\begin{aligned}&i\psi _x+\alpha _{2}K_2(\psi ,\psi ^*)=i\psi _x+\alpha _{2}(\psi _{tt}\nonumber \\&\quad +\,2|\psi |^2\psi )=0, \end{aligned}$$
(4)

which includes the lowest-order dispersion and self-phase modulation terms. Further, if only \(\alpha _2\) and \(\alpha _3\) are nonzero, we have the integrable Hirota equation [46]:

$$\begin{aligned}&i\psi _x+\alpha _{2}(\psi _{tt}+2|\psi |^2\psi )-i\alpha _3(\psi _{ttt}\nonumber \\&\quad +\,6|\psi |^2\psi _t)=0. \end{aligned}$$
(5)

Adding the fourth-order operator, \(K_4,\) into Eq. (5), gives the Lakshmanan–Porsezian–Daniel (LPD) equation [47, 48], and so on.

Again, the coefficients \(\alpha _n\) are finite and arbitrary. However, physical applications, in general, require dispersive effects to decrease rapidly in strength with increasing order n. Convergence will thus not be an issue in practice for series involving \(\alpha _n,\) and we will therefore be comfortable leaving the operator F for the whole equation (1), as well as any other associated parameters, in the form of an infinite series when necessary.

While the operators \(K_n\) in (3) rapidly become more complicated and the resulting differential equation of order n becomes much harder to solve, exact solutions can be found explicitly by using already known solutions to the NLSE as a guide, and a large class of breather and soliton solutions are already known [41, 42]. In previous works [41, 42], we have seen that the effect of nonzero odd order operators is to transform t as \(t\mapsto t+vx\) with v being a function of all coefficients \(\alpha _{2n+1}\). The effect of the nonzero even order operators is to transform x as \(x\mapsto Bx,\) with B being a function of the parameters \(\alpha _{2n}\).

In this work, we extend this approach to a general family of second-order solutions, so we introduce parameters \(B_1\) and \(B_2,\) and \(v_1\) and \(v_2\), to play an analogous role for the two distinct breather components. This enables us to generalise the 2-breather to the infinite extension of the NLSE, and we now proceed to the analysis of these solutions.

3 The 2-breather solution

Higher analogues of the Akhmediev breathers can be obtained through iterations of the Darboux transformation [49, 50]. After transforming the plane wave solution \(e^{ix}\) with a Darboux transformation, with an eigenvalue \(\lambda \) such that \(\lambda ^2\ne -1,\) and carrying out this transformation twice, we get the 2-breather solution to the basic NLSE. This can then be generalised to the 2-breather solution of the extended equation. The general 2-breather solution is of the form

$$\begin{aligned} \psi (x,t)=\left\{ 1+\frac{G(x,t)+iH(x,t)}{D(x,t)}\right\} e^{i\phi x}, \end{aligned}$$
(6)

where

$$\begin{aligned} G(x,t)= & {} -(\kappa _1^{\;2}-\kappa _2^{\;2})\bigg \{\frac{\kappa _1^{\;2}\delta _2}{\kappa _2} \cosh \delta _1B_1x\cos \kappa _2t_2 \nonumber \\&-\,\frac{\kappa _2^{\;2}\delta _1}{\kappa _1}\cosh \delta _2B_2x\cos \kappa _1t_1 \nonumber \\&-\,(\kappa _1^{\;2}-\kappa _2^{\;2})\cosh \delta _1B_1x\cosh \delta _2B_2x\bigg \},\nonumber \\ \end{aligned}$$
(7)
$$\begin{aligned} H(x,t)= & {} -2(\kappa _1^{\;2}-\kappa _2^{\;2})\bigg \{\frac{\delta _1\delta _2}{\kappa _2} \sinh \delta _1B_1x\cos \kappa _2t_2 \nonumber \\&-\,\frac{\delta _1\delta _2}{\kappa _1}\sinh \delta _2B_2x\cos \kappa _1t_1 \nonumber \\&-\,\delta _1\sinh \delta _1B_1x\cosh \delta _2B_2x \nonumber \\&+\,\delta _2\cosh \delta _1B_1x\sinh \delta _2B_2x\bigg \}, \end{aligned}$$
(8)
$$\begin{aligned} D(x,t)= & {} 2(\kappa _1^{\;2}+\kappa _2^{\;2})\frac{\delta _1\delta _2}{\kappa _1\kappa _2}\cos \kappa _1t_1\cos \kappa _2t_2 \nonumber \\&+\,4\delta _1\delta _2(\sinh \delta _1B_1x\sinh \delta _2B_2x\nonumber \\&+\,\sin \kappa _1t_1\sin \kappa _2t_2)-(2\kappa _1^{\;2}-\kappa _1^{\;2}\kappa _2^{\;2}\nonumber \\&+\,\kappa _2^{\;2}) \cosh \delta _1B_1x\cosh \delta _2B_2x \nonumber \\&-\,2(\kappa _1^{\;2}-\kappa _2^{\;2})\bigg \{\frac{\delta _1}{\kappa _1} \cosh \delta _2B_2x\cos \kappa _1t_1 \nonumber \\&-\, \frac{\delta _2}{\kappa _2}\cosh \delta _1B_1x\cos \kappa _2t_2\bigg \}, \end{aligned}$$
(9)

Here \(\kappa _1\) and \(\kappa _2\) are the modulation parameters,

$$\begin{aligned} \delta _m=\tfrac{1}{2}\kappa _m\sqrt{4-\kappa _m^{\;2}} \end{aligned}$$

is the growth rate of the modulational instability for each breather component, and the shorthand notation \(t_m\) indicates \(t_m=t+v_mx\) for \(m=1,2.\) Note that whenever \(t_m\) appears, we have ignored a constant of integration, and we have also done the same whenever \(\delta _mB_mx\) appears. The most general solution allows for the replacements \(t_m\mapsto t_m-T_m\), and \(\delta _mB_mx\mapsto \delta _mB_m(x-X_m),\) where \(T_m\) and \(X_m\) are real constants which determine relative positions along the axes of t and x,  respectively, which we might include to incorporate a time delay in one breather component, for instance. For the time being, we set these constants to be both zero without substantial loss, to address their significance later.

The phase factor \(\phi \) is independent of the modulation, since this part has no physical effect on the modulation when it is real, and here it takes the same real value as it does for the plane wave solution, i.e.

$$\begin{aligned} \phi =\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) \alpha _{2n}. \end{aligned}$$
(10)

The values \(B_m\) determine the modulation frequency of each component, and the parameters \(v_m,\) although they cannot be considered velocities in the usual sense, introduce a tilt to \(|\psi |\) relative to the axes of x and t. They are given explicitly by

$$\begin{aligned} B_m&=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) nF\left( 1-n,1;\tfrac{3}{2};\tfrac{1}{4}\kappa _m^{\;2}\right) \alpha _{2n}, \end{aligned}$$
(11)
$$\begin{aligned} v_m&=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)F\left( -n,1;\tfrac{3}{2};\tfrac{1}{4}\kappa _m^{\;2}\right) \alpha _{2n+1}, \end{aligned}$$
(12)

with \(m=1,2,\) where F(a, b; c; z) is the Gaussian hypergeometric function. Note that there is a simple relationship between \(v_m\) and \(B_m\): The coefficient of \(\alpha _{2n}\) in \(B_m\) is twice the coefficient of \(\alpha _{2n-1}\) in \(v_m.\) The first two terms of \(B_m\) for the two-breather solution have been previously given in [51]. Our new solution extends these coefficients to arbitrary orders of dispersion and nonlinearity.

Fig. 1
figure 1

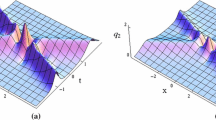
The 2-breather solution (6) of Eq. (1). The modulation parameters are at a ratio \(\kappa _1:\kappa _2=1:2\). Parameters of the equation are: \(\alpha _2=\tfrac{1}{2},\)\(\alpha _3=\tfrac{1}{6},\)\(\alpha _4=\tfrac{1}{24},\)\(\alpha _5=\tfrac{1}{30},\)\(\alpha _6=\tfrac{1}{144},\) with all higher \(\alpha _n=0.\) The wave profile is tilted in the (x, t)-plane due to the nonzero \(v_m\)

Full size image

Also notice that the parameters are the same functions of \(\kappa _m,\) for both \(m=1,2.\) This is at least suggested by symmetry. If two successive Darboux transformations generate a 2-breather solution, then there must be two independent eigenvalues, corresponding to two independent modulation parameters. Physically, we could reason that there should be no way of knowing which breather component is which, so the order in which each component was generated by Darboux transformation should be equally irrelevant. If so, it should then follow that \(B_1\) is the same function of \(\kappa _1\) as \(B_2\) is of \(\kappa _2,\) and similar for \(v_1\) and \(v_2\), and this would also imply that \(B_m\) and \(v_m\) are the same functions as for the single-breather solution, which are already known [42]. It is worth considering whether this property extends to the general n-breather solution: i.e. whether, in general, we can find \(B_1,\dots ,B_n\) and \(v_1,\dots ,v_n\) which are the same functions of their respective modulation parameters \(\kappa _1,\dots ,\kappa _n,\) but we do not answer this question here (Fig. 1).

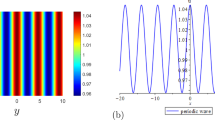
The growth rate \(\delta _m\) in both components will be real when \(\kappa _m\) is real, but the eigenvalues of the Darboux transformation are free to take any complex value at all, although the transformations are trivial when the eigenvalues are real, and thus so are the modulation parameters. Real-valued modulation parameters correspond to Akhmediev breathers, whereas imaginary-valued modulation parameters correspond to Kuznetsov–Ma solitons, the functional form of the breathers being otherwise equivalent. An example which shows the difference between real and imaginary modulation parameters is given in Fig. 2. In Fig. 3, we give an example of the effects of altering the ratio of the modulation of the two components.

Fig. 2
figure 2

A collision between an Akhmediev breather and Kuznetsov–Ma soliton, with \(\kappa _1=1,\) and \(\kappa _2=i.\) Here \(\alpha _n=1/n!\) up to \(n=8,\) with all higher \(\alpha _n=0\)

Full size image
Fig. 3
figure 3

The 2-breather solution with \(\alpha _n=1/n!\) up to \(n=8,\) with all higher \(\alpha _n=0,\) but now with \(\kappa _1=\tfrac{3}{2},\) and \(\kappa _2=1\)

Full size image

4 Breather-to-soliton conversion

If we choose parameters \(\alpha _n\) such that \(B_m=0,\) the 2-breather solution may then behave in a way which is unique to the extension of the nonlinear Schrödinger equation [51], in the sense that it is only when higher orders of dispersion and nonlinearity are accounted for that it is possible to take \(B_m=0\) without obtaining a trivial or otherwise degenerate solution.

For example, if we choose \(\alpha _2\) such that \(B_2=0\) for all \(\kappa _2,\) then writing \(B_1=B,\) it is easy to show that B must take the value

$$\begin{aligned} B=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n+2\\ n+1\end{array}}\right) (n+1)E \left( -n,1;\tfrac{3}{2};\tfrac{1}{4}\kappa _1^{\;2}|\tfrac{1}{4}\kappa _2^{\;2} \right) \alpha _{2n+2}, \end{aligned}$$

where we define the function E as the difference of hypergeometric functions:

$$\begin{aligned} E(a,b;c;z_1|z_2)=F(a,b;c;z_1)-F(a,b;c;z_2). \end{aligned}$$

We can then simplify the general 2-breather solution considerably. We obtain

$$\begin{aligned} G(x,t)&=(\kappa _1^{\;2}-\kappa _2^{\;2})\bigg \{\frac{\kappa _1^{\;2} \delta _2}{\kappa _2}\cosh \delta _1Bx\cos \kappa _2t_2 \nonumber \\&\quad -\frac{\kappa _2^{\;2}\delta _1}{\kappa _1}\cos \kappa _1t_1 -(\kappa _1^{\;2}-\kappa _2^{\;2})\cosh \delta _1Bx\bigg \}, \nonumber \\ H(x,t)&=2\delta _1(\kappa _1^{\;2}-\kappa _2^{\;2})\sinh \delta _1Bx \bigg (1-\frac{\delta _2}{\kappa _2}\cos \kappa _2t_2\bigg ), \nonumber \\ D(x,t)&=2(\kappa _1^{\;2}+\kappa _2^{\;2})\frac{\delta _1\delta _2}{\kappa _1\kappa _2}\cos \kappa _1t_1\cos \kappa _2t_2 \nonumber \\&\quad +\,4\delta _1\delta _2\sin \kappa _1t_1\sin \kappa _2t_2 \nonumber \\&\quad -\,(2\kappa _1^{\;2}-\kappa _1^{\;2}\kappa _2^{\;2}+\kappa _2^{\;2}) \cosh \delta _1Bx \nonumber \\&\quad -\,2(\kappa _1^{\;2}-\kappa _2^{\;2})\bigg (\frac{\delta _1}{\kappa _1} \cos \kappa _1t_1 \nonumber \\&\quad -\,\frac{\delta _2}{\kappa _2}\cosh \delta _1Bx\cos \kappa _2t_2\bigg ). \end{aligned}$$
(13)

An example of this solution is given in Fig. 4. The difference of this solution from the one shown in Fig. 1 is that the wave profiles at \(x\rightarrow \pm \infty \) are not plane waves. The periodic set of tails from each breather maximum extends to infinity, reminiscent of periodically repeating solitons. This is the phenomenon that is known as breather-to-soliton conversion [51]. Clearly, these ‘solitons’ do not have a separate spectral parameter related to them.

Fig. 4
figure 4

A wave profile of a ‘breather-to-soliton conversion.’ We use the same set of parameters as in Fig. 3, except \(\alpha _2\) is now chosen such that \(B_2=0.\) This choice extends to infinity the tails of the breathers that would otherwise decay

Full size image

5 The 2-breather solution in the semirational limit

When one of the modulation parameters, say \(\kappa _2,\) tends to zero, we obtain the semirational limit, i.e. a solution obtained as a combination of polynomials and circular or hyperbolic functions. Then, writing \(\kappa \) for \(\kappa _1\), and \(\delta \) for \(\delta _1,\) the functions G, H, and D become

$$\begin{aligned} G(x,t)= & {} \tfrac{1}{8}\kappa ^2\{\kappa ^2(1+4t_2^{\;2}+4B_2^{\;2}x^2)-1\}\cosh \delta B_1x \nonumber \\&+\,\kappa \delta \cos \kappa t_1,\nonumber \\ H(x,t)= & {} 2\kappa B_2x(\delta \cos \kappa t_1-\kappa \cosh \delta B_1x) \nonumber \\&+\,\tfrac{1}{4}\delta \kappa ^2(1+4t_2^{\;2}+4B_2^{\;2}x^2)\sinh \delta B_1x\nonumber \\ D(x,t)= & {} \frac{\delta }{\kappa }\{4-\tfrac{1}{4}\kappa ^2(1+4t_2^{\;2}+4B_2^{\;2}x^2)\} \cos \kappa t_1 \nonumber \\&+\,4\delta B_2x\sinh \delta B_1x+\delta t_2\sin \kappa t_1 \nonumber \\&-\,\{4+\tfrac{1}{4}\kappa ^2(1+4t_2^{\;2}+4B_2^{\;2}x^2)\}\cosh \delta B_1x,\nonumber \\ \end{aligned}$$
(14)

and the parameters \(B_2\) and \(v_2\) are reduced to

$$\begin{aligned} B_2=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) n\alpha _{2n}, \end{aligned}$$
(15)

and

$$\begin{aligned} v_2=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)\alpha _{2n+1}. \end{aligned}$$
(16)

This semirational 2-breather solution is a superposition of a Peregrine solution with the Akhmediev breather, since taking the limit \(\kappa _2\rightarrow 0\) reduces the frequency of one of the breathers to zero, meaning that it is transformed to a Peregrine solution. A plot of this solution is shown in Fig. 5. Here, the central feature is roughly the second-order rogue wave while the peaks away from the origin belong to the remaining first-order breather.

Fig. 5
figure 5

The 2-breather solution in the semirational limit. Here the nonzero modulation parameter is \(\kappa =1,\) with \(\alpha _n\) the same as in Fig. 1. It can be considered as a superposition of the Akhmediev breather with the Peregrine solution

Full size image

6 The degenerate two-breather limit

If both eigenvalues of the Darboux transformation are taken to be equal, so that both modulation parameters \(\kappa _m\) are also equal, we obtain the case of degenerate breathers. Direct calculations provide no solution. In this case, one modulation parameter should instead be taken as a small perturbation from the other, say \(|\kappa _1-\kappa _2|=\varepsilon .\) Then, we take the limit as the perturbation \(\varepsilon \) becomes arbitrarily small, so that the solution remains well defined at all times. Namely, if we put \(\kappa _1=\kappa ,\) and \(\kappa _2=\kappa +\varepsilon ,\) we have

$$\begin{aligned} B_2=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) nF(1-n,1;\tfrac{3}{2};\tfrac{1}{4} (\kappa +\varepsilon )^2)\alpha _{2n}, \end{aligned}$$

and

$$\begin{aligned} v_2=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)F(-n,1;\tfrac{3}{2};\tfrac{1}{4} (\kappa +\varepsilon )^2)\alpha _{2n+1}. \end{aligned}$$

Next, recalling the identity

$$\begin{aligned} \frac{d}{\mathrm{d}z}F(a,b;c;z)=\frac{ab}{c}F(a+1,b+1;c+1;z) \end{aligned}$$

take the Maclaurin series of G(x, t), H(x, t) and D(x, t) with respect to \(\varepsilon .\) In the limit as \(\varepsilon \rightarrow 0,\) the ratio of these series will be a well-defined solution with equal eigenvalues; it is thus sufficient to consider only the lowest-order non-vanishing terms in the series expansion for D(x, t) in \(\varepsilon ,\) which in this case happen to be the coefficients of \(\varepsilon ^2\). By this method, we obtain the degenerate 2-breather solution in form (6) with

$$\begin{aligned} G(x,t)= & {} 2\kappa ^2\bigg [1+\cosh 2\delta Bx+\bigg \{\bigg (\kappa B-\frac{2\delta ^2}{\kappa }B \nonumber \\&-\,\delta ^2B'\bigg )x\sinh \delta Bx \nonumber \\&-\,\frac{\kappa }{\delta }\left( 1-\frac{\delta ^2}{\kappa ^2}\right) \cosh \delta Bx\bigg \}\cos \kappa (t+vx) \nonumber \\&-\,\{t+(v+\kappa v')x\}\delta \cosh \delta Bx\sin \kappa (t+vx)\bigg ], \nonumber \\ H(x,t)= & {} 2\kappa \bigg [\left\{ \left( \frac{2\delta ^2}{\kappa ^2}-1\right) \kappa B+2\delta ^2B'\right\} x \nonumber \\&+\,\tfrac{1}{2}\delta \bigg \{\tfrac{1}{2}\left( \frac{2\delta ^2}{\kappa ^2} -1\right) Bx-\frac{\delta ^2}{\kappa }B'\bigg \}x\cosh \delta Bx \nonumber \\&\,\times \cos \kappa (t+vx)+\frac{\kappa }{\delta }\bigg (\frac{2\delta ^2}{\kappa ^2}-1\bigg )\sinh 2\delta Bx \nonumber \\&-\,\delta ^2\sinh \delta Bx\{\cos \kappa (t+vx) \nonumber \\&+\,\kappa \sin \kappa (t+vx)\} \{t+(v+\kappa v')x\}\bigg ]\nonumber , \\ D(x,t)= & {} \frac{\kappa ^2}{32\delta ^2}\bigg [-8\kappa ^2\left( 1+\frac{\delta ^2}{\kappa ^2}\right) -\frac{64\delta ^4}{\kappa ^2}(t+vx)^2 \nonumber \\&-\,64\delta ^2\bigg (1-\frac{2\delta ^2}{\kappa ^2}\bigg )^2B^2x^2-32\cosh 2\delta Bx \nonumber \\&-\,\frac{128\delta ^2}{\kappa }\bigg \{\bigg (2-\frac{4\delta ^2}{\kappa ^2} \bigg )B-\frac{\delta ^2}{\kappa }B'\bigg \}x\sinh \delta Bx\nonumber \\&\,\times \cos \kappa (t+vx)-32\delta \bigg \{\kappa \cos \kappa (t+vx) \nonumber \\&+\,\frac{4\delta ^2}{\kappa ^2}\{t+(v+\kappa v')x\}\sin \kappa (t+vx)\bigg \}\nonumber \\&\,\cosh \delta Bx+ \frac{16\delta ^2}{\kappa ^2}\bigg \{2\cos 2\kappa (t+vx)\nonumber \\&+\,\bigg (8\bigg (1-\frac{2\delta ^2}{\kappa ^2}\bigg )\kappa BB'x \nonumber \\&-\,4\delta ^2B'^2\bigg )\kappa ^2x-4v'\{2t+(v+\kappa v')x\}\bigg )\bigg \}\bigg ],\nonumber \\ \end{aligned}$$
(17)

where \(B=B_1\) and we use \(B'\) and \(v'\) to denote the partial derivatives of \(B_2\) and \(v_2\) with respect to \(\varepsilon \) evaluated at the point \(\varepsilon =0,\) i.e. when \(\kappa _2\rightarrow \kappa .\) That is,

$$\begin{aligned} B'=\tfrac{1}{3}\kappa \sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) n(1-n)F(2-n,2; \tfrac{5}{2};\tfrac{1}{4}\kappa ^2)\alpha _{2n}, \end{aligned}$$

and

$$\begin{aligned} v'=-\tfrac{1}{3}\kappa \sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)nF(1-n,2; \tfrac{5}{2};\tfrac{1}{4}\kappa ^2)\alpha _{2n+1}, \end{aligned}$$

etc. We drop the subscripts due to the fact that as \(\varepsilon \rightarrow 0\) both modulation parameters take equal values anyway. A plot of this solution is given in Fig. 6.

Fig. 6
figure 6

The degenerate 2-breather solution. We take the set of \(\alpha _n\) the same as in Fig. 1, and the modulation parameters \(\kappa _1=\kappa _2=\tfrac{1}{2}.\) The two breathers collide with the high peak at the origin due to the synchronised phases

Full size image

The degenerate breather solution is a one-parameter family of solutions which represents the collision of two breathers with the same modulation parameter \(\kappa \), or, equivalently, with equal frequencies. It can be considered a generalisation of the known 2-soliton solution for the class I extension of the nonlinear Schrödinger equation [52].

7 Second-order rogue wave solution

When the frequency of the degenerate breather tends to zero, the spacing between the successive peaks in Fig. 6 becomes infinitely large, pushing them out to infinity. What remains at the origin is the second-order rogue wave. In order to derive this solution, we take the limit \(\kappa \rightarrow 0\) in expressions (17). However, calculations show that this limit cannot be found directly. In order to find it, we repeatedly apply l’Hôpital’s rule to the degenerate breather solution as \(\kappa \rightarrow 0\). The derivatives of G,  H,  and D with respect to \(\kappa \) at the point \(\kappa =0\) vanish up to \(O(\varepsilon ^6)\). The resulting functions G, H,  and D become polynomials:

$$\begin{aligned} G(x,t)&=12\{-3+24(3B^2-BB''-vv'')x^2 \nonumber \\&\quad +\,80B^4x^4-192v''xt+96B^2x^2(t+vx)^2 \nonumber \\&\quad +\,24(t+vx)^2+16(t+vx)^4\}, \end{aligned}$$
(18)
$$\begin{aligned} H(x,t)&=576B''x+2304B''x(t+vx)^2-24Bx\{15 \nonumber \\&\quad -\,8(B+16B'')Bx^2-16B^4x^4 \nonumber \\&\quad +\,192v''x(t+vx)-32B^2x^2(t+vx)^2 \nonumber \\\,&\quad +\,24(t+vx)^2-16(t+vx)^4\}, \end{aligned}$$
(19)
$$\begin{aligned} D(x,t)&=-\,9-36\{11B^2-48BB''+64B''^2 \nonumber \\&\quad -\,16(v-v'')v''\}x^2-48\{9B^4-6B^2v^2 \nonumber \\&\quad +\,16(3v^2-B^2)BB''+16(v^2-3B^2)vv''\}x^4 \nonumber \\&\quad -\,64(B^4+3B^2v^2+3v^4)B^2x^6+576v''xt \nonumber \\&\quad -\,768v''xt^3+288(B^2-8BB''-8vv'')x^2t^2 \nonumber \\&\quad -\,192B^2x^2t^4+576\{(B-8B'')Bv \nonumber \\&\quad +\,4(B^2-v^2)v''\}x^3t-768B^2vx^3t^3 \nonumber \\&\quad -\,192(B^2+6v^2)B^2x^4t^2-384(B^2 \nonumber \\&\quad +\,2v^2)B^2vx^5t-108(t+vx)^2 \nonumber \\&\quad -\,48(t+vx)^4-64(t+vx)^6, \end{aligned}$$
(20)

where, in the same limit as \(\kappa \rightarrow 0,\)

$$\begin{aligned} B&=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) n\alpha _{2n},\\ v&=\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)\alpha _{2n+1}. \end{aligned}$$

The first-order derivatives \(B'\) and \(v'\) vanish as \(\kappa \rightarrow 0,\) but the second-order derivatives still remain, and in the limit as \(\kappa \rightarrow 0\) are

$$\begin{aligned} B''&=-\frac{1}{3}\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) n(n-1)\alpha _{2n},\\ v''&=-\frac{1}{3}\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n\\ n\end{array}}\right) (2n+1)n\alpha _{2n+1}. \end{aligned}$$

This solution is shown in Fig. 7. It is, naturally, the second-order rogue wave, but slanted and rescaled in the (x, t)-plane relative to the second-order rogue wave of the NLSE [53, 54].

Fig. 7
figure 7

The second-order rogue wave, Eqs. (18), (19), (20), obtained from the degenerate 2-breather solution shown in Fig. 6 in the limit \(\kappa \rightarrow 0,\) with some stretching due to higher-order effects

Full size image

8 Rogue wave triplets

It is well known that the general nth order rogue wave has the remarkable property of being able to split into \(\tfrac{1}{2}n(n+1)\) first-order components [55]. The second-order rogue wave discussed above is only a particular case of a more general rogue wave structure, where all three first-order components are located at the origin and have merged into one single peak. In order to obtain the more general solution where the three components are not merged together, known as the rogue wave triplet [56], we re-introduce the constants of integration into the general 2-breather solution, i.e.

$$\begin{aligned} \delta _mB_mx&\mapsto \delta _m(B_mx-\varepsilon X_m),\\ t+v_mx&\mapsto t-T_m\varepsilon +v_mx, \end{aligned}$$

where \(X_m\) and \(T_m\) are arbitrary and the parameter \(\varepsilon \) is introduced to make sure that the Taylor series in the degenerate limit still vanishes up to \(O(\varepsilon ^2).\) The values of \(X_m\) and \(T_m\) determine the location of the components of the breather components. They add additional free parameters to the solution which we have previously given for the restricted case in which \(X_m=T_m=0.\) Notice also that we do not make the replacement \(x\mapsto x-X_m\varepsilon \) directly, but, for simplicity’s sake, instead define \(X_m\) to account for the higher-order terms in \(B_m\).

In order to further simplify parametrisation, we assume that \(X_m\) and \(T_m\) are functions of the modulation parameter \(\kappa \) and are of the order \(O(\kappa )\). Then, defining free parameters \(\xi \) and \(\eta \) independent of \(\kappa ,\) such that

$$\begin{aligned} \kappa \xi&=48(X_1-X_2),\\ \kappa \eta&=48(T_1-T_2), \end{aligned}$$

we have in the limit as \(\kappa \rightarrow 0\) the rogue wave triplet solution in the form

$$\begin{aligned} \psi (x,t)=\left\{ 1+\frac{{\hat{G}}(x,t)+i{\hat{H}}(x,t)}{{\hat{D}}(x,t)} \right\} e^{i\phi x}, \end{aligned}$$
(21)

with

$$\begin{aligned} {\hat{G}}(x,t)= & {} G(x,t)-48\xi Bx-48\eta (t+vx), \end{aligned}$$
(22)
$$\begin{aligned} {\hat{H}}(x,t)= & {} H(x,t)+12\xi -48\xi B^2x^2 \nonumber \\&-\,96\eta Bx(t+vx)+48\xi (t+vx)^2, \end{aligned}$$
(23)
$$\begin{aligned} {\hat{D}}(x,t)= & {} D(x,t)-(\xi ^2+\eta ^2)+12\{\xi (3B-4B'') \nonumber \\&-\,4\eta v''\}x+16\xi B^3x^3+12\eta (1+4B^2x^2)\nonumber \\&\,\times (t+vx)-48\xi Bx(t+vx)^2 \nonumber \\&-\,16\eta (t+vx)^3, \end{aligned}$$
(24)

where \({\hat{G}},\)\({\hat{H}}\) and \({\hat{D}}\) now contain two new free parameters, \(\xi \) and \(\eta ,\) which determine the separation of the fundamental rogue wave components in the triplet [56], and where G,  H and D are as given in Eqs. (18)–(20), for the particular case in which \(\xi =\eta =0\). An example of the formation of rogue wave triplets, corresponding to nonzero \(\xi \) and \(\eta ,\) is shown in Fig. 8. When both \(\xi =0\) and \(\eta =0\), all three components merge at the origin, as in Fig. 7.

Fig. 8
figure 8

The second-order rogue wave triplet (21), with separation parameters \(\xi =-\eta =480,\) and the extended equation parameters given by \(\alpha _2=\tfrac{1}{2},\)\(\alpha _3=\tfrac{1}{27},\)\(\alpha _4=\tfrac{1}{50},\)\(\alpha _5=\tfrac{1}{81},\)\(\alpha _6=\tfrac{1}{200},\)\(\alpha _7=\tfrac{1}{343}\). For this choice of parameters, we have \(B=\tfrac{77}{50},\)\(v=\tfrac{1324}{1323},\)\(B''=-\tfrac{7}{25}\) and \(v''=-\tfrac{2894}{3969}\)

Full size image

Generally, the coefficient B in Eq. (21) determines the degree of localisation along the x-axis. Larger values of B will correspond to narrower peaks, whereas smaller values of B will correspond to broader peaks and \(B=0\) to minimal localisation. A point of interest here is that it is again possible to choose a parametrisation for which B is any fixed constant. If we choose, for instance,

$$\begin{aligned} \alpha _2=c-\frac{1}{2}\sum _{n=1}^{\infty }\left( {\begin{array}{c}2n+2\\ n+1\end{array}}\right) (n+1)\alpha _{2n+2}, \end{aligned}$$

we end up with \(B=c,\) where c is a free parameter. However, \(B''\) is entirely independent of the choice of c, since the coefficient of \(\alpha _2\) in \(B''\) is zero. As the simplest example, we consider the completely de-localised case, \(B=0,\) with \(B''\) remaining arbitrary. The rogue wave solution then reduces to (21) with

$$\begin{aligned} {\hat{G}}(x,t)&=G_0(x,t)-48\eta (t+vx),\\ {\hat{H}}(x,t)&=H_0(x,t)+12\xi +48\xi (t+vx)^2,\\ {\hat{D}}(x,t)&=D_0(x,t)-(\xi ^2+\eta ^2)-48(\xi B''+\eta v'')x \\&\quad +12\eta (t+vx)-16\eta (t+vx)^3. \end{aligned}$$

where

$$\begin{aligned} G_0(x,t)&=12\{-3-192v''x(t+vx)+24(t+vx)^2 \\&\quad +16(t+vx)^4\},\\ H_0(x,t)&=576B''x\{1+4(t+vx)^2\},\\ D_0(x,t)&{=}-\,9{-}576\{4B''^2{+}v''^2\}x^2{+}576v''x(t+vx) \\&\quad -\,768v''x(t+vx)^3-108(t+vx)^2 \\&\quad -\,48(t+vx)^4-64(t+vx)^6. \end{aligned}$$

Here, \(G_0,\)\(H_0\) and \(D_0\) are as given for the case where the components are merged and \(B=0\), and \({\hat{G}},\)\({\hat{H}},\)\({\hat{D}}\) incorporate the shifting of the first-order components through \(\xi \) and \(\eta .\)

Fig. 9
figure 9

The second-order rogue wave solution with ‘soliton’-like tails when \(\alpha _2\) is chosen such that \(B=0,\) and \(\xi =\eta =0.\) Other parameters are the same as in Fig. 8

Full size image

When \(B=0\), the second-order rogue wave acquires soliton-like tails similar to those in Fig. 4. When, additionally, \(\xi =\eta =0,\) rogue waves merge at the origin to form a second-order rogue wave with extended tails. This case is shown in Fig. 9. When \(\xi \) or \(\eta \) is not zero, the components split, resulting in the disappearance of the central peak. This case is shown in Fig. 10. Here, the central peak is absent but the long tails remain, consisting of de-localised first-order components.

Fig. 10
figure 10

The second-order rogue wave solution with ‘soliton’-like tails when \(B=0,\) but now \(\xi =\eta =48\)

Full size image

9 Conclusions

We have derived the general 2-breather solution for the class I infinitely extended nonlinear Schrödinger equation, and given many limiting cases, namely breather-to-soliton conversions, the semirational limit, the degenerate 2-breather, and, probably most importantly, the general second-order rogue wave solution. These solutions completely describe a large family of second-order solutions to the class I extension of the NLSE, and exhibit rich behaviour.

These results provide a more detailed analysis of the formation of nonlinear wave structures such as breathers and rogue waves when higher-order effects come into play, and leave a large range of future related work wide open.