1 Introduction

Nonlinear evolution equations (NLEEs) have been attractive in science and engineering [1,2,3,4]. Soliton and rational solutions for some NLEEs have been structured [5,6,7]. Soliton solutions describe various vital nonlinear nature phenomena [8, 9]. Upon taking long wave limits, rational solutions can be created from those solitons [9, 10], which include lump solutions, rationally localized solutions in all directions of the space and particularly rogue waves [11, 12]. Lump solutions emerge in many physical phenomena, such as plasma, shallow water wave, optic media and Bose–Einstein condensate [13]. Lump solutions have been found for kinds of integrable equation that have exponentially localized in certain direction [14, 15].

The research to lump solution has not been well developed, because it is very complex to solve the lump solution of NLEEs. Recently Ma [16] introduced a method to obtain the lump solutions of NLEEs by using the Hirota bilinear form. By utilizing this way, Ma et al. explored the lump solutions and the interaction solutions of NLEEs [17,18,19,20,21,22,23,24,25]. Other researchers successfully obtained the lump solutions and interaction solutions of NLEEs by symbolic computation as well [26,27,28,29,30,31,32,33,34,35].

We consider the \((2+1)\)-dimensional generalized fifth-order KdV equation [36] as follows:

$$\begin{aligned} u_{t}+ \alpha u_{xxxxx}+\beta uu_{xxx}+\gamma u_{x}u_{xx} +\delta u^2 u_{x}+u_{y}=0.\nonumber \\ \end{aligned}$$
(1)

Equation (1) describes motions of long waves in shallow water under gravity field and in a two-dimensional nonlinear lattice, where \(\alpha , \beta ,\gamma , \delta \) are the coefficients of the fifth-order dispersion term and the high-order nonlinear term, which are arbitrary nonzero real numbers. When model (1) is only considered one-dimensional space, we can get the fifth-order KdV equation as follows [37, 38]

$$\begin{aligned} u_{t}+ \alpha u_{xxxxx}+\beta uu_{xxx}+\gamma u_{x}u_{xx} +\delta u^2 u_{x}=0. \end{aligned}$$
(2)

Nonlinear equation (2) is an important mathematical model with wide applications in fluid mechanics, quantum mechanics, ion physics, nonlinear optics and other disciplines [39]. Equation (2) contains many practical models. The forms include the Lax equation, SK equation, SKPD equation, KK equation, KKPD equation and the Ito equation, such as Lax equation [40]:

$$\begin{aligned}&u_{t}+ u_{xxxxx}+\gamma uu_{xxx}+2\gamma u_{x}u_{xx}\nonumber \\&\quad +\,\gamma ^2\frac{3}{10} u^2 u_{x}=0. \end{aligned}$$
(3)

and Kaup–Kupershmidt equation [41]:

$$\begin{aligned} u_{t}+ u_{xxxxx}+\gamma uu_{xxx}+\gamma u_{x}u_{xx}+\gamma ^2\frac{1}{5} u^2 u_{x}=0.\nonumber \\ \end{aligned}$$
(4)

and Sawada–Kotera equation [42].

When \(\alpha =1, \beta =15, \delta =45, \gamma =15\) in Eq. (1), we obtain the following equation

$$\begin{aligned}&u_{t}+u_{xxxxx}+15uu_{xxx}+15u_{x}u_{xx}\nonumber \\&\quad +\,45u^2 u_{x}+u_{y}=0. \end{aligned}$$
(5)

In the present paper, we will discuss the lump solution and two classes of interaction solutions to \((2+1)\)-dimensional generalized fifth-order KdV equation (5).

2 Lump solution of the \((2+1)\)-dimensional generalized KdV equation

By using the following bilinear transformation:

$$\begin{aligned} u=2[\ln f(x,y,t)]_{xx}, \end{aligned}$$
(6)

Equation (5) became Hirota bilinear equation

$$\begin{aligned}&B_{\mathrm{KdV}}(f):\left( D_{x}D_{t}+D_{x}D_{y}+D_{x}^6\right) f\cdot f\nonumber \\&\quad =2(f_{xt}f-f_{x}f_{t})+2(f_{xy}f-f_{x}f_{y})\nonumber \\&\qquad +\,2f_{xxxxxx}f-12f_{xxxxx}f_{x}+30 f_{xxxx}f_{xx}\nonumber \\&\qquad -\,20f^2_{xxx}=0, \end{aligned}$$
(7)

where the operator D:

$$\begin{aligned}&D_{t}^{m} D_{x}^{n}a(t,x) \cdot b(t,x)\\&\quad =\frac{\partial ^m}{\partial s^m}\frac{\partial ^n}{\partial y^{n}}a(t+s,x+y)\\&\qquad b(t-s,x-y)|_{s=0,y=0}, m,n=0,1,2,3,\ldots \end{aligned}$$

In order to get the quadratic function solution of Hirota bilinear equation (7), we assume

$$\begin{aligned} f= & {} g^{2}+h^{2}+a_9,g=a_1 x+a_2 y+a_3 t+a_4,\nonumber \\ h= & {} a_5 x+a_6 y+a_7 t+a_8, \end{aligned}$$
(8)

where \(a_i\ (i=1,2,\ldots ,9)\) are real constants. It is noticed that \(g^2 + a_5\) cannot generate any analytic solutions, which are a kind of rational function localized in all directions of the space.

By substituting (8) into (7) and handling all the coefficients of different polynomials of x, y, t to zero, we obtain a set of algebraic equations for \(a_i\ (i=1,2,\ldots ,9)\). Solving the set of algebraic equations by mathematics yields the following solutions of \(a_i\ (i=1,2,\ldots ,9)\).

$$\begin{aligned} a_{1}= & {} a_1, a_{2}=\frac{a_1a_6}{a_5}, a_{3}=-\frac{a_{1}a_6}{a_5}, a_{4}=a_4,\nonumber \\ a_{5}= & {} a_5, a_{6}=a_{6}, a_{7}=-a_6, a_{8}=a_8 ,a_{9}=a_{9}, \end{aligned}$$
(9)

where \(a_{1},a_{4},a_{5}(\ne 0),a_{6},a_{8},a_9\) are arbitrary constants.

Substituting (9) into (8), we obtain a kind of positive quadratic function solution f of Eq. (7)

$$\begin{aligned} f= & {} \left[ a_4+a_1x-\frac{a_1a_6(y-t)}{a_5}\right] ^2\nonumber \\&+\,[a_8+a_5x+a_6(t-y)]^2+a_9, \end{aligned}$$
(10)

and the resulting class of quadratic function solutions, in turn, yields a class of lump solutions to \((2+1)\)-dimensional generalized KdV equation (5) via transformation (6):

$$\begin{aligned} u=-\frac{8(a_{1} g+a_{5} h)^{2}-4 (a_{1}^{2}+a_{5}^{2}) f}{f^{2}}, \end{aligned}$$
(11)

where the function f is defined by (10). Note that the lump solution in (11) is analytic if the parameter \(a_{5}\ne 0, a_9>0\). Quite evidently, we can get at any given time t the above lump solutions \(u\rightarrow 0\) if and only if the corresponding sum of squares \(g^{2}+h^{2}\rightarrow \infty \).

When \(a_{1},a_{4},a_{5},a_{6},a_{8},a_9\) are special value, we obtain two special pairs of positive quadratic function solutions and lump solutions as follows.

1. A selection of the parameters:

$$\begin{aligned} a_{1}=1, a_{4}=1, a_{5}=2, a_{6}=3, a_{8}=5, a_{9}=1 \end{aligned}$$

leads to

$$\begin{aligned} f_1(x,y,t)= & {} \frac{1}{4}(2x-3y+3t+2)^2\\&+\,(2x-3y+3t+5)^2+1, \end{aligned}$$

and the lump solution

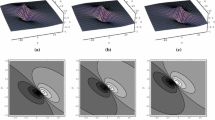
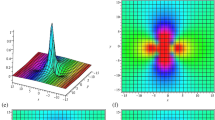
$$\begin{aligned} u_1(x,y,t)=-\frac{16[428+225t^2+100x^2+225y^2+660y+20x(22+15y)-30t(22+10x+15y)]}{[(2x+3y-3t+2)^2+4(2x+3y-3t+5)^2+4]^2}.\qquad \qquad \end{aligned}$$
(12)

The profile of \(u_1(x,y,t)\), its profiles, density and y-axis plots are shown in Fig. 1.

Fig. 1
figure 1

(Color online) Lump solution (12) with \(t = 0\). (Left) Perspective view of lump soliton (12). (Middle) Overhead view of the wave. (Right) The wave along the y-axis with \(x=-1\) (green), \(x=0\) (blue) and \(x=1\) (pink)

Full size image
Fig. 2
figure 2

(Color online) Lump solution (15) with \(t = 1\). (Left) Perspective view of lump soliton (15). (Middle) Overhead view of the wave. (Right) The wave along the y-axis with \(x=-1\) (green), \(x=0\) (blue) and \(x=1\) (pink)

Full size image
Fig. 3
figure 3

(Color online) Perspective view of lump-soliton solution (19). a Solution (19) with \(t = 0\). b Solution (19) with \(t = 3\). c Solution (19) with \(t = 6\). d Solution (19) with \(t = 10\). e Solution (19) with \(t = 15\). f Solution (19) with \(t = 20\)

Full size image

2. Another selection of the parameters:

$$\begin{aligned} a_{1}= & {} -1, a_{4}=-4, a_{5}=-7,a_{6}=-3,\nonumber \\ a_{8}= & {} 0, a_{9}=7, \end{aligned}$$
(13)

leads to

$$\begin{aligned} f_2(x,y,t)= & {} \frac{1}{49}(7x-3y+3t+28)^{2}\nonumber \\&+\,(7x-3y+3t)^{2}+7, \end{aligned}$$
(14)

and the lump solution

$$\begin{aligned}&u_2(x,y,t)\nonumber \\&\quad =\frac{-8[-27391+11250t^2+61250x^2+4200y+11250y^2+700x(14+75y)-300t(14+175x+75y)]}{49[(7x+3y-3t)^{2}+\frac{1}{49}(7x+3y-3t+28)^{2}+7]^2}.\nonumber \\ \end{aligned}$$
(15)

The profile of \(u_2(x,y,t)\), its profiles, density and y-axis plots are shown in Fig. 2.

3 Lump-soliton solutions of the \((2+1)\)-dimensional generalized KdV equation

Interaction solutions of the \((2+1)\)-dimensional generalized KdV equation will be studied in this section. In order to obtain the interaction solutions between lump solution and solitary wave solution, we assume f(x, y, t) as a combination of hyperbolic cosine function and positive quadratic function:

$$\begin{aligned} f= & {} (a_1 x+a_2 y+a_3 t+a_4)^{2}+(a_5 x+a_6 y+a_7 t+a_8)^{2}\nonumber \\&+\cosh (\zeta _1x+\zeta _2y+\zeta _3t+\zeta _4)+a_9, \end{aligned}$$
(16)

where \(a_i\ (i=1,2,\ldots ,9), \zeta _i\ (i=1,\ldots ,4)\) are real constants.

Substituting (16) into (7) with a direct symbolic computation, we get the following solutions:

$$\begin{aligned} a_2= & {} \frac{a_4a_6}{a_8}, a_3=-a_2, a_6=-a_7, \zeta _1=0,\nonumber \\ \zeta _2= & {} -\zeta _3,a_i=a_i\ (i=1,4,5,8,9),\zeta _4=\zeta _4, \end{aligned}$$
(17)

where \(a_{1},a_{4},a_{5}, a_8(\ne 0), a_{9},\zeta _{3},\zeta _4\) are arbitrary constants. Then, the exact interaction solution of u is expressed as follows:

$$\begin{aligned} u=\frac{-8[a_5a_8(a_5x+a_6y-a_6t+a_8)+a_1^2a_8x+a_1a_4(a_8+a_6y-a_6t)]^2}{a_8^2f^2}+\,4(a_1^2+a_5^2)\frac{1}{f}, \end{aligned}$$
(18)

where

$$\begin{aligned} f= & {} \left[ a_1x+\frac{a_4}{a_8}(a_8+a_6y-a_6t)\right] ^2\\&+\,(a_5x+a_6y-a_6t+a_8)^2\\&+\,\cosh [\zeta _3 (t-y)+\zeta _4]+a_9. \end{aligned}$$

To illustrate the interaction solutions between lump and line solitons, we choose the parameters as follows:

$$\begin{aligned} a_1= & {} 1,a_4=-1, a_5=4, a_6=1, a_8=3,\nonumber \\ a_9= & {} 6, \zeta _3=2, \zeta _4=2. \end{aligned}$$
(19)

Profiles of (18) with parameters (19) are shown in Figs. 3 and 4

Figure 3 exhibits the interaction between hyperbolic functions and the positive quadratic functions. We can see the soliton finally drowns or swallows up the lump soliton with the evolution of time t. The interaction between two solitary waves is nonelastic (Fig. 5).

Fig. 4
figure 4

(Color online) Overhead view and contour plot of lump-soliton solution (19). a, d Solution (19) with \(t = 0\). b, e Solution (19) with \(t = 8\). c, f Solution (19) with \(t = 15\)

Full size image
Fig. 5
figure 5

Profile and contour plot of lump–kink solution (23). a Solution (23) with \(t =-10\). b, I Solution (23) with \(t = 0\). II Solution (23) with \(t = 7\). c, III Solution (23) with \(t =20\). d Solution (23) with \(t = 28\). e Solution (23) with \(t =45\). f Solution (23) with \(t = 58\)

Full size image

4 Lump–kink solutions of the \((2+1)\)-dimensional generalized KdV equation

The interaction between a lump and a stripe of \((2+1)\)-dimensional generalized KdV equation (5) will be studied in this section. To seek the interaction solution of Eq. (5), we begin with

$$\begin{aligned} f= & {} (a_1 x+a_2 y+a_3 t+a_4)^{2}\nonumber \\&+\,(a_5 x+a_6 y+a_7 t+a_8)^{2}\nonumber \\&+\,\exp (\zeta _1x+\zeta _2y+\zeta _3t+\zeta _4)+a_9, \end{aligned}$$
(20)

where \(a_i\ (i=1,2,\ldots ,9), \zeta _i\ (i=1,\ldots ,4)\) are real constants.

Substituting (20) into Eq. (7) with a direct symbolic computation, we obtain the following set of solutions for the parameters \(a_i, \zeta _i\):

$$\begin{aligned} a_3=-a_2, a_6=-a_7, \zeta _1=0, \zeta _2=-\zeta _3. \end{aligned}$$
(21)

Then we obtain the mixed lump–kink solution of Eq. (5)

$$\begin{aligned} u=\frac{4(a_1^2+a_5^2)f-8[a_1(a_1x+a_3t-a_3y+a_4)+a_5(a_5x+a_7t-a_7y+a_8)]^2}{f^2}, \end{aligned}$$

where f is given in (20), and \( a_1, a_2, a_4, a_5, a_6, a_8, a_9, \zeta _3,\zeta _4\) are arbitrary real constants.

When we choose the following special value for the parameters:

$$\begin{aligned} \zeta _3= & {} \frac{5}{4}, \zeta _4=\frac{1}{2}, a_1=3, a_3=3, a_4=2,\nonumber \\ a_5= & {} -1, a_7=-2, a_8=4, a_9=1, \end{aligned}$$
(22)

then we obtain

$$\begin{aligned} u=\frac{8\left[ 101+5\exp \left( \frac{1}{2}+\frac{5}{4}t -\frac{5}{4}y\right) -56t^{2}-20x-50x^{2}-2t(32+55x-56y)+64y+110xy-56y^2\right] }{\left[ 1+\exp \left( \frac{1}{2}+\frac{5}{4}t-\frac{5}{4}y\right) +(2+3t+3x-3y)^2+(-4+2t+x-2y)^2\right] ^2}.\nonumber \\ \end{aligned}$$
(23)

To get the collision phenomenon, \(a_3^2+a_7^2+\zeta _3\ne 0\) is indispensable. So the asymptotic behavior of u can be obtained, the solution \(u\rightarrow 0\) as \(t\rightarrow \infty \). The asymptotic behavior shows that the lump is finally drowned or swallowed up by the stripe along with the change of time.

5 Conclusion

In this paper, a kind of lump solutions and two classes of interaction solutions to \((2+1)\)-dimensional generalized KdV equation (5) are studied with the aid of symbolic computation system Mathematica. Firstly, using the transformation \(u=2[\ln f(x,y,t)]_{xx}\), we obtained the bilinear form of the \((2+1)\)-dimensional KdV equation. By determining the positive quadratic function solutions of bilinear equation (7), we have derived the lump solution of Eq. (5). The result included six arbitrary parameters, and these parameters guaranteed analyticity and rational localization of the lump solution. Secondly, we presented the interaction solutions between positive quadratic function and hyperbolic cosine function and showed the process of interaction. Finally, we successfully constructed the interaction solutions between lumps and kinks of Eq. (5). When time t increases to big enough, the lump solitary wave solution disappears, and only the kink solitary wave solution exists. For such phenomenon, the asymptotic behavior shows that the lump is finally drowned or swallowed up by the stripe along with the change of time. The above phenomenon shows that the interaction between two solitary waves is nonelastic [43,44,45]. These results help to understand the propagation of nonlinear waves in fluid mechanics and enrich the dynamic changes of high-dimensional nonlinear wave fields. Also it shows that the method can be used for many other NLEEs in mathematical physics.