1 Introduction

The development of different kinds of adaptive controller shows a clear tendency toward the research of control methods with high autonomy. The pursuit for highly autonomous control is to achieve the control goal for unknown systems without the requirement of the prior mathematical model of the system and further preliminaries of the system dynamic behavior like the exact description of the changing environment of the system. If the autonomous control can be realized, the whole control process will be robust, flexible, and efficient, no manual design process is needed. As stabilization is the basic task of the control problem, this paper is focused on designing an autonomous stabilizer.

High autonomy is defined by the following four requirements/key aspects (for control design in the context of stabilization):

  • The dynamic behavior of the unknown system to be controlled has to be learned by the desired algorithm only with the knowledge about the input and output (I/O) measurements. It should be mentioned that in most practical cases the dynamic behavior of the learned system describes only the local dynamics of the system to be controlled accurately, which means it cannot be globally accurate. Therefore the desired controller should be able to learn the system dynamic behavior online, in order to update the actual dynamic behavior. With this capability, the dynamics of time-variant systems can also be learned online assuming a suitable relation between the time variance and the adaption behavior of the learning system.

  • Using the learned system dynamic behavior, the desired controller should be able to do multi-step prediction of the system outputs with different input values with acceptable accuracy. The predicted system outputs are required for judging the stability of the system future motion with desired inputs and for determining the optimal input values for several upcoming time steps.

  • The stability of the concerned system should be related to the upcoming motion predicted using the learned local dynamic behavior. Furthermore, the required stability criteria should be realized in a data-driven manner. This results from the fact that in this contribution it is assumed that the system model is not known, so only the knowledge about the I/O behavior can be used for the whole approach.

  • The desired control inputs for the upcoming time steps should be directly and optimally determined.

Several data-based adaptive controller design methods have already been developed trying to achieve the expectation as described above for nonlinear systems, like virtual reference feedback tuning (VRFT) [5, 21], iterative learning control (ILC) [3, 26–28], iterative feedback tuning (IFT) [9, 19] , model-free adaptive control (MFAC) [10], real-time particle filter (RTPF) [13], and adaptive dynamic programming (ADP) [11, 14, 16] etc. Unfortunately, none of these methods can realize the expectation without any shortage related to the high autonomy. The approaches require different assumptions (about the system’s behavior) or will lead to different limitations with respect to their application. In order to explain it more clearly, a brief introduction of each method is given in the sequel. Finally, the difference of the novel approach to previously published approaches of others will be briefly pointed out.

Establishing VRFT approach [5], an optimal controller is determined among a special controller class according to collected data of the considered nonlinear unknown SISO system. The VRFT approach can be extended for MIMO systems, but, according to [21], is restricted to an equal number of inputs and outputs. The process to determine the controller is realized without off-line identification of the system model, so the system is assumed as time-invariant. The given data have to include enough information of the systems dynamic behavior to guarantee optimal controller behavior. Additionally, it is assumed that the I/O behavior of the nonlinear system is smooth and invertible. Such requirements have to be achieved in practice, which is difficult to realize due to the assumed complexity of unknown systems. Moreover, the stability of the controlled system is not discussed within this approach.

The main idea of the ILC approach [26] is to update the desired control input according to the output measurements iteratively for each discrete time step using always the same initial conditions of the system dynamic behavior for each iteration, which is an imperative fundamental assumption of ILC [27, 28]. A priori knowledge about the bounding functions of the uncertainties of the system dynamic behavior is required for the learning process [26], so ILC is not a complete model-free approach. On the one hand, the perfect tracking (as advantage) of the desired system outputs can be realized using ILC without any identification of the system model. On the other hand, ILC cannot be used online because the outputs cannot always be measured within the same initial conditions of the system states and the same control environment within one discrete time step in practice. As a consequence, ILC-based approaches have to be combined with identification methods to achieve online applicability as shown in [3]. The advantage of the perfect tracking is missing because of not avoidable identification error.

The IFT approach [9, 19] is also an adaptive control method without included identification process. The structure of the controller is predefined. The parameters of the controller are optimized during each time step based on three experimental tests done in parallel. This approach is not applied and developed for nonlinear MIMO systems as well as for time-variant systems.

Model-free adaptive control (MFAC) [10] approach was developed as an extension of adaptive control to realize tracking tasks for a class of discrete-time MIMO nonlinear systems assuming an identical number of inputs and outputs. Using MFAC, the known dynamical structure of the nonlinear system model is not required, even the identification of the system model is not needed. A series of linearized local dynamic models of the closed-loop system along the dynamic operation points is established with online I/O measurements without training process. A suitable linearization structure is chosen directly among different possibilities of dynamic linearization technique (DLT) with pseudo-partial derivative (PPD). Each possibility uses different PPD matrices to describe the system model. All kinds of PPD matrices should be diagonally dominant. In order to guarantee this condition, the given I/O data should include suitable information about the system dynamic behavior which needs additional afford to be guaranteed in practice. Each possibility of DLT leads to its own controller structure, whose parameters are determined according to the linearized data model updated using the online I/O measurement. Using MFAC algorithm, BIBO stability of the closed-loop system is considered.

The RTPF approach [13] is usually applied for system dynamic estimation including specially robot localization problems. The dynamic behavior of the unknown system can be represented and predicted as the posterior probability densities of the measured system samples, which is sampled according to the inputs and sensor data collected by the dynamical system/robot moving around a given set of possible outputs. If the sampling of the required samples of an unknown nonlinear dynamical system can be achieved successfully, suitable inputs for the desired outputs can be determined from the predictive densities directly. A given set for all possible outputs of dynamical system is not always available. With such a given set a sampling process which include enough information of the system dynamic is also expensive for online process. Furthermore, the stability of the controlled system is not considered.

The ADP approach [14, 16] consists of three neural networks, which are used separately for model identification, updating of the optimal cost function related to the control law, and updating of the control law. Using ADP the computational requirement is large because of the use of three neural networks, of which the approximating accuracy should be guaranteed. Additionally, the stability of the closed-loop system is not considered in the controller design. In order to solve this problem, robust ADP was developed [11] for controlling nonlinear systems with dynamic uncertainties. The system model is assumed to consist of two parts: unknown system dynamics with measured states and unknown system dynamics with unmeasured states. With the help of an iterative technique called policy iteration and nonlinear small-gain theorem, both parts are considered during the controller design to stabilize the closed-loop system at the origin. However, this method can only be used for SIMO systems.

In order to overcome the shortages or to develop an alternative of the existing methods, a cognitive stabilizer has been developed and proposed recently for a class of nonlinear dynamical MIMO discrete system. With the use of a cognitive framework, the requirements of high autonomy (including mainly the assumption that no model information is used) should be fulfilled. The key idea for the cognitive aspect of the framework is to match the definition of cognition, which is a distinctive feature of cognitive systems [25]: “being able to understand what is going on and what to do to next. Cognition in the engineering context means the capability of perceiving the environment, assimilating information by discovering and structuring knowledge, and autonomously making rational decisions of how to act” [1]. This definition is closely related to similar one developed in information science, as given from Strube [24]. The cognition-based framework is developed in the context of stabilization in order to achieve the expectation of the high autonomy stated above. A controller based on such framework used for stabilization task will be denoted as cognitive stabilizer. Previous publications of the authors Nowak (née Shen) and Söfkker are related to similar topics. In [22], the cognitive stabilizer is developed firstly using a simple but not optimal algorithm applied to a SIMO simulation example. In [18], the cognitive stabilizer is improved with another algorithm and applied to a SIMO chaotic nonlinear system numerically.

In this contribution, the approach is extended by the authors in order to realize all the expectations for the first time. Different realizations of each module and the whole framework are discussed and compared. They are applied to a chaotic MIMO nonlinear system. The similarities between former works and this publication are small and result from focusing the same idea but using different algorithms.

This paper is organized as follows: The concept of the cognitive-based framework for stabilization is explained in Sect. 2; the realizations for each module of the cognitive-based framework are presented in Sect. 3; the cognitive stabilizer is applied to a Lorenz system. The corresponding simulation results are shown in Sect. 4. Summary and conclusion are given in Sect. 5.

2 Concept of a cognitive-based framework for stabilization

Different definitions of stabilization in the control research area are known. Due to the fact that from the point of view of the cognitive control design besides the measurements no information about the system to be controlled is used, it is necessary to define the stabilization problem which should be solved in the context of cognitive stabilizer clearly.

2.1 Stabilization problem

The considered class of time-variant discrete nonlinear dynamical MIMO systems is given by

$$\begin{aligned} x(k+1)=f(x(k), u(k))\text {,} \end{aligned}$$
(1)

where \(f(\cdot )\) denotes the nonlinear system discrete dynamic, \(x(k)\in \mathfrak {R}^n\) the state vector, k the current discrete time step, and \(u(k)\in \mathfrak {R}^m\) the control input. The stabilization problem should be solved by designing a suitable control input vector

$$\begin{aligned} u(k) = u(x(k), x(k-1),\ldots ,x(k-l)) \end{aligned}$$
(2)

with l as an integer which is smaller than k such that \(x_\mathrm{a}\) as an arbitrary state of the system to be controlled becomes an asymptotically stable equilibrium point of the controlled system.

It is assumed that the function \(f(\cdot )\) is unknown, the state vector x are measured and the system is fully controllable.

2.2 Cognition-based framework for stabilization

In order to solve the stabilization problem above, the cognition-based framework for stabilization is developed in [22] and shown repeatedly in Fig. 1. The details of each module and their interconnections are illustrated in the sequel.

Fig. 1
figure 1

Cognition-based framework for stabilization [22]

Full size image

As shown in the figure, in the external environment, the system to be controlled is an unknown system, which means that the related mathematical model is not known neither to the stabilizer nor to the designer, and therefore the system model is not used. The inputs and outputs including the disturbances as well as the given goal of the stabilization task are the only information about the unknown system which are used for design and are transmitted during operation to the cognitive stabilizer.

The cognitive stabilizer consists of the four modules (“perception and interpretation,” “expert knowledge,” “planning” as well as “execution”) and their interconnections. This modules/functionalities and their interaction are typical for cognitive frameworks as defined in [4]. The I/O measurements are firstly gathered, analyzed, and stored as the system dynamic behavior information by using dynamic identifier in the module “perception and interpretation.” Such information (learned using the I/O measurements) is able to present the previous system dynamic behavior with high accuracy and to predict the dynamic behavior for a certain multi-step prediction horizon. To guarantee the stability of the controlled system, a suitable knowledge about state stability is used in the module “expert knowledge” to judge weather the former control inputs to be updated can achieve the control goal: stabilize the system at the desired equilibrium point of the controlled system. The judging process does not need the model of the system but only the stored information about the system in the module “perception and interpretation.” In the module “planning,” the strategy for choosing the optimal control input which can satisfy the requirement in the module “expert knowledge” is defined to reach the goal dynamics of the controlled system efficiently. Finally, the input signal is generated by the module “execution” according to the defined strategy. Each module in the framework can be realized separately by applying different methods.

3 Realization of the modules of the cognitive-based framework

The detailed possible realization methods for each module of the framework above will be given in this section.

3.1 Realization of the module “perception and interpretation”

Various kinds of methods can identify the system dynamics of unknown nonlinear systems with the I/O measurements online, such as radial basis function neural networks, dynamic recurrent neural networks, nonlinear autoregressive exogenous model recurrent neural networks (NARX-RNN), Gaussian process regression (GPR), support vector machine, real-time particle filter, and dynamic linearization technique. Each of these methods is characterized by specific advantages and disadvantages. In this paper, NARX-RNN [8, 23], GPR [7, 12, 20], and a combined identifier based on NARX-RNN and GPR are combined to realize the module perception and interpretation. Other methods possibly to be combined will be discussed in the future work.

3.1.1 Nonlinear autoregressive exogenous model recurrent neural networks (NARX-RNN)

Using recurrent neural networks (RNN), the dynamical system behavior can be trained without a high-level memory also for high-dimensional nonlinear systems [8]. Nonlinear autoregressive exogenous models as a kind of RNN can be applied not only for the system dynamic behavior training but also for multi-step-ahead prediction of the system states with high accuracy using new system inputs [23]. A brief introduction of NARX-RNN is given in the sequel.

During a training process, the input vectors of the NARX-RNN are defined as

$$\begin{aligned} x(k-1)= & {} [x(k-1),\ldots ,x(k-l-1)]\text { and} \nonumber \\ u(k-1)= & {} [u(k-1),\ldots ,u(k-l-1)]\text {.} \end{aligned}$$
(3)

The output vector of the NARX-RNN is defined as

$$\begin{aligned} x(k)= & {} [x(k),\ldots ,x(k-l)]\text {,} \end{aligned}$$
(4)

where l denotes the size of the training horizon. The measured states and inputs of the system of the past l discrete time steps are considered for the training phase. The active functions \(f_1\), \(f_2\) and the number of the neurons \(\eta \) in the hidden layer of the neural network are predefined.

The structure of the relation between the output vector and the input vectors is predefined by NARX-RNN as

$$\begin{aligned} x(k)= & {} f_2(W_3\cdot f_1(W_1\cdot u(k-1)+W_2\cdot x(k-1)\nonumber \\&+\,b_1) {} +b_2)\text {,} \end{aligned}$$
(5)

with \(W_1\), \(W_2\), and \(W_3\) as weighting matrices and \(b_1\) and \(b_2\) as bias vectors.

In the training phase, the weighting matrices and bias are adapted using back-propagation-through-time algorithm. In the prediction phase, the new system state vector for the next discrete time step \(\hat{x}(k+1)\) is predicted using the trained weighting matrices and bias with a new system input vector \(u_d(k)\). Iteratively, the system states in the multi-step prediction horizon (horizon size s) are predicted using the real system states from the training horizon and the previous predicted system states as

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{c} \hat{x}(k+s) \\ \hat{x}(k+s-1) \\ \vdots \\ \hat{x}(k+1) \\ x(k) \\ \vdots \\ x(k+s-l) \\ \end{array} \right]&=f_2 \left( W_3\cdot f_1 \left( W_1 \left[ \begin{array}{c} u_d(k+s-1) \\ u_d(k+s-2) \\ \vdots \\ u_d(k) \\ u(k-1) \\ \vdots \\ u(k+s-l-1) \\ \end{array} \right] \right. \right. {} \\&\qquad \left. \left. +\, W_2 \left[ \begin{array}{c} \hat{x}(k+s-1) \\ \hat{x}(k+s-2) \\ \vdots \\ \hat{x}(k) \\ x(k-1) \\ \vdots \\ x(k+s-l-1) \\ \end{array} \right] +b_1 \right) +b_2 \right) .\\ \end{aligned}\nonumber \\ \end{aligned}$$
(6)

Using the NARX-RNN algorithm, the system dynamic behavior for every multi-step prediction horizon can be trained. The states of the unknown nonlinear system can be predicted online according to the new system inputs.

This algorithm can also be applied to approximate the inverse relation between the system inputs and outputs [18] as

$$\begin{aligned} \begin{aligned} \left[ \begin{array}{c} \hat{u}_d(k+s-1) \\ \hat{u}_d(k+s-2) \\ \vdots \\ \hat{u}_d(k) \\ u(k-1) \\ \vdots \\ u(k+s-l) \\ \end{array} \right]&=f_2 \left( W_3\cdot f_1 \left( W_1 \left[ \begin{array}{c} x_d(k+s) \\ x_d(k+s-1) \\ \vdots \\ x_d(k+1) \\ x(k) \\ \vdots \\ x(k+s-l+1) \\ \end{array} \right] \right. \right. {} \\&\qquad \left. \left. +\,W_2 \left[ \begin{array}{c} \hat{u}_d(k+s-2) \\ \hat{u}_d(k+s-1) \\ \vdots \\ \hat{u}_d(k) \\ u(k-1) \\ \vdots \\ u(k+s-l-1) \\ \end{array} \right] +b_1 \right) +b_2 \right) ,\\ \end{aligned}\nonumber \\ \end{aligned}$$
(7)

where \(\hat{u}_d(p)|_{p=k\text {, }\ldots \text {, } k+s-1}\) denotes the predicted desired system input and \(x_d(p)|_{p=k+1\text {, }\ldots \text {, } k+s}\) the desired system state.

It should be mentioned that during the training phase, the approximation results are validated to guarantee that the weighting matrices and bias are suitable enough to approximate the system dynamics with high accuracy. In the prediction phase, no validation process to check weather the predicted states are accurate enough is given. Therefore, a simple but efficient additional validation for the predicted states is defined here. Assume \(\Delta x_{\mathrm{max}, q}=\text {max}\left| x_q(i+s)-x_q(i)\right| \) with \(q=1 \ldots r \text { and } i=1 \ldots k\), the predicted system states are considered as not accurate enough (not correct) if the condition

$$\begin{aligned} \left| \hat{x}_q(k+s)-\hat{x}_q(k)\right| >\lambda \Delta x_{\mathrm{max}, q} \end{aligned}$$
(8)

is fulfilled, where \(\lambda \) is a predefined tolerance parameter. The idea of this kind of validation is explained from a practical point of view. Each system shows its own dynamics and energy limits in the output (here also denoted as the state) side generated from the input side. Therefore in a time period with a certain length the predicted change of the system outputs can normally not be larger than any past change within any time period of the same length.

3.1.2 Gaussian process regression (GPR)

Gaussian process is a statistic process, which is defined by [20] as “a collection of random variables, any finite number of which has a joint Gaussian distribution.” According to [7, 12, 20], a brief introduction and the application of GPR are given in the following.

Here two new matrices are defined additionally to explain the use of GPR:

$$\begin{aligned} \hat{X}(k+1)= & {} [\hat{x}(k+1),\ldots ,\hat{x}(k+s)] \text { and}\end{aligned}$$
(9)
$$\begin{aligned} U_d(k)= & {} [u_d(k),\ldots ,u_d(k+s-1)]. \end{aligned}$$
(10)

Applying Gaussian process to learn and predict the system dynamic behavior, the multi-step-ahead prediction problem to define

$$\begin{aligned} \hat{X}(k+1)=f(k,X(k),U_d(k)) \end{aligned}$$
(11)

can be reformulated as a probabilistic problem to define the distributions of each element of \(\hat{X}(k+1)\) presented by the marginal likelihood [20] defined as

$$\begin{aligned} \text {marginal likelihood}=\frac{\text {likelihood}\times \text {prior}}{\text {posterior}} \end{aligned}$$
(12)

with

$$\begin{aligned}&p(f(U_d(k))|X(k),U(k-1)) \nonumber \\&\quad =\frac{p(X(k)|f(U_d(k),U(k-1)))p(f(U_d(k)))}{P(X(k)|U(k-1))}[12].\nonumber \\ \end{aligned}$$
(13)

The predicted distribution of \(\hat{X}(k+1)\) can be rewritten with a joint Gaussian distribution like

$$\begin{aligned}&\hat{X}(k+1)|U_d(k)\sim \mathcal {N} (\mathbb {E}_{U_d}[\mu (U_d)],\end{aligned}$$
(14)
$$\begin{aligned}&\mathbb {E}_{U_d}[\sigma ^2(U_d)]+\text {var}_{U_d}[\mu (U_d)]) \end{aligned}$$
(15)

with the mean \(\mu \) and the variance \(\sigma ^2\) for each prediction step. According to [12], the mean and the variance can be determined by

$$\begin{aligned} \mu \left( U_d\right)&= c\left( U_d\right) ^\mathrm{T}C^{-1}X(k) \nonumber \\ \sigma ^2\left( U_d\right)&= c'\left( U_d\right) -c\left( U_d\right) ^\mathrm{T}C^{-1}c\left( U_d\right) +v_0\text {.} \end{aligned}$$
(16)

The matrix C is a nonnegative definite covariance matrix determined with a certain covariance function c which is chosen as

$$\begin{aligned} c=v_1\exp \left[ -\frac{1}{2}\sum \limits _{d=1}^{D}w_d(u^p-u^q)^2\right] +v_0\text {,} \end{aligned}$$
(17)

where \(u^p\) and \(u^q\) are different input vectors among \(u(k-1),\ldots ,u(k-l-1)\) and \(u_d(k),\ldots ,u_d(k+s-1)\) as well as \(w_1\dots w_D\), \(v_0\), and \(v_1\) the hyperparameters to be trained by maximization of the marginal likelihood. The detailed calculation derivation is given in [7].

With the determined mean \(\mathbb {E}_{U_d}[\mu (U_d)]\) and variance \(\mathbb {E}_{U_d}[\sigma ^2(U_d)]+\text {var}_{U_d}[\mu (U_d)]\) for the multi-step-prediction probability, the system dynamic behavior can be trained and predicted without the use of a given system structure model.

It should be mentioned that the prediction result by using GPR is highly accurate only if the training input data are standard normal distributed. Because the system is described as Gaussian process describing the data with Gaussian/normal distribution better than with non-Gaussian distribution. Additionally, GPR can only be applied directly to MISO systems and repeatedly to MIMO systems (separate prediction process for each output).

3.1.3 Combined identifier

Both NARX-RNN and GPR has to be combined suitably for data-driven multi-step-ahead prediction tasks. In order to apply for different systems the most suitable one under different conditions automatically, a combined identifier based on both NARX-RNN and GPR is developed. The principle idea is explained as shown in Fig. 2.

Fig. 2
figure 2

Flowchart of the combined identifier

Full size image

In the initial training process, GPR is considered firstly to identify the system dynamic behavior with the training data measured from the unknown system. In order to guarantee the identification accuracy, the negative log marginal likelihood of the identified system outputs is checked online. If it is not small enough, the covariance function of the GP or its hyperparameters should be changed until the log marginal likelihood is small enough.

If the identification process is completed, the identified Gaussian process with its covariance function and hyperparameters are used to predict the system dynamics with certain test input data and the corresponding test output data. Considering the whole cognitive stabilizer, the type of the test input data could be defined according to the required form of the control inputs generated in the modules “planning and execution.” For example, the control inputs are determined according to the control goal for each step separately, which means the value of the control input vectors may be stepwise unique, and the test input data should be a standard uniform distributed random signals with the similar form of the control inputs. Similarly, if the control inputs with the same value are determined for each s steps, the test input data should be random step signal serials.

The test prediction result is evaluated according to the average absolute relative error (ARE). If the ARE of the predicted system outputs is not small enough, the training input and output data may not have enough information about the system dynamics behavior. In this case the whole training process will be repeated until suitable training data are defined. Otherwise, the training data should be saved and used for online prediction.

Applied for the online prediction process, GPR is used to predict the system outputs with the control inputs for the first \(k_\mathrm{c}\) steps, which are predefined or given experimentally. To guarantee the prediction accuracy, an additional validation process is used to verify whether the GPR can predict the system outputs with acceptable accuracy. Due to the fact that the real system outputs for the future steps cannot be measured during the online prediction process, Eq. (8) based only on the predicted system outputs and the real system outputs in the past is used as the condition for not acceptable prediction result. If the prediction results are not acceptable, NARX-RNN will be used for the same prediction task. If the new prediction result is better (evaluated using Eq. 8) than the former one using GPR, the new one will be treated as the suitable one. Otherwise, the old one will be taken as the predicted result.

A step number \(k_\mathrm{c}\) is determined for the case that the prediction result using GPR should always be repeated using NARX-RNN. After \(k_\mathrm{c}\) steps, the prediction process using both methods can be reduced by only using NARX-RNN.

Using this strategy, the suitable method for the identification can be selected automatically in the online process with guaranteed accuracy. The corresponding simulation examples will be shown in Sect. 5 to demonstrate the related performance.

3.2 Realization of stability criterion

As mentioned in the introduction, the considered systems to be stabilized are nonlinear discrete systems. Quadratic stability related to nonlinear discrete systems is considered in the module “expert knowledge” of the cognition-based framework.

Quadratic stability is defined [2] as: “The system described by \(x(k+1)=f(x(k))\) is called quadratic stable if there exists a positive definite matrix P, such that along the solution of the nonlinear discrete-time system the vector function

$$\begin{aligned} v(x(k))=x(k)^{T}Px(k) \end{aligned}$$
(18)

satisfies

$$\begin{aligned} \Delta v(x(k))=v(x(k+1))-v(x(k))\le 0\text {.''} \end{aligned}$$
(19)

The function v(x(k)) is the Lyapunov function for the actual discrete system considered. Evidently, assuming a positive definite matrix P,

(20)

will be considered to establish the Lyapunov function.

In order to realize this criterion in a data-driven manner, data-driven quadratic stability criterion [29] and a certain Lyapunov function with coordinate transformation [18] are developed.

3.2.1 Data-driven quadratic stability criterion

The main idea of data-driven quadratic stability criterion is to establish a relationship between the measured system states and the quadratic stability of trajectories of a nonlinear discrete-time systems directly by utilizing a geometric method. According to [29], a brief introduction is given in the sequel.

In order to present such a criterion in a data-driven manner, a geometric method is used and the corresponding necessary definitions is stated at first:

Definition 1

“A negative open half space \(h^{-}\) [15] is the half space of the n-dimensional Euclidean space \(E^{n}\) containing the complete set of points below a non-vertical hyperplane h in \(E^{n}\). If a vector w is located in a negative open half space, its inner products with all the vectors located in the space \(R^{n+}\) are less than zero.”

Definition 2

“A subset \(C_\mathrm{s}\) of a vector space V is a convex cone if and only if \(p_{1}x+p_{2}y\) belongs to \(C_\mathrm{s}\), for any positive scalars \(p_{1}\), \(p_{2}\), and any x, y in C.”

With these geometric definitions, the quadratic stability of the system states can be judged using a geometric approach as given in the sequel.

It is assumed that the system states are fully measurable and free of noise. The controlled system

$$\begin{aligned} x(k + 1) = f(x(k), u(x(k), x(k-1),\ldots ,x(k-l)) ) \end{aligned}$$
(21)

and an arbitrary physical possible state \(x_\mathrm{a}\) of the system to be controlled are considered. The system to be controlled should be stabilized at the state \(x_\mathrm{a}\) which is also the equilibrium point of the controlled system. According to the first definition, only the stability of the original point \(x_0=0\) of the space h can be evaluated. Therefore, the state variables are transformed firstly into a new coordinate as \(x_\mathrm{new}=x_\mathrm{old}-x_\mathrm{a}\). In this case, \(x_\mathrm{new}=x_0=0\) defines exactly \(x_\mathrm{old}=x_\mathrm{a}\).

The criterion is defined with the definitions mentioned above: The origin \(x_0 = 0\) is an asymptotically stable equilibrium point of the system related to the motion observed, if and only if every vector w is contained in a convex cone which is located in a negative open half space \(h^{-}\). A similar proof regarding the controlled system is given in [29]. The vector w is obtained by the transformation of all system states x, \(x\ne 0\) with

$$\begin{aligned} w=\text {diag}[\varphi f(x)]\varphi x \end{aligned}$$
(22)

using \(\varphi \) as an orthogonal matrix.

3.2.2 A certain Lyapunov function with coordinate transformation

Another possibility to realize the quadratic stability in a data-driven manner is to design a Lyapunov function which can satisfy the requirements given in Eqs. (19) and (20) only using the system measurements. A suitable Lyapunov function as illustrated in [18] is

$$\begin{aligned} v(e(k))=e^\mathrm{T}(k)\cdot e(k)\text {,} \end{aligned}$$
(23)

using \(e(k)=w-x(k)\) with w as the reference vector of the system outputs. A transformation of the state variables \(x_\mathrm{new}=x_\mathrm{old}-x_\mathrm{a}\) into the new coordinates similar to the data-driven quadratic stability criterion is also necessary. With this transformation, the reference vector can always be defined as \(w{=}x_0{=}[0 \text {, }\ldots \text {, }0]\) which means that e(t) can be defined as \(-x(t)\). The Lyapunov function is redefined in the new coordinates as

(24)

which satisfies the conditions in (20) with all system states.

The resulting problem is to define a suitable vector \(x(k+1)\) to satisfy the condition (19) as

$$\begin{aligned} \big \Vert x(k+1)\big \Vert \mathop {<}\limits ^{!}\big \Vert x(k)\big \Vert \text {.} \end{aligned}$$
(25)

From the control point of view, a suitable range of the desired system states \(x_d(k+1)\) can be determined using the inequality (25), which can guarantee the quadratic stability of the motion of the system. Therefore, the new control input can be found with the help of the inverse control technique within a suitable range of \(x_d(k+1)\). This kind of realization can only be used together with the inverse learning process as given in Sect. 3.1.

Both stability criteria are suitable for data-driven stability evaluation. The data-driven quadratic stability criterion is used to evaluate arbitrary predicted system states at each time step. Using the second criterion, a suitable exactitude range of the desired system outputs can be calculated. However, the inverse model of the system has to be generated first. Both criteria allow the evaluation to define a suitable corresponding input. The application of the two stability criteria of the cognitive stabilizer will be explained in the following subsection.

3.3 Realization of “planning and execution”

The input variables of the system to be realized are bounded from the physical point of view in a certain interval denoted by [a, b]. The task of the module “planning and execution” is to determine those suitable control input series within [a, b] which enables the controlled system to satisfy the chosen stability criterion and the most suitable control input (as optimal solution) among the suitable control input series. It is assumed that the optimal solution is related to a quadratic cost function as

$$\begin{aligned} J=\left( x_d^{T}(k+1) Q x_d(k+1)+u_d^{T}(k) R u_d(k)\right) \text {,} \end{aligned}$$
(26)

where Q and R are positive definite weighting matrices. This cost function is one kind of representation of the system energy consisting of the state energy \(x_d^{T}(k+1) Q x_d(k+1)\) and the input energy \(u_d^{T}(k) R u_d(k)\). The optimal solution is therefore the one which is determined among the suitable input series related to the stability criterion and minimizes the cost function (26).

Two different strategies (exhaustive grid search and inverse dynamic optimal control method) are considered. Both are applied for the module “planning” and the module “execution.”

3.3.1 Exhaustive grid search method

Considering the system input signals, the bounded interval \([a_j, b_j]\) with \(j=1 \ldots m\) distinguishing the input signal \(u_j\) separately. If all bounded intervals are partitioned into several subintervals without intersections as

$$\begin{aligned}{}[a_j,\quad a_j+\Delta u_j, \ldots , b_j] \end{aligned}$$
(27)

with a suitable interval \(\Delta u_j\) for each input (denote \(\Delta U\) for all inputs), the number of the possible input values is finite. The method of exhaustive grid search can be used to determine optimization target (26) as firstly detailed in [22] and therefore briefly repeated in the sequel.

The endpoint of each subinterval will be considered as a possible value of the corresponding input signal. The cost function (26) and the stability of the predicted motion are calculated and evaluated for all possible values \(\Delta u_j\) of all inputs (\(u_j\)) and the corresponding predicted outputs. The possible input vectors able to generate a stable behavior are stored in a set \(U_\mathrm{s}\). The input vector among \(U_\mathrm{s}\) minimizing the cost function is denoted as the optimal solution of the control input vector and will be generated in the module “execution.”

Using this kind of strategy, the optimal control input can be found and the stability of the controlled system can be guaranteed. In order to reduce the computational load of the algorithm, the use of the exhaustive grid search method is simplified and illustrated as flowchart in Fig. 3.

Fig. 3
figure 3

Flowchart of the cognitive stabilizer using exhaustive grid search method

Full size image

As the next step following the initial training process using the system identifier, the norm of the current system states x(k) has to be checked firstly for each prediction horizon to improve the calculation efficiency. Using the stability criterion, a coordinate transformation with the desired equilibrium point of the controlled system as the original point is required in the whole process. It is larger than a predefined distance \(\delta \), which means if the system states are not close to the equilibrium point of the controlled system (\( \big \Vert x(k)\big \Vert >\delta \)) or the absolute values of the system states are not small enough, the realizable interval of the system inputs [a, b] with a given sample interval \(\Delta U\) is used as the elements in set \(U_\mathrm{s}\). As mentioned before, the system identifier cannot predict the system without prediction error. If the absolute values of the real system states are larger than the difference of different possible system input vector values, the prediction results can be similar. So the related suitable inputs are around all possible input vector values for the case \( \big \Vert x(k)\big \Vert >\delta \). Using a larger sample interval, the number of the elements in \(U_\mathrm{s}\) can be reduced so a suitable input vector can be found. If \( \big \Vert x(k)\big \Vert \) is smaller than \(\delta \), a relative small boundary [a, b] and a small sample interval \(\Delta U\) should be used. In this case, the absolute values of the system states are relative small. Therefore, the accuracy of the predicted results with different system inputs with small \(\Delta U\) can be guaranteed and therefore used to find the most suitable input vector stabilizing the system at the desired equilibrium point. Therefore, a small boundary interval [a, b] is used in this case in order to improve the computational efficiency. After the adjustment of [a, b] and \(\delta \), the set \(U_\mathrm{s}\) for the possible inputs is determined.

With respect to the computational load, the calculation of the cost function is less intensive than that of the stability check. The applied numerical calculation steps required are as follows: (1) The system states related to the possible input vectors are predicted using the learned dynamic system behavior; (2) ranking of the cost function values according to the predicted system states is determined as next step; (3) the stability of the motion of the predicted system is checked according to the generated ranking; (4) as long as the stability criterion is fulfilled, the stability check is stopped; (5) the corresponding input vector is determined and executed as the optimal input vector for the next s steps. Evidently, it is necessary to train the dynamic system behavior again for each prediction horizon to detect changes of the unknown system or its environment online.

Using this strategy, the computational requirements can be reduced and the relative optimal control input, which can guarantee the stability of the motion, can be planned.

3.3.2 Inverse dynamic optimal control method

If the inverse dynamics of the system can be predicted with suitable accuracy, the stability criterion providing a range of the desired stable system states can be used. Comparing to the exhaustive grid search method, it is not required to check the stability of the predicted motion of all possible control input separately. The control strategy firstly applied in [18] denoted as inverse dynamic optimal control method is developed.

The inverse dynamics of the system are identifiable and predictable for the given desired system states \(x_d(k+1)=[x_d(k+1),\ldots ,x_d(k+s)]\) for each prediction horizon, the desired system input matrix is determined as

$$\begin{aligned} u_d(k)=f(k, [x(k) x_d(k+1)], u(k)]\text {.} \end{aligned}$$
(28)

Similar to the system input values, restrictions of the system states may be also required using a certain boundary range. Therefore, a new condition for the possible range of any desired system states \(x_d(k+p)\) with \(p\in [1\ldots s]\) as

$$\begin{aligned} \big \Vert x_d(k+p)\big \Vert \mathop {\le }\limits ^{!} \big \Vert x(k+p-1)\big \Vert +\epsilon (k+p) \end{aligned}$$
(29)

is used. The boundary \(\epsilon (k+p)\) can be determined approximately according to the previous system behavior as

$$\begin{aligned} \epsilon (k+p)=\bigg \Vert \Big [ \left\| x_1 \right\| _\infty \quad \left\| x_2 \right\| _\infty \quad \cdots \quad \left\| x_n \right\| _\infty \Big ] \bigg \Vert \end{aligned}$$
(30)

with \(x_n=[x_n(1)\quad x_n(2) \quad \cdots \quad x_n(k+p)]\).

The optimal desired system inputs are determined minimizing the cost function \(u_d(k+p-1)=\text {argmin }J\) with the inequality constrains (29) in combination with the stability criterion using the active set algorithm [6]. A flowchart of the algorithm introduced is illustrated in Fig. 4.

Fig. 4
figure 4

Flowchart of the cognitive stabilizer using direct input optimization with inverse model

Full size image

After the initial training process using the chosen system identifier for the inverse model of the system, the norm of the current system states x(k) will also be firstly checked for each prediction horizon similarly like using the exhaustive grid search method. A coordinate transformation with the desired equilibrium point of the controlled system as original point is needed to fulfill the stability criterion. If \( \big \Vert x(k)\big \Vert >\delta \), the stable range \([\alpha \text { } \beta ]\) of the desired system states is determined using the stability criterion according to Eq. (29) for the next step. The optimal desired system input vector according to the desired system state vector among \([\alpha \text { } \beta ]\) using the identified system model for the next step is determined by minimizing the cost function. Repeating iteratively this process p times, the optimal desired system input matrix can be determined for the next s steps. If \( \big \Vert x(k)\big \Vert <\delta \), additionally an integral controller is applied. The difficulty to predict the system dynamics with a high accuracy results from small absolute values of the system transformed states and the optimal desired input vector searched among the whole physical possible range \([a \text { } b]\). Therefore, an integral controller (I-controller) with a certain gain vector \(K_\mathrm{I}\) is applied due to its advantages of eliminating static control error. Using this strategy, the optimal control inputs \(U_d(k)\) for the prediction horizon can always be executed. Evidently, a training process for each prediction horizon is also required here.

4 Simulation results

The proposed cognitive stabilizer is applied to a benchmark nonlinear chaotic MIMO system—Lorenz system, which has 3 states, 2 inputs and 3 different equilibrium points and is described by

$$\begin{aligned} \dot{x} = \begin{pmatrix} -\sigma x_1 + \sigma x_2+u_1\\ -x_1 x_3 - x_2 + r x_1+u_2\\ x_1 x_2 - b x_3 \end{pmatrix}\text {, } x(t=0)=x_0. \end{aligned}$$
(31)

The parameters are given for the simulation as \(\sigma =10\), \(r=28\), and \(b=\frac{8}{3}\). The three equilibrium points of the uncontrolled system are \(P_1=(0,0,0)\), \(P_2=(8.4853, 8.4853, 27)\), and \(P_3=(-8.4853, -8.4853, 27)\). The desired control task is to stabilize the Lorenz system at one arbitrary equilibrium point.

Assuming a sample time of \(T_\mathrm{s}=10^{-3}\)s, a training time \(T_\mathrm{t}=0.5\)s, \(\eta =30\), \(\alpha =0\), \(s_n=0.05\), the initial condition of the outputs \({\hbox {ini}}=[-10\) 10 25], \(s=5\), and the covariance function

$$\begin{aligned} c=v_1\exp \left[ -\frac{1}{2}\sum \limits _{d=1}^{m}w_d(u^p-u^q)^2\right] +v_0, \end{aligned}$$
(32)

the cognitive identifier is applied first separately to the Lorenz system with a standard normal distributed random input training data and step control input test data. The results obtained from the training and predictions phases are shown in Fig. 5 to demonstrate the performance of the combined identifier.

Fig. 5
figure 5

Comparison of real and predicted outputs using combined identifier. (Color figure online)

Full size image

The input and real output data are denoted with black lines. The predicted system outputs using GPR (blue points) and using NARX-RNN (green points) are shown. The accepted predicted outputs (red points) indicate clearly that the combined identifier can be used for predicting the outputs of nonlinear dynamical MIMO system with acceptable accuracy.

Between \(k=500\) and \(k=600\), the system outputs are predicted using GPR with high accuracy except by \(k=515\), \(k=520\), \(k=525\), and \(k=590\), as denoted by blue points. Therefore, NARX-RNN is used to guarantee the prediction accuracy. Only the not acceptable predicted outputs by using GPR are replaced with the predicted results by using NARX-RNN. For example, for \(k=515\), only the first and second predicted outputs using GPR are not suitable enough and are replaced by the predicted results using NARX-RNN. There is no need to take the predicted result using NARX-RNN for the third output. For the remaining part \(k=600\) only NARX-RNN is used, the corresponding results are acceptable. The result of this strategy in terms of the absolute prediction error is shown in Fig. 6.

Fig. 6
figure 6

Comparison of the absolute prediction error by using GPR and NARX-RNN. (Color figure online)

Full size image

For comparison, the prediction error using GPR is given (red lines) as well as the prediction error using NARX-RNN (blue lines). It can be detected from the figures that for the first 100 prediction steps, the not acceptable predicted system outputs using GPR can be detected and corrected using NARX-RNN during the online prediction process. The acceptable predicted system outputs using GPR show higher accuracy than those using NARX-RNN.

In this case, the ARE of the whole process is 0.3059 for \(x_1\), 0.3614 for \(x_2\), and 0.0187 for \(x_3\) using this kind of combined identifier. It can be concluded that the prediction accuracy can be guaranteed (by using validation processes) and optimized (by using GPR for the possible cases).

As mentioned in Sect. 2, each module of the cognitive framework can be realized using different methods and combined by autonomous communication. In this paper, 2 kinds of realization for the whole framework are given:

  • (I) Learning (by training) and predicting the system dynamic behavior using cognitive identifier, judging the quadratic stability of the predicted system motion using data-driven quadratic stability criterion, and defining of the optimal control input vector using Exhaustive Grid Search Method

  • (II) Learning the system inverse dynamic behavior using NARX-RNN, determining the desired system output vector related to the quadratic stability of the system motion using a certain Lyapunov function with coordinate transformation and the learned system inverse dynamic behavior, as well as defining of the optimal control input vector using direct input optimization.

Using the realization (I), the stabilization of Lorenz system at \(P_1\) will be simulated and the corresponding simulation results will be illustrated in Fig. 7 at first.

Fig. 7
figure 7

Time history of the Lorenz system by using the realization (I) of the proposed cognitive stabilizer (desired equilibrium point: \(P_1\)). (Color figure online)

Full size image

In this simulation, the following parameter values are taken: \(l=500\), \(Ts = 10^{-3}s\), the initial system states \({\hbox {ini}}=[-30\) 30 35], \(s = 5\), \(h = 100\), Q and R as unit matrices, and \(u\in [-2000\) 2000].

As shown in Fig. 7, the origin of the time history of the outputs denotes the equilibrium point \(P_1\). The free motion of the Lorenz system is indicated in green. It becomes clear that the system behavior will not move to any of its equilibrium point without control input. During the training period (here denoted with black-colored line), the standard normal distributed random inputs are given to the combined identifier in order to train the combined identifier. After the training period, the actual closed-loop response of the system (blue line) approaches the origin using the proposed controller after about 0.2 s.

To check the performance of the proposed realization of the cognitive stabilizer furthermore, the Lorenz system will be stabilized from \(P_1\) to an other equilibrium point \(P_2\) as well as from \(P_2\) to P3 as shown in Fig. 8.

Fig. 8
figure 8

Time history of the Lorenz system by using the realization (I) of the proposed cognitive stabilizer (desired equilibrium point: \(P_1 \rightarrow P_2 \rightarrow P_3\)). (Color figure online)

Full size image

Similar to the stabilization process by \(P_1\), a standard normal distributed random input value series will be given for l steps starting at \(k=2501\) (black lines). The system identifier uses only the knowledge about the system states nearby the origin till \(k=2500\) and can therefore not estimate the model of the system in the new situation without training. After the short training process, the Lorenz system can be stabilized from \(P_1\) to \(P_2\) as well as from \(P_2\) to \(P_3\) by repeating the process once again. If \(P_2\) or \(P_3\) is considered as the initial value of the free motion of the system, the Lorenz system will stay at the equilibrium (green line).

Using the realization (II), the stabilization of Lorenz system at \(P_2\) is simulated and the corresponding simulation results are illustrated in Fig. 9.

Fig. 9
figure 9

Time history of the Lorenz system by using realization (II) of the proposed cognitive stabilizer (desired equilibrium point: \(P_2\)). (Color figure online)

Full size image

In this simulation, the following parameter values are taken: \(l=500\), \(Ts = 10^{-4}s\), the initial system states \({\hbox {ini}}=[-30\) 30 40], \(s = 5\), Q and R as unit matrices, and \(u\in [-2000\) 2000].

During the training period denoted (black lines), the combined identifier is trained to be able to estimate the inverse model of the real system with high accuracy. After the training period, the free motion of the system is denoted (green lines). The actual closed-loop response of the system (blue lines) approaches the desired system state \(P_2\) using the proposed realization after about 0.35 s.

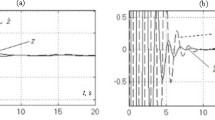
Using combined identifier to train the inverse model of the system for every prediction horizon, the closed-loop response of the system states can follow the desired system states with high accuracy. The performance of the inverse model estimation is indicated more clearly in Fig. 10, where the time history of \(x_2\) of the first 0.2s is shown. The error between the closed-loop response of the system states (blue line) and the desired system states (red points) is very small.

Fig. 10
figure 10

Phase portrait of the second state of the Lorenz system by using the realization (II) of the proposed cognitive stabilizer. (Color figure online)

Full size image

For this kind of realization, the Lorenz system also will be stabilized from the equilibrium point \(P_2\) to \(P_3\) started at \(t=2s\). The corresponding simulation results are shown in Fig. 11. After the required training process and about 0.1 s control process, the Lorenz system is stabilized during the transition from \(P_2\) to \(P_3\).

Fig. 11
figure 11

Time history of the Lorenz system by using the realization (II) of the proposed cognitive stabilizer (desired equilibrium point: \(P_2 \rightarrow P_3\)). (Color figure online)

Full size image

The proposed cognitive stabilizer was also applied to a benchmark nonlinear system—inverted pendulum system, and the corresponding successful simulation results are given in [22] with the realization (I) and in [18] with the realization (II).

In order to evaluate the performance of the proposed cognitive stabilizer furthermore, some ideal nonlinear switched systems can be considered for the simulation in future work. The corresponding results can be compared with other methods developed for the similar control task such as the one given in [17].

5 Summary

The novel concept of cognitive stabilizer which is developed to realize control design for stabilizing nonlinear dynamical MIMO systems with high autonomy is introduced, developed, and evaluated. The advantages and disadvantages of the existing data-based adaptive controller design methods are discussed. Different kinds of methods for realization the modules of the cognitive framework are introduced. Two kinds of realization of the cognitive stabilizer are presented. The proposed approach establishes a strong improvement of stabilizing approaches with respect to the computational load and the robustness.

Examples are given, showing the performance of the proposed controller. Using simulations, it is shown that the Lorenz system can be stabilized online at its arbitrary equilibrium point using both realizations. The combined identifier can predict the system dynamic behavior with acceptable accuracy during the online control process. The suitable control inputs are determined with respect to given cost functions. The stability of the motion of the system is guaranteed.

The approach proposed in this contribution is successfully developed and applied for stabilization tasks by the authors to realize all the expectations of the high autonomy. The approach can be used for unknown nonlinear dynamical MIMO discrete systems gaining only the knowledge about the I/O measurements. It is suitable for online control process to guarantee the stability of the closed-loop system in the whole control process.