1 Introduction

Integrable equations possess Wronskian solutions [1], by basing on Hirota bilinear forms [2]. Among such interesting and important solutions are solitons, positons and complexitons [3,4,5], and interaction solutions between different kinds of exact solutions describe more interesting nonlinear phenomena [1]. Surprisingly, integrable equations can also have algebraically localized solutions, called lump solutions [6, 7]. The Hirota bilinear formulation plays a crucial role in generating all those exact solutions, and usually, trial and error is a way to go with [8].

Nonlinear equations arising from physically relevant situations and possessing lump solutions contain the KP equation I [6, 9], the three-dimensional three-wave resonant interaction [10], the BKP equation [11, 12], the Davey–Stewartson equation II [13] and the Ishimori-I equation [14]. In particular, the KP equation of the following form:

$$\begin{aligned} (u_t+6uu_x+u_{xxx})_x-u_{yy}=0, \end{aligned}$$
(1.1)

has the lump solution [6]:

$$\begin{aligned} u=4\frac{-[x+ay+(a^2-b^2)t]^2+b^2(y+2at)^2+3/b^2}{\{[x+ay+(a^2-b^2)t]^2 +b^2(y+2at)^2+3/b^2\}^2},\nonumber \\ \end{aligned}$$
(1.2)

where a and b are real free parameters. General rational solutions to integrable equations have been generated from the Wronskian formulation, the Casoratian formulation and the Grammian or Pfaffian formulation (see [2, 7]). Typical examples include the KdV equation and the Boussinesq equation in (1+1)-dimensions, the KP equation in (2+1)-dimensions, and the Toda lattice equation in (0+1)-dimensions (see, e.g., [1, 15]). New attempts have also been made to search for rational solutions to other integrable and near-integrable equations, particularly in higher dimensions, by direct analytical approaches including the tanh-function method, the \(\frac{G'}{G}\)-expansion method, and the exp-function method without using Hirota bilinear forms (see, e.g., [16,17,18,19]). Links of rational solutions between integrable and near-integrable equations could also exist (see, e.g., [20]). Bilinear Bäcklund transformations are applied to rational solutions to (3+1)-dimensional generalized KP equations (see, e.g., [21]), and direct searches have been made for general rational solutions to nonlinear equations determined by generalized bilinear equations (see, e.g., [22,23,24,25]).

In this paper, we would like to consider interaction solutions between lumps and line solitons of the KP equation and generate five classes of interaction solutions by symbolic computations with Maple, which exhibit more diverse nonlinear phenomena. We will start from the Hirota bilinear form of the KP equation, and compute linear combination solutions to the bilinear KP equation by making linear combinations of quadratic functions and the hyperbolic cosine. Concluding remarks will be given finally in the last section.

2 Interaction solutions

The KP equation

$$\begin{aligned} P_{KP}(u):= (u_t+6uu_x+u_{xxx})_{x}-u_{yy} =0 \end{aligned}$$
(2.1)

is among the entire Sato KP hierarchy [26] and can be transformed into a Hirota bilinear equation [2]:

$$\begin{aligned} B_{KP}(f):= & {} \left( D_{x}D_t+D_{x}^4-D_y^2\right) f\cdot f \nonumber \\= & {} 2\left( f_{xt}f-f_tf_x+f_{xxxx}f-4f_{xxx}f_x\right. \nonumber \\&\left. +\,3{f_{xx}}^2-f_{yy}f+{f_{y}}^2\right) =0, \end{aligned}$$
(2.2)

under the transformation

$$\begin{aligned} u=2(\ln f)_{xx}=\frac{2\left( f_{xx}f-{f_x}^2\right) }{f^2}. \end{aligned}$$
(2.3)

This is also one of characteristic transformations adopted in Bell polynomial theories of soliton equations (see, e.g., [27, 28]), and in fact, we have

$$\begin{aligned} P_{KP}(u)=\Bigl (\frac{B_{KP}(f) }{f^2}\Bigr )_{xx} . \end{aligned}$$

Therefore, when f solves the bilinear KP Eq. (2.2), \(u=2(\ln f)_{xx}\) will present a solution to the KP Eq. (2.1).

The Hirota perturbation technique and symmetry constraints allow us to present soliton solutions and dromion-type solutions (see, e.g., [29,30,31,32]). In what follows, we focus on computing interaction solutions between lumps and line solitons to the KP Eq. (2.1) through searching for linear combination solutions to the bilinear KP Eq. (2.2) with symbolic computations, by making linear combinations of quadratic functions and the hyperbolic cosine.

We apply the computer algebra system Maple to look for linear combination solutions to the bilinear KP Eq. (2.2). We take an ansatz

$$\begin{aligned} f={\xi _1} ^2+{\xi _2}^2+ \cosh \xi _3+a_{13}, \end{aligned}$$
(2.4)

where three wave variables are defined by

$$\begin{aligned} \left\{ \begin{array}{l} \xi _1=a_{1}x+a_{2}y+a_{3}t+a_{4},\\ \xi _2=a_{5}x+a_{6}y+a_{7}t+a_{8},\\ \xi _3= a_{9}x+a_{10}y+a_{11}t+a_{12},\end{array} \right. \end{aligned}$$
(2.5)

the \(a_i\)’s being real constants to be determined. We consider two cases where taking \(a_{10}=0\) or \(a_{11}=0\). Direct Maple symbolic computations generate the following set of solutions for the parameters \(a_i\)’s:

$$\begin{aligned}&\displaystyle \Bigl \{ a_{{1}}=a_{{1}},\ a_{{2}}=-{\frac{a_{{6}}a_{{5}}}{a_{{1}}}},\ a_ {{3}}=-{\frac{{a_{{6}}}^{2}}{a_{{1}}}},\\&\quad a_{{4}}=a_{{4}},\ a_{{5}}=a_{{5} },\ a_{{6}}=a_{{6}}, \Bigr . \\&\,\, \displaystyle \Bigl . \ \ a_{{7}}=-{\frac{a_{{5}}{a_{{6}}}^{2}}{{a_{{1}}}^{2} }},\ a_{{8}}=a_{{8}},\ a_{{9}}={\frac{b\, a_{{6}}}{a_{{1}}}}, \\&\quad a_{{10}}=0,\ a_{{11}}=-{\frac{{a_{{6}}}^{3} }{9\, b\, {a_{{1}}}^{3}}}, \Bigr . \\&\,\, \displaystyle \Bigl . \ \ a_{ {12}} =a_{{12}},\ a_{{13}}\\&\quad ={\frac{36\,{a_{{1}}}^{8}+72\,{a_{{1}}}^ {6}{a_{{5}}}^{2}+36\,{a_{{1}}}^{4}{a_{{5}}}^{4}+{a_{{6}}}^{4}}{12\, {a_{{1} }}^{2}{a_{{6}}}^{2} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) }} \Bigr \}, \end{aligned}$$

upon taking \(a_{10}=0\), and the following four sets of solutions for the parameters \(a_i\)’s:

$$\begin{aligned}&\displaystyle \Bigl \{ a_{{1}}=0,\ a_{{2}}={\frac{ c \, a_{{7}} }{ 2\, a_{{9}}}}, \ a_{{3}}=\pm c \, a_{{7}}, \ a_{{4}}=a_{{4}},\\&\quad a_{{5}}=-{\frac{a_{{ 7}}}{2\, {a_{{9}}}^{2}}},\ a_{{6}}=\mp {\frac{a_{{7}}}{2 \, a_{{9}}}}, \Bigr . \\&\displaystyle \Bigl . \ \ a_{{7}}= a_{{7}},\ a_{{8}}=a_{{8}},\ a_{{9}}=a_{{9}},\ a_{{10}}=\pm {a_{{9}}}^{2}, \\&\quad a_{{11} }=0,\ a_{{12}}=a_{{12}},\ a_{{13}}={\frac{4\,{a_{{9}}}^{12}+{ a_{{7}}}^{4}}{ 4 \, {a_{{7}}}^{2}{a_{{9}}}^{6}}} \Bigr \} , \\&\displaystyle \Bigl \{ \ \ a_{{1}}={\frac{ b\, a_{{6}}}{a_{{9}}}},\ a_{{2}}=\pm b\, a_{{6}},\ a_{{3}}=- {\frac{2\, a_{{6}}a_{{9}}}{3\, c }},\\&\quad a_{{4}}=a_{{4}},\ a_{{5}} =0,\ a_{{6}}=a_{{6}}, \Bigr . \\&\displaystyle \Bigl . \ \ a_{{7}}=\pm 2\,a_{{6}}a_{{9}},\ a_{{8}}=0,\ a_{{9}}=a_{{9}} ,\ a_{{10}}=\pm {a_{{9}}}^{2},\\&\quad a_{{11}}=0,\ a_{{12}}=a_{{12}},\ a_{{13}}={\frac{9\,{a_{{9}}}^{8}+4\,{a_{{6}}}^{4}}{12\, {a_{{6}}}^{2}{a_{{9}}} ^{4}}} \Bigr \} ,\\&\displaystyle \Bigl \{ \ \ a_{{1}}=c\, a_{{5}} ,\ a_{{2}}=0,\ a_{{3}}=-4\,c\, a_{{5}}{a_{{9}}}^{2} ,\\&\quad a_{{4}}=a_{{4}},\ a_{{5}}=a_{{5}},\ a_{{6}}=\pm 4\,a_{{5} }a_{{9}}, \Bigr . \\&\displaystyle \Bigl . \ \ a_{{7}}=4\,a_{{5}}{a_{{9}}}^{2},\ a_{{8}}=a_{{8}},\ a_{{9}}=a_{{9 }},\ a_{{10}}=\pm {a_{{9}}}^{2},\\&\quad a_{{11}}=0,\ a_{{12}}=a_{{12}},\ a_{{13} }={\frac{64\,{a_{{5}}}^{4}+{a_{{9}}}^{4}}{16\, {a_{{5}}}^{2}{a_{{9}} }^{2}}} \Bigr \} ,\\&\displaystyle \Bigl \{ \ \ a_{{1}}= {\frac{\mp a_{{5}}a_{{9}}- a_{{6}}}{3\, b\, a_{{9}} }}, \ a_{{2}}=b\, ( 4\,a_{{5}}a_{{9}}\pm a_{{6}} ) ,\\&\quad a_{{3}}={\frac{2\, a_{{9}} ( \mp 2\,a_{{5}}a_{{9}} + a_{{6 }} ) }{3\, b }},\ a_{{4 }}=a_{{4}}, \Bigr . \\&\displaystyle \Bigl . \ \ a_{{5}}=a_{{5}},\ a_{{6}}=a_{{6}},\ a_{{7}}=-4\,a_{{5}}{a_{{9}} }^{2}\mp 2\,a_{{6}}a_{{9}},\\&\quad a_{{8}}=a_{{8}},\ a_{{9}}=a_{{9}}, \ a_{{10}}=\mp {a_{ {9}}}^{2},\ a_{{11}}=0, \Bigr . \end{aligned}$$
$$\begin{aligned}&\displaystyle a_{{12}}=a_{{12}},a_{{13}}\\&\quad ={\frac{ 64\,{a_{{5}}}^{4}{a_{{9}}}^{4}+9\,{a_{{9}}}^{8}\pm 64\,{a_{{5}}}^{3}a_{{6 }}{a_{{9}}}^{3}+48\,{a_{{5}}}^{2}{a_{{6}}}^{2}{a_{{9}}}^{2}\pm 16\,a_{{5} }{a_{{6}}}^{3}a_{{9}}+4\,{a_{{6}}}^{4}}{12\, {a_{{9}}}^{4} ( 4\,{a_{{5 }}}^{2}{a_{{9}}}^{2}+2\,a_{{5}}a_{{6}}a_{{9}}+{a_{{6}}}^{2} ) }} \Bigr \}, \end{aligned}$$

upon taking \(a_{11}=0\). In all above sets of solutions for the parameters \(a_i\)’s, the constants b and c are determined by

$$\begin{aligned} 3\,b^2-1=0,\ c^2 -{3}=0, \end{aligned}$$
(2.6)

and an equation \(a_i=a_i\) means that the parameter \(a_i\) is arbitrary provided that any other expressions using \(a_i\) make sense.

These sets of solutions for the parameters generate five classes of linear combination solutions \(f_i,\ 1\le i\le 5,\) defined by (2.4) and (2.5), to the bilinear KP Eq. (2.2), and then the resulting combination solutions present five classes of interaction solutions \(u_i,\ 1\le i\le 5\), under the transformation (2.3), to the KP Eq. (2.1). Each of the latter four sets of solutions for the parameters \(a_i\)’s contain the plus and minus signs, and both the constants b and c have two values. Therefore, various kinds of interaction solutions could be constructed explicitly this way.

The analyticity of the interactions solutions is automatically guaranteed for the first four classes and the last fifth class with the plus sign and can easily be achieved for the last fifth class with the minus sign, if we choose the parameters to ensure \(a_{13}>0\). We point out that the presented interaction solutions do not approach zero in all directions in the independent variable space since a line soliton is involved, and they form a peak at finite times due to the existence of a lump solution.

For the first class of interaction solutions and the fifth class of interaction solutions with the minus sign, let us choose the following two special sets of parameters:

$$\begin{aligned}&a_1=\frac{1}{2},\ a_4=a_5=0,\ a_6=-\frac{1}{2} ,\ \\&\quad a_8=0, \ a_{12}=1,\ b=\frac{\sqrt{3}}{3}, \end{aligned}$$

and

$$\begin{aligned}&a_4=0,\ a_5=1,\ a_6=-\frac{1}{2},\ a_8=0, \ \\&\quad a_9=-\frac{1}{2} ,\ a_{12}=1 ,\ b=\frac{\sqrt{3}}{3}, \end{aligned}$$

the second of which leads to \(a_{13}=\frac{65}{16}\), which is positive, indeed. The corresponding two special interaction solutions to the KP Eq. (2.1) read

$$\begin{aligned}&u_{1}= \frac{( 24\, x^2 {+}24\, y^2 -48\, xt +24\, t^2 +248 ) \cosh \xi _3 }{{g_1}^2} {-} \frac{96\sqrt{3} \,(-x {+} t) \sinh \xi _3 {+}36\,x^2 -36\,y^2 -72\,xt {+}36\, t^2 {-}252}{{g_1}^2}\nonumber \\ \end{aligned}$$
(2.7)
Fig. 1
figure 1

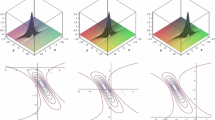
Profiles of (2.7) with \(t=0,5,10\): 3d plots (top) and contour plots (bottom)

Full size image

with

$$\begin{aligned} g_1= & {} 3\,{x}^{2} +3\, y^2 -6\,xt+3\,{t}^{2}\nonumber \\&+\,12\,\cosh \xi _3 +13,\ \xi _3=\frac{\sqrt{3}}{9}\, ( t-3\,x ) +1 ,\nonumber \\ \end{aligned}$$
(2.8)

and

$$\begin{aligned} u_{5,-}= & {} \frac{2\, \bigl [2+\frac{1}{4} \cosh (\frac{1}{2} \, x -\frac{1}{4}\, y -1) \bigr ]}{g_2}\nonumber \\&-\,\frac{2\, \bigl [ 2\,x-y-t+\frac{1}{2} \sinh ( \frac{1}{2} \, x -\frac{1}{4}\, y -1) \bigr ]^2 }{{g_2}^2}\nonumber \\ \end{aligned}$$
(2.9)

with

$$\begin{aligned} g_2= & {} \left( \frac{\sqrt{3}}{2} \,y-\frac{\sqrt{3}}{2} \, t \right) ^{2}+ \left( x -\frac{1}{2} \, y-\frac{1}{2}\, t \right) ^{2}\nonumber \\&+\cosh \left( \frac{1}{2} \, x -\frac{1}{4} \,y- 1 \right) +{\frac{65}{16}}, \end{aligned}$$
(2.10)

respectively.

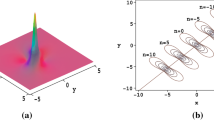
Three 3-dimensional plots and contour plots of the solution \(u_1\) at \(t= 0,5,10\) and the solution \(u_{5,-}\) at \(t= 0,10,15\) are shown in Figs. 1 and 2, respectively.

Fig. 2
figure 2

Profiles of (2.9) with \(t=0,10,15\): 3d plots (top) and contour plots (bottom)

Full size image

3 Concluding remarks

Through the Hirota formulation and symbolic computations with Maple, we constructed five classes of interaction solutions between lumps and line solitons to the KP equation explicitly, and the resulting classes of interaction solutions supplement the existing lump solutions in the literature.

On the one hand, we point out that the case of taking \(a_9=0\) leads to a class of trivial interaction solutions:

$$\begin{aligned} f= & {} ( a_{{3}} t+a_{{4}} ) ^{2}+ ( a_{{7}}t+a_{{8}} ) ^{2}\\&+\,\cosh ( a_{{11}}t+a_{{12}} ) +a_{{13}} , \end{aligned}$$

which is independent of the spatial variables. However, if we do not take any reduction, we could not work out any linear combination solution to the bilinear KP equation on personal computers. On the other hand, if we change the Hirota derivatives in (2.2) into generalized bilinear derivatives [33], all previous computations would be different in the case of the KP-like equation [23], though lump solutions generated from quadratic functions remain the same. It is also interesting to find linear combination solutions to other generalized bilinear and trilinear differential equations, formulated in terms of general bilinear derivatives [33], which should be pretty different from resonant solutions [34, 35].

Linear combination solutions could present interesting rogue wave solutions to the associated nonlinear equations under the transformations \(u= 2(\ln f)_x\) and \(u= 2(\ln f)_{xx}\). It is recognized that higher-order rogue wave solutions are connected with generalized Wronskian solutions [36] and generalized Darboux transformations [37], and higher-order generalizations of lump solutions and rogue waves can also be generated from the Fredholm determinant formulation [38]. All of these motivate us to compute more general interaction solutions to the KP equation. There is a long way to go to classify exact solutions to the KP equation.