1 Introduction

Well functional transportation system plays an important role in assisting people’s daily life and has been widely used to assess the creditworthiness of the degree of a city’s modernization. Over the last decades, traffic problems have attracted considerable attention where the conflict between resource, environment and the demand of transportation becomes more apparent. In order to study the substance of various traffic phenomenon deeply, a great number of traffic engineers, physicists and mathematicians throw themselves into the studies of the traffic flow dynamics in the frame of car- following behaviors [1,2,3,4,5,6,7,8,9,10,11]. Recently, many new traffic flow models and theoretical approaches have been developed with very gratifying results [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38].

It is observed that traffic jams occur and propagate as density waves when car density is higher than a critical value. Traffic jams in large-size cities have become a serious social problem attracting extensive attention of researchers from different backgrounds. The perturbation method has been used to investigate the morphology of traffic jams. Kerner and Konhäuser have found the single-pulse density wave by means of simulations, while Komatsu and Sasa derived the modified Korteweg–de Vries (KdV) equation from the optimal velocity model to represent traffic jams in terms of kink-density wave.

In order to efficiently suppress the formation of traffic jams, some efforts have been made to extend the original optimal velocity model. An important direction improving is to consider the cooperatively driving control which incorporates the traffic information of other vehicles by use of the system of information and communication technologies (ICT) in an environment of intelligent transportation system (ITS), with examples of several typical scholars as Nagatani, Li, Tang, Peng and Ge, etc [12,13,14,15,16,17,18,19,20,21,22]. However, the implementation of the cooperatively driving control highly depends on the quality of the communication network. A vehicle cannot still carry out the cooperatively driving control without the traffic data from other vehicles. In this particular case, an alternative scheme for suppressing traffic jams is to take advantage of traffic information of the considered vehicle itself as a source of control of stabilizing [39, 40]. We have been moving in this direction and have developed an extended optimal velocity model taking into account the historical velocity difference [38]. The improved model can stabilize traffic flow only utilizing the traffic data of the considered vehicle, i.e., the traffic flow can be stabilized only by each vehicle’s self-stabilizing control, without helps of the cooperatively driving control from others.

Self-stabilizing control is very crucial for the improvement of traffic flow stability because of its implementation dispensing with external factors. Self-stabilizing control in historical velocity difference can help to reduce the speed fluctuation between two successive time points, which finally deduces to the stable stage of whole traffic flow. But, do there exist other regulations for self-stabilizing control by using the considered vehicle’s traffic data other than traffic velocity? Can other new consideration of self-stabilizing control further stabilize traffic system on the basis of the self-stabilizing control in historical velocity difference? Here we shall concentrate our attention on such direction. We find that the driver needs to continuously adjust his optimal velocity according to the distance to the immediately preceding vehicle in the course of driving. The optimal velocities of each vehicle at two successive time points should be exactly same when the traffic flow is totally stable, which gives us a hint that the historical optimal velocity difference may be a desirable candidate target in further self-stabilizing control for traffic system. These analyses indicate that the self-stabilizing control in historical traffic data (the velocity and the optimal velocity of the considered vehicle) is necessary.

In this paper, we improve a historical velocity self-stabilizing control model to considering two self-stabilizing control methods and study the effect of the historical traffic data on the traffic behavior. We explore the new model’s ability against a small perturbation and compare it with the existing traffic flow model considering cooperatively driving control. In addition, we apply nonlinear analysis to the improved model and derive the modified KdV equation near the critical point by means of the perturbation method. We conduct the direct simulations to verify the results of theoretical analysis.

This paper is organized as follows. In Sect. 2, the improved optimal velocity model is proposed to consider the historical velocity and historical optimal velocity for the purpose to self-stabilizing control. The linear stability analysis of the proposed model is conducted, and the stability condition is obtained and discussed in Sect. 3. The self-stabilizing control dependence of the kink solution for traffic jams is obtained from the method of nonlinear analysis in Sect. 4. Numerical simulations are carried out in Sect. 5 to validate the analytic results of theory. Finally, we conclude our paper in Sect. 6.

2 Car-following model with self-stabilizing control

As basic and important representatives of microscopic approaches, car-following theories have been given considerable attention over past decades. Car-following model describes traffic flow at high level of detail from the point of individual drivers and vehicles. Bando et al. presented a favorable and famous car-following model called optimal velocity model (OVM) [1], which is a time-continuous model whose acceleration equation is given by

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}=a[V(\Delta x_n (t))-v_n (t)] \end{aligned}$$
(1)

where a is the sensitivity of a driver. The basic idea of the model is that each vehicle controls the acceleration \(\hbox {d}v_n (t)/\hbox {d}t\) of itself at time t to reduce the difference between the current velocity \(v_n (t)\) and an optimal velocity \(V(\Delta x_n (t))\), which depends on the distance \(\Delta x_n (t)\) of the immediately preceding vehicle.

Without loss of generality, the optimal velocity function \(V(\Delta x_n (t))\) is a monotonically increasing function and it has an upper bound. According to the original OVM, the optimal velocity function takes a hyperbolic tangent function as

$$\begin{aligned} V(\Delta x_n (t))=\frac{v_{\max } }{2}\left[ \tanh (\Delta x_n (t)-h_\mathrm{c} )+\tanh (h_\mathrm{c})\right] \nonumber \\ \end{aligned}$$
(2)

where \(h_\mathrm{c} =5\) is the safety distance and \(v_{\max } =2\) is the maximal velocity.

Here, we will pursue the mode of self-stabilizing control that suppresses traffic jams induced by small perturbations via the data of the considered vehicle’s own. We consider the historical velocity and historical optimal velocity of each vehicle as a potentially useful factor for stabilizing traffic flow and reducing traffic jams in the process of the interaction among vehicles. The stabilizing mode with the help of motion information of the considered vehicle belongs to the category of self-stabilizing control, which eliminates the dependence of the adjacent vehicles. In order to explore the effect of self-stabilizing control in historical traffic data, we develop an extended optimal velocity model, whose dynamics equation is

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}= & {} a\left[ {V(\Delta x_n (t))-v_n (t)} \right] \nonumber \\&+\,\lambda \left[ {V(\Delta x_n (t))-V(\Delta x_n (t-t_0 ))} \right] \nonumber \\&+\,m\left[ v_n (t)-v_n (t-t_0 )\right] \end{aligned}$$
(3)

where \(t_0 \) is the time gap between the current time t and the historical time \(t-t_0 \) and \(\Delta V_n =V(\Delta x_n (t))-V(\Delta x_n (t-t_0 ))\) represents the self-stabilizing control in the historical optimal velocity difference between the current optimal velocity \(V(\Delta x_n (t))\) and the historical optimal velocity \(V(\Delta x_n (t-t_0 ))\) of the nth vehicle. \(\Delta v_n =v_n (t)-v_n (t-t_0 )\) is the self-stabilizing control in the historical velocity difference of the considered vehicle. We expect the historical optimal velocity difference term \(\Delta V_n \) can further affect the traffic stability in suppressing traffic jams based on the self-stabilizing control in historical velocity difference, and they are introduced into our extended model with the constant coefficients \(\lambda \) and m.

The optimal velocity reflects a driver’s desiring speed when he drives on a motorway at a given headway. The velocity denotes the shifting of the displacement of the considered vehicle. The recorded data of a vehicle show the optimal velocity, and the velocity of all vehicles are running at a constant speed when the traffic flow is stable. The self-stabilizing control terms on the right-hand side of Eq. (3) are expected to enhance the performance in suppressing traffic jams and reduce the time cost from an unstable state to a stable one. The traffic flow can be stabilized only by each vehicle’s self-stabilizing control, without help of the cooperatively driving control from others.

3 Linear stability analysis

Small disturbance in speed or headway appears in the running of the vehicle flow inevitably, which induces heavy traffics with density waves naturally. Linear stability analysis method is usually used to analyze the traffic flow model’s ability against a small perturbation. Here, we analyze the proposed car-following model in a linear approach of stability analysis and explore whether the self-stabilizing control in historical optimal velocity difference can further stabilize traffic system on the basis of the self-stabilizing control in historical velocity difference.

In order to carry out the stability analysis easily, we introduce the linear analyzing process of the extended traffic flow model briefly. First of all, we change the expressing form of Eq. (3) as follows:

$$\begin{aligned}&f_n (\Delta x_n (t),v_n (t),\Delta x_n (t-t_0 ))\nonumber \\&\quad =a\left[ {V(\Delta x_n (t))-v_n (t)} \right] \nonumber \\&\qquad +\,\lambda \left[ {V(\Delta x_n (t))-V(\Delta x_n (t-t_0 ))} \right] \nonumber \\&\qquad +\,m[v_n (t)-v_n (t-t_0 )] \end{aligned}$$
(4)

A desired traffic flow is based on the situation that all vehicles move at the same velocity. The evolution of the traffic flow which is added a small disturbance could reach a stable equilibrium situation finally if the stability criterion is met, in which the speed of the considered vehicle is given by \(v_n =v_n^e \) and its headway is given by \(\Delta x_n (t)=\Delta x_n (t-t_0 )=\Delta x_n^e \). Moreover, the acceleration of each vehicle should be zero as expressed as \(f_n (\Delta x_n^e ,\Delta v_n^e ,\Delta x_n^e )=0\). It is assumed that \(\delta \Delta x_n (t)\),\(\delta v_n (t)\) and \(\delta \Delta x_n (t-t_0 )\) are small deviations from the steady-state solution: \(\Delta x_j (t)=\Delta x_j ^{e}+\delta \Delta x_j (t)\),\(v_j (t)=V_j (\Delta x_j ^{e})+\delta v_j (t)\) and \(\Delta x_j (t-t_0 )=\Delta x_j ^{e}+\delta \Delta x_j (t-t_0 )\). Based on that, we conduct the first-order Taylor expansion of Eq. (4) and obtain the following form:

$$\begin{aligned} \frac{\hbox {d}\delta v\left( t \right) }{\hbox {d}t}= & {} \underbrace{f_n \left( \Delta x_n^e ,\Delta v_n^e ,\Delta x_n^e \right) }_{=0}-(m-a)\delta v_n \left( t \right) \nonumber \\&+\,(a+\lambda )V^{\prime }(\Delta x_n^e )\delta \Delta x_n \left( t \right) \nonumber \\&-\,\lambda V^{\prime }(\Delta x_n^e )\delta \Delta x_n \left( {t-t_0 } \right) -m\delta v_n \left( {t-t_0 } \right) \nonumber \\ \end{aligned}$$
(5)

Supposed that \(\delta \Delta x_n (t)=\Delta X_n \hbox {e}^{in\omega +kt}\),\(\delta v_n (t)=V_n \hbox {e}^{in\omega +kt}\) and \(\delta \Delta x_n (t-t_0 )=\Delta x_n \hbox {e}^{in\omega +k\left( {t-t_0 } \right) }\), where \(V_n \) and \(\Delta X_n \) are constant. Considering that \(\Delta x_n (t)=x_{n-1} (t)-x_n (t)\) and \(\tfrac{\mathrm{d}\Delta x}{\mathrm{d}t}=v_{n-1} -v_n \), we can obtain:

$$\begin{aligned} \Delta X_j =\frac{V_{j-1} \hbox {e}^{-i\omega }-V_j }{k} \end{aligned}$$
(6)

Substituting Eq. (6) into Eq. (5), we can get:

$$\begin{aligned}&V_n \left( k^{2}-(m-a)k+(a+\lambda )V^{\prime }(\Delta x_n^e )\right. \nonumber \\&\qquad \left. -\,\lambda V^{\prime }(\Delta x_n^e )\hbox {e}^{-kt_0 }+km\hbox {e}^{-kt_0 } \right) \nonumber \\&\quad = V_{n-1} \hbox {e}^{-i\omega }\left( {(a+\lambda )V^{\prime }(\Delta x_n^e )-\lambda V^{\prime }(\Delta x_n^e )\hbox {e}^{-kt_0 }} \right) \nonumber \\ \end{aligned}$$
(7)

In our model, the traffic flow is homogeneous flow, so all vehicles have the same velocity in the stationary situation. That is \(V_n =V_{n-1} \). We can simplify Eq. (7)as follows:

$$\begin{aligned}&k^{2}+(m-a)k+(a+\lambda )V^{\prime }(\Delta x_n^e )\nonumber \\&\qquad -\,\lambda V^{\prime }(\Delta x_n^e )\hbox {e}^{-kt_0 }+km\hbox {e}^{-kt_0 }\nonumber \\&\quad = \hbox {e}^{-i\omega }\left( {(a+\lambda )V^{\prime }(\Delta x_n^e )-\lambda V^{\prime }(\Delta x_n^e )\hbox {e}^{-kt_0 }} \right) \end{aligned}$$
(8)

Solving Eq. (8) with k, we only consider the case of the k with \(\omega \) varying. It is concluded from Eq. (8) that when \(\omega \rightarrow 0\), \(\lambda \rightarrow 0\). Let us derive the long wave expansion of k, which is determined by order around \(i\omega \). Then extending a power series solution \(k=i\omega k_1 +(i\omega )^{2}k_2 +\cdots \), \(\hbox {e}^{-iw}=1-iw-\frac{w^{2}}{2!}\), and \(\hbox {e}^{-kt_0 }\,\hbox {=}\,1+\left( {-\,kt_0 } \right) +\frac{\left( {-kt_0 } \right) ^{2}}{2!}\), and substitute them into Eq. (8), the first- and second-order \(i\omega \) are obtained. We set the first-order o(w)and the second \(o(w^{2})\)terms as zero.

$$\begin{aligned}&o(\omega )=0\Rightarrow \quad k_1 =-V^{\prime }(\Delta x_n^e ) \end{aligned}$$
(9)
$$\begin{aligned}&o(\omega ^{2})=0\Rightarrow \quad \frac{-k_2 }{k_1^2 \left( {V^{\prime }(\Delta x_n^e )} \right) }=\frac{1}{2}\left( {\frac{1}{V^{\prime }(\Delta x_n^e )}} \right) ^{2}\nonumber \\&-\frac{1}{aV^{\prime }(\Delta x_n^e )}-\frac{t_0 a(\lambda +m)V^{\prime }(\Delta x_n^e )}{\left( {aV^{\prime }(\Delta x_n^e )} \right) ^{2}} \end{aligned}$$
(10)

Stability condition indicates that the real value R(k) of k should be \(R(k)\le 0\), So it could be presented that \(k_1 \le 0,\,k_2 \ge 0\). It is obvious that \(k_1 \le 0\) is satisfied absolutely in the extended car-following model. The key point of the stability condition is \(k_2 \ge 0\), which makes Eq. (10) satisfy

$$\begin{aligned} \frac{-k_2 }{k_1^2 \left( {V^{\prime }(\Delta x_n^e )} \right) }= & {} \frac{1}{2}\left( {\frac{1}{V^{\prime }(\Delta x_n^e )}} \right) ^{2}-\frac{1}{aV^{\prime }(\Delta x_n^e )}\nonumber \\&-\,\frac{t_0 a(\lambda +m)V^{\prime }(\Delta x_n^e )}{\left( {aV^{\prime }(\Delta x_n^e )} \right) ^{2}}\le 0 \end{aligned}$$
(11)

One is convinced that \(k_2 \ge 0\) is always guaranteed if

$$\begin{aligned}&\frac{1}{2}\left( {\frac{1}{V^{\prime }(\Delta x_n^e )}} \right) ^{2}-\frac{1}{aV^{\prime }(\Delta x_n^e )}\nonumber \\&\quad -\frac{t_0 a(\lambda +m)V^{\prime }(\Delta x_n^e )}{\left( {aV^{\prime }(\Delta x_n^e )} \right) ^{2}}>0 \end{aligned}$$
(12)

According to Eq. (12), the stability condition for the traffic flow with self-stabilizing control in historical optimal velocity difference is presented as follows:

$$\begin{aligned} {V}^{\prime }(\Delta x_n^e )<\frac{a}{2(1-t_0 (\lambda +m))} \end{aligned}$$
(13)

Comparing stability criterion Eq. (13) with that of only considering the self-stabilizing control in the historical velocity difference [38], we can find that the stable region of the extended model is enlarged to the region

$$\begin{aligned} \frac{a}{2(1-t_0 m)}<{V}^{\prime }(\Delta x_n^e )<\frac{a}{2(1-t_0 (\lambda +m))} \end{aligned}$$
(14)

Obviously, considering the historical optimal velocity difference, the traffic flow can be further stabilized on the basis of the self-stabilizing control in the historical velocity difference of the considered vehicle, which means double self-stabilizing control model provides a better performance in jams suppressing than single self-stabilizing control.

Fig. 1
figure 1

Neutral stability lines in the headway-sensitivity space for different \((\lambda +m)\) with a fixed value of time gap \(t_0 =1.0\,\hbox {s}\)

Full size image

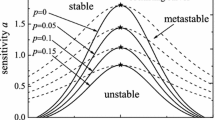
Stability criterion (13) gives the critical boundary between the stable region and the unstable one, which brings us a choice to discuss the relationship on the traffic stability and self-stabilizing control. We have derived that the stability of the traffic system can be enhanced with the increasing in the sum of two control coefficients \(\lambda \) and m. Figure 1 indicates the neutral stability lines in the space (\(\Delta x_n^e ,a)\) for different \(\lambda +m\) with the time gap \(t_0 =1.0\) s. The apex of each curve denotes the critical point as shown in Fig. 1, the region above the neutral stability line is stable region while the region below the line falls into the unstable region as a small disturbance is intervened into uniform traffic flow. From Fig. 1, we can conclude that the critical points and the neutral stability lines become lower gradually with the increasing in \((\lambda +m)\) which means that the self-stabilizing control in the historical traffic data (the optimal velocity and the velocity of the considered vehicle) can improve the stability of traffic system.

Figure 2 shows the neutral stability curves for different time gap \(t_0 \), where the control coefficients satisfy \(\lambda +m=0.2\). Obviously, the time gap also has an important influence on the traffic stability, and the stability regions are enlarged with the increasing of the time gap \(t_0 \), which is similar to that of only considering the self-stabilizing control model in historical velocity difference [38]. However, an important conclusion can be drawn that the stability improvement for the increasing in the sum of the two control coefficients and the time gap is limited. Traffic flow would return to the unstable state if the product of \(\lambda +m\) and \(t_0 \) satisfies \((\lambda +m)t_0 >1\).

Fig. 2
figure 2

Neutral stability lines in the headway-sensitivity space for different time gap \(t_0\), where two coefficients satisfy \(\lambda +m=0.2\)

Full size image

In order to illustrate the advantages of the proposed model better, we compare the self-stabilizing control method with the cooperatively driving control in optimal velocity. Peng et al. [13] presented a car-following model which considers the optimal velocity difference of the two adjacent vehicles utilizing the communication system of transportation system. To have a better comparison, we simplify their model as follows:

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}= & {} a[V(\Delta x_n )-v_n (t)]\nonumber \\&+\,k[V(\Delta x_{n+1} )-V(\Delta x_n )] \end{aligned}$$
(15)

where k is the control coefficient of the optimal velocity difference of the considered vehicle and its immediately preceding one. The stability criterion of model (15) is derived as

$$\begin{aligned} {V}^{\prime }(\Delta x_n^e )<\frac{a}{2}+k \end{aligned}$$
(16)

Comparing stability criteria (16) and (13), two findings can be summarized as follows:

  1. (1)

    Although two vehicle control modes can improve the stability of traffic flow, the cooperatively driving control of each vehicle relies heavily on endless supplies of the optimal velocity data from the preceding one. Once the real-time communication environment cannot be guaranteed, Peng’s control mode is hard to be carried on. The self-stabilizing control mode has the unparalleled advantage on the dependence on external data compared with cooperatively driving control.

  2. (2)

    Self-stabilizing control mode offers greater flexibility and scaling for implementing. The proposed car-following model has two variable and adjustable factors, while cooperatively driving control model has only one regulator. In other words, in the case of limited control strength \(\lambda \) (or m), self-stabilizing control can still suppress traffic jams by adjusting the time gap \(t_0 \).

4 Nonlinear analysis

In the part of linear stability analysis, we get stability criterion (13), in which we can know that the traffic stability can be improved by each vehicle’s self-stabilizing control. In this section, we conduct nonlinear analysis about the proposed model. When stability criterion (13) is not met, the vehicle flow will form density waves at some particular position on road. Nonlinear wave equation can be derived to describe the kink-antikink solution of these density waves. In order to examine the self-stabilizing control dependence of the kink solution for traffic jams, the nonlinear analysis is carried out to study the slowly varying behavior for the long waves in the unstable region, with the help of a small positive scaling parameter \(\varepsilon \). The simplest way to describe the long wavelength modes is the long-wave expansion.

It is convenient to rewrite Eq. (3) by using the asymmetric forward difference as follows:

$$\begin{aligned}&x_j \left( {t+2\tau } \right) -x_j \left( {t+\tau } \right) \nonumber \\&\quad =\tau V(\Delta x_j )+\lambda \tau ^{2}\left[ {V\left( {\Delta x_j (t)} \right) -V\left( {\Delta x_j (t-t_0 )} \right) } \right] \nonumber \\&\qquad +\,m\tau \left[ x_j \left( {t+\tau } \right) -x_j \left( t \right) \right. \nonumber \\&\qquad \left. -\,x_j \left( {t+\tau -t_0 } \right) +x_j \left( {t-t_0 } \right) \right] \end{aligned}$$
(17)

We introduce slow scales for space variable j and time variable t, and define the slow variables X and T for \(0<\varepsilon \le 1\) as follows:

$$\begin{aligned} X=\varepsilon (j+bt),\quad T=\varepsilon ^{3}t \end{aligned}$$
(18)

where b is a constant to be determined. We can set the headway as follows:

$$\begin{aligned} \Delta x_j =h+\varepsilon R\left( {X,T} \right) \end{aligned}$$
(19)

and further rewrite the Eq. (17) as:

$$\begin{aligned}&\Delta x_j \left( {t+2\tau } \right) -\Delta x_j \left( {t+\tau } \right) \nonumber \\&\quad =\tau \left[ {V(\Delta x_{j+1} )-V(\Delta x_j )} \right] \nonumber \\&\qquad +\,\lambda \tau ^{2}\left[ V\left( {\Delta x_{j+1} (t)} \right) -V\left( {\Delta x_j (t)} \right) \right. \nonumber \\&\qquad \left. -\,V\left( {\Delta x_{j+1} (t-t_0 )} \right) +V\left( {\Delta x_j (t-t_0 )} \right) \right] \nonumber \\&\qquad +\,m\tau \left[ \Delta x_j \left( {t+\tau } \right) \right. \nonumber \\&\qquad \left. -\,\Delta x_j \left( t \right) -\Delta x_j \left( {t+\tau -t_0 } \right) +\Delta x_j \left( {t-t_0 } \right) \right] \nonumber \\ \end{aligned}$$
(20)

Substituting Eqs. (18) and (19) into Eq. (20), and making the Taylor expansions to the fifth order of \(\varepsilon \), one can obtain the following nonlinear partial differential equation:

$$\begin{aligned}&\varepsilon ^{2}\left( {-b+{V}^{\prime }} \right) \partial _x R+\varepsilon ^{3}\left( {-\frac{3}{2}b^{2}\tau +\frac{V^{\prime }}{2}+(\lambda +m)b^{2}\tau t_0 } \right) \partial _X^2 R \nonumber \\&\quad +\,\varepsilon ^{4}\left\{ {-\partial _T R+\left( {-\frac{7b^{3}\tau ^{2}}{6}+\frac{V^{\prime }}{6}+\frac{\lambda \tau }{6}\left[ {3bt_0 -3b^{2}t_0 ^{2}} \right] +\frac{mb^{3}}{6}\left[ {3\tau ^{2}t_0 -3\tau t_0 ^{2}} \right] } \right) \partial _X^3 R-\frac{{V}^{\prime \prime \prime }}{6}\partial _X R^{3}} \right\} \nonumber \\&\quad +\,\varepsilon ^{5}\left\{ {\begin{array}{l} \left( {2mb\tau t_0 -3b\tau -\lambda \tau V^{\prime }t_0 } \right) \partial _T \partial _X R-\left[ {\begin{array}{l} \frac{15b^{4}\tau ^{3}}{24}-\frac{V^{\prime }}{24}-\frac{\lambda \tau }{24}\left[ {-3(bt_0 )^{3}+6(bt_0 )^{2}-3bt_0 } \right] \\ +\frac{mb^{4}}{24}\left[ {4\tau ^{3}t_0 -6\tau ^{2}t_0 ^{2}+4\tau t_0 ^{3}} \right] \\ \end{array}} \right] \partial _X^4 R \\ +\left( {\frac{V^{\prime \prime \prime }}{12}+\frac{V^{\prime \prime \prime }bt_0 \lambda \tau }{6}} \right) \partial _X^2 R^{3} \\ \end{array}} \right\} =0\nonumber \\ \end{aligned}$$
(21)

where \(V^{\prime }=V^{\prime }(h_\mathrm{c} )\) and \(V^{\prime \prime \prime }=V^{\prime \prime \prime }(h_\mathrm{c} )\).

By taking \(b={V}^{\prime }\), the second- and third-order terms of \(\varepsilon \) are eliminated from Eq. (21). We consider the neighborhood of the critical point \(\tau _\mathrm{c} \):

$$\begin{aligned} \frac{\tau }{\tau _\mathrm{c} }=1+\varepsilon ^{2} \end{aligned}$$
(22)

Equation (21) can be rewritten as follows:

$$\begin{aligned}&\varepsilon ^{4}\left\{ {-\partial _T R+\left( {-\frac{7b^{3}\tau _\mathrm{c} ^{2}}{6}+\frac{V^{\prime }}{6}+\frac{\lambda \tau _\mathrm{c} }{6}\left[ {3bt_0 -3b^{2}t_0 ^{2}} \right] +\frac{mb^{3}}{6}\left( {3\tau _\mathrm{c} ^{2}t_0 -3\tau _\mathrm{c} t_0 ^{2}} \right) } \right) \partial _X^3 R-\frac{{V}^{\prime \prime \prime }}{6}\partial _X R^{3}} \right\} \nonumber \\&\quad +\,\varepsilon ^{5}\left\{ {\begin{array}{l} \left( {\lambda b^{2}\tau _\mathrm{c} t_0 V^{\prime }-\frac{3}{2}b^{2}\tau _\mathrm{c} } \right) \partial _X^2 R+\left( {\frac{V^{\prime \prime \prime }}{12}+\frac{V^{\prime \prime \prime }bt_0 \lambda \tau _\mathrm{c} +2mb\tau _\mathrm{c} t_0 }{6}} \right) \partial _X^2 R^{3} \\ -\left[ {\begin{array}{l} \frac{15b^{4}\tau _\mathrm{c} ^{3}}{24}-\frac{V^{\prime }}{24}-\frac{\lambda \tau _\mathrm{c} }{24}\left[ {-3(bt_0 )^{3}+6(bt_0 )^{2}-3bt_0 } \right] \\ +\frac{mb^{4}\left( {4\tau _\mathrm{c} ^{3}t_0 -6\tau _\mathrm{c} ^{2}t_0 ^{2}+4\tau _\mathrm{c} t_0 ^{3}} \right) }{24} \\ \end{array}} \right] \partial _X^4 R \\ +\left( {2mb\tau _\mathrm{c} t_0 -3b\tau _\mathrm{c} -\lambda \tau V^{\prime }t_0 } \right) \left[ {\left( {\begin{array}{l} -\frac{7b^{3}\tau _\mathrm{c} ^{2}}{6}+\frac{V^{\prime }}{6}+\frac{\lambda \tau _\mathrm{c} }{6}\left[ {3bt_0 -3b^{2}t_0 ^{2}} \right] \\ +\frac{+mb^{3}\left( {3\tau _\mathrm{c} ^{2}t_0 -3\tau _\mathrm{c} t_0 ^{2}} \right) }{6} \\ \end{array}} \right) \partial _X^4 R-\frac{{V}^{\prime \prime \prime }}{6}\partial ^{2}_X R^{3}} \right] \\ \end{array}} \right\} =0 \end{aligned}$$
(23)

The coefficients of \(\partial _X^3 R,\partial _X R^{3},\partial _X^2 R,\partial _X^4 R,\partial _X^2 R^{3}\) is set as \(-g_1 ,g_2 ,g_3 ,g_4 ,g_5 \), respectively. Equation (24) can be rewritten

$$\begin{aligned}&\varepsilon ^{4}\left[ {\partial _T R-g_1 \partial _X^3 R+g_2 \partial _X R^{3}} \right] \nonumber \\&\quad +\,\varepsilon ^{5}\left[ {g_4 \partial _X^4 R+g_3 \partial _X^2 R+g_5 \partial _X^2 R^{3}} \right] =0 \end{aligned}$$
(24)

In order to derive the regularized mKdV equation with higher-order correction, we make the following transformations for Eq. (24) :

$$\begin{aligned} T^{\prime }= & {} -\left( {-\frac{7b^{3}\tau _\mathrm{c} ^{2}}{6}+\frac{V^{\prime }}{6}+\frac{\lambda \tau _\mathrm{c} \left( {3bt_0 -3b^{2}t_0 ^{2}} \right) }{6}+\frac{mb^{3}\left( {3\tau _\mathrm{c} ^{2}t_0 -3\tau _\mathrm{c} t_0 ^{2}} \right) }{6}} \right) T \end{aligned}$$
(25)
$$\begin{aligned} R^{\prime }= & {} -\left( {\frac{-7b^{3}\tau _\mathrm{c} ^{2}+V^{\prime }+\lambda \tau \left( {3bt_0 -3b^{2}t_0 ^{2}} \right) +mb^{3}\left( {3\tau _\mathrm{c} ^{2}t_0 -3\tau _\mathrm{c} t_0 ^{2}} \right) }{{V}^{\prime \prime \prime }}} \right) ^{\frac{1}{2}}R \end{aligned}$$
(26)

Thus we obtain the standard mKdV equations:

$$\begin{aligned} \partial _{{T}^{\prime }} {R}^{\prime }=\partial _X^3 {R}^{\prime }-\partial _X {R}^{\prime 3}-\varepsilon M\left[ {R^{\prime }} \right] \end{aligned}$$
(27)

where

$$\begin{aligned} M\left[ {R^{\prime }} \right] =\frac{1}{g_1 }\left[ {g_3 \partial _X^2 R^{\prime }+g_4 \partial _X^4 R^{\prime }+\frac{g_1 g_5 }{g_2 }\partial _X^2 R^{\prime 3}} \right] \nonumber \\ \end{aligned}$$
(28)
Fig. 3
figure 3

Space-time evolutions of the headway profile after a sufficient time \(t=9.9\times 10^{5}\) according to the proposed model for a \(\lambda +m=0.0\), b \(\lambda +m=0.05\), c \(\lambda +m=0.1\), and d \(\lambda +m=0.15\), respectively. \((t_0 =1.0, a=1.5)\)

Full size image
Fig. 4
figure 4

Snapshots of headway configuration of all vehicles at time steps \(t=9.9\times 10^{5}\) for a \(\lambda +m=0.0\), b \(\lambda +m=0.05\), c \(\lambda +m=0.1\), and d \(\lambda +m=0.15\), respectively. (\(t_0 =1.0\), \(a=1.5)\)

Full size image

Equation (27) is the mKdV equation with an \(\mathrm{O}\left( \varepsilon \right) \) correction term on the right-hand side. If we ignore the \(\mathrm{O}\left( \varepsilon \right) \) terms in Eq. (24), we get the mKdV equation with a kink solution as the desired solution

$$\begin{aligned} {R}^{\prime }_0 \left( {X,{T}^{\prime }} \right) =\sqrt{c}\tanh \sqrt{\frac{c}{2}}\left( {X-c{T}^{\prime }} \right) \end{aligned}$$
(29)

Next, assuming that \({R}^{\prime }(X,{T}^{\prime })={R}^{\prime }_0 (X,{T}^{\prime })+\varepsilon {R}^{\prime }_1 (X,{T}^{\prime })\), we take into account the \(\mathrm{O}\left( \varepsilon \right) \) correction. In order to determine the selected value of the propagation velocity c for the kink solution, it is necessary to satisfy the solvability condition

$$\begin{aligned} \left( {{R}^{\prime }_0 ,M[{R}^{\prime }_0 ]} \right) \equiv \int _{-\infty }^{+\infty } {\hbox {d}X{R}^{\prime }_0 M[{R}^{\prime }_0 ]} =0 \end{aligned}$$
(30)

where \(M[{R}^{\prime }_0 ]=M[{R}^{\prime }]\) for Eq. (28).

Fig. 5
figure 5

Time evolutions of the headway profile according to the proposed model for a \(t_0 =0.0\), b \(t_0 =0.3\), c \(t_0 =0.6\), and d \(t_0 =1.0\), respectively. (\(\lambda =0.15\), \(a=1.5)\)

Full size image

By performing the integration, we obtain the selected velocities

$$\begin{aligned} c=\frac{5g_2 g_3 }{2g_2 g_4 -3g_1 g_5 } \end{aligned}$$
(31)

We can obtain the value of propagation velocity for any vehicle by substituting the value \(g_1 ,g_2 ,g_3 ,g_4 ,g_5 \) into Eq. (31).

We can obtain the solution of the mKdV equation as:

$$\begin{aligned} R\left( {X,T} \right) =\sqrt{\frac{g_1 c}{g_2 }}\tanh \left[ {\sqrt{\frac{c}{2}}(X-cg_1 T)} \right] \end{aligned}$$
(32)

From the extended OVM, We can know \(V^{\prime }=v_{\max } /2\) and \({V}^{\prime \prime \prime }=-v_{\max } \), and the corresponding amplitude c of the kink–antikink soliton solution is computed by

$$\begin{aligned} A=\sqrt{\frac{g_1 c}{g_2 }\left| {\frac{\tau }{\tau _\mathrm{c} }-1} \right| } \end{aligned}$$
(33)

The kink–antikink solution represents the coexisting phase consisting of the freely moving phase with low density and the jammed phase with high density. Their headways are given by\(\Delta x=h_\mathrm{c} \pm A\).

5 Numerical simulation

Theoretical analyses have shown that the traffic flow can be more stable by considering double self-stabilizing control, under the limited condition of \((\lambda +m)t_0 <1\) . On the basis of the linear stability analysis, simulations are conducted to verify the correctness of the theoretical results in Sect. 3. In order to simplify many processes for the analysis in specifying boundary conditions, we perform simulations under a periodic boundary condition. We assume a platoon of vehicles runs in a ring road according to the extended model considering the self-stabilizing control in historical traffic data. We solve Eq. (3) numerically with optimal velocity function Eq. (2) by the method of the fourth-order-Runge–Kurra.

A small disturbance induced by a vehicle is introduced for the purpose of analyzing the stability for the proposed model of traffic flow. At the beginning, all vehicles run on a single lane without overtaking and inflowing, with the same initial headway and velocity. It is assumed that all vehicles run with the initial arrangement as follows:

$$\begin{aligned} \Delta x_j (0)= & {} \Delta x_j (1)=5.0\,\hbox {m}, \quad \left( {j\ne 50,51} \right) \end{aligned}$$
(34)
$$\begin{aligned} \Delta x_j (0)= & {} \Delta x_j (1)=5.0-0.1, \quad \left( {j=50} \right) \end{aligned}$$
(35)
$$\begin{aligned} \Delta x_j (0)= & {} \Delta x_j (1)=5.0+0.1, \quad \left( {j=51} \right) \end{aligned}$$
(36)

where the total number of vehicle is \(N=100\).

Firstly, we fix \(t_0 =1.0\) to demonstrate the effect of self-stabilizing control on the traffic stability. The inequality of \((\lambda +m)t_0 <1\) should be guaranteed when we choose different sums of two control coefficients \(\lambda \) and m. In Fig. 3, the patterns a–d show the space-time evolution of the headway for \(\lambda +m=0.0,\) 0.05, 0.1 and 0.15, respectively, where the sensitivity \(a=1.5\). In patterns a–c, the traffic flow is unstable while density waves appearing, since stability criterion (13) is unsatisfied for given parameters. The traffic flow state added a small disturbance transits from the initial uniform flow to the inhomogeneous kink-antikink traffic jams, which corresponds to the nonlinear analytical results in Sect. 4. In addition, the amplitude of the headway waves decreases with increasing of the sum of two control coefficient as shown in Fig. 4, in which all subplots correspond to those in Fig. 3, respectively. When the sum of two control coefficients is further increased to \(\lambda +m=0.15\), the kink-antikink density waves not occur in the pattern d of Figs. 3 and 4. It means that the traffic stability becomes better and better with more self-stabilizing control in historical traffic data, which is consistent with the theoretical analysis.

Next, we choose \(\lambda +m=0.15\) to explore the effect of the time gap \(t_0 \) on the stability of traffic system of single lane. Also, the condition \((\lambda +m)t_0 <1\) should be met when the time gap \(t_0 \) is set in the simulations. The patterns a–d in Fig. 5 show the space-time evolution of the headway after a sufficient time steps \(t=9.9\times 10^{5}\) for the time gap \(t_0 =0.0, 0.3, 0.6\) and 1.0, respectively, where the sensitivity \(a=1.5\). In patterns a–c, the traffic flow is unstable because stability criterion (13) is not satisfied. The kink-antikink headway waves occur as the form of traffic jams propagating backward. When the time gap changes to the value of \(t_0 =1.0\), the traffic system is stable with the headway waves disappearing and the traffic flow stay uniform flow over the whole time space. Figure 6 gives the snapshot of the headway profile at time \(t=9.9\times 10^{5}\) with all subplots corresponding to those in Fig. 5, respectively. We can observe that the amplitude of the headway wave decreases with increasing the time gap \(t_0 \). It demonstrates sufficiently that the time gap has an important effect on the traffic flow stability, and the whole traffic can be stabilized with the increasing in time gap. This result is in good agreement with the theoretical analysis.

Fig. 6
figure 6

Snapshots of headway configuration of all vehicles at time steps \(t=9.9\times 10^{5}\) a \(t_0 =0.0\), b \(t_0 =0.3\), c \(t_0 =0.6\), and d \(t_0 =1.0\), respectively. (\(\lambda =0.15\), \(a=1.5)\)

Full size image
Fig. 7
figure 7

The space-time evolution of the headway after the time steps \(t=9.9\times 10^{5}\) with the control coefficient \(\lambda +m=1.0\) and the time gap \(t_0 =1.5\)

Full size image

From stability criterion (13) of the extended model, the conclusion can be addressed that the effect of the self-stabilizing control on traffic stability should satisfy certain condition that the product of \(\lambda +m\) and \(t_0 \) is less than 1. It means our proposed model cannot support a stable traffic flow against small disturbances when the product is greater than 1. We can perform simulation to verify the conclusion by choosing the parameters of \(\lambda +m\) and \(t_0 \) to meet the condition that \((\lambda +m)t_0 >1\). Figure 7 shows the space-time evolution of the headway after the time steps \(t=9.9\times 10^{5}\) with the control coefficient \(\lambda +m=1.0\) and the time gap \(t_0 =1.5\). It can be easily found that the homogeneous steady flow finally evolves to drastic changes of the headway waves finally which is in good agreement with theoretical analysis.

Fig. 8
figure 8

Time-space evolutions of all vehicle for the cooperatively driving control (a) and the self-stabilizing control (b–d). (space evolutions of all vehicle for the cooperatively driving) \(k=0.125\); (b) \(\lambda +m=0.125, t_0 =0.5\); (c) \(\lambda +m=0.125, t_0 =1.0\);(c) \(\lambda +m=0.125, t_0 =1.5\)

Full size image

Theoretical analysis shows that the self-stabilizing control mode comes greater flexibility than that of cooperatively driving control. Here, we choose the same control strength for the cooperatively driving control and the self-stabilizing control to investigate the suppressing performance of jam waves induced by a small disturbance. The time-space evolution of all vehicles for the cooperatively driving control and the self-stabilizing control, are denoted by Fig. 8a–c, respectively. The data are obtained by recording the positions of vehicles during 990,000–1,000,000 steps. The control factor in subplot (a) is chosen for the cooperatively driving control with \(k=0.125\), and two control factors in subplot (b) are selected for the self-stabilizing control with \(\lambda +m=0.125\) and \(t_0 =0.5\). It is obvious that the stop-and-go waves appear on both simulations, for the reason that the control strength is not great enough to meet with stability criteria (13) and (16). However, we can observe that the stop-and-go wave which appears in subplot (b) is increasingly suppressed in subplot (c) and disappears in subplot (d), with another regulator \(t_0 \) changing from \(t_0 =0.5\) to \(t_0 =1.5\), which fully verified that the self-stabilizing control is more flexible to eliminate traffic jams in the case of limited control strength.

6 Summary

In this paper, we proposed an extended car-following model which takes into account of the self-stabilizing control in historical traffic data: the historical optimal velocity and the historical velocity of the considered vehicle. Linear stability analysis of the proposed model was conducted by the traditional theoretical derivation and finds that the traffic flow can be stabilized by the self-stabilizing control in the historical traffic data, just like the cooperatively driving control. It was also found that the time gap between the current time and the historical time has a significant effect on the stability criterion. We also summarized the strengths of the self-stabilizing control in the implementation, in comparison with cooperatively driving control. In addition, from the nonlinear analysis to the proposed model, the historical optimal velocity and historical velocity dependence of the propagating kink solutions for jam waves was obtained by deriving the modified KdV equation near critical point by using the reductive perturbation method. Finally, theoretical results were confirmed by direct simulations.