1 Introduction

In recent years, the modeling of traffic flow has attracted considerable attention in the field of physical science and engineering [1–3]. This increasing interest is stimulated not only by its practical application for optimizing traffic facilities and management, but also by the observed many interesting nonequilibrium phenomena, such as phase transition, hysteresis effect and stop-and-go waves in traffic flow [4–8].

In order to understand the mechanism and characteristics of the complex phenomena in traffic flow, many traffic models have been proposed, including macroscopic models (e.g., hydrodynamic models [9–13]) in which traffic flow is viewed as a compressible fluid formed by vehicles, and microscopic models (e.g., cellular automaton models [14–18] and car-following models [19–24]) where an individual vehicle is conceived to be a particle and the vehicle traffic is regarded as a system of interacting particles driven far from equilibrium. Since the car-following models can be easily implemented for numerical investigation and theoretical analysis, they have been widely applied to describe the driver’s individual behavior. Among them, the most well-known one is the optimal velocity (for short, OV) model [19], which has successfully revealed the dynamic evolution of traffic jam. However, comparison with empirical data shows that too high acceleration and unrealistic deceleration occur in the OV model. After that, many researchers have attempted to improve the OV model. Helbing and Tilch [20] introduced a negative velocity difference term into the OV model and developed the generalized force (for short, GF) model. But the GF model cannot explain the traffic phenomenon that if the leading vehicle is much faster, then the following vehicle will not brake, even if its headway is smaller than the safety distance. For this reason, Jiang et al. [21] proposed a more realistic full velocity difference (for short, FVD) model by further considering the effect of velocity difference and found that the stability of traffic flow is apparently improved and the results are in good agreement with the field data. Subsequently, many new car-following models were developed to describe the nature of traffic more realistically. Some of them were extended by considering the information of vehicle or road obtained by intelligent transportation system (for short, ITS) (e.g., inter-vehicle communication, multiple headway and relative velocity information [25–29]), and the others were improved by considering driver’s behaviors (e.g., anticipation, reaction-time delay and sensory memory effects [30–34]) and attributions (e.g., the driver’s bounded rationality, aggressive and conservative characteristics [35–37]).

However, these models rarely consider the influence of the honk effect on the driver’s behavior. In real traffic, when a vehicle hinders its following vehicle from moving at its current velocity, the following vehicle may honk its horn. Once the preceding driver hears the horn, the driver will probably change lane or accelerate according to the traffic state at that time. Although this phenomenon seldom occurs in the developed countries, it can often be observed in many developing countries (e.g., China). Thus, it is necessary to consider the honk effect to analyze the car-following behavior. Recently, Tang et al. [38] developed an extended the OV model with the honk effect, which shows that the honk effect can enhance the equilibrium velocity and flow when the traffic density is moderate. Thereafter, Tang et al. [39] further presented an improved car-following model to explore the impacts of the honk effect on the stability of traffic flow. The analytical and numerical results show that the honk effect can improve the stability of traffic flow. To further study the driver’s characteristics under honk environment, Wen et al. [40] proposed a modified OV model based on Tang’s model [39] by considering the timid or aggressive features of drivers behavior on traffic flow. However, some key factors of the honk effect have not been considered in the above models, e.g., the effect of velocity difference between the current and preceding vehicles. In fact, it has been widely proved that considering velocity difference in the model can improve the stability of traffic flow. Besides, the OV functions of the preceding and following vehicles have not been distinguished completely. As we know, the movement behavior of the preceding vehicle and the honk of the following one, which have different effects on the current vehicle, should be considered separately. Therefore, the different OV functions should be adopted in the course of modeling [41]. In addition, to our knowledge, the honk effect on the formation mechanism of density wave of traffic jam has not been explored in the car-following models up to now.

The aim of this paper is to provide a new insight to analyze qualitatively and explore theoretically how drivers adjust their micro-driving behavior based on the real-time traffic situation when hearing the horn of following vehicle. The paper is organized as follows: A new car-following model is introduced by considering the honk effect in Sect. 2. Then, the linear stability theory is employed to obtain the neutral stability condition in Sect. 3. The mKdV equation is obtained by applying the reductive perturbation method, and the evolution feature of traffic jam is described by the kink–antikink wave in Sect. 4. In Sect. 5, numerical simulations are performed to verify analytical results, and the intrinsic mechanism of the corresponding phase transition is explored. Finally, some conclusions are drawn.

2 Model

In 1995, Bando et al. [19] proposed the famous OV model to describe car-following behavior on a single-lane highway. The dynamical equation of the OV model is as follows:

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}=a\left[ {V\left( {\Delta x_n (t)} \right) -v_n (t)} \right] \end{aligned}$$
(1)

where \(x_{n}(t)\) and \(v_{n}(t)\) are the position and the velocity of the nth vehicle at time t, respectively. a denotes the sensitivity of the driver and is given by the inverse of the delay time \(\tau \), namely \(a=1/\tau \), \(\Delta x_n (t)=x_{n+1} (t)-x_n (t)\) is the headway between the leading vehicle \(n+1\) and the following one n, and \(V(\cdot )\) refers to the optimal velocity function.

Based on the OV model, Helbing and Tilch [20] in 1998 proposed a generalized force (GF) model. Its formulation is as follows:

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}= & {} a\left[ {V\left( {\Delta x_n (t)} \right) -v_n (t)} \right] \nonumber \\&+\lambda H({-\Delta v_n (t)})\Delta v_n (t) \end{aligned}$$
(2)

where \(H(\cdot )\) is the Heaviside function. It is a discontinuous function whose value is zero for negative argument and one for other arguments, i.e., \(H(x)\hbox {=}\left\{ {{\begin{array}{l} {{\begin{array}{ll} \hbox {0}&{} {x<0} \\ \end{array} }} \\ {{\begin{array}{ll} \hbox {1}&{} {x\ge 0} \\ \end{array} }} \\ \end{array} }} \right. \), and \(\Delta v_n (t)=v_{n+1} (t)-v_n (t)\) is the velocity difference of two successive vehicles, and \(\lambda \) is the responding factor to the velocity difference. The simulation results indicate that the GF model is poor in anticipating the kinematic wave speed and the delay time of car motion.

In 2001, by introducing positive relative velocity into the GF model, Jiang et al. [21] developed the full velocity difference (FVD) model as follows:

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}=a\left[ {V\left( {\Delta x_n (t)} \right) -v_n (t)} \right] +\lambda \Delta v_n (t) \end{aligned}$$
(3)

Compared with the OV and GF models, the results show that the FVD model is more realistic.

The aforementioned models can describe some complex traffic phenomena. However, these models cannot reflect the impacts of the honk effect on the car-following behavior realistically. How does this scenario affect the traffic dynamics in a single-lane highway? This is an interesting but still open problem.

Motivated by above reason, we propose a new car-following model to simulate single-lane traffic flow by taking into account the honk effect. The model is governed by the following partial equation:

$$\begin{aligned} \frac{\hbox {d}v_n (t)}{\hbox {d}t}= & {} a[ V_F ( {\Delta x_n ( t )} )( {1-p} )+V_B ( {\Delta x_{n-1} ( t )} )\nonumber \\&H( h_c-\Delta x_{n-1} ( t ) )p-v_n (t) ]+\lambda \Delta v_n ( t )\nonumber \\ \end{aligned}$$
(4)

where \(h_{c}\) is the safety distance; \(V_F ( {\Delta x_n ( t )} )\) is the OV function describing the forward looking effect, which is equivalent to the \(V( {\Delta x_n ( t )} )\) in Eq. (3) and \(V_B ( {\Delta x_{n-1} ( t )} )\), as the OV function describing the honk effect of the following vehicle, is similar to the backward looking effect of the current vehicle proposed by Nakayama [41] and can increase the velocity of the current vehicle when the headway of the following vehicle becomes small, here \(\Delta x_{n-1} (t)\) can be obtained by ITS (e.g., inter-vehicle communication [25, 26]). Note that the parameter p represents the weight of the honk effect, i.e., as \(\Delta x_{n-1} (t)<h_c \), the possible probability for following vehicle to honk the horn, which also indirectly reflects the relative roles of the two OV functions. In this paper, we take \(p\in \left[ {0,0.3} \right] \), which reflects the fact that in realistic situation, on the one hand, the probability to honk the horn is rare; on the other hand, even if the honk effect appears, the forward looking effect (i.e., the headway and relative velocity between the current and preceding vehicles) is still more important than the honk effect of the following vehicle in the single-lane traffic flow. The larger the p is, the more obvious the honk effect is. When p=0 (i.e., without the honk effect of the following vehicle), the new model is completely in accordance with the FVD model [21]. Besides that, \(H({h_c -\Delta x_{n-1} (t)})=\left\{ {{\begin{array}{l} {{\begin{array}{ll} 0&{} {\Delta x_{n-1} (t)>h_c } \\ \end{array} }} \\ {{\begin{array}{ll} 1&{} {\Delta x_{n-1} ( t )\le h_c } \\ \end{array} }} \\ \end{array} }} \right. \) is regarded as a factor to add the honk effect term of the dynamical Eq. (4), which means that when the following vehicle is very fast and near to the current vehicle (i.e., \(\Delta x_{n-1} (t)<h_c )\), it may honk its horn with probability p to urge the current one to accelerate motion. So the honk effect plays an important role only if the headway is less than a certain distance between the successive vehicles, which is set as the safety distance \(h_{c}\).

In this paper, the same optimal velocity function proposed by Bando et al. [19] is used as follows.

$$\begin{aligned}&V_F \left( {\Delta x_n (t)} \right) \hbox {=}\frac{v_{\max } }{2}\nonumber \\&\quad \left[ {\tanh \left( {\Delta x_n (t)-h_c } \right) +\tanh ({h_c })} \right] \end{aligned}$$
(5)
$$\begin{aligned}&\quad V_B \left( {\Delta x_{n-1} (t)} \right) \hbox {=}\frac{v_{\max } }{2}\nonumber \\&\quad \left[ {-\tanh \left( {\Delta x_n (t)-h_c } \right) +\tanh ({h_c })} \right] \end{aligned}$$
(6)

where \(v_\mathrm{max}=2\) is the maximal velocity and \(h_{c}=4\) is the safety distance.

3 Linear stability analysis

In general, the stability analysis method has been widely used in macroscopic models and microscopic models to theoretically study traffic instabilities [42, 43]. It is also worth mentioning that the stability analysis using microscopic models usually refers to the string stability of a platoon of vehicles following each other, which is also equivalent to the flow stability analysis using macroscopic models. In this paper, the same linear stability analysis [27] is applied to investigate the influence of honk effect on traffic flow. To do so, the stability of the uniform flow is considered. The uniform traffic flow is defined by such a state that all the vehicles moving with the constant headway b and the optimal velocity \(V_F (b)({1-p})+V_B (b)p\) on a circular road. Obviously, the steady-state solution for Eq. (4) is given by

$$\begin{aligned} x_n^0 (t)=bn+\left[ {V_F (b)\left( {1-p} \right) +V_B (b)p} \right] t,b=\frac{L}{N}\nonumber \\ \end{aligned}$$
(7)

where N is the total number of vehicles, and L is the length of the road.

Suppose \(y_n (t)\)is a small deviation from the steady-state solution \(x_n^0 (t)\), then the perturbed solution is

$$\begin{aligned} x_n (t)=x_n^0 (t)+y_n (t) \end{aligned}$$
(8)

Substituting Eqs. (7) and (8) into Eq. (4), then the linearized equation is obtained

$$\begin{aligned} \frac{\hbox {d}^{\hbox {2}}y_n (t)}{\hbox {d}t^{2}}= & {} a\left[ {V}'_F (b)\Delta y_n (t)({1-p})+{V}'_B (b)\Delta y_{n-1} (t)\right. \nonumber \\&\left. H({h_c -b-\Delta y_{n-1} (t)})p-\frac{\hbox {d}y_n (t)}{\hbox {d}t} \right] \nonumber \\&+\lambda \frac{\hbox {d}\left( {\Delta y_n (t)} \right) }{\hbox {d}t} \end{aligned}$$
(9)

where \(\Delta y_n (t)=y_{n+1} (t)-y_n (t)\) and \({V}'(b)=\left. {\left[ {{\hbox {d}V({\Delta x_n })}/{\hbox {d}\Delta x_n }} \right] } \right| _{\Delta x_n =b} \). Here, we mainly focus on the condition \(b<h_c -\Delta y_{n-1} \).

By expanding \(y_n (t)\)in the Fourier models:\(y_n (t)=\exp ({ikn+zt})\), one can obtain the following equation:

$$\begin{aligned}&z^{2}-z\left[ {\lambda ({e^{ik}-1})-a} \right] -a\bigg [ {V}'_F (b)({e^{ik}-1})\left( {1-p} \right) \nonumber \\&\quad +{V}'_B (b)({1-e^{-ik}})p \bigg ]=0 \end{aligned}$$
(10)

Expanding \(z=z_1 (ik)+z_2 (ik)^{2}+\cdots \), and inserting it into Eq. (10), the first-order and second-order terms of ik are obtained, respectively:

$$\begin{aligned} z_1= & {} {V}'_F (b)({1-p})+{V}'_B \left( b \right) p \end{aligned}$$
(11)
$$\begin{aligned} z_2= & {} \frac{1}{2}\left[ {{V}'_F (b)\left( {1-p} \right) -{V}'_B (b)p} \right] +\frac{1}{a}\left( {z_1 \lambda -z_1^2 } \right) \nonumber \\ \end{aligned}$$
(12)

When \(z_2 <0\), the uniform steady-state flow becomes unstable for the long wavelength modes. When \(z_2 >0\), the uniform traffic flow is stable. Thus, the neutral stability condition for the new model is derived as follows:

$$\begin{aligned} a= & {} 2\frac{\left[ {{V}'_F (b)({1-p})+{V}'_B (b)p} \right] ^{2}}{{V}'_F (b)( {1-p} )-{V}'_B (b)p}\nonumber \\&-2\lambda \frac{{V}'_F \left( b \right) ({1-p})+{V}'_B (b)p}{{V}'_F ( b )({1-p})-{V}'_B (b)p} \end{aligned}$$
(13)

Thus, the homogeneous traffic flow is stable under a small disturbance if the following condition is satisfied:

$$\begin{aligned}&a>2\frac{\left[ {{V}'_F (b)({1-p})+{V}'_B (b)p} \right] ^{2}}{{V}'_F (b)( {1-p} )-{V}'_B (b)p}\nonumber \\&\quad -2\lambda \frac{{V}'_F ( b)({1-p})+{V}'_B (b)p}{{V}'_F ( b )({1-p})-{V}'_B (b)p} \end{aligned}$$
(14)

Here, note that the stable traffic meeting above stable condition might actually still show short-wave lengths instability [42]. As \(p=0,a>2{V}'_F (b)-2\lambda \), the result of stable condition is the same as that of the FVD model [21].

Fig. 1
figure 1

Phase diagram in the headway-sensitivity space. The solid lines, dotted lines and asterisks indicate the neutral stability curves, the coexisting curves and the critical point, respectively

Full size image

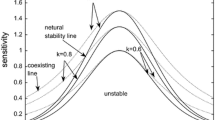
Figure 1 shows the neutral stability curves in the headway-sensitivity space under different values of p when \(\lambda =0.2\). The solid lines and dotted lines represent the neutral stability cures and the coexisting curves, respectively. The apex of each curve indicates the existence of a critical point \((h_c ,a_c )\) denoted by asterisks. Figure 1 shows that the phase diagram is divided into three regions by the solid lines and dotted lines: The first is the stable region above the coexisting curve, the second is the metastable region between the neutral stability line and the coexisting line, and the third is the unstable region below the neutral stability line. In the stable region, traffic jams do not occur when small disturbances are added. While in the metastable and unstable regions, the traffic flow is unstable and will evolve into congestion with time. In addition, the unstable region shrinks gradually with increase in p, which indicates the stability of the uniform traffic flow has been strengthened, and traffic jam is effectively suppressed. When p=0, the critical point and the neutral stability lines are consistent with those in the FVD model [21].

Fig. 2
figure 2

Plot of \(a_{c}\) against p, where \(\lambda =0.2\)

Full size image

In order to further explore the impacts of the honk effect on the stability of traffic flow, the relationship between the critical value \(a_{c}\) and the parameter p can be obtained from Eq. (13), i.e., \(a_c =2\frac{\left[ {{V}'_F ({h_c })\left( {1-p} \right) +{V}'_B ({h_c })p} \right] ^{2}}{{V}'_F \left( {h_c } \right) ({1-p})-{V}'_B \left( {h_c } \right) p}-2\lambda \frac{{V}'_F ({h_c })\left( {1-p} \right) +{V}'_B ({h_c })p}{{V}'_F \left( {h_c } \right) ({1-p})-{V}'_B ({h_c })p}\), and Fig. 2 gives the plot of critical sensitivity \(a_{c}\) against p, where \(\lambda =0.2\). From Fig. 2, it can be seen clearly that the critical sensitivity \(a_{c}\) decreases with increasing p, which means the stability regions are enlarged and the honk effect can improve the stability of traffic flow.

4 Nonlinear analysis

For further analysis and discussion, Eq. (4) can be rewritten as

$$\begin{aligned}&\frac{\hbox {d}^{2}\Delta x_n (t)}{\hbox {d}t^{2}}=a\left\{ (1-p)\left[ {V_F ({\Delta x_{n+1} ( \hbox {t})} )-V_F ({\Delta x_n ( \hbox {t})} )} \right] \right. \nonumber \\&\qquad \left. +p\left[ {V_B ({\Delta x_n ( \hbox {t})} )-V_B ({\Delta x_{n-1} ( \hbox {t})} )} \right] -\frac{\hbox {d}\Delta x_n (t)}{\hbox {d}t} \right\} \nonumber \\&\qquad +\lambda \left( {\frac{\hbox {d}\Delta x_{n+1} (t)}{\hbox {d}t}-\frac{\hbox {d}\Delta x_n (t)}{\hbox {d}t}} \right) \end{aligned}$$
(15)

We apply the reductive perturbation method to Eq. (15) and focus on the system behavior near the critical point \(\left( {h_c,a_c}\right) \). The small positive scaling parameter \(\varepsilon \) is introduced, which represents the deviation from the critical point \(a_c\). We introduce slow scales for space variables n and time variable t [7, 8] and define slow variables X and T as

$$\begin{aligned} X=\varepsilon (n+bt) \hbox { and } T=\varepsilon ^{3}t, 0<\varepsilon \ll 1 \end{aligned}$$
(16)

where b is a constant to be determined. The headway is set as

$$\begin{aligned} \Delta x_n (t)=h_c +\varepsilon R({X,T}). \end{aligned}$$
(17)

By expanding each term in Eq. (15) to the fifth order of \(\varepsilon \), one obtains

$$\begin{aligned}&\frac{\hbox {d}\Delta x_n (t)}{\hbox {d}t}=b\varepsilon ^{2}\partial _X R+\varepsilon ^{4}\partial _T R \end{aligned}$$
(18)
$$\begin{aligned}&\frac{\hbox {d}\Delta x_{n+1} (t)}{\hbox {d}t}=b\varepsilon ^{2}\partial _X R+b\varepsilon ^{3}\partial _X^2 R\nonumber \\&+\varepsilon ^{4}\left( {\frac{1}{2}b\partial _X^3 R+\partial _T R} \right) \nonumber \\&+\varepsilon ^{5}\left( {\frac{1}{6}b\partial _X^4 R+\partial _X \partial _T R} \right) \end{aligned}$$
(19)
$$\begin{aligned}&\frac{\hbox {d}^{2}\Delta x_n (t)}{\hbox {d}t^{2}}=b^{2}\varepsilon ^{3}\partial _X^2 R+2b\varepsilon ^{5}\partial _X \partial _T R \end{aligned}$$
(20)
$$\begin{aligned}&\Delta x_{n+1} (t)=h_c +\varepsilon R+\varepsilon ^{2}\partial _X R+\frac{1}{2}\varepsilon ^{3}\partial _X^2 R\nonumber \\&+\frac{1}{6}\varepsilon ^{4}\partial _X^3 R+\frac{1}{24}\varepsilon ^{5}\partial _X^4 R \end{aligned}$$
(21)
$$\begin{aligned}&\Delta x_{n-1} (t)=h_c +\varepsilon R-\varepsilon ^{2}\partial _X R+\frac{1}{2}\varepsilon ^{3}\partial _X^2 R\nonumber \\&-\frac{1}{6}\varepsilon ^{4}\partial _X^3 R+\frac{1}{24}\varepsilon ^{5}\partial _X^4 R \end{aligned}$$
(22)
$$\begin{aligned}&V_F (\Delta x_n )=V_F (h_c )+\varepsilon {V}'_F R+\frac{V_F^{{\prime }{\prime }{\prime }} }{6}\varepsilon ^{3}R^{3} \end{aligned}$$
(23)
$$\begin{aligned}&V_F (\Delta x_{n+1} )=V_F (h_c )+\varepsilon {V}'_F R+\varepsilon ^{2}{V}'_F \partial _X R\nonumber \\&+\varepsilon ^{3}\left( {\frac{{V}'_F }{2}\partial _X^2 R+\frac{{V}'''_F }{6}R^{3}} \right) \nonumber \\&+\varepsilon ^{4}\left( {\frac{{V}'_F }{6}\partial _X^3 R+\frac{V_F^{{\prime }{\prime }{\prime }} }{6}\partial _X R^{3}} \right) \nonumber \\&+\varepsilon ^{5}\left( {\frac{{V}'_F }{24}\partial _X^4 R+\frac{{V}'''_F }{12}\partial _X^2 R^{3}} \right) \end{aligned}$$
(24)
$$\begin{aligned}&V_B (\Delta x_n )=V_B (h_c )+\varepsilon {V}'_B R+\frac{V_B^{{\prime }{\prime }{\prime }} }{6}\varepsilon ^{3}R^{3} \end{aligned}$$
(25)
$$\begin{aligned}&V_B (\Delta x_{n-1} )=V_B (h_c )+\varepsilon {V}'_B R-\varepsilon ^{2}{V}'_B \partial _X R\nonumber \\&+\varepsilon ^{3}\left( {\frac{{V}'_B }{2}\partial _X^2 R+\frac{V_B^{{\prime }{\prime }{\prime }} }{6}R^{3}} \right) \nonumber \\&-\varepsilon ^{4}\left( {\frac{{V}'_B }{6}\partial _X^3 R+\frac{V_B^{{\prime }{\prime }{\prime }} }{6}\partial _X R^{3}} \right) \nonumber \\&+\varepsilon ^{5}\left( {\frac{{V}'_B }{24}\partial _X^4 R+\frac{{V}'''_B }{12}\partial _X^2 R^{3}} \right) \end{aligned}$$
(26)

where \({V}'_F ={V}'_F ({h_c })=\left[ {{\hbox {d}V_F (\Delta x_n )}/{\hbox {d}\Delta x_n }} \right] \left| {_{\Delta x_n =h_c } } \right. \), \({V}'''_F ={V}'''_F ({h_c })=\left[ {{\hbox {d}^{3}V_F ({\Delta x_n })}/{\hbox {d}^{3}\Delta x_n }} \right] \left| {_{\Delta x_n =h_c } } \right. \), \({V}'_B ={V}'_B ({h_c })=\left[ {{\hbox {d}V_B (\Delta x_n )}/{\hbox {d}\Delta x_n }} \right] \left| {_{\Delta x_n =h_c } } \right. \), \({V}'''_B ={V}'''_B ({h_c })=\left[ {{\hbox {d}^{3}V_B ({\Delta x_n })}/{\hbox {d}^{3}\Delta x_n }} \right] \left| {_{\Delta x_n =h_c } } \right. \).

By substituting Eqs. (18) and (26) into Eq. (15) and making the Taylor expansion to the fifth order of \(\varepsilon \), one can obtain the following nonlinear partial differential equation:

$$\begin{aligned}&\varepsilon ^{2}(b-m_1 )\partial _X R+\varepsilon ^{3}\left( {\frac{b^{2}}{a}-\frac{m_2 }{2}-\frac{b}{a}\lambda } \right) \partial _X^2 R \nonumber \\&\quad +\varepsilon ^{4}\left( {\partial _T R-\left( {\frac{m_1 }{6}+\frac{b\lambda }{2a}} \right) \partial _X^3 R-\frac{m_3 }{6}\partial _X R^{3}} \right) \nonumber \\&\quad +\varepsilon ^{5}\left( \frac{2b-\lambda }{a}\partial _X \partial _T R-\left( {\frac{m_2 }{24}+\frac{b\lambda }{6a}} \right) \partial _X^4 R\right. \nonumber \\&\quad \left. -\frac{m_4 }{12}\partial _X^2 R^{3} \right) =0 \end{aligned}$$
(27)

where \(m_1 =({1-p})V_F^{\prime } +pV_B^{\prime } \), \(m_2 =(1-p)V_F^{\prime } -pV_B^{\prime } \), \(m_3 =\left( {1-p} \right) V_F^{{\prime }{\prime }{\prime }} +pV_B^{{\prime }{\prime }{\prime }} \), \(m_4 =\left( {1-p} \right) V_F^{{\prime }{\prime }{\prime }} -pV_B^{{\prime }{\prime }{\prime }} \).

Near the critical point \(({\Delta x_c ,a_c })\), let \(a_c =a({1+\varepsilon ^{2}})\). By taking \(b=m_1 \), the second-order and third-order terms of \(\varepsilon \) can be eliminated from Eq. (27) and result in the following equation:

$$\begin{aligned}&\varepsilon ^{4}\left( {\partial _T R-g_1 \partial _X^3 R+g_2 \partial _X R^{3}} \right) \nonumber \\&\quad +\varepsilon ^{5}\left( {g_3 \partial _X^2 R+g_4 \partial _X^4 R+g_5 \partial _X^2 R^{3}} \right) =0 \end{aligned}$$
(28)

where \(g_1 =\frac{m_1 }{6}+\frac{\lambda m_1 }{2a_c }\), \(g_2 =-\frac{m_3 }{6}\), \(g_3 =\frac{m_2 }{2}\), \(g_4 =\frac{m_1 ^{2}-m_1 \lambda }{3a_c }+\frac{2\lambda m_1 ^{2}-\lambda ^{2}m_1 }{2a_c^2 }-\frac{m_2 }{24}\), \(g_5 =\frac{2m_1 m_3 -\lambda m_3 }{6a_c }-\frac{m_4 }{12}\),

Fig. 3
figure 3

Space–time evolution of the headway for different values of p

Full size image

In order to obtain the standard mKdV equation with higher correction, we make the following transformations to Eq. (28):

$$\begin{aligned} T=\frac{{T}'}{g_1 },R(X,T)=\sqrt{\frac{g_1 }{g_2 }}{R}'(X,{T}') \end{aligned}$$
(29)

Thus, we obtain the following regularized equation:

$$\begin{aligned} \partial _{{T}'} {R}'-\partial _X^3 {R}'+\partial _X {R}'^{3}+\varepsilon M\left[ {{R}'} \right] =0 \end{aligned}$$
(30)

where \(M\left[ {{R}'} \right] =\frac{1}{g_1 }\left[ {g_3 \partial _X^2 {R}'+g_4 \partial _X^4 {R}'+\frac{g_1 g_5 }{g_2 }\partial _X^2 {R}'^{3}} \right] \). If we ignore the \(O(\varepsilon )\) terms in Eq. (30), it becomes the standard mKdV equation with a kink solution as the desired solution:

$$\begin{aligned} {R}'_0 (X,{T}')=\sqrt{c}\tanh \left[ {\sqrt{\frac{c}{2}}(X-c{T}')} \right] \end{aligned}$$
(31)

In order to determine the selected value of the propagation velocity c for the kink solution Eq. (31), it is necessary to consider the solvability condition [7, 8],

$$\begin{aligned} ({{R}'_0 ,M\left[ {{R}'_0 } \right] })\equiv \int _{-\infty }^{+\infty } {\hbox {d}X{R}'_0 } M\left[ {{R}'_0 } \right] =0 \end{aligned}$$
(32)

where \(M\left[ {{R}'_0 } \right] =M\left[ {{R}'} \right] \). By performing the integration, one can obtain the selected velocity c,

$$\begin{aligned} c=\frac{5g_2 g_3 }{2g_2 g_4 -3g_1 g_5 } \end{aligned}$$
(33)

Hence, the kink–antikink solution of mKdV equation is obtained as follows:

$$\begin{aligned} R(X,T)=\sqrt{\frac{g_1 c}{g_2 }}\tanh \sqrt{\frac{c}{2}}\left( {X-cg_1 T} \right) \end{aligned}$$
(34)

By rewriting each variable to the original Eq. (17), the kink–antikink solution of headway is

$$\begin{aligned} \Delta x_n =h_c +\sqrt{\frac{g_1 c}{g_2 }( {\frac{a_c }{a}-1} )}\tanh \sqrt{\frac{c}{2}( {\frac{a_c }{a}-1} )}\nonumber \\ \left[ {n+\left( {1-cg_1 \left( {\frac{a_c }{a}-1}\right) t} \right) } \right] \end{aligned}$$
(35)

The amplitude A of the kink–antikink solution is described by

$$\begin{aligned} A=\sqrt{\frac{g_1 c}{g_2 }({\frac{a_c }{a}-1})} \end{aligned}$$
(36)

The kink–antikink solution represents the coexisting phase involving both the freely moving phase and congested phase. The coexisting curve can be described by \(\Delta x_n =h_c \pm A\) in the headway-sensitivity space and is shown in Fig. 1 by the dotted lines.

5 Simulation and discussion

To verify the theoretical results and reveal the influence of honk effect on traffic flow, numerical simulation is performed for the new model described by Eq. (4) by using the fourth-order Runger–Kutta method where the time interval is taken as\(\Delta t=1/{20}\). The periodic boundary is adopted, and the related parameters are taken as \(a=1,\lambda =0.2\). The initial conditions are chosen as follows:

\(\Delta x_n (0)=4, \Delta x_n ( 1 )=\Delta x_n ( 0 )=4\) for \(n\ne 50,51\); \(\Delta x_n ( 1 )=4+0.1\) for \(n=50; \Delta x_n ( 1 )=4-0.1\) for \(n=5\hbox {1}\), where the total car number is \(N=100\).

Figure 3 shows the space–time evolution of the headway after \(t=10,000\) time steps for different values of p. The patterns (a) to (d) in Fig. 3 correspond to \(p = 0, 0.05, 0.1\) and 0.15, respectively. Figure 3 clearly shows that the traffic flow is unstable in patterns (a)–(c), because the linear stability condition of Eq. (14) is not satisfied at \(a=1\), and the initial homogeneous flow will evolve into traffic jam under a small perturbation. The propagating behavior of traffic jam can be described by the kink–antikink solution of the mKdV equation. However, in pattern (d), the density waves disappear and the traffic flow is uniform over the whole space with the same sensitivity, which indicates that the honk effect can suppress effectively the traffic jam and enhance the stability of traffic flow. This qualitative conclusion is the same as that in Tang’s model [39].

Fig. 4
figure 4

Headway profile of the density wave at \(t=10,200\) corresponding to Fig. 3

Full size image

Figure 4 shows headway profile of the density wave at \(t=10,200\) corresponding to Fig. 3. We can find that the amplitude of FVD model (i.e., \(p=0\)) fluctuates much more widely than those (i.e., \(p\ne 0\)) of the new model, which indicates that the stability is improved by introducing the honk effect. Furthermore, with the increasing value of p, the fluctuation of headway is reduced obviously. In particular, when \(p=0.15\), the stop-and-go phenomenon disappears and traffic flow becomes uniform state due to the satisfaction of the stability condition (14). All these results are consistent with the above analysis.

Fig. 5
figure 5

Hysteresis loops for different values of p

Full size image

In order to further prove that the honk effect can improve the stability of traffic flow, the hysteresis phenomena of traffic flow are explored. Figure 5 shows the velocity-headway trajectory corresponding to the cases \(p = 0, 0.05, 0.1\) and 0.15, respectively. After sufficiently long time, the traffic state is close to stationary where the motions of vehicles organize hysteresis loops. The hysteresis loop will gradually be reduced with the increase in p, which indicates that the honk effect plays positive function on the stabilization of traffic flow. In particular, when \(p=0.15\), the stability condition [see Eq. (14)] is satisfied, the loop will shrink into a point H on the optimal velocity curve, and the traffic flow is a stable state. Therefore, the simulation results are in good agreement with the theoretical analysis.

6 Conclusions

In this paper, we proposed an extended car-following model to simulate traffic flow under honk environment. To do so, two optimal velocity functions describing the forward looking effect and the honk effect of the following vehicle are introduced, respectively. The stability of traffic flow and the density waves were investigated analytically through the linear stability theory and nonlinear analysis method. The mKdV equation near the critical point has been derived to describe the traffic jam. Furthermore, the numerical results are in good agreement with the theoretical analysis, which indicates that the honk effect plays an important role in improving the stability of traffic flow and suppressing the traffic jam.

However, the present work is limited on single lane, and the lane-changing behaviors as well as the driver’s attributions (e.g., aggressive and conservative characteristics) have not been considered. Moreover, the obtained results are qualitative. In the future, this model will be further extended to investigate the above problems.