Linear and nonlinear stability analysis of a car-following model considering velocity difference of two adjacent lanes

Abstract

An improved optimal velocity model, which considers the velocity difference of two adjacent lanes, is presented in this paper. Using linear stability theory, the stability criterion of the new model is obtained and the neutral stability curves are plotted. By applying the reductive perturbation method, the nonlinear stability of the proposed model is also investigated and the soliton solution of the modified Korteweg–de Vries equation near the critical point is obtained to characterize the unstable region. All the theoretical analysis and numerical results demonstrate that the proposed model can characterize traffic following behaviors effectively and achieve better stability.

1 Introduction

Over the decades, the research on car-following has attracted considerable attention [2, 4]. Various traffic models have been developed, and numerous empirical tests have been conducted. As early as 1953, Pipes [34] did pioneering work to mathematically derive dynamic equations which can be used to describe several motions of the leading vehicle. Chandler et al. [3] later expanded Pipes’ model and developed the California model which considers the delay time of vehicles. Herman [16] proposed a double look-ahead model which involves the nearest and next nearest cars in front and simulated the model using computer for the first time. Subsequently, many researchers (e.g., Gazis [8, 9], Edie [7], Newell [31, 32], et al.) made great contributions to the car-following theory [5, 14, 29, 30, 38].

Among hundreds of car-following models, the optimal velocity (OV) model developed by Bando et al. [1] has been widely accepted due to its simplicity, innovativeness, and great performance of describing the car-following behavior. Komatsu and Sasa [20] employed the OV model to study traffic congestion. Helbing and Tilch [15] applied the basic concept of the OV model and developed a generalized force (GF) model, which achieved good agreement with the empirical data. Nagatani et al. [28] deduced a difference equation from the OV model to describe highway traffic flow. Lenz et al. [22] extended the OV model by incorporating multi-vehicle interactions and the results indicated that the size of the stable region had been increased. Muramastu and Nagatani [24] analyzed the density wave numerically and analytically and obtained Korteweg-de Vries (KdV) equation for the OV model. Recently, Jiang et al. [18] studied a full velocity difference (FVD) model concerning both positive and negative velocities and addressed the problems of too high acceleration and unrealistic deceleration that appear in the OV model. Ge et al. [11] studied three different types of OV models using three nonlinear wave equations including KdV, Burgers and mKdV, and concluded two generally verified solutions for the KdV and mKdV equations. Furthermore, Peng et al. [33] proposed an optimal velocity difference (OVD) model; Zheng et al. [42] analyzed an anticipation driving car-following (AD-CF) model; Tang et al. [36] studied the driving behavior under an accident and proposed a car-following model with inter-vehicle communication (IVC); and Yu et al. [40] presented a full velocity difference and acceleration (FVDA) model which considers headway, velocity difference and acceleration of the leading car.

However, most of existing car-following models only concern car-following behaviors for single lane. Only little work considers the interaction between the major lane and neighbor lane(s). Tang et al. [37] considered the lateral distance of two lanes and obtained the stability condition via linear stability theory and nonlinear perturbation equation. Ge et al. [13] proposed a car-following model incorporating lateral distance between the motor and adjacent non-motor lane without isolation belts. Jia et al. [17] considered the lateral influence by introducing a combination of optimal velocity functions of two adjacent lanes.

Apparently, the vehicle velocity of the adjacent lane has impact on the driving behaviors of vehicles on the major lane. Typically, if the vehicles on the adjacent lane increase velocity suddenly, the drivers on the major lane might speed up in order to catch up the adjacent vehicles or slow down since they might think the adjacent vehicles need to change lane. On the contrary, if the vehicles on the adjacent lane reduce velocity abruptly, the drivers on the major lane might also slow down since they might think there is a traffic jam or accident ahead. In either way, the drivers on the major lane adjust their speeds due to the velocity change of the vehicles on the adjacent lane. In other words, the major lane velocity is influenced by the vehicle velocity on adjacent lanes.

In order to characterize above-mentioned behavior, in this paper, we propose an expanded car-following model, named lane velocity difference (LVD) model, which describes the influence caused by the velocity difference between the major and adjacent lanes. We will first analyze the stability condition of the proposed LVD model by using linear stability theory, followed by investigating its nonlinear stability by using the reductive perturbation method. From the nonlinear stability analysis, we can obtain the kink solution of the modified mKdV equation near the critical point. With the kink solution, traffic flow state can be divided into stable, metastable and unstable three regions. Several simulations will be also carried out to illustrate analytical results.

The remainder of the paper is organized as follows. Section 2 reviews some classic car-following models followed by a description of the proposed LVD model. Sections 3 and 4 present the stability condition of the proposed model and analyze the density wave of traffic flow by using the mKdV equation. In Sect. 5, several simulation experiments are conducted to verify our analytic results. Lastly, Sect. 6 concludes this paper with some remarks.

2 Mathematical model

In this section, we present an extended car-following model (i.e., the LVD model), which considers the relative velocity between the major and adjacent lanes.

As proposed by Chowdhury et al. [4], a common dynamic equation of a car-following model is given by

$$\begin{aligned} {\ddot{x}}={{f}_{sti}}\left( {{v}_{n}},{\Delta } {{x}_{n}},{\Delta } {{v}_{n}} \right) , \end{aligned}$$

(1)

where the function ${{f}_{sti}}$ indicates the response to the stimulus received by the $n\hbox {th}$ vehicle. For single-lane car-following models, the stimulus generally consists of the speed of the $n\hbox {th}$ vehicle ${{v}_{n}}$, the relative velocity between vehicles n and $n+1$, ${\Delta } {{v}_{n}}={{v}_{n+1}}-{{v}_{n}}$, and the relative distance (i.e., headway) between vehicles n and $n+1$, ${\Delta } {{x}_{n}}={{x}_{n+1}}-{{x}_{n}}$ between successive vehicles. Note, different car-following models might have different ${{f}_{sti}}$ functions, which include different relative parameters [6, 23, 43].

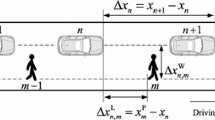
To consider the influence of the velocity difference between the major and adjacent lanes, as shown in Fig. 1, Eq. (1) can be generalized as follows:

$$\begin{aligned} {\ddot{x}}={{f}_{sti}}\left( {{v}_{n}},{\Delta }{{x}_{n}},{\Delta } {{v}_{n}},{\Delta }v_{n}^{\mathrm {LVD}} \right) , \end{aligned}$$

(2)

where ${\Delta } v_{n}^{\mathrm {LVD}}={{{\bar{v}}}_{m}^\text{ L }}-{{v}_{n}}$ represents the relative velocity between the vehicles on the major and adjacent lanes; ${{{\bar{v}}}_{m}^{\mathrm {L}}}=\hbox {mean}(v_{m}^{\mathrm {L}},v_{m+1}^\mathrm{L},\ldots ,v_{m+s-1}^{\text{ L }})$ is the average speed of m lateral vehicles on the adjacent lane near the nth vehicle on the major lane, where $v_{m}^{\mathrm {L}}$ indicates the velocity of the mth car on the adjacent lane and s represents the number of the cars on the adjacent lane which can be observed by and generate impact on the nth vehicle on the major lane. Note the average speed of several vehicles ${{{\bar{v}}}_{m}^{\mathrm {L}}}$, instead of a particular vehicle velocity $v_{m}^{\mathrm {L}}$ of the adjacent lane, is used in our model to indicate velocity difference. This is simply because the influence from the adjacent lane might come from multiple vehicles. Most car-following models for single lane only consider the impact from the nearest leading vehicle since most of drivers only pay attention to the nearest front vehicle and the view other vehicles has been blocked by the nearest one. But when considering the impact from the adjacent lane, the drivers on the major lane very likely can observe several vehicles driving on the adjacent lane. So an average speed of these vehicles better describes the overall influence caused by the velocity difference from the adjacent lane.

Fig. 1

Sketch map of a two-lane traffic. ${\Delta } x_n=x_{n+1}-x_n$ denotes the vehicle headway on the major lane, where $x_n$ indicates the position of the nth car on the major lane. ${\Delta } x_{m}^{\mathrm {L}}=x_{m+1}^{\mathrm {L}}-x_{m}^{\mathrm {L}}$ represents the vehicle headway on the adjacent lane, where $x_{m}^{\mathrm {L}}$ indicates the position of the mth car on the adjacent lane. ${\Delta } x_{n}^{\mathrm {LVD}}=x_{m}^{\mathrm {L}}-x_{n}$ indicates the distance between the nth car on the major lane and mth car on the adjacent lane

To derive the mathematical expression of Eq. (2), we first refer to a simple single-lane car-following model proposed by Newell [32] and Whitham [39]:

$$\begin{aligned} \frac{\hbox {d}{{x}_{n}}(x+\tau )}{\hbox {d}t}=V\left( {\Delta } {{x}_{n}}(t) \right) , \end{aligned}$$

(3)

where ${{x}_{n}}(t)$ is the position of the nth car at time t, $V\left( {\Delta } {{x}_{n}}(t) \right)$ is the optimal velocity function incorporating various of the headways on the same lane, and $\tau$ is the delay time, i.e., the time lag before reaching the optimal velocity. This model essentially indicates that it takes the delay time $\tau$ for a driver to adjust the vehicle velocity and reach the optimal velocity which is determined purely based on the observed headway (${\Delta } x_n(t)$).

Clearly, many other factors, such as acceleration, deceleration, relative velocity between successive vehicles etc., have impacted the final value of the optimal velocity, as suggested by [12, 35, 37]. In this paper, we further consider the impact from the relative velocity between the major and adjacent lanes. By considering all abovementioned impact factors, Eq. (3) can be expanded to a more general differential equation:

$$\begin{aligned} \frac{\hbox {d}{{x}_{n}}(t+\tau )}{\hbox {d}t}=V\left( {\Delta } {{x}_{n}}(t),{\Delta } {{v}_{n}}(t), {\Delta } v_{n}^{\mathrm {LVD}}(t) \right) . \end{aligned}$$

(4)

If we assume a linear relationship between the optimal velocity and two relative velocities (i.e., $V({\Delta } x_n(t),$ ${\Delta } v_n(t),{\Delta } v_n^{\mathrm {LVD}}(t))=V({\Delta } x_n(t))+\lambda _1{\Delta } v_n(t)+\lambda _2 \tau {\Delta } v_n^{\mathrm {LVD}}(t))$ [18, 19, 41], and apply Taylor expanding to Eq. (4), we can get the following differential format of the proposed LVD model:

$$\begin{aligned} \frac{{{\hbox {d}}^{2}}{{x}_{n}}(t)}{\hbox {d}{{t}^{2}}}= & {} \alpha \left[ V\left( {\Delta } {{x}_{n}}(t) \right) -{{v}_{n}}(t)\right] \nonumber \\&+\,{{k}_{1}}{\Delta } {{v}_{n}}(t)+{{\lambda }_{2}}{\Delta } v_{n}^{\mathrm {LVD}}(t), \end{aligned}$$

(5)

where ${{k}_{1}}={{{\lambda }_{1}}}/{\tau }, \;{{\lambda }_{1}}$ is the response coefficient of the relative velocity between successive vehicles, and ${{\lambda }_{2}}$ is the response coefficient of the relative velocity between vehicles on the major and adjacent lanes. Note $\lambda _1,\lambda _2$ are constants independent of time, velocity and position.

Note the assumption of a linear combination of the optimal velocity and relative velocities has been suggested by much other research. For example, by assuming a linear relationship between the optimal velocity and the relative velocity between successive vehicles (i.e., $V({\Delta } x_n(t), {\Delta } v_n(t))=V({\Delta } x_n(t))+\lambda _1{\Delta } v_n(t)$), Xu [41] derived the following relative velocity (RV) car-following model:

$$\begin{aligned} \frac{{{\hbox {d}}^{2}}{{x}_{n}}(t)}{\hbox {d}{{t}^{2}}}=\alpha \left[ V\left( {\Delta } {{x}_{n}}(t) \right) -\frac{\hbox {d}{{x}_{n}}(t)}{\hbox {d}t} \right] +k_1{{{\Delta } v}_{n}}(t).\nonumber \\ \end{aligned}$$

(6)

The RV model has the exactly same format as the simplified FVD model proposed by Jiang et al. [18, 19], who derived the model based on the GF model [15]. By comparing with our model [Eq. (5)] and the RV model [Eq. (6)], we can see that the proposed LVD model will be degenerated to the RV model (or FVD model), if $\lambda _2$ is set as 0, i.e., ignoring the influence of the relative velocity between the major and adjacent lanes. Furthermore, if $\lambda _1=\lambda _2=0$, the LVD model will be converted to the original OV model [see Eq. (3)]. The consistency between the proposed LVD, RV, and OV models further confirms the rationality of the proposed LVD model.

For the purpose of convenience, the dynamic equation Eq. (5) needs to be discretized and then rewritten as the following difference equation through the asymmetric forward difference [4, 26]:

$$\begin{aligned} {{x}_{n}}(t+2\tau )= & {} {{x}_{n}}(t+\tau )+\tau V\left( {\Delta } {{x}_{n}}(t) \right) \nonumber \\&+{{\lambda }_{1}}\left( {\Delta } {{x}_{n}}(t+\tau )\right. \nonumber \\&-\left. {\Delta } {{x}_{n}}(t) \right) +{{\lambda }_{2}}\nonumber \\&\times \tau \left( \frac{1}{s}\sum \limits _{j=1}^{s}{{\Delta } {x_{m+j-1}^{\mathrm {L}}}(t)} -{\Delta } {{x}_{n}}(t)\right) ,\nonumber \\ \end{aligned}$$

(7)

where ${\Delta } {{x}_{m+j-1}^{\mathrm {L}}}(t)={{x}_{m+j}^{\text{ L }}}(t)-{{x}_{m+j-1}^{\text{ L }}}(t)$ is the headway between the $(m+j-1)-\hbox {th}$ and $(m+j)$th cars on the adjacent lane. Since the response coefficients $\lambda _1,\;\lambda _2$ are sensitive to the headway, the following step functions are assumed:

$$\begin{aligned} \lambda _1=\left\{ \begin{array}{ll} \beta ,&{}\quad {\Delta } x_{n}<s_c,\\ 0,&{} \quad {\Delta } x_{n}\ge s_c,\\ \end{array}\right. \qquad \lambda _2=\left\{ \begin{array}{ll} \delta ,&{}\quad {\Delta } x_{n}^{\mathrm {L}}<s_c,\\ 0,&{} \quad {\Delta } x_{n}^{\mathrm {L}}\ge s_c.\\ \end{array}\right. \end{aligned}$$

where $\beta ,\; \delta$ are predetermined response coefficients, and $s_c$ is a critical headway. The above step functions essentially indicate that if the distance between the proceeding and following cars (i.e., headway) is too large (i.e., greater than a critical distance), the velocity difference between two successive vehicles will have no influence to the car-following behavior of the following car; similarly, if the distance between the car on the adjacent lane and the car on the major lane (similar to headway) goes beyond a critical distance, the velocity difference between these two cars will have no influence to the car-following behavior of the car on the major lane. Note here the critical headway $s_c$ is assumed the same for both $\lambda _1$ and $\lambda _2$, but certainly different critical headways could be assigned to $\lambda _1$ and $\lambda _2$ to indicate the drivers’ different response behaviors to the relative velocity of the vehicles on the same or different lane.

For computational convenience, Eq. (7) can be rewritten as:

$$\begin{aligned} {\Delta } {{x}_{n}}(t+2\tau )= & {} {\Delta } {{x}_{n}}(t+\tau )\nonumber \\&+\,\tau \left[ V\left( {\Delta } {{x}_{n+1}}(t) \right) -V\left( {\Delta } {{x}_{n}}(t) \right) \right] \nonumber \\&+\,{{\lambda }_{1}}\left( {\Delta } {{x}_{n+1}}(t+\tau ) -{\Delta } {{x}_{n+1}}(t)\right. \nonumber \\&\left. -\,{\Delta } {{x}_{n}}(t+\tau )+{\Delta } {{x}_{n}}(t) \right) +{{\lambda }_{2}}\tau \nonumber \\&\times \, \bigg ( \frac{1}{s}\sum \limits _{j=1}^{s}{\left( {\Delta } {{x}_{m+j}^{\text{ L }}}(t)-{\Delta } {{x}_{m+j-1}^{\text{ L }}}(t) \right) }\nonumber \\&-\,\left( {\Delta } {{x}_{n+1}}(t)-{\ Delta} {{x}_{n}}(t)\right) \bigg ). \end{aligned}$$

(8)

As suggested by [12, 26], the optimal velocity function $V({\Delta } x_n)$ can be formulated as:

$$\begin{aligned} V\left( {\Delta } {{x}_{n}} \right) =\frac{{{v}_{\max }}}{2}\left[ \tanh \left( {\Delta } {{x}_{n}}-{{h}_{c}} \right) +\tanh \left( {{h}_{c}} \right) \right] , \end{aligned}$$

(9)

where ${{h}_{c}}$ is a safety distance and ${{v}_{\max }}$ is a maximum velocity. Equation (9) assumes a monotonically increasing function with an upper bound of ${\lim _{{\Delta } {{x}_{n}}\rightarrow \infty }}\,V\left( {\Delta } {{x}_{n}} \right) =v_{\mathrm{max}}/{2}\left( 1+\tanh \left( {{h}_{c}} \right) \right)$. Note that Eq. (9) has a turning point (i.e., inflection point) at ${\Delta } {{x}_{n}}={{h}_{c}}:\;{V}''\left( {{h}_{c}} \right) = {{\left[ {{\hbox {d}^{2}}V\left( {\Delta } {{x}_{n}} \right) }/{\hbox {d}{\Delta } x_{n}^{2}}\; \right] }_{{\Delta } {{x}_{n}}={{h}_{c}}}}=0$, which is a critical point where the mKdV equation of Eq. (7) can be obtained.

3 Linear stability analysis

This section is to investigate the stability of the proposed LVD model by applying a linear stability analysis method [12, 25]. Here we assume no lane changing and no overtaking, and we only consider the stability of the uniform traffic flow on each lane. The solution of the uniformly steady state of Eq. (7) is given by

$$\begin{aligned}&x_{n}^{(0)}(t) =hn+V\left( h \right) t,\quad \hbox {with}\quad h={L}/{{{N}_{1}}}; \nonumber \\&x_{m}^{\mathrm {L}(0)}(t) ={{h}_{l}}m+V_{l}\left( h_l \right) t,\quad \hbox {with}\quad {{h}_{l}}={L}/{{{N}_{2}}},\nonumber \\ \end{aligned}$$

(10)

where $h,{{h}_{l}}$ represent the constant headways of two successive vehicles in the major and adjacent lanes, respectively; ${{N}_{1}},{{N}_{2}}$ indicate the number of cars in the major and adjacent lanes, respectively; $V,V_{l}$ denote the optimal velocities for the vehicles on the major and adjacent lanes, respectively; and L is the road length.

Adding small deviations ${{y}_{n}}(t),{{{y}}_{m}^{\mathrm {L}}}(t)$ to the uniform solutions described in Eq. (10), we get updated solutions: ${{x}_{n}}(t)=x_{n}^{(0)}(t)+{{y}_{n}}(t),\;{{x}_{m}^{\mathrm {L}}}(t)=x_{m}^{\mathrm {L} (0)}(t)+{{{y}}_{m}^{\text{ L }}}(t);$ and $\left| {{y}_{n}}(t) \right| ,\;\left| {{{{y}}}_{m}^\mathrm{L}}(t)\right| \ll 1$ [1, 22]. With the updated solutions, the linear stability equation for Eq. (8) can be obtained:

$$\begin{aligned}&{\Delta } {{y}_{n}}(t+2\tau )\nonumber \\&\quad = {\Delta }{{y}_{n}}(t+\tau )+\tau {V}'\left( {\Delta } {{y}_{n+1}}(t)-{\Delta } {{y}_{n}}(t) \right) \nonumber \\&\qquad +\,{{\lambda }_{1}}\left( {\Delta } {{y}_{n+1}}(t+\tau )\right. \nonumber \\&\qquad \left. -\,{\Delta }{{y}_{n+1}}(t)-{\Delta } y_n(t+\tau )+{\Delta } {{y}_{n}}(t) \right) +\lambda _2\tau \nonumber \\&\qquad \cdot \left( \frac{1}{s}\sum \limits _{j=1}^{s}{\left( {\Delta } {{ y}_{m+j}^{\mathrm {L}}}(t)-{\Delta } {{ y}_{m+j-1}^{\text{ L }}}(t) \right) }\right. \nonumber \\&\qquad \left. -\,\left( {\Delta } {{y}_{n+1}}(t)-{\Delta } {{y}_{n}}(t)\right) \right) , \end{aligned}$$

(11)

where ${V}'$ is the derivative of optimal velocity $V({\Delta } {{x}_{n}})$ at ${\Delta } x=h$, ${\Delta } {{y}_{n}}(t)={{y}_{n+1}}(t)-{{y}_{n}}(t)$, and ${\Delta } {{y}_{m}^{\mathrm {L}}}(t)={{y}_{m+1}^{\mathrm {L}}}(t)-{{y}_{m}^{\mathrm {L}}}(t)$. Since ${{y}_{n}}(t)$ and ${{{y}}_{m}^{\mathrm {L}}}(t)$ are very small perturbations and ${{y}_{n}}(t),\;{{{y}}_{m}^{\mathrm {L}}}(t)\propto \exp \{ikn+zt\}$, we can let ${\Delta } {{y}_{n}}(t)=A \exp \{ikn+zt\}$, ${\Delta } {{{y}}_{m}^{\mathrm {L}}}(t)\cong \gamma A\exp \{ikn+zt\}$, where $\gamma$ represents the average strength coefficient which describes the perturbations between the major and adjacent lanes. $\gamma$ is critical for this model since it normalizes the perturbations between the major and adjacent lanes. By assuming explicit functions for ${\Delta } {{y}_{n}}$, and ${\Delta } {{{y}}_{m}^{\mathrm {L}}}$, Eq. (11) can be expanded to:

$$\begin{aligned} {{e}^{2z\tau }}= & {} {{e}^{z\tau }}+{V}'\left( {{e}^{ik}}-1 \right) \tau \nonumber \\&+\,{{\lambda }_{1}}\left( {{e}^{ik+z\tau }}-{{e}^{ik}}-{{e}^{z\tau }}+1 \right) \nonumber \\&+\,{{\lambda }_{2}}\tau \left( \frac{\gamma }{s}\sum \limits _{j=1}^{s}\right. \nonumber \\&\times \,\left. {\left( {{e}^{ikj}}-{{e}^{ik(j-1)}} \right) } -({{e}^{ik}}-1)\right) . \end{aligned}$$

(12)

Further expanding z with $z={{z}_{1}}(ik)+{{z}_{2}}{{(ik)}^{2}}+\cdots$ [25, 41], we have

$$\begin{aligned} {{z}_{1}}= & {} {V}'+{{\lambda }_{2}}\left( \gamma -1 \right) ,\nonumber \\ {{z}_{2}}= & {} -\frac{3}{2}{{z}_{1}}^{2}\tau +\frac{{{V}'}}{2}+{{\lambda }_{1}}{{z}_{1}}+{{\lambda }_{2}}\cdot \frac{\gamma s-1}{2}. \end{aligned}$$

(13)

From Eq. (13): if ${{z}_{2}}$ is negative, the uniformly steady-state flow is unstable for long-wavelength modes; and if ${{z}_{2}}$ is positive, the uniform flow is stable. The neutral stability condition is given by $z_2=0$:

$$\begin{aligned} \tau =\frac{{V}'+2{{\lambda }_{1}}{{z}_{1}}+{{\lambda }_{2}}(\gamma s -1)}{3z_{1}^{2}}. \end{aligned}$$

(14)

In Eq. (14), the delay time $\tau$ is a critical value and usually is written as $\tau _c$. Its inverse $(1/\tau _c)$ is called the critical sensitivity ($\alpha _c$). From Eq. (14), the unstable and stable condition are:

$$\begin{aligned} \tau> & {} \frac{{V}'+2{{\lambda }_{1}}{{z}_{1}}+{{\lambda }_{2}}(\gamma s -1)}{3z_{1}^{2}},\end{aligned}$$

(15)

$$\begin{aligned} \tau< & {} \frac{{V}'+2{{\lambda }_{1}}{{z}_{1}}+{{\lambda }_{2}}(\gamma s -1)}{3z_{1}^{2}}. \end{aligned}$$

(16)

Fig. 2

Phase diagram of different car-following models. The solid line represents the OV model ($\lambda _1=\lambda _2=0$); the dash line indicates the RV model ($\lambda _1=0.2$, $\lambda _2=0$); and the circle line denotes the LVD model ($\lambda _1=0.2$, $\lambda _2=0.2$, $\gamma =0.4$, $s=1$)

Note that the stability condition Eq. (14) in this paper is similar to the stability conditions of the OV model (see Eq. (12) in Ref. [1]) and RV model (see Eq. (11a) in Ref. [41]). For comparison, Fig. 2 plots the stability regions for OV, RV, and LVD models respectively. As shown in the figure, the LVD has the largest stable region. The finding indicates that by considering the velocity difference between the major and adjacent lanes, the proposed LVD model reduces the unstable region and makes the cars running more stable under the same condition.

As described before, the derivative of optimal velocity Eq. (9) can be obtained: $V'({\Delta } x_n)=\frac{v_{\mathrm{max}}}{2}[1-\hbox {tanh}^2({\Delta } x_n-h_c)]$. From this equation, we can see that at the turning point $h=h_c$, the derivative $V'$ of Eq. (9) has the maximum value, i.e., $v_{\mathrm{max}}/2$. Therefore, from the Eqs. (14) and (16), for any car density, the uniform flow is always stable when $\alpha >\alpha _c$. Figure 3 shows the neutral stability lines in the space of $({\Delta } x, \alpha )$ for different $\lambda _2$ with $v_{\mathrm{max}}=3$, and $h_c=4$. The solid curves in the figure represent the neutral stability lines with different values of $\lambda _2$. The areas covered by the solid lines decrease with the increase of $\lambda _2$, and the apex of each curve denotes the critical point. Outside the each curve, the traffic flow is stable, and inside the each curve, the traffic flow is unstable. From the figure, we can see that with the increase of $\lambda _2$, the area of stable region is increasing. This clearly indicates that by considering the impact of the relative velocity between the major and adjacent lanes, the proposed LVD model is more stable.

Fig. 3

Neutral stability lines in the headway-sensitivity. The solid lines represent the neutral stability lines for various of $\lambda _2$, where the safety distance $h_c=4$ and the maximum velocity $v_{\mathrm{max}}=3$

4 Nonlinear stability analysis

A nonlinear stability analysis of the proposed LVD model is further conducted by using the reductive perturbation method [12]. The analysis essentially provides the solution of the mKdV equation which describes the kink density wave. Based on the coarse-grained scales for long-wavelength models, we consider the slowly varying behavior at long-wavelength near the critical point $\left( {{h}_{c}},{{a}_{c}} \right)$ and introduce slow scales for space variable n and time variable t [12, 25, 37]. Then the slow variables X and T are defined as below:

$$\begin{aligned} X=\varepsilon \left( n+bt \right) \quad \hbox {and}\quad T={{\varepsilon }^{3}}t,\;0 < \varepsilon \ll 1, \end{aligned}$$

(17)

where b is a to-be-determined constant. Adding a small fluctuation $\varepsilon R(X,T)$ as a function of space X and time T, the headway can be written as [27]:

$$\begin{aligned} {\Delta } {{x}_{n}}\left( t \right) ={{h}_{c}}+\varepsilon R\left( X,T \right) . \end{aligned}$$

(18)

By expanding Eq. (8) to the fifth order of $\varepsilon$ and replacing X and T by Eqs. (17) and (18), respectively, we can derive the following nonlinear partial differential equation:

$$\begin{aligned}&{{\varepsilon }^{2}} \left[ b-{V}'-{{\lambda }_{2}}\left( \gamma -1 \right) \right] \nonumber \\&\quad \times {{\partial }_{X}}R+{{\varepsilon }^{3}}\left( \frac{3{{b}^{2}}\tau }{2}-\frac{{{V}'}}{2}-{{\lambda }_{1}}b\right. \nonumber \\&\quad \left. -{{\lambda }_{2}}\cdot \frac{\gamma s -1}{2} \right) \partial _{X}^{2}R +{{\varepsilon }^{4}}\nonumber \\&\quad \times \left[ {{\partial }_{T}}R+\left( \frac{7{{b}^{3}}{{\tau }^{2}}}{6}-\frac{{{V}'}}{6}-\frac{{{\lambda }_{1}}b\left( 1+b\tau \right) }{2}\right. \right. \nonumber \\&\quad \left. \left. -\,{{\lambda }_{2}}\cdot \frac{\gamma {{s}^{2}}-1}{6} \right) \partial _{X}^{3}R\right. \nonumber \\&\quad \left. -\,\frac{{{V}'''}}{6}{{\partial }_{X}}{{R}^{3}} \right] +{{\varepsilon }^{5}}\Big [ \left( 3b\tau -{{\lambda }_{1}} \right) {{\partial }_{X}}{{\partial }_{T}}R\nonumber \\&\quad \left. +\,\left( \frac{5{{b}^{4}}{{\tau }^{3}}}{8}-\frac{{{V}'}}{24}-{{\lambda }_{1}}\cdot \frac{b\left( 2{{b}^{2}}{{\tau }^{2}}+3b\tau +2 \right) }{12}\right. \right. \nonumber \\&\quad \left. -\,{{\lambda }_{2}}\cdot \frac{\gamma {{s}^{3}}-1}{24} \right) \partial _{X}^{4}R -\frac{{{V}'''}}{12}\partial _{X}^{2}{{R}^{3}} \Big ]=0, \end{aligned}$$

(19)

where ${V}'=dV({\Delta } {{x}_{n}})/d({\Delta } {{x}_{n}}){{|}_{{\Delta } x={{h}_{c}}}}$, ${V}'''={{d}^{3}}V({\Delta } {{x}_{n}})$ $/d{{({\Delta } {{x}_{n}})}^{3}}{{|}_{{\Delta } x={{h}_{c}}}}$. Near the critical point $\left( {{h}_{c}},{{a}_{c}} \right)$, by taking $\tau =(1+{{\varepsilon }^{2}}){{\tau }_{c}}$ and $b={V}'+{{\lambda }_{2}}(\gamma -1 )$, Eq. (19) can be simplified as

$$\begin{aligned}&{{\varepsilon }^{4}}\left( {{\partial }_{T}}R-{{g}_{1}}\partial _{X}^{3}R+{{g}_{2}}{{\partial }_{X}}{{R}^{3}} \right) \nonumber \\&\quad +\,{{\varepsilon }^{5}}\left( {{g}_{3}}\partial _{X}^{2}R+{{g}_{4}}\partial _{X}^{2}{{R}^{3}}+{{g}_{5}}\partial _{X}^{4}R \right) =0, \end{aligned}$$

(20)

where ${{g}_{1}}=\left( \frac{{{V}'}}{6}+\frac{{{\lambda }_{1}}b\left( 1+b{{\tau }_{c}} \right) }{2}+\frac{{{\lambda }_{2}}\left( \gamma {{s}^{2}-1} \right) }{6}-\frac{7{{b}^{3}}\tau _{c}^{2}}{6} \right)$, ${{g}_{2}}=-\frac{{{V}'''}}{6}$, ${{g}_{3}}=\frac{3{{b}^{2}}{{\tau }_{c}}}{2}$, ${{g}_{4}}=\frac{6b{{\tau }_{c}}-2{{\lambda }_{1}}-1}{12}{V}'''$, ${{g}_{5}}=-\frac{23}{8}{{b}^{4}}\tau _{c}^{3}+\frac{12b{{\tau }_{c}}-4{{\lambda }_{1}}-1}{24}{V}'+{{\lambda }_{1}}\Big ( \frac{5{{b}^{2}}{{\tau }_{c}}}{4}+\frac{5{{b}^{3}}\tau _{c}^{2}}{2}-\frac{{{\lambda }_{1}}b\left( 1+b\tau _c \right) }{2}-\frac{b}{6} \Big )+{{\lambda }_{2}}\cdot \frac{\left( 12b{{\tau }_{c}}-4{{\lambda }_{1}} \right) \left( \gamma {{s}^{2}}-1 \right) -(\gamma {{s}^{3}}-1)}{24}$.

We make the following transformation for Eq. (20)

$$\begin{aligned} {T}'={{g}_{1}}T,\quad R=\sqrt{\frac{{{g}_{1}}}{{{g}_{2}}}}{R}', \end{aligned}$$

(21)

then we obtain the regularized equation

$$\begin{aligned}&{{\partial }_{{{T}'}}}{R}'-\partial _{X}^{3}{R}'+{{\partial }_{X}}{{{R}'}^{3}}+\varepsilon \left( \frac{{{g}_{3}}}{{{g}_{1}}}\partial _{X}^{2}{R}'+\frac{{{g}_{4}}}{{{g}_{2}}}\partial _{X}^{2}{{{{R}'}}^{3}}\right. \nonumber \\&\left. +\frac{{{g}_{5}}}{{{g}_{1}}}\partial _{X}^{4}{R}' \right) =0. \end{aligned}$$

(22)

Omitting the $O(\varepsilon )$ term in Eq. (22), we get the mKdV equation:

$$\begin{aligned} {{{R}'}_{0}}\left( X,{T}' \right) =\sqrt{c}\tanh \sqrt{\frac{c}{2}}\left( X-c{T}' \right) , \end{aligned}$$

(23)

where c is a propagation velocity of the kink–antikink soliton solution, and c is determined by the $O(\varepsilon )$ term.

In order to determine the value of c, it is necessary to consider the solvability condition [11, 25]:

$$\begin{aligned}&\left( {{{{R}'}}_{0}},M[{{{{R}'}}_{0}}] \right) \nonumber \\&\quad =\int _{-\infty }^{\infty }{dX{{{{R}'}}_{0}}(X,{T}')M[{{{{R}'}}_{0}}(X,{T}')]}=0, \end{aligned}$$

(24)

where $M[{{{R}'}_{0}}]=\frac{{{g}_{3}}}{{{g}_{1}}}\partial _{X}^{2}{R}'+\frac{{{g}_{4}}}{{{g}_{2}}}\partial _{X}^{2}{{{R}'}^{3}}+\frac{{{g}_{5}}}{{{g}_{1}}}\partial _{X}^{4}{R}'$.

Integrating Eq. (24), we obtain the selected velocity

$$\begin{aligned} c=\frac{5{{g}_{2}}{{g}_{3}}}{2{{g}_{2}}{{g}_{5}}-3{{g}_{1}}{{g}_{4}}}, \end{aligned}$$

then, based on Eq. (21), the solution of the mKdV equation (20) is given by

$$\begin{aligned} R\left( X,T \right) =\sqrt{\frac{{{g}_{1}}c}{{{g}_{2}}}}\cdot \tanh \sqrt{{c}/{2}\;}\left( X-c{{g}_{1}}T \right) . \end{aligned}$$

(25)

According to Eq. (9), we find that ${V}'={{{v}_{\max }}}/{2}, {V}'''=-{{v}_{\max }}$. Thus, the amplitude A of the kink solution is given by

$$\begin{aligned} A= & {} {{\left[ \frac{{{g}_{1}}c}{{{g}_{2}}}\left( \frac{{{a}_{c}}}{a}-1 \right) \right] }^{{1}/{2}\;}}\quad \hbox {with}\\ {{a}_{c}}= & {} \frac{3{{\left( {{v}_{\max }}+2{{\lambda }_{2}}\left( \gamma -1 \right) \right) }^{2}}}{2{{v}_{\max }}+4{{\lambda }_{1}}\left( {{v}_{\max }}+2{{\lambda }_{2}}\left( \gamma -1 \right) \right) +4{{\lambda }_{2}}(\gamma s-1)}. \end{aligned}$$

Therefore, the kink–antikink density wave soliton solution of the headway is given by

$$\begin{aligned} {\Delta } {{x}_{n}}(t)= & {} {{h}_{c}}+\sqrt{\frac{{{g}_{1}}c}{{{g}_{2}}}\left( \frac{{{\alpha }_{ c}}}{\alpha }-1 \right) }\tanh \Big \{ \sqrt{\frac{c}{2}\left( \frac{{{\alpha }_{ c}}}{\alpha }-1 \right) }\nonumber \\&\cdot \left[ n+\left( 1-c{{g}_{1}}\left( \frac{{{\alpha }_{c}}}{\alpha }-1 \right) \right) t \right] \Big \}. \end{aligned}$$

(26)

Fig. 4

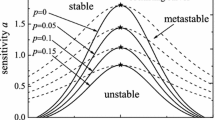
Phase diagram of the headway ${\Delta } x$ and sensitivity $\alpha$. The coexisting curves and neutral stability curves are represented by the dotted lines and solid lines, respectively. With an identical $\lambda _2$, the coexisting and neutral stability curves divide the whole region into three parts: where the region above the coexisting curve is stable, the region under the neutral stability curve is unstable, and the region between the coexisting and neutral stability curves is metastable

Figure 4 shows a phase diagram of the headway ${\Delta } x$ and sensitivity $\alpha$. The coexisting and neutral stability curves are represented by the dotted and solid lines, respectively. The coexisting curves are derived from the solution of the mKdV equation. The coexisting phase consists of freely moving phase with low density and congested phase with high density. The headways in freely moving phase and congested phase are denoted by ${\Delta } x={{h}_{c}}+A$ and ${\Delta } x={{h}_{c}}-A$, respectively. As shown in the figure, with an identical $\lambda _2$, the coexisting and neutral stability curves divide the whole region into three parts: the region above the coexisting curve is stable, the region under the neutral stability curve is unstable, and the region between the coexisting and neutral stability curves is metastable.

Table 1 The relation of the critical sensitivity $\alpha _c$ and the propagation velocity c with the number of the concerning vehicles in the adjacent lane s

We further investigate whether the number of concerning vehicles in the adjacent lane (i.e., s) will have impact on the values of the critical sensitivity $\alpha _c$ and propagation velocity c. Table 1 lists the values of the critical sensitivity $\alpha _c$ and the propagation velocity c with the varying values of s. From the table, we can see that the critical sensitivity $\alpha _c$ increases with the increasing value of s, and the propagation velocity c changes irregularly with the various s. Note a suitable value of s needs to be determined in order to cater for the need of the different versions of car-following systems. Obviously, if $s=1$, the minimum value of the critical sensitivity $\alpha _c$ can be obtained, but the corresponding value of propagation velocity c may not be an appropriate value in the special case [28]. Therefore, for the sake of definiteness and without loss of generality, we introduce a variable s in our model to cover different car-following systems.

5 Simulation

In this section, we carry out a serial of numerical simulations to describe the proposed LVD model. Referring to the work of Konishi [21], Ge [10] and Xue [41], the initial parameters are set as:

In major lane: $v_{\mathrm{max}}=4\,\hbox {m/s},\, h_c=4\,\hbox {m},\, a=2\,\hbox {s}^{-1},$ $v_n(0)=2\,\hbox {m/s}$, $N=50$, $T=0.1\,\hbox {s}$, where N is the number of simulation cars, T is a sampling time (also known as an interval time) which selects data at a regular interval from the simulation test.

For the adjacent lane, we assume that all the vehicles have the same initial values and keep the same traffic characteristics during the whole simulation time. In other words, all the vehicles on the major and adjacent lanes travel homeostatically with identical velocity and headway when the dynamic system is stable. To test the model, during the simulation, it is assumed that a velocity disturbance appears, namely, the leading car stops suddenly. In detail, we first let all vehicles run uniformly without any extra disturbance for $0\le n<1000$ (i.e., $0\le nT<100$), then let the leading car stop suddenly for a short time ($100\le nT\le 103$), and then the leading car recovers its initial velocity.

Fig. 5

Velocity-time plots for the LVD model (a) and RV model (b). The leading car stops suddenly at time $nT=100\sim 103$ s with a $\lambda _1=0.2,\;\lambda _2=0.2$, and b $\lambda _1=0.2$, $\lambda _2=0$. With time increasing, the red solid line $v_3$ represents the velocity profile of the 3th car ahead, the blue dotted line $v_{25}$ indicates the velocity profile of the 25th car ahead, and the green dash line $v_{50}$ denotes the velocity profile of the 50th car ahead

Fig. 6

Space-time patterns for the LVD model (a) and RV model (b). The leading car stops suddenly at time $nT=100\sim 103$s with a $\lambda _1=0.2,\;\lambda _2=0.2$, and b $\lambda _1=0.2$, $\lambda _2=0$. The horizontal axis indicates the distances between the leading car and each following car. The longitudinal axis represents simulation time including the disturbance time period. Each curve is corresponding to one of simulated vehicles and denotes the change of distance between the observed and leading cars with the change of time. The red dotted lines (i.e., horizontal lines) in the two figures indicate the end of distance change

Figure 5 shows the velocity-time patterns of the 3th, 25th, 50th cars generated by the LVD model (Fig. 5a) and RV model (Fig. 5b), corresponding to the parameters of $\lambda _2=0.2$ and $\lambda _2=0$, respectively. From the figure, we can observe the go-and-stop wave, oscillating behavior and traffic jam phenomena. Both LVD and RV models can capture traffic jam and velocity changes of the following cars. The figure also shows that compared with the RV model (Fig. 5b), the amplitude of velocity fluctuation in LVD model is relatively smaller. This indicates that the cars in LVD model run more smoothly and achieve stable status earlier.

To further investigate the space-time evolution of the traffic flow, we plot the distances between the first leading and each following car over the change of time. Figure 6 shows the space-time patterns for the LVD and RV models. From the figure, we observe the change of the space-time evolution and find that the disturbance propagates backward when the leading car stops suddenly at time $nT=100 \sim 103$. The figure also indicates that distance fluctuation in the LVD model terminates earlier than that in the RV model. Taking the 50th car (the last one) as an example, in the LVD model the headway between the leading car and the 50th car returns back to a constant at around 145 s; but for the RV model the terminal time of the disturbance is about 155s. This observation indicates that under the same simulation condition, the LVD model is more stable than the RV model.

Fig. 7

Velocity-time plot for different $\lambda _2$ and different cars. A curve containing two colors and corresponding to a value of $\lambda _2$ represents velocity changes of the 25th and 51th car with simulation time. The solid line indicates velocity-time evolution of 25th and 51th car when $\lambda _2=0$, the dotted line indicates velocity-time evolution of 25th and 51th car when $\lambda _2=0.2$, and the dash line indicates velocity-time evolution of 25th and 51th car when $\lambda _2=0.4$

Next, in order to simulate actual traffic with more realistic data and compensate the shortage of Eq. (9), in which the control parameters are unrealistic as pointed by [17, 33], a different optimal velocity function proposed by Kontishi [21] is introduced:

$$\begin{aligned} V\left( {\Delta } {{x}_{n}} \right) =\frac{{{v}_{\max }}}{2}\left[ 1+H\left( 2\cdot \frac{{\Delta } x_n-h_c}{\zeta }\right) \right] , \end{aligned}$$

(27)

where H is a saturation function and given by

$$\begin{aligned} H\left( \rho \right) = \left\{ \begin{array}{ll} 1,&{}\quad \rho >1,\\ \rho ,&{}\quad -1\le \rho \le 1,\\ -1,&{}\quad \rho <-1. \end{array} \right. \end{aligned}$$

The parameters in simulation experiment are set as:

In major lane: $v_{\mathrm{max}}=33.6\,\hbox {m/s},$ $h_c=25\,\hbox {m},$ $\alpha =2 \,\hbox {s}^{-1},$ $v_n(0)=20\,\hbox {m/s},$ $N=51$, $\zeta = 23.3\,\hbox {m}$, $T=0.1\,\hbox {s}$, where $\zeta$ is a distance parameter.

We assume that all vehicles in the adjacent lane travel uniformly and steadily with an identical headway and a steady speed. The disturbance is generated when the velocity of the first leading car drops to 10 suddenly during time 100–103 s. Figure 7 shows the velocity-time plots of different values of $\lambda _2$ for 25th and 51th cars. From the figure, we can see that the amplitude of the velocity fluctuation decreases with the increasing value of $\lambda _2$. This indicates that by considering the relative velocity from the adjacent lane, vehicles can run more homeostatically with a smaller amplitude of velocity fluctuation.

Figure 8 shows the velocities of all vehicles at some particular times. Each line presents the velocity of each vehicle at a particular time. As shown in the figure, when the first leading car slows down suddenly at time 100 s, the velocity of the first leading car drops down to 10 and the velocities of other cars still keep the same initial speed of 20. After five seconds, the first leading car recovers its previous speed, but the 6th and nearby cars begins to slow down. It is not hard to see that the velocity disturbance propagates backwards; and with the time going by, the amplitude of velocity disturbance decreases gradually.

Fig. 8

Vehicle velocities at some particular simulation times. Each line represents the velocities of all vehicles at a given moment. The figure denotes the velocity evolution of all cars with time passing

6 Summary

Car-following modeling is an important research subject for exploring the way out of traffic jam and for developing a benign cooperative driving system. This research extends the original OV model and develops a new LVD model which considers the relative velocity of two adjacent lanes. Particularly, this research introduces the average strength coefficient $\gamma$ to describe the perturbation relationship between the major and adjacent lanes for the purpose of modeling the influence caused by the velocity difference between the major and adjacent lanes. The linear and nonlinear stability analysis are also conducted in this research to obtain a neutral stability condition and mKdV equation for the proposed model. Furthermore, this research derives both the neutral stability and coexisting lines with varying response factor $\lambda _2$ to define three regions, i.e., stable, metastable and unstable. At the end, through simulation, this research demonstrates that the proposed new car-following model which considers lane velocity difference can enhance traffic stability. The future work will be focusing on modeling the influence of the pedestrians and cyclists from the adjacent lanes.