1 Introduction

Traffic flow has been widely studied over the decades [1,2,3,4,5,6,7,8]. Many models, such as fluid [9,10,11,12], car-following [13,14,15,16,17,18,19,20] and cellular automation (CA) [21,22,23,24], have been developed. Among them, car-following has attracted much attention due to its intuitive physical meaning [25,26,27]. While most of the existing car-following models assume a simplified environment in which vehicles are only impacted by surrounding vehicles, the true traffic in urban cities indeed is more complex and a mixed one of not only vehicles, but pedestrians and bicycles. Clearly, research on mixed traffic, particularly the car-following behaviors with pedestrians on adjacent lane, is needed but very limited, and this research aims to address this challenge.

During the past decades, various car-following models have been developed since Reuschel [28] and Pipes [29] first proposed the follow-the-leader model in single lane. But most of them only consider the impact from surrounding vehicles. For example, Chandler et al. [30] proposed the California model which considers the delay time of vehicles in following behavior; Newell et al. [31] modeled car-following behavior as a general mathematical equation which involves the velocity–headway relations; Bando et al. [32] later developed the optimal velocity (OV) model which has been widely adopted due to its simplicity, intuitiveness and innovativeness [33,34,35,36,37,38], and Jiang et al. [39] developed a full velocity difference (FVD) model by taking the positive velocity difference factor into account. Jiang’s FVD model is generally considered superior to OV and generalized force (GF) models [40] for characterizing real car-following behaviors [41,42,43]. Therefore, many researchers improved the FVD model to better describe real traffic phenomena. For instance, Zhou [44] expanded FVD model by introducing drivers’ visual angle. The new model is more realistic by effectively explaining some complex traffic phenomena. Furthermore, Peng et al. [45] presented a car-following model by considering anticipation effect which could avoid the negative velocity and headway and remove collision through numerical simulation, and Yu et al. [46] incorporated the relative velocity fluctuation into an improved FVD model to better design an advanced adaptive cruise control strategy.

Since the late decade, some researchers begin to study the interactions between vehicles and pedestrians [47, 48], but most of them were focusing on uncontrolled intersections and crosswalks. For example, Helbing et al. [49] investigated the oscillations and delays of pedestrian and vehicle flows from a macro-dynamic viewpoint during pedestrians crossing the road; Chen et al. [50] developed a modified bidirectional pedestrian model to describe the interactions between vehicles and pedestrians at uncontrolled midblock crosswalks; Zhang et al. [51] designed a cooperative planning model incorporating pedestrians and vehicles in an evacuation network; Ito and Nishinari [52] used CA model to describe the interactions between vehicles and pedestrians in congested intersections; Xin et al. [53] employed the CA model to describe the evolution process of mixed-pedestrian–vehicle flow in un-signalized crosswalks; and Jin et al. [54] applied the OV model to propose a visual angle model by taking the effect of the pedestrians crossing behaviors into account.

Although pedestrians crossing the road certainly have impacts on vehicles’ behaviors, pedestrians walking on the adjacent lane could also create some significant impacts on driving behaviors, particularly car-following. Drivers have to pay attention to both surrounding vehicles and the pedestrians or bicycles on adjacent lanes to avoid any potential conflicts. In such a complicated environment full of both motorized and non-motorized vehicles, drivers could behave significantly differently. Particularly, drivers might choose different following gaps and reduce driving speed, leading to different car-following behaviors, which cannot be modeled by traditional car-following models. However, very little work has been done in this subject. Jiang et al. [55, 56] modeled similar phenomenon during cars emerging into a narrow channel using the lattice gas model, but they did not capture the dynamic characteristics of the vehicle flow because their attention was paid on pedestrians behaviors during evacuation.

Considering pedestrians or bicycles walking on adjacent lanes is common in many urban cities, modeling such interactions has become desired. This research aims to fill in this gap by proposing an improved car-following model which specifically considers the impact of pedestrians and bicycles walking on adjacent lanes. The proposed model is derived from the stimulus equation proposed by Chowdhury et al. [57] by adding the influential factors generated from pedestrians and bicycles on adjacent lanes for both lateral and longitudinal directions. The linear and nonlinear analysis shows that the new model can successfully describe the car-following behaviors under the circumstance of surrounding pedestrians and bicycles and archives better stability. Furthermore, our testing results also show that the extended car-following model can better characterize the traffic behavior involving lateral pedestrians.

The improved model is expected to greatly contribute to the improvement of the safety and control of the complicated mixed-vehicle–pedestrian traffic in urban cities. For example, the proposed model can be used to determine the new and more appropriate speed limit for urban streets with vehicles surrounding by pedestrians and bicycles, due to abnormal driving behaviors in such complicated circumstance. Furthermore, the new model can be used to improve the travel time estimation for arterials with pedestrians and bicycles on the adjacent lanes. This is much needed for urban traffic control.

The remainder of this paper is organized as follows. Section 2 presents the mathematical equation of the proposed model, followed by the linear and nonlinear stability analysis in Sect. 3 and Sect. 4, respectively. The analysis also obtains the stability condition and soliton solution of the modified Korteweg–de Vries (mKdV) equation. Section 5 carries out several simulation experiments to verify the analytic results. Finally, Sect. 6 concludes this research.

2 Mathematical model

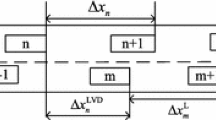
The proposed model considers the impact of the pedestrians or bicycles walking on adjacent lane. Note we assume there is no physical barrier between vehicle lane and pedestrian lane except lane markings, and vehicles and pedestrians could share a widened same lane with pedestrians walking on one side, as shown in Fig. 1.

The proposed model is based on a common dynamic equation proposed by Chowdhury et al. [57]:

$$\begin{aligned} \ddot{x}={{f}_{sti}}\left( {{v}_{n}}, \Delta {{x}_{n}},\Delta {{v}_{n}} \right) , \end{aligned}$$
(1)

where \(\ddot{x}\) is the acceleration and \({{f}_{sti}}\) is the stimulus function for the nth car. Equation (1) indicates that the nth vehicle’s action, i.e., acceleration, is stimulated by the velocity of the nth car (\({{v}_{n}}\)), velocity difference (\(\Delta {{v}_{n}}={{v}_{n+1}}-{{v}_{n}}\)), and the headway (\(\Delta {{x}_{n}}={{x}_{n+1}}-{{x}_{n}}\)) between the \((n+1)\)th (i.e., preceding) and nth car (i.e., following) cars. Here \({{x}_{n}}\) is the position of the nth car. Note, assuming different stimuli, such as acceleration, deceleration and lateral distance, Eq. (1) could convert to different versions of car-following models [14, 42, 58].

Fig. 1
figure 1

Sketch map of the mixed-pedestrian–vehicle flow. \({{x}_{n}},\; x_{m}^{\text {P}}\) are the positions of car n and pedestrian m, respectively; \(\Delta {{x}_{n}}={{x}_{n+1}}-{{x}_{n}}\) indicates the headway between car n (i.e., the following car) and car \(n+1\) (i.e., the preceding car); \(\Delta x_{n,m}^{\text {W}}\) represents the lateral headway (i.e., distance) between vehicle n and pedestrian m; \(\Delta x_{n,m}^{\text {L}}=x_{m}^{\text {P}}-{{x}_{n}}\) represents the longitudinal headway (i.e., distance) between the vehicle n and pedestrian m

Full size image

Following the Chowdhury’s format, the influence of adjacent pedestrians can be formulated by adding two pedestrian-related stimuli to Eq. (1): one is the lateral headway (i.e., distance) between vehicle and pedestrian (\(\Delta x_{n,m}^{\text {W}}\)), and the other is the longitudinal headway (i.e., distance) between vehicle and pedestrian (\(\Delta x_{n,m}^{\text {L}}\)), as described in Eq. (2):

$$\begin{aligned} \ddot{x}={{f}_{sti}}\left( {{v}_{n}},\Delta {{x}_{n}},\Delta {{v}_{n}},\Delta x_{n,m}^{\mathrm{L}},\Delta x_{n,m}^{\mathrm{W}} \right) . \end{aligned}$$
(2)

Note, this model assumes no crossing for pedestrians unless there are crosswalks. Thus, we do not concern the crossing behavior of pedestrians.

Equation (2) can be elaborated using the explicit stimulus function proposed by Newell [31] and Whitham [59]:

$$\begin{aligned} \frac{\mathrm{d}{{x}_{n}}(t+\tau )}{\mathrm{d}t}=V\left( \Delta {{x}_{n}}(t) \right) , \end{aligned}$$
(3)

where \({{x}_{n}}(t)\) is the position of car n at time t, \(V\left( \Delta {{x}_{n}}(t) \right) \) is an optimal velocity function considering the headway of the successive cars and \(\tau \) is delay time. Essentially, this model explains that a driver adjusts the current speed to an optimal one based on the headway with a delay time of \(\tau \).

For our model, the optimal velocity is determined by not only the headway between following and leading vehicles, but also the velocity difference between successive cars and both lateral and longitudinal headways between vehicles and adjacent pedestrians, i.e.,

$$\begin{aligned} \frac{\mathrm{d}{{x}_{n}}(t+\tau )}{\mathrm{d}t}=V\left( \Delta {{x}_{n}},\Delta {{v}_{n}},\Delta x_{n,m}^{\mathrm{L}},\Delta x_{n,m}^{\mathrm{W}} \right) . \end{aligned}$$
(4)

To simplify Eq. (4) and for better stability analysis, we adopt the following optimal velocity function V suggested by [26, 60]:

$$\begin{aligned} V\left( \Delta {{x}_{n}} \right) =\frac{{{v}_{\max }}}{2}\left[ \tanh \left( \Delta {{x}_{n}}-{{h}_{c}} \right) +\tanh \left( {{h}_{c}} \right) \right] , \end{aligned}$$
(5)

where \({{h}_{c}}\) is a safety distance and \({{v}_{\max }}\) is a maximum velocity. \(V\left( \Delta {{x}_{n}} \right) \) is a monotonically increasing function since \({V}'\left( \Delta {{x}_{n}} \right) ={{{v}_{\max }}}/{2}\;[1-{{\tanh }^{2}}(\Delta {{x}_{n}}-{{h}_{c}})]\), the first-order derivative of \(V\left( \Delta {{x}_{n}} \right) \), is nonnegative regardless of the value of \(\Delta {{x}_{n}}\). In addition, Eq. (5) has an upper bound, i.e., \(\underset{\Delta {{x}_{n}}\rightarrow \infty }{\mathop {\lim }}\,V\left( \Delta {{x}_{n}} \right) ={{{v}_{\max }}}/{2}\;\left( 1+\tanh \left( {{h}_{c}} \right) \right) \). A turning point can be further determined at \({V}''\left( {{h}_{c}} \right) ={{\left[ {{\mathrm{d}}^{2}}V\left( \Delta {{x}_{n}} \right) /\mathrm{d}{{\left( \Delta {{x}_{n}} \right) }^{2}} \right] }_{\Delta {{x}_{n}}={{h}_{c}}}}=0\). As we will show later, the turning point is crucial for analyzing the nonlinear steady of the proposed model.

As pointing out by Sawada (see Eq. (2) in [61]), Li et al. (see Eq. (4) in [62]), Peng et al. (see Eq. (6) in [15]) and Jin et al. (see Eq. (2) in [63]), the optimal velocity function with multi-parameters can be linearized by adding adjustable weights to each optimal velocity function with single parameter. Note, the optimal velocity in their papers is only a function of distance, but not including velocity. Therefore, a linearized form of Eq. (4) can be formulated as follows according to [58, 64, 65]:

$$\begin{aligned}&V\left( \Delta {{x}_{n}},\Delta {{v}_{n}},\Delta x_{n,m}^{\mathrm{L}},\Delta x_{n,m}^{\mathrm{W}} \right) =pV\left( \Delta {{x}_{n}} \right) \nonumber \\&\quad +qV\left( \Delta x_{n,m}^{\mathrm{L}} \right) +rV\left( \Delta x_{n,m}^{\mathrm{W}} \right) +\lambda \Delta {{v}_{n}},\nonumber \\ \end{aligned}$$
(6)

where \(p,\; q,\;r\) are the weights of three optimal functions of headway between successive vehicles, lateral headway between vehicle and pedestrian, and longitudinal headway between vehicle and pedestrian, respectively, and \(\lambda \) is the response coefficient of the relative velocity between successive vehicles. Note, \(\lambda \) is a constant independent of time, velocity and position.

Applying Taylor expansion with first- and second-order to Eq. (4), and combining Eq. (6), we can obtain the following differential equation:

$$\begin{aligned} \frac{{{\mathrm{d}}^{2}}{{x}_{n}}(t)}{\mathrm{d}{{t}^{2}}}= & {} \alpha \Big [ pV\left( \Delta {{x}_{n}} \right) +qV\left( \Delta x_{n,m}^{\mathrm{L}} \right) +rV\left( \Delta x_{n,m}^{\mathrm{W}} \right) -\frac{\mathrm{d}{{x}_{n}}(t)}{\mathrm{d}t} \Big ]\nonumber \\&+\, k\Delta {{v}_{n}}, \end{aligned}$$
(7)

where \(\alpha \) is a sensitivity of a driver and \(\alpha ={1}/{\tau }\), and \(k={\lambda }/{\tau }\).

Note \(p+q+r=1\). Also, we assume:

$$\begin{aligned} q= & {} 0,\qquad \hbox {if} \ \Delta x_{n,m}^{\mathrm{L}}>{{l}_{c}}; \\ r= & {} 0,\qquad \hbox {if} \ \Delta x_{n,m}^{\mathrm{W}}>{{d}_{c}}, \end{aligned}$$

where \({{l}_{c}}\), \({{d}_{c}}\) are the preset critical longitudinal and lateral headways between the observed vehicle and the preceding pedestrian. These assumptions simply indicate that if the lateral distance between the following car and the preceding pedestrian is too large (i.e., greater than the critical distance \({{d}_{c}}\)), the pedestrian has no impact on the car when the car overtakes the pedestrian. Similarly, if the longitudinal distance between the observed car and preceding pedestrian is larger than the critical distance \({{l}_{c}}\), the adjacent pedestrian has no impact on the driver. Note Eq. (7) is a degenerated form of Eq. (3) in [64], which has been widely cited by other car-following research. Furthermore, the assumption \(p+q+r=1\) indicates that the driver pays no extra attention to other influence other than these three headways [15].

For computational convenience, Eq. (7) needs to be discretized and rewritten as the following difference equation using the asymmetric forward difference [33, 66]:

$$\begin{aligned}&{{x}_{n}}\left( t+2\tau \right) -{{x}_{n}}(t+\tau )\nonumber \\&\quad =\tau \left( pV\left( \Delta {{x}_{n}}(t) \right) +qV\left( \Delta x_{n,m}^{\mathrm{L}}(t) \right) +rV\left( \Delta x_{n,m}^{\mathrm{W}}(t) \right) \right) \nonumber \\&\qquad +\, \lambda \left( \Delta {{x}_{n}}\left( t+\tau \right) -\Delta {{x}_{n}}(t) \right) . \end{aligned}$$
(8)

For better linear and nonlinear stability analysis, Eq. (8) can be rewritten as:

$$\begin{aligned}&\Delta {{x}_{n}}\left( t+2\tau \right) -\Delta {{x}_{n}}(t+\tau )\nonumber \\&\quad =\tau \Big \{ p\left[ V\left( \Delta {{x}_{n+1}}(t) \right) -V\left( \Delta {{x}_{n}}(t) \right) \right] \nonumber \\&\qquad +q\left[ V\left( \Delta x_{n+1,m+1}^{\mathrm{L}}(t) \right) -V\left( \Delta x_{n,m}^{\mathrm{L}}(t) \right) \right] \nonumber \\&\qquad +r\left[ V\left( \Delta x_{n+1,m+1}^{\mathrm{W}}(t) \right) -V\left( \Delta x_{n,m}^{\mathrm{W}}(t) \right) \right] \Big \} \nonumber \\&\qquad +\lambda \Big ( \Delta {{x}_{n+1}}\left( t+\tau \right) -\Delta {{x}_{n+1}}(t)\nonumber \\&\qquad -\Delta {{x}_{n}}\left( t+\tau \right) +\Delta {{x}_{n}}(t) \Big ). \end{aligned}$$
(9)

3 Linear stability analysis

In this section, the stability of the proposed model is investigated by applying a linear stability analysis method [26, 67]. Herein, we assume no lane changing and no overtaking. For the stability analysis, we first assume that both vehicle and pedestrian flow are uniform. Then following [40], in an ideal homogeneous state each pedestrian and vehicle will keep a certain space to the preceding and following pedestrians. Thus, the solution of the uniform steady state of Eq. (8) is presented as follows:

$$\begin{aligned}&x_{n}^{(0)}=hn+V(h)t,\quad \quad \mathrm{with}\quad h=L/{{N}_{1}}; \end{aligned}$$
(10)
$$\begin{aligned}&x_{m}^{\mathrm{P}(0)}={{h}_{p}}m+{{V}_{p}}({{h}_{p}})t,\quad \quad \mathrm{with}\quad {{h}_{p}}=L/{{N}_{2}},\nonumber \\ \end{aligned}$$
(11)

where \(h,\; {{h}_{p}}\) are constant headways of successive vehicles and successive pedestrians, respectively; \({{N}_{1}},\;{{N}_{2}}\) represent the number of cars and pedestrians in mixed flow, respectively; \(V,\; {{V}_{p}}\) denote the optimal velocities of the vehicles and pedestrians, respectively; and L is the road length.

By adding small deviations \({{y}_{n}}(t),\; y_{m}^{\mathrm{P}}(t)\) to the uniform solutions Eqs. (10) and (11), the updated solutions of the positions of vehicles and pedestrians are given by:

$$\begin{aligned}&{{x}_{n}}(t)=x_{n}^{(0)}(t)+{{y}_{n}}(t), \end{aligned}$$
(12)
$$\begin{aligned}&x_{m}^{\mathrm{P}}(t)=x_{m}^{\mathrm{P}(0)}(t)+y_{m}^{\mathrm{P}}(t), \end{aligned}$$
(13)

where \(|{{y}_{n}}(t)|,\; |y_{m}^{\mathrm{P}}(t)|\ll 1\) [32].

Based on the above equations (10)–(13), Eq. (9) can be rewritten as:

$$\begin{aligned}&\Delta {{y}_{n}}\left( t+2\tau \right) -\Delta {{y}_{n}}(t+\tau )\nonumber \\&\quad =\tau \big \{ p{V}'\left[ \Delta {{y}_{n+1}}(t)-\Delta {{y}_{n}}(t) \right] \nonumber \\&\qquad +q\beta {V}'\left[ \Delta {{y}_{n+1}}(t)-\Delta {{y}_{n}}(t) \right] \nonumber \\&\qquad +r\eta {V}'\left[ \Delta {{y}_{n+1}}(t)-\Delta {{y}_{n}}(t) \right] \big \} \nonumber \\&\qquad +\lambda \big ( \Delta {{y}_{n+1}}\left( t+\tau \right) -\Delta {{y}_{n+1}}(t)\nonumber \\&\qquad -\Delta {{y}_{n}}\left( t+\tau \right) +\Delta {{y}_{n}}(t) \big ), \end{aligned}$$
(14)

where \({V}'\) denotes the derivative of \(V\left( \Delta {{x}_{n}} \right) \) at \(\Delta {{x}_{n}}=h\), \(\Delta {{y}_{n}}(t)={{y}_{n+1}}(t)-{{y}_{n}}(t)\), \(\beta \) represents the average strength coefficient which describes the disturbance relationship between the headway of successive cars and the longitudinal headway of the observed car and the preceding pedestrian, and \(\eta \) indicates the average strength coefficient which describes the disturbance relationship between the headway of successive cars and the lateral headway of the observed car and the preceding pedestrian. Note, we can also apply the mean-field theory, which replaces all interactions by any one of the factors with an average or effective interaction, to combine two types of particles (i.e., pedestrians and vehicles) as one from the macroscopic view, as suggested by Tang et al. [35].

By assuming an explicit function for \(\Delta {{y}_{n}}(t)=A \) \(\cdot \exp \{ikn+zt\}\), Eq. (14) can be rewritten as:

$$\begin{aligned} {{e}^{2zt}}-{{e}^{zt}}= & {} \tau \Big [ p{V}'\left( {{e}^{ik}}-1 \right) +q{V}'\beta \left( {{e}^{ik}}-1 \right) \nonumber \\&+\,r{V}'\eta \left( {{e}^{ik}}-1 \right) \Big ]\nonumber \\&+\,\lambda \left( {{e}^{ik+z\tau }}-{{e}^{ik}}-{{e}^{z\tau }}+1 \right) . \end{aligned}$$
(15)

Then by expanding z with \(z={{z}_{1}}(ik)+{{z}_{2}}{{(ik)}^{2}}+\cdots \) [65], Eq. (15) can be transformed into:

$$\begin{aligned}&{{z}_{1}}=\left( p+q\beta +r\eta \right) {V}', \nonumber \\&{{z}_{2}}= -\frac{3\tau }{2}z_{1}^{2}+\frac{{{z}_{1}}}{2}+\lambda {{z}_{1}}. \end{aligned}$$
(16)

For long-wavelength modes, if \({{z}_{2}}\) is negative, the uniform steady flow becomes unstable; if \({{z}_{2}}\) is positive, the uniform flow keeps stable state. Setting the neutral stability condition at \({{z}_{2}}=0\), we have:

$$\begin{aligned} \tau =\frac{2\lambda +1}{3\left[ \left( p+q\beta +r\eta \right) {V}' \right] }. \end{aligned}$$
(17)

In Eq. (17), the delay time \(\tau \) is called the critical value and is usually written as \({{\tau }_{c}}\), which will be used for nonlinear stability analysis in Sect. 4. Its inverse is called the critical sensitivity \(({{\alpha }_{c}}={1}/{{{\tau }_{c}}})\). For small disturbances with long wavelengths, both unstable and stable conditions can be derived as follows:

$$\begin{aligned}&\tau >\frac{2\lambda +1}{3\left[ \left( p+q\beta +r\eta \right) {V}' \right] }, \end{aligned}$$
(18)
$$\begin{aligned}&\tau <\frac{2\lambda +1}{3\left[ \left( p+q\beta +r\eta \right) {V}' \right] }. \end{aligned}$$
(19)

From Eq. (5), the derivative \({V}'\) of the optimal velocity V has a maximum value, i.e., \({{{v}_{\max }}}/{2}\;\). Submitting the maximum velocity into Eq. (19), we can find that the uniform flow is always stable for any car density if \(\tau <\frac{2(2\lambda +1)}{3\left[ \left( p+q\beta +r\eta \right) {{v}_{\max }} \right] }\). Note, the stability condition for Eq. (17) in this paper is similar to the neutral stability conditions of the OV model proposed by Bando (see Eq. (12) in [32]) and the relative velocity (RV) model proposed by Xue (see Eq. (11a) in [64]).

It is worth mentioning that both differential equation (7) and difference equations (8) and (9) can be used to analyze the linear stability condition. Due to different structures and physical meaning of differential and difference equations, they could generate different stability conditions as stated by Nagatani [4] and Ge [68]. Taking OV model [32] as an example, its stability condition derived from differential equation is \(\tau <{1}/{2V'(h)}\;\), while the stability condition derived from difference equation is \(\tau <{1}/{3V'(h)}\;\). However, which stability condition is optimal is still an open question. As suggested by [67, 69], we adopt the difference equation model in this paper. One of reasons is that, we believe, using difference equation can more conveniently conduct computer simulation and nonlinear stability analysis in next section.

Moreover, we would like to point out that here we apply the long-wavelength stability analysis, instead of the short-wavelength stability analysis as suggested by many other researchers [30, 70]. It has been argued that applying different wavelength stability analyses could generate different stable conditions [71]. Indeed, it is true that the “stable” traffic under the long-wavelength stability condition may still unstable under the short-wavelength stability condition. For instance, Berg et al. [72] claimed that the macroscopic hydrodynamic model has an instability, which is resulted from short-wavelength fluctuations, but such instability is not presenting in the classical car-following model. However, if the short-wavelength fluctuations are properly regularized as suggested by [73], such instability could disappear. We only apply the long-wavelength stability analysis to study the linear stability of the proposed model because this method has been widely used in many publications for both macroscopic and microscopic models [74,75,76].

Fig. 2
figure 2

Neutral stability curves with different sets of \((\lambda , p, q, r)\). The solid line corresponds to (0, 1, 0, 0), the dash line to (0.2, 1, 0, 0) and the circle line to (0.2, 0.8, 0.1, 0.1), where \({{v}_{\max }}=3\ \mathrm{m/s},\; {{h}_{c}}=4\ \mathrm{m},\; \beta =0.5,\; \eta =0.1\)

Full size image

Figure 2 shows the neutral stability curves with different sets of \((\lambda , p, q, r)\). The solid line corresponds to (0, 1, 0, 0), which is in line with the OV model, the dash line to (0.2, 1, 0, 0), which agrees with the RV model, and the circle line to (0.2, 0.8, 0.1, 0.1), which takes into account the interactions of adjacent pedestrians. Among the three lines, a characteristic curve (i.e., the line with circle marks) of our model has the largest stable region (i.e., the smallest unstable region). The finding means that by incorporating the adjacent pedestrian interaction into the original car-following model, the traffic flow becomes more stable than that without considering lateral pedestrians.

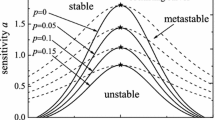
In Fig. 3, the solid curves represent the neutral stability lines in headway-sensitivity pattern and the apex of each curve denotes the critical point. The increase in stability region is presented in the figure with the increase in q as well as the decrease in r when p is a preset value. The space beyond each curve indicates the stable region, where the traffic flow is free; the opposite area indicates unstable region, where the traffic flow is congested. Figure 3 represents that if drivers pay more attention on the longitudinal distance than lateral distance between the car and the preceding pedestrian, i.e., with the increase in weight q of longitudinal distance, the traffic flow will become more unstable.

Fig. 3
figure 3

Neutral stability lines in space of \((\Delta {{x}_{n}}, \alpha )\) when \(p=0.6\). The solid curves represent the neutral stability lines with different values of q and r at \(p=0.6\)

Full size image

4 Nonlinear stability analysis

In this section, by using the reductive perturbation met-hod [68, 77], a nonlinear stability analysis of the proposed model is conducted. The soliton of the mKdV equation that describes the kink density wave can be obtained via the nonlinear stability analysis. Applying the coarse-grained scales for long-wavelength modes, we investigate the slowly varying behavior at long-wavelength near the critical point \(\left( {{h}_{c}},{{\alpha }_{c}} \right) \) and introduce slow scales for space variable n and time variable t [78]. The corresponding slow variables X and T are defined as follows:

$$\begin{aligned} X=\varepsilon (n+bt)\quad \mathrm{and}\quad T={{\varepsilon }^{3}}t,\quad 0<\varepsilon \ll 1, \end{aligned}$$
(20)

where b is a to-be-determined constant. Adding a small fluctuation \(\varepsilon R(X,T)\) as a function of space X and time T, the headway can be given by [79]:

$$\begin{aligned} \Delta {{x}_{n}}\left( t \right) ={{h}_{c}}+\varepsilon R\left( X,T \right) . \end{aligned}$$
(21)

Employing Eqs. (20) and (21), we expand Eq. (9) to the fifth order of \(\varepsilon \) and then obtain the following nonlinear partial differential equation:

$$\begin{aligned}&{{\varepsilon }^{2}}\left[ b-{V}'\left( p+q\beta +r\eta \right) \right] {{\partial }_{X}}R\nonumber \\&\quad +{{\varepsilon }^{3}}\left[ \frac{3{{b}^{2}}\tau }{2}-\frac{(p+q\beta +r\eta ){V}'}{2}-\lambda b \right] \partial _{X}^{2}R \nonumber \\&\quad +{{\varepsilon }^{4}}\Big [ {{\partial }_{T}}R+\left( \frac{7{{b}^{3}}{{\tau }^{2}}}{6}-\frac{(p+q\beta +r\eta ){V}'}{6}-\frac{\lambda ({{b}^{2}}\tau +b)}{2} \right) \partial _{X}^{3}R\nonumber \\&\quad -\frac{{{V}'''}}{6}{{\partial }_{X}}{{R}^{3}} \Big ]+{{\varepsilon }^{5}}\Big [ (3b\tau -\lambda ){{\partial }_{X}}{{\partial }_{T}}R\nonumber \\&\quad +\left( \frac{5{{b}^{4}}{{\tau }^{3}}}{8}-\frac{(p+q\beta +r\eta ){V}'}{24}-\frac{\lambda (2{{b}^{3}}{{\tau }^{2}}+3{{b}^{2}}\tau +2b)}{12} \right) \partial _{X}^{4}R\nonumber \\&\quad -\frac{{{V}'''}}{12}\partial _{X}^{2}{{R}^{3}} \Big ]=0\ , \end{aligned}$$
(22)

where \({V}'''\) is the third derivative of optimal velocity \(V(\Delta {{x}_{n}})\) at \(\Delta {{x}_{n}}={{h}_{c}}\).

Near the critical point \(({{h}_{c}},{{\alpha }_{c}})\), by taking \(\tau =(1+{{\varepsilon }^{2}}){{\tau }_{c}}\) and \(b={V}'(p+q\beta +r\eta )\), Eq. (22) can be simplified as:

$$\begin{aligned}&{{\varepsilon }^{4}}\left[ {{\partial }_{T}}R-{{g}_{1}}\partial _{X}^{3}R+{{g}_{2}}{{\partial }_{X}}{{R}^{3}} \right] \nonumber \\&\quad +{{\varepsilon }^{5}}\left[ {{g}_{3}}\partial _{X}^{2}R+{{g}_{4}}\partial _{X}^{2}{{R}^{3}}+{{g}_{5}}\partial _{X}^{4}R \right] =0, \end{aligned}$$
(23)

where \({{g}_{1}}=\frac{(p+q\beta +r\eta ){V}'}{6}+\frac{\lambda ({{b}^{2}}{{\tau }_{c}}+b)}{2}-\frac{7{{b}^{3}}\tau _{c}^{2}}{6}\), \({{g}_{2}}=-\frac{{{V}'''}}{6}\), \({{g}_{3}}=\frac{3{{b}^{2}}{{\tau }_{c}}}{2}\), \({{g}_{4}}=\frac{6b{{\tau }_{c}}-{2{\lambda }_{1}-1}}{12}{V}'''\), \({{g}_{5}}=\frac{12b{{\tau }_{c}}-4\lambda -1}{24}{V}'-\frac{23{{b}^{4}}\tau _{c}^{3}}{8}+\lambda \left( \frac{5{{b}^{2}}{{\tau }_{c}}}{4}+\frac{5{{b}^{3}}\tau _{c}^{2}}{2}-\frac{b}{6} \right) -\frac{{{\lambda }^{2}}b(1+b{{\tau }_{c}})}{2}\).

If we make the following transformation for Eq. (23):

$$\begin{aligned} {T}'={{g}_{1}}T,\quad R=\sqrt{\frac{{{g}_{1}}}{{{g}_{2}}}}{R}', \end{aligned}$$
(24)

then we obtain the regularized equation as below:

$$\begin{aligned} \begin{array}{ll} &{}{{\partial }_{{{T}'}}}{R}'-\partial _{X}^{3}{R}'+{{\partial }_{X}}{{{R}'}^{3}}\\ &{}\quad +\,\varepsilon \left( \frac{{{g}_{3}}}{{{g}_{1}}}\partial _{X}^{2}{R}'+\frac{{{g}_{4}}}{{{g}_{2}}}\partial _{X}^{2}{{{{R}'}}^{3}}+\frac{{{g}_{5}}}{{{g}_{1}}}\partial _{X}^{4}{R}' \right) =0. \end{array} \end{aligned}$$
(25)

Omitting the \({\mathrm O}(\varepsilon )\) term in Eq. (25), we get the mKdV equation with a kink solution as the desired solution:

$$\begin{aligned} {{{R}'}_{0}}\left( X,{T}' \right) =\sqrt{c}\tanh \sqrt{\frac{c}{2}}\left( X-c{T}' \right) , \end{aligned}$$
(26)

where c is a propagation velocity of the kink–antikink soliton solution and is determined by the \({\mathrm O}(\varepsilon )\) term.

In order to obtain the value of c, it is necessary to consider the solvability condition [33, 80]:

$$\begin{aligned}&\left( {{{{R}'}}_{0}},M[{{{{R}'}}_{0}}] \right) \nonumber \\&\quad =\int _{-\infty }^{\infty }{\mathrm{d}}X{{{R}'}_{0}}\left( X,{T}' \right) M\left[ {{{{R}'}}_{0}}\left( X,{T}' \right) \right] =0, \end{aligned}$$
(27)

where \(M[{{{R}'}_{0}}]=\frac{{{g}_{3}}}{{{g}_{1}}}\partial _{X}^{2}{R}'+\frac{{{g}_{4}}}{{{g}_{2}}}\partial _{X}^{2}{{{R}'}^{3}}+\frac{{{g}_{5}}}{{{g}_{1}}}\partial _{X}^{4}{R}'\).

By integrating Eq. (27), the velocity c is obtained:

$$\begin{aligned} c=\frac{5{{g}_{2}}{{g}_{3}}}{2{{g}_{2}}{{g}_{5}}-3{{g}_{1}}{{g}_{4}}}. \end{aligned}$$
(28)

Hence, the solution of Eq. (23) is derived as follows:

$$\begin{aligned} R\left( X,T \right) =\sqrt{\frac{{{g}_{1}}c}{{{g}_{2}}}}\cdot \tanh \sqrt{\frac{c}{2}}\left( X-c{{g}_{1}}T \right) . \end{aligned}$$
(29)

Based on Eq. (5), we know that \({V}'={{{v}_{\max }}}/{2},\; {V}'''=-{{v}_{\max }}\). Thus, the amplitude A of the kink soliton is followed by:

$$\begin{aligned} A={{\left[ \frac{{{g}_{1}}c}{{{g}_{2}}}\left( \frac{{{\alpha }_{c}}}{\alpha }-1 \right) \right] }^{1/2}}\mathrm{with }\quad {{\alpha }_{c}}=\frac{3\left( p+q\beta +r\eta \right) {{v}_{\max }}}{2(2\lambda +1)}.\nonumber \\ \end{aligned}$$
(30)

Therefore, the kink–antikink density wave soliton solution of the headway is given by:

$$\begin{aligned} \Delta {{x}_{n}}(t)= & {} {{h}_{c}}+\sqrt{\frac{{{g}_{1}}c}{{{g}_{2}}}\left( \frac{{{\alpha }_{c}}}{\alpha }-1 \right) }\tanh \Big \{ \sqrt{\frac{c}{2}\left( \frac{{{\alpha }_{c}}}{2}-1 \right) }\nonumber \\&\times \left[ n+\left( 1-c{{g}_{1}}\left( \frac{{{\alpha }_{c}}}{\alpha }-1 \right) \right) t \right] \Big \}. \end{aligned}$$
(31)
Fig. 4
figure 4

Phase diagram of the space of \((\Delta {{x}_{n}},\; \alpha )\). The dash lines indicate the coexisting curves, and the solid lines represent the neutral stability curves. The solid and dash lines with a same color share an identical peak (also called a critical point). This pair of lines divides the whole region into three parts: stable, unstable and metastable regions

Full size image

Applying the linear steady condition and soliton solution of the headway, Fig. 4 presents a phase diagram of \((\Delta {{x}_{n}},\ \alpha )\) with three state regions. For the convenience of analysis, by taking \(q=0.1\), the figure shows the variation tendency with different p and r. The dash lines (also called coexisting lines) are derived from the solution of the mKdV equation, and solid lines (also called neutral steady lines) are resulted from the linear steady condition. Combining the dash and solid lines with the same color, the two lines with the same peak (i.e., critical point) divide the whole region into three parts: the region above the dash line is stable, the region under the solid line is unstable, and the region between the dash and solid lines is metastable. The metastable state is a coexisting phase including the freely moving phase with low traffic density and the congested phase with high traffic density. Theoretically, the headways in free and congested phases are denoted by \(\Delta x_{n}(t)={{h}_{c}}+A\) and \(\Delta x_{n}(t)={{h}_{c}}-A\), respectively.

5 Simulation

In this section, numerical simulations are employed to verify the result of the stability analysis. In order to use real traffic data, we apply another optimal velocity function proposed by Kontishi et al. [81], which is derived from Eq. (5) [32, 82] as follows:

$$\begin{aligned} {{V}^{\mathrm{op}}}\left( \Delta {{x}_{n}}(t) \right) =\frac{{{v}_{\max }}}{2}\left[ 1+H\left( 2\cdot \frac{\Delta {{x}_{n}}(t)-\eta }{\xi } \right) \right] , \end{aligned}$$
(32)

where the saturation function H(x) is described as

$$\begin{aligned} H(x)=\left\{ \begin{array}{ll} 1,\qquad &{} x>1; \\ x, \qquad &{} -1\le x\le 1; \\ -1, \qquad &{} x<-1. \\ \end{array} \right. \end{aligned}$$
(33)

In fact, Eq. (32) is deduced from \(V(\Delta x)=16.8 [\tanh 0.086(\Delta x-25)+0.913]\), which is used in the car-following experiment and determined by the observed data on Japanese motorways in [25, 82, 83]. These values are compatible with the simulation parameters of vehicles in this paper and are presented in Table 1. Besides, T is sampling time (also known as an interval time) and used to select data at a regular interval. Table 2 shows the simulation parameters of pedestrians. These values were suggested by related studies in the field of social behavior [84, 85] to meet the practical experience.

Table 1 Simulation parameters of vehicles
Full size table
Table 2 Simulation parameters of pedestrians
Full size table

As suggested by Kontishi et al. [81] and Ge [86], a motorcade consisted of 11 cars is assumed traveling on a mixed-pedestrian–vehicle lane to investigate the traffic pattern changes influenced by the adjacent pedestrians. In order to examine the proposed model better, two simulation scenarios are provided:

  1. (1)

    Scenario of only a few pedestrians on the street, and the motorcade passes adjacent pedestrians one by one. In this situation, we investigate the changes of vehicle feature influenced by a few adjacent pedestrians. This scenario is similar to some real situations such as a few pedestrians walking at night, or in rainy days, etc. on roadside.

  2. (2)

    Scenario of a large crowd of people walking along the roadside. In this situation, we study vehicle behaviors influenced by adjacent pedestrians flow during the following three time intervals: cars begin to enter, cars drive through, and cars drive away. This scenario is similar to some real situations such as the crowd leaving from a stadium, theater, or other gathering place.

Fig. 5
figure 5

Velocity–time plots for various parameters: a \(p=0.6,\ q=0.3,\ r=0.1\) and b \(p=0.6,\ q=0.2, \ r=0.2\). The blue solid line represents velocity change of the 2nd car, the green dash line indicates velocity change of the 5th car, the pink dot-and-dash line denotes the velocity change of the 8th car, and the dotted line shows the velocity change of the 11th car (i.e., the last car of the motorcade)

Full size image
Fig. 6
figure 6

Headway–time evolution for various parameters when \(p=0.6\): a \(q=0.3,\; r=0.1\) and b \(q=0.2,\; r=0.2\)

Full size image

For both scenarios, the initial conditions are set as followed by the values suggested in [81]: \({{v}_{n}}(0)=20 \;\mathrm{m/s}\), \({{x}_{11}}(0)=0\) (i.e., the last car of the motorcade is located at origin and at initial time), \(\Delta {{x}_{n}}(0)={v\xi }/{{{v}_{\max }}}\;-{\xi }/{2}\;+\eta \) for \(n\ne 1\), \(\Delta {{x}_{1}}(t)={v\xi }/{{{v}_{\max }}}-{\xi }/{2}+\eta \) for any t (i.e., during the simulation time, the headway between the leading and successive cars is a constant which is determined by relative parameters). We assume that all vehicles have the same initial velocity and headway before incorporating the adjacent preceding pedestrians. That is to say, all vehicles run uniformly without extra disturbance at the early stage. When they begin to pass over adjacent pedestrians in mixed-pedestrian–vehicle lane, the characteristics of traffic flow will be drastically changed.

5.1 Scenario 1

In the first step, we carry out the simulation for scenario 1 and investigate the evolution characteristics of traffic flow.

Figures 5a, b shows the velocity–time patterns for the 2nd, 5th, 8th and 11th (i.e., the last car) cars by assuming \(p=0.6,\; q=0.3,\; r=0.1\) and \(p=0.6,\; q=0.2,\; r=0.2\), respectively. Figure 5 shows that when the motorcade overtakes an adjacent pedestrian, the traffic shock wave of uniformly traveling vehicles generates fluctuation, and the velocity change of the selected cars are different. This figure essentially demonstrates the evolution of oscillation behavior and traffic jam. Note, under condition of \(p=0.6,\; q=0.2,\;r=0.2\) (Fig. 5b), the amplitude of velocity fluctuation is relative smaller. This indicates that the cars run more smoothly and recover stable status earlier compared to the situation in Fig. 5a.

Figure 6 shows three-dimensional space–time evolutions of the headway for various values of \(q,\; r\), including (a) \(q=0.3,\; r=0.1\) and (b) \(q=0.2,\ \ r=0.2\) with \(p=0.6\). From both figures, we can observe the change of the space–time evolutions and find that the disturbances propagate backward when the motorcade passes the adjacent pedestrian. The amplitude of the headway fluctuation in Fig. 6a is larger than that in Fig. 6b. From Figs. 5 and 6, we can find that when \( q=0.2,\; r=0.2\), the cars run more smoothly with smaller fluctuation than that in case with \(\ q=0.3,\;r=0.1\). This finding is consisted with the results during linear stability analysis (see Fig. 3).

Fig. 7
figure 7

Temporal velocity pattern of four cars. The blue solid line represents velocity change of the 2nd car, the green dash line indicates velocity change of the 5th car, the pink dot-and-dash line denotes the velocity change of the 8th car, and the dotted line shows the velocity change of the 11th car

Full size image

5.2 Scenario 2

In the second step, we carry out the simulation for scenario 2 and investigate the dynamic behavior of a motorcade which consists of 11 cars. As is mentioned above, pedestrians are assumed walking uniformly and steadily along the roadside. The oscillation behavior of cars occurs when the leading car encounters the tail of the queued pedestrians.

Figure 7 shows the velocity–time plots for the 2nd, 5th, 8th, 11th cars. For better observation and analysis, we only choose the four cars instead of all vehicles. As shown in the figure, during 100–400s, the vehicles encounter the pedestrians, and then, the cars speeds slow down. During 400–700s, all vehicles are running through the crowd and their speeds remain a relatively low values. In this stage, the headway between successive pedestrians is much smaller than car headway, and the car speed is faster than any pedestrian. From the macroscopic perspective, the pedestrians flow seems like a long barrier. In fact, in this period, the vehicles flow is influenced by each pedestrian with extremely short interval (due to short pedestrian headway) so the velocity fluctuation curve of each car looks like a straight line. During 700–1000s, cars pass by the crowd in succession, and their speeds recover to the initial velocity via a series of complicated velocity fluctuations.

To further analyze traffic flow behavior, Fig. 8 presents the change of distances between the leading car and each following car with the change of time. As shown in the figure, each curve has two bumps due to the distance fluctuation. The first bump occurs when the leading/first car encounters pedestrians and has to decline the speed, leading that the distances between the leading and each following cars become smaller. The second bump occurs when the leading car leaves the crowd and recovers to its initial speed, leading that the distances between the leading and each following cars become larger.

Figure 9 presents headway–time curves of each car in three-dimensional space. Compared with Fig. 8, we focus on observing the headway evolution between the successive cars with time increasing. The graph is composed of convex and concave surfaces which are consistent with each cars headway change profile. Through this figure, we can see the headway change patterns of all cars intuitionally.

Fig. 8
figure 8

Space–time plots for a motorcade passing by the pedestrian crowd. The horizontal axis indicates the distances between the leading and each following cars. The longitudinal axis denotes simulation time including encountering, driving through and leaving the crowd. Each curve represents the fluctuation of the distance between the first and each following car

Full size image
Fig. 9
figure 9

Headway–time patterns for each following car in three-dimensional space

Full size image

According to these simulation experiments, we find that in mixed lane of pedestrians and vehicles, the traffic flow is influenced by the adjacent pedestrian(s). Velocities and headways evolve with the time. The results show that with pedestrians walking on adjacent lanes, the drivers usually slow down to ensure the safety of pedestrians and themselves. This finding indicates that taking into account the lateral and longitudinal influences from adjacent pedestrians could improve traffic safety and help resolve traffic congestion.

6 Conclusions

Pedestrians or bicycles walking on adjacent lanes is common in urban cities; therefore, modeling the interactions between vehicles and adjacent pedestrians has become important. This research proposes an improved car-following model which specifically considers the impact of pedestrians and bicycles walking on adjacent lanes based on the OV model. In particular, we introduce two additional stimuli generated by adjacent pedestrians, i.e., lateral and longitudinal distances between the car and preceding pedestrian, to the OV model. With the proposed new model, we further conduct the linear and nonlinear stability analyses to obtain a serial of neutral steady curves and coexisting curves. Lastly, we evaluate the proposed model through simulation for two typical and practical scenarios. This results show that the proposed model can successfully describe mixed traffic flow behaviors and improves traffic steady to avoid traffic accidents and jams.

The extended model is expected to greatly contribute to the improvement of the safety and control of the complicated mixed-vehicle–pedestrian traffic in urban cities. There could be many potential applications of the proposed model. For example, the new model can be used to determine a more appropriate speed limit for urban streets with vehicles surrounding by pedestrians and bicycles, due to abnormal driving behaviors in such complicated circumstance. In addition, the new model can be used to improve the travel time estimation for arterials with pedestrians and bicycles on the adjacent lanes. This is important for urban traffic performance measure and control.

However, this paper is mainly focusing on theoretical development. So only simulation studies are presented to evaluate the proposed model. Although in our simulation, real traffic data were used, we clearly understand that using field data and conducting field experiments could better validate the proposed model. Therefore, an important part of our future research work will be focusing on applying field data to calibrate and verify the proposed models in order to better characterize the car-following behavior for mixed traffic.