1 Introduction

Distributed parameter estimation is gathered more increased interest in the wireless sensor networks (WSNs) application areas. It just relies on the local information exchange between neighbouring sensors. It, hence, eliminates the necessity of a powerful fusion center to collect and process the data from the entire sensor network and, as such, decreases the communications power and bandwidth of the conventional centralized approach while preserving similar performance. There are two widely considered topologies, diffusion and incremental, for distributed estimation over adaptive networks. [1]. However, amongst these structures, diffusion topologies show superior performance over incremental topologies in terms of robustness to the nodes and link failures and are manageable to distributed implementations [2]. As a result, diffusion-based adaptive networks are widely studied that can learn and adapt from consecutive data streaming and exhibit good tracking capability and fast convergence rates. Besides, based on the diffusion structure, different diffusion techniques have been presented, such as the diffusion recursive least squares (D-RLS) [3], diffusion least mean square (D-LMS) [4], diffusion Kalman filter [5], diffusion affine projection (D-APA) [6], and diffusion improved multiband-structured subband adaptive filter (D-IMSAF) [7]. The convex combination of two D-LMS algorithms is proposed in [8] to overcome the tradeoff between the convergence rate and steady-state error in the traditional D-LMS algorithm. Two D-LMS algorithms with different step sizes are combined in this algorithm, resulting in a lower steady-state error and faster convergence rate at the cost of increased computational complexity. Also, motivated by the idea of combining adaptive algorithms, [9] proposed an affine combination framework for diffusion topologies, where affine combination coefficients are adjusted based on the minimum mean-square-error (MSE) criterion. This combined diffusion structure enjoys the best characteristics of all component strategies. Since the conventional diffusion adaptive networks experience a significant performance degeneration in the presence of impulsive noise, robust D-RLS algorithms are developed in [10] to enhance the performance in such noisy scenarios. In another approach, to mitigate the performance deterioration experienced in diffusion adaptive networks in the presence of impulsive noise, [11] proposed a diffusion-based affine projection M-estimate algorithm, which employs a robust M-estimate based cost function. Paper [12] has studied the performance analysis of diffusion adaptive networks by considering the communication delays of the links between nodes. This paper presents the stability conditions in the mean and mean-square sense. This paper shows that the delayed D-LMS algorithm could converge under the same step-sizes limitation of the conventional D-LMS algorithm without considering delays. The transient performance of the D-LMS algorithm for the non-stationary systems has been studied in [13], where each node employs the different types of cyclostationary white non-Gaussian signals.

In [14], the authors have developed the zeroth-order (ZO)-diffusion algorithm by utilizing the gradient-free approach to the adaptation phase of the conventional diffusion structure. Furthermore, a modification of the stochastic variance reduced gradient (SVRG) named time-averaging SVRG (TA-SVRG) is provided in [14] for streaming data processing. Finally, the TA-SVRG algorithm has been applied in the ZO-diffusion to decrease the estimation variance and enhance the convergence rate.

Distributed diffusion adaptive techniques are implemented in two phases: the combination phase, in which each sensor combines its neighbourhood information, and the adaptation phase, in which each sensor updates its estimate based on an adaptive rule. The performance of diffusion networks could be enhanced by developing combination policies that set the combination coefficients based on the data quality. Accordingly, the design of combination coefficients has been considered in the literature [15,16,17,18].

As discussed, the above-mentioned papers have been developed to estimate the elements of an unknown parameter vector of interest in a distributed manner. These cooperative methods utilize a simple assumption that the dimension of the unknown vector or the tap-length is known a priori. So, they overlook one crucial point: in some contexts, the optimal length of the desired parameter is also unknown, similar to its elements. On this basis, the tap-length estimation problem has been considered in the distributed context based on diffusion [19,20,21] and incremental strategies [22, 23].

However, in some cases, for reasons such as power storage (since power consumption is a critical concern in WSNs), such variable tap length approaches are not applicable. So a suppositional length for the unknown vector is considered at each sensor. Usually, the exact length of the filter is unknown in advance, so it is possible to apply in each sensor node a deficient tap-length adaptive filter, i.e., an adaptive filter whose tap-length is smaller than that of the unknown desired vector length.

In distributed adaptive filter settings, the steady-state study for deficient length scenarios has been conducted only in incremental-based adaptive networks [24]. Despite the importance of studying the deficient length scenario for diffusion LMS algorithm, in almost all diffusion adaptive networks theoretical analysis, it is supposed that the length of the adaptive filter is the same as that of the unknown desired vector. On the other hand, theoretical findings on sufficient tap-length diffusion adaptive algorithms could not necessarily apply to the practical deficient length cases. Accordingly, from practical aspects, it becomes very critical to analyze and quantify the statistical behavior of the deficient length diffusion adaptive algorithms.

On this basis, in this paper, we study the deficient length diffusion LMS adaptive networks’ performance in the steady state. More precisely, we derive closed-form expressions for the EMSE and MSD for each node to explain the efficiency of length deficiency on the steady-state performance of each node. This study shows that setting the tap length smaller than its actual value leads to drastic degradation of the steady-state EMSE and MSD in diffusion adaptive networks. Also, unlike the full-length case, where the steady-state MSD and EMSE decrease significantly with the step size reduction, this study shows that in the deficient-length scenario, there are no significant improvements in the steady-state performance by reducing the step size. Consequently, according to this study, the tap length plays a key role in diffusion adaptive networks since the performance deterioration due to deficient selection of tap length could not be compensated by an adjustment in the step size.

NotationAs a convenience to the reader, Tables 1 and 2 list the main acronyms and symbols used in this paper.

Table 1 List of main acronyms
Full size table
Table 2 The main symbols
Full size table

2 Background

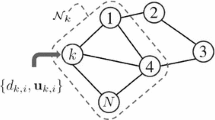
Consider a network of J sensors implemented in a diffusion structure to estimate the unknown vector \({\varvec{w}}_{{L_{opt}}}^o\) of length \({L_{opt}}\). It is supposed that the network nodes have no prior information about the length \({L_{opt}}\), and each node is equipped with a filter of length \( N\leqslant {L_{opt}}\). Considering the Combine-Then-Adapt (CTA) strategy, the filter coefficients update equation in diffusion adaptive networks would be as [2]:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \varvec{\varphi }_k^{(i - 1)} = \sum \limits _{\ell \in {\jmath _k}} {{c_{k,\ell }}\varvec{\psi }_\ell ^{(i - 1)}} \\ {\varvec{\psi }_k ^{(i)} = \varvec{\varphi }_k^{(i - 1)} + {\mu _k}{\varvec{u}}_{k,i}^*\left( {{d_k}(i) - {{\varvec{u}}_{k,i}}\varvec{\varphi }_k^{(i - 1)}} \right) } \end{array}} \right. \end{aligned}$$
(1)

where the \(N \times 1\) column vector \(\varvec{\psi }_k ^{(i)}\) represents the deficient-length local estimate of \({\varvec{w}}_{{L_{opt}}}^o\) at sensor k and time i, and where \( {\jmath _k}\) stands for the topologically connected nodes to node k (the neighborhood of sensor k, including itself). Note that, in (1), all vectors have length N. In (1), the positive constant \({\mu _k}\) is the step-size at sensor k, and the local combiners \(\{c_{k,\ell } \geqslant 0 \}\) meet the requirement \(\sum _{\ell =1}^{J} {{c_{k,\ell }}} = 1\). The combiners \(\{c_{k,\ell }\}\) are collected in a matrix \(C=[c_{k,\ell }]\) that reflects the network topology. In (1), the data are supposed to follow the linear model [25]:

$$\begin{aligned} {{d}_k}(i) = {{\varvec{u}}_{{L_{opt}}k,i}}{\varvec{w}}_{{L_{opt}}}^o + {{v}_k}(i) \end{aligned}$$
(2)

In this equation, \({{v}_k}(i)\) represents white background noise with zero-mean and variance \(\sigma _{v,k}^2\), which is assumed to be independent of \( {{\varvec{u}}_{{L_{opt}}\ell ,j}}\) for all \(\ell ,j\).

In (2), \( {{\varvec{u}}_{{L_{opt}}k,i}}\) is a vector of length \({L_{opt}}\), and \({{\varvec{u}}_{k,i}}\) consists of N first elements of \( {{\varvec{u}}_{{L_{opt}}k,i}}\). In this regard, \({\varvec{u}}_{L_{opt}k,i}\) could be written as \({\varvec{u}}_{L_{opt}k,i}=\left[ {\varvec{u}}_{k,i},\ {\bar{{\varvec{u}}}}_{k,i}\right] \), where \({\varvec{u}}_{k,i}=\left[ u_k\left( i\right) ,u_k\left( i-1\right) ,...,u_k\left( i-N+1\right) \right] \) and \({\bar{{\varvec{u}}}}_{k,i}=\left[ u_k\left( i-N\right) ,...,u_k\left( i-L_{opt}+1\right) \right] \), with \(u_k\left( i\right) \) representing the ith element of \({\varvec{u}}_{k,i}\).

3 Steady-state analysis of deficient tap-length CTA diffusion LMS algorithm

Now, we intend to analyze the steady-state behavior of the CTA diffusion LMS algorithm when a conjectural deficient length is applied for the unknown parameter. In this regard, the unknown vector is treated as the composition of two vectors stacked on top of each other as \(\left[ \begin{matrix}{\varvec{w}}_N^{\left( 1\right) }\\ {\varvec{w}}_{L_{opt}-N}^{\left( 2\right) }\\ \end{matrix}\right] \), where \({\varvec{w}}_N^{\left( 1\right) }\) consists of the first N entries of \({\varvec{w}}_{{L_{opt}}}^o\), and \({\varvec{w}}_{L_{opt}-N}^{\left( 2\right) }\) consists of the \( {L_{opt}-N}\) final elements.

To assess the steady-state performance, we analyze the MSD and EMSE measures for each sensor k, which are defined as [2]:

$$\begin{aligned} {\text {MSD}_k=E\left\{ {\left\| {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{L_{opt},k}\right\| }^2\right\} } \end{aligned}$$
(3a)
$$\begin{aligned} {\text {EMSE}_k=E\left\{ {\left| {{{\varvec{u}}}}_{L_{opt},k,i}{\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{L_{opt},k}\right| }^2\right\} } \end{aligned}$$
(3b)

where \({\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{L_{opt},k}\) is defined as:

$$\begin{aligned}{} & {} {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{L_{opt},k}=-{\varvec{w}}_{{L_{opt}}}^o+\left[ \begin{array}{c} {{\varvec{\psi }}}^{\left( i-1\right) }_k \\ {{{\varvec{0}}}}_{\left( L_{opt}-N\right) \times 1} \end{array} \right] \nonumber \\{} & {} =\left[ \begin{array}{c} -{{{\varvec{w}}}}^{\left( 1\right) }_N \\ -{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N} \end{array} \right] \nonumber \\{} & {} +\left[ \begin{array}{c} {{\varvec{\psi }}}^{\left( i-1\right) }_k \\ {{{\varvec{0}}}}_{\left( L_{opt}-N\right) \times 1} \end{array} \right] =\left[ \begin{array}{c} {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k} \\ -{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N} \end{array} \right] \end{aligned}$$
(4)

where \({\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}={{\varvec{\psi }}}^{\left( i-1\right) }_k-{{{\varvec{w}}}}^{\left( 1\right) }_N\). With the definition of \({\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{L_{opt},k}\), (3) could be rewritten as:

$$\begin{aligned}{} & {} {{\text {MSD}}_k=E\left\{ {\left\| {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}\right\| }^2\right\} +{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2} \end{aligned}$$
(5a)
$$\begin{aligned}{} & {} \quad {\text {EMSE}}_k=E\left\{ {\left| \left[ \begin{array}{cc} {{{\varvec{u}}}}_{k,i}&{\overline{{{\varvec{u}}}}}_{k,i} \end{array} \right] \left[ \begin{array}{c} {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k} \\ -{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N} \end{array} \right] \right| }^2\right\} =E\left\{ {\left| {{{\varvec{u}}}}_{k,i}{\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}-{\overline{{{\varvec{u}}}}}_{k,i}{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right| }^2\right\} \nonumber \\{} & {} =E\left\{ {\left\| {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}\right\| }^2_{R_{{{{\varvec{u}}}}_k}}\right\} +{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2_{R_{{\overline{{{\varvec{u}}}}}_k}} \end{aligned}$$
(5b)

where \(R_{{{{\varvec{u}}}}_k}=E\left\{ {{{\varvec{u}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}\right\} \) and \(R_{{\overline{{{\varvec{u}}}}}_k}=E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}{\overline{{{\varvec{u}}}}}_{k,i}\right\} \). The components of the regressors are assumed to be uncorrelated zero-mean Gaussian processes with variance \({\sigma }^2_{u,k}\). It is also assumed that \({\varvec{u}}_{{L_{opt}}k,i}\) is independent of \({\varvec{u}}_{{L_{opt}}\ell ,j}\) for \( k\ne \ell \) and \(i\ne j\). This assumption will imply the independence of \({\varvec{u}}_{k,i}\) from \({\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}\). To proceed, we rewrite (1) as:

$$\begin{aligned} \varvec{\varphi }_k^{(i - 1)}&= \sum \limits _{\ell \in {\jmath _k}} {{c_{k,\ell }}\varvec{\psi }_\ell ^{(i - 1)}} \nonumber \\ {{\varvec{\psi }}}^{\left( i\right) }_k&={{\varvec{\varphi }}}^{\left( i-1\right) }_k+\mu _k{{{\varvec{u}}}}^*_{k,i}\left[ \left( {{{\varvec{u}}}}_{L_{opt},k,i}{{{\varvec{w}}}}^o_{L_{opt}}+v_k(i)\right) -{{{\varvec{u}}}}_{k,i}{{\varvec{\varphi }}}^{\left( i-1\right) }_k\right] \nonumber \\&={{\varvec{\varphi }}}^{\left( i-1\right) }_k+\mu _k{{{\varvec{u}}}}^*_{k,i}\left[ \left[ \begin{array}{cc} {{{\varvec{u}}}}_{k,i}&{\overline{{{\varvec{u}}}}}_{k,i} \end{array} \right] \left[ \begin{array}{c} {{{\varvec{w}}}}^{\left( 1\right) }_N \nonumber \\ {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N} \end{array} \right] +v_k(i)-{{{\varvec{u}}}}_{k,i}{{\varvec{\varphi }}}^{\left( i-1\right) }_k\right] \nonumber \\&={{\varvec{\varphi }}}^{\left( i-1\right) }_k+\mu _k{{{\varvec{u}}}}^*_{k,i}\left[ {{{\varvec{u}}}}_{k,i}{{{\varvec{w}}}}^{\left( 1\right) }_N+{\overline{{{\varvec{u}}}}}_{k,i}{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}-{{{\varvec{u}}}}_{k,i}{{\varvec{\varphi }}}^{\left( i-1\right) }_k+v_k(i)\right] \nonumber \\&=\sum _{\ell \in {\jmath }_k}{c_{k,\ell }{{\varvec{\psi }}}^{\left( i-1\right) }_{\ell }}+\mu _k{{{\varvec{u}}}}^*_{k,i}\nonumber \\&\quad \left[ -{{{\varvec{u}}}}_{k,i}\left( \sum _{\ell \in {\jmath }_k}{c_{k,\ell }\left( {{\varvec{\psi }}}^{\left( i-1\right) }_{\ell }-{{{\varvec{w}}}}^{\left( 1\right) }_N\right) }\right) +{\overline{{{\varvec{u}}}}}_{k,i}{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}+v_k(i)\right] \end{aligned}$$
(6)

where the condition \({\sum _{\ell \in {\jmath }_k}{c_{k,\ell }}=1}\) is imposed. Let us subtract \({{{\varvec{w}}}}^{\left( 1\right) }_N\) from both sides of (6):

$$\begin{aligned} \begin{aligned} {\overline{{\varvec{\psi }}}}^{\left( i\right) }_{N,k}=\sum _{\ell \in {\jmath }_k}{c_{k,\ell }{\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,\ell }}&-\mu _k{{{\varvec{u}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}\sum _{\ell \in {\jmath }_k}{c_{k,\ell }{\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,\ell }} \\&+\mu _k{{{\varvec{u}}}}^*_{k,i}{\overline{{{\varvec{u}}}}}_{k,i}{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}+\mu _k{{{\varvec{u}}}}^*_{k,i}v_k\left( i\right) \end{aligned} \end{aligned}$$
(7)

For ease of analysis, we define some quantities:

$$\begin{aligned} {{{\varvec{U}}}}_i&={{\text {diag}}}\left\{ {{{\varvec{u}}}}_{1,i},\dots ,{{{\varvec{u}}}}_{J,i}\right\} \ \ \ \ \ \ \ \ \ \ \ \ \ {{\overline{{{\varvec{U}}}}}_i= {{\text {diag}}}\left\{ {\overline{{{\varvec{u}}}}}_{1,i},\dots ,{\overline{{{\varvec{u}}}}}_{J,i}\right\} } \\ {{\varvec{D}}}&={{\text{diag}}}\left\{ \mu _1I_N,\dots ,\mu _JI_N\right\} \ \ \ \ \ \ \ \ \ \ {\overline{{{\varvec{D}}}}={{\text {diag}}}\left\{ \mu _1I_{L_{opt}-N},\dots ,\mu _JI_{L_{opt}-N}\right\} } \\ {\overline{{\varvec{\varPsi }}}}^{\left( i\right) }_N&={\text {col}}\left\{ {\overline{{\varvec{\psi }}}}^{\left( i\right) }_{N,1},\dots ,{\overline{{\varvec{\psi }}}}^{\left( i\right) }_{N,J}\right\} \ \ \ \ \ \ \ \ \ \ {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N} ={\text {col}}\left\{ {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N},\dots ,{{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\} \\ {{{\varvec{V}}}}_i&={\text {col}}\left\{ {{{\varvec{v}}}}_1(i),\dots ,{{{\varvec{v}}}}_J(i)\right\} \end{aligned}$$

Let \(C=\{c_{k,\ell } \}\) represents the combination coefficient matrix; we also define \({G=C\bigotimes I_N}\), where \(\bigotimes \) represents the standard Kronecker product.

With the expressed notation, we rewrite (7) as:

$$\begin{aligned} {{\overline{{\varvec{\varPsi }}}}^{\left( i\right) }_N=G{\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N-D{{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_iG{\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N+D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i{{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}+D{{{\varvec{U}}}}^*_i{{{\varvec{V}}}}_i} \end{aligned}$$
(8)

Also, with the expressed notation, the local MSD and EMSE at sensor k can be rewritten as:

$$\begin{aligned} {\text {MSD}_k=E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{{{\text {diag}}}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) N},I_N,{{{\varvec{0}}}}_{\left( J-k\right) N}\right\} }\right\} +{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2} \end{aligned}$$
(9a)
$$\begin{aligned} \begin{aligned} \text {EMSE}_k=E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{{{\text {diag}}}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) N},R_{{{{\varvec{u}}}}_k},{{{\varvec{0}}}}_{\left( J-k\right) N}\right\} }\right\} \\\quad+{\left\| {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\right\| }^2_{{{\text {diag}}}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) \left( L_{opt}-N\right) },R_{{\overline{{{\varvec{u}}}}}_k},{{{\varvec{0}}}}_{\left( J-k\right) \left( L_{opt}-N\right) }\right\} } \end{aligned} \end{aligned}$$
(9b)

Also, to characterize the network performance, the network MSD and EMSE could be considered as:

$$\begin{aligned}{\text {MSD}}^{Net}=\frac{1}{J}\sum ^J_{k=1}{{MSD}_k}=\frac{1}{J}\sum ^J_{k=1}{E\left\{ {\left\| {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}\right\| }^2\right\} }+{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2\nonumber =\frac{1}{J}E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{I_{NJ}}\right\} +{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2 \end{aligned}$$
(10a)
$$\begin{aligned}&\quad \text {EMSE}^{Net}=\frac{1}{J}\sum ^J_{k=1}{{EMSE}_k} =\frac{1}{J}\sum ^J_{k=1}{E\left\{ {\left\| {\overline{{\varvec{\psi }}}}^{\left( i-1\right) }_{N,k}\right\| }^2_{R_{{{{\varvec{u}}}}_k}}\right\} }+\frac{1}{J}\sum ^J_{k=1}{{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2_{R_{{\overline{{{\varvec{u}}}}}_k}}} \nonumber \\&\quad = \frac{1}{J}E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{R_{{{\varvec{U}}}}}\right\} +\frac{1}{J}{\left\| {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\right\| }^2_{R_{\overline{{{\varvec{U}}}}}} \end{aligned}$$
(10b)

where \( R_{\varvec{U}} = E\left\{ {{\varvec{U}}_{i}^{*} {\varvec{U}}_{i} } \right\} = {\text{diag}}\left\{ {{\text{R}}_{{{{{\varvec{u}}}}_{{{1}}} }} , \ldots ,{\text{R}}_{{{{{\varvec{u}}}}_{{\text{J}}} }} } \right\} \) and \({R_{\overline{{{\varvec{U}}}}}=E\left\{ {\overline{{{\varvec{U}}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} ={{\text {diag}}}\left\{ R_{{\overline{{{\varvec{u}}}}}_1},\dots ,R_{{\overline{{{\varvec{u}}}}}_J}\right\} }\).

What all these measures have in common is the weighted norm \({{\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{\sum }}\). On this basis, evaluating the weighted norm on both sides of (8) and then taking expectations yields the following relation:

$$\begin{aligned} \begin{aligned} E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i\right) }_N\right\| }^2_{\sum }\right\}&=E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{\widetilde{\sum }}\right\} \\&+{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N} \\&+E\left\{ {{{\varvec{V}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{{{\varvec{V}}}}_i\right\} \end{aligned} \end{aligned}$$
(11)

where

$$\begin{aligned} \widetilde{\sum }=G^*\sum G-G^*\sum DE\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_i\right\} G \nonumber \\ -G^*E\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_i\right\} D\sum G+G^*E\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_i\right\} G \end{aligned}$$
(12)

The term \({{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\) on the right-hand side of (11) is due to the deficient length adaptive filter application at each node. This term, which contains all the omitted entries of the unknown vector, does not appear in the sufficient length scenario.

To proceed, we calculate the moments in the relations (11) and (12). First, \(E\left\{ {{{\varvec{V}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{{{\varvec{V}}}}_i\right\} \) could be evaluated as [25]:

$$\begin{aligned} \begin{aligned} E\left\{ {{{\varvec{V}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{{{\varvec{V}}}}_i\right\}&=\text {tr}\left\{ D\ E\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{V}}}}_i{{{\varvec{V}}}}^*_i{{{\varvec{U}}}}_i\right\} D\sum \right\} \\&=\text {tr}\left\{ D\ E\left\{ {{{\varvec{U}}}}^*_iR_{{{\varvec{V}}}}{{{\varvec{U}}}}_i\right\} D\sum \right\} \\&=\text {tr}\left\{ D\left( R_{{{\varvec{V}}}}\bigotimes I_N\right) \ E\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_i\right\} D\sum \right\} \\&=\text {tr}\left\{ D^2\left( R_{{{\varvec{V}}}}\bigotimes I_N\right) \ E\left\{ {{{\varvec{U}}}}^*_i{{{\varvec{U}}}}_i\right\} \sum \right\} \\&=\text {tr}\left\{ D^2\left( R_{{{\varvec{V}}}}\bigotimes I_N\right) R_{{{\varvec{U}}}}\sum \right\} \\&={\left( {\text{bvec}}\left\{ D^2\left( R_{{{\varvec{V}}}}\bigotimes I_N\right) R_{{{\varvec{U}}}}\right\} \right) }^T\ {\text{bvec}}\{\sum \} \end{aligned} \end{aligned}$$
(13)

where \({R_{{{\varvec{V}}}}=E\left\{ {{{\varvec{V}}}}_i{{{\varvec{V}}}}^*_i\right\} ={{\text {diag}}}\left\{ \sigma ^2_{v,1},\dots ,\sigma ^2_{v,J}\right\} }\)

To evaluate \({{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\), we start by assessing \({\varUpsilon \mathrm{=}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_i\sum {{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} }\) as:

$$\begin{aligned}&k\ne \ell ; \nonumber \\&\quad {\varUpsilon }_{k\ell }=E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}{\sum }_{k\ell }{{{\varvec{u}}}}^*_{\ell ,i}{\overline{{{\varvec{u}}}}}_{\ell ,i}\right\} =E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}\}{\sum }_{k\ell }E\{{{{\varvec{u}}}}^*_{\ell ,i}{\overline{{{\varvec{u}}}}}_{\ell ,i}\right\} =0 \end{aligned}$$
(14)
$$\begin{aligned}&\quad \quad k=\ell ;{\varUpsilon }_{kk} =E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}{\sum }_{kk}{{{\varvec{u}}}}^*_{k,i}{\overline{{{\varvec{u}}}}}_{k,i}\right\} =E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}\text {tr}\left\{ {{{\varvec{u}}}}_{k,i}{\sum }_{kk}{{{\varvec{u}}}}^*_{k,i}\right\} {\overline{{{\varvec{u}}}}}_{k,i}\right\} \nonumber \\&\quad =E\left\{ {\overline{{{\varvec{u}}}}}^*_{k,i}{\overline{{{\varvec{u}}}}}_{k,i}\right\} \text {tr}\left\{ E\left\{ {{{\varvec{u}}}}^*_{k,i}{{{\varvec{u}}}}_{k,i}\right\} {\sum }_{kk}\right\} =R_{{\overline{{{\varvec{u}}}}}_k}\text {tr}\left\{ R_{{{{\varvec{u}}}}_k}{\sum }_{kk}\right\} \end{aligned}$$
(15)

where \({\varUpsilon }_{k\ell }\) is the \(k\ell \)-block of \({\varUpsilon }\). Therefore, \({{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\) could be calculated as:

$$\begin{aligned} \begin{aligned}&{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}={{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\overline{D}\varUpsilon \overline{D}{{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N} \\&=\text {tr}\left\{ {{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\overline{D}\varUpsilon \overline{D}{{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\right\} \\&=\text {tr}\left\{ {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\overline{D}\varUpsilon \overline{D}\right\} \\&={\left( {\text{bvec}}\left\{ {\left( {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\right) }^T\right\} \right) }^T{\text{bvec}}\left\{ \overline{D}\varUpsilon \overline{D}\right\} \\&={\left( {\text{bvec}}\left\{ {\left( {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\right) }^T\right\} \right) }^T\left( \overline{D}\bigodot \overline{D}\right) {\text{bvec}}\{\varUpsilon \} \end{aligned} \end{aligned}$$
(16)

We could express \({\text{bvec}}\{\varUpsilon \}\) as \({b{{vec}}}\left\{ \varUpsilon \right\} =\text {col}\left\{ {{\varvec{\gamma }}}_1,\dots ,{{\varvec{\gamma }}}_J\right\} \), where:

$$\begin{aligned} {{{\varvec{\gamma }}}_k=\text {col}\left\{ {{{\varvec{0}}}}_{{\left( L_{opt}-N\right) }^2\left( k-1\right) \times 1},{\overline{{{\varvec{r}}}}}_k{{{\varvec{r}}}}^T_k \sigma _{kk},{{{\varvec{0}}}}_{{\left( L_{opt}-N\right) }^2\left( J-k\right) \times 1}\right\} } \end{aligned}$$
(17)

where \(\sigma _{kk}=\text {vec}\left\{ {\sum }_{kk}\right\} \), \({{{\varvec{r}}}}_k=\text {vec}\left\{ R_{{{{\varvec{u}}}}_k}\right\} \), and \({\overline{{{\varvec{r}}}}}_k=\text {vec}\{R_{{\overline{{{\varvec{u}}}}}_k}\}\). It follows that

$$\begin{aligned} \begin{aligned} {{\varvec{\gamma }}}_k&={\varGamma }_k \sigma _k \\&= {{\text {diag}}}\left\{ {{{\varvec{0}}}}_{{\left( L_{opt}-N\right) }^2\left( k-1\right) \times N^2\left( k-1\right) },{\overline{{{\varvec{r}}}}}_k{{{\varvec{r}}}}^T_k,{{{\varvec{0}}}}_{{\left( L_{opt}-N\right) }^2\left( J-k\right) \times N^2\left( J-k\right) }\right\} \sigma _k \end{aligned} \end{aligned}$$
(18)

where \({\sigma _k=\text {col}\left\{ \sigma _{1k},\ \sigma _{2k},\dots ,\sigma _{Jk}\right\} }\). So, \({\text{bvec}}\{\varUpsilon \}\) could be rewritten as:

$$\begin{aligned} {{b\text {vec}}\left\{ \varUpsilon \right\} ={\text {{diag}}}\left\{ {\varGamma }_1,{\varGamma }_2,\dots ,{\varGamma }_J\right\} {\text{bvec}}\{\sum \}=\digamma {\text{bvec}}\{\sum \}} \end{aligned}$$
(19)

Consequently, we find that:

$$\begin{aligned} {{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}E\left\{ {\overline{{{\varvec{U}}}}}^*_i{{{\varvec{U}}}}_iD\sum D{{{\varvec{U}}}}^*_i{\overline{{{\varvec{U}}}}}_i\right\} {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\nonumber \\ ={\left({\text {bvec}}\left\{ {\left( {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\right) }^T\right\} \right) }^T\left( \overline{D}\bigodot \overline{D}\right) \digamma \ {\text {bvec}}\{\sum \} \end{aligned}$$
(20)

Also, applying the block vectorization operator bvec to \(\widetilde{\sum }\) in (12) will result in [25]:

$$\begin{aligned} \begin{aligned} \text {bvec}\{\ \widetilde{\sum } \}&=\left( G^T\bigodot G^*\right) {\text{bvec}}\{\sum \}\\&-\left( G^T\bigodot G^*\right) \left( DR_{{{\varvec{U}}}}\bigodot I_{JN}\right) {\text {bvec}}\{\sum \} \\&-\left( G^T\bigodot G^*\right) \left( I_{JN}\bigodot R_{{{\varvec{U}}}}D\right) \text {bvec}\{\sum \} \\&+\left( G^T\bigodot G^*\right) \left( D\bigodot D\right) {{\mathcal {B}}}\ \text {bvec}\{\sum \} \end{aligned} \end{aligned}$$
(21)

where \({{\mathcal {B}}}={\text {diag}}\left\{ {\mathfrak {B}}_1,{\mathfrak {B}}_2,\dots ,{\mathfrak {B}}_J\right\} \), and

$$\begin{aligned} {{\mathfrak {B}}_k= {\text {diag}}\left\{ {\mathfrak {b}}^{\left( 1\right) }_k,\dots ,{\mathfrak {b}}^{\left( J\right) }_k\right\} } \end{aligned}$$
(22)

where \(\mathfrak {b}^{\left( \ell \right) }_k\) is given by

$$\begin{aligned} {{\mathfrak {b}}^{(\ell )}_k=\left\{ \begin{array}{l} {{{\varvec{r}}}}_k{{{\varvec{r}}}}^T_k+\beta R_{{{{\varvec{u}}}}_k}\bigotimes R_{{{{\varvec{u}}}}_k}\ \ \ \ \ \ \ \ell =k \\ R_{{{{\varvec{u}}}}_{\ell }}\bigotimes R_{{{{\varvec{u}}}}_k}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ell \ne k \end{array} \right. } \end{aligned}$$
(23)

where \(\beta =2\) for real regressors and \(\beta =1\) for complex data.

Substituting the resulting moments in (11) and (12) leads to the following relation for deficient length diffusion LMS adaptive networks.

$$\begin{aligned} {E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i\right) }_N\right\| }^2_{\text {bvec}\{\sum \}}\right\} =E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( i-1\right) }_N\right\| }^2_{{{\mathcal {S}}}\ \text {bvec}\{\sum \}}\right\} +{{\mathcal {Z}}}\ \text {bvec}\{\sum \}} \end{aligned}$$
(24)

where

$$\begin{aligned} \begin{aligned} {{\mathcal {S}}}&=\left( G^T\bigodot G^*\right) \\&\quad \times \left[ I-\left( DR_{{{\varvec{U}}}}\bigodot I_{JN}\right) -\left( I_{JN}\bigodot R_{{{\varvec{U}}}}D\right) +\left( D\bigodot D\right) {{\mathcal {B}}}\right] \end{aligned} \end{aligned}$$
(25)

and

$$\begin{aligned} \begin{aligned} {{\mathcal {Z}}}&={\left( \text {bvec}\left\{ {\left( {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}{{{\mathcal {W}}}}^{*\left( O\right) }_{L_{opt}-N}\right) }^T\right\} \right) }^T\left( \overline{D}\bigodot \overline{D}\right) \digamma \\&\quad +{\left( \text {bvec}\left\{ D^2\left( R_{{{\varvec{V}}}}\bigotimes I_N\right) \ \ R_{{{\varvec{U}}}}\right\} \right) }^T \end{aligned} \end{aligned}$$
(26)

In steady-state, (24) yields to

$$\begin{aligned} {E\left\{ {\left\| {\overline{{\varvec{\varPsi }}}}^{\left( \infty \right) }_N\right\| }^2_{(I-{{\mathcal {S}}})\ \text {bvec}\{\sum \}}\right\} ={{\mathcal {Z}}}\ \text {bvec}\{\sum \}} \end{aligned}$$
(27)

Therefore, the network and local MSD and EMSE could be evaluated as:

$$\begin{aligned}{} & {} {\text {MSD}^{Net}=\frac{1}{J}{{\mathcal {Z}}}{(I-{{\mathcal {S}}})}^{-1}\text {bvec}\{I_{JN}\}+{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2} \end{aligned}$$
(28)
$$\begin{aligned}{} & {} \quad {\text {EMSE}^{Net}=\frac{1}{J}{{\mathcal {Z}}}{(I-{{\mathcal {S}}})}^{-1}\text {bvec}\{R_U\}+\frac{1}{J}{\left\| {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\right\| }^2_{R_{\overline{{{\varvec{U}}}}}}} \end{aligned}$$
(29)
$$\begin{aligned}{} & {} \quad \text {MSD}_k={{\mathcal {Z}}}{(I-{{\mathcal {S}}})}^{-1}\text {bvec}\left\{ \text {diag}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) N},I_N,{{{\varvec{0}}}}_{\left( J-k\right) N}\right\} \right\} +{\left\| {{{\varvec{w}}}}^{\left( 2\right) }_{L_{opt}-N}\right\| }^2 \end{aligned}$$
(30)
$$\begin{aligned}{} & {} \quad \text {EMSE}_k ={{\mathcal {Z}}}{(I-{{\mathcal {S}}})}^{-1}\text {bvec}\left\{ \text {diag}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) N},R_{{{{\varvec{u}}}}_k},{{{\varvec{0}}}}_{\left( J-k\right) N}\right\} \right\} \nonumber \\{} & {} +{\left\| {{{\mathcal {W}}}}^{\left( O\right) }_{L_{opt}-N}\right\| }^2_{\text {diag}\left\{ {{{\varvec{0}}}}_{\left( k-1\right) \left( L_{opt}-N\right) },R_{{\overline{{{\varvec{u}}}}}_k},{{{\varvec{0}}}}_{\left( J-k\right) \left( L_{opt}-N\right) }\right\} } \end{aligned}$$
(31)

4 Simulation results

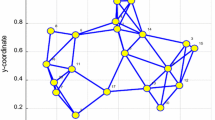
This section compares the theoretical derivations with the computer experiments. All simulations are performed in MATLAB© software and examined in the HP laptop with Windows 10 Pro 64-bit, with Processor Intel®-coreTM i5-3340M CPU @ 2.70GHz and 8GB of RAM. All expectations are resulted from averaging over 100 independent runs. We consider a network with \(J=10\) sensors where each sensor runs a local filter with N taps to estimate the unknown vector \(w_{{L_{opt}}}^o=col\{1, 1, ..., 1 \} / \sqrt{L_{opt}}\) with length \({L_{opt}=10}\). The zero-mean Gaussian noise and regressors are independent in space, and i.i.d. in time. Their statistics profile and the network topology are illustrated in Fig. 1. The step size at each sensor is set to \(\mu _k=0.01\). Also, for the local combiners \(\{c_{k,\ell } \geqslant 0 \}\), the Metropolis rule is utilized as [25]:

$$\begin{aligned} {c_{k,\ell }} = \left\{ {\begin{array}{*{20}{l}} {1/{\max ({j_k},{j_\ell })}}{\quad \,\,}if{\,}k \ne \ell {\,}are{\,}linked\\ {0{\qquad \qquad \qquad \quad \quad \,}if{\,}k{\,}and{\,}\ell {\,}are{\,}not{\,}linked}\\ {1 - \!\! \!\! \sum \limits _{m \in {\jmath _k}\backslash \left\{ k \right\} } \!\! \!\! \!\!{{c_{k,m}}} {\quad \quad \,\,}if{\,}k = \ell } \end{array}} \right. \end{aligned}$$
(32)

where \({j_k}\) Indicates the degree of node k, i.e., \(j_k = | {\jmath _k}|\).

Fig. 1
figure 1

Network topology a, and statistical settings b for \(J=10\) sensors

Full size image

Figure 2 shows the steady-state MSD per node, where every node runs an adaptive filter of lengths \(N=5\), \(N=8\) (to model the deficient length scenario), and \(N=10\) (which implies the sufficient length scenario). As can be seen from this figure, there is a good match between simulation and theoretical results. Also, this figure confirms that by decreasing the tap-length from its actual value, the steady-state MSD deteriorates drastically, such that, for only two units of length reduction (\(N=8\)), the steady-state MSD in node \(\#1\) decreases from −51.49 to −6.98 dB.

Fig. 2
figure 2

The steady-state local MSD vs. node for \(N=5\) a, \(N=8\) b, and \(N=10\) c

Full size image

A similar achievement is observed for the EMSE evaluation criterion, illustrated in Fig. 3. This figure confirms the close match between simulation and theoretical results of the EMSE measure. According to Fig. 3, similar to MSD, by decreasing the tap length from its actual value, the performance from the steady-state EMSE point of view degrades considerably. For example, for node \(\#7\), as indicated in Fig. 3, for tap lengths \(N=3\), \(N =7\), and \(N =10\), the steady-state EMSE is −3.75, −7.54, and −53.55 dB, respectively.

It is evident from Figs. 2 and 3 that the steady-state MSD and EMSE are sensitive to the sensor statistics in both sufficient and deficient length scenarios.

Fig. 3
figure 3

The steady-state local EMSE vs. node for \(N=3\) a, \(N=7\) b, and \(N=10\) c

Full size image

The dependency of the steady-state MSD and EMSE on the filter tap-length is seen clearly in Fig. 4. According to this figure, the steady-state measures are improved as the tap length tends to its actual value. However, this improvement occurs slowly for \(N<{L_{opt}}\), changing the length from 9 to 10 improves the value of the steady-state measures by about 41 dB.

Fig. 4
figure 4

Network MSD a, and Network EMSE b per N

Full size image

Figures 5 and 6 show another interesting finding concerning deficient length diffusion LMS adaptive networks: in the case of deficient length, the steady-state MSD and EMSE curves continue to grow at a slower rate as \(\mu \) increases. These figures also reveal the acceptable matching between simulation and theoretical findings. Also, we can see from these figures that, by tending the tap length to its optimum value, the performance increases as expected. As can be seen from Fig. 5, by decreasing the step size from 0.01 to 0.001, the network MSD is improved by about 10.483 dB in the case of sufficient length, but this improvement is about 0.006 dB in the case of deficient length N = 6.

Fig. 5
figure 5

Network MSD vs. \(\mu \) for deficient length aand full length b scenarios

Full size image
Fig. 6
figure 6

Network EMSE vs. \(\mu \) for deficient length a and full length b scenarios

Full size image

5 Concluding remarks

In this paper, we studied the steady-state behavior of the deficient length diffusion LMS algorithm. We provided a closed-form expression for the EMSE and MSD of each node to clarify the efficiency of length deficiency on the steady-state performance of each sensor. The results verified the dependency of the steady-state MSD and EMSE on the filter tap length. It was concluded that the performance of diffusion adaptive networks is considerably affected in the deficient length scenario, or equivalently, the steady-state measures are improved as the tap length tends to its actual value. Unlike the full-length case, where the steady-state MSD and EMSE decrease significantly with the step size reduction, this research showed that in the deficient-length scenario, there are no considerable improvements in the steady-state performance by reducing the step size, or equivalently, in the case of deficient length, the steady-state MSD and EMSE curves continue to grow at a slower rate as step-size increases. Therefore, it can be concluded that the tap length plays a critical role in diffusion adaptive networks since the performance deterioration due to the deficient selection of tap length could not be compensated by an adjustment in the step size.