1 Introduction

Intelligent sensor networks are widely used in various fields, such as environmental detection, climate detection, and signal detection and control, due to their low cost, practicality, and network adaptability. However, the presence of various noises can significantly affect the accuracy of information processing in sensors, leading to estimation deviations. Active noise suppression techniques have gained significant attention [17].

Distributed adaptive filter algorithms based on adaptive networks, which utilize noise measurement data from nodes to estimate potential parameter vectors, have emerged as a research hotspot due to the advances in adaptive filter theory. The distributed least mean square (DLMS) algorithm was proposed [17]. However, the DLMS algorithm still suffers from the limitations of fixed step sizes in the LMS algorithm, as it fails to optimize the convergence speed and stability error simultaneously.

To address the limitations mentioned above and minimize the loss of network information, researchers have proposed improved algorithms utilizing impulse noise detection methods. For instance, the diffusion robust variable step size LMS (DRVSS-LMS) algorithm [14] was introduced. However, this algorithm requires prior knowledge of the output error, including its mean, variance, and distribution. Another approach, the diffusion sign error LMS (DSE-LMS) algorithm, was proposed in reference [21] based on the minimization of the mean absolute error (MAE) criterion. By designing the cost function using the \( L_{1} \) norm of the error, this algorithm effectively eliminates the interference of impulse noise through the sign operation during the adaptive step. However, the DSE-LMS algorithm exhibits slow convergence speed and large steady-state error due to its adaptive update process relying solely on the error signal’s sign. Additionally, the robust diffusion LMS (RDLMS) algorithm presented in reference [3] derives from minimizing the pseudo-Huber function, which approximates the Huber function and ensures a continuous derivative.

Several methods have been proposed for non-Gaussian noise scenarios. The FxLMP algorithm [16] effectively converges by utilizing the error P-norm. Hui introduced the FxlogLMS algorithm [32], which models the steady-state distribution of \( \alpha \) as a logarithmic process and performs a logarithmic transformation of the collected impact noise. Hadi proposed an algorithm [36] that enhances the robustness of network nodes against impulse noise. However, these methods suffer from fixed step sizes, resulting in slow convergence and large steady-state error.

To achieve high convergence speed and small steady-state error, this study proposes a convex combination LMS algorithm based on the distributed diffusion strategy (CCLMS-DDS). By introducing convex combination into the distributed algorithm, this approach effectively balances the convergence speed and steady-state error, addressing the limitations of existing algorithms.

1.1 Related Studies

The classification of nonlinear filters can be categorized into three main groups: function expansion filters, recursive filters, and bilinear filters. Function expansion filters, such as Volterra and functional link artificial neural network (FLANN) filters, are known for their low computational load and linear output-weights relationship [4, 7, 11, 22, 26, 29]. Among them, Volterra filters outperform FLANN filters in handling crossing nonlinearities. Several function expansion filters have been developed to improve noise control in nonlinear active noise control (NANC) systems, including the Chebyshev filter [7], exponential functional link network (EFLN) filter [22], general FLANN filter [26], and mirror Fourier nonlinear (EMFN) filter [4].

Inspired by function expansion filters, researchers have introduced recursive filters [5, 6, 12, 27, 37] and function expansion bilinear (FEB) filters [13, 15, 19, 28] to further enhance control performance. FEB filters have shown remarkable applicability in NANC systems [12], but their practical implementation is hindered by high computational load and the bounded input bounded output (BIBO) stability problem. On the other hand, recursive filters have gained considerable attention due to their superior complexity and clear theoretical mechanism. Notable examples of recursive filters include the recursive second-order Volterra (RSOV) filter [37], recursive FLANN (RFLANN) filter [27], recursive EMFN (REMFN) filter [5], and recursive EMFN filter with linear infinite impulse response (IIR) section (REMFNL) filter [12].

Several algorithms have been proposed to control noise based on different estimation and cost functions. The FxLMM algorithm utilizes the objective function of an M estimation function [9, 30], while a nonlinear active noise control algorithm employs a P-norm Wiener filter algorithm with a continuous logarithmic cost function [18]. Another approach introduces variable step sizes in an LMS algorithm using incremental and diffusion strategies [24]. Saeed et al. [23] propose variable step size methods based on combinations of nonlinear functions, such as sigmoid and exponential functions, to achieve adaptive step sizes in the iterative process. However, these methods suffer from deficiencies, such as sensitivity to environmental noise and algorithm deviation caused by significant step size variations.

To address the limitations of variable step size methods, researchers have proposed variable step size methods suitable for impulse noise environments [14, 31, 33, 35]. Huang et al. [14] design an adaptive iterative method for step sizes and impulse noise detection thresholds, preventing impulse interference through threshold judgment. Although these methods exhibit good performance in impulse noise environments, they are computationally intensive. Garcia et al. [1] introduce the concept of convex combination into adaptive filtering algorithms, leading to a class of adaptive algorithms for convex combination with promising results. Zhao et al. [38] propose an algorithm utilizing convex combination for noise control in neural networks. Yu et al. [34] modify thresholds using a distributed recursion scheme, improving algorithm performance in the presence of impulsive noise. Guo et al. [12] propose an improved recursive even mirror Fourier nonlinear filter for nonlinear active noise control (NANC) by employing a convex combination of feedforward and feedback subsections. However, these algorithms are primarily designed for central algorithms, resulting in low reliability and scalability in networked systems.

To address these limitations, we introduce the concept of convex combinations in distributed networks, combining the advantages of both approaches. Through efficient calculations, we achieve the desired effect of reducing the step size.

1.2 Contributions of this Study

The proposed CCLMS-DDS algorithm in this study consists of two stages: adapt and combine. In the adapt phase, individual nodes estimate parameters and update local estimates using measurements from neighboring nodes. In the combine stage, the distributed strategy assigns weight values based on adjacent nodes and combines them to generate a new weight estimate. Compared to the DLMS algorithm, the algorithm proposed in this study offers the following advantages:

  1. 1.

    In the adapt stage, a convex combination approach is introduced for parameter estimation. This allows for dynamic adjustment of the filter’s step size based on the uncertain external noise characteristics. As a result, the algorithm achieves rapid convergence in the initial phase of operation and adapts to a smaller step size near the steady state, effectively reducing the steady-state error. Therefore, this algorithm successfully addresses the contradiction between fast convergence and low steady-state error, broadening its applicability.

  2. 2.

    In the combine stage, information from neighboring nodes is fused, resulting in higher accuracy in the final parameter estimation compared to a centralized algorithm. The theoretical proof provides the corresponding mathematical derivation supporting this claim.

1.3 Structure of this Study

This paper is structured as follows. Section 1 presents the introduction, providing an overview of the research. In Sect. 2, the problem formulation and relevant background are discussed. Section 3 introduces the CCLMS-DDS algorithm, outlining its key features and operation principles. The performance analysis is presented in Sect. 4, where the algorithm’s convergence and stability properties are thoroughly examined. Section 5 presents the simulation experiments conducted to evaluate the algorithm’s performance, followed by an analysis of the experimental results. Finally, Sect. 6 summarizes the study, highlighting the key findings and contributions.

2 Question Formulation and Relevant Context

2.1 LMS Algorithm

The LMS algorithm is a well-known adaptive filtering technique that utilizes input signals to dynamically adjust filter weights for signal processing purposes. By performing statistical analysis on the input and system-generated signals, the L-order filter aims to meet predefined standards and achieve desired signal processing effects.

Let \( x\left( i\right) \) denote the input signal, and the system’s output signal \( y\left( i\right) \) is obtained by combining weighted versions of past input signals, as shown in Eq. (1):

$$\begin{aligned} y\left( i\right) =\sum \limits ^L \omega _{m}x\left( i-m\right) . \end{aligned}$$
(1)

The error signal \( e\left( i\right) \) is defined as the difference between the desired output signal \( d\left( i\right) \) and the system’s actual output signal \( y\left( i\right) \), as given by Eq. (2):

$$\begin{aligned} e\left( i\right) =d\left( i\right) -y\left( i\right) =d\left( i\right) -\sum \limits ^L \omega _{m}x\left( i-m\right) . \end{aligned}$$
(2)

To update the filter’s weight vector, Eq. (3) is employed:

$$\begin{aligned} \omega \left( i+1\right) =\omega \left( i\right) +2\mu e\left( i\right) x\left( i\right) , \end{aligned}$$
(3)

where \( \mu \) represents the step size of the filter.

2.2 Sensor Network Model

In this section, we present the sensor network model used in this study. The sensor network consists of M nodes, denoted as \( \delta =\left\{ 1,\ldots ,M\right\} \), which are deployed across observation areas with computing, communicating, and sensing capabilities.

To enable direct communication between nodes, a communication range distance of \( \pi _{r} \) is assumed. The network’s structure is described by a graph \( \kappa =\left( \delta ,\zeta \right) \), where \( \zeta \subset \delta \times \delta \) represents the edge set of the network. If two nodes p and q satisfy the condition \( \left( p,q\right) \in \kappa \), they are considered interconnected.

The neighboring nodes of node p, denoted as \( H_{p} \), are defined as the set of nodes connected directly to node p, as shown in Eq. (4):

$$\begin{aligned} H_{p}=\left\{ q\in \delta \mid \left( p,q\right) \in \zeta \right\} . \end{aligned}$$
(4)

It is worth noting that node p is also considered its own neighbor. Each node is aware of its immediate neighbors but does not possess knowledge about the complete communication structure of the entire network. Assuming interconnectivity among the networks, there exists a sequence of boundaries between any two nodes p and q, denoted as \( \left( p,u_{1}\right) , \left( u_{1},u_{2}\right) ,\ldots , \left( u_{m},q\right) \) in \( \zeta \).

In summary, this section outlines the sensor network model employed in the study, emphasizing the communication range, network structure represented by a graph, and the concept of neighboring nodes.

2.3 Diffusion Strategy

In the context of distributed estimation, various strategies are employed to tackle network parameter estimation problems. Among them, consensus, incremental, and diffusion strategies have gained significant attention. In this section, we focus on the diffusion strategy and its relevance to the research topic.

The incremental distribution system, discussed in previous studies [17], relies on a network ring topology to establish the sequence of estimates for each node, update their estimation tasks, and evaluate algorithm efficiency through theoretical analysis.

Schizas proposed a novel algorithm based on the consensus strategy, and its implementation process was thoroughly analyzed [20]. Mateos conducted a stability analysis of the consensus algorithm and provided theoretical confirmation of its effectiveness [25]. While both the incremental and consensus strategies have their merits, the diffusion strategy stands out due to its flexibility in network structure.

In line with the diffusion strategy, Sayed introduced the DLMS algorithm [8]. This algorithm has been specifically designed to leverage the advantages of the diffusion strategy for network parameter estimation.

In summary, this section highlights the diffusion strategy as a key component of distributed estimation. It provides an overview of the incremental and consensus strategies, leading to the introduction of the DLMS algorithm based on the diffusion strategy.

3 A Convex Combination LMS Algorithm Based on the Distributed Diffusion Strategy

The LMS algorithm, known for its simplicity and fast convergence speed, exhibits favorable performance in Gaussian distributions. However, when subjected to non-Gaussian white noise, the algorithm’s adjustment accuracy is affected, and conventional error-based second-order moment algorithms fail to achieve proper convergence. This leads to a significant degradation or even invalidation of the LMS algorithm’s performance. Existing alternative algorithms often suffer from either excessive computation or unsatisfactory parameter selection, further complicating the issue.

To address these limitations, this study proposes an innovative approach that leverages the concept of convex combinations. By combining filters with large and small step sizes based on weight ratios, the proposed algorithm continually adjusts its convergence speed and steady-state errors in response to the type of external noise. This effectively resolves the challenge of simultaneously achieving high convergence speed and low steady-state errors.

By dynamically adapting to the characteristics of non-Gaussian noise, the proposed CCLMS-DDS algorithm overcomes the limitations of traditional LMS algorithms. It offers a promising solution that balances the trade-off between convergence speed and steady-state errors, thereby improving the algorithm’s overall performance. The details of the algorithm formulation and its mathematical analysis will be presented in the following sections.

3.1 Convex Combination Adaptation Phase

The filter structure utilizing the convex combination is depicted in Fig. 1, where two filters are connected in parallel. The filter with a large step size is denoted as \( \omega _{1}\left( i\right) \), while the filter with a small step size is represented by \( \omega _{2}\left( i\right) \). The output signals from the two LMS filters are \( y_{1}\left( i\right) \) and \( y_{2}\left( i\right) , \) respectively, and the final output value of the filter after the convex combination is denoted as \( y\left( i\right) \). The input signal from the external source is \( x\left( i\right) \), which passes through both filters. The desired signal is \( d\left( i\right) \), and the error signal is calculated as \( e\left( i\right) =d\left( i\right) -y\left( i\right) \). The weight coefficient \( \lambda \left( i\right) \) controls the proportion of the two filters and adapts to the environment.

Fig. 1
figure 1

The schematic diagram of the convex combination filter structure

Full size image

By employing the principle of convex combination, the output can be expressed as:

$$\begin{aligned} y\left( i\right) =\lambda \left( i\right) y_{1}\left( i\right) +\left[ 1-\lambda \left( i\right) \right] y_{2}\left( i\right) . \end{aligned}$$
(5)

Similarly, the output error can be obtained as:

$$\begin{aligned} e\left( i\right) =\lambda \left( i\right) e_{1}\left( i\right) +\left[ 1-\lambda \left( i\right) \right] e_{2}\left( i\right) . \end{aligned}$$
(6)

The core of the proposed algorithm lies in achieving a balance between fast convergence and minimal steady-state error. Consequently, the parameter \( \lambda \left( i\right) \) needs to be variable. In the initial stage, the filter with the larger step size dominates, allowing for quick convergence. As the algorithm approaches stability and the steady-state error decreases, the parameter \( \lambda \left( i\right) \) is adjusted to give priority to the filter with the smaller step size. Consequently, the overall algorithm error is reduced. The parameter \( \lambda \left( i\right) \) gradually transitions from 1 to 0, following the sigmoid function:

$$\begin{aligned} \lambda \left( i\right) =sgm\left[ \delta \left( i\right) \right] =\frac{1}{1+e^{-\delta \left( i\right) }}, \end{aligned}$$
(7)

Here, \( \delta \left( i\right) \) is a dynamically adjusted variable determined by the error signal and the outputs of the filters. To minimize the mean square error [2], the stochastic gradient method of the LMS error is utilized for adjustment, and \( \delta \left( i\right) \) is adaptively updated based on the error signal \( e\left( i\right) \), as well as the output values \( y_{1}\left( i\right) \) and \( y_{2}\left( i\right) \) of the two filters. The recursive formula for \( \delta \left( i\right) \) is given by:

$$\begin{aligned} \delta \left( i+1\right)&=\delta (i)-\frac{\mu _{\alpha }}{2}\frac{\partial e^2(i)}{\partial \delta (i)} \end{aligned}$$
(8)
$$\begin{aligned}&=\delta (i)-\frac{\mu _{\alpha }}{2}\frac{\partial e^2(i)}{\partial \lambda (i)}\frac{\partial \lambda (i)}{\partial \delta (i)}\end{aligned}$$
(9)
$$\begin{aligned}&=\delta \left( i\right) +\mu _{\alpha }e\left( i\right) \left[ y_{1}\left( i\right) -y_{2}\left( i\right) \right] \lambda \left( i\right) \left[ 1-\lambda \left( i\right) \right] , \end{aligned}$$
(10)

where \( \mu _{\alpha } \) is a positive constant. To confine the mixed parameter \( \lambda \left( i\right) \) within the convergent range of the algorithm, a sigmoidal function is employed. This effectively suppresses random gradient noise. The final filter weight update formula is described as follows:

$$\begin{aligned} \omega _{j}\left( i+1\right) =\omega _{j}\left( i\right) +\mu _{j}x\left( i\right) e_{j}\left( i\right) , \end{aligned}$$
(11)

where \( j=1,2 \).

By combining two single filters with different step sizes using the concept of a convex combination, a convex combination filter is designed. This approach enables the filter to achieve fast convergence with minimal steady-state error. The implementation steps are as follows:

$$\begin{aligned}&\mu _{\alpha }>0 \end{aligned}$$
(12)
$$\begin{aligned}&y_{1}(i)-y_{2}(i)=[\omega _{1}(i)-\omega _{2}(i)]x(i)>0\end{aligned}$$
(13)
$$\begin{aligned}&\lambda (i)[1-\lambda (i)]>0 \end{aligned}$$
(14)

1. Based on these equations, the functional relationship between \( \delta \) and e depicted in Fig. 2, and the monotonicity of variable \( \delta \) being influenced solely by e, the algorithm initially increases \( \delta \) and \( \lambda \) when

$$\begin{aligned} e(i) = d(i) - y(i) > 0. \end{aligned}$$
(15)

This leads to an increased proportion of the filter with the large step size (\( y_{1}(i) \)), resulting in higher y(i) . Consequently, the filter with the large step size dominates, leading to a higher convergence speed.

Fig. 2
figure 2

The functional relationship between \( \lambda \) and \( \delta \)

Full size image

2. Conversely, when

$$\begin{aligned} e(i) = d(i) - y(i) < 0, \end{aligned}$$
(16)

indicating that y(i) is too large, e decreases according to the functional relationship in Fig. 2, resulting in a decrease in \( \lambda \). Consequently, the proportion of the filter with the small step size (\( y_{1}(i) \)) increases, leading to a decrease in y(i) . In this case, the filter with the small step size dominates. After the algorithm converges for a certain period, the mixing parameter of the filter is automatically adjusted, increasing the proportion of the filter with the small step size. As a result, the overall filter’s step size decreases, leading to a slower convergence speed and a smaller steady-state error. The combined convex filter achieves a balance between a small steady-state error and a high convergence speed.

Next, we consider the convex combination as a filter and derive the relationship between the overall filter weight update and the input. This relationship can be obtained from Eq. (5) as follows:

$$\begin{aligned} y_{j}(i)= & {} \omega _{j}(i)x(i), j=1,2, \end{aligned}$$
(17)
$$\begin{aligned} y(i)= & {} \omega (i)x(i)\end{aligned}$$
(18)
$$\begin{aligned}= & {} \lambda (i)y_{1}(i)+[1-\lambda (i)]y_{2}(i)\end{aligned}$$
(19)
$$\begin{aligned}= & {} \lambda (i)\omega _{1}(i)x(i)+[1-\lambda (i)]\omega _{2}(i)x(i)\end{aligned}$$
(20)
$$\begin{aligned}= & {} {\lambda (i)\omega _{1}(i)+[1-\lambda (i)]\omega _{2}(i)}x(i), \end{aligned}$$
(21)

so we can derive

$$\begin{aligned} \omega \left( i\right) =\lambda \left( i\right) \omega _{1}\left( i\right) +\left[ 1-\lambda \left( i\right) \right] \omega _{2}\left( i\right) ; \end{aligned}$$
(22)

by substituting (11) into (22), we can obtain the updated formula for \( \omega (i+1) \).

$$\begin{aligned} \omega \left( i+1\right)&=\lambda \left( i\right) \omega _{1}\left( i+1\right) +\left[ 1-\lambda \left( i\right) \right] \omega _{2}\left( i+1\right) \end{aligned}$$
(23)
$$\begin{aligned}&=\lambda \left( i\right) \left[ \omega _{1}\left( i\right) +\mu _{1}e_{1}\left( i\right) x(i)\right] +\left[ 1-\lambda \left( i\right) \right] \left[ \omega _{2}\left( i\right) +\mu _{2}e_{2}\left( i\right) x(i)\right] . \end{aligned}$$
(24)

After substituting (6), the following equation is obtained

$$\begin{aligned} \omega \left( i+1\right)&=\lambda \left( i\right) \left[ \omega _{1}\left( i\right) +\mu _{1}e_{1}\left( i\right) x(i)\right] +\left[ 1-\lambda \left( i\right) \right] \left[ \omega _{2}\left( i\right) +\mu _{2}e_{2}\left( i\right) x(i)\right] \end{aligned}$$
(25)
$$\begin{aligned}&=\lambda (i)\omega _{1}(i)+[1-\lambda (i)]\omega _{2}(i)\nonumber \\&\quad +\lambda (i)\mu _{1}e_{1}(i)x(i)+[1-\lambda (i)]\mu _{2}e_{2}(i)x(i)\end{aligned}$$
(26)
$$\begin{aligned}&=\omega (i)+\lambda (i)\mu _{1}e_{1}(i)x(i)+[1-\lambda (i)]\mu _{2}e_{2}(i)x(i)\end{aligned}$$
(27)
$$\begin{aligned}&=\omega (i)+\lambda (i)\mu _{1}e_{1}(i)x(i)-\lambda (i)\mu _{2}e_{1}(i)x(i)\nonumber \\&\quad +\lambda (i)\mu _{2}e_{1}(i)x(i)+[1-\lambda (i)]\mu _{2}e_{2}(i)x(i)\end{aligned}$$
(28)
$$\begin{aligned}&=\omega (i)+\lambda (i)\mu _{1}e_{1}(i)x(i)-\lambda (i)\mu _{2}e_{1}(i)x(i)\nonumber \\&\quad +{\lambda (i)e_{1}(i)+[1-\lambda (i)]e_{2}(i)}\mu _{2}x(i)\end{aligned}$$
(29)
$$\begin{aligned}&=\omega (i)+\lambda (i)\mu _{1}e_{1}(i)x(i)-\lambda (i)\mu _{2}e_{1}(i)x(i)+\mu _{2}e(i)x(i)\end{aligned}$$
(30)
$$\begin{aligned}&=\omega \left( i\right) +\left( \mu _{2}+\frac{\lambda (i)\left( \mu _{1}-\mu _{2}\right) e_{1}\left( i\right) }{e\left( i\right) }\right) e\left( i\right) x(i). \end{aligned}$$
(31)

Therefore, the final filter has a step size \( \mu \left( i\right) =f\left( i\right) =\mu _{2}+\frac{\lambda (i)\left( \mu _{1}-\mu _{2}\right) e_{1}\left( i\right) }{e\left( i\right) } \).

3.2 Combination Phase

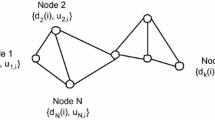
Let us consider a sensor network consisting of N nodes, where each node \( k\in \left\{ 1,2,\ldots ,N\right\} \) represents a different node in the network. At time i, the parameter value obtained by node k is denoted as \( d_{k}\left( i\right) \), and there is an input vector \( u_{k,i} \) for node k, equivalent to the input vector x in the LMS algorithm, where \( u_{k,i} \) is an \( L\times 1 \) dimensional vector. Additionally, the accurate weight value of the network filter \( \omega ^0 \) is also represented as an \( L\times 1 \) dimensional vector. The input–output model for node k can be expressed as follows:

$$\begin{aligned} d_{k}\left( i\right) =u_{k,i}^{T}\omega ^0+\xi _{k}\left( i\right) . \end{aligned}$$
(32)

Here, \( \xi _{k}\left( i\right) \) represents Gaussian noise with a mean of 0 and variance \( \sigma _{k,i}^2 \). The main objective of distributed estimation is to use the external observations \( \left( u_{k,i},d_{k}\left( i\right) \right) \) to estimate \( \omega ^0 \) and approach its accurate value. Two strategies have been proposed for calculating the estimated value of \( \omega ^0 \): Adapt-Then-Combine (ATC) and Combine-Then-Adapt (CTA). The ATC strategy has been shown to provide better estimation accuracy compared to the CTA strategy [10]. (In order to substantiate the theoretical superiority of the Adaptive-Then-Combine (ATC) strategy over the Combine-Then-Adapt (CTA) strategy in handling performance within distributed networks, we have included additional experiments and provided corresponding simulation results in Sect. 5.3.) Therefore, this study directly utilizes and analyzes the ATC strategy.

The ATC strategy can be described as follows:

$$\begin{aligned} \varphi _{k,i}= & {} \omega _{k,i-1}+\mu _{k}\sum u^*_{l,i}\left( d_{l}\left( i\right) -u_{l,i}\omega _{k,i-1}\right) , \end{aligned}$$
(33)
$$\begin{aligned} \omega _{k,i}= & {} \sum a_{k,l}\varphi _{l,i}, \end{aligned}$$
(34)

where \( \mu _{k}=\mu (i)=\mu \left[ e(i)\right] =f\left[ e(i)\right] =\mu _{2}+\frac{\lambda \left( \mu _{1}-\mu _{2}\right) e_{1}\left( i\right) }{e\left( i\right) } \).

Equation (33) represents the adaptation phase, where each node independently uses the observations \( \left( u_{k,i},d_{k}\left( i\right) \right) \) to calculate an intermediate estimate \( \varphi _{k,i} \). Equation (34) represents the combination phase. Each node has the ability to communicate with its neighboring nodes and receive their parameter estimates. The node assigns weights to the received estimates and combines them to produce a new estimate. The coefficient \( \left\{ a_{k,l}\right\} \) determines the amount of intermediate estimate \( \varphi _{k,i} \) exchanged between node k and its neighboring nodes \( l\in N_{k} \). The weight coefficient \( \left\{ a_{k,l}\right\} \) should be greater than 0. Matrix A, with dimensions M, is used to select a subset of intermediate estimates for transmission. Assuming N-dimensional intermediate estimates need to be selected as a subset to be sent to neighboring nodes, the diagonal elements of matrix A consist of N ones, while the remaining \( M-N \) elements are zeros. This allows neighboring nodes to choose the subset to be transmitted. If all diagonal elements are ones, it indicates that all neighboring nodes need to send their intermediate estimates, subject to the following conditions:

$$\begin{aligned} a_{k,l}=0,l\notin N_{k},1^{T}A=1^{T}. \end{aligned}$$
(35)

The communication mode between nodes is determined by the weight coefficients, and the network topology of the wireless sensor network influences the size of the coefficient matrix. The weight coefficient matrix is generated using the Metropolis rule, as shown in Eq. (36):

$$\begin{aligned} a_{k,l}=\left\{ \begin{array}{l} \frac{1}{max\left( r_{k},r_{l}\right) }, l\in N_{k}, l\ne k\\ 1-\sum \limits _{l\in N_{k}, l\ne k} c_{k,l}, l=k\\ 0,l\notin N_{k} \end{array}, \right. \end{aligned}$$
(36)

where \( r_{k} \) and \( r_{l} \) are the degrees of nodes k and l, respectively. By utilizing the distributed strategy, effective decentralization can be achieved, and the computing tasks can be evenly distributed among each node, thereby improving estimation speed and reducing estimation errors caused by single-node estimation. Furthermore, in a distributed network, each node has computing power, so the overall network remains unaffected if a node fails, thereby enhancing network robustness.

Algorithm 1
figure a

A Convex Combination LMS Algorithm Based on the Distributed Diffusion Strategy

Full size image

4 Performance Analysis

4.1 Convergence Analysis

In this section, we analyze the convergence of the weight coefficient vector in Eq. (3). By taking the expectation on both sides, we obtain the following equation:

$$\begin{aligned} E\left\{ \omega (i+1)\right\} =E\left\{ \omega (i)\right\} +2\mu E\left\{ e(i)x(i)\right\} =(I-2\mu R_{xx})E\left\{ \omega (i)\right\} +2\mu R_{xd}, \end{aligned}$$
(37)

where the identity matrix is denoted as I,

$$\begin{aligned} R_{xd}=E\left\{ d(i)x(i)\right\} ,R_{xx}=E\left\{ x(i)x^{T}(i)\right\} . \end{aligned}$$
(38)

By substituting \( i=0 \), we obtain:

$$\begin{aligned} E\left\{ \omega (1)\right\} =(I-2\mu R_{xx})E\left\{ \omega (0)\right\} +2\mu R_{xd}, \end{aligned}$$
(39)

Similarly, for \( i=1 \), we have:

$$\begin{aligned} E\left\{ \omega (2)\right\} =(I-2\mu R_{xx})E\left\{ \omega (1)\right\} +2\mu R_{xd}, \end{aligned}$$
(40)

Starting with \( E\left\{ \omega (0)\right\} =\omega (0) \), we can iterate the process and obtain:

$$\begin{aligned} E\left\{ \omega (i+1)\right\} =(I-2\mu Q\varLambda Q^{-1})^{i+1}\omega (0)+2\mu \sum \limits _{j=0}^{i}(I-2\mu Q\varLambda Q^{-1})^{j}R_{xd}. \end{aligned}$$
(41)

Here, \( R_{xx} \) can be decomposed into a quadratic form as

$$\begin{aligned} R_{xx}=Q\varLambda Q^{T}=Q\varLambda Q^{-1}, \end{aligned}$$
(42)

where Q is an orthogonal unitary matrix and \( \varLambda \) represents the eigenmatrix of \( R_{xx} \). \( \lambda \) denotes the eigenvalues of \( \varLambda \).

Using the relationship with the identity matrix, we have:

$$\begin{aligned} (I-2\mu Q\varLambda Q^{-1})^{i}= & {} Q(I-2\mu \varLambda )^{i} Q^{-1}, \end{aligned}$$
(43)
$$\begin{aligned} \sum _{j=0}^{inf} (I-2\mu Q\varLambda Q^{-1})^{j}= & {} Q(2\mu \varLambda )^{-1}Q^{-1}. \end{aligned}$$
(44)

If the diagonal elements of the matrix are less than 1 (achieved by controlling \( \mu \)), we can observe that:

$$\begin{aligned}{} & {} \lim \limits _{i\longrightarrow \inf } (I-2\mu \varLambda )^{i+1}=0, \end{aligned}$$
(45)
$$\begin{aligned}{} & {} R_{xx}^{-1}=Q\varLambda ^{-1}Q^{-1}. \end{aligned}$$
(46)

By substituting the identities of Eqs. (43) and (44) into Eq. (41), we obtain:

$$\begin{aligned} E\left\{ \omega (i+1)\right\} =Q\varLambda ^{-1}Q^{-1}R_{xd}=R_{xx}^{-1}R_{xd}=\omega _{opt}. \end{aligned}$$
(47)

As time progresses, the solution of the weight vector gradually converges to the Wiener solution, represented by \( \omega _{opt} \). The diagonal elements in \( (I-2\mu \varLambda ) \) are less than 1, which ensures convergence:

$$\begin{aligned} 0<\mu <\frac{1}{\lambda _{max}}, \end{aligned}$$
(48)

where \( \lambda _{max} \) is the maximum eigenvalue of \( R_{xx} \). The step size \( \mu \) plays a crucial role in determining the convergence speed.

Before proving the convergence of a distributed network, we need to establish the following assumptions:

1. The input vectors of all nodes \( u_{k,i} \) are independently and uniformly distributed, with the property \( E\left\{ u_{k,i}u_{k,i}^{T}\right\} =R_{u,k} \).

2. The input Gaussian white noise \( \xi _{k}(i) \) and the input \( u_{k,i} \) of node k are independent, and the \( \xi _{k}(i) \) of all nodes are also independent. We have the following relationships:

$$\begin{aligned} \begin{array}{c} \varDelta {\omega }_{k,i}=\omega ^{0}-\omega _{k,i},\\ \varDelta {\varphi }_{k,i}=\varphi ^{0}-\varphi _{k,i}. \end{array} \end{aligned}$$
(49)

By substituting Eq. (49) into Eqs. (33) and (4), we obtain Eq. (50):

$$\begin{aligned} \begin{array}{c} \varDelta {\varphi }_{k,i}=(I_{M}-\mu _{k}u_{k,i}u_{k,i}^{T})\varDelta {\omega }_{k,i-1}+\mu _{k}u_{k,i}v_{k,t},\\ \varDelta {\omega }_{k,i}=\sum _{l\in N_{k},l\ne k}a_{l,k}\varDelta {\varphi }_{l,i}. \end{array} \end{aligned}$$
(50)

Next, we introduce the following diagonal matrix:

$$\begin{aligned} M=diag\left\{ \mu _{1}I_{M},\ldots ,\mu _{N}I_{M}\right\} . \end{aligned}$$
(51)

We also introduce the following matrices:

$$\begin{aligned} D_{i}= & {} blockdiag\left\{ u_{l,i}^* u_{l,i},\ldots ,u_{N,i}^* u_{N,i}\right\} , \end{aligned}$$
(52)
$$\begin{aligned} g_{i}= & {} col\left\{ u_{l,i}v_{l,i},\ldots ,u_{N,i}v_{N,i}\right\} , \end{aligned}$$
(53)
$$\begin{aligned} \bar{G_{i}}= & {} G_{i}\otimes I_{M}, \end{aligned}$$
(54)
$$\begin{aligned} G_{i}= & {} \left( \begin{array}{ccc} a_{1,1,i}&{}\cdots &{}a_{1,N,i}\\ :&{}\ddots &{}:\\ a_{N,1,i}&{}\cdots &{}a_{N,N,i} \end{array}\right) , \end{aligned}$$
(55)

where \( \otimes \) represents the Kronecker product and \( I_{M} \) represents the M dimensions identity matrix, and the vector

$$\begin{aligned} \varDelta {\omega }_{i}=col\left\{ \varDelta {\omega }_{1,i},\ldots ,\varDelta {\omega }_{N,i}\right\} . \end{aligned}$$
(56)

Using the Kronecker product and the introduced matrices, we have the equation:

$$\begin{aligned} \varDelta {\omega }_{i}=\bar{G}_{i}(I_{MN}-MU_{i})\varDelta {\omega }_{i-1}+\bar{G}_{i}Lb_{i}. \end{aligned}$$
(57)

Considering the independence of\( \varDelta {\omega }_{i},U_{i} \) and \( \bar{G}_{i} \) based on the first two assumptions, we can average Eq. (57) and obtain the following equation:

$$\begin{aligned} E\left\{ \varDelta {\omega }_{i}\right\} =(\bar{G}_{i}\otimes I_{M})(I_{MN}-MR)E\left\{ \varDelta {\omega }_{i-1}\right\} , \end{aligned}$$
(58)

where

$$\begin{aligned} R=blockdiag\left\{ R_{1},\ldots ,R_{n}\right\} . \end{aligned}$$
(59)

The calculation yields:

$$\begin{aligned} ({G}_{i}\otimes I_{M})I_{MN}=I_{MN}, \end{aligned}$$
(60)

where \( {G}_{i}\otimes I_{M} \) denotes a positive value, and by satisfying the inequality

$$\begin{aligned} \left| \lambda _{max}\left\{ I_{MN}-MR\right\} \right| <1, \end{aligned}$$
(61)

we can finally obtain an unbiased solution. In conclusion, the convergence condition for \( \lambda _{max}(A) \), representing the eigenvalue of the Hermitian matrix A, is given by:

$$\begin{aligned} 0<\mu _{i}<\frac{2}{\lambda _{max}\left\{ R_{i}\right\} }. \end{aligned}$$
(62)

4.2 Complexity Comparison

This section presents an analysis of the computational complexity of the CCLMS-DDS algorithm. The aim is to enhance the robustness of the DLMS algorithm in unknown external environments and ensure reliable estimation performance. However, the introduction of additional steps in the convex combination phase leads to increased computation time compared to the DLMS algorithm.

Table 1 provides the complexity of each node’s computation in each iteration when using the CCLMS-DDS algorithm. Table 2 compares the complexity between the DLMS algorithm and the CCLMS-DDS algorithm in each iteration. The results indicate that the computational complexity of the proposed algorithm is higher than that of the DLMS algorithm. This difference arises from the inclusion of two filter calculations.

Although both the DLMS algorithm and the CCLMS-DDS algorithm are relatively straightforward to implement, the DLMS algorithm encounters challenges when dealing with unknown external environments. Specifically, it struggles to strike a balance between low steady-state error and high convergence speed. In contrast, the proposed algorithm addresses this issue by increasing the computational complexity of the filter.

Overall, the CCLMS-DDS algorithm offers improved performance in unknown external environments, but it comes at the cost of higher computational complexity.

Table 1 Single iteration complexity of the CCLMS-DDS algorithm
Full size table
Table 2 Complexity comparison between the CCLMS-DDS algorithm and the DLMS algorithm
Full size table

5 Simulation and Result

Simulation experiments were conducted on the MATLAB platform to validate the feasibility of the proposed algorithm and to compare it with existing algorithms.

5.1 The Impact of Different Step Size Settings on the Performance of the LMS Algorithm

In order to investigate the impact of different step size settings on the performance of the LMS algorithm, various step sizes were tested and their effects were analyzed. Table 3 provides an overview of the different step size settings, while Table 4 presents the settings for the noise signal.

Firstly, when the step size of the LMS algorithm is set to 0.05, as shown in Fig.  3, the convergence speed is significantly faster compared to previous settings. It reaches the convergence state in approximately 50 iterations. However, an issue arises with a subsequent occurrence of severe jitter in the MSE. This indicates the presence of a large error in the MSE, leading to a significant steady-state error between stable and accurate values.

Table 3 Filter parameter settings
Full size table
Table 4 Noise signal settings
Full size table
Fig. 3
figure 3

MSE of the filter whose step size is 0.05

Full size image

Secondly, when the step size of the LMS algorithm is set to 0.005, as depicted in Fig.  4, the convergence speed becomes excessively slow.

Furthermore, in comparison to the filter with a large step size of 0.05, the convex combination filter exhibits a slower iteration speed, as shown in Fig.  5. It takes around 300 iterations to reach a steady state. However, once convergence is achieved, the stability is robust, and the steady-state error is effectively suppressed at -30 dB. Compared to the filter with a step size of 0.005, the convex combination filter converges faster. The filter with a step size of 0.005 requires 1200 iterations to converge, while the convex combination filter reaches a steady state in 300 iterations. Moreover, after reaching a steady state, the steady-state error is controlled at -30 dB.

The simulation results highlight the impact of different step size settings on the performance of the LMS algorithm. The convex combination filter demonstrates improved convergence speed and steady-state error suppression compared to the filters with larger or smaller step sizes. These findings support the effectiveness of the proposed algorithm in achieving desirable performance characteristics.

Fig. 4
figure 4

MSE of the filter whose step size is 0.005

Full size image
Fig. 5
figure 5

MSE of the algorithm proposed in this paper

Full size image

5.2 Performance Improvement of Algorithms with Convex Combination Strategy

The convex combination strategy, as discussed in the previous theoretical analysis, plays a crucial role in achieving a balance between convergence speed and steady-state error by continuously adjusting the weights between filters based on external conditions and errors. The performance of the LMS algorithm is affected by the statistical characteristics of the input signal. To address the challenges in parameter selection and ensure filter convergence, Widrow et al. introduced the normalized LMS (NLMS) algorithm by incorporating a normalization operation, allowing for a flexible step size selection (\( 0<\mu <2 \)) independent of the input signal’s statistical characteristics. In our simulation experiments, we compare our proposed algorithm with the NLMS algorithm, as depicted in Fig. 6.

The convergence and stability time of both the NLMS algorithm and our proposed algorithm are nearly identical, approximately 400 iterations, which is significantly faster than the 1200 iterations required by the conventional LMS algorithm. It is worth noting that our proposed method exhibits a faster convergence speed than the NLMS algorithm prior to reaching stability, highlighting the significant advantages of our approach utilizing the convex combination strategy.

The results clearly demonstrate the substantial superiority of our proposed method utilizing the convex combination strategy over the NLMS algorithm. These findings provide valuable insights for the design of adaptive filtering algorithms that achieve enhanced convergence speed and stability, especially in the presence of varying input signal statistics. Further research and application of the convex combination strategy have the potential to contribute to the development of advanced adaptive filtering techniques, thereby improving their performance in real-world scenarios.

Fig. 6
figure 6

Performance improvement of algorithms with convex combination strategy

Full size image

5.3 The Impact of Different Strategies and Step Size Settings on the Performance of the DLMS Algorithm

In this study, we conducted experiments to evaluate the performance of the DLMS algorithm and the proposed method. The parameters used for both algorithms were as follows: \( N=20 \) nodes in the network, Gaussian input signals with zero mean, a filter order of \( M=5 \), and Gaussian noise \( v_{k}(i) \) with a variance of \( [-2,-1]dB \). The input signals at the nodes followed a Gaussian distribution with a variance of \( \sigma ^{2}=1 \).

As mentioned in Sect. 3.2, the ATC strategy has shown superior performance compared to the CTA strategy in distributed networks. To further validate this claim, additional experiments were conducted and presented in Fig. 7. The figure illustrates the network MSE performance curves of the DLMS algorithm under the non-cooperative approach, ATC strategy, and CTA strategy, respectively. The results clearly demonstrate that both the ATC and CTA strategies achieve comparable convergence speeds, but the ATC strategy outperforms the CTA strategy in terms of steady-state error reduction. Moreover, the performance of both strategies surpasses that of the non-cooperative approach, highlighting the effectiveness of information exchange among nodes in improving estimation performance. These experimental findings further support the practical relevance of the ATC strategy in distributed networks.

Fig. 7
figure 7

The performance comparison of DLMS algorithms with different strategies

Full size image

For the DLMS algorithm, step sizes \( \mu _{k} \) of 0.05, 0.005, and 0.01 were set for all nodes. In the proposed method, the parameter \( \alpha \) was set to 4, and the step sizes for the two filters were \( \mu _{1}=0.05 \) and \( \mu _{2}=0.005 \), respectively. The network MSE, which indicates estimation accuracy, was used to evaluate the performance, with smaller MSE values indicating more accurate estimation. Each simulation result represents the average of 10 independent experiments.

Before directly comparing the DLMS algorithm and the proposed method, we first analyzed the impact of different step sizes on the performance of the DLMS algorithm. This analysis aimed to determine the optimal parameters for the DLMS algorithm. Additional experimental simulations were conducted, and the results, depicted in Figs. 8 and 9, indicate that a larger step size (e.g., \( \mu _{k}=0.05 \)) leads to faster convergence but poorer steady-state error performance. Conversely, a smaller step size (e.g., \( \mu _{k}=0.005 \)) results in slower convergence but better steady-state error performance. It is evident that the DLMS algorithm with a fixed step size cannot achieve a satisfactory balance between convergence speed and steady-state performance.

Fig. 8
figure 8

The performance comparison between the DLMS algorithm and the proposed algorithm under different step sizes

Full size image
Fig. 9
figure 9

The performance comparison of the DLMS algorithm and the proposed algorithm for each node under different step sizes

Full size image

5.4 Performance Comparison of the Proposed Algorithm in Gaussian Noise Environment with Similar Approaches

In the considered network with \( N=20 \) nodes, each node’s input vector \( u_{k,i} \) follows a zero-mean Gaussian process. The filter order is set to \( M=5 \), and the variance of Gaussian noise \( \upsilon _{k}(i) \) ranges from \(-\,20\) to \(-\,15 dB \). The input signals of each node and the variance of Gaussian noise are shown in Fig. 10. The simulation results are obtained from averaging 200 independent experiments.

In this section, we compare the performance of the proposed method with similar algorithms. Specifically, we consider the DRVSS-LMS algorithm [14] with parameters \( \alpha =2.6 \) and \( \lambda =0.99 \), as well as the RDLMS algorithm [3] with parameter \( \delta =0.9 \).

Fig. 10
figure 10

Variance of input signal and noise in the network nodes

Full size image

Figure  11a and b presents the performance comparison of different algorithms under Gaussian noise conditions. Figure  11a shows the network MSE curves of the proposed algorithm and similar algorithms in a Gaussian noise environment, while Fig.  11b illustrates the steady-state MSE of each node in the network under Gaussian noise conditions.

From the figures, it is evident that the DSE-LMS algorithm exhibits the poorest steady-state estimation performance among the five algorithms, with a slower convergence speed. This can be attributed to the DSE-LMS algorithm’s use of the sign function in the gradient calculation, which filters both abnormal error information contaminated by impulse noise and normal error information. As a result, the DSE-LMS algorithm experiences slow convergence due to a small gradient in the early stages and significant steady-state error caused by a large gradient in the steady-state phase.

In contrast, the proposed algorithm employs the convex combination strategy, which reduces computational complexity and dynamically adjusts the weight of the convex combination filter. It achieves a faster convergence speed compared to the other four algorithms (excluding the DLMS algorithm) and approaches the convergence speed of the DLMS algorithm. Moreover, in the steady-state phase, the proposed algorithm exhibits lower steady-state error than the DLMS algorithm. This demonstrates a successful balance between convergence speed and steady-state error.

These results highlight the superiority of the proposed algorithm in achieving an optimal trade-off between convergence speed and steady-state error. The findings further validate the effectiveness and practical applicability of the proposed algorithm in real-world scenarios.

Fig. 11
figure 11

The performance comparison of different algorithms under Gaussian noise conditions

Full size image

5.5 Performance Comparison with the DLMS Algorithm Based on Impulse Noise

The Bernoulli–Gaussian model is commonly used to describe impulse noise distribution, which combines Bernoulli distribution and Gaussian distribution to model impulse noise as contaminated Gaussian noise. In this model, the background noise \( v_{k}(i) \) consists of two components:

$$\begin{aligned} v_{k}(i)=\upsilon _{k}(i)+I_{k}(i), \end{aligned}$$
(63)

zero-mean Gaussian noise \( \upsilon _{k}(i) \) and impulse noise \( I_{k}(i) \), which is independent of the input vector and Gaussian noise. Impulse noise \( I_{k}(i) \) is expressed as

$$\begin{aligned} I_{k}(i)=\theta _{k}(i)q_{k}(i) \end{aligned}$$
(64)

, where \( \theta _{k}(i) \) follows a Bernoulli distribution with probability \( Pr[\theta _{k}(i)]=p_{k} \), and \( q_{k}(i) \) is zero-mean Gaussian noise with variance \( \zeta _{k}.\sigma _{k,i}^2 \). The power of impulse noise is significantly higher than that of Gaussian noise \( \nu _{k}(i) \). Figure 12a, b illustrates the background noise representation for \( p_{k}=0.06 \) and \( p_{k}=0.12 \).

Fig. 12
figure 12

The background noise contaminated with impulsive noise of varying occurrence probabilities. The X-axis represents the noise samples, while the Y-axis denotes the magnitude of the noise

Full size image

The impact of impulse noise is visually depicted in Fig.  12a and b, where the darkened areas represent the regions of impulse noise occurrence. The occurrence probability of impulse noise at each node, \( p_{k} \), influences the overall noise characteristics of the network. A higher occurrence probability, such as \( p_{k}=0.12 \), results in more frequent impulse noise occurrences and affects a larger portion of the network.

The Bernoulli–Gaussian model provides a valuable framework for accurately modeling and analyzing impulse noise in practical scenarios, enabling better understanding of communication systems in the presence of impulse noise.

The subsequent sections will further analyze and evaluate the effects of impulse noise on communication system performance, emphasizing the importance of mitigating these effects and proposing effective techniques to enhance system performance in such challenging environments.

The influence of different occurrence probabilities of impulse noise on the DLMS algorithm under the Bernoulli–Gaussian model is investigated. In this context, \( p_{k}=0 \) represents the absence of impulse noise, where the background noise follows a Gaussian distribution. Nonzero probability values indicate the likelihood of impulse noise occurrence. The graph reveals that even with a very low occurrence probability, the DLMS algorithm experiences a significant increase in steady-state error. As the occurrence probability increases, the algorithm’s performance further deteriorates, potentially leading to algorithmic failure.

Figure  13 illustrates the relationship between the occurrence probability of impulse noise and the steady-state error of the DLMS algorithm. The steady-state error shows a substantial increase as the occurrence probability of impulse noise grows. This vulnerability of the DLMS algorithm to impulse noise, even at low occurrence probabilities, indicates the need for effective mitigation strategies and robust algorithms to address impulse noise scenarios and prevent performance degradation.

These observations underscore the importance of addressing impulse noise in practical communication systems, especially when the occurrence probability is non-negligible. Mitigating the effects of impulse noise and developing robust algorithms capable of handling such scenarios are crucial research directions for improving the performance and reliability of communication systems.

Fig. 13
figure 13

The relationship between the occurrence probability of impulse noise and the steady-state error of the DLMS algorithm

Full size image

Figure 14a and b compares the performance of various algorithms under the condition that the occurrence probability of impulse noise is \( p_{k}=0.1 \). Figure 14a presents the network MSE comparison of the proposed algorithm and similar algorithms in the Bernoulli–Gaussian noise environment, while Fig. 14b compares the steady-state MSE of each node in the network under the same noise conditions.

From Fig. 14a and b, it can be observed that in the presence of impulse noise, the DLMS algorithm exhibits significant performance deterioration, rendering it ineffective in estimation tasks. In contrast, both the DRVSS-LMS algorithm and the RDLMS algorithm show slight degradation in steady-state estimation performance but still demonstrate robustness against impulse noise interference compared to the Gaussian noise scenario.

The proposed algorithm in this study and the DSE-LMS algorithm exhibit consistent steady-state estimation performance under the Bernoulli–Gaussian noise environment, indicating their strong robustness. Furthermore, the proposed algorithm achieves faster convergence speed and smaller steady-state error compared to the other algorithms.

These findings highlight the resilience of the proposed algorithm and its ability to handle impulse noise, demonstrating its superiority in achieving accurate and reliable estimations in practical applications.

Fig. 14
figure 14

The performance comparison of different algorithms under Bernoulli–Gaussian noise conditions

Full size image

6 Conclusion

In conclusion, this study has presented a novel convex combination distributed LMS algorithm that addresses the challenges of convergence speed and steady-state error in sensor networks. By leveraging the distributed diffusion strategy and incorporating the concept of convex combination, our algorithm has achieved decentralized and robust estimation performance.

The experimental results have demonstrated the feasibility and effectiveness of the proposed algorithm in various scenarios. We have shown that the convex combination distributed LMS algorithm outperforms existing algorithms in terms of convergence speed, steady-state error, and resilience against impulse noise interference. The algorithm strikes a balance between convergence speed and estimation accuracy, offering improved performance compared to the traditional DLMS algorithm.

While the proposed algorithm has shown promising results, there are areas for further improvement and research. Firstly, future work could focus on enhancing the convergence speed without compromising the overall performance. This can be achieved by exploring adaptive step size control techniques, such as variable step sizes based on the network conditions, to accelerate convergence while maintaining stability.

Secondly, reducing the steady-state error remains an important objective. Investigating advanced regularization methods or incorporating adaptive algorithms that adaptively adjust the algorithm’s parameters during operation could help minimize the steady-state error and enhance the accuracy of the estimation results.

Additionally, considering the computational complexity of the proposed algorithm is essential for practical implementation. Future research can explore techniques to optimize the algorithm’s computational requirements, such as employing parallel computing architectures or developing efficient algorithms that strike a better balance between performance and computational cost.

Furthermore, the application of the convex combination distributed LMS algorithm can be extended to non-stationary environments or nonlinear systems. Addressing these challenges will require adapting the algorithm to handle time-varying or nonlinear characteristics, potentially through the use of adaptive filtering techniques or advanced machine learning algorithms.

In conclusion, the convex combination distributed LMS algorithm offers a valuable contribution to the field of adaptive filtering in sensor networks. While further research is needed to enhance convergence speed, reduce steady-state error, and optimize computational complexity, the algorithm’s potential for improved estimation performance is evident. By addressing these research directions, we can advance the algorithm’s practical applicability and foster its adoption in real-world scenarios, contributing to the development of more efficient and reliable sensor network systems.