1 Introduction

The applications of distributed adaptive networks have become very widespread and long lasting and this issue made the study of their performance a crucial topic of research [1,2,3,4,5]. The ability of distributed tracking and estimation of these networks can and will be an aid to measure and estimate almost every desirable entity. These measurements and estimations will take place in various conditions. For example if we want to work on a wireless platform, we must face the challenges of wireless communication channels.

Channel estimation is a vital part of all wireless communication systems. Without channel estimation, the communication will suffer from channel impairments and the direct results will be the reduction in data transfer rate and the decline in the estimation performance. Studying channel effects on adaptive networks is a hot topic of research. In some papers channels in these networks have been considered to be severely noisy [1, 6], others considered deeply faded channels [3, 4]. Fading for a wireless adaptive network may occur when the nodes are far from each other or moving with respect to each other [4, 5]. Consequently, channel estimation and equalization for wireless adaptive networks is essential. When we work in fading environments, it is important to know that we must deal with non-stationary conditions [7], because fading channel taps are usually non-stationary. Up until now the performance analysis of distributed networks have been mostly presented for stationary environments and estimating stationary variables. However, recently the performance of sensor networks have been investigated in non-stationary variable estimation [1, 2]. However, none of these references mentioned a feasible application of non-stationary entity estimation.

There are two major distributed cooperation strategies for adaptive networks [8], the first one is incremental strategy which allows nodes to share data in a Hamiltonian cycle [5]. The other cooperation strategy is the diffusion scheme that allows nodes to communicate with more than two neighboring nodes and this makes the network robust to link failures [9, 10]. The performance of both of these strategies under non-stationary conditions were investigated in [2]. By considering these investigations, in [11, 12] the authors performed channel estimation with incremental strategy and presented results for estimating Rayleigh flat fading channels. In this paper our aim is to perform channel estimation with diffusion strategy which is more practical in implementation.

In [3, 5] it was assumed that channel side information for nodes is not available at all and consequently the performance of simulated sensor network is highly degraded in comparison with the simulations of [4]. Also, In [4] it was assumed that we have channel side information in each node and channel equalization is available but it is not mentioned that how we can estimate channel gains at each node, in this paper we will show how this can be done with diffusion strategy and this paper completes the argument in [4].

Our main contribution in this work is the estimation of the fading channels with diffusion adaptive algorithms and applying the theoretical calculations of non-stationary entity estimation to this task. Up until now several models have been presented for modeling Rayleigh and Rician fading channels [13] but it must be noted that these models are not always non-stationary. In this paper we considered a non-stationary model for our Rayleigh fading channels and used the accurate results for autocorrelation functions in deriving covariance matrixes of these channels, then we applied tracking performance analysis with estimating their time varying channel taps. All in all, in this paper we want to know how we can model and verify channel estimation results and our aim in this paper is to derive closed form relations for the steady-state fading channel estimation performance of diffusion LMS algorithm and comparing the results with channel estimation simulations. The remaining of this paper is prepared as follows:

In part II we will have a brief overview of diffusion adaptive estimation of a stationary data in distributed sensor networks. In part III we describe the non-stationary channel model that is considered in this paper. In part IV we study the tracking performance of diffusion LMS algorithm and overview the derivation of theoretical Steady-state performance results. In part V we presented our simulation examples for tracking of time varying weights and Rayleigh fading channel estimation. Part VI contains our concluding remarks.

Notation We used boldface letters for random variables and plain text letters for deterministic quantities. Upper case letters are also used for matrixes. We used the notation \({\mathbb{E}}\left[ . \right]\) to denote expectation operation, \(\left( . \right)^{*}\) to denote complex conjugation for scalars and complex conjugate transposition for matrixes, \(Tr\left( . \right)\) to denote trace of matrixes, ⊗ to denote Kronecker product and \(vec\left( . \right)\) to denote a vector formed by stacking the columns of its matrix argument. The notation \(diag\left\{ \ldots \right\}\) denotes a diagonal matrix formed by its elements and the notation \(col\left\{ \ldots \right\}\) denotes a column vector formed by its arguments. In addition, we used weighted norm notation as \(\left\| x \right\|_{\Sigma }^{2} = x^{*}\Sigma x\).

2 Problem Statement

In diffusion strategy each node can communicate with several neighboring nodes. Consider a network of N nodes distributed in an area like Fig. 1. This is also the diffusion network topology that we used for our simulations.

Fig. 1
figure 1

The topology of a diffusion adaptive network with 20 nodes

Full size image

Take (k) as sensor index, then each node will have access to time realizations \(\left\{ {d_{k} \left( i \right), u_{k,i} } \right\}\) of \(\left\{ {\varvec{d}_{k} \left( i \right),\varvec{u}_{k,i} } \right\}\) measurements. For each sensor \(\varvec{d}_{k}\) is a scalar quantity and \(,\varvec{u}_{k}\) is a \(1 \times M\) vector. The data model for stationary case represents the relation between these measurements through a linear equation [8]:

$$\varvec{d}_{k} \left( i \right) = \varvec{u}_{k,i} w^{o} + \varvec{v}_{k} \left( i \right)$$
(1)

where \(w^{o}\) is the \(M \times 1\) desired unknown stationary vector and \(\varvec{v}_{k} \left( i \right)\) is white noise with variance \(\sigma_{v,k}^{2}\). For each specific task, this weight vector can be modeled with respect to the conditions of the problem. For example in the channel estimation task, the weight vector must be produced using the standard channel models. In part 3 we will explain the weigh vector model for Rayleigh fading channels.

The following independence assumptions are taken into consideration: (1) For \(k = 1, \ldots ,N\) and \(i \ge 1\), the regressors \(\varvec{u}_{k,i}\) are independent of node indices \(k\) and iterations \(i\). (2) The observation noises \(\varvec{v}_{k} \left( i \right)\) for all nodes \(k = 1, \ldots ,N\) and all iterations \(i \ge 1\) are zero mean Gaussian processes and are independent of each other and all regressors.

In stationary case the objective of the adaptive network is to estimate the desired deterministic vector \(w^{o}\) through minimizing the mean square error:

$$w^{o} = \mathop {\text{argmin}}\limits_{w} \frac{1}{N}\mathop \sum \limits_{k = 1}^{N} {\mathbb{E}}\left| {\varvec{d}_{k} - \varvec{u}_{k} w} \right|^{2}$$
(2)

The optimal weight is then:

$$w^{o} = \left( {\mathop \sum \limits_{k = 1}^{N} R_{u,k} } \right)^{ - 1} \left( {\mathop \sum \limits_{k = 1}^{N} R_{du,k} } \right)$$
(3)

where \(R_{u,k} = {\mathbb{E}}\left( {\varvec{u}_{k}^{*} \varvec{u}_{k} } \right)\) and \(R_{du,k} = {\mathbb{E}}\left( {\varvec{d}_{k} \varvec{u}_{k}^{*} } \right)\) are correlation terms. In the non-stationary case, this optimal weight vector changes with time and our task is to track its variations. Here we study two prominent diffusion strategies:

2.1 Adapt then Combine Strategy

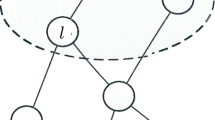
In the diffusion cooperation mode, each node uses the information from all adjacent nodes and there are two main policies for combining this information. One is the adapt then combine (ATC) strategy, here if we consider \(\psi_{k,i}\) as the local estimation of unknown vector at node \(k\) and iteration \(i\), node k performs a combination of all neighboring node estimations. This combination can be expressed by the following equation [2]:

$$\varvec{\psi}_{k,i} = \mathop \sum \limits_{{l \in {\mathcal{N}}_{k} }} a_{k,l} \varvec{\phi}_{l,i}$$
(4)

where \(a_{k,l}\) are the combination coefficients, \({\mathcal{N}}_{k}\) is the size of the neighborhood of node \(k\) and \(\phi_{l,i}\) is the individual estimation of each node and it is achieved by:

$$\varvec{\phi}_{k,i} =\varvec{\psi}_{k,i - 1} + \mu_{k} \varvec{u}_{k,i}^{*} \left( {\varvec{d}_{k} \left( i \right) - \varvec{u}_{k,i}\varvec{\psi}_{k,i - 1} } \right)$$
(5)

This procedure can be seen for node k in Fig. 2:

Fig. 2
figure 2

The ATC diffusion strategy

Full size image

İt is important to mention that choosing different values for the combination coefficients (\(a_{k,l}\)) will affect the performance of diffusion algorithms. In our simulations we used the Uniform policy for determining these coefficients. In this policy we have:

$$a_{l,k} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{n_{k} }}, } \hfill & { l \in {\mathcal{N}}_{k} } \hfill \\ {0,} \hfill & { otherwise} \hfill \\ \end{array} } \right.$$
(6)

where \(n_{k} \triangleq \left| {{\mathcal{N}}_{k} } \right|\) is the size of the neighborhood of node \(k\). We can see that all the neighbors of node \(k\) are assigned the same weight, \(\frac{1}{{n_{k} }}\).

2.2 Combine then Adapt Strategy

If we change the order of steps in the ATC algorithm, we achieve the combine then adapt (CTA) strategy which is given as bellow:

At each iteration \(i \ge 0\) and for each node \(k\) repeat:

  1. 1.

    Combine local estimations:

    $$\varvec{\phi}_{k,i - 1} = \mathop \sum \limits_{{l \in {\mathcal{N}}_{k} }} a_{k,l}\varvec{\psi}_{l,i - 1}$$
    (7)
  2. 2.

    Adapt the local estimation:

    $$\varvec{\psi}_{k,i} = \varvec{\phi}_{k,i - 1} + \mu_{k} \varvec{u}_{k,i}^{*} \left( {\varvec{d}_{k} \left( i \right) - \varvec{u}_{k,i} \varvec{\phi}_{k,i - 1} } \right)$$
    (8)

This strategy is depicted for node k in Fig. 3:

Fig. 3
figure 3

The CTA diffusion strategy

Full size image

The same uniform combination policy as in (6) for \(a_{k,l}\) is considered here.

3 Non-stationary Weight Vector Models

One of the uses of analyzing channel estimation with diffusion networks is to understand how well we can track a non-stationary entity. So far we mentioned that the goal of adaptive distributed networks can be stated as estimating the unknown vector \(w^{o}\). This task is taken into consideration in many papers and for different environment conditions [1,2,3,4,5, 11]. Recently the performance of adaptive networks for non-stationary variable estimation is investigated in [2] where the unknown vector varies with time. This variation with time can be described as first order Markov process [14]:

$$\varvec{w}_{i}^{o} = \alpha \varvec{w}_{i - 1}^{o} +\varvec{\eta}_{i}$$
(9)

where \(\alpha\) is a fixed parameter of the model (close to one) and \(\varvec{\eta}_{i}\) is a zero mean random sequence with covariance matrix \(R_{\eta }\). It is important to mention that if we take \(\alpha\) very close to one, we obtain the Random-walk model:

$$\varvec{w}_{i}^{o} = \varvec{w}_{i - 1}^{o} +\varvec{\eta}_{i}$$
(10)

This assumption is widely used in adaptive literature and without this assumption; the developed performance analysis will be inaccurate. In this case, the goal of our network is to follow and estimate this time varying vector and for this reason it is more likely to be a difficult task. So many applications can be assumed for the estimating a non-stationary value and in this paper we assigned channel estimation task for diffusion LMS algorithm. Therefore, in this paper for the first time we used diffusion strategy for fading channel estimation and related it to the tracking performance. As we want to present the performance analysis of adaptive networks in estimating non-stationary fading channel types, we must find the fading models that are non-stationary because there are also fading channel models that are wide sense stationary [13]. Here we explain the Rayleigh fading channel model and its relation with non-stationary data model:

3.1 Rayleigh Fading Channel Model

In [7] a non-stationary model for Rayleigh fading channel is described where the channel coefficients (or the impulse response of channel) are calculated as:

$$h\left( n \right) = \gamma x\left( n \right)\delta \left( {n - n_{0} } \right)$$
(11)

where \(\gamma\) is path loss and \(n_{0}\) is the channel delay. \(x\left( n \right)\) is a time varying sequence and its amplitude \(\left| {x\left( n \right)} \right|\) is assumed to have Rayleigh distribution which is given as:

$$f_{{\left| {\varvec{x}\left( n \right)} \right|}} \left( {\left| {\varvec{x}\left( n \right)} \right|} \right) = \left| {\varvec{x}\left( n \right)} \right|e^{{{\raise0.7ex\hbox{${ - \left| {\varvec{x}\left( n \right)} \right|^{2} }$} \!\mathord{\left/ {\vphantom {{ - \left| {\varvec{x}\left( n \right)} \right|^{2} } 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} ,\quad \left| {\varvec{x}\left( n \right)} \right| \ge 0$$
(12)

The phase of this distribution is uniformly distributed within [\(- \;\pi ,\pi ]\). The auto correlation of the sequence \(x\left( n \right)\) is equal to zeroth-order Bessel function:

$$\varvec{r}\left( k \right) = {\mathbb{E}}\left[ {\varvec{x}\left( n \right)\varvec{x}\left( {n - k} \right)} \right] = J_{0} \left( {2\pi f_{D} T_{s} k} \right), k = \; \ldots ,\; - \;1,\;0,\;1,\; \ldots$$
(13)

where \(f_{D}\) is the Doppler frequency, \(T_{s}\) is the sampling period and \(J_{0} \left( . \right)\) is zeroth-order the Bessel function.

Now if we want to estimate this channel model, the first order AR model for \(x\left( n \right)\) is:

$$\varvec{x}\left( k \right) = \alpha .\varvec{x}\left( {k - 1} \right) + \varvec{e}\left( k \right)$$
(14)

where \(\varvec{e}\left( k \right)\) is a white noise process with the variance of \(\sigma_{e}^{2} = \left( {1 - \alpha^{2} } \right)\) and \(\left( \alpha \right)\) is obtained as:

$$\alpha = \frac{r\left( 1 \right)}{r\left( 0 \right)}$$
(15)

In this equation, \(r\left( k \right)\) is defined in (13) and \(r\left( 0 \right) = 1\). In [7] the first order AR model is given as:

$$\varvec{x}\left( n \right) = \varvec{r}\left( 1 \right)\varvec{x}\left( {n - 1} \right) + \sqrt {1 - \left| {\varvec{r}\left( 1 \right)} \right|^{2} } \varvec{ v}\left( n \right)$$
(16)

where \(\varvec{v}\left( n \right)\) is a white noise process with unit variance. Now we can assume a \(M \times 1\) weight vector with the entries of these Rayleigh fading coefficients like: \(\varvec{w}_{i}^{o} = \left[ {x_{1} \left( n \right) x_{2} \left( n \right) \ldots x_{M} \left( n \right)} \right]^{'}\). All the entries of this vector change with time and as the coefficients change at the same rate, the above approximation indicates that the variations in weight vector could be approximated as:

$$\varvec{w}_{i}^{o} = \alpha \varvec{w}_{i - 1}^{o} +\varvec{\eta}_{i}$$
(17)

where the covariance matrix of \(\varvec{\eta}_{i}\) is:

$$R_{\eta } = \left( {1 - \alpha^{2} } \right)I$$
(18)

with \(\alpha = r\left( 1 \right)\) and \(I\) to be a unit matrix. It is obvious that the maximum value of \(\alpha\) is one and as the value of \(\alpha\) decreases the diagonal elements of \(R_{\eta }\) increase. Here for the first time we reveal how increasing Doppler frequency can make the performance of channel estimation more difficult and even sometimes impossible. For this reason we introduce the Degree of Non-stationarity (DN) [14]. For each node:

$$DN_{k} \triangleq \sqrt {\frac{{Tr(R_{u,k} R_{\eta } ) }}{{\sigma_{v,k}^{2} }}}$$
(19)

If \(DN_{k}\) is less than one for all nodes, then the network can track the variations in channel, but if it is more than unity, then the variations are to fast for the network and therefore the convergence becomes unstable. In simulation part we will describe this issue with examples. It means that convergence depends on the diagonal elements of \(R_{\eta }\) and consequently to Doppler frequency and sampling period.

4 Steady-State Analysis

In this part we analyze the steady-state error performance of diffusion LMS algorithm in tracking the non-stationary channel model. In order to present theoretical analysis for tracking performance, we consider the general diffusion LMS algorithm given by [1, 2]:

$$\begin{aligned} & \varvec{\phi}_{k,i - 1} = \mathop \sum \limits_{{l \in {\mathcal{N}}_{k} }} a_{1,lk} \varvec{w}_{l,i - 1} \hfill \\& \varvec{\psi}_{k,i} = \varvec{\phi}_{k,i - 1} + \mu_{k} \varvec{u}_{k,i}^{*} \left( {\varvec{d}_{k} \left( i \right) - \varvec{u}_{k,i} \varvec{\phi}_{k,i - 1} } \right) \hfill \\ &\varvec{w}_{k,i} = \mathop \sum \limits_{{l \in {\mathcal{N}}_{k} }} a_{2,lk}\varvec{\psi}_{l,i} \hfill \\ \end{aligned}$$
(20)

In these relations \(\left\{ {a_{1,lk} ,a_{2,lk} } \right\}\) are combination coefficients corresponding to elements of combination \(N \times N\) matrices \(A_{1}\), \(A_{2}\). By altering these combination matrices we can achieve different diffusion algorithms that is, if we choose \(A_{1} = I_{N}\) and \(A_{2} = A\), we obtain ATC diffusion algorithm. Also, if we consider \(A_{1} = A\) and \(A_{2} = I_{N}\) we obtain CTA diffusion algorithm. In these relations, the combination coefficients using (6) give rise to the \(N \times N\) combination matrix \(A = \left[ {a_{l,k} } \right]\) and \(I_{N}\) represents \(N \times N\) identity matrix. These considerations are important when we want to match theoretical and simulation results.

For non-stationary entity estimation when the optimum weight vector varies with time, the following weight error vectors are defined:

$$\tilde{\varvec{\phi} }_{k,i} \triangleq \varvec{w}_{i}^{o} - \varvec{\phi}_{k,i} ,\quad \tilde{\varvec{\psi }}_{k,i} \triangleq \varvec{w}_{i}^{o} -\varvec{\psi}_{k,i} ,\quad \tilde{\varvec{w}}_{k,i} \triangleq \varvec{w}_{i}^{o} - \varvec{w}_{k,i}$$
(21)

We analyze the tracking performance of adaptive networks using Mean square deviation (MSD) and Excess mean square error (EMSE) defined as:

$$MSD_{k} = {{\mathbb{E}}}\left\| {\tilde{\varvec{w}}_{k,\infty } } \right\|_{I}^{2}$$
(22)
$$EMSE_{k} = {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{k,\infty } } \right\|_{{R_{u,k} }}^{2}$$
(23)

If we collect the errors of all nodes in single matrixes we get:

$$\tilde{\varvec{\phi}}_{i}\, \triangleq \, col\left\{ {\tilde{\varvec{\phi}}_{1,i} , \ldots ,\tilde{\varvec{\phi}}_{N,i} } \right\},\quad \tilde{\varvec{\psi }}_{i} \, \triangleq \, col\left\{ {\tilde{\varvec{\psi }}_{1,i} , \ldots ,\tilde{\varvec{\psi }}_{N,i} } \right\},\quad \tilde{\varvec{w}}_{i} \, \triangleq \, col\left\{ {\tilde{\varvec{w}}_{1,i} , \ldots ,\tilde{\varvec{w}}_{N,i} } \right\}$$
(24)

In addition, we define:

$${\mathcal{M}} \, \triangleq \, diag\left\{ {\mu_{1} I_{M} ,\mu_{2} I_{M} , \ldots ,\mu_{N} I_{M} } \right\}$$
(25)
$${\boldsymbol{\mathcal{R}}}_{i} \, \triangleq \, diag\left\{ {\varvec{u}_{1,i}^{*} \varvec{u}_{1,i} ,\varvec{u}_{2,i}^{*} \varvec{u}_{2,i} , \ldots ,\varvec{u}_{N,i}^{*} \varvec{u}_{N,i} } \right\}$$
(26)
$$\varvec{s}_{i} \, \triangleq \, col\left\{ {\varvec{u}_{1,i}^{*} \varvec{v}_{1} \left( i \right),\varvec{u}_{2,i}^{*} \varvec{v}_{2} \left( i \right), \ldots ,\varvec{u}_{N,i}^{*} \varvec{v}_{N} \left( i \right)} \right\}$$
(27)

The recursion for network error vector is given by:

$$\tilde{\varvec{w}}_{i} = {\boldsymbol{\mathcal{B}}}_{i} \tilde{\varvec{w}}_{i - 1} - {\mathcal{G}}\varvec{s}_{i} , i \ge 0$$
(28)

in this recursion we have:

$$\begin{aligned} {\boldsymbol{\mathcal{B}}}_{i} = A_{2}^{T} \left( {I_{NM} - {\mathcal{M}}{\boldsymbol{\mathcal{R}}}_{i} } \right){\mathcal{A}}_{1}^{T} \hfill \\ {\mathcal{G}} = {\mathcal{A}}_{2}^{T} {\mathcal{M}} \hfill \\ {\mathcal{A}}_{1} = A_{1} \otimes I_{M} , {\mathcal{A}}_{2} = A_{2} \otimes I_{M} \hfill \\ \end{aligned}$$
(29)

We have \({\mathbb{E}}\varvec{s}_{i} = 0\) because of the independence of regressors and noises. By taking expectation from (28) we get:

$${\mathbb{E}}\tilde{\varvec{w}}_{i} = {\boldsymbol{\mathcal{B}}}_{i} {\mathbb{E}}\tilde{\varvec{w}}_{i - 1}$$
(30)

Our contribution in steady-state analysis of tracking the non-stationary channel begins here. For estimating a fading channel with Random-walk model we have:

$$\varvec{\zeta}_{i} = col\left\{ {\varvec{\eta}_{i} , \ldots ,\varvec{\eta}_{i} } \right\} = {\mathbb{I}}_{N} \otimes\varvec{\eta}_{i} \quad \quad \left( {NM \times 1} \right)$$
$${\mathbb{I}}_{N} = col\left\{ {1,1, \ldots ,1} \right\}$$
(31)

where \(\varvec{\eta}_{i}\) is described in (9) and (17). The relation (30) for a non-stationary variable tracking becomes:

$${\mathbb{E}}\tilde{\varvec{w}}_{i} = {\boldsymbol{\mathcal{B}}}_{i} {\mathbb{E}}\left\{ {\tilde{\varvec{w}}_{i - 1} +\varvec{\zeta}_{i} } \right\}$$
(32)

In [2] the variance relation for diffusion adaptation in stationary condition is given as:

$${\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i} } \right\|_{\sigma }^{2} \,= {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i - 1} } \right\|_{{F_{dif} \sigma }}^{2} + \left[ {vec\left( {{\mathcal{Y}}^{T} } \right)} \right]^{T} \sigma$$
(33)

where we have:

$$F_{dif} \approx {\mathcal{B}}^{T} \otimes {\mathcal{B}}^{*} ,\quad {\mathcal{Y}} = {\mathcal{G}\mathcal{S}\mathcal{G}}^{T} ,\quad {\mathcal{S}} = {\mathbb{E}}\left\{ {s_{i} s_{i}^{*} } \right\}$$
(34)

Also, \({\mathbb{E}}\left\{ {{\boldsymbol{\mathcal{B}}}_{i} } \right\} = {\mathcal{B}}\). If we assume:

$$\sigma = vec\left(\Sigma \right)$$
(35)

where \(\Sigma\) is a \(NM \times NM\) non-negative matrix, then \(\sigma\) becomes a \(N^{2} M^{2} \times 1\) vector. We can write (33) as:

$${\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i} } \right\|_{\Sigma }^{2}\, = {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i - 1} } \right\|_{{\Sigma ^{{\prime }} }}^{2} + \left[ {vec\left( {{\mathcal{Y}}^{T} } \right)} \right]^{T} \sigma$$
(36)

where we have:

$${\varSigma \prime } = vec\left( {F_{dif} \sigma } \right) = vec\left( {\sigma^{\prime}} \right)$$
(37)

In non-stationary condition the variance relation is given by [1]:

$${\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i} } \right\|_{\Sigma }^{2}\, = {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i - 1} } \right\|_{{\Sigma ^{{\prime }} }}^{2} \,+ \, {\mathbb{E}}\left\| {\zeta_{i} } \right\|_{{\Sigma ^{{\prime }} }}^{2} + \left[ {vec\left( {{\mathcal{Y}}^{T} } \right)} \right]^{T} \sigma$$
(38)

in this relation we have \({\mathbb{E}}\left\| {\zeta_{i} } \right\|_{{\Sigma ^{{\prime }} }}^{2}\, = {\mathbb{E}}Tr\left( {\zeta_{i} \zeta_{i}^{*}\Sigma ^{{\prime }} } \right)\). Also, we can write [1]:

$$\Sigma ^{{\prime }} = {\mathcal{A}}_{1} {\mathcal{A}}_{2} {\varSigma \mathcal{A}}_{2}^{T} {\mathcal{A}}_{1}^{T} + {\mathcal{O}}\left( {\mathcal{M}} \right) + {\mathcal{O}}\left( {{\mathcal{M}}^{2} } \right)$$
(39)

where \({\mathcal{O}}\left( {\mathcal{M}} \right)\) denotes a term on the order of \({\mathcal{M}}\) and \({\mathcal{O}}\left( {{\mathcal{M}}^{2} } \right)\) denotes a term on the order of \({\mathcal{M}}^{2}\).The last two terms of relation (39) can be omitted for small step sizes and then:

$${\mathbb{E}}\left\| {\zeta_{i} } \right\|_{{\Sigma ^{{\prime }} }}^{2} \, = {\mathbb{E}}Tr\left( {\zeta_{i} \zeta_{i}^{*}\Sigma ^{{\prime }} } \right) = Tr\left( {{\mathcal{A}}_{2}^{T} {\mathcal{A}}_{1}^{T} {\mathcal{R}}_{\zeta } {\mathcal{A}}_{1} {\mathcal{A}}_{2}\Sigma } \right)$$
(40)

By defining:

$${\mathcal{R}}_{\varvec{\zeta}} \, \triangleq \, {\mathbb{E}}\varvec{\zeta}_{i}\varvec{\zeta}_{i}^{*} = \left( {{\mathbb{I}}_{N} {\mathbb{I}}_{N}^{T} } \right) \otimes R_{\eta }$$
(41)

where \(R_{\eta }\) is the covariance matrix of \(\varvec{\eta}_{i}\) given in (18). We have:

$${\mathcal{A}}_{2}^{T} {\mathcal{A}}_{1}^{T} {\mathcal{R}}_{\zeta } {\mathcal{A}}_{1} {\mathcal{A}}_{2} = \left( {A_{2}^{T} \otimes I_{M} \left( {A_{1}^{T} \otimes I_{M} } \right) \left( {{\mathbb{I}}_{N} {\mathbb{I}}_{N}^{T} } \right) \otimes R_{\eta } } \right) \times \left( {A_{1} \otimes I_{M} } \right)\left( {A_{2} \otimes I_{M} } \right)$$
(42)

we can write [1]:

$$Tr\left( {{\mathcal{R}}_{\zeta }\Sigma } \right) = \left[ {vec\left( {{\mathcal{R}}_{\zeta }^{T} } \right)} \right]^{T} \sigma$$
(43)

Using this equality relation (36) transforms to:

$${\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i} } \right\|_{\Sigma }^{2} \, = {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i - 1} } \right\|_{{\Sigma ^{{\prime }} }}^{2} + \left[ {vec\left( {{\mathcal{Y}}^{T} + {\mathcal{R}}_{\zeta }^{T} } \right)} \right]^{T} \sigma$$
(44)

also:

$${\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i} } \right\|_{\upsigma}^{2} \, = {\mathbb{E}}\left\| {\tilde{\varvec{w}}_{i - 1} } \right\|_{{F_{dif} \sigma }}^{2} + \left[ {vec\left( {{\mathcal{Y}}^{T} + {\mathcal{R}}_{\zeta }^{T} } \right)} \right]^{T} \sigma$$
(45)

By defining the following block matrices:

$$\begin{aligned} {\mathcal{J}}_{k} \, \triangleq \, diag\left\{ {0_{M} , \ldots ,0_{M} ,I_{M} ,0_{M} , \ldots ,0_{M} } \right\} \hfill \\ {\mathcal{T}}_{k} \, \triangleq \, diag\left\{ {0_{M} , \ldots ,0_{M} ,R_{u,k} ,0_{M} , \ldots ,0_{M} } \right\} \hfill \\ \end{aligned}$$
(46)

and using them as weighting matrices like \(\left( {I - F_{dif} } \right)\sigma = vec\left( {{\mathcal{J}}_{k} } \right) or vec\left( {{\mathcal{T}}_{k} } \right)\), for MSD and EMSE respectively, we can finally arrive to these steady-state error values of diffusion adaptation strategy in estimating a non-stationary channel.

$$MSD_{k} = \left[ {vec\left( {{\mathcal{Y}}^{T} + {\mathcal{R}}_{\zeta }^{T} } \right)} \right]^{T} \left( {I - F_{dif} } \right)^{ - 1} vec\left( {{\mathcal{J}}_{k} } \right)$$
(47)
$$EMSE_{k} = \left[ {vec\left( {{\mathcal{Y}}^{T} + {\mathcal{R}}_{\zeta }^{T} } \right)} \right]^{T} \left( {I - F_{dif} } \right)^{ - 1} vec\left( {{\mathcal{T}}_{k} } \right)$$
(48)

we can see the effect of \({\mathcal{R}}_{\varvec{\zeta}}\) in these equations which is related to channel covariance matrix \(R_{\eta }\) (given in 18) and it is correspondingly related to Doppler frequency and sampling period of the estimated channel. It means that for a given \(f_{D}\) and \(T_{s}\) we can find the diagonal values of \(R_{\eta }\) matrix and directly incorporate them in (47) and (48).

5 Simulation Results

Now it is time to simulate non-stationary channel tracking with distributed network. We consider a network with 20 active nodes working in a diffusion cooperation strategy. All simulation results are averaged over 100 Monte Carlo runs. The steady-state curves are obtained by averaging the last 200 iteration results of simulations [5]. The variance of noise is considered to be the same for all nodes and we have \(\sigma_{v,k}^{2} = 0.01\), this assumption is different from the assumption of noisy links in [3]. In addition, the step-size is considered to be fixed and it is equal to 0.0045. The regressors \(u_{k,i }\) are generated by independent realizations of a Gaussian distribution with a covariance matrix \(R_{u,k}\) whose eigenvalue spread is between 1 and 5. The estimated channel vector is Rayleigh modeled with size \(M = 4\).

For different Doppler frequency and sampling period quantities, we have different performances. In [12] it is mentioned for operating frequencies between 100 MHz and 2 GHz, the Doppler frequency shift \(f_{D}\) can be as large as 128 Hz. In our simulations we consider the Doppler frequency to be between 10 and 40 Hz. Also in [7] sampling period \(T_{s}\) considered between \(10^{ - 6}\) and \(10^{ - 3}\) s. In this case, the diagonal entries of covariance matrix \(R_{\eta }\) from zeroth-order Bessel function of (13) will be between 0.9843 and 1.

In Fig. 4 we presented our channel estimation results for 5 different cases of Doppler frequency and sampling periods. It can be seen that as the Doppler frequency and sampling period increase, the performance of adaptive network degrades and for the two top curves the convergence becomes unstable or it can be said that the network does not converge when the non-stationarity grows. As we mentioned before, the degree of non-stationarity plays an important role in the convergence or divergence of the adaptive algorithms.

Fig. 4
figure 4

The effect of degree of non-stationarity in the performance of network

Full size image

Also, when the non-stationarity is low, the performance of convergence becomes very similar to the stationary case and in the lowest curve of Fig. 4 it can be seen than the theoretical values of the Stationary channel estimation match with the simulation results of the estimation of a channel that is weakly non-stationary.

In Figs. 5 and 6 we compared the theoretical and simulation results of channel estimation when the channels are highly non-stationary and mildly non-stationary, respectively. As it can be seen from these figures, in both cases the theoretical results almost match the simulation results and this shows the credibility of presented calculations for a certain range of non-stationarity degree.

Fig. 5
figure 5

Matching the theoretical and simulation results of Rayleigh channel estimation

Full size image
Fig. 6
figure 6

Matching the theoretical and simulation results of Rayleigh channel estimation

Full size image

Also, in all cases we can see that the performance of ATC diffusion algorithm is better than CTA algorithm.

6 Conclusion

In this paper we analyzed the performance of diffusion LMS algorithm in tracking Rayleigh channels modeled as non-stationary variables. Previously, this task was done with incremental cooperation strategy and with this paper, we completed the channel estimation analysis with adaptive networks. As we mentioned, the diffusion strategy is a more practical scheme to deploy for various tasks. We showed that as the degree of non-stationarity in channel grows, the performance of the network degrades and becomes unstable. For this reason the impacts of sampling period and Doppler frequency on the convergence of network are investigated and we came to the conclusion that if the degree of non-stationarity exceeds unity, as a result of large Doppler frequency, the tracking of channel variations will be difficult and even impossible. Finally, we insist on the fact that for matching theoretical and simulation results, the time varying unknown vector must follow a Random-Walk process, and the analysis for tracking of a Markov process is yet to be developed in our future works.