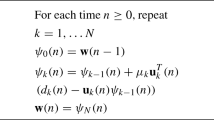1 Introduction

A wireless sensor network (WSN) is composed of a large number of small, low-cost sensors with integrated sensing, processing, and communication abilities [1]. These capabilities make it possible to use WSNs in many applications such as physiological monitoring, environmental monitoring, conditional-based maintenance, smart spaces, military, precision agriculture, transportation, factory instrumentation, and inventory tracking [7]. In most of these applications, we deal with the estimation of an unknown parameter using noisy measurements that are collected across sensors. Such a problem can be solved by either a centralized approach or a distributed one. In the centralized solution, every node in the network transmits its measurements to a central fusion center for processing. The central processor would then perform the required estimation tasks and send the results back to the other node. This approach has a critical point of failure at the fusion center and requires large amount of energy for communication. On the other hand, in distributed solution, each node communicates only with its closest neighbors and processing is carried out locally at every node. It is generally believed that in a WSN, the energy required for local computation is much less than what is used for communications. Furthermore, energy consumption is a critical issue in WSNs, so distributed solutions are much desirable for such situations. Moreover, in many applications, it is necessary to perform estimation task in a constantly changing environment without having a statistical model for the underlying processes of interest. This issue requires the distributed processing to be adaptive. Networks in which all nodes are equipped with the adaptive capabilities are called adaptive networks, networks with distributed adaptive estimation algorithms. Using cooperative processing in conjunction with adaptive filtering per node not only enables the tracking of the variations in the environment but also the topology of the network.

Distributed adaptive estimation algorithms could be categorized based on the mode of cooperation between the nodes and the adaptive filter that they use, such as incremental least mean-square (LMS) algorithm [12], incremental recursive least squares (RLS) algorithm [18], incremental affine projection-based adaptive (APA) algorithm [11], diffusion LMS algorithm [13], and diffusion RLS algorithm [4]. In an incremental mode of cooperation, information is sequentially circulated from one node to the adjacent node, but in a diffusion implementation, each node communicates with all its neighbors as dictated by the network topology. Each of these schemes has their own advantages and disadvantages. From the adaptive algorithm point of view which is used in the nodes, LMS algorithm has low computational cost, is robust, and has good tracking performance, but it suffers from slow initial convergence. On the other hand, RLS algorithm has faster convergence rate but the major drawback of RLS is surely its high computational complexity. Compared to the RLS algorithm, the APA algorithm has less computational cost at each node, has reduced internode communications, and memory cost is low while it retains an acceptable steady-state performance. In addition, this algorithm shows improved performance as compared to LMS algorithm in the highly correlated input case. From the cooperation mode approach point of view, the main advantage of the incremental mode of cooperation is its ability to reduce the required energy and communication resources, but it has one major drawback. This algorithm needs to establish a cyclic path through the network, which in large-size networks is a NP-hard problem, and is not guaranteed to exist in general case. In addition, cyclic paths are not robust to node or link failure. In comparison, in diffusion strategies, no cyclic path is required, and these schemes are scalable, robust to node or link failure, and are more amenable to distributed implementation. Nevertheless, diffusion-based methods need more communication resources and suffer from low convergence problem. However, some work has been done to overcome the disadvantages of the incremental and diffusion methods. For example, [14] relaxes the requirement to establish a cyclic path over the network by defining a random cooperation walk over the nodes, while keeping nearly the same mean-square performance. In order to save energy and communication resources in diffusion cooperation mode, in [15], a probabilistic diffusion algorithm is developed that lets the nodes to communicate only with a subset of their direct neighbors chosen at random. [17] rather than picking nodes at random proposes a dynamic technique that enables the node to choose from among its neighbors those that are likely to lead to the best MSD performance. Also, hierarchical diffusion algorithm [5], multilevel diffusion algorithm [6], and diffusion algorithm with adaptive combiner [19] are proposed in order to improve the performance of diffusion algorithm. The effect of noisy links on the performance of incremental and diffusion adaptive networks is studied in [9] and [10]. The importance of such study stems from this fact that the performance of distributed adaptive estimation algorithm can drastically be deteriorated in the presence of noisy links [9, 10].

In all of the previous works [4–6, 9–15, 17–19], it is assumed that the length of the adaptive filter at each node is equal to that of the unknown parameter. Actually, the length of the unknown parameter is unknown similar to its coefficients. So, in many practical situations, at each node, a deficient length adaptive filter, whose length is less than that of the unknown parameter, is employed.

In principle, the minimum mean-squared error (MMSE) is a monotonic non-increasing function of the tap-length, but the decrease in the MMSE due to the tap-length increase always becomes trivial when the tap-length is long enough. Obviously, it is not suitable to have too long a filter, as it not only unnecessarily increases the complexity but also introduces more adaption noise. Therefore, there exists an optimum tap-length, \(L_{\mathrm{opt}}\), that best balances the steady-state performance and complexity. Usually, one does not know what is the optimum filter length; therefore, each node is equipped with an adaptive filter with \(M\) coefficients, where we assume \(M<L_{\mathrm{opt}} \). In other words, at each node, a deficient length adaptive filter is employed. Since the theoretical results in the sufficient length case do not necessarily apply to the realistic deficient length situation, so in this paper we study the performance of the deficient length DILMS algorithm. More precisely, we derive a closed-form expression for the MSD to explain the steady-state performance at each individual node. However, for a non-distributive adaptive filter case, such an analysis has been done [2, 3, 8, 16], but this analysis in the distributive adaptive network domain is challenging due to the fact that the nodes in every neighborhood interact with one another, and therefore, a successful analysis must take into account both the temporal and spatial interconnectedness of the data. Different nodes will converge to different MSD levels, reflecting the statistical diversity of the data and the different noise levels. Although the authors in [20–22] compensated the unstructured uncertainty (i.e., nonlinear friction, external disturbances, and/or unmodeled dynamics), they did not consider the unknown length of the unknown parameter. In these works, the goal was to have the inertia load to track any specified smooth motion trajectory \(x_{\mathrm{1d}}\) as close as possible, where \(x_{\mathrm{1d}} \) is a one-dimensional (time-varying) scalar; in other words, the dimension of \(x_\mathrm{1d} \) is known. However, in our paper, we assume that the dimensions of parameters like that are also unknown. Simulation results support our theoretical analysis.

Notation: For the ease of reference, the main symbols used in this paper are listed below

\(col\{ .\}\) :

Column vector;

\(E\{ . \}\) :

Statistical expectation;

\(\Vert .\Vert ^{2}\) :

Squared Euclidean norm operation;

\(\left| . \right| ^{2}\) :

Absolute squared operation;

\(\mathbf{0}_{M\times 1} \) :

\(M\times 1\) Zero vector;

\(\mathbf{0}_{1\times M} \) :

\(1\times M\) Zero vector;

\(\mathbf{0}_{M\times L} \) :

\(M\times L\) Zero matrix;

\(I_L \) :

\(L\times L\) Identity matrix;

\((.)^{*}\) :

Conjugation for scalars and Hermitian transpose for matrices;

2 Deficient Length DILMS Algorithm

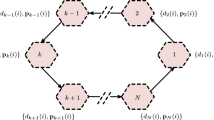
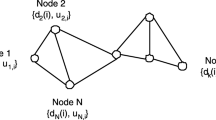
Consider a set of \(N\) sensors that are randomly distributed over a region. The purpose was to estimate an \(L_{\mathrm{opt}} \times 1\) unknown vector \(\varvec{w}_{L_\mathrm{opt}}^o \) from multiple measurements collected at \(N\) nodes in the network. We assume that both the coefficients and length \(L_{\mathrm{opt}} \) of the unknown parameter \(\varvec{w}_{L_{\mathrm{opt}} }^o \) are unknown. Since the length \(L_{\mathrm{opt}} \) is unknown, so a conjectural length \({M}\) for the unknown parameter is considered at each node, where \(M<L_{\mathrm{opt}} \). Also, suppose that each node \(k\) has access to time realizations \(\left\{ {d_k \left( i \right) ,\varvec{u}_{k,i} } \right\} \) of zero-mean spatial data \(\left\{ {d_k ,\varvec{u}_k } \right\} \), where each \(d_k \) is a scalar measurement and each \(\varvec{u}_k \) is a \(1\times M\) row regression vector.

Collecting the regression and measurement data into global matrices results

$$\begin{aligned}&\varvec{U}\triangleq col\left\{ {\varvec{u}_1 ,\varvec{u}_2 ,\ldots \varvec{u}_N } \right\} \quad \left( {N\times M} \right) \end{aligned}$$
(1)
$$\begin{aligned}&\varvec{d}\triangleq col\left\{ {d_1 ,d_2 ,\ldots d_N } \right\} \quad \left( {N\times 1} \right) \end{aligned}$$
(2)

The objective was to estimate the \(M\times 1\) vector \(\varvec{w}\) that solves

$$\begin{aligned} arg\mathop {\min }\limits _{\varvec{w}} J({\mathbf {w}}) \end{aligned}$$
(3)

where

$$\begin{aligned} J(\varvec{w})=E\left\{ \big \Vert {\varvec{d}-\varvec{Uw} \big \Vert ^{2}}\right\} \end{aligned}$$
(4)

The optimal solution \(\varvec{w}^{\varvec{o}}\) satisfies the normal equations [12]

$$\begin{aligned} \varvec{r}_{du} =\varvec{R}_u \varvec{w}^{\varvec{o}} \end{aligned}$$
(5)

where \(\varvec{w}^{\varvec{o}}\) has length \(M\), and

$$\begin{aligned} \varvec{R}_u =E\left\{ {\varvec{U}^{*}\varvec{U}} \right\} ,\quad \varvec{r}_{du} =E\left\{ {\varvec{U}^{*}\varvec{d}} \right\} \!. \end{aligned}$$
(6)

Note that in order to use (5) to compute \(\varvec{w}^{\varvec{o}}\), each node must have access to the global statistical information \(\left\{ {\varvec{r}_{du} ,\varvec{R}_u } \right\} \), which in turn requires more communications between nodes and computational resources. Moreover, such an approach does not enable the network to respond to changes in statistical properties of data. In [12], a distributed incremental LMS (DILMS) strategy with a cyclic estimator structure is proposed as

$$\begin{aligned} \varvec{\psi } _k^{(i)} =\varvec{\psi } _{k-1}^{(i)} +\mu _k \varvec{u}_{k,i}^*\left( {d_k \left( i \right) -\varvec{u}_{k,i} \varvec{\psi } _{k-1}^{\left( i \right) } } \right) ,\quad k \in {\mathcal {N}} \end{aligned}$$
(7)

where \(\varvec{\psi }_k^{(i)} \) is the \(M\times 1\) local estimate at node \(k\) and time \(i\). For each time \(i\), each node \(k\) utilizes the local data \(d_k \left( i \right) \), \(\varvec{u}_{k,i} \) and \(\varvec{\psi }_{k-1}^{\left( i \right) } \) received from the \(\left( {k-1} \right) \)th node to obtain \(\varvec{\psi }_k^{(i)} \). At the end of this cycle, \(\varvec{\psi }_N^{(i)} \) is employed as the initial condition for the next time instant at node \(k=1\). In (7), \(\mu _k \) denotes the local step size at node \(k\), which is a positive small real number.

3 Performance Analysis of Deficient Length DILMS

As mentioned, we assume that there is an optimal length for \(\varvec{w}_{L_{\mathrm{opt}} }^o \) as \(L_{\mathrm{opt}} \), where the presumed filter length \(M\) is not equal to it. We are going to analyze this condition in the context of incremental adaptive network.

3.1 Data Model and Assumptions

To perform the performance analysis, it is necessary to assume a model for the data as it is commonly done in the literature of adaptive algorithms. In the subsequent analysis, the following assumptions will be considered.

  1. 1)

    We assume a linear measurement model as

$$\begin{aligned} d_k \left( i \right) =\varvec{u}_{L_{\mathrm{opt}} k,i} \varvec{w}_{L_{\mathrm{opt}} }^o +v_k \left( i \right) . \end{aligned}$$
(8)

where \(v_k \left( i \right) \) is some temporal and spatial white noise sequence with zero mean and variance \(\sigma _{v,k}^2 \) and is independent of \(\varvec{u}_{L_{\mathrm{opt}} \ell ,j} \) and \(d_\ell \left( j \right) \) for all \(\ell ,j\). The linear model (8) is also called stationary model in which the unknown parameter \(\varvec{w}_{L_{\mathrm{opt}} }^o \) is fixed and statistics of the various input and noise signals are time-invariant. In (8), \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) is a vector with length equal to \(L_{\mathrm{opt}} \) as

$$\begin{aligned} \varvec{u}_{L_{\mathrm{opt}} k,i} =\left[ {u_k \left( i \right) ,u_k \left( {i-1} \right) ,\ldots ,u_k \left( {i-L_{\mathrm{opt}} +1} \right) } \right] \end{aligned}$$
(9)

and \(\varvec{u}_{k,i} \) consists of \(M\) first coefficients of \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) as

$$\begin{aligned} \varvec{u}_{k,i} =\left[ {u_k \left( i \right) ,u_k \left( {i-1} \right) ,\ldots ,u_k \left( {i-M+1} \right) } \right] \end{aligned}$$
(10)
  1. 2)

    \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) is independent of \(\varvec{u}_{L_{\mathrm{opt}} \ell ,i} \) for \(k\ne \ell \).

  2. 3)

    \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) is independent of \(\varvec{u}_{L_{\mathrm{opt}} k,j} \) for \(i\ne j\).

  3. 4)

    The components of \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) are drawn from a zero-mean white Gaussian process with variance \(\sigma _{u,k}^2 \), in other words the covariance matrix of \(\varvec{u}_{L_{\mathrm{opt}} k,i} \) is \(\varvec{R}_{u,k} =\sigma _{u,k}^2 \varvec{I}\).

According to these assumptions, we are interested in the evaluation of the MSD for the steady-state condition for every node \(k\).

3.2 Performance Analysis

To proceed, we define the following local error signal at each node \(k\) as

$$\begin{aligned} e_k \left( i \right) =d_k \left( i \right) -\varvec{u}_{k,i} \varvec{\psi }_{k-1}^{\left( i \right) } \end{aligned}$$
(11)

This signal measures the estimation error in approximating \(d_k \left( i \right) \) by using information available locally, i.e., \(\varvec{u}_{k,i} \varvec{\psi }_{k-1}^{\left( i \right) } \). By this definition, (7) can be written as

$$\begin{aligned} \varvec{\psi } _k^{(i)} =\varvec{\psi } _{k-1}^{(i)} +\mu _k \varvec{u}_{k,i}^*e_k (i) \quad k\in {\mathcal {N}} \end{aligned}$$
(12)

To carry out the performance analysis, we partition the unknown parameter \(\varvec{w}_{L_{\mathrm{opt}} }^o \) as

$$\begin{aligned} \left[ {{\begin{array}{c} \widehat{\varvec{w}}_M \\ \widetilde{\varvec{w}}_{L_{\mathrm{opt}}-M} \\ \end{array} }} \right] \end{aligned}$$
(13)

where \(\widehat{\varvec{w}}_M \) is the \(M\) first coefficients of \(\varvec{w}_{L_{\mathrm{opt}} }^o \); in other words, \(\widehat{\varvec{w}}_M \) is the part of \(\varvec{w}_{L_{\mathrm{opt}} }^o \) that is modeled by \(\varvec{\psi }_k^{(i)}\) in each node, and \(\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \) is the part of \(\varvec{w}_{L_{\mathrm{opt}} }^o \) that is excluded in the estimation of \(\varvec{w}_{L_{\mathrm{opt}} }^o \) in each node. This partitioning makes it easy to work with vectors that have different lengths. By this partitioning, (11) could be written as

$$\begin{aligned} e_k \left( i \right)&= \varvec{u}_{L_{\mathrm{opt}} k,i} \varvec{w}_{L_{\mathrm{opt}} }^o -\varvec{u}_{k,i} \varvec{\psi } _{k-1}^{\left( i \right) } +v_k \left( i \right) \nonumber \\&= \varvec{u}_{L_{\mathrm{opt}} k,i} \left[ {{\begin{array}{c} {\widehat{\varvec{w}}_M } \\ {\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] -\varvec{u}_{L_{\mathrm{opt}} k,i} \left[ {{\begin{array}{c} {\varvec{\psi } _{k-1}^{\left( i \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] +v_k \left( i \right) \nonumber \\&= -\varvec{u}_{L_{\mathrm{opt}} k,i} \left[ {{\begin{array}{c} {\varvec{\psi } _{k-1}^{\left( i \right) } -\widehat{\varvec{w}}_M } \\ {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] +v_k \left( i \right) =-\varvec{u}_{L_{\mathrm{opt}} k,i} \left[ {{\begin{array}{c} {\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) } } \\ {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] +v_k \left( i \right) \nonumber \\&= -\varvec{u}_{L_{\mathrm{opt}} k,i} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } +v_k \left( i \right) \end{aligned}$$
(14)

The vector \(\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \) measures the difference between the weight estimate at node \(k-1\) and the desired solution \(\varvec{w}_{L_{\mathrm{opt}} }^o \). The vector \(\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) } \) is also a measure of difference between weights, but it only uses the coefficients of \(\varvec{w}_{L_{\mathrm{opt}} }^o \) that are modeled by \(\varvec{\psi } _k^{(i)} \).

Substituting (14) into (12) results

$$\begin{aligned} \varvec{\psi }_k^{(i)} =\varvec{\psi }_{k-1}^{(i)} -\mu _k \varvec{u}_{k,i}^*\varvec{u}_{L_{\mathrm{opt}} k,i} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } +\mu _k v_k \left( i \right) \varvec{u}_{k,i}^*\end{aligned}$$
(15)

Padding the vectors with length \(M\) in (15) by \(L_{\mathrm{opt}} -M\) zeros results vectors with length \(L_{\mathrm{opt}} \) that allows subtraction of \(\varvec{w}_{L_{\mathrm{opt}} }^o \) from both sides of (15), so we have

$$\begin{aligned} \left[ {{\begin{array}{c} {\varvec{\psi } _k^{\left( i \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] -\varvec{w}_{L_{\mathrm{opt}} }^o&= \left[ {{\begin{array}{c} {\varvec{\psi } _{k-1}^{\left( i \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] -\varvec{w}_{L_{\mathrm{opt}} }^o -\mu _k \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \nonumber \\&\varvec{u}_{L_{\mathrm{opt}} k,i} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } +\mu _k v_k \left( i \right) \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \end{aligned}$$
(16)

and according to the definition of \(\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \), we have

$$\begin{aligned} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( i \right) } =\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } -\mu _k \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \varvec{u}_{L_{\mathrm{opt}} k,i} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } +\mu _k v_k \left( i \right) \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \end{aligned}$$
(17)

by defining

$$\begin{aligned} \Lambda _k (i)=I_{L_{\mathrm{opt}} } -\mu _k \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \varvec{u}_{L_{\mathrm{opt}} k,i} \end{aligned}$$
(18)

The Eq. (17) can be written as

$$\begin{aligned} \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( i \right) } ={\Lambda }_k (i)\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } +\mu _k v_k \left( i \right) \left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \end{aligned}$$
(19)

We are interested in the evaluation of the MSD in the steady-state condition for every node \(k\). This quantity is defined as

$$\begin{aligned} \text{ MSD }_k =E\left\{ \big \Vert {\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) }} \big \Vert ^{2}\right\} \end{aligned}$$
(20)

In order to derive an expression for this quantity, we write \(\big \Vert {\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( i \right) }}\big \Vert ^{2}\) as

$$\begin{aligned} \big \Vert {\bar{\varvec{\psi }}^{\left( i \right) }_{L_{\mathrm{opt}} ,k}}\big \Vert ^{2}&= \bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1} {\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \nonumber \\&+\,\mu _k v_k \left( i\right) \bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1} {\Lambda }^{*}_k (i)\left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }} \right] \nonumber \\&+\,\mu _k v_k \left( i \right) \left[ {{\begin{array}{ll} {\varvec{u}_{k,i} }&{} {\varvec{0}_{1\times \left( {L_{\mathrm{opt}} -M} \right) } } \\ \end{array} }} \right] {\Lambda }_k \left( i \right) \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) }\nonumber \\&+\,\mu _k^2 v_k^2 (i)\big \Vert \varvec{u}_{k,i}\big \Vert ^{2} \end{aligned}$$
(21)

To proceed, we should take expectations from both sides of (21). For this, we use the assumptions (1)–(4), and from these assumptions, several results can be inferred as follows

  • Result 1 Since the matrix \({\Lambda }_k \left( i \right) \) only consists of the regression vectors, it is independent of measurement noise \(v_k \left( i \right) \).

  • Result 2 From \(\varvec{\psi } _{k-1}^{(i)} =\varvec{\psi } _{k-2}^{(i)} +\mu _{k-1} \varvec{u}_{k-1,i}^*\left( {d_{k-1} \left( i \right) -\varvec{u}_{k-1,i} \varvec{\psi } _{k-2}^{\left( i \right) } } \right) \), it is clear that \(\varvec{\psi } _{k-1}^{(i)} \) only depends on the measurements \(d_\ell \left( j \right) \) of node \(k-1\) and its previous nodes in current iteration, and also on the measurements of its previous iterations. So, from assumption (1), the noise \(v_k \left( i \right) \) will be independent of \(\varvec{\psi } _{k-1}^{(i)} \) and \(\bar{\varvec{\varvec{\psi }}}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \).

  • Result 3 Since \(\varvec{\psi } _{k-1}^{(i)} \) only depends on the regression vectors \(\varvec{u}_{\ell ,j} \) of node \(k-1\) and previous nodes in current iteration, and the regressions of previous iterations, so from assumptions (2) and (3), it is clear that \(\varvec{u}_{k,i} \) and so \({\Lambda }_k \left( i \right) \) are independent from \(\varvec{\psi } _{k-1}^{(i)} \) and \(\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \).

Using the assumptions (1)–(4) and their results, and taking expectations of both sides of (21), leads to

$$\begin{aligned} E\left\{ \big \Vert \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( i \right) }\big \Vert ^{2}\right\} \!=\! E\left\{ {\bar{{\varvec{\psi }}}^{{*}^{\left( i \right) }}}_{{L_{\mathrm{opt}} ,k-1}} {\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } \right\} +\mu _k^{2} E\left\{ {v_k^{2} (i)} \right\} E\left\{ \big \Vert {\varvec{u}_{k,i}\big \Vert ^{2}} \right\} \end{aligned}$$
(22)

To proceed, we need to evaluate the moments in the right-hand side of (22). From result (3), we have

$$\begin{aligned} E\left\{ {\bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1} {\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } } \right\} =E\left\{ {\bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1}E\left[ {{\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) } \right] \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } } \right\} \end{aligned}$$
(23)

So, first we calculate the following expectation

$$\begin{aligned} E\left\{ {{\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) } \right\}&= I_{L_{\mathrm{opt}} } -\mu _k E\left\{ {\left[ {{\begin{array}{c} {\varvec{u}_{k,i}^*} \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times 1} } \\ \end{array} }}\right] \varvec{u}_{L_{\mathrm{opt}} k,i} } \right\} \nonumber \\&-\,\mu _k E\left\{ {\varvec{u}_{L_{\mathrm{opt}} k,i}^*\left[ {{\begin{array}{cc} {\varvec{u}_{k,i} }&{} {\varvec{0}_{1\times \left( {L_{\mathrm{opt}} -M} \right) } }\\ \end{array} }} \right] } \right\} \nonumber \\&+\,\mu _k^2 E\left\{ {\varvec{u}_{L_{\mathrm{opt}} k,i}^*\varvec{u}_{L_{\mathrm{opt}} k,i} \big \Vert \varvec{u}_{k,i} \big \Vert ^{2}} \right\} \end{aligned}$$
(24)

As shown in the Appendix, the following relation holds true for this expectation as

$$\begin{aligned} E\left\{ {{\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) } \right\} =\left[ {{\begin{array}{cc} {\beta _k I_M }&{} {\varvec{0}_{M\times \left( {L_{\mathrm{opt}} -M} \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times M} }&{} {\eta _k I_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] \end{aligned}$$
(25)

where

$$\begin{aligned} \beta _k =1-2\mu _k \sigma _{u,k}^2 +\mu _k^2 \sigma _{u,k}^4 \left( {M+2} \right) \end{aligned}$$
(26)

and

$$\begin{aligned} \eta _k =1+\mu _k^2 \sigma _{u,k}^4 M \end{aligned}$$
(27)

On the other hand, from \(\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } =\left[ {{\begin{array}{l} {\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) } } \\ {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] \) we have

$$\begin{aligned} \big \Vert \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) }\big \Vert ^{2}=\big \Vert \bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) }\big \Vert ^{2}+\big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2} \end{aligned}$$
(28)

Using (25) and (28) in (23), we get

$$\begin{aligned}&E\left\{ {\bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1} {\Lambda }^{*}_k \left( i \right) {\Lambda }_k \left( i \right) \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } } \right\} \nonumber \\&=E\left\{ {\bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{L_{\mathrm{opt}} ,k-1} \left[ {{\begin{array}{cc} {\beta _k I_M }&{} {\varvec{0}_{M\times \left( {L_{\mathrm{opt}} -M} \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times M} }&{} {\eta _k I_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] \bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) } } \right\} \nonumber \\&=E\left\{ {\left[ {{\begin{array}{cc} {\bar{\varvec{\psi }}^{{*}^{\left( i \right) } }_{M,k-1}}&{} {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}^*}\\ \end{array} }} \right] \left[ {{\begin{array}{cc} {\beta _k I_M }&{} {\varvec{0}_{M\times \left( {L_{\mathrm{opt}} -M} \right) } } \\ {\varvec{0}_{\left( {L_{\mathrm{opt}} -M} \right) \times M} }&{} {\eta _k I_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] \times \left[ {{\begin{array}{l} {\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) } } \\ {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] } \right\} \nonumber \\&=E\left\{ {\left[ {{\begin{array}{cc} {\beta _k \bar{\varvec{\psi }}^{{*}^{\left( i \right) }}_{M,k-1}}&{} {-\eta _k \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}^*} \\ \end{array} }} \right] \left[ {{\begin{array}{c} {\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) } } \\ {-\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} } \\ \end{array} }} \right] } \right\} \nonumber \\&=\beta _k E\left\{ \big \Vert {\bar{\varvec{\psi }}_{M,k-1}^{\left( i \right) }}\big \Vert ^{2} \right\} +\eta _k \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2} \nonumber \\&=\beta _k E\left\{ \big \Vert {\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) }}\big \Vert ^{2} \right\} +\left( {\eta _k -\beta _k } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2} \end{aligned}$$
(29)

Substituting (29) into (22) results

$$\begin{aligned} E\left\{ \big \Vert \bar{\varvec{\psi }}^{\left( i \right) }_{L_{\mathrm{opt}} ,k}\big \Vert ^{2} \right\} =\beta _k E\left\{ \big \Vert \bar{\varvec{\psi }}^{\left( i \right) }_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2} \right\} +\left( {\eta _k -\beta _k } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2}+\tau _k \end{aligned}$$
(30)

where

$$\begin{aligned} \tau _k =\mu _k^2 \sigma _{v,k}^2 \sigma _{u,k}^2 M \end{aligned}$$
(31)

Now, we rewrite (30) in a summarized form as

$$\begin{aligned} E\left\{ \big \Vert {\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( i \right) } \big \Vert ^{2}} \right\} =\beta _k E\left\{ \big \Vert {\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k-1}^{\left( i \right) }\big \Vert ^{2}} \right\} +f_k \end{aligned}$$
(32)

where

$$\begin{aligned} f_k =\left( {\eta _k -\beta _k } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2}+\tau _k \end{aligned}$$
(33)

Since we are interested in the steady-state analysis, as \(\left( {i\rightarrow \infty } \right) \) in (32), so with assumption of \({\varvec{P}}_{L_{\mathrm{opt}} ,k} =\bar{\varvec{\psi }}_{L_{\mathrm{opt}} ,k}^{\left( \infty \right) } \), (32) can be written as

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k} \big \Vert ^{2}} \right\} =\beta _k E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2}} \right\} +f_k \end{aligned}$$
(34)

Observe, however, that (34) is a coupled equation: it involves both \(E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k} \big \Vert ^{2}} \right\} \) and \(E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2}} \right\} \), i.e., information from two spatial locations. To resolve this difficulty, we take the advantage of the ring topology [11, 12, 18]. Thus, by iterating (34), we have

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,1} \big \Vert ^{2}} \right\}&= \beta _1 E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,N} \big \Vert ^{2}} \right\} +f_1 \nonumber \\ E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,2} \big \Vert ^{2}} \right\}&= \beta _2 E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,1} \big \Vert ^{2}} \right\} +f_2 \\&\qquad {\vdots } \nonumber \\ E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-2} \big \Vert ^{2}} \right\}&= \beta _{k-2} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-3} \big \Vert ^{2}} \right\} +f_{k-2}\nonumber \\ E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\}&= \beta _{k-1} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-2}\big \Vert ^{2}} \right\} +f_{k-1} \nonumber \\ \vdots&\nonumber \\ E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,N}\big \Vert ^{2}} \right\}&= \beta _N E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,N-1} \big \Vert ^{2}} \right\} +f_N\nonumber \end{aligned}$$
(35)

Observe that according to (35), \(E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\} \) can be expressed in terms of \(E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-3} \big \Vert ^{2}} \right\} \) as

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\} =\beta _{k-1} \beta _{k-2} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-3} \big \Vert ^{2}} \right\} +\beta _{k-1} f_{k-2} +f_{k-1} \end{aligned}$$
(36)

By iterating in this manner, we have

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2}} \right\}&= \beta _{k-1} \beta _{k-2} \ldots \beta _1 \beta _N \beta _{N-1} \ldots \beta _k E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\} \nonumber \\&+\,\beta _{k-1} \beta _{k-2} \ldots \beta _1 \beta _N \beta _{N-1} \ldots \beta _{k+1} f_k \nonumber \\&+\,\beta _{k-1} \beta _{k-2} \ldots \beta _1 \beta _N \beta _{N-1} \ldots \beta _{k+2} f_{k+1} \nonumber \\&+\,\ldots +\beta _{k-1} \beta _{k-2} \ldots \beta _1 \beta _N f_{N-1} +\beta _{k-1} \beta _{k-2} \ldots \beta _1 f_N \nonumber \\&+\,\beta _{k-1} \beta _{k-2} \ldots \beta _2 f_1 +\beta _{k-1} \beta _{k-2} \ldots \beta _4 \beta _3 f_2 \nonumber \\&+\,\ldots +\beta _{k-1} \beta _{k-2} f_{k-3} +\beta _{k-1} f_{k-2} +f_{k-1} \end{aligned}$$
(37)

Now, for each node \(k\), we define a set of \(N\) quantities as

$$\begin{aligned} \Pi _{k,\ell } \triangleq \beta _{k-1} \beta _{k-2} \ldots \beta _1 \beta _N \beta _{N-1} \ldots \beta _{k+\ell } \beta _{k+\ell -1} ,\quad \ell =1,\ldots ,N \end{aligned}$$
(38)

and if we define \(s_k \) as

$$\begin{aligned} s_k \triangleq \Pi _{k,2} f_k + \Pi _{k,3}f_{k+1} +\ldots + \Pi _{k,N-1} f_{k-3} + \Pi _{k,N} f_{k-2} + f_{k-1} \end{aligned}$$
(39)

From (37)–(39), we have

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2}} \right\} =\Pi _{k,1} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1}\big \Vert ^{2}} \right\} +s_k \end{aligned}$$
(40)

From (40), we derive an expression for the desired steady-state MSD as

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\} =\left( {1-\Pi _{k,1} } \right) ^{-1}s_k \end{aligned}$$
(41)

3.3 Discussions on Derived Theoretical Results

Due to the complicated form of the resulting relationship for the steady-state MSD, it is not easy to achieve useful information about the use of deficient length adaptive filter in each node. In order to obtain a clear view about the effect of deficient length application, we simplify the equation (41). For this purpose, we assume that \(\mu _k =\mu ,\forall k\in {\mathcal {N}}\) and \(\varvec{R}_{u,k} =\sigma _u^2 \varvec{I}\). Also, we assume that \(\mu \) is small enough, so that the \(\mu ^{2}\) term can be ignored in \(\beta _k \). With these assumptions, \(\beta _k \) could be approximated as

$$\begin{aligned} \beta _k =1-2\mu \sigma _u^2 \end{aligned}$$
(42)

as a result, \(\Pi _{k,1} \) could be approximated as

$$\begin{aligned} \Pi \triangleq \beta _1 \beta _2 \ldots \beta _N =\left( {1-2\mu \sigma _u^2 } \right) ^{N} \approx \left( {1-2\mu N\sigma _u^2 } \right) \end{aligned}$$
(43)

Similarly, using these assumption, \(s_k \) becomes

$$\begin{aligned} s_k&\approx \mathop \sum \limits _{k=1}^N f_k\nonumber \\&= \mathop \sum \limits _{k=1}^N \left( {2\mu \sigma _u^2 \left( {1-\mu \sigma _u^2 } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \big \Vert ^{2}+M\mu ^{2}\sigma _u^2 \sigma _{v,k}^2 } \right) \end{aligned}$$
(44)

Now, by substituting (43) and (44) into (41), we obtain

$$\begin{aligned} E\left\{ \big \Vert {{\varvec{P}}_{L_{\mathrm{opt}} ,k-1} \big \Vert ^{2}} \right\}&= \frac{1}{2\mu N\sigma _u^2 }\mathop \sum \limits _{k=1}^N \left( {2\mu \sigma _u^2 \left( {1-\mu \sigma _u^2 } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \big \Vert ^{2}+M\mu ^{2}\sigma _u^2 \sigma _{v,k}^2 } \right) \nonumber \\&= \left( {1-\mu \sigma _u^2 } \right) \big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M}\big \Vert ^{2}+\frac{M\mu }{2N}\mathop \sum \limits _{k=1}^N \sigma _{v,k}^2 \end{aligned}$$
(45)

Now, several results are implied from (45) as

  1. 1)

    The first term on the right-hand side of (45) is indeed the additional error due to the deficient length application. This term consists of all the omitting coefficients of unknown parameter, namely \(\widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \) in the estimation process. Whenever the considered length for the adaptive filter in each node, namely \(M\), is less than \(L_{\mathrm{opt}} \), this term will be large. In other words, as much the selected length is more deficient, the error will increase.

  2. 2)

    Unlike the full length case \(\left( {M=L_{\mathrm{opt}} } \right) \), in which as \(\mu \) approaches to zero, the steady-state MSD tends toward zero. It is observed that, in the deficient length case with \(\mu \rightarrow 0\), the steady-state MSD will tend toward a constant term \(\big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \big \Vert ^{2}\).

4 Simulations

In this section, we do some simulations and compare the results with theory and show that the derived theoretical expression for MSD can predict the steady-state performance of the deficient length DILMS algorithm. To this aim, we deploy a distributed network with \(N=20\) sensors each running as an adaptive filter with \(M\) taps to estimate the \(L_{\mathrm{opt}} \times 1\) unknown parameter \(\varvec{w}^{\varvec{o}}_{L_{\mathrm{opt}}} =col\left\{ {1,1,\ldots ,1} \right\} /\sqrt{L_{\mathrm{opt}} }\) where \(L_{\mathrm{opt}} =10\). The measurement data \(\left\{ {d_k \left( i \right) } \right\} \) are generated according to model (8), and the regressors are assumed to be independent zero-mean Gaussians with covariance matrix as \(\varvec{R}_{u,k} =\sigma _{u,k}^2\, \varvec{I}\). The observation noise variances \(\sigma _{v,k}^2 \) and \(\sigma _{u,k}^2 \) are shown in Fig. 1. The steady-state curves are obtained by averaging the last 500 instantaneous samples of 3,500 iterations. All of the simulation results are averaged over 100 independent Monte Carlo runs and the theoretical curves are obtained from (41). The steady-state MSD curves in node k for different tap-length \(M\) are shown in Figs. 2 and 3 for step size \(\mu _k =0.02\) and \(\mu _k =0.005\), respectively.

Fig. 1
figure 1

Observation noise profile \(\varvec{\sigma }_{\varvec{v,k}}^{\varvec{2}} \), and \(\varvec{\sigma } _{\varvec{u,k}}^{\varvec{2}} \)

Full size image

Figures 2 and 3 show that there is a good match between theory and simulations. We can see from Fig. 3 that, for \(M=9,8,7\) and \(6\), the steady-state MSD values for node \(k=1\) are \(-9.665\), \(-6.772\), \(-5.004\), and \(-3.791\) dB, respectively. This implies that, as much the considered length for the adaptive filter in each node, namely \(M\), is less than \(L_{\mathrm{opt}} \), the steady-state MSD will increase. In fact, this is the confirmation for the first result, as we mentioned, as much the selected length is more deficient, the error will increase. In order to do a comparison, the steady-state MSD in node k for the case of no deficiency of the filter length, i.e., \(M=L_{\mathrm{opt}} \), is also shown in these figures. Comparing these figures shows that the realistic condition, i.e., deficient length, can drastically deteriorate the performance of DILMS algorithm in term of MSD. These simulations justify the derived theoretical results.

Fig. 2
figure 2

Steady-state MSD versus node for different tap-length, \(\mu _k =0.02\)

Full size image
Fig. 3
figure 3

Steady-state MSD versus node for different tap-length, \(\mu _k =0.005\)

Full size image

These results could be used to assign a value for the step size for all the nodes. Nodes showing poor performance, or having high noise level, can be assigned with small step sizes; in the limit, they could become simply relay nodes.

The steady-state MSD versus different values of \(\mu \) for node \(k=1\) are plotted in Figs. 4 and 5 for two cases \(M=8\) (\(M<L_{\mathrm{opt}} )\) and \(M=L_{\mathrm{opt}} \), respectively. (In this case, we used \(\sigma _{u,k}^2 \in ( {0,.4} ],\) but the other setup parameters are the same as those in the previous simulations). Again, as it is clear from these figures, simulation results coincide very well to the graphs of the theoretical analysis. On the other hand, as mentioned in the second result, comparison of Figs. 4 and 5 shows that unlike the full length case \(\left( {M=L_{\mathrm{opt}} } \right) \), in which as \(\mu \) approach to zero, the steady-state MSD tends toward zero, it is observed that in the deficient length case, as \(\mu \rightarrow 0\), the steady-state MSD will approach toward a constant term \(\big \Vert \widetilde{\varvec{w}}_{L_{\mathrm{opt}} -M} \big \Vert ^{2}\) (here, it is equal to \(-6.9897\) dB).

Fig. 4
figure 4

Steady-state MSD versus \(\mu \) for node \(k=1\), \(M=8\)

Full size image
Fig. 5
figure 5

Steady-state MSD versus \(\mu \) for node \(k=1\), \(M=L_{\mathrm{opt}} \)

Full size image

5 Conclusions

In this paper, we have presented a theoretical analysis of the DILMS algorithm, in the case when there is a mismatch between the length of the adaptive filter at each node and the length of the unknown parameter. Based on our analysis, we have derived a closed-form expression for the MSD to explain the steady-state performance at each individual node. In practical physical systems, a conjectural length for an unknown parameter is usually considered, and indeed, our derived expression for the MSD predicts the performance of physical systems for this realistic condition. Our simulation results show there is a good match between our derived expression and computer simulations. The most important results of our analysis were that, in comparison with the sufficient length case, the steady-state MSD includes an additional term that arises from the deficient length application. This term includes all the coefficients of the unknown parameter that are omitted in the estimation process. As the length of the adaptive filter assigned to each node becomes more and more deficient, this term will become larger and larger. The results also show that, unlike the sufficient length case, as the step size tends toward zero, the steady-state MSD tends toward a nonzero constant value. It must be noted that different learning rules such as RLS can also be applied in the context of a distributed network with incremental topology.