1 Introduction

In most applications of wireless sensor networks (WSNs), we are encountered with estimating the desired parameter. In some scenarios, to perform the processing required for this estimate, sensors send their information to a central processing unit (e.g., cluster head or fusion center). Then, the processing of these gathered data, which inherently have temporal and spatial correlations, are performed in a centralized manner in this central unit [2, 3]. This amount of communication between the sensors and the central processor consumes a significant amount of bandwidth and energy, which is critical for a network of limited power sensors. Therefore, the need for a distributed solution to prolong the network lifetime is undeniable. In a distributed method, the amount of data exchanges is significantly reduced, so that each sensor communicates only with a subset of its one-hop neighbors. It is dictated by the network topology, that each sensor is permitted to communicate with which of its neighbors. Two useful topologies that enable learning and adaptation over networks in real-time are the diffusion and incremental topologies [13]. In an incremental structure, each node communicates with only one adjacent node. So, in this structure, data flows sequentially from one sensor to a neighboring sensor [32]. This form of cooperation requires a cyclic design of cooperation between the sensors, which is an NP-hard problem. Also, cyclic paths are not robust to link or node failures. Therefore, a diffusion strategy can be preferred in which each sensor has access to data of all its neighbors. In this scheme, each sensor can communicate with all its neighbors as dictated by the network structure. So, in this strategy, no cyclic path is required; this scheme is scalable, robust to link or node failures, and is more flexible to distributed implementation. This form of cooperation usually involves two stages: an adaption stage where sensors use their measurements to update their estimation. A combination stage where sensors combine the estimates from their neighbors to make a new estimate [7, 8, 16, 24, 33]. Diffusion recursive least square (RLS) algorithm [14, 30], diffusion least mean square (LMS) algorithm[34], diffusion affine projection-based adaptive (APA) algorithm [1], diffusion distributed conjugate gradient-based algorithms [36], jointly sparse single-task[11] and multitask [12, 20] recovery algorithms are examples of widely used algorithms employing diffusion strategy.

With the advent of adaptive networks based on incremental and diffusion strategies, extensive research has been conducted in this field. For example, paper [17] investigates the implementation of Active Noise Control (ANC) systems over an incremental adaptive network, using the distributed version of the Multiple Error Filtered-x Least Mean Square (MEFxLMS) algorithm. In [5], the constrained stability approach is applied for distributed ANC systems employing an incremental communication topology.

In the mentioned algorithms, the length of the unknown vector is assumed to be fixed and known a priori at each node. However, this assumption is not suitable for many applications where the optimum filter length is unknown or variable. The tap-length, or the size of the unknown parameter, significantly affects the performance of the distributed networks. If the number of filter coefficients is kept fix at a smaller value due to motives such as reduced computational load, which is a necessity for WSNs, the mean-square error (MSE) will increase as a result of this length deficiency [9, 10], whereas a larger tap-length increases the computational cost and the excess MSE (EMSE). Therefore, there exists an optimal length that best balances the conflicting necessities of performance and complexity. Based on this, structure adaptation algorithms were proposed, with the idea that although the minimum MSE is a monotonic non-increasing function of the filter length, it decreases slightly as the filter length increases when the tap-length is sufficiently large. On the other hand, having a large tap-length is not suitable as it not only undesirably increases computational complexity but also provides more adaption noise. In the stand-alone adaptive filter context, several algorithms have been proposed[31, 38] to find such an optimal tap-length. These algorithms have finally advanced into the FT variable-length algorithm [37]. The FT algorithm has the required conditions to be considered as a popular variable-length algorithm. This algorithm is very similar to the LMS technique, so it is often called an LMS style variable tap-length algorithm. This algorithm is as simple as the LMS algorithm, and at the same time, it has a good performance[19, 29]. Therefore, it is not unexpected that in the context of the adaptive networks, among all variable tap-length algorithms, only this algorithm is considered for structure adaptation. This algorithm is presented in the distributed context in both incremental [22] and diffusion strategies [21].

Note that the concept of variable tap-length algorithms is different from the variable step-size algorithms proposed to satisfy the conflicting requirements of low misadjustment and fast convergence rate [6, 28].

FT algorithm contains several parameters that influence the performance of the algorithm. Therefore, the proper selection of these parameters is very critical in achieving acceptable performance. One of these parameters is the error width, which controls the trade-off between the convergence rate and the steady-state tap-length bias. Another critical parameter is the tap-length adaptation step-size. This parameter provides a trade-off between steady-state tap-length fluctuation and the convergence rate of the tap-length. Therefore, selecting a fixed value for these parameters cannot provide the superior performance of this algorithm comprehensively. Therefore, to eliminate these trade-offs, a variable approach is proposed for the selection of these parameters. In the proposed method, these parameters are adjusted to achieve a fast convergence in the initial stages of the algorithm, and a less tap-length fluctuation and accurate tap-length estimation in the steady-state.

There are several works for error-width adaptation [18, 23, 27], and tap-length step-size adaptation [4, 25, 35].

In [23], the error width is adapted based on the mean squared error estimation. But, this algorithm affects by the interference of system error and could not indicate the accurate state of iteration at the same time. The reported method in [27] could eliminate the system noise interference and enhance the convergence performance. But, in this method, the error width is affected by the previous instant error value. So this approach may not accurately indicate the current changes and may have a specific passive influence on tap-length updating in the initial iterations. On this basis, [18] proposed an approach that adjusts error width using fragment-full error (FE) to solve the challenges associated with [23] and [27].

In [25], the tap-length adjustment error (TAE) is served as a criterion to adapt the tap-length step-size. To be robust against independent noise disturbance, the authors in [25] have used the estimation of the TAE correlation between two consecutive iterations to adjust the tap-length step-size. By arguing that in a time-varying scenario, the changes in the variance of input signal or the tap-coefficients will require the retuning of tap-length step-size, paper [4] exploited a normalized tap-length step-size in length update procedure. In [35], a variable tap-length step-size method is proposed, where the tap-length step-size is adjusted by the difference between squared output error and squared segmented estimation error, and is limited by a sigmoid function.

The presented methods in [4, 18, 23, 25, 27, 35] are all in the context of stand-alone adaptive filters, but, in the context of diffusion adaptive networks, this matter has been left out of consideration. It motivates us to consider the variable parameter concept in the diffusion fractional tap-length scenario.

Note that, in the proposed method, the adaptation of the parameters is performed in a cooperative and distributed manner. This distributed adaptation will result in the superior performance of the proposed algorithm.

The roadmap of the remainder of this paper is as follows. The preliminaries on the FT algorithm is provided in Sect. 2. In Sect. 3, we present a variable tap-length algorithm with adaptive error width and adaptive tap-length adaptation step-size based on the gradient vector norm. Section 4 provides the steady-state analysis. In Sect. 5, computer simulations are conducted, and finally, in Section 6, we conclude this paper.

2 Preliminaries

Suppose a network consists of N nodes. Here, the purpose of this network is to obtain an estimate of the desired parameter \(w_{{L_{opt}}}^o\) and its length \({L_{opt}}\). It is to be highlighted that the estimation of both the tap-weights and tap-length of the unknown parameter \(w_{{L_{opt}}}^o\) is considered here. However, the adaption criterion for weights and length could be separated, and the selection criterion for one does not depend on the selection criterion of the other. First, we assume that the tap-length is L, which is searched by the length search solution discussed later. We also assume that at every time \(i > 0\), each node k has access to a scalar measurement \({d_k}(i)\),and a \(1 \times L\) regression vector \({u_{k,i}}\), where they are assumed to be time realizations of zero-mean random processes \(\{ {\mathbf {d}_k},{\mathbf {u}_k}\}\). These measurements are related to the unknown parameter by

$$\begin{aligned} {\mathbf {d}_k}(i) = {\mathbf {u}_{{L_{opt}}k,i}}w_{{L_{opt}}}^o + {\mathbf {v}_k}(i) \end{aligned}$$
(1)

where \({\mathbf {v}_k}(i)\) accounts for the zero-mean noise and modeling error with variance \(\sigma _{v,k}^2\) which is assumed independent over space and time and independent of the regressors. In ()the subscript \({L_{opt}}\) implies that the length of the vector \({\mathbf {u}_{{L_{opt}}k,i}}\) is \({L_{opt}}\). Collecting the signals into global matrices result in:

$$\begin{aligned} \mathbf {U}&\buildrel \varDelta \over = col\{ {\mathbf {u}_1},{\mathbf {u}_2},...,{\mathbf {u}_N}\} \quad (N \times L)\nonumber \\ \mathbf {d}&\buildrel \varDelta \over = col\{ {\mathbf {d}_1},{\mathbf {d}_2},...,{\mathbf {d}_N}\} \quad (N \times 1) \end{aligned}$$
(2)

where \(col\{ \cdot \cdot \cdot \}\) stands for a vector resulted by stacking the specified vectors. By considering the linear least-mean-squares estimation problem:

$$\begin{aligned} \mathop {\arg \min }\limits _w {J_L}(\mathbf {w}) \quad with \quad {J_L}(\mathbf {w}) = E\{ {\left\| {\mathbf {d} - \mathbf {U} \mathbf {w}} \right\| ^2}\} \end{aligned}$$
(3)

reference [26] proposed a diffusion distributed LMS strategy as:

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} \varvec{\phi }_k^{(i - 1)} = \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}\varvec{\psi }_\ell ^{(i - 1)}} \\ {\varvec{\psi }_\ell ^{(i)} = \varvec{\phi }_k^{(i - 1)} + {\mu _k}\varvec{u}_{k,i}^*\left( {{d_k}(i) - {\varvec{u}_{k,i}}\varvec{\phi }_k^{(i - 1)}} \right) } \end{array}} \right. \end{aligned}$$
(4)

where \(\aleph _k\) accounts for the neighborhood of node k, which is defined as the collection of all sensors topologically connecting to node k, including itself. According to (4), the diffusion strategy is implemented in two steps: In the first step, each node linearly combines the local estimates gathered from its neighbors. This step fuses data from sensors across the network into node k. In the second step, the resulting aggregate at node k is fed into the local adaptive filter to adapt the local data measured at sensor k.

In (4) the local combiners \(\{c_{k,\ell }\}\) satisfy \(\sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}} = 1\). The combiners \(\{c_{k,\ell }\}\) give rise to a matrix \(C=[c_{k,\ell }]\) that contains the network topology information. There are several rules for choosing these combiners. In this paper, we utilize the Metropolis rule as [26]:

$$\begin{aligned} {c_{k,\ell }} = \left\{ {\begin{array}{*{20}{l}} 1/{\max ({n_k},{n_\ell })}\quad if{\,}k \ne \ell {\,}are{\,}linked\\ {0{\qquad \qquad \qquad }if{\,}k{\,}and{\,}\ell {\,}are{\,}not{\,}linked}\\ {1 - \!\! \!\! \sum \limits _{m \in {\aleph _k}\backslash \left\{ k \right\} } \!\! \!\! \!\!{{c_{k,m}}} {\quad }if{\,}k = \ell } \end{array}} \right. \end{aligned}$$
(5)

where \({n_k}\) and \({n_\ell }\), respectively, denote the degree of node k and \({\ell }\), i.e., the cardinality of \({\aleph _k}\) and \({\aleph _\ell }\).

Now we consider the tap-length estimation problem. It is common to use the segmented cost function to find the optimal tap-length. Because the tap-length is unknown, we temporarily assume that to be equal to L. With this assumption, the segmented cost function is defined as:

$$\begin{aligned} J_M^{(L)}(\mathbf {w}) \buildrel \varDelta \over = E\{ {\left\| {\mathbf {d} - {\mathbf {U}_M}{\mathbf {w}_M}} \right\| ^2}\} \end{aligned}$$
(6)

where \(1 \le M \le L\), \({\mathbf {w}_M}\) and \({\mathbf {U}_M}\) are vectors consisting of the first M elements/columns of \({\mathbf {w}}\) and \({\mathbf {U}}\), respectively. The underlying principle of the FT algorithm is to determine the length L such that:

$$\begin{aligned} min\{ L|J_{(L - \varDelta )}^{(L)}(\mathbf {w}) - J_L^{(L)}(\mathbf {w}) \le \varepsilon \} \end{aligned}$$
(7)

where \(\varepsilon \) is a small positive specified by the system requirements, and \(\varDelta \) is a positive integer to avoid the local minima tap-length.

Reference [21] presents a distributed solution based on diffusion strategy to solve (9):

$$\begin{aligned} \begin{array}{l} {l_{k,f}}(i - 1) = \sum \limits _{\ell \in {\aleph _k}} {{b_{\ell ,k}}{L_{\ell ,f}}(i - 1)} \\ {L_{k,f}}(i) = {l_{k,f}}(i - 1) - {\alpha _k} + {\gamma _k}\left( {e_{{L_k}(i) - {\varDelta _k}}^2\left( {{\varvec{\psi }_{k,i - 1}}} \right) - e_{{L_k}(i)}^2\left( {{\varvec{\psi }_{k,i - 1}}} \right) } \right) \end{array} \end{aligned}$$
(8)

where

$$\begin{aligned} \begin{array}{l} {e_{{L_k}(i)}}\left( {{\varvec{\psi }_{k,i - 1}}} \right) = {d_k}(i) - {\varvec{u}_{k,i}}{\varvec{\psi }_{k,i - 1}}\\ {e_{{L_k}(i) - {\varDelta _k}}}\left( {{\varvec{\psi }_{k,i - 1}}} \right) = {d_k}(i) - {\varvec{u}_{k,i}}(1:{L_k}(i) - {\varDelta _k}){\varvec{\psi }_{k,i - 1}}(1:{L_k}(i) - {\varDelta _k}) \end{array} \end{aligned}$$
(9)

where \({\varvec{u}_{k,i}}(1:{L_k}(i) - {\varDelta _k})\) and \({\varvec{\psi }_{k,i - 1}}(1:{L_k}(i) - {\varDelta _k})\) are vectors consisting of the first \({L_k}(i) - {\varDelta _k}\) elements of \( {\varvec{u}_{k,i}}\) and \( {\varvec{\psi }_{k,i - 1}}\), respectively. In (8), the parameters \(\alpha _k\) and \(\gamma _k\) are small positive values. The parameter \(\alpha _k\) is the leakage factor of node k and is used to prevent an increase in length to a large undesirable value. The parameter \(\gamma _k\) is the length adaption step-size of node k. In (8) the local combiners \(\{b_{k,\ell }\}\) satisfy \(\sum \limits _{\ell \in {\aleph _k}} {{b_{k,\ell }}} = 1\). There are several rules for choosing these combiners. In this paper, we utilize the relative-degree rule as [15]:

$$\begin{aligned} {b_{k,\ell }} = \left\{ {\begin{array}{*{20}{l}} {{n_\ell }}\big / {\sum \limits _{m \in {\aleph _k}}\! \! {{n_m}} }{\qquad }if{\,}\ell \in {\aleph _k}\\ {0{\qquad \qquad \qquad { otherwise}}} \end{array}} \right. \end{aligned}$$
(10)

In (8), \({L_{\ell ,f}}(i )\) and \({l_{k,f}}(i)\) are the local and integrated fractional tap-length estimates, and the integer tap-length is adjusted by

$$\begin{aligned} {L_k}(i) = \left\{ {\begin{array}{*{20}{l}} {\left\lfloor {{L_{k,f}}(i)} \right\rfloor {,}{\quad }if{\,}\left| {{L_k}(i - 1) - {L_{k,f}}(i)} \right| > {\delta _k}}\\ {{L_k}(i - 1){\qquad { otherwise}}} \end{array}} \right. \end{aligned}$$
(11)

where \(\left\lfloor {.} \right\rfloor \) rounds the embraced value to the nearest integer. Here, \(\delta _k\) is the small local integer and is usually set to one.

3 Proposed Method

The given LMS style algorithm in (8) is a powerful approach to estimate the fractional tap-length in a diffusion strategy. However, the fact that its performance is affected by several parameters challenges the effectiveness of this algorithm. The value of the leakage factor \(\alpha _k\) in (8) must be small enough so that the steady-state tap-length is not reduced too much, and large enough to prevent the “wandering” issue during the learning stage. Generally, the choice of this parameter was not critical, and values between 0.001 and 0.01 are good choices for the leakage factor in each node. Therefore, in this paper, we do not want to impose an additional computational burden on the nodes by updating the leakage factor, because the power limitation in wireless sensor networks is a critical issue. Instead, we will focus on the two key parameters, length adaptation step-size \(\gamma _k\), and error width \(\varDelta _k\). The error width controls the trade-off between the convergence rate and the steady-state tap-length bias. The tap-length adaptation step-size controls the trade-off between the tap-length convergence rate and steady-state tap-length fluctuation. A large \(\varDelta _k\) accelerates the convergence rate of the tap-length learning and equips the algorithm with the ability to escape from the possible suboptimal tap-lengths. Besides, a smaller \(\varDelta _k\) than the estimation of the optimal tap-length will result in a steady-state tap-length that is not significantly biased. About the role of \(\gamma _k\) in the algorithm, a large \(\gamma _k\) accelerates the convergence rate of the tap-length learning but results in high steady-state fluctuation of the tap-length. Besides, a smaller \(\gamma _k\), although, leads to a low steady-state tap length fluctuation but results in a slow convergence rate. So, this motivates us to propose a diffusion variable tap-length method with variable parameters rather than fixed, where the tap-length adaptation step-size and the error width are set in the large values during the initial iterations, and they reduce step by step to approach the smaller values in the steady-state. For this purpose, we need a measure to control these variations. Various criteria can be used for this purpose, among which the gradient vector is a suitable measure. It is well-known that the squared norm of the smoothed gradient vector tracks the variation of the mean square deviation. Hence, it is an excellent candidate to control the tap-length adaptation step-size and error width. In this paper, we propose a diffusion tap-length update with variable parameters method based on the gradient vector in which the tap length adaptation step-size and error width are adjusted to be proportional to the estimated smoothed gradient vector norm square. Since the Euclidean norm of the gradient vector is large in initial iterations and approaches to a small amount at steady-state, so by proportionate the parameters with it, all the goals we pursue will be met. In the sense that, since the proposed measure provides large \(\varDelta _k\) and \(\gamma _k\) at initial iterations, the fast convergence rate of the tap-length learning is achieved, and also this large \(\varDelta _k\) for each node prevents the tap-length from trapping in the sub-optimal value. On the other hand, the proposed measure provides a small \(\varDelta _k\) and \(\gamma _k\) at steady-state, which leads to the unbiased estimated tap-length and low steady-state fluctuation of the tap-length. Another point to consider is the strategy used to update these parameters. These parameters can be updated independently in each node without the cooperation of other nodes. However, we can take advantage of the spatial diversity to update these parameters. In the proposed method, we use the diffusion strategy for the adaptation of these parameters. So, these parameters are updated in a distributed manner with the cooperation of all nodes.

Accordingly, in the proposed method, first, each node linearly combines the local estimated smoothed instantaneous gradient vector gathered from its neighbors as

$$\begin{aligned} { \varvec{\rho }_k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \varvec{\rho }_\ell }(i-1)} \end{aligned}$$
(12)

where the vector \({\varvec{\rho }_k}(i)\) is the smoothed gradient vector, and \({ \varvec{\rho }_k ^{(a)}}(i)\) is the aggregated gradient vector at node k. Thanks to this step, the estimation of the smoothed gradient vector enjoys spatial diversity. Then, the resulting aggregate at node k is updated as

$$\begin{aligned} {\varvec{\rho }_k}(i) = {\beta _k}{ \varvec{\rho }_k ^{(a)}}(i) + (1 - {\beta _k}){e_{{L_k}(i)}}\left( {{\varvec{\psi }_{k,i - 1}}} \right) {\varvec{u}_{k,i}} \end{aligned}$$
(13)

where the smoothing parameter \({\beta _k}\) is selected very close to the unit. Thus, (13) corresponds to a low pass filtering, which decreases the noise influence on the gradient vector estimation and leads to a more stable parameter adaptation. Note that the length of the vector \({ \varvec{\rho }_k ^{(a)}}(i)\) is adjusted in each iteration according to the estimated tap-length.

We also implement the strategy of aggregating neighbors’ local estimates for updating the parameters \(\varDelta _k\) and \(\gamma _k\). On this basis, each node first calculates the aggregated estimations

$$\begin{aligned} { \varDelta _k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \varDelta _\ell }(i-1)} \end{aligned}$$
(14)

and

$$\begin{aligned} { \gamma _k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \gamma _\ell }(i-1)} \end{aligned}$$
(15)

where \(\varDelta _k(i)\) and \(\gamma _k(i)\) are the estimated error width and tap-length adaptation step-size at node k and iteration i, respectively. The parameters \({ \varDelta _k ^{(a)}}(i)\) and \({ \gamma _k ^{(a)}}(i)\) are the aggregated error width and tap-length adaptation step-size at node k and iteration i, respectively. Using the resulted aggregates, \(\varDelta _k(i)\) and \(\gamma _k(i)\) are updated, respectively, as

$$\begin{aligned} {\varDelta _k}(i) = \left\lfloor {{\theta _k}{ \varDelta _k ^{(a)}}(i) + {\kappa _k}\left\| {{ \varvec{\rho }_k}(i)} \right\| } \right\rfloor \end{aligned}$$
(16)

and

$$\begin{aligned} {\gamma _k}(i) = {\tau _k}{ \gamma _k ^{(a)}}(i)+ {\eta _k}\left\| {{ \varvec{\rho }_k}(i)} \right\| \end{aligned}$$
(17)

where \(0<{\tau _k}<1\), \(0<{\theta _k}<1\), \({\eta _k}\) and \({\kappa _k}\) are positive constants.

As is clear from (12)–(17), the proposed algorithm is fully distributed and is performed with the cooperation of all nodes. So that each node first takes the neighbors’ local estimates, aggregates them as (12), (14), and (15) and then updates the aggregated results as (13), (16), and (17). Note that both \(\varDelta _k(i)\) and \(\gamma _k(i)\) are updated with the same measure according to the above relations, and no separate measures are considered for each. The reason for this is to avoid additional calculations, and consequently, to avoid extra power consumption. This common measure, the Euclidean norm of the smoothed gradient vector, will provide large initial and small steady-state values for both \(\varDelta _k(i)\) and \(\gamma _k(i)\) . As a result, fast tap-length convergence, low steady-state fluctuations, and unbiased steady-state tap-length estimation will be provided.

The proposed diffusion variable tap-length method with variable parameters is summarized as follows:

$$\begin{aligned}&\varvec{\phi }_k^{(i - 1)} = \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}\varvec{\psi }_\ell ^{(i - 1)}} \end{aligned}$$
(18a)
$$\begin{aligned}&{l_{k,f}}(i - 1) = \sum \limits _{\ell \in {\aleph _k}} {{b_{\ell ,k}}{L_{\ell ,f}}(i - 1)} \end{aligned}$$
(18b)
$$\begin{aligned}&{ \varvec{\rho }_k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \varvec{\rho }_\ell }(i-1)} \end{aligned}$$
(18c)
$$\begin{aligned}&{ \varDelta _k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \varDelta _\ell }(i-1)} \end{aligned}$$
(18d)
$$\begin{aligned}&{ \gamma _k ^{(a)}}(i)= \sum \limits _{\ell \in {\aleph _k}} {{c_{k,\ell }}{ \gamma _\ell }(i-1)} \end{aligned}$$
(18e)
$$\begin{aligned}&{\varvec{\psi }_k ^{(i)} = \varvec{\phi }_k^{(i - 1)} + {\mu _k}\varvec{u}_{k,i}^*\left( {{d_k}(i) - {\varvec{u}_{k,i}}\varvec{\phi }_k^{(i - 1)}} \right) } \end{aligned}$$
(18f)
$$\begin{aligned}&{e_{{L_k}(i)}}\left( {{\varvec{\psi }_{k,i }}} \right) = {d_k}(i) - {\varvec{u}_{k,i}}{\varvec{\psi }_{k,i }} \end{aligned}$$
(18g)
$$\begin{aligned}&{\varvec{\rho }_k}(i) = {\beta _k}{ \varvec{\rho }_k ^{(a)}}(i) + (1 - {\beta _k}){e_{{L_k}(i)}}\left( {{\varvec{\psi }_{k,i}}} \right) {\varvec{u}_{k,i}} \end{aligned}$$
(18h)
$$\begin{aligned}&{\varDelta _k}(i) = \left\lfloor {{\theta _k}{ \varDelta _k ^{(a)}}(i) + {\kappa _k}\left\| {{ \varvec{\rho }_k}(i)} \right\| } \right\rfloor \end{aligned}$$
(18i)
$$\begin{aligned}&{\gamma _k}(i) = {\tau _k}{ \gamma _k ^{(a)}}(i)+ {\eta _k}\left\| {{ \varvec{\rho }_k}(i)} \right\| \qquad \qquad \end{aligned}$$
(18j)
$$\begin{aligned}&{e_{{L_k}(i) - {\varDelta _k}}}\left( {{\varvec{\psi }_{k,i - 1}}} \right) = {d_k}(i) - {\varvec{u}_{k,i}}(1:{L_k}(i) - {\varDelta _k}){\varvec{\psi }_{k,i}}(1:{L_k}(i) - {\varDelta _k}) \end{aligned}$$
(18k)
$$\begin{aligned}&{L_{k,f}}(i) = {l_{k,f}}(i - 1) - {\alpha _k} + {\gamma _k}\left( {e_{{L_k}(i) - {\varDelta _k}}^2\left( {{\varvec{\psi }_{k,i }}} \right) - e_{{L_k}(i)}^2\left( {{\varvec{\psi }_{k,i }}} \right) } \right) \end{aligned}$$
(18l)
$$\begin{aligned}&{L_k}(i) = \left\{ {\begin{array}{*{20}{l}} {\left\lfloor {{L_{k,f}}(i)} \right\rfloor {,}{\quad }if{\,}\left| {{L_k}(i - 1) - {L_{k,f}}(i)} \right| > {\delta _k}}\\ {{L_k}(i - 1){\qquad { otherwise}}} \end{array}} \right. \end{aligned}$$
(18m)

This proposed algorithm proceeds as follows. Each node k, at each iteration i, performs the following steps:

1) Receives the estimates \(\varvec{\psi }_\ell ^{(i - 1)}\), \({L_{\ell ,f}}(i - 1) \), \({ \varvec{\rho }_\ell }(i-1)\), \({ \varDelta _\ell }(i-1)\), and \({ \gamma _\ell }(i-1)\) from its neighbors \(\{ \ell \in {\aleph _k} \}\).

2) Computes the convex combination of estimates received from its neighbors according to (18a)-(18e).

3) Adapts its current aggregate weight estimate \(\varvec{\phi }_k^{(i - 1)}\) using its local data available at the time i, to obtain a new tap-weight estimate \(\varvec{\psi }_k ^{(i)}\).

4) Using the estimated weight vector \(\varvec{\psi }_k ^{(i)}\), this node updates the error estimation according to (18g), which is used to estimate the smoothed gradient vector according to (18h).

5) The Euclidean norm of the estimated gradient vector is used alongside with the aggregate estimates \( { \varDelta _k ^{(a)}}(i)\) and \({ \gamma _k ^{(a)}}(i)\) in (18i) and (18j) to update the error width \({\varDelta _k}(i)\) and the tap-length adaptation step-size \({\gamma _k}(i)\).

6) Using the updated \({\varDelta _k}(i)\) and \(\varvec{\psi }_k ^{(i)}\), this node updates the segmented error according to (18k).

7) Finally, the local tap-length is computed according to (18l) and (18m), and the length of the vectors are adjusted accordingly.

This iteration is concluded when node k exchanges \(\varvec{\psi }_k ^{(i )}\), \({L_{k ,f}}(i ) \), \({ \varvec{\rho }_k }(i)\), \({ \varDelta _k }(i)\), and \({ \gamma _k }(i)\) with its neighbors \(\{ \ell \in {\aleph _k} \}\).

4 Steady-State Analysis

This section provides a steady-state analysis. This approximate analysis is intended to give an insight into the effect of the parameters on the steady-state tap-length adaptation step-size and error width. This analysis is convincing to put the boundaries on error width and tap-length step-size. For the convenience of the analysis, we consider several assumptions as

A1) \({\mathbf {u}}_{L_{opt}k,i}\) is independent of \({\mathbf {u}}_{L_{opt}\ell ,j}\) for \(k\ne \ell \), and \(i\ne j \).

A2) The regressors \({\mathbf {u}}_{L_{opt}k,i}\) are Gaussian with the eigendecomposition \(R_{u,k}=Q_{k}\varLambda _{k}Q_{k}^*\), where \( Q_{k}\) is unitary and \(\varLambda _{k}\) is a diagonal matrix with the eigenvalues of \(R_{u,k}\).

A3) The steady-state excess mean squared error is enough smaller than the noise variance, and consequently, the error \({e_{{L_k}(i)}}\left( {{\varvec{\psi }_{k,i }}} \right) \) in each node is approximately equal to the noise \( {\mathbf {v}_k}(i)\). Note that this assumption is only feasible when the step size is so small. Nevertheless, it provides the insight we investigate

Equations (18h)-(18j) combine the updates of several interconnected algorithms and also the network topology. Therefore, subsequent analysis tends to be challenging. To proceed with this analysis, we define the following global quantities.

$$\begin{aligned} \begin{aligned} {\varGamma }^i&\triangleq col\left\{ \gamma _1\left( i\right) , \gamma _2\left( i\right) ,\ \dots ,\gamma _N\left( i\right) \right\} \\ {\varDelta }^i&\triangleq col\left\{ {\varDelta }_1\left( i\right) ,{\varDelta }_2\left( i\right) ,\ \dots ,\ {\varDelta }_N\left( i\right) \right\} \\ {\mathrm{P}}^i&\triangleq col\left\{ {{\varvec{\rho }}}_1\left( i\right) ,{\varvec{\rho }}_2\left( i\right) ,\ \dots ,\ {\varvec{\rho }}_N\left( i\right) \right\} \\ \mathrm{B}&\triangleq diag\left\{ \beta _1I_{L\left( \infty \right) },\beta _2I_{L\left( \infty \right) },\dots ,\beta _NI_{L\left( \infty \right) }\right\} \\ {{\varvec{e}}}^i&\triangleq col\left\{ {e_{{L_1}(i)}}\left( {{\varvec{\psi }_{1,i }}} \right) ,{e_{{L_2}(i)}}\left( {{\varvec{\psi }_{2,i }}} \right) ,\ \dots ,\ {e_{{L_N}(i)}}\left( {{\varvec{\psi }_{N,i }}} \right) \right\} \\ \varTheta&\triangleq diag\left\{ \theta _1,\theta _2,\dots ,\theta _N\right\} \\ \mathrm{T}&\triangleq diag\left\{ \tau _1, \tau _2,\dots ,\tau _N\right\} \end{aligned} \begin{aligned} {\varGamma }^{\left( a\right) ,i}&\triangleq col\left\{ \gamma ^{\left( a\right) }_1\left( i\right) , \gamma ^{\left( a\right) }_2\left( i\right) ,\ \dots ,\ \gamma ^{\left( a\right) }_N\left( i\right) \right\} \\ {\varDelta }^{\left( a\right) ,i}&\triangleq col\left\{ {\varDelta }^{\left( a\right) }_1\left( i\right) ,\ {\varDelta }^{\left( a\right) }_2\left( i\right) ,\ \dots ,\ {\varDelta }^{\left( a\right) }_N\left( i\right) \right\} \\ {\mathrm{P}}^{\left( a\right) ,i}&\triangleq col\left\{ {{\varvec{\rho }}}^{\left( a\right) }_1\left( i\right) ,\ {{\varvec{\rho }}}^{\left( a\right) }_2\left( i\right) ,\ \dots ,\ {{\varvec{\rho }}}^{\left( a\right) }_N\left( i\right) \right\} \\ U_i&\triangleq diag\left\{ {{\mathbf{u}}}_{1,i},\ {{\mathbf{u}}}_{2,i},\dots ,{{\mathbf{u}}}_{N,i}\right\} \\ {{\mathbf{v}}}^i&\triangleq col\left\{ v_1\left( i\right) ,v_2\left( i\right) ,\ \dots ,\ v_N\left( i\right) \right\} \\\ {\mathrm{K}}_\kappa&\triangleq diag\left\{ \kappa _1, \kappa _2,\dots ,\kappa _N\right\} \\ {\mathrm{H}}_\eta&\triangleq diag\left\{ \eta _1, \eta _2,\dots ,\eta _N\right\} \end{aligned} \end{aligned}$$
(19)

With these definitions, relations (18c) and (18h) admit the global description as follow:

$$\begin{aligned} \begin{array}{l} {\mathrm{P}}^{\left( a\right) ,i}=G{\mathrm{P}}^{i-1} \\ {\mathrm{P}}^i=\mathrm{B}{\mathrm{P}}^{\left( a\right) ,i}+\left( I-\mathrm{B}\right) U^T_i{\mathrm{e}}^i \\ \end{array} \end{aligned}$$
(20)

or, in an equivalent compact form: c

$$\begin{aligned} {\mathrm{P}}^i=\mathrm{B}G{\mathrm{P}}^{i-1}+\left( I-\mathrm{B}\right) U^T_i{\mathrm{e}}^i \end{aligned}$$
(21)

with \(G\triangleq C\otimes I_{L\left( \infty \right) } \), where \(\otimes \) stands for the Kronecker product. By assuming \( {\mathrm{P}}^0=0\), (21) can be written as

$$\begin{aligned} {\mathrm{P}}^i=\sum ^i_{n=0}{{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n{\mathrm{e}}^n} \end{aligned}$$
(22)

The mean squared norm of the smoothed gradient is obtained as

$$\begin{aligned} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} =\sum ^i_{m=0}{\sum ^i_{n=0}{E\left\{ {\left( {\mathrm{e}}^m\right) }^TU_m\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-m}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n{\mathrm{e}}^n\right\} }} \end{aligned}$$
(23)

The subsequent analysis considers the summand at the steady-state. So, by assuming that the algorithm has converged, we have:

$$\begin{aligned}&E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} =\sum ^i_{m=0}{\sum ^i_{n=0}{E\left\{ {\left( {{\mathbf{v}}}^m\right) }^TU_m\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-m}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n{{\mathbf{v}}}^n\right\} }} \nonumber \\&\quad =\sum ^i_{m=0}{\sum ^i_{n=0}{E\left\{ tr\left\{ {\left( {{\mathbf{v}}}^m\right) }^TU_m\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-m}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n{{\mathbf{v}}}^n\right\} \right\} }}\nonumber \\&\quad =\sum ^i_{m=0}{\sum ^i_{n=0}{E\left\{ tr\left\{ {{\mathbf{v}}}^n{\left( {{\mathbf{v}}}^m\right) }^TU_m\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-m}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n\right\} \right\} }} \nonumber \\&\quad =\sum ^i_{m=0}{\sum ^i_{n=0}{tr\left\{ E\left\{ {{\mathbf{v}}}^n{\left( {{\mathbf{v}}}^m\right) }^T\right\} E\left\{ U_m\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-m}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n\right\} \right\} }}\nonumber \\ \end{aligned}$$
(24)

and since the noise signal is independent over time

$$\begin{aligned} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} =\sum ^i_{n=0}{tr\left\{ {\varLambda }_vE\left\{ U_n\left( I-\mathrm{B}\right) {\left( G\mathrm{B}\right) }^{i-n}{\left( \mathrm{B}G\right) }^{i-n}\left( I-\mathrm{B}\right) U^T_n\right\} \right\} } \end{aligned}$$
(25)

where \({\varLambda }_v=diag\left\{ \sigma ^2_{v,1},\sigma ^2_{v,2},\dots ,\sigma ^2_{v,N}\right\} \). By defining \(H^{i-n}={\left( G\mathrm{B}\right) }^{i-n}{\left( \mathrm{B}G\right) }^{i-n}\), (25) can be written as

$$\begin{aligned} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} =\sum ^i_{n=0}{tr\left\{ {\varLambda }_vE\left\{ U_n\left( I-\mathrm{B}\right) H^{i-n}\left( I-\mathrm{B}\right) U^T_n\right\} \right\} } \end{aligned}$$
(26)

Considering assumption (A2), let to define:

$$\begin{aligned} \begin{aligned} \overline{U_i}&=U_i\mathrm{Q} \\ {\overline{H}}^{i-n}&={\mathrm{Q}}^TH^{i-n}\mathrm{Q} \\ \overline{\left( I-\mathrm{B}\right) }&={\mathrm{Q}}^T\left( I-\mathrm{B}\right) \mathrm{Q=}\left( I-\mathrm{B}\right) \end{aligned} \end{aligned}$$
(27)

where \(\mathrm{Q}=diag\left\{ Q_1,Q_2,\dots ,\ Q_N\right\} \). Due to the unitary property of \(\mathrm{Q}\), i.e., \( {\mathrm{Q}}^T\mathrm{Q}=\mathrm{Q}{\mathrm{Q}}^T=I\), the expectation in (26) can be written as

$$\begin{aligned} \begin{array}{l} E\left\{ U_n\mathrm{Q}{\mathrm{Q}}^T\left( I-\mathrm{B}\right) \mathrm{Q}{\mathrm{Q}}^TH^{i-n}\mathrm{Q}{\mathrm{Q}}^T\left( I-\mathrm{B}\right) \mathrm{Q}{\mathrm{Q}}^TU^T_n\right\} \\ =E\left\{ {\overline{U}}_n\left( I-\mathrm{B}\right) {\overline{H}}^{i-n}\left( I-\mathrm{B}\right) {\overline{U}}^T_n\right\} \end{array} \end{aligned}$$
(28)

The \(k \ell \) entry of this expectation is given by

$$\begin{aligned} \begin{array}{l} {\left( E\left\{ {\overline{U}}_n\left( I-\mathrm{B}\right) {\overline{H}}^{i-n}\left( I-\mathrm{B}\right) {\overline{U}}^T_n\right\} \right) }_{k\ell }=\left\{ \begin{array}{c} 0\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ k\ne \ell \\ {\left( 1-\beta _k\right) }^2tr\left\{ {\varLambda }_k{\overline{H}}^{i-n}_{kk}\right\} \ \ \ \ \ \ \ \ \ \ \ \ k=\ell \end{array} \right. \end{array} \end{aligned}$$
(29)

where \({\overline{H}}^{i-n}_{k \ell }\) is the \(k \ell \) -block of \(\overline{H}^{i-n}\). So that the summand in (26) gives

$$\begin{aligned} tr\left\{ {\varLambda }_vE\left\{ U_n\left( I-\mathrm{B}\right) H^{i-n}\left( I-\mathrm{B}\right) U^T_n\right\} \right\} ={{\mathbf{z}}}^T{\overline{{\mathbf{h}}}}^{i-n} \end{aligned}$$
(30)

with \({\overline{{\mathbf{h}}}}^{i-n}=bvec\left\{ {\overline{H}}^{i-n}\right\} \), \({\mathbf{z}}=\text {bvec}\left\{ R_v{\left( I-\mathrm{B}\right) }^2\varLambda \right\} \), \(\varLambda =diag\left\{ {\varLambda }_1,{\varLambda }_2,\dots ,\ {\varLambda }_N\right\} \) and \(R_v={\varLambda }_v\odot I_{L\left( \infty \right) }\). Here, \(\odot \) denotes the block Kronecker product, and bvec stands for block vector operator which is defined for a given matrix

$$\begin{aligned} X=\left[ \begin{array}{cccc} X_{11} &{} X_{12} &{} \cdots &{} X_{1N} \\ X_{21} &{} X_{22} &{} \cdots &{} X_{2N} \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ X_{N1} &{} X_{N2} &{} \cdots &{} X_{NN} \end{array} \right] \end{aligned}$$
(31)

as

$$\begin{aligned} \text {bvec}\left\{ X\right\} =\left[ \begin{array}{c} X_1 \\ X_2 \\ \vdots \\ X_N \end{array} \right] \end{aligned}$$
(32)

with \(X_{\ell }=col\left\{ \text {vec}\left\{ X_{1\ell }\right\} ,\text { vec}\left\{ X_{2\ell }\right\} ,\dots ,\text { vec}\left\{ X_{N\ell }\right\} \right\} \), where vec stands for the standard vector operator. vector operator (30) in (26) results in

$$\begin{aligned} \begin{array}{l} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} =\sum ^i_{n=0}{{{\mathbf{z}}}^T{\overline{{\mathbf{h}}}}^{i-n}}={{\mathbf{z}}}^T\sum ^i_{n=0}{{\overline{{\mathbf{h}}}}^{i-n}}={{\mathbf{z}}}^T \text {bvec}\left\{ \sum ^i_{n=0}{{\overline{H}}^{i-n}}\right\} \end{array} \end{aligned}$$
(33)

If all nodes use the same value for \(\beta _k = \beta \), the matrix \(\mathrm B\) can be replaced by \(\mathrm{B}\mathrm{=}\beta I\) which gives rise to

$$\begin{aligned} {\overline{H}}^{i-n}={\mathrm{Q}}^TH^{i-n}\mathrm{Q}={\mathrm{Q}}^T{\left[ {\left( \beta G\right) }^2\right] }^{i-n}\mathrm{Q} \end{aligned}$$
(34)

From (33) and (34), the steady-state mean squared norm of the smoothed gradient results as

$$\begin{aligned} E\left\{ {\left\| {\mathrm{P}}^{\infty }\right\| }^2\right\} ={{\mathbf{z}}}^T \text {bvec}\left\{ {\mathrm{Q}}^T\sum ^{\infty }_{n=0}{{\left[ {\left( \beta G\right) }^2\right] }^{i-n}}\mathrm{Q}\right\} ={{\mathbf{z}}}^T \text {bvec} \left\{ {\mathrm{Q}}^T{\left( I-{\left( \beta G\right) }^2\right) }^{-1}\mathrm{Q}\right\} \end{aligned}$$
(35)

Using the global description for (18i) and (18j), and tacking expectations of both sides of them at steady-state, and assuming that the steady-state \({\mathrm{P}}^i\) be a vector of (not necessarily independent) Gaussian random variables, leads to

$$\begin{aligned} E\{{\varDelta }^i\}=\varTheta C{E\{\varDelta }^{i-1}\} +\sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)} \sqrt{ \frac{1}{NL_{opt}} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} } {\mathrm{K}}_\kappa {\mathbf{1}} \end{aligned}$$
(36)

and

$$\begin{aligned} E\{{\varGamma }^i\}=\mathrm{T}C{E\{\varGamma }^{i-1}\}+ \sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)} \sqrt{ \frac{1}{NL_{opt}} E\left\{ {\left\| {\mathrm{P}}^i\right\| }^2\right\} } {\mathrm{H}}_\eta {\mathbf{1}} \end{aligned}$$
(37)

In which we have used \({\varDelta }^{\left( a\right) ,i}=C{\varDelta }^{i-1}\) and \({\varGamma }^{\left( a\right) ,i}=C{\varGamma }^{i-1} \). Here,\({\mathbf{1}}\) denotes an \(N \times 1\) vector whose entries are all unity. By substituting (35) in (36), and (37) we will have

$$\begin{aligned} {\varDelta }^{\infty }= & {} \sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)} \sqrt{ \frac{1}{NL_{opt}} {{\mathbf{z}}}^T\text {bvec}\left\{ {\mathrm{Q}}^T{\left( I-{\left( \beta G\right) }^2\right) }^{-1}\mathrm{Q}\right\} } {\left( I-\varTheta C\right) }^{-1}{\mathrm{K}}_\kappa {\mathbf{1}} \end{aligned}$$
(38)
$$\begin{aligned} {\varGamma }^{\infty }= & {} \sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)} \sqrt{ \frac{1}{NL_{opt}} {{\mathbf{z}}}^T\text {bvec}\left\{ {\mathrm{Q}}^T{\left( I-{\left( \beta G\right) }^2\right) }^{-1}\mathrm{Q}\right\} }{\left( I-\mathrm{T}C\right) }^{-1}{\mathrm{H}}_\eta {\mathbf{1}} \end{aligned}$$
(39)

Let to define global error width and global tap-length adaptation step-size as the average of these quantities over all nodes:

$$\begin{aligned} {\varDelta }_{Net}\left( \infty \right)= & {} \frac{1}{N}\sum ^N_{k=1}{{\varDelta }_k\left( \infty \right) }=\frac{1}{N}{{\mathbf{1}}}^T{\varDelta }^{\infty } \end{aligned}$$
(40)
$$\begin{aligned} \varGamma _{Net}\left( \infty \right)= & {} \frac{1}{N}\sum ^N_{k=1}{\gamma _k\left( \infty \right) }=\frac{1}{N}{{\mathbf{1}}}^T{\varGamma }^{\infty } \end{aligned}$$
(41)

Therefore, (38)- (41) lead to

$$\begin{aligned} {\varDelta }_{Net}\left( \infty \right)= & {} \frac{1}{N} \sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)}\nonumber \\&\sqrt{ \frac{1}{NL_{opt}} {{\mathbf{z}}}^T\text {bvec}\left\{ {\mathrm{Q}}^T{\left( I-{\left( \beta G\right) }^2\right) }^{-1}\mathrm{Q}\right\} } {{\mathbf{1}}}^T {\left( I-\varTheta C\right) }^{-1}{\mathrm{K}}_\kappa {\mathbf{1}} \qquad \end{aligned}$$
(42)
$$\begin{aligned} \varGamma _{Net}\left( \infty \right)= & {} \frac{1}{N} \sqrt{2} \frac{\varGamma ((L_{opt}+1)/2)}{\varGamma (L_{opt}/2)}\nonumber \\&\sqrt{ \frac{1}{NL_{opt}} {{\mathbf{z}}}^T\text {bvec}\left\{ {\mathrm{Q}}^T{\left( I-{\left( \beta G\right) }^2\right) }^{-1}\mathrm{Q}\right\} } {{\mathbf{1}}}^T{\left( I-\mathrm{T}C\right) }^{-1}{\mathrm{H}}_\eta {\mathbf{1}}\qquad \end{aligned}$$
(43)

Considering Eq.(42) and Eq.(43), several parameters need to be selected suitably to ensure a large \({\varDelta _k}\left( i \right) \) and \({{\gamma _k}\left( i \right) }\) at initial iterations of adaptation and after immediate variations, which accelerates the tap-length convergence. Also, these proper choice of parameters should ensure a small \({\varDelta _k}\left( i \right) \) and \({{\gamma _k}\left( i \right) }\) for each node at steady-state to guarantee a small bias and small fluctuations, but not too small to make the tap-length update insensitive to instantaneous changes. The proposed algorithm is presented here to solve the problem of selecting two parameters \({\varDelta _k}\left( i \right) \) and \({{\gamma _k}\left( i \right) }\). But now their selection depends on several other parameters, the simultaneous choice of them affects the steady-state values and, of course, the transient conditions of the algorithm. One way to overcome this problem is to constraint this parameter as \({\varDelta _k}\left( i \right) \mathrm{{ }} = \mathrm{{ }}\max \left( {\min \left( {{\varDelta _k}\left( i \right) ,\mathrm{{ }}{\varDelta _{\max }}} \right) ,\mathrm{{ }}{\varDelta _{\min }}} \right) \), where \( 0< {\varDelta _{\min }} < {\varDelta _{\max }}\) and \({\gamma _k}\left( i \right) \mathrm{{ }} = \mathrm{{ }}\max \left( {\min \left( {{\gamma _k}\left( i \right) ,\mathrm{{ }}{\gamma _{\max }}} \right) ,\mathrm{{ }}{\gamma _{\min }}} \right) \), where \(0< {\gamma _{\min }} < {\gamma _{\max }}\). The upper bands are selected to guarantee that the algorithm does not fail, and the lower bands are chosen to ensure the feasibility of the algorithm. As the simulations will show in the next section, this restriction solves the problem of selecting different parameters. At the same time, the expected performance of the algorithm is obtained.

5 Simulation Results

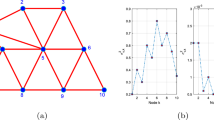
To show the performance of the proposed method, we perform several simulations in this section. First, the performance of the proposed method is tested under the low noise condition for two different optimal tap-length cases. Then, the performance of the proposed method under high noise conditions is tested. The last experiment is conducted to test the tracking behavior of the proposed algorithm, where the optimal tap-length changes unpredictably. The network topology with \(N=20\) sensors is shown in Fig 1a. The measurement noises and regressors are considered uncorrelated Gaussian processes with zero-mean, independent in space and time across the network. The regressor variances are depicted in Fig 1b.

Fig. 1
figure 1

Network topology (a), and regressor variances (b) for \(N=20\) nodes

Full size image

Low noise condition with \({L_{opt}=200}\): First we consider the low noise condition, where the noise variances in each node are scaled to realize high signal-to-noise ratios (SNRs) as is shown in Fig2a. The unknown vector \(w_{{L_{opt}}}^o\) of length \({L_{opt}=200}\) is drawn from a zero-mean white Gaussian sequence with variance 0.003. The parameters are set as \( {\mu _k}=0.008, {\alpha _k} = 0.006, {\beta _k}= 0.995, {\theta _k}=0.94, {\kappa _k}=60, {\tau _k}=0.95, {\eta _k}=50, \gamma _{\min }=5, {\gamma _{\max }}=35, {\varDelta _{\min }}=2, {\varDelta _{\max }}=30 \).

Fig. 2
figure 2

The SNRs across the sensors in the network for (a) low-noise case, and (b) high-noise case

Full size image

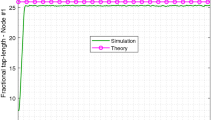
Figure 3 depicts the evolution curves for different methods over diffusion adaptive networks, including the proposed algorithm, and conventional FT algorithm with \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k}= {\gamma _{\min }})\), \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k} = {\gamma _{\max }})\), \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\min }})\), and \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\). The results are averaged over 100 independent Monte Carlo experiments. The global average fractional tap-length and global average mean-square deviation (MSD) are defined, respectively, as

$$\begin{aligned} L_f^{Net}(i)= & {} \frac{1}{N}\sum \limits _{k = 1}^N {{L_{k,f}}(i)} \end{aligned}$$
(44)
$$\begin{aligned} MS{D^{Net}}(i)= & {} \frac{1}{N}\sum \limits _{k = 1}^N {E\left\{ {{{\left\| {\varvec{w}_{{L_{opt}}}^o -\varvec{\psi } _{k,i}} \right\| }^2}} \right\} } \end{aligned}$$
(45)

As we can see from Figure 3, the proposed algorithm converges as fast as the diffusion FT method with the fixed-parameter \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\), while the steady-state tap-length in the proposed method does not have the same bias as the fixed-parameter \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\). By reducing the \(\varDelta _k\) and \({\gamma _k}\) from the \({\varDelta _{\max }}\) and \({\gamma _{\max }}\) in the fixed-parameter diffusion FT, the convergence slows down, and as can be seen from Fig. 3 it converges slowly, and of course, the length of the steady-state is biased due to the large \({\varDelta _k}\). In order not to have a steady-state bias, the \({\varDelta _k}\) must be reduced to the \({\varDelta _{\min }}\), but in the meantime, if \({\gamma _k}\) is selected as the \({\gamma _{\min }}\), convergence will not occur. For the case \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k} = {\gamma _{\max }})\), although the steady-state bias is not expected, the convergence will be greatly reduced. Therefore, the proposed algorithm enjoys fast convergence similar to the diffusion FT with fixed-parameters \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) and has less steady-state bias similar to the diffusion FT with \({\varDelta _k} = {\varDelta _{\min }}\).

Figure 4 compares the performance of the proposed method with the algorithms presented in [18] and [35]. For the algorithm presented in [18], the parameters are set as \(\lambda =0.95, \varDelta _{\max }=30, \varDelta (\infty )=2, C=1, \gamma =35, \lambda _1=0.9, \lambda _2=0.95\). For the algorithm presented in [35], the parameters are set as \(\gamma _M =35, \gamma _m=5, \tau =1, \beta =0.99, \varDelta =30\). For a fair comparison, the other parameters are considered the same for all algorithms. As can be seen, compared to the other algorithms, the proposed method shows better performance in terms of both convergence rate and steady-state error.

Figure 5 shows the evolution curves of \({\varDelta _k(i)} \) and \({\gamma _k(i)} \). These parameters initiate from large values, and with the convergence of the algorithm, they end in smaller values which are suitable for steady-state condition. Note that, since both \(\varDelta _k(i)\) and \(\gamma _k(i)\) are updated with the same measure, they follow the same path of convergence.

Note that, by increasing \({\tau _k}\) or \({\eta _k}\) the width of \({\gamma _k}\) in Fig.4 increases. By decreasing these parameters, we will have a narrower \({\gamma _k}\) with a smaller peak, such that the peak will not reach its maximum. Also, \({\theta _k}\) and \({\kappa _k}\) have a similar effect on \(\varDelta _k\). As the \({\beta _k}\) increases, the peaks of \({\gamma _k}\) and \(\varDelta _k\) become narrower, and they will converge slowly.

Fig. 3
figure 3

The evolution curves of global tap-length (a) and MSD (b) under the low-noise condition, where \(L_{opt}=200\)

Full size image
Fig. 4
figure 4

The evolution curves of global tap-length (a) and MSD (b) for different algorithms

Full size image
Fig. 5
figure 5

Evolution curves of \(\gamma _k(i)\) and \(\varDelta _k(i)\) of the proposed method

Full size image

Low noise condition with \({L_{opt}=100}\):

In the second simulation, the unknown parameter length is considered to be \(L_{opt}=100\). The setup of this simulation is the same as those in the previous simulation except for \( {\mu _k}=0.01, {\alpha _k} = 0.01, {\beta _k}= 0.95\), and \( {\varDelta _{\max }}=20 \). The evolution curves for the proposed algorithm, and conventional FT with \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k}= {\gamma _{\min }})\), \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k} = {\gamma _{\max }})\), \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\min }})\), and \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) are depicted in Fig 5 . The definition for the global average fractional tap-length follows that in (44), and the global average MSE is defined as

$$\begin{aligned} MS{E^{Net}}(i) = \frac{1}{N}\sum \limits _{k = 1}^N {\left( {E\left\{ {{{\left| {{\varvec{u}_{{L_{opt}},k,i}}\left( {\varvec{w}_{{L_{opt}}}^o - \varvec{\psi } _{k,i}} \right) } \right| }^2}} \right\} + \sigma _{v,k}^2} \right) } \end{aligned}$$
(46)

This simulation shows that the proposed algorithm outperforms the fixed-parameters diffusion FT regardless of the unknown vector length.

Fig. 6
figure 6

The evolution curves of global tap-length (a) and MSE (b) under the low-noise condition, where \(L_{opt}=100\)

Full size image

High-noise condition:

In the third simulation, a high-noise setting is employed, where noise variances are scaled to realize low SNRs, as is shown in Fig.2b. The setup of this simulation is the same as those in the first simulation except for \( {\mu _k}=0.006\), \( {\alpha _k} = 0.04 \), and \( {\beta _k} = 0.997 \). The evolution curves for the proposed algorithm, and conventional FT with \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k}= {\gamma _{\min }})\), \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k} = {\gamma _{\max }})\), \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\min }})\), and \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) are depicted in Fig 7. This simulation shows the effect of large \({\gamma _k} \) on the steady-state performance. As is clear from Fig 7, the fixed parameters diffusion FT algorithm with \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) exhibits large fluctuations for steady-state tap-length under high noise condition. On the other hand, reducing the parameter \({\gamma _k} \) slows down the convergence rate. However, the proposed algorithm has a high convergence thanks to the large \({\gamma _k} \) in the initial iterations and will stay away from the steady-state fluctuations by tending the \({\gamma _k} \) to a smaller value.

Fig. 7
figure 7

The evolution curves of global tap-length (a) and MSD (b) under the high-noise condition

Full size image
Fig. 8
figure 8

The evolution curves of global tap-length (a) and MSD (b), where the optimal tap-length changes unpredictably

Full size image

Evaluating the tracking behavior of the algorithm:

In the last experiment, we test the tracking behavior of the proposed method. The unknown vector is the same as that in the first simulation, which is drawn from a zero-mean white Gaussian signal with variance of 0.003, but the tap-length changes at the 7000th time instant from 150 to 250, and at the 14000th time instant from 250 to 150, and 81 coefficients of \(w_{{L_{opt}}}^o\) are set to zero to model a sparse system, i.e., \(w_{{250}}^o(150:230) = 0\). The setup of this simulation is the same as those in the first simulation except for \( {\mu _k}=0.005\), \( {\alpha _k} = 0.05 \) and \( {\beta _k} = 0.96\). The evolution curves for the proposed algorithm, and conventional FT with \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k}= {\gamma _{\min }})\), \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k} = {\gamma _{\max }})\), \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\min }})\), and \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) are depicted in Fig. 8.

As can be seen, to converge, track the time-varying scenario and deal with the sparsity, both large parameters for \({\varDelta _k}\) and \({\gamma _k}\) must be selected. But, the diffusion FT with fixed- parameters \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) leads to large steady-state bias. The proposed algorithm similar to the diffusion FT with fixed- parameters \(({\varDelta _k} = {\varDelta _{\max }}, {\gamma _k} = {\gamma _{\max }})\) converges fast and similar to the diffusion FT with fixed- parameters \(({\varDelta _k} = {\varDelta _{\min }}, {\gamma _k}= {\gamma _{\min }})\) enjoys from low steady-state bias. This indicates the outstanding performance of the proposed method compared to the diffusion FT with fixed- parameters.

6 Conclusions

This paper proposed an automatic scheme for selecting the parameters of the distributed fractional tap-length algorithm for adaptive wireless networks with diffusion strategy. In the proposed algorithm, error width and length adaptation step-size parameters are adjusted based on the estimated gradient vector. The error width controls the trade-off between the convergence and the steady-state tap-length bias, and the tap-length adaptation step-size provides a trade-off between tap-length fluctuation in steady-state and the convergence of the tap-length. Hence, taking a fixed value for these parameters cannot provide better performance for this algorithm. On this basis, to eliminate these trade-offs, a variable strategy is proposed for determining these parameters. In the proposed approach, these parameters are adapted to obtain an accelerated convergence in the initial iterations of the algorithm, and a less tap-length fluctuation and accurate tap-length estimation in the steady-state. The proposed method is fully distributed and implemented in diffusion cooperation. This distributed adaptation will result in the superior performance of the proposed algorithm.