The free vibration analysis of hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells

Abstract

In this research, the natural frequency responses of joined hemispherical–cylindrical–conical shells made of composite three-phase materials have been dealt with in the framework of First-Order Shear Deformation Theory (FOSDT). The joined hemispherical–cylindrical–conical shells are assumed to be made of hybrid porous nanocomposite material with three phases including a matrix of epoxy, macroscale carbon fiber, and nanoscale 3D Graphene Foams (3GFs). For getting the equivalent mechanical properties of the Hybrid Matrix (HM) including polymer epoxy and 3GFs, the well-known rule of the mixture is used. In addition, the effect of porosity throughout the HM is considered using two novel and one well-known porosity distribution pattern. Moreover, the HM is reinforced with transversely isotropic macroscale carbon fibers in which the Halpin–Tsai scheme is used for multiscale homogenization procedure. The governing equations of motion associated with hybrid porous nanocomposite joined hemispherical–cylindrical–conical structures are figured out by implementing Donnell-type shell formulation and Hamilton’s approach. Moreover, an efficient and well-known semi-analytical solution method entitled Generalized Differential Quadrature Method (GDQM) is employed to solve the governing differential equations. To verify the proposed formulation some well-known benchmarks, especially those are composed of homogenous materials have been analyzed, and a good agreement has been achieved. Besides, some other new and applicable problems are considered to investigate the effects of different parameters including various boundary conditions, patterns of porosity distributions, and geometric properties of structure on the vibration behavior of joined shells.

1 Introduction

Shell structures are widely used in the engineering industry, some examples are pressure tanks, submarine and ship hulls, plane wings and hulls, pipes, outer surfaces of rockets, vehicle tires, reinforced concrete roofs, and liquid tanks. Hence, the shell structures having different geometric properties have extensively attracted the attention of many researchers in various fields of modern technology [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22].

The vibration behavior of shell structures has been studied for several decades using many shell theories and formulations. The shell structures usually confront more complicated dynamic behaviors due to the curvature and thickness. Therefore, it is believable that axial constraints can be effective in the predominantly radial mode. Therefore, much research has been implemented to study the linear and nonlinear vibrations of homogenous and composite shell structures with different geometries. In addition, there are three different schemes including analytical, semi-analytical, and numerical to solve the governing equations. Among them, semi-analytical approaches have fascinated the interest of many researchers because of their higher potential and lower time and computational costs. To solve the complex Partial Differential Equations (PDEs), different numerical approximation methods are categorized into two approaches including numerical analysis and semi-analytical solutions. The Finite-Element Method and Finite-Difference technique are numerical analyses used for solving different complicated PDEs associated with various types of structure [23,24,25,26,27,28]. Due to the requirement of many elements or intervals in these approaches, the computational time is too high. Other techniques have been designed to minimize computing time by applying lesser meshes. Liew et al. [29] studied the free vibration of conical shells utilizing the Ritz method. Irie et al. [30] obtained the natural frequencies of conical shells with variable thickness. Civalek [31] proposed a discrete singular convolution method to investigate the vibration of rotating conical shells. Differential Quadrature Method (DQM), which is a special case of the finite difference method, is one of the most applicable semi-analytical solution methods for mechanical problems and it was introduced by Bellman et al. [32] for the first time. Then, Shu and Richards [33] overcame the drawbacks of DQM by proposing the Generalized Differential Quadrature Method (GDQM), which has been using by many researchers in different problems of engineering [34,35,36,37]. Du et al. [38] employed this method for structural analysis first and foremost. Shu [39] calculated the responses of conical shells employing GDQM. Bagheri et al. [40] used this efficient method for solving different PDEs of the free vibration problem of the conical shell. Moreover, the behavior of simple cylindrical shells with different boundary conditions was investigated numerically in various studies [41,42,43]. Furthermore, the buckling load and natural frequencies of conical shells with different boundary conditions were also investigated numerically in many other studies [44,45,46,47,48,49,50]. Lam et al. [51] analyzed the vibration of the truncated conical panels with different boundary conditions using GDQM. Hua and Lam [52, 53] used GDQM to implement the rotating effect on frequencies of conical shells. Viola and Artioli [54] used GDQM for the modal analysis of FSDT curved shells. Artioli and his coworkers [55, 56] examined the mechanical behaviors of the isotropic homogenous conical shells based on the Reissner–Mindlin hypothesis and applying GDQM.

Joined shells are alternative types of shell structures in which two or more shells with different geometries are coupled with each other. These types of structures have a wide range of applications in many fields of engineering, especially aerospace, mechanical, ocean, nuclear, and civil engineering. Irie et al. [57] presented the pioneer study on the free vibration analysis of joined conical–cylindrical shells. Kamat et al. [58] employed the principles of Bolotin’s method for analyzing the laminated composite joined conical–cylindrical structures. Lee et al. [59] used Flugge shell theory and Rayleigh’s energy method to obtain the vibration parameters of joined cylindrical–spherical shell structures. Wu et al. [60] determined the vibration characteristics of spherical–cylindrical–spherical structures applying Fourier series and Chebyshev polynomials displacement functions as admissible displacement fields in the framework of Reissner–Naghdi’s thin shell theory. Bagheri et al. [61] utilized the GDQM for examining the natural frequencies of homogeneous joined conical–conical shells. Bagheri et al. [62] obtained the natural frequency of the coupled conical–cylindrical–conical shells implementing GDQM. Li et al. [63] studied the vibration of the coupled spherical–cylindrical structure applying the Ritz technique. Pang et al. [64] solved the governing equations of free vibration of spherical–cylindrical–spherical shells having arbitrary boundary conditions simulated with the penalty method using the Rayleigh–Ritz method. Rezaiee-Pajand et al. [65] reported the vibration parameters of functionally graded carbon nanotubes coupled with conical–conical shells employing the GDQM. Furthermore, numerical solutions have also been presented for these types of structures [66,67,68].

During recent decades, composite materials have been widely used in many structures of engineering because of their superior properties such as high strength and low weight. These advantages attracted the attention of several researchers to study the mechanical behaviors of composite structures having different geometries in micro/macro scales [69,70,71,72,73]. Composites can be manufactured in several ways, one of these ways is the construction of isotropic-nonhomogeneous composite having three parts two nano- and a macro-scale material. These phases include a matrix is made of polymer, macro-, and nano-measure fibers. The mixture of polymer matrix and nanoscale fiber augmentation is identified as Hybrid Matrix (HM). Rafiee et al.[74] performed geometrically nonlinear analysis of plates made of hybrid nanocomposite piezoelectric materials in the framework of the first shear deformation theory. Ebrahimi and Habibi [75] investigated the nonlinear thermomechanical behavior of hybrid nanocomposite plates using the multiscale method. Gholami and Ansari [76] studied the nonlinear bending behavior of multiscale hybrid nanocomposite plates adopting von Kármán principles. Dabbagh et al. [77] obtained the natural frequencies of multiscale hybrid nanocomposite beams using the Finite-Element Method (FEM). Karimiasl et al. [78] performed the dynamic hygro-thermomechanical analysis of doubly curved structures made of hybrid nanocomposite materials. The production of nanocomposites involves several complex steps, and some technical problems may be met in the manufacturing process of nanocomposites that cause porosity. The presence of porosities inside nanocomposites results in the decrease of the strength of the material. Therefore, the examination of the effect of porosity on the structures is a major issue [79,80,81,82,83,84,85].

As a result of the search of open literature, it is seen that the vibration of joined hemispherical–cylindrical–conical shells composed of hybrid porous nanocomposite materials has not been studied yet. Especially, the effects of the use of distinct types of composite materials and various multiscale homogenization approaches have not been investigated. Besides, three-phase hybrid nanocomposite materials in many structures, especially shell-like structures still need to be developed numerically, while the stated issue can be solved using an efficient semi-analytical solution method of GDQM. For this context, the free vibration analysis of hybrid porous nanocomposite joined hemispherical–cylindrical–conical composite shells is examined using a semi-analytical solution approach in this paper. First, the considered hybrid porous nanocomposite material, i.e., a three-phase composite material is made of two main parts including Hybrid Matrix (HM) and transversely isotropic macroscale AS4 carbon fiber, is defined, and the related formulations are obtained. Namely, parts of the composite shell are homogenized using the well-known Halpin–Tsai multiscale approach, as well as the rule of mixture method is employed to obtain the equivalent mechanical properties of HM, which is manufactured by 3502-epoxy polymer and nanoscale 3D Graphene Foams (3GFs). After figuring out the equivalent mechanical and physical attributes to the three-phase material, the governing equations of motion of joined composite shell are derived applying Donnell’s shell theory and Hamilton’s principles. Then, the governing differential equations of motion are numerically solved using the well-known semi-analytical method of GDQM. The solution procedure is completely presented. A computer program is developed using this procedure to unravel the diverse complex and enforceable moot points. Finally, several examinations are considered to confirm the given formulation and procedure. Further, some other new, complex, and applicable joined shell problems with different geometric, material, and boundary conditions are examined to affirm the authenticity, accuracy, and sufficiency of the recommended formulation as well.

2 The properties of the Hybrid Matrix

HM are manufactured in two parts including polymer and nanofiller synthesizers. In this study, the polymeric 3502-epoxy resin is utilized for the polymer part of HM material [86]. Nanofiller materials are classified into several types, and 3D Graphene Foam (3GF) is one of the nanofillers that can be used in hybrid materials. In addition, the 3GFs enhance the performance and mechanical properties of HM materials.

The equivalent mechanical properties of HM are figured out by utilizing the well-known rule of the mixture as follows:

$$ E_{{HM}}^{0} = E_{m} (1 - V_{{Gr}} ) + E_{{Gr}} V_{{Gr}} $$

(1)

$$ \rho _{{HM}}^{0} = \rho _{m} (1 - V_{{Gr}} ) + \rho _{{Gr}} V_{{Gr}} $$

(2)

$$ \nu _{{HM}}^{0} = \nu _{m} (1 - V_{{Gr}} ) + \nu _{{Gr}} V_{{Gr}} , $$

(3)

where $E_{m}$, $E_{{Gr}}$, and $E_{{HM}}^{0}$ represent Young’s modulus of the matrix, 3GFs, and HM, respectively. Besides, the density of HM, matrix, and 3GFs are shown with $\rho _{{HM}}^{0}$,$\rho _{m}$ and $\rho _{{Gr}}$, respectively. On the other hand, $\nu _{{HM}}^{0}$, $\nu _{m}$ and $\nu _{{Gr}}$ represent Poisson’s ratio of HM, matrix, and 3GFs, respectively.

The volume fraction of 3GFs is calculated as follows:

$$ V_{{Gr}} = \frac{{w_{{Gr}} }}{{w_{{Gr}} + ({{\rho _{{Gr}} } \mathord{\left/ {\vphantom {{\rho _{{Gr}} } {\rho _{m} )}}} \right. \kern-\nulldelimiterspace} {\rho _{m} )}} - w_{{Gr}} ({{\rho _{{Gr}} } \mathord{\left/ {\vphantom {{\rho _{{Gr}} } {\rho _{m} )}}} \right. \kern-\nulldelimiterspace} {\rho _{m} )}}}}, $$

(4)

where $w_{{Gr}}$ defines the weight fraction of 3GFs.

Note that the total volume fraction of 3GFs and matrix is equal to one based on the rule of mixture ($V_{{Gr}} + V_{m} = 1$).

The shear module of HM is found as follows:

$$ G_{{HM}}^{0} = \frac{{E_{{HM}}^{0} }}{{2(1 + \nu _{{HM}}^{0} )}}. $$

(5)

In this study, three different patterns are used to demonstrate the distribution of porosity in 3GFs and polymers constructing HM material. These porosity skeleton forms are defined as pattern-I, pattern-II, and pattern-III [87,88,89].

It is worthy to mention that the mechanical properties of HM are influenced by the porosity distribution along with the thickness of the structure.

To determine the mechanical properties of HM regarding porosity pattern-I, the following expressions can be given as follows:

$$ E_{{HM}}^{{\rm I}} (\eta ) = E_{{HM}}^{0} \left[ {1 - \xi _{{\rm I}} \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right] $$

(6)

$$ G_{{HM}}^{{\rm I}} (\eta ) = G_{{HM}}^{0} \left[ {1 - \xi _{{\rm I}} \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right] $$

(7)

$$ \rho _{{HM}}^{{\rm I}} (\eta ) = \rho _{{HM}}^{0} \left[ {1 - \mu _{{\rm I}} \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right], $$

(8)

where Young’s and shear modulus, and density of porous HM using pattern-I are defined as $E_{{HM}}^{{\rm I}}$, $G_{{HM}}^{{\rm I}}$, and $\rho _{{HM}}^{{\rm I}}$, respectively. Moreover, $\xi _{{\rm I}}$ and $\mu _{{\rm I}}$ are Young’s modulus and density factors of porosity about pattern-I.

Figure 1 depicts the variation of Young’s modulus and density of porous HM according to pattern-I along the thickness direction.

Fig. 1

The variation of (a) Young’s modulus and (b) density of porous HM according to pattern-I along the thickness direction

The mechanical and physical properties of HM according to the pattern-II distribution of porosity along the thickness can be given as follows:

$$ E_{{HM}}^{{{\rm I}{\rm I}}} (\eta ) = E_{{HM}}^{0} \left\{ {1 - \xi _{{{\rm I}{\rm I}}} \left[ {1 - \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right]} \right\} $$

(9)

$$ G_{{HM}}^{{{\rm I}{\rm I}}} (\eta ) = G_{{HM}}^{0} \left\{ {1 - \xi _{{{\rm I}{\rm I}}} \left[ {1 - \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right]} \right\} $$

(10)

$$ \rho _{{HM}}^{{{\rm I}{\rm I}}} (\eta ) = \rho _{{HM}}^{0} \left\{ {1 - \mu _{{{\rm I}{\rm I}}} \left[ {1 - \cos \left( {\frac{{\pi \eta }}{h}} \right)} \right]} \right\}, $$

(11)

where $E_{{HM}}^{{{\rm I}{\rm I}}}$, $G_{{HM}}^{{{\rm I}{\rm I}}}$ and $\rho _{{HM}}^{{{\rm I}{\rm I}}}$, respectively, represent the Young’s and shear modulus, and density of porous HM about the pattern-II. The factors of Young’s modulus and density for the pattern-II are defined with $\xi _{{{\rm I}{\rm I}}}$ and $\mu _{{{\rm I}{\rm I}}}$, respectively.

The variation of Young’s modulus and density of HM including porosity according to the pattern-II along the thickness is illustrated in Fig. 2.

Fig. 2

The variation of (a) Young’s modulus and (b) density of porous HM according to pattern-II along the thickness direction

The mechanical and physical properties of porous HM according to the pattern-III distribution of porosity can be given as follows:

$$ E_{{HM}}^{{{\rm I}{\rm I}{\rm I}}} = E_{{HM}}^{0} \xi _{{{\rm I}{\rm I}{\rm I}}} $$

(12)

$$ G_{{HM}}^{{{\rm I}{\rm I}{\rm I}}} = G_{{HM}}^{0} \xi _{{{\rm I}{\rm I}{\rm I}}} $$

(13)

$$ \rho _{{HM}}^{{{\rm I}{\rm I}{\rm I}}} = \rho _{{HM}}^{0} \mu _{{{\rm I}{\rm I}{\rm I}}} . $$

(14)

The variation of Young’s modulus and density of HM including porosity according to the pattern-III along the thickness is illustrated in Fig. 3.

Fig. 3

The variation of (a) Young’s modulus and (b) density of porous HM according to pattern-III along the thickness direction

The relation between Young’s modulus of HM and porous HM with the density of HM and porous HM for each pattern of porosity distribution can be found with the following expression [90,91,92,93]:

$$ \frac{{E_{{HM}}^{i} (z)}}{{E_{{HM}}^{0} }} = \left( {\frac{{\rho _{{HM}}^{i} (z)}}{{\rho _{{HM}}^{0} }}} \right)^{{2.73}} \,\,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(15)

On the other hand, the relation between the elastic modulus and density factors in each pattern of porosity distribution can be found as follows:

$$ \left[ {\begin{array}{*{20}l} {1 - \mu _{{\rm I}} \cos \left( {\frac{{\pi z}}{h}} \right) = \sqrt[{2.73}]{{1 - \xi _{{\rm I}} \cos \left( {\frac{{\pi z}}{h}} \right)}}} & {{\text{Pattern}} - {\rm I}} \\ {1 - \mu _{{{\rm I}{\rm I}}} \left\{ {1 - \cos \left( {\frac{{\pi z}}{h}} \right)} \right\} = \sqrt[{2.73}]{{1 - \xi _{{{\rm I}{\rm I}}} \left\{ {1 - \cos \left( {\frac{{\pi z}}{h}} \right)} \right\}}}} & {{\text{Pattern}} - {\rm I}{\rm I}} \\ {\mu _{{{\rm I}{\rm I}{\rm I}}} = \sqrt[{2.73}]{{\xi _{{{\rm I}{\rm I}{\rm I}}} }}} & {\,\,{\text{Pattern}} - {\rm I}{\rm I}{\rm I}} \\ \end{array} } \right.. $$

(16)

In addition, the relations between Young’s modulus factors of each pattern of porosity distribution with the other can be determined as follows:

$$ \left[ {\begin{array}{*{20}l} {\int\limits_{0}^{{\frac{h}{2}}} {\sqrt[{2.73}]{{1 - \xi _{{{\rm I}{\rm I}}} \left\{ {1 - \cos \left( {\frac{{\pi z}}{h}} \right)} \right\}}}\,dz = \int\limits_{0}^{{\frac{h}{2}}} {\sqrt[{2.73}]{{1 - \xi _{{\rm I}} \cos \left( {\frac{{\pi z}}{h}} \right)}}\,dz} } } \\ {\int\limits_{0}^{{\frac{h}{2}}} {\sqrt[{2.73}]{{\xi _{{{\rm I}{\rm I}{\rm I}}} }}\,dz = \int\limits_{0}^{{\frac{h}{2}}} {\sqrt[{2.73}]{{1 - \xi _{{\rm I}} \cos \left( {\frac{{\pi z}}{h}} \right)}}\,dz} } } \\ \end{array} } \right.. $$

(17)

Table 1 reports the values of Young’s modulus factors of all three patterns versus Eq. (17). It is observed that the values of $\xi _{{II}}$ enhanced with the increasing the values of $\xi _{I}$, and the values of $\xi _{{II}}$ tends to ($\sim 1$). The domain of $\xi _{I}$ is assigned to be $[0,0.65]$.

Table 1 The coefficient of porosity patterns

The mechanical properties of 3D Graphene Foams and 3506-epoxy resin materials are reported in Table 2.

Table 2 The mechanical properties of nanofiller and matrix materials

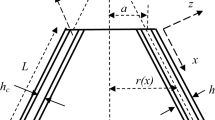
3 Homogenization of HM with AS4 carbon fibers

The special type of materials is formed in three phases by mixing polymeric matrix, macro-filler fiber, and micro-filler 3GFs. Therefore, HM material can be reinforced with fibers. In addition, HM material is reinforced with the use of macroscale particles which can improve the mechanical properties of HM. Multiscale analysis can be used to find the effective mechanical properties of this type of material. The mechanical properties of the fibers can be categorized into three groups of isotropic, transversely isotropic, and anisotropic materials. Transversely isotropic AS4 carbon fibers have continuous, high strength, high strain, and PAN-based properties. Therefore, it can be employed for improving the behavior of HM materials [86]. Based on this, Young’s modulus of transversely isotropic fiber can be assumed to be $E_{{{\text{fiber}}}}^{{\text{1}}} {\text{,}}\,E_{{{\text{fiber}}}}^{{\text{2}}} = E_{{{\text{fiber}}}}^{{\text{3}}}$. In addition, the shear modulus of this group is represented with $G_{{{\text{fiber}}}}^{{{\text{23}}}} ,G_{{{\text{fiber}}}}^{{{\text{12}}}} = G_{{{\text{fiber}}}}^{{13}}$. Furthermore, $\nu _{{fiber}}^{{12}} = \nu _{{fiber}}^{{13}} ,\,\nu _{{fiber}}^{{23}}$ represent Poisson’s ratio of transversely isotropic fibers.

There are many multiscale techniques, Halpin–Tsai is one of these methods which is employed in this research to evaluate the equivalent three-phase material mechanical properties. On the other hand, the Halpin–Tsai homogenization approach determines the mechanical properties of three-phase materials by utilizing Hill’s Young’s modulus parameters [94,95,96,97,98].

Appropriately, Hill’s parameters of HM material are calculated as follows:

$$ k_{{HM}} = \frac{{E_{{HM}}^{i} }}{{2(1 - \nu _{{HM}}^{0} - 2(\nu _{{HM}}^{0} )^{2} )}}\,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(18)

$$ l_{{HM}} = \frac{{\nu _{{HM}}^{0} E_{{HM}}^{i} }}{{(1 - \nu _{{HM}}^{0} - 2(\nu _{{HM}}^{0} )^{2} )}} = 2\nu _{{HM}}^{0} k_{{HM}} \,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(19)

$$ m_{{HM}} = G_{{HM}}^{i} = \frac{{E_{{HM}}^{i} }}{{2(1 + \nu _{{HM}}^{0} )}} = (1 - 2\nu _{{HM}}^{0} )k_{{HM}} \,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(20)

$$ n_{{HM}} = \frac{{(1 - \nu _{{HM}}^{0} )E_{{HM}}^{i} }}{{(1 - \nu _{{HM}}^{0} - 2(\nu _{{HM}}^{0} )^{2} )}} = 2(1 - \nu _{{HM}}^{0} )\;k_{{HM}} \,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(21)

$$ p_{{HM}} = G_{{HM}}^{i} = \left(1 - 2\nu _{{HM}}^{0} \right)k_{{HM}} = m_{{HM}} \,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I}. $$

(22)

On the other hand, Hill’s factors of transversely isotropic AS4 carbon fiber are given as follows:

$$ k_{{{\text{fiber}}}} = \frac{{E_{{{\text{fiber}}}}^{2} }}{{2\left(1 - \nu _{{{\text{fiber}}}}^{{23}} - 2\nu _{{{\text{fiber}}}}^{{21}} \nu _{{{\text{fiber}}}}^{{12}}\right )}} $$

(23)

$$ l_{{{\text{fiber}}}} = \frac{{\nu _{{{\text{fiber}}}}^{{12}} E_{{{\text{fiber}}}}^{2} }}{{\left(1 - \nu _{{{\text{fiber}}}}^{{23}} - 2\nu _{{{\text{fiber}}}}^{{21}} \nu _{{{\text{fiber}}}}^{{12}}\right )}} = 2\nu _{{{\text{fiber}}}}^{{12}} k_{{{\text{fiber}}}} $$

(24)

$$ m_{{{\text{fiber}}}} = \frac{{E_{{{\text{fiber}}}}^{2} }}{{2\left(1 + \nu _{{{\text{fiber}}}}^{{23}}\right )}} = \frac{{1 - \nu _{{{\text{fiber}}}}^{{23}} - 2\nu _{{{\text{fiber}}}}^{{21}} \nu _{{{\text{fiber}}}}^{{12}} }}{{1 + \nu _{{{\text{fiber}}}}^{{23}} }}k_{{{\text{fiber}}}} $$

(25)

$$ n_{{{\text{fiber}}}} = \frac{{E_{{{\text{fiber}}}}^{1}\left (1 - \nu _{{{\text{fiber}}}}^{{23}} \right)}}{{1 - \nu _{{{\text{fiber}}}}^{{23}} - 2\nu _{{{\text{fiber}}}}^{{21}} \nu _{{{\text{fiber}}}}^{{12}} }} = 2\left(1 - \nu _{{{\text{fiber}}}}^{{23}}\right )\frac{{E_{{{\text{fiber}}}}^{1} }}{{E_{{{\text{fiber}}}}^{2} }}k_{{{\text{fiber}}}} $$

(26)

$$ p_{{{\text{fiber}}}} = G_{{{\text{fiber}}}}^{{{\text{12}}}} . $$

(27)

In addition, the effective Hill’s parameters in terms of HM and AS4 carbon fibers are obtained as follows:

$$ k_{{{\text{eff}}}} = \frac{{k_{{HM}} (k_{{{\text{fiber}}}} + m_{{HM}} )(1 - V_{{{\text{fiber}}}} ) + k_{{{\text{fiber}}}} \left(k_{{HM}} + m_{{HM}}\right )V_{{{\text{fiber}}}} }}{{\left(k_{{{\text{fiber}}}} + m_{{HM}}\right )\left(1 - V_{{{\text{fiber}}}} \right) + \left(k_{{HM}} + m_{{HM}} \right)V_{{{\text{fiber}}}} }} $$

(28)

$$ l_{{{\text{ef}}f}} = V_{{{\text{fiber}}}} l_{{{\text{fiber}}}} + (1 - V_{{{\text{fiber}}}} ) + \frac{{l_{{{\text{fiber}}}} - l_{{HM}} }}{{k_{{{\text{fiber}}}} - k_{{HM}} }}(k_{{{\text{eff}}}} - V_{{{\text{fiber}}}} k_{{{\text{fiber}}}} - (1 - V_{{{\text{fiber}}}} )k_{{HM}} ) $$

(29)

$$ m_{{eff}} = m_{{HM}} \frac{{2V_{{fiber}} m_{{fiber}} (k_{{HM}} + m_{{HM}} ) + 2(1 - V_{{fiber}} )m_{{fiber}} m_{{HM}} + (1 - V_{{fiber}} )k_{{HM}} (m_{{fiber}} + m_{{HM}} )}}{{2V_{{fiber}} m_{{HM}} (k_{{HM}} + m_{{HM}} ) + 2(1 - V_{{fiber}} )m_{{fiber}} m_{{HM}} + (1 - V_{{fiber}} )k_{{HM}} (m_{{fiber}} + m_{{HM}} )}} $$

(30)

$$ n_{{{\text{eff}}}} = V_{{{\text{fiber}}}} n_{{{\text{fiber}}}} + (1 - V_{{{\text{fiber}}}} )n_{{HM}} + \left( {\frac{{l_{{{\text{fiber}}}} - l_{{HM}} }}{{k_{{{\text{fiber}}}} - k_{{HM}} }}} \right)^{2} (k_{{{\text{eff}}}} - V_{{{\text{fiber}}}} k_{{{\text{fiber}}}} - (1 - V_{{{\text{fiber}}}} )k_{{HM}} ) $$

(31)

$$\begin{array}{l} {p_{{\rm{eff}}}} = \frac{{({p_{{\rm{fiber}}}} + {p_{HM}}){p_{HM}}(1 - {V_{{\rm{fiber}}}}) + 2{p_{{\rm{fiber}}}}{p_{HM}}{V_{{\rm{fiber}}}}}}{{({p_{{\rm{fiber}}}} + {p_{HM}})(1 - {V_{{\rm{fiber}}}}) + 2{p_{HM}}{V_{{\rm{fiber}}}}}}\\ {p_{fiber}} = G_{fiber}^{12}. \end{array}$$

(32)

The effective mechanical properties of three-phase material are determined employing the Halpin–Tsai approach with the following expressions:

$$ E_{{\text{1}}}^{{{\text{eff}}}} = E_{{{\text{fiber}}}}^{{\text{1}}} V_{{{\text{fiber}}}} + E_{{Hm}}^{i} (1 - V_{{{\text{fiber}}}} )\,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I} $$

(33)

$$ E_{{\text{2}}}^{{{\text{eff}}}} = \frac{{4(n_{{{\text{eff}}}} k_{{{\text{eff}}}} - l_{{{\text{eff}}}} ^{2} )m_{{{\text{eff}}}} }}{{(k_{{{\text{eff}}}} + m_{{{\text{eff}}}} )n_{{{\text{eff}}}} - l_{{{\text{eff}}}} ^{2} }} $$

(34)

$$ \nu _{{{\text{12}}}}^{{{\text{eff}}}} = \nu _{{{\text{fiber}}}}^{{12}} V_{{{\text{fiber}}}} + \nu _{{Hm}}^{0} (1 - V_{{{\text{fiber}}}} ) $$

(35)

$$ G_{{{\text{eff}}}}^{{{\text{12}}}} = G_{{{\text{eff}}}}^{{{\text{13}}}} = p_{{{\text{eff}}}} $$

(36)

$$ G_{{eff}}^{{23}} = m_{{eff}} $$

(37)

$$ \rho _{{{\text{eff}}}} = \rho _{{{\text{fiber}}}} V_{{{\text{fiber}}}} + \rho _{{Hm}}^{i} (1 - V_{{{\text{fiber}}}} )\,\,\,\,\,\,\,{\text{for}}\,\,\,i = {\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I}. $$

(38)

The mechanical properties of the transversely isotropic AS4 carbon fibers material are reported in Table 3.

Table 3 The mechanical properties of carbon fiber material

The variation of engineering constants of 3506-epoxy resin-AS4 carbon fibers-3D Graphene Foams three-phase material along the thickness direction of the joined shell is illustrated in Fig. 4 for two different patterns of porosity.

Fig. 4

The variation of equivalent mechanical properties along the thickness direction of joined shell, (a) longitudinal Young’s modulus, (b) transverse Young’s modulus, (c) in-plane shear modulus, (d) out-of-plane shear modulus

4 The fundamental relations and expressions

One of the most applicable shells is joined shell structures due to their superior performance and high proficiency, and the joined hemispherical–cylindrical–conical structure is one of these structures. The joined shells have wide applications in aerospace, mechanics, and civil engineering. On the other hand, employing new forms of materials such as three-phase hybrid matrix nanocomposite materials can improve the behavior of these serviceable structures as well.

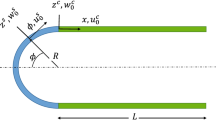
Figure 5 depicts the paradigm of nanocomposite three-phase hybrid porous joined hemispherical–cylindrical–conical shell.

Fig. 5

The scheme of HM-carbon fiber nanocomposite joined hemispherical–cylindrical–conical shell structure

In this work, the FOSDT and Donnell’s shell theory are employed to solve the joined hemispherical–cylindrical–conical shell formulation. Therefore, the displacement field of this structure is found as follows:

$$ \begin{array}{*{20}c} \begin{gathered} U_{1}^{i} (\zeta _{i} ,\theta ,\eta ,t) = u_{1}^{i} (\zeta _{i} ,\theta ,t) + \eta \Psi _{\zeta }^{i} (\zeta _{i} ,\theta ,t) \hfill \\ U_{2}^{i} (\zeta _{i} ,\theta ,\eta ,t) = u_{2}^{i} (\zeta _{i} ,\theta ,t) + \eta \Psi _{\theta }^{i} (\zeta _{i} ,\theta ,t) \hfill \\ U_{3}^{i} (\zeta _{i} ,\theta ,\eta ,t) = u_{3}^{i} (\zeta _{i} ,\theta ,t). \hfill \\ \end{gathered} & {{\text{for}}\,\,\,\,i = co,cy,hs} \\ \end{array} $$

(39)

where $U_{1}^{i} ,U_{2}^{i} ,U_{3}^{i}$ define the hemispherical–cylindrical–conical shell displacements in various directions, respectively. In addition, the mid-surface displacements along the directions of $\zeta _{i} ,\theta ,\eta$ are represented by $u_{1}^{i} ,u_{2}^{i} ,u_{3}^{i}$, respectively. $\Psi _{\zeta }^{i} ,\Psi _{\theta }^{i}$ are the mid-surface transversely normal rotations about $\theta ,\zeta _{i}$ directions, respectively. The axes of the longitudinal, circumferential, and normal directions of the hemispherical–cylindrical–conical shells defined at the mid-surface are indicated with $\zeta _{i} ,\theta ,\eta$, respectively. The longitudinal directions for cylindrical and conical parts of this structure are defined $0 \le \zeta _{{cy}} \le L_{{cy}} ,0 \le \zeta _{{co}} \le L_{{co}}$ while $\vartheta \le \zeta _{{hs}} \le \frac{\pi }{2}$ is used for the domain of longitudinal direction of hemispherical one. Accordingly, the geometrical properties of joined hemispherical–cylindrical–conical shell structure are shown in Fig. 6.

Fig. 6

The geometrical characteristics of joined hemispherical–cylindrical–conical shells

The strain fields of hemispherical, cylindrical, and conical shells in terms of mid-surface strains and curvatures are found utilizing Donnell’s approach and FSDT as follows:

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\varepsilon _{\zeta }^{i} } \\ {\varepsilon _{\theta }^{i} } \\ {\gamma _{{\zeta \theta }}^{i} } \\ {\gamma _{{\zeta \eta }}^{i} } \\ {\gamma _{{\theta \eta }}^{i} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{\zeta }^{i} } \\ {\bar{\varepsilon }_{\theta }^{i} } \\ {\bar{\gamma }_{{\zeta \theta }}^{i} } \\ {\bar{\gamma }_{{\zeta \eta }}^{i} } \\ {\bar{\gamma }_{{\theta \eta }}^{i} } \\ \end{array} } \right\} + \eta \left\{ {\begin{array}{*{20}c} {\chi _{\zeta }^{i} } \\ {\chi _{\theta }^{i} } \\ {\chi _{{\zeta \theta }}^{i} } \\ {\chi _{{\zeta \eta }}^{i} } \\ {\chi _{{\theta \eta }}^{i} } \\ \end{array} } \right\}} & {{\text{for}}\,\,\,\,{\text{i = co,cy,hs}}} \\ \end{array} , $$

(40)

where $\bar{\varepsilon }_{\zeta }^{i} ,\bar{\varepsilon }_{\theta }^{i}$ indicate the normal strains of mid-surface along with $\zeta _{i} ,\theta$ directions, respectively, while an in-plane shear strain is defined by $\bar{\gamma }_{{\zeta \theta }}^{i}$.$\bar{\gamma }_{{\zeta \eta }}^{i} ,\bar{\gamma }_{{\theta \eta }}^{i}$ represent the out-of-plane shear strains. The curvatures of each part of the hemispherical–cylindrical–conical are depicted with $\chi _{\zeta }^{i} ,\chi _{\theta }^{i} ,\chi _{{\zeta \theta }}^{i} ,\chi _{{\zeta \eta }}^{i} ,\chi _{{\theta \eta }}^{i}$, respectively. The relation between strains and displacements of mid-surface of the cylindrical part of joined hemispherical–cylindrical–conical can be found employing Donnell’s shell theory and FOSDT as follows:

$$ \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{\zeta }^{{cy}} } \\ {\bar{\varepsilon }_{\theta }^{{cy}} } \\ {\bar{\gamma }_{{\zeta \theta }}^{{cy}} } \\ {\bar{\gamma }_{{\zeta \eta }}^{{cy}} } \\ {\bar{\gamma }_{{\theta \eta }}^{{cy}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{1}^{{cy}} }}{{\partial \zeta _{{cy}} }}} \\ {\frac{1}{R}\frac{{\partial u_{2}^{{cy}} }}{{\partial \theta }} + \frac{{u_{3}^{{cy}} }}{R}} \\ {\frac{{\partial u_{2}^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{1}{R}\frac{{\partial u_{1}^{{cy}} }}{{\partial \theta }}} \\ {\frac{{\partial u_{3}^{{cy}} }}{{\partial \zeta _{{cy}} }} + \Psi _{\zeta }^{{cy}} } \\ {\frac{1}{R}\frac{{\partial u_{3}^{{cy}} }}{{\partial \theta }} - \frac{{u_{2}^{{cy}} }}{R} + \Psi _{\theta }^{{cy}} } \\ \end{array} } \right\}. $$

(41)

On the other hand, the above relation can be re-written in the form of the conical part as follows:

$$ \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{\zeta }^{{co}} } \\ {\bar{\varepsilon }_{\theta }^{{co}} } \\ {\bar{\gamma }_{{\zeta \theta }}^{{co}} } \\ {\bar{\gamma }_{{\zeta \eta }}^{{co}} } \\ {\bar{\gamma }_{{\theta \eta }}^{{co}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{1}^{{co}} }}{{\partial \zeta _{{co}} }}} \\ {\frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial u_{2}^{{co}} }}{{\partial \theta }} + \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}u_{1}^{{co}} + \frac{{\cos (\Theta )}}{{R(\zeta _{{co}} )}}u_{3}^{{co}} } \\ {\frac{{\partial u_{2}^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial u_{1}^{{co}} }}{{\partial \theta }} - \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}u_{2}^{{co}} } \\ {\frac{{\partial u_{3}^{{co}} }}{{\partial \zeta _{{co}} }} + \Psi _{\zeta }^{{co}} } \\ {\frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial u_{3}^{{co}} }}{{\partial \theta }} - \frac{{\cos (\Theta )}}{{R(\zeta _{{co}} )}}u_{2}^{{co}} + \Psi _{\theta }^{{co}} } \\ \end{array} } \right\}. $$

(42)

Conversely, the hemispherical part mid-surface strain and displacement relations can be figured out as follows:

$$ \left\{ {\begin{array}{*{20}c} {\bar{\varepsilon }_{\zeta }^{{hs}} } \\ {\bar{\varepsilon }_{\theta }^{{hs}} } \\ {\bar{\gamma }_{{\zeta \theta }}^{{hs}} } \\ {\bar{\gamma }_{{\zeta \eta }}^{{hs}} } \\ {\bar{\gamma }_{{\theta \eta }}^{{hs}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{1}{R}\frac{{\partial u_{1}^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{{u_{3}^{{hs}} }}{R}} \\ {\frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial u_{2}^{{hs}} }}{{\partial \theta }} + \frac{{\cot (\zeta _{{hs}} )}}{R}u_{1}^{{hs}} + \frac{{u_{3}^{{hs}} }}{R}} \\ {\frac{1}{R}\frac{{\partial u_{2}^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial u_{1}^{{hs}} }}{{\partial \theta }} - \frac{{\cot (\zeta _{{hs}} )}}{R}u_{2}^{{hs}} } \\ {\frac{1}{R}\frac{{\partial u_{3}^{{hs}} }}{{\partial \zeta _{{hs}} }} + \Psi _{\zeta }^{{hs}} - \frac{{u_{1}^{{hs}} }}{R}} \\ {\frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial u_{3}^{{hs}} }}{{\partial \theta }} - \frac{{u_{2}^{{hs}} }}{R} + \Psi _{\theta }^{{hs}} } \\ \end{array} } \right\}. $$

(43)

The relation between the curvatures and mid-surface displacements of cylindrical part can be expressed using Donnell’s shell theory and FOSDT as follows:

$$ \left\{ {\begin{array}{*{20}c} {\chi _{\zeta }^{{cy}} } \\ {\chi _{\theta }^{{cy}} } \\ {\chi _{{\zeta \theta }}^{{cy}} } \\ {\chi _{{\zeta \eta }}^{{cy}} } \\ {\chi _{{\theta \eta }}^{{cy}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \Psi _{\zeta }^{{cy}} }}{{\partial \zeta _{{cy}} }}} \\ {\frac{1}{R}\frac{{\partial \Psi _{\theta }^{{cy}} }}{{\partial \theta }}} \\ {\frac{{\partial \Psi _{\theta }^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{1}{R}\frac{{\partial \Psi _{\zeta }^{{cy}} }}{{\partial \theta }}} \\ 0 \\ 0 \\ \end{array} } \right\}. $$

(44)

Based on these assumptions, the above relation can be re-written for the conical part as follows:

$$ \left\{ {\begin{array}{*{20}c} {\chi _{\zeta }^{{co}} } \\ {\chi _{\theta }^{{co}} } \\ {\chi _{{\zeta \theta }}^{{co}} } \\ {\chi _{{\zeta \eta }}^{{co}} } \\ {\chi _{{\theta \eta }}^{{co}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \Psi _{\zeta }^{{co}} }}{{\partial \zeta _{{co}} }}} \\ {\frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial \Psi _{\theta }^{{co}} }}{{\partial \theta }} + \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}\Psi _{\zeta }^{{co}} } \\ {\frac{{\partial \Psi _{\theta }^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial \Psi _{\zeta }^{{co}} }}{{\partial \theta }} - \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}\Psi _{\theta }^{{co}} } \\ 0 \\ 0 \\ \end{array} } \right\}. $$

(45)

The curvatures and mid-surface displacements relation related to the hemispherical part is formulated as the following expressions:

$$ \left\{ {\begin{array}{*{20}c} {\chi _{\zeta }^{{hs}} } \\ {\chi _{\theta }^{{hs}} } \\ {\chi _{{\zeta \theta }}^{{hs}} } \\ {\chi _{{\zeta \eta }}^{{hs}} } \\ {\chi _{{\theta \eta }}^{{hs}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{1}{R}\frac{{\partial \Psi _{\zeta }^{{hs}} }}{{\partial \zeta _{{hs}} }}} \\ {\frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial \Psi _{\theta }^{{hs}} }}{{\partial \theta }} + \frac{{\cot (\zeta _{{hs}} )}}{R}\Psi _{\zeta }^{{hs}} } \\ {\frac{1}{R}\frac{{\partial \Psi _{\theta }^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial \Psi _{\zeta }^{{hs}} }}{{\partial \theta }} - \frac{{\cot (\zeta _{{hs}} )}}{R}\Psi _{\theta }^{{hs}} } \\ 0 \\ 0 \\ \end{array} } \right\}. $$

(46)

The stress–strain relation of the joined hemispherical–cylindrical–conical shell can be obtained employing Hook’s law as follows:

$$ \left[ {\begin{array}{*{20}c} {\sigma _{\zeta }^{i} } \\ {\sigma _{\theta }^{i} } \\ {\tau _{{\zeta \theta }}^{i} } \\ {\tau _{{\zeta \eta }}^{i} } \\ {\tau _{{\theta \eta }}^{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {C_{{11}} (\eta )} & {C_{{12}} (\eta )} & 0 & 0 & 0 \\ {C_{{12}} (\eta )} & {C_{{22}} (\eta )} & 0 & 0 & 0 \\ 0 & 0 & {C_{{44}} (\eta )} & 0 & 0 \\ 0 & 0 & 0 & {C_{{55}} (\eta )} & 0 \\ 0 & 0 & 0 & 0 & {C_{{66}} (\eta )} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\varepsilon _{\zeta }^{i} } \\ {\varepsilon _{\theta }^{i} } \\ {\gamma _{{\zeta \theta }}^{i} } \\ {\gamma _{{\zeta \eta }}^{i} } \\ {\gamma _{{\theta \eta }}^{i} } \\ \end{array} } \right], $$

(47)

where the $C_{{ij}}$ is the coefficient of HM nanocomposite porous hybrid three-phase material. Due to the porosity of HM throughout the thickness of the hemispherical–cylindrical–conical shell, these parameters are written in the terms of $\eta$ as follows:

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{{11}} (\eta ) = \frac{{E_{1}^{{eff}} (\eta )}}{{1 - \nu _{{12}}^{{eff}} (\eta )\nu _{{21}}^{{eff}} (\eta )}},} & {C_{{22}} (\eta ) = \frac{{E_{2}^{{eff}} (\eta )}}{{1 - \nu _{{12}}^{{eff}} (\eta )\nu _{{21}}^{{eff}} (\eta )}},} \\ \end{array} } & {C_{{12}} (\eta ) = \frac{{\nu _{{12}}^{{eff}} (\eta )E_{1}^{{eff}} (\eta )}}{{1 - \nu _{{12}}^{{eff}} (\eta )\nu _{{21}}^{{eff}} (\eta )}},} \\ \end{array} } \\ {\begin{array}{*{20}c} {C_{{44}} (\eta ) = G_{{23}}^{{eff}} (\eta ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{{55}} (\eta ) = G_{{13}}^{{eff}} (\eta ),\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,} & {C_{{66}} (\eta ) = G_{{12}}^{{eff}} (\eta )} \\ \end{array} } \\ \end{array} $$

(48)

The force and moment resultants of each part of the hemispherical–cylindrical–conical shell can be obtained applying the stresses integration along with the thickness of the shell as follows:

$$ \begin{gathered} \left[ {\begin{array}{*{20}c} {{\rm N}_{\zeta }^{i} } \\ {{\rm N}_{\theta }^{i} } \\ {{\rm N}_{{\zeta \theta }}^{i} } \\ \end{array} } \right] = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left[ {\begin{array}{*{20}c} {\sigma _{\zeta }^{i} } \\ {\sigma _{\theta }^{i} } \\ {\tau _{{\zeta \theta }}^{i} } \\ \end{array} } \right]d\eta } ,\,\,\,\,\left[ {\begin{array}{*{20}c} {{\rm M}_{\zeta }^{i} } \\ {{\rm M}_{\theta }^{i} } \\ {{\rm M}_{{\zeta \theta }}^{i} } \\ \end{array} } \right] = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\eta .\left[ {\begin{array}{*{20}c} {\sigma _{\zeta }^{i} } \\ {\sigma _{\theta }^{i} } \\ {\tau _{{\zeta \theta }}^{i} } \\ \end{array} } \right]d\eta } ,\,\,\,\, \hfill \\ \left[ {\begin{array}{*{20}c} {Q_{{\zeta \eta }}^{i} } \\ {Q_{{\theta \eta }}^{i} } \\ \end{array} } \right] = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\kappa \left[ {\begin{array}{*{20}c} {\sigma _{{\zeta \eta }}^{i} } \\ {\sigma _{{\theta \eta }}^{i} } \\ \end{array} } \right]d\eta } \,\,\,\,\,\,\,\,{\text{for}}\,\,\,\,{\text{i = co,cy,hs}} \hfill \\ \end{gathered} $$

(49)

where ${\rm N}_{\zeta }^{i} ,{\rm N}_{\theta }^{i}$ are the resultant axial forces while ${\rm N}_{{\zeta \theta }}^{i}$ stands for the resultant shear force.$Q_{{\zeta \eta }}^{i} ,Q_{{\theta \eta }}^{i}$ define the resultant transversely shear forces of joined hemispherical–cylindrical–conical shell. The resultant moment and torsion are shown via ${\rm M}_{\zeta }^{i} ,{\rm M}_{\theta }^{i}$ and ${\rm M}_{{\zeta \theta }}^{i}$, respectively. The resultants of force and moment of the joined hemispherical–cylindrical–conical shell can be formulated in terms of mid-surface strains using a transformation matrix. Substituting Eqs. (40) and (47) into Eq. (49), the following expression is found for each part of the shell:

$$ \left[ {\begin{array}{*{20}c} {{\rm N}_{\zeta }^{i} } \\ {{\rm N}_{\theta }^{i} } \\ {{\rm N}_{{\zeta \theta }}^{i} } \\ {{\rm M}_{\zeta }^{i} } \\ {{\rm M}_{\theta }^{i} } \\ {{\rm M}_{{\zeta \theta }}^{i} } \\ {Q_{{\zeta \eta }}^{i} } \\ {Q_{{\theta \eta }}^{i} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\rm A}_{{11}} } & {{\rm A}_{{12}} } & 0 & {\bar{{\rm A}}_{{11}} } & {\bar{{\rm A}}_{{12}} } & 0 & 0 & 0 \\ {{\rm A}_{{12}} } & {{\rm A}_{{22}} } & 0 & {\bar{{\rm A}}_{{12}} } & {\bar{{\rm A}}_{{22}} } & 0 & 0 & 0 \\ 0 & 0 & {{\rm A}_{{66}} } & 0 & 0 & {\bar{{\rm A}}_{{66}} } & 0 & 0 \\ {\bar{{\rm A}}_{{11}} } & {\bar{{\rm A}}_{{12}} } & 0 & {\bar{\bar{{\rm A}}}_{{11}} } & {\bar{\bar{{\rm A}}}_{{12}} } & 0 & 0 & 0 \\ {\bar{{\rm A}}_{{12}} } & {\bar{{\rm A}}_{{22}} } & 0 & {\bar{\bar{{\rm A}}}_{{12}} } & {\bar{\bar{{\rm A}}}_{{22}} } & 0 & 0 & 0 \\ 0 & 0 & {\bar{{\rm A}}_{{66}} } & 0 & 0 & {\bar{\bar{{\rm A}}}_{{66}} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\kappa {\rm A}_{{44}} } & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & {\kappa {\rm A}_{{55}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\bar{\varepsilon }_{\zeta }^{i} } \\ {\bar{\varepsilon }_{\theta }^{i} } \\ {\bar{\gamma }_{{\zeta \theta }}^{i} } \\ {\chi _{\zeta }^{i} } \\ {\chi _{\theta }^{i} } \\ {\chi _{{\zeta \theta }}^{i} } \\ {\bar{\gamma }_{{\theta \eta }}^{i} } \\ {\bar{\gamma }_{{\zeta \eta }}^{i} } \\ \end{array} } \right]\,\,\,\,{\text{for}}\,\,\,\,{\text{i = co,cy,hs}}{\text{.}} $$

(50)

In this work, the shear factor $\kappa$ is assumed to be $\frac{5}{6}$, and the stiffness factors $\left( {{\rm A}_{{ij}} ,\bar{{\rm A}}_{{ij}} ,\bar{\bar{{\rm A}}}_{{ij}} } \right)$ are expressed as follows:

$$ \begin{array}{*{20}c} {\left[ {\begin{array}{*{20}c} {{\rm A}_{{ij}} } \\ {\bar{{\rm A}}_{{ij}} } \\ {\bar{\bar{{\rm A}}}_{{ij}} } \\ \end{array} } \right] = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left[ {\begin{array}{*{20}c} {C_{{ij}} (\eta )} \\ {\eta C_{{ij}} (\eta )} \\ {\eta ^{2} C_{{ij}} (\eta )} \\ \end{array} } \right]\,d\eta } } & {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{i,j = 1,2,4,5,6}}} \\ \end{array} . $$

(51)

5 The equations of motion

The joined hemispherical–cylindrical–conical shell-governing equations of motion are derived by employing Hamilton’s principle and Donnell’s approach in this research [99]. The basic formulation of this principle is given by

$$ \begin{gathered} \delta \int\limits_{{t_{1} }}^{{t_{2} }} {[{\rm K}_{i} - (V_{i} + \Pi _{i} )]dt = 0} \hfill \\ {\text{for}}\,\,\,\,\,\,\,\,\,{\text{i = co,cy,sh,}} \hfill \\ \end{gathered} $$

(52)

where $\delta {\rm K}_{i}$ defines the kinetic energy and can be expressed for each part of joined hemispherical–cylindrical–conical shell as follows:

$$ \begin{gathered} \delta {\rm K}_{i} = \int\limits_{{V_{i} }} {\rho _{{eff}}^{{({\rm I},{\rm I}{\rm I},{\rm I}{\rm I}{\rm I})}} (\eta )(\mathop {U_{1}^{i} }\limits^{.} \delta \mathop {U_{1}^{i} }\limits^{.} + } \mathop {U_{2}^{i} }\limits^{.} \delta \mathop {U_{2}^{i} }\limits^{.} + \mathop {U_{3}^{i} }\limits^{.} \delta \mathop {U_{3}^{i} }\limits^{.} )dV_{i} \hfill \\ {\text{for}}\,\,\,\,\,\,\,\,\,{\text{i = co,cy,sh,}} \hfill \\ \end{gathered} $$

(53)

where (^.) indicates the derivative with respect to time.

In addition, $\delta \Pi _{i}$ is the strain energy of each segment of the structure and expressed as follows:

$$ \begin{gathered} \delta \Pi _{i} = \int\limits_{{A_{i} }} {\int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {[\sigma _{\zeta }^{i} \delta \varepsilon _{\zeta }^{i} + \sigma _{\theta }^{i} \delta \varepsilon _{\theta }^{i} + \tau _{{\zeta \theta }}^{i} \delta \gamma _{{\zeta \theta }}^{i} + \kappa \tau _{{\zeta \eta }}^{i} \delta \gamma _{{\zeta \eta }}^{i} + \kappa \tau _{{\theta \eta }}^{i} \delta \gamma _{{\theta \eta }}^{i} ]\,d\eta dA_{i} } } \hfill \\ {\text{for}}\,\,\,\,\,\,\,{\text{i = co,cy,hs}}{\text{.}} \hfill \\ \end{gathered} $$

(54)

Based on Hamilton’s principle the following statements can be expressed as follows:

$$ \begin{gathered} {\text{at}}\,\,\,\,\,t = t_{1} ,t_{2} :\,\,\,\,\,\delta u_{1}^{i} = \delta u_{2}^{i} = \delta u_{3}^{i} = \delta \Psi _{\zeta }^{i} = \delta \Psi _{\theta }^{i} \hfill \\ {\text{for}}\,\,\,\,\,\,\,{\text{i = co,cy,hs}}{\text{.}} \hfill \\ \end{gathered} $$

(55)

Moreover, using Eqs. (50), (52)–(54), performing the integration along the thickness direction, and employing Green-Gauss theory, the governing differential equations of motion of cylindrical segment of the joined hemispherical–cylindrical–conical shell is found as follows:

$$ \begin{gathered} \delta u_{1}^{{cy}} :\frac{{\partial {\rm N}_{\zeta }^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{cy}} }}{{\partial \theta }}\frac{1}{R} = I_{1} \ddot{u}_{1}^{{cy}} + I_{2} \ddot{\Psi }_{\zeta }^{{cy}} \hfill \\ \delta u_{2}^{{cy}} :\frac{{\partial {\rm N}_{\theta }^{{cy}} }}{{\partial \theta }}\frac{1}{R} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{{Q_{{\theta \eta }}^{{cy}} }}{R} = I_{1} \ddot{u}_{2}^{{cy}} + I_{2} \ddot{\Psi }_{\theta }^{{cy}} \hfill \\ \delta u_{3}^{{cy}} :\frac{{\partial Q_{{\zeta \eta }}^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{1}{R}\frac{{\partial Q_{{\theta \eta }}^{{cy}} }}{{\partial \theta }} - \frac{{{\rm N}_{\theta }^{{cy}} }}{R} = I_{1} \ddot{u}_{3}^{{cy}} \hfill \\ \delta \Psi _{\zeta }^{{cy}} :\frac{{\partial {\rm M}_{\zeta }^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{{\partial {\rm M}_{{\zeta \theta }}^{{cy}} }}{{\partial \theta }}\frac{1}{R} - Q_{{\zeta \eta }}^{{cy}} = I_{2} \ddot{u}_{1}^{{cy}} + I_{3} \ddot{\Psi }_{\zeta }^{{cy}} \hfill \\ \delta \Psi _{\theta }^{{cy}} :\frac{{\partial {\rm M}_{{\zeta \theta }}^{{cy}} }}{{\partial \zeta _{{cy}} }} + \frac{{\partial {\rm M}_{\theta }^{{cy}} }}{{\partial \theta }}\frac{1}{R} - Q_{{\theta \eta }}^{{cy}} = I_{2} \ddot{u}_{2}^{{cy}} + I_{3} \ddot{\Psi }_{\theta }^{{cy}} . \hfill \\ \end{gathered} $$

(56)

Furthermore, the governing differential equations of motion for the conical part of joined hemispherical–cylindrical–conical shell can be found using the same above-mentioned procedure as follows:

$$ \begin{gathered} \delta u_{1}^{{co}} :\frac{{\partial {\rm N}_{\zeta }^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{co}} }}{{\partial \theta }}\frac{1}{{R(\zeta _{{co}} )}} + \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}({\rm N}_{\zeta }^{{co}} - {\rm N}_{\theta }^{{co}} ) = I_{1} \ddot{u}_{1}^{{co}} + I_{2} \ddot{\Psi }_{\zeta }^{{co}} \hfill \\ \delta u_{2}^{{co}} :\frac{{\partial {\rm N}_{\theta }^{{co}} }}{{\partial \theta }}\frac{1}{{R(\zeta _{{co}} )}} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{co}} }}{{\partial \zeta _{{co}} }} + 2\frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}{\rm N}_{{\zeta \theta }}^{{co}} + \frac{{\cos (\Theta )}}{{R(\zeta _{{co}} )}}Q_{{\theta \eta }}^{{co}} = I_{1} \ddot{u}_{2}^{{co}} + I_{2} \ddot{\Psi }_{\theta }^{{co}} \hfill \\ \delta u_{3}^{{co}} :\frac{{\partial Q_{{\zeta \eta }}^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{1}{{R(\zeta _{{co}} )}}\frac{{\partial Q_{{\theta \eta }}^{{co}} }}{{\partial \theta }} + \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}Q_{{\zeta \eta }}^{{co}} - \frac{{\cos (\Theta )}}{{R(\zeta _{{co}} )}}{\rm N}_{\theta }^{{co}} = I_{1} \ddot{u}_{3}^{{co}} \hfill \\ \delta \Psi _{\zeta }^{{co}} :\frac{{\partial {\rm M}_{\zeta }^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{{\partial {\rm M}_{{\zeta \theta }}^{{co}} }}{{\partial \theta }}\frac{1}{{R(\zeta _{{co}} )}} + \frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}({\rm M}_{\zeta }^{{co}} - {\rm M}_{\theta }^{{co}} ) - Q_{{\zeta \eta }}^{{co}} = I_{2} \ddot{u}_{1}^{{co}} + I_{3} \ddot{\Psi }_{\zeta }^{{co}} \hfill \\ \delta \Psi _{\theta }^{{co}} :\frac{{\partial {\rm M}_{{\zeta \theta }}^{{co}} }}{{\partial \zeta _{{co}} }} + \frac{{\partial {\rm M}_{\theta }^{{co}} }}{{\partial \theta }}\frac{1}{{R(\zeta _{{co}} )}} + 2\frac{{\sin (\Theta )}}{{R(\zeta _{{co}} )}}{\rm M}_{{\zeta \theta }}^{{co}} - Q_{{\theta \eta }}^{{co}} = I_{2} \ddot{u}_{2}^{{co}} + I_{3} \ddot{\Psi }_{\theta }^{{co}} . \hfill \\ \end{gathered} $$

(57)

On the other hand, the governing equations of motion associated to the hemispherical part of the shell can be obtained utilizing the similar mathematical operation concerning the others segment of joined hemispherical–cylindrical–conical shell as follows:

$$ \begin{gathered} \delta u_{1}^{{hs}} :\frac{1}{R}\frac{{\partial {\rm N}_{\zeta }^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{hs}} }}{{\partial \theta }}\frac{1}{{R\sin (\zeta _{{hs}} )}} + \frac{{\cot (\zeta _{{hs}} )}}{R}({\rm N}_{\zeta }^{{hs}} - {\rm N}_{\theta }^{{hs}} ) + \frac{{Q_{{\zeta \eta }}^{{hs}} }}{R} = I_{1} \ddot{u}_{1}^{{hs}} + I_{2} \ddot{\Psi }_{\zeta }^{{hs}} \hfill \\ \delta u_{2}^{{hs}} :\frac{{\partial {\rm N}_{\theta }^{{hs}} }}{{\partial \theta }}\frac{1}{{R\sin (\zeta _{{hs}} )}} + \frac{{\partial {\rm N}_{{\zeta \theta }}^{{hs}} }}{{\partial \zeta _{{hs}} }} + 2\frac{{\cot (\zeta _{{hs}} )}}{R}{\rm N}_{{\zeta \theta }}^{{hs}} + \frac{{Q_{{\theta \eta }}^{{hs}} }}{R} = I_{1} \ddot{u}_{2}^{{hs}} + I_{2} \ddot{\Psi }_{\theta }^{{hs}} \hfill \\ \delta u_{3}^{{hs}} :\frac{1}{R}\frac{{\partial Q_{{\zeta \eta }}^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{1}{{R\sin (\zeta _{{hs}} )}}\frac{{\partial Q_{{\theta \eta }}^{{hs}} }}{{\partial \theta }} + \frac{{\cot (\zeta _{{hs}} )}}{R}Q_{{\zeta \eta }}^{{hs}} - \frac{{({\rm N}_{\theta }^{{hs}} + {\rm N}_{\zeta }^{{hs}} )}}{R} = I_{1} \ddot{u}_{3}^{{hs}} \hfill \\ \delta \Psi _{\zeta }^{{hs}} :\frac{1}{R}\frac{{\partial {\rm M}_{\zeta }^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{{\partial {\rm M}_{{\zeta \theta }}^{{hs}} }}{{\partial \theta }}\frac{1}{{R\sin (\zeta _{{hs}} )}} + \frac{{\cot (\zeta _{{hs}} )}}{R}({\rm M}_{\zeta }^{{hs}} - {\rm M}_{\theta }^{{hs}} ) - Q_{{\zeta \eta }}^{{hs}} = I_{2} \ddot{u}_{1}^{{hs}} + I_{3} \ddot{\Psi }_{\zeta }^{{hs}} \hfill \\ \delta \Psi _{\theta }^{{hs}} :\frac{1}{R}\frac{{\partial {\rm M}_{{\zeta \theta }}^{{hs}} }}{{\partial \zeta _{{hs}} }} + \frac{{\partial {\rm M}_{\theta }^{{hs}} }}{{\partial \theta }}\frac{1}{{R\sin (\zeta _{{hs}} )}} + 2\frac{{\cot (\zeta _{{hs}} )}}{R}{\rm M}_{{\zeta \theta }}^{{hs}} - Q_{{\theta \eta }}^{{hs}} = I_{2} \ddot{u}_{2}^{{hs}} + I_{3} \ddot{\Psi }_{\theta }^{{hs}} . \hfill \\ \end{gathered} $$

(58)

It should be noted that the inertia coefficients ($I_{i}$) of the structure can be found as follows:

$$ \left[ {\begin{array}{*{20}c} {I_{1} } \\ {I_{2} } \\ {I_{3} } \\ \end{array} } \right] = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\rho _{{eff}}^{{(I,II,II)}} (\eta )\left[ {\begin{array}{*{20}c} 1 \\ \eta \\ {\eta ^{2} } \\ \end{array} } \right]d\eta } . $$

(59)

5.1 The boundary conditions

According to the type of structures in this study, the boundary conditions are differentiated by various forms. Based on this issue, joined shells are assumed to be restrained with Clamped (C), Simply supported (S), and Free (F) ends. The mathematical expressions of these boundary conditions for the ends of the joined hemispherical–cylindrical–conical shell structure are given as follows:

$$ \begin{gathered} F_{{hs}} :{\rm N}_{\zeta }^{{hs}} = {\rm N}_{{\zeta \theta }}^{{hs}} = Q_{{\zeta \eta }}^{{hs}} = {\rm M}_{\zeta }^{{hs}} = {\rm M}_{{\zeta \theta }}^{{hs}} = 0 \hfill \\ S_{{hs}} :\,\,\,u_{1}^{{hs}} = u_{2}^{{hs}} = u_{3}^{{hs}} = {\rm M}_{\zeta }^{{hs}} = \Psi _{\theta }^{{hs}} = 0 \hfill \\ C_{{hs}} :\,\,\,u_{1}^{{hs}} = u_{2}^{{hs}} = u_{3}^{{hs}} = \Psi _{\zeta }^{{hs}} = \Psi _{\theta }^{{hs}} = 0 \hfill \\ F_{{co}} :{\rm N}_{\zeta }^{{co}} = {\rm N}_{{\zeta \theta }}^{{co}} = Q_{{\zeta \eta }}^{{co}} = {\rm M}_{\zeta }^{{co}} = {\rm M}_{{\zeta \theta }}^{{co}} = 0 \hfill \\ S_{{co}} :\,\,\,u_{1}^{{co}} = u_{2}^{{co}} = u_{3}^{{co}} = {\rm M}_{\zeta }^{{co}} = \Psi _{\theta }^{{co}} = 0 \hfill \\ C_{{co}} :\,\,\,u_{1}^{{co}} = u_{2}^{{co}} = u_{3}^{{co}} = \Psi _{\zeta }^{{co}} = \Psi _{\theta }^{{co}} = 0. \hfill \\ \end{gathered} $$

(60)

5.2 Coupling conditions

The coupling conditions of joined hemispherical–cylindrical–conical shells can be found for each part including hemispherical–cylindrical and cylindrical–conical parts. Note that these conditions are considered, separately.

First, the displacement conditions at the connection of hemispherical–cylindrical shells are given as follows:

$$ \begin{gathered} u_{1}^{{hs}} = u_{1}^{{cy}} \hfill \\ u_{2}^{{hs}} = u_{2}^{{cy}} \hfill \\ u_{3}^{{hs}} = u_{3}^{{cy}} \hfill \\ \Psi _{\zeta }^{{hs}} = \Psi _{\zeta }^{{cy}} \hfill \\ \Psi _{\theta }^{{hs}} = \Psi _{\theta }^{{cy}} . \hfill \\ \end{gathered} $$

(61)

Then, the conditions used for movement at the connection of cylindrical–conical shells are as follows:

$$ \begin{gathered} u_{1}^{{cy}} = u_{1}^{{co}} \cos (\Theta ) - u_{3}^{{co}} \sin (\Theta ) \hfill \\ u_{3}^{{cy}} = u_{1}^{{co}} \sin (\Theta ) + u_{3}^{{co}} \cos (\Theta ) \hfill \\ u_{2}^{{cy}} = u_{2}^{{co}} \hfill \\ \Psi _{\zeta }^{{cy}} = \Psi _{\zeta }^{{co}} \hfill \\ \Psi _{\theta }^{{cy}} = \Psi _{\theta }^{{co}} . \hfill \\ \end{gathered} $$

(62)

Furthermore, the compatible conditions for resultant forces and moments at the connection of hemispherical–cylindrical can be defined as follows:

$$ \begin{gathered} {\rm N}_{\zeta }^{{hs}} = {\rm N}_{\zeta }^{{cy}} \hfill \\ Q_{{\zeta \eta }}^{{hs}} = Q_{{\zeta \eta }}^{{cy}} \hfill \\ {\rm M}_{\zeta }^{{hs}} = {\rm M}_{\zeta }^{{cy}} \hfill \\ {\rm N}_{{\zeta \theta }}^{{hs}} = {\rm N}_{{\zeta \theta }}^{{cy}} \hfill \\ {\rm M}_{{\zeta \theta }}^{{hs}} = {\rm M}_{{\zeta \theta }}^{{cy}} . \hfill \\ \end{gathered} $$

(63)

Moreover, the consistent conditions related to the force and moment resultants at the intersection of cylindrical–conical are accessed by

$$ \begin{gathered} {\rm N}_{\zeta }^{{cy}} = {\rm N}_{\zeta }^{{co}} \cos (\Theta ) - Q_{{\zeta \eta }}^{{co}} \sin (\Theta ) \hfill \\ Q_{{\zeta \eta }}^{{cy}} = {\rm N}_{\zeta }^{{co}} \sin (\Theta ) + Q_{{\zeta \eta }}^{{co}} \cos (\Theta ) \hfill \\ {\rm M}_{\zeta }^{{cy}} = {\rm M}_{\zeta }^{{co}} \hfill \\ {\rm N}_{{\zeta \theta }}^{{cy}} = {\rm N}_{{\zeta \theta }}^{{co}} \hfill \\ {\rm M}_{{\zeta \theta }}^{{cy}} = {\rm M}_{{\zeta \theta }}^{{co}} . \hfill \\ \end{gathered} $$

(64)

The natural frequencies of joined hemispherical–cylindrical–conical shells can be calculated by solving the governing differential equations of motion. Hence, these equations can be obtained by applying the relation between the resultants of force and the moment in terms of mid-surface displacements. In addition, the following expressions are considered for the displacement fields of the structure:

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {u_{1}^{i} (\zeta _{i} ,\theta ,t)} \\ {u_{2}^{i} (\zeta _{i} ,\theta ,t)} \\ {u_{2}^{i} (\zeta _{i} ,\theta ,t)} \\ {\Psi _{\zeta }^{i} (\zeta _{i} ,\theta ,t)} \\ {\Psi _{\theta }^{i} (\zeta _{i} ,\theta ,t)} \\ \end{array} } \right\} = \cos (\omega _{n} t)\left[ {\begin{array}{*{20}c} {\sin (n\theta )} & 0 & 0 & 0 & 0 \\ 0 & {\cos (n\theta )} & 0 & 0 & 0 \\ 0 & 0 & {\sin (n\theta )} & 0 & 0 \\ 0 & 0 & 0 & {\sin (n\theta )} & 0 \\ 0 & 0 & 0 & 0 & {\cos (n\theta )} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\bar{U}_{1}^{i} (\zeta _{i} )} \\ {\bar{U}_{2}^{i} (\zeta _{i} )} \\ {\bar{U}_{3}^{i} (\zeta _{i} )} \\ {\bar{\Psi }_{\zeta }^{i} (\zeta _{i} )} \\ {\bar{\Psi }_{\theta }^{i} (\zeta _{i} )} \\ \end{array} } \right\} \hfill \\ \,\,\,\, \hfill \\ {\text{for}}\,\,\,\,{\text{i = co,cy,hs,}} \hfill \\ \end{gathered} $$

(65)

where $\omega _{n} ,n$ are the natural frequency and the circumferential wave number of joined shells, respectively.

It should be noted that the governing equations of motion of each part of this joined structure can be transformed concerning the $\bar{U}_{1}^{i} (\zeta _{i} ),\bar{U}_{2}^{i} (\zeta _{i} ),\bar{U}_{3}^{i} (\zeta _{i} ),\bar{\Psi }_{\zeta }^{i} (\zeta _{i} ),\bar{\Psi }_{\theta }^{i} (\zeta _{i} )$ functions utilizing Eq. (65). After that, the obtained governing equations only depend on the longitudinal direction, which can be found for each segment of the joined hemispherical–cylindrical–conical shell. Accordingly, the natural frequencies of this structure can be determined by solving 15 equations (5 for hemispherical, 5 for cylindrical, and 5 for conical segments), simultaneously. In addition, the related equations are given in Appendix I.

6 The solution procedure

In this work, the differential equations of motions related to the joined hemispherical–cylindrical–conical shell are solved by applying a qualified semi-analytical solution, namely GDQM. It should also be noted that the GDQM technique is used for derivative equations of motion and implemented boundary and coupled conditions based on using grid points. The GDQM is continued by the Lagrangian polynomials and Chebyshev–Gauss–Lobatto to realize weighting coefficients and grid points distribution pattern, respectively. On this basis, the governing equations of motion associated with the joined hemispherical–cylindrical–conical shell can be written for each grid point as follows:

$$ \left[ {\Re _{{dd}} } \right]\left[ {{\rm X}_{d} } \right] + \left[ {\Re _{{db}} } \right]\left[ {{\rm X}_{b} } \right] + \left[ {\Re _{{dc}} } \right]\left[ {{\rm X}_{c} } \right] = \omega _{n} ^{2} \left[ {M_{{dd}} } \right]\left[ {{\rm X}_{d} } \right], $$

(66)

where $\left[ {\Re _{{dd}} } \right]$ and $\left[ {\Re _{{dd}} } \right]$ are interior point stiffness and mass matrices, respectively. The inner stiffness matrix due to stiffness of intersection grids is represented by $\left[ {\Re _{{dc}} } \right]$. In addition, $\left[ {{\rm X}_{d} } \right]$, $\left[ {{\rm X}_{b} } \right]$ and $\left[ {{\rm X}_{c} } \right]$ indicate the displacement vector of the interior, boundary, and connective conditions, respectively. On the other hand, the interior stiffness matrix as a product of the stiffness of boundary points is defined by $\left[ {\Re _{{db}} } \right]$. It should be noticed that five equations are built for each part of joined hemispherical–cylindrical–conical shell structure. Hence, there are 15 equations for the joined hemispherical–cylindrical–conical shell. Furthermore, each grid point should be filled in these 15 equations. In addition, by applying GDQM and considering boundary and coupling conditions, the following equations can be defined:

$$ \left[ {\Re _{{bb}} } \right]\left[ {{\rm X}_{b} } \right] + \left[ {\Re _{{bd}} } \right]\left[ {{\rm X}_{d} } \right] + \left[ {\Re _{{bc}} } \right]\left[ {{\rm X}_{c} } \right] = 0 $$

(67)

$$ \left[ {\Re _{{cc}} } \right]\left[ {{\rm X}_{c} } \right] + \left[ {\Re _{{cd}} } \right]\left[ {{\rm X}_{d} } \right] + \left[ {\Re _{{cb}} } \right]\left[ {{\rm X}_{b} } \right] = 0, $$

(68)

where the stiffness matrices of boundary and connective points are represented by $\left[ {\Re _{{bb}} } \right]$ and $\left[ {\Re _{{cc}} } \right]$, respectively.

Moreover, $\left[ {\Re _{{bd}} } \right]$ and $\left[ {\Re _{{bc}} } \right]$ are the boundary stiffness matrices including the stiffness of interior and connection points. The connective stiffness matrices caused by the stiffness of interior and boundary grids are shown with $\left[ {\Re _{{cd}} } \right]$ and $\left[ {\Re _{{cb}} } \right]$, respectively.

Furthermore, there are ten boundary conditions related to the end restrains of the joined hemispherical–cylindrical–conical shell, as well as 20 connection conditions are also employed for the structure. Note that there are several methods to include the boundary and connection conditions in the differential equations of motion.

The governing equations of interior points can be obtained by substituting relations (67) and (68) into (66). Therefore, the natural frequencies of joined hemispherical–cylindrical–conical shells are obtained applying the eigenvalue of the linear governing equations of motion as follows:

$$ \left| {\Re ^{{eff}} - \omega _{n} M^{{eff}} } \right| = 0 $$

(69)

in which

$$ \begin{gathered} \left[ {\Re ^{{eff}} } \right] = \left[ {\Re _{{dd}} } \right] + \{ \left[ {\Re _{{db}} } \right](\left[ {\Re _{{bb}} } \right] - \left[ {\Re _{{bc}} } \right]\left[ {\Re _{{cc}} } \right]^{{ - 1}} \left[ {\Re _{{cb}} } \right])^{{ - 1}} (\left[ {\Re _{{bd}} } \right] - \left[ {\Re _{{bc}} } \right]\left[ {\Re _{{cc}} } \right]^{{ - 1}} \left[ {\Re _{{cd}} } \right])\} \hfill \\ + [\left[ {\Re _{{dc}} } \right]( - (\left[ {\Re _{{cc}} } \right]^{{ - 1}} )(\left[ {\Re _{{cd}} } \right] + \{ \left[ {\Re _{{cb}} } \right](\left[ {\Re _{{bb}} } \right] - \left[ {\Re _{{bc}} } \right]\left[ {\Re _{{cc}} } \right]^{{ - 1}} \left[ {\Re _{{cb}} } \right])^{{ - 1}} \hfill \\ (\left[ {\Re _{{bd}} } \right] - \left[ {\Re _{{bc}} } \right]\left[ {\Re _{{cc}} } \right]^{{ - 1}} \left[ {\Re _{{cd}} } \right])\} ))] \hfill \\ ~~\left[ {M^{{eff}} } \right] = \left[ {M_{{dd}} } \right]. \hfill \\ \end{gathered} $$

(70)

Finally, the dimension of the effective stiffness matrix is $15N - 30$. In addition, N stands for the number of total grids. Accordingly, there are 15 grids are employed to the discretization of the shell structures [100]. Afterward, the dimension of the effective stiffness matrix is found as 195-by-195.

7 Results and discussion

At first, some comparison studies are performed with the available results of open literature to verify the proposed formulation. Then, some new, applicable, and complicated problems associated with nonhomogeneous and homogenous joined hemispherical–cylindrical–conical shells are solved numerically to show the high accuracy and capability of the proposed formulation. The effects of different boundary conditions, material properties, and geometrical characteristics on the vibrational behavior of joined shells are also discussed. Here, F, S, and C represent the free, simply supported, and clamped boundary conditions, respectively.

7.1 Verification study

This example deals to verify the proposed formulation and solution method comparing the natural frequency of the hemispherical–cylindrical–conical structure having the following geometrical and material properties with the results of [66, 68]. The boundary condition of the shell is supposed to be F–F:

$$ \begin{gathered} ^{{R = 1,\,\,\,\,L_{{cy}} = 2.5,\,\,\,\,R_{{co}}^{1} = 0.4,\,\,\,\,\,h = 0.01,\,\,\,\,\,\,\Theta = - \frac{\pi }{6},\,\,\,\,\,\vartheta = \left\{ {0,\frac{\pi }{6},\frac{\pi }{4}} \right\}}} \hfill \\ E = 69.58\,({\text{GPa}}),\,\,\,\,\nu = 0.31,\,\,\,\,\rho = 2700\,({\text{kgm}}^{{{{ - 3}}}} ). \hfill \\ \end{gathered} $$

The results are reported in Table 4. It is seen that there is a good agreement between the results of the present study and the results of the references.

Table 4 The natural frequencies of isotropic joined hemispherical–cylindrical–conical shells under F–F boundary conditions

7.2 Convergence study

In this example, the results of the natural frequency of the joined hemispherical–cylindrical–conical shells are compared with the results of the structure modeled in a commercial FEM software called ABAQUS. This analysis is performed under the C–F boundary conditions. The results related to the first mode of the circumferential wave number of 0, 1, 2, 3, and 4 are reported. The material and geometric properties of the structure are the same as in the earlier example, as well as two different values of thickness including 0.02 and 0.05 are considered.

Table 5 reports the natural frequency of the homogenous joined hemispherical–cylindrical–conical shells under C–F boundary conditions. In addition, the mode shapes of the joined shells with thickness value 0.02 are also illustrated in Fig. 7.

Table 5 The natural frequencies of isotropic joined hemispherical–cylindrical–conical shells under C–F boundary conditions

Fig. 7

The variation of mode shapes of the joined isotropic hemispherical–cylindrical–conical shell under C–F boundary conditions (a) occurred in the second wave number (47.424 Hz), (b) occurred in the third wave number (91.606 Hz), (c) occurred in the fourth wave number (95.941 Hz), (d) occurred in the second mode of third wave number (142.99 Hz), (e) occurred in the second mode of the second wave number (147.41 Hz)

7.3 The effect of different patterns of porosity distribution

The main goal of this example is to study the effect of three different patterns of porosity distribution on the natural frequencies of joined hemispherical–cylindrical–conical shells. Different types of boundary conditions are considered in this part. The volume fraction of fibers is assumed to equal 0.6. The results associated with the first mode of the first ten circumferential waves are obtained. The geometric characteristics of the shell are as follows:$^{{R = 1,\,\,\,\,L_{{cy}} = 2.5,\,\,\,\,L_{{co}} = 1,\,\,\,\,\,h = 0.01,\,\,\,\,\,\,\Theta = - \frac{\pi }{6},\,\,\,\,\,\vartheta = \frac{\pi }{6}}} .$

In the first part, the responses related to the boundary condition of C–C are presented for different porosity patterns. Table 6 reports the natural frequency of the joined shells constructed with hybrid matrix nanocomposite shells including porosity with different patterns of distribution.

Table 6 The natural frequencies of the first ten wave numbers of hybrid porous nanocomposite joined hemispherical–cylindrical–conical shell versus various porosity patterns

It is seen that the natural frequencies of the joined shell decrease with the increasing porosity factor in all patterns. In the second part, different boundary conditions are considered for the structure with the porosity factor of 0.6. Figure 8 depicts the variation of the natural frequency of the structure with different boundary conditions.

Fig. 8

The variation of natural frequencies of the first ten wave numbers of hybrid porous nanocomposite joined shell under different boundary conditions, (a) C–C, (b) C–F, (c) F–C, (d) F–F, (e) F–S, (f) S–F

The lowest values of the natural frequency of the joined shell are obtained under C–C boundary conditions for the first pattern of porosity distribution in the fifth circumferential wave number, while for the sixth circumferential wave in the second and third patterns of porosity distribution. Furthermore, for the boundary conditions of C–F and F–C, the lowest frequency of the joined shell is reported for the second circumferential wave number for all patterns of porosity distribution. This parameter is minimized at the first circumferential wave as the boundary condition of the structure is S–F, F–S, or F–F for all patterns of porosity distribution.

7.4 The effect of the meridional angle of the hemispherical part

This example studies the effect of the meridional angle of the hemispherical part of the joined shell on the natural frequency of the hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells having the first pattern of the porosity distribution with the porosity factor of 0.1, as well as the volume fraction of the AS4 carbon fibers is equal to 0.6. The geometric properties of the joined shell are considered as follows:$^{{R = 1,\,\,\,\,L_{{cy}} = 2.5,\,\,\,\,L_{{co}} = 1,\,\,\,\,\,\Theta = - \frac{\pi }{6}}} .$

At first, the thickness of the structure is assumed to be 0.01 and different boundary conditions are considered. The results are found for the first mode of the first circumferential wave number and presented in Table 7.

Table 7 The first mode of the first wave number of pattern-I hybrid porous nanocomposite joined hemispherical–cylindrical–conical versus the different meridional angles of hemispherical under various boundary conditions

Then, different values of thickness including 0.01, 0.02, 0.05, and 0.1 are considered for the C–C joined hemispherical–cylindrical–conical shell. The results associated with the first mode of the first five circumferential waves are illustrated in Fig. 9.

Fig. 9

The variation of natural frequencies of the first five wave numbers versus hemispherical meridional angle with different shell thicknesses, (a) thickness = 0.01, (b) thickness = 0.02, (c) thickness = 0.05, (d) thickness = 0.1

It is seen that for all values of the shell thickness, increasing the values of meridional angle of the hemispherical part increases the natural frequency of the structure. Moreover, the lowest frequency of the structure having the thickness of 0.01, 0.02, 0.05, and 0.1 is found for the fifth, fourth, third, and first circumferential waves, respectively.

7.5 The effect of shell thickness

This example investigates the effect of thickness variation on the natural frequencies of the hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells. In this example, the first pattern of the porosity distribution with the coefficient of 0.1 is employed, the volume fraction of AS4 carbon fibers is also supposed to be 0.6, and the following geometric characteristics are considered: $^{{R = 1,\,\,\,\,L_{{cy}} = 2.5,\,\,\,\,L_{{co}} = 1,\,\,\,\,\,\Theta = - \frac{\pi }{6},\,\,\,\,\,\vartheta = \frac{\pi }{6}}} .$

At first, all types of boundary conditions are studied, and results of natural frequency related to the first circumferential wave number of the first mode are given in Table 8.

Table 8 The first mode of the first wave number of pattern-I hybrid porous nanocomposite joined hemispherical–cylindrical–conical versus different shell thicknesses under various boundary conditions

Then, the results of the natural frequency of the hemispherical–cylindrical–conical shells associated with the first five circumferential waves of the first mode are obtained for the boundary conditions of C–C, C–F, F–C, and F–S and illustrated in Fig. 10.

Fig. 10

The variation of the first mode of the first five wave numbers versus various shell thicknesses under different boundary conditions, (a) C–C, (b) C–F, (c) F–C, (d) F-S

It is noticed that in all cases, increasing the thickness of the structure increases the natural frequency of the shell. In addition, in the case of the C–C boundary conditions, increasing the thickness of the structure causes that the lowest natural frequency of shell is obtained for the different number of circumferential waves. On the other hand, in the cases of C–F and F–C and the thickness of 0.01, the lowest natural frequency is found in the second circumferential wave while this parameter is obtained in the first circumferential wave for other values of shell thickness.

7.6 The effect of semi-vertex angle of the conical part

This example examines the effect of variation of the semi-vertex angle of the conical part on the natural frequency of the hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells. Note that the porosity coefficient of the material is assumed to be 0.1, and the first pattern of porosity distribution is considered. The geometric characteristics of the structure are also taken to be: $^{{R = 1,\,\,\,\,L_{{cy}} = 2.5,\,\,\,\,L_{{co}} = 1}} .$

The results of this study are divided into two steps. At the first step, the effect of the semi-vertex angle of conical on the natural frequency is investigated for two cases. The first case is related to the C–C boundary condition with the shell thickness of 0.01, 0.05, and 0.1. In the second case, the boundary conditions of C–F and F–C are also employed with the shell thickness of 0.01. The meridional angle of the hemispherical part is taken to be 30°. Figure 11 illustrates the natural frequencies of the structure associated with the first five circumferential waves of the first mode.

Fig. 11

The variation of natural frequencies of the first mode of the first five wave numbers of hybrid porous (pattern-I) nanocomposite joined hemispherical–cylindrical–conical shell in terms of the variation of semi-vertex angle of conical part (a) C–C condition and thickness = 0.01, (b) C–C condition and thickness = 0.05, (c) C–C condition and thickness = 0.1, (d) C–F condition and thickness = 0.01, (e) F–C condition and thickness = 0.01

It is seen that the highest values of the natural frequency of the shell are found for the case of C–C boundary condition and with the shell thickness of 0.01 in the first, second, third, fourth, and fifth circumferential waves when the semi-vertex angle of the conical part is equal to 50°, 60°, 30°, 20°, and 10°, respectively. On the other hand, the structure with the boundary condition of C–C and shell thickness of 0.05 and 0.1 has the lowest natural frequency in the second, third, fourth, and fifth circumferential waves when the semi-vertex angle of conical is equal to 0°. Furthermore, the lowest values of the natural frequency of the shell are obtained under the boundary condition of C–F with the shell thickness of 0.01, and the semi-vertex angle of 0° can be obtained at the second, third, fourth, and fifth circumferential waves. In the case of F–C boundary condition and with the shell thickness of 0.01, the highest natural frequency of the structure is found in the first and second circumferential waves when the semi-vertex angle of the conical part is equal to 0°, in the third and fifth circumferential waves when the semi-vertex angle of conical is equal to 10° and in the fourth circumferential wave when the semi-vertex angle of conical is equal to 20°.

At the second step, the natural frequency related to the first circumferential wave of the first mode of the shell under the boundary conditions of C–C and F–C, with the shell thickness of 0.1 and meridional angle of the hemispherical part of 0°, 30°, 45°, and 60°. The results are presented in Fig. 12.

Fig. 12

The variation of the first mode of the first wave numbers of hybrid porous (pattern-I) nanocomposite joined shell in terms of variation of semi-vertex angle of conical versus different hemispherical meridional angle with shell thickness equal to 0.1, (a) C–C, (b) F–C

It is seen that in the cases of C–C and F–C boundary conditions, increasing the meridional angle of the hemispherical part increases the natural frequency of the joined shell. In addition, the highest values of the natural frequency of the joined shell are found in the semi-vertex angle of 20°. In the case of the C–C boundary condition, it is seen that the lowest and highest values of the natural frequency of the joined shell are obtained for the semi-vertex angle of − 90° and + 90°, respectively.

8 Conclusions

This paper was dedicated to studying the free vibration behavior of the hybrid porous nanocomposite joined hemispherical–cylindrical–conical shells composed of three-phase material including a matrix of epoxy, macroscale carbon fiber, and nanoscale 3GFs. The effect of shear deformation was considered using FSDT. The rule of the mixture and Halpin–Tsai homogenization multiscale approaches were employed to, respectively, obtain the equivalent mechanical properties of HM and equivalent material properties of HM reinforced with macroscale carbon fibers. Based on Donnell’s shell theory and applying Hamilton’s principles, the governing equations of motion related to the joined shells were established. Then, the well-known semi-analytical solution method of GDQM was used to solve the governing differential equations of motion. The procedure of this method was completely presented, and a computer program was developed according to the boundary and coupling conditions. To confirm the proposed formulation, some benchmark problems were solved, and the obtained results were compared with the results of open literature. Furthermore, several new and applicable joined shells were analyzed to investigate the effect of different parameters including material and geometrical properties and boundary conditions on the natural frequencies of hybrid porous nanocomposite joined shells.

Briefly, the following outcomes can be given:

• The natural frequencies of the joined shell decrease with the increasing porosity factor in all patterns.

• Increment of the values of meridional angle of the hemispherical part increases the natural frequency of the joined structure for all values of the shell thickness.

• Increment of the thickness of the structure increases the natural frequency of the shell in all cases.

• Increment of the meridional angle of the hemispherical part increases the natural frequency of the joined shell in the cases of C–C and F–C boundary conditions.

Appendix I

The governing differential equations of joined hemispherical–cylindrical–conical shells in terms of displacement functions are given by

$$ \begin{gathered} \left( {\frac{1}{{R^{2} }}} \right)\{ A_{{11}} \bar{U}^{{cy}} _{{1,\zeta _{{cy}} \zeta _{{cy}} }} R^{2} + \bar{A}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{cy}} \zeta _{{cy}} }}^{{cy}} R^{2} \hfill \\ \quad - nR(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{cy}} }}^{{cy}} - nR(A_{{12}} + A_{{66}} )\bar{U}^{{cy}} _{{2,\zeta _{{cy}} }} \hfill \\ \quad + RA_{{12}} \bar{U}^{{cy}} _{{3,\zeta _{{cy}} }} + (\bar{U}^{{cy}} _{1} A_{{22}} + \bar{\Psi }_{\zeta }^{{cy}} \bar{A}_{{22}} ) \hfill \\ \quad - n^{2} A_{{66}} \bar{U}^{{cy}} _{1} - \bar{\Psi }_{\zeta }^{{cy}} n^{2} \bar{A}_{{66}} \} = I_{1} \omega _{n} ^{2} \bar{U}^{{cy}} _{1} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{cy}} \hfill \\ \end{gathered} $$

(71)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} }}} \right)\{ \bar{A}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{cy}} \zeta _{{cy}} }}^{{cy}} R^{2} + A_{{66}} \bar{U}^{{cy}} _{{2,\zeta _{{cy}} \zeta _{{cy}} }} R^{2} \hfill \\ \quad + nR(A_{{12}} + A_{{66}} )\bar{U}^{{cy}} _{{1,\zeta _{{cy}} }} + nR(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{cy}} }}^{{cy}} \hfill \\ \quad - n\bar{U}^{{cy}} _{2} (\kappa A_{{44}} + A_{{22}} ) + n\bar{U}^{{cy}} _{3} (\kappa A_{{44}} + A_{{22}} )\} \hfill \\ \quad + ( - n^{2} \bar{A}_{{22}} + R\kappa A_{{44}} )\bar{\Psi }_{\theta }^{{cy}} \hfill \\ \;\;\;= I_{1} \omega _{n} ^{2} \bar{U}^{{cy}} _{2} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{cy}} \hfill \\ \end{gathered} $$

(72)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} }}} \right)\{ \kappa A_{{55}} R^{2} \bar{U}^{{cy}} _{{3,\zeta _{{cy}} \zeta _{{cy}} }} + (R[R\kappa A_{{55}} - \bar{A}_{{12}} )\bar{\Psi }_{{\zeta ,\zeta _{{cy}} }}^{{cy}} \hfill \\ \quad - RA_{{12}} \bar{U}^{{cy}} _{{1,\zeta _{{co}} }} - \bar{U}^{{cy}} _{3} A_{{22}} - \bar{A}_{{22}} n\bar{\Psi }_{\theta }^{{cy}} \hfill \\ \quad + \bar{U}^{{cy}} _{2} (\kappa A_{{44}} + A_{{22}} )n \hfill \\ \quad - ((nA_{{44}} \bar{\Psi }_{\theta }^{{cy}} )R + A_{{44}} n^{2} \bar{U}^{{cy}} _{3} )\kappa \} \hfill \\ \;\;\;= I_{1} \omega _{n} ^{2} \bar{U}^{{cy}} _{3} \hfill \\ \end{gathered} $$

(73)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} }}} \right)\{ \bar{A}_{{11}} \bar{U}^{{cy}} _{{1,\zeta _{{cy}} \zeta _{{cy}} }} R^{2} + \bar{\bar{A}}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{cy}} \zeta _{{cy}} }}^{{cy}} R^{2} \hfill \\ \quad - nR(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{cy}} }}^{{cy}} - nR(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{cy}} _{{2,\zeta _{{cy}} }} \hfill \\ \quad + ( - R^{2} A_{{55}} \kappa + \bar{A}_{{12}} R)\bar{U}^{{cy}} _{3} - n^{2} \bar{A}_{{66}} \bar{U}^{{cy}} _{1} \hfill \\ \quad - R^{2} A_{{55}} \kappa \bar{\Psi }_{\zeta }^{{cy}} - \bar{\Psi }_{\zeta }^{{cy}} n^{2} \bar{\bar{A}}_{{66}} \} \hfill \\ \;\;\;= I_{2} \omega _{n} ^{2} \bar{U}^{{cy}} _{1} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{cy}} \hfill \\ \end{gathered} $$

(74)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} }}} \right)\{ \bar{\bar{A}}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{cy}} \zeta _{{cy}} }}^{{cy}} R^{2} + \bar{A}_{{66}} \bar{U}^{{cy}} _{{2,\zeta _{{cy}} \zeta _{{cy}} }} R^{2} \hfill \\ \quad + nR(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{cy}} _{{1,\zeta _{{cy}} }} + nR(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{cy}} }}^{{cy}} \hfill \\ \quad - R^{2} \bar{\Psi }_{\theta }^{{cy}} \kappa A_{{44}} - n^{2} \bar{\bar{A}}_{{22}} \bar{\Psi }_{\theta }^{{cy}} \hfill \\ \quad - \kappa A_{{44}} (n\bar{U}^{{cy}} _{3} - \bar{U}^{{cy}} _{2} )R - \bar{U}^{{cy}} _{2} n^{2} \bar{A}_{{22}} \hfill \\ \quad + \bar{U}^{{cy}} _{3} n\bar{A}_{{22}} \} = I_{2} \omega _{n} ^{2} \bar{U}^{{cy}} _{2} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{cy}} \hfill \\ \end{gathered} $$

(75)

$$ \begin{gathered} \left( {\frac{1}{{R(\zeta _{{co}} )^{2} }}} \right)\{ A_{{11}} \bar{U}^{{co}} _{{1,\zeta _{{co}} \zeta _{{co}} }} R(\zeta _{{co}} )^{2} + \bar{A}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{co}} \zeta _{{co}} }}^{{co}} R(\zeta _{{co}} )^{2} \hfill \\ - nR(\zeta _{{co}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{co}} }}^{{co}} - nR(\zeta _{{co}} )(A_{{12}} + A_{{66}} )\bar{U}^{{co}} _{{2,\zeta _{{co}} }} \hfill \\ \quad + \sin (\Theta )R(\zeta _{{co}} )A_{{11}} \bar{U}^{{co}} _{{1,\zeta _{{co}} }} + \cos (\Theta )R(\zeta _{{co}} )A_{{12}} \bar{U}^{{co}} _{{3,\zeta _{{co}} }} \hfill \\ \quad + \sin (\Theta )R(\zeta _{{co}} )\bar{A}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{co}} }}^{{co}} + ( - A_{{22}} \bar{U}^{{co}} _{3} \cos (\Theta ) + ((\bar{A}_{{22}} + \bar{A}_{{66}} )\bar{\Psi }_{\theta }^{{co}} \hfill \\ \quad + \bar{U}^{{co}} _{2} (A_{{22}} + A_{{66}} ))n)\sin (\Theta ) + (\bar{U}^{{co}} _{1} A_{{22}} + \bar{\Psi }_{\zeta }^{{co}} \bar{A}_{{22}} )\cos (\Theta )^{2} \hfill \\ \quad + ( - n^{2} A_{{66}} - A_{{22}} )\bar{U}^{{co}} _{1} - \bar{\Psi }_{\zeta }^{{co}} (n^{2} \bar{A}_{{66}} + \bar{A}_{{22}} )\} = I_{1} \omega _{n} ^{2} \bar{U}^{{co}} _{1} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{co}} \hfill \\ \end{gathered} $$

(76)

$$ \begin{gathered} \left( {\frac{1}{{R(\zeta _{{co}} )^{2} }}} \right)\{ \bar{A}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{co}} \zeta _{{co}} }}^{{co}} R(\zeta _{{co}} )^{2} + A_{{66}} \bar{U}^{{co}} _{{2,\zeta _{{co}} \zeta _{{co}} }} R(\zeta _{{co}} )^{2} \hfill \\ \quad + nR(\zeta _{{co}} )(A_{{12}} + A_{{66}} )\bar{U}^{{co}} _{{1,\zeta _{{co}} }} + nR(\zeta _{{co}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{co}} }}^{{co}} \hfill \\ \quad + \sin (\Theta )R(\zeta _{{co}} )\bar{A}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{co}} }}^{{co}} + \sin (\Theta )R(\zeta _{{co}} )A_{{66}} \bar{U}^{{co}} _{{2,\zeta _{{co}} }} \hfill \\ \quad + \cos (\Theta )R(\zeta _{{co}} )\kappa A_{{44}} \bar{\Psi }_{\theta }^{{co}} + (\bar{\Psi }_{\theta }^{{co}} \bar{A}_{{66}} - \bar{U}^{{co}} _{2} (\kappa A_{{44}} - A_{{66}} ))\cos (\Theta )^{2} \hfill \\ \quad + n\bar{U}^{{co}} _{2} (\kappa A_{{44}} + A_{{22}} )\cos (\Theta ) + n((A_{{22}} + A_{{66}} )\bar{U}^{{co}} _{1} \hfill \\ \quad + \bar{\Psi }_{\zeta }^{{co}} (\bar{A}_{{22}} + \bar{A}_{{66}} )\sin (\Theta ) + ( - n^{2} \bar{A}_{{22}} - \bar{A}_{{66}} )\bar{\Psi }_{\theta }^{{co}} - \bar{U}^{{co}} _{2} (n^{2} A_{{22}} + A_{{66}} )\} \hfill \\ \;\;\;= I_{1} \omega _{n} ^{2} \bar{U}^{{co}} _{2} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{co}} \hfill \\ \end{gathered} $$

(77)

$$ \begin{gathered} \left( {\frac{1}{{R(\zeta _{{co}} )^{2} }}} \right)\{ \kappa A_{{55}} R(\zeta _{{co}} )^{2} \bar{U}^{{co}} _{{3,\zeta _{{co}} \zeta _{{co}} }} + (R(\zeta _{{co}} )[R(\zeta _{{co}} )\kappa A_{{55}} - \bar{A}_{{12}} \cos (\Theta ))\bar{\Psi }_{{\zeta ,\zeta _{{co}} }}^{{co}} \hfill \\ \quad - R(\zeta _{{co}} )\cos (\Theta )A_{{12}} \bar{U}^{{co}} _{{1,\zeta _{{co}} }} + \sin (\Theta )R(\zeta _{{co}} )\kappa A_{{55}} \bar{U}^{{co}} _{{3,\zeta _{{co}} }} \hfill \\ \quad - \bar{U}^{{co}} _{3} \cos (\Theta )^{2} A_{{22}} + (( - A_{{22}} \bar{U}^{{co}} _{1} - \bar{A}_{{22}} \bar{\Psi }_{\zeta }^{{co}} )\sin (\Theta ) \hfill \\ \quad + (\bar{A}_{{22}} \bar{\Psi }_{\theta }^{{co}} + \bar{U}^{{co}} _{2} (\kappa A_{{44}} + A_{{22}} ))n)\cos (\Theta ) \hfill \\ \quad - ((nA_{{44}} \bar{\Psi }_{\theta }^{{co}} - A_{{44}} \bar{\Psi }_{\zeta }^{{co}} \sin (\Theta ))R(\zeta _{{co}} ) + n^{2} \bar{U}^{{co}} _{3} )\kappa \} \hfill \\ \;\;\;= I_{1} \omega _{n} ^{2} \bar{U}^{{co}} _{3} \hfill \\ \end{gathered} $$

(78)

$$ \begin{gathered} \left( {\frac{1}{{R(\zeta _{{co}} )^{2} }}} \right)\{ \bar{A}_{{11}} \bar{U}^{{co}} _{{1,\zeta _{{co}} \zeta _{{co}} }} R(\zeta _{{co}} )^{2} + \bar{\bar{A}}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{co}} \zeta _{{co}} }}^{{co}} R(\zeta _{{co}} )^{2} \hfill \\ \quad - nR(\zeta _{{co}} )(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{co}} }}^{{co}} - nR(\zeta _{{co}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{co}} _{{2,\zeta _{{co}} }} \hfill \\ \quad + ( - R(\zeta _{{co}} )^{2} A_{{55}} \kappa + \bar{A}_{{12}} \cos (\Theta )R(\zeta _{{co}} ))\bar{U}^{{co}} _{3} \hfill \\ \quad + \sin (\Theta )R(\zeta _{{co}} )\bar{A}_{{11}} \bar{U}^{{co}} _{{1,\zeta _{{co}} }} + \sin (\Theta )R(\zeta _{{co}} )\bar{\bar{A}}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{co}} }}^{{co}} \hfill \\ \quad - R(\zeta _{{co}} )^{2} A_{{55}} \kappa \bar{\Psi }_{\zeta }^{{co}} + ( - \bar{A}_{{22}} \bar{U}^{{co}} _{3} \cos (\Theta ) \hfill \\ \quad + ((\bar{\bar{A}}_{{22}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{\theta }^{{co}} + \bar{U}^{{co}} _{2} (\bar{A}_{{22}} + \bar{A}_{{66}} ))n)\sin (\Theta ) \hfill \\ \quad + (\bar{U}^{{co}} _{1} \bar{A}_{{22}} + \bar{\Psi }_{\zeta }^{{co}} \bar{\bar{A}}_{{22}} )\cos (\Theta )^{2} - (n^{2} A_{{66}} + A_{{22}} )\bar{U}^{{co}} _{1} + \bar{\Psi }_{\zeta }^{{co}} ( - n^{2} \bar{\bar{A}}_{{66}} - \bar{\bar{A}}_{{22}} )\} \hfill \\ \;\;\;= I_{2} \omega _{n} ^{2} \bar{U}^{{co}} _{1} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{co}} \hfill \\ \end{gathered} $$

(79)

$$ \begin{gathered} \left( {\frac{1}{{R(\zeta _{{co}} )^{2} }}} \right)\{ \bar{\bar{A}}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{co}} \zeta _{{co}} }}^{{co}} R(\zeta _{{co}} )^{2} + \bar{A}_{{66}} \bar{U}^{{co}} _{{2,\zeta _{{co}} \zeta _{{co}} }} R(\zeta _{{co}} )^{2} \hfill \\ \quad + nR(\zeta _{{co}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{co}} _{{1,\zeta _{{co}} }} + nR(\zeta _{{co}} )(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{co}} }}^{{co}} \hfill \\ \quad + \sin (\Theta )R(\zeta _{{co}} )\bar{\bar{A}}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{co}} }}^{{co}} + \sin (\Theta )R(\zeta _{{co}} )\bar{A}_{{66}} \bar{U}^{{co}} _{{2,\zeta _{{co}} }} \hfill \\ \quad - R(\zeta _{{co}} )^{2} \bar{\Psi }_{\theta }^{{co}} \kappa A_{{44}} - \kappa A_{{44}} (n\bar{U}^{{co}} _{3} - \cos (\Theta )\bar{U}^{{co}} _{2} )R(\zeta _{{co}} ) \hfill \\ \quad + n((\bar{A}_{{22}} + \bar{A}_{{66}} )\bar{U}^{{co}} _{1} + \bar{\Psi }_{\zeta }^{{co}} (\bar{\bar{A}}_{{22}} + \bar{\bar{A}}_{{66}} )\sin (\Theta ) \hfill \\ \quad + (\bar{\Psi }_{\theta }^{{co}} \bar{\bar{A}}_{{66}} + \bar{U}^{{co}} _{2} (\bar{A}_{{66}} )\cos (\Theta )^{2} + \cos (\Theta )\bar{U}^{{co}} _{3} n\bar{A}_{{22}} \hfill \\ \quad + ( - n^{2} \bar{\bar{A}}_{{22}} - \bar{\bar{A}}_{{66}} )\bar{\Psi }_{\theta }^{{co}} - \bar{U}^{{co}} _{2} (n^{2} \bar{A}_{{22}} + \bar{A}_{{66}} )\} \hfill \\ \;\;\; = I_{2} \omega _{n} ^{2} \bar{U}^{{co}} _{2} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{co}} \hfill \\ \end{gathered} $$

(80)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} \sin (\zeta _{{hs}} )^{2} }}} \right)\{ ( - \cos (\zeta _{{hs}} )^{2} A_{{11}} + A_{{11}} )\bar{U}^{{hs}} _{{1,\zeta _{{hs}} \zeta _{{hs}} }} + ( - \cos (\zeta _{{hs}} )^{2} \bar{A}_{{11}} + \bar{A}_{{11}} )\bar{\Psi }_{{\zeta ,\zeta _{{hs}} \zeta _{{hs}} }}^{{hs}} \hfill \\ \quad - (\cos (\zeta _{{hs}} )^{2} - 1)(\kappa A_{{55}} + A_{{11}} + A_{{12}} )\bar{U}^{{hs}} _{{3,\zeta _{{hs}} }} - n\sin (\zeta _{{hs}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{hs}} }}^{{hs}} \hfill \\ \quad - n\sin (\zeta _{{hs}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{hs}} _{{2,\zeta _{{hs}} }} + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )A_{{11}} \bar{U}^{{hs}} _{{1,\zeta _{{hs}} }} \hfill \\ \quad + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )\bar{A}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{hs}} }}^{{hs}} + ((\kappa A_{{55}} + A_{{12}} - A_{{22}} )\bar{U}^{{hs}} _{1} \hfill \\ \quad + \bar{\Psi }_{\zeta }^{{hs}} ( - \kappa A_{{55}} R + \bar{A}_{{12}} - \bar{A}_{{22}} ))\cos (\zeta _{{hs}} )^{2} + (\bar{U}^{{hs}} _{3} (A_{{11}} + A_{{22}} )\sin (\zeta _{{hs}} ) \hfill \\ \quad + ((\bar{A}_{{22}} + \bar{A}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} + \bar{U}^{{hs}} _{2} (A_{{22}} + A_{{66}} )n)\cos (\zeta _{{hs}} ) + \hfill \\ \quad ( - n^{2} A_{{66}} - \kappa A_{{55}} - A_{{12}} )\bar{U}^{{hs}} _{1} - \bar{\Psi }_{\zeta }^{{hs}} ( - \kappa A_{{55}} R + n^{2} \bar{A}_{{66}} + \bar{A}_{{12}} )\} \hfill \\ \;\;\;= I_{1} \omega _{n} ^{2} \bar{U}^{{hs}} _{1} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{hs}} \hfill \\ \end{gathered} $$

(81)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} \sin (\zeta _{{hs}} )^{2} }}} \right)\{ ( - \cos (\zeta _{{hs}} )^{2} \bar{A}_{{66}} + \bar{A}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{hs}} \zeta _{{hs}} }}^{{hs}} + ( - \cos (\zeta _{{hs}} )^{2} A_{{66}} + A_{{66}} )\bar{U}^{{hs}} _{{2,\zeta _{{hs}} \zeta _{{hs}} }} \hfill \\ \quad + n\sin (\zeta _{{hs}} )(A_{{12}} + A_{{66}} )\bar{U}^{{hs}} _{{1,\zeta _{{hs}} }} + n\sin (\zeta _{{hs}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{hs}} }}^{{hs}} \hfill \\ \quad + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )\bar{A}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{hs}} }}^{{hs}} + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )A_{{66}} \bar{U}^{{hs}} _{{2,\zeta _{{hs}} }} \hfill \\ \quad + (( - \kappa A_{{44}} R - 2\bar{A}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} + \bar{U}^{{hs}} _{2} (\kappa A_{{44}} - 2A_{{66}} ))\cos (\zeta _{{hs}} )^{2} \hfill \\ \quad + ((A_{{22}} + A_{{66}} )\bar{U}^{{hs}} _{1} + \bar{\Psi }_{\zeta }^{{hs}} (\bar{A}_{{22}} + \bar{A}_{{66}} ))n\cos (\zeta _{{hs}} ) + \hfill \\ \quad n\bar{U}^{{hs}} _{3} (\kappa A_{{44}} + A_{{12}} + A_{{22}} )\sin (\zeta _{{hs}} ) + (\kappa A_{{44}} R - n^{2} \bar{A}_{{22}} + \bar{A}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} \hfill \\ \quad - \bar{U}^{{hs}} _{2} (n^{2} A_{{22}} + \kappa A_{{44}} - A_{{66}} )\} = I_{1} \omega _{n} ^{2} \bar{U}^{{hs}} _{2} + I_{2} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{hs}} \hfill \\ \end{gathered} $$

(82)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} \sin (\zeta _{{hs}} )^{2} }}} \right)\{ ( - \cos (\zeta _{{hs}} )^{2} \kappa A_{{55}} + \kappa A_{{55}} )\bar{U}^{{hs}} _{{3,\zeta _{{hs}} \zeta _{{hs}} }} \hfill \\ \quad + (\cos (\zeta _{{hs}} )^{2} - 1)(\kappa A_{{55}} + A_{{11}} + A_{{12}} )\bar{U}^{{hs}} _{{1,\zeta _{{hs}} }} \hfill \\ \quad + (\cos (\zeta _{{hs}} )^{2} - 1)( - \kappa A_{{55}} R + \bar{A}_{{11}} + \bar{A}_{{12}} )\bar{\Psi }_{{\zeta ,\zeta _{{hs}} }}^{{hs}} \hfill \\ \quad + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )\kappa A_{{55}} \bar{U}^{{hs}} _{{3,\zeta _{{hs}} }} + \bar{U}^{{hs}} _{3} (A_{{11}} + 2A_{{12}} + A_{{22}} )\cos (\zeta _{{hs}} )^{2} \hfill \\ \quad - ((\kappa A_{{55}} + A_{{22}} + A_{{12}} )\bar{U}^{{hs}} _{1} + \bar{\Psi }_{\zeta }^{{hs}} ( - \kappa A_{{55}} R + \bar{A}_{{22}} + \bar{A}_{{12}} ))\sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} ) \hfill \\ \quad + n(( - \kappa A_{{44}} R + \bar{A}_{{22}} + \bar{A}_{{12}} )\bar{\Psi }_{\theta }^{{hs}} + \bar{U}^{{hs}} _{2} (\kappa A_{{44}} + A_{{12}} + A_{{22}} ))\sin (\zeta _{{hs}} ) \hfill \\ \quad - \bar{U}^{{hs}} _{3} (\kappa n^{2} A_{{44}} + A_{{11}} + 2A_{{12}} + A_{{22}} )\} = I_{1} \omega _{n} ^{2} \bar{U}^{{hs}} _{3} \hfill \\ \end{gathered} $$

(83)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} \sin (\zeta _{{hs}} )^{2} }}} \right)\{ ( - \cos (\zeta _{{hs}} )^{2} \bar{A}_{{11}} + \bar{A}_{{11}} )\bar{U}^{{hs}} _{{1,\zeta _{{hs}} \zeta _{{hs}} }} + ( - \cos (\zeta _{{hs}} )^{2} \bar{\bar{A}}_{{11}} + \bar{\bar{A}}_{{11}} )\bar{\Psi }_{{\zeta ,\zeta _{{hs}} \zeta _{{hs}} }}^{{hs}} \hfill \\ \quad + (\cos (\zeta _{{hs}} )^{2} - 1)(\kappa A_{{55}} R + \bar{\bar{A}}_{{11}} + \bar{\bar{A}}_{{12}} )\bar{U}^{{hs}} _{{3,\zeta _{{hs}} }} - n\sin (\zeta _{{hs}} )(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{hs}} }}^{{hs}} \hfill \\ \quad - n\sin (\zeta _{{hs}} )(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{U}^{{hs}} _{{2,\zeta _{{hs}} }} + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )\bar{A}_{{11}} \bar{U}^{{hs}} _{{1,\zeta _{{hs}} }} \hfill \\ \quad + \sin (\zeta _{{hs}} )\cos (\zeta _{{hs}} )\bar{\bar{A}}_{{11}} \bar{\Psi }_{{\zeta ,\zeta _{{hs}} }}^{{hs}} + ((\kappa A_{{55}} R + \bar{A}_{{12}} - \bar{A}_{{22}} )\bar{U}^{{hs}} _{1} \hfill \\ \quad + \bar{\Psi }_{\zeta }^{{hs}} ( - \kappa A_{{55}} R^{2} + \bar{\bar{A}}_{{12}} - \bar{\bar{A}}_{{22}} ))\cos (\zeta _{{hs}} )^{2} + (\bar{U}^{{hs}} _{3} (\bar{A}_{{11}} + \bar{A}_{{22}} )\sin (\zeta _{{hs}} ) \hfill \\ \quad + n((\bar{\bar{A}}_{{22}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} + \bar{U}^{{hs}} _{2} (\bar{A}_{{22}} + \bar{A}_{{66}} )))\cos (\zeta _{{hs}} ) + \hfill \\ \quad ( - n^{2} \bar{A}_{{66}} - \kappa A_{{55}} R - \bar{A}_{{12}} )\bar{U}^{{hs}} _{1} - \bar{\Psi }_{\zeta }^{{hs}} ( - \kappa A_{{55}} R^{2} + n^{2} \bar{\bar{A}}_{{66}} + \bar{\bar{A}}_{{12}} )\} \hfill \\ \;\;\; = I_{2} \omega _{n} ^{2} \bar{U}^{{hs}} _{1} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\zeta }^{{hs}} \hfill \\ \end{gathered} $$

(84)

$$ \begin{gathered} \left( {\frac{1}{{R^{2} \sin (\zeta _{{hs}} )^{2} }}} \right)\{ ( - \cos (\zeta _{{hs}} )^{2} \bar{\bar{A}}_{{66}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\theta ,\zeta _{{hs}} \zeta _{{hs}} }}^{{hs}} + ( - \cos (\zeta _{{hs}} )^{2} \bar{A}_{{66}} + A_{{66}} )\bar{U}^{{hs}} _{{2,\zeta _{{hs}} \zeta _{{hs}} }} \hfill \\ \quad + n\sin (\zeta _{{hs}} )(\bar{A}_{{12}} + \bar{A}_{{66}} )\bar{U}^{{hs}} _{{1,\zeta _{{hs}} }} + n\sin (\zeta _{{hs}} )(\bar{\bar{A}}_{{12}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{{\zeta ,\zeta _{{hs}} }}^{{hs}} \hfill \\ \quad + \sin (\zeta _{{hs}} )\cos (\vartheta )\bar{\bar{A}}_{{66}} \bar{\Psi }_{{\theta ,\zeta _{{hs}} }}^{{hs}} + \sin (\zeta _{{hs}} )\cos (\vartheta \zeta _{{hs}} )\bar{A}_{{66}} \bar{U}^{{hs}} _{{2,\zeta _{{hs}} }} \hfill \\ \quad + (( - \kappa A_{{44}} R^{2} - 2\bar{\bar{A}}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} - \bar{U}^{{hs}} _{2} (\kappa A_{{44}} R + 2A_{{66}} ))\cos (\zeta _{{hs}} )^{2} \hfill \\ \quad + ((\bar{A}_{{22}} + \bar{A}_{{66}} )\bar{U}^{{hs}} _{1} + \bar{\Psi }_{\zeta }^{{hs}} (\bar{\bar{A}}_{{22}} + \bar{\bar{A}}_{{66}} ))n\cos (\zeta _{{hs}} ) - \hfill \\ \quad n\bar{U}^{{hs}} _{3} (\kappa A_{{44}} R - \bar{A}_{{12}} - \bar{A}_{{22}} )\sin (\zeta _{{hs}} ) + ( - \kappa A_{{44}} R^{2} - n^{2} \bar{\bar{A}}_{{22}} + \bar{\bar{A}}_{{66}} )\bar{\Psi }_{\theta }^{{hs}} \hfill \\ \quad - \bar{U}^{{hs}} _{2} (n^{2} A_{{22}} - \kappa A_{{44}} R - A_{{66}} )\} = I_{2} \omega _{n} ^{2} \bar{U}^{{hs}} _{2} + I_{3} \omega _{n} ^{2} \bar{\Psi }_{\theta }^{{hs}} \hfill \\ \end{gathered} $$

(85)