Formulation and evaluation of a new four-node quadrilateral element for analysis of the shell structures

Abstract

Shell structures are lightweight constructions which are extensively used by engineering. Due to this reason presenting an appropriate shell element for analysis of these structures has become an interesting issue in recent decades. This study presents a new rectangular flat shell element called ACM-SQ4 obtained by combining bending and membrane elements. The bending element is a well-known plate bending element called ACM which is based on the classical thin-plate theory and the membrane element is an unsymmetric quadrilateral element called US-Q4θ, the test function of this element is improved by the Allman-type drilling DOFs and a rational stress field is used as the element’s trial function. Finally, some numerical benchmark problems are used to evaluate the performance of the proposed flat shell element. The obtained results show that despite its simple formulation, the proposed element has reasonable accuracy and acceptable convergence in comparison with other shell elements.

1 Introduction

Nowadays, shell structures (the structures that are thin in thickness and have considerable length in other two directions) are widely used in engineering, specifically in the automotive and construction industries [1]. Due to their geometrical complexity, various loading conditions and mixed boundary conditions, analytical methods cannot meet the engineer’s needs. Accordingly, numerical methods are the best solution to analyze such structures, among numerical methods finite element method is a conventional selection for engineers. Using an appropriate element which has reasonable accuracy and fast convergence is one of the serious challenges in the finite element method therefore, different kinds of elements were proposed by researchers. For instance, Carrera and Petrolo [2] presented a modified beam element for the numerical analysis of shell structures. Using a combination of the edge-based smoothed finite element (ES-FEM) and the node-based smoothed finite element (NS-FEM) Nguyen et al. [3] developed a triangular shell element with acceptable accuracy in benchmark problems. Hernandez et al. [4] evaluated the dynamic behavior of the cylindrical shell using finite element method. A practical study was done by Yuqi et al. [5] on flange earring steel plates in deep-drawing process using the triangular shell element.

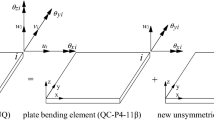
In general, shell elements used in the finite element analysis of shell structures are flat shell element [6], curved shell element [7], axisymmetric shell element [8] and degenerated solid element [9], the merits and demerits of each type are detailed in Gallagher research [10]. Among the shell elements, flat shell elements are quite popular element for analyses of shell structures due to the simplicity of formulation and reasonable computational costs. In small deformation the stretching and bending deformation can be considered independently for a flat shell element, hence the element can be developed by combining membrane and bending elements. Using the element combining method, Botaz et al. [11] proposed the DKQ16 square element and evaluated its accuracy by numerical benchmark problems. In another research [12] they introduced new flat shell elements by using discrete Kirchhoff pentagonal and hexagonal plate elements and combining them with RP5 and RH6 membrane elements, respectively, then evaluated the accuracy of each one through some numerical benchmark problems. Zengjie and Wanji [13] evaluated the performance of a new triangular shell element using some numerical problems. The shell element was formed by assemblage of the RDKTM bending element and CST membrane element. Sabourin et al. [14] introduced a new quadrilateral shell element called DKS16, which is the superposition of a modified DKT12 membrane element and quadrilateral S4 element, the accuracy of the proposed element evaluated using some geometrically nonlinear benchmark problems. For geometrically nonlinear analysis of composite plates Wang and Sun [15] introduced a new flat shell element using a four-node membrane element based on the quadrilateral area coordinate method and combining it with a four-node bending element based on the Timoshenko beam function. Zhang et al. [16] proposed a new triangular shell element through combining an ANDES-based membrane element and a refined nonconforming element method-based bending element then the performance of the proposed element was evaluated by experimental results and some numerical problems. Hamadi et al. [17] introduced a flat shell element called ACM_RSBE5 through the superposition of elements and examined its accuracy using experimental results. Yan et al. [18] introduced a quadrilateral flat shell element by combination of a HDF (hybrid displacement function) plate bending element and a HSF (hybrid stress function) membrane element, called HDF-HSF, then the performance of the element evaluated through numerical standard problems.

Using drilling degrees of freedom in element is one of the main improvement method in shell structural analysis. Allman [19] enhanced the performance of CST element in numerical analyses of problems by adding the drilling degree of freedom to each node of the element. 18DOF triangular flat shell element was presented by Providas and Kattis [20] through combining a triangular plate bending element and a new triangular membrane element which was obtained by a novel approach for adding the drilling rotations to the CST element. Pimpinelli [21] proposed a flat shell element which was the combination of DKQ plate bending element and a new strain-based membrane element with drilling degrees of freedom, the accuracy of the proposed element tested using numerical problems. A new quadrilateral membrane element with drilling rotations introduced by Madeo et al. [22]. The element was based on the mixed Hellinger–Reissner variational formulation and was less sensitive to the mesh distortion. Choi et al. [23] assessed the performance of the new hybrid Trefftz plane element with drilling degrees of freedom by some benchmark problems. For the nonlinear analysis of reinforced concrete structures Rojas et al. [24] presented a quadrilateral membrane element with drilling degrees of freedom using a blended field interpolation for the displacements over the element.

Adding mid-side nodes between those in the corners is another improvement method in the shell elements. This method improves the element accuracy in the analyses of shell structures; however, it increases the computational costs. As an example, Nestorovic et al. [25] proposed a nine-node triangular degenerated shell element based on the Reissner–Mindlin theory to analyze composite structures. Areias et al. [26] presented a nine-node shell element that was improved in both out-of-plane and in-plane bending cases by mixed formulation. They also showed the robustness of the proposed element is adequate for crack propagation simulation. For geometrically nonlinear analysis of shell structures Kim et al. [27] proposed an eight-node shell element, the ANS method was employed in the proposed element to eliminate various locking problems. Li et al. [28] have presented a 9-node curved shell element based on the co-rotational formulation to analyze shell structures then examined the performance of the proposed element by some numerical problems. For the nonlinear analysis of shell structures Li et al. [29] proposed a six-node triangular shell element based on the Reissner–Mindlin theory and the assumed strain method, in formulation of the proposed element rigid body rotation were excluded from the local nodal variables. The effort of these studies was introducing an element with simple formulation, appropriate accuracy and reasonable convergence that are the main issue of the present study.

The present study proposes a novel flat shell element defined by 24 degrees of freedom (3 translations and 3 rotations for each node) called ACM-SQ4 which is the superposition of quadrilateral bending and membrane elements, the most important feature of the superposition method is the introduction of a new element with simple formulation. In this method at first, the parents elements should be checked to have appropriate performance then should be investigated whether this combination leads to a shell element with reasonable performance or not. The membrane element proposed by Shang and Ouyang [30] is an unsymmetric four-node low-order element with drilling degrees of freedom, called US-Q4θ. The test function of the membrane element is a new type of displacement field which was improved by drilling degrees of freedom. The element’s trial function is a rational stress field which was computed by the analytical solution of plane problem. Moreover, the quasi-conforming method was used to express the relations between the assumed stress field and the nodal degrees of freedom. The bending element presented by Clough and Adini [31] is a nonconforming plate bending element based on the Kirchhoff plate theory, named ACM. Finally, the performance of the proposed element is evaluated through some numerical benchmark problems.

2 Formulation

As mentioned earlier, the proposed flat shell element is a combination of US-Q4θ membrane and ACM plate bending elements, correspondingly the element stiffness matrix is a combination of those elements. As shown in Fig. 1, each node of the shell element has 6 degrees of freedom.

Fig. 1

Detail of the element composition

The general element equation for membrane element is shown in Eq. (1).

$$ {\mathbf{K}}_{\text{m}} {\mathbf{q}}_{\text{m}} = {\mathbf{f}}_{\text{m}} , $$

(1)

where ${\mathbf{K}}_{\text{m}}$, ${\mathbf{q}}_{\text{m}}$ and ${\mathbf{f}}_{\text{m}}$ are the stiffness matrix, the nodal displacement and the element load vector of the membrane element, respectively. The general element equation of the plate bending element is written as

$$ {\mathbf{K}}_{\text{p}} {\mathbf{q}}_{\text{p}} = {\mathbf{f}}_{\text{p}} , $$

(2)

where ${\mathbf{K}}_{\text{p}}$, ${\mathbf{q}}_{\text{p}}$ and ${\mathbf{f}}_{\text{p}}$ are the stiffness matrix, the nodal displacement and the element load vector of the plate bending element, respectively. By superposition of the membrane and plate bending equations, the force–displacement relationship of the flat shell element is defined as follows

$$ {\mathbf{Kq}} = {\mathbf{f}}, $$

(3)

where ${\mathbf{K}}$, ${\mathbf{q}}$ and ${\mathbf{f}}$ are the stiffness matrix, the nodal displacement and the element load vector of the flat shell element, respectively. The sub-matrix of the stiffness matrix for the ith node of the shell element is

$$ {\mathbf{K}}_{i} = \left[ {\begin{array}{*{20}c} {k_{11}^{\text{m}} } & {k_{12}^{\text{m}} } & 0 & 0 & 0 & {k_{13}^{\text{m}} } \\ {k_{21}^{\text{m}} } & {k_{22}^{\text{m}} } & 0 & 0 & 0 & {k_{23}^{\text{m}} } \\ 0 & 0 & {k_{11}^{\text{p}} } & {k_{12}^{\text{p}} } & {k_{13}^{\text{p}} } & 0 \\ 0 & 0 & {k_{21}^{\text{p}} } & {k_{22}^{\text{p}} } & {k_{23}^{\text{p}} } & 0 \\ 0 & 0 & {k_{31}^{\text{p}} } & {k_{32}^{\text{p}} } & {k_{33}^{\text{p}} } & 0 \\ {k_{31}^{\text{m}} } & {k_{32}^{\text{m}} } & 0 & 0 & 0 & {k_{33}^{\text{m}} } \\ \end{array} } \right],\quad (i = 1 - 4), $$

(4)

where $k_{jl}^{\text{m}}$ and $k_{jl}^{\text{p}}$ are elements of ${\mathbf{K}}_{\text{m}}$ and ${\mathbf{K}}_{\text{p}}$ for the ith node, respectively. Elements of the nodal displacement vector of the element for the ith node are

$$ {\mathbf{q}}_{i} = \{ \begin{array}{*{20}c} {q_{1}^{\text{m}} } & {q_{2}^{\text{m}} } & {q_{1}^{\text{p}} } & {q_{2}^{\text{p}} } & {q_{3}^{\text{p}} } & {q_{3}^{\text{m}} } \\ \end{array} \} ,(i = 1 \sim 4), $$

(5)

where $q_{j}^{\text{m}}$ and $q_{j}^{\text{p}}$ are the elements of ${\mathbf{q}}_{\text{m}}$ and ${\mathbf{q}}_{\text{p}}$ for the ith node, respectively. It is necessary to describe a rotation matrix $({\varvec{\uplambda}})$ to transform structural quantities including displacement, force, etc., between local coordinate system and global coordinate system. The elements of the rotation matrix $(l_{i} ,m_{i} \;{\text{and}}\;n_{i} )$ are the cosines of the angles between local and global coordinate axes; details of the rotation matrix computation are presented by Cook [32].

$$ {\varvec{\uplambda}} = \left[ {\begin{array}{*{20}c} {l_{1} } & {m_{1} } & {n_{1} } \\ {l_{2} } & {m_{2} } & {n_{2} } \\ {l_{3} } & {m_{3} } & {n_{3} } \\ \end{array} } \right] $$

(6)

Accordingly, the stiffness matrix $({\mathbf{K}}_{\text{global}} )$, nodal displacement $({\mathbf{q}}_{\text{global}} )$ and element load vector $({\mathbf{f}}_{\text{global}} )$ of the shell element in global coordinate system can be obtained from their local forms

$$ \varvec{K}_{\text{global}} { = }{\mathbf{T}}^{\text{T}} {\mathbf{K}}_{\text{local}} {\mathbf{T}}, $$

(7)

$$ \varvec{q}_{\text{global}} = \varvec{T}^{\text{T}} \varvec{q}_{\text{local}} , $$

(8)

$$ \varvec{f}_{\text{global}} = \varvec{T}^{\text{T}} \varvec{f}_{\text{local}} , $$

(9)

where

$$ {\mathbf{T}}\varvec{ = }\left[ {\begin{array}{*{20}c} {\varvec{\uplambda}} & {} & {} & {} & {} & {} & {} & {} \\ {} & {\varvec{\uplambda}} & {} & {} & {} & {} & \varvec{0} & {} \\ {} & {} & {\varvec{\uplambda}} & {} & {} & {} & {} & {} \\ {} & {} & {} & {\varvec{\uplambda}} & {} & {} & {} & {} \\ {} & {} & {} & {} & {\varvec{\uplambda}} & {} & {} & {} \\ {} & {} & {} & {} & {} & {\varvec{\uplambda}} & {} & {} \\ {} & \varvec{0} & {} & {} & {} & {} & {\varvec{\uplambda}} & {} \\ {} & {} & {} & {} & {} & {} & {} & {\varvec{\uplambda}} \\ \end{array} } \right]_{{24{ \times }24}} . $$

(10)

2.1 The plate bending component

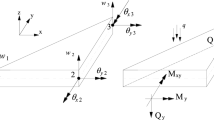
The bending part of the proposed shell element is a 12DOF nonconforming quadrilateral plate bending element, called ACM. As shown in Fig. 2, the nodal degrees of freedom variables of the bending element are $w_{i}$,$\theta_{xi}$ and $\theta_{yi}$, where $w_{i}$,$\theta_{xi} (\partial w_{i} /\partial \theta_{y} )$ and $\theta_{yi} ( - \partial w_{i} /\partial \theta_{x} )$ are the translation along the z-axis and bending rotations along the x- and y-axes for the ith node, respectively. The ACM element is chosen because it has simple formulation and appropriate accuracy in bending-dominated problems among the bending elements.

Fig. 2

The plate bending element geometry and nodal degrees of freedom

The nodal displacement vector of the plate bending element is

$$ {\mathbf{q}}_{\text{p}}^{\text{T}} = \{ \begin{array}{*{20}c} {w_{1} } & {\theta_{x1} } & {\theta_{y1} } & {w_{2} } & {\theta_{x2} } & {\theta_{y2} } & {w_{3} } & {\theta_{x3} } & {\theta_{y3} } & {w_{4} } & {\theta_{x4} } & {\theta_{y4} } \\ \end{array} \} . $$

(11)

The plate bending element is a non-conforming element based on the Kirchhoff plate theory [33], a significant advantage of this element is the simple formulation of assumed displacement field that provides reasonable accuracy in bending problems. Accordingly, the deflection of the element considered in the z direction (without any stretching) and assumed to be a function of x and y only, w = w(x, y). The assumed displacement field is a fourth-order polynomial expression in terms of the 12 parameters (since the bending element has 12 degrees of freedom) as follows

$$ w(x,y) = a_{1} + a_{2} x + a_{3} y + a_{4} x^{2} + a_{5} xy + a_{6} y^{2} + a_{7} x^{3} + a_{8} x^{2} y + a_{9} xy^{2} + a_{10} y^{3} + a_{11} x^{3} y + a_{12} xy^{3} . $$

(12)

The constants $a_{i}$ can be evaluated through the 12 simultaneous equations linking the values of $w_{i}$, $\theta_{xi}$ and $\theta_{yi} .$ The matrix form of the equations is:

$$ \left\{ {\begin{array}{*{20}c} {w_{i} } \\ {\theta_{xi} } \\ {\theta_{yi} } \\ {w_{j} } \\ {\begin{array}{*{20}c} . \\ . \\ \end{array} } \\ {\theta_{yn} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 1 & {x_{i} } & {y_{i} } & {x_{i}^{2} } & {x_{i} y_{i} } & {y_{i}^{2} } & {x_{i}^{3} } & {x_{i}^{2} y_{i} } & {x_{i} y_{i}^{2} } & {y_{i}^{3} } & {x_{i}^{3} y_{i} } & {x_{i} y_{i}^{3} } \\ 0 & 0 & 1 & 0 & {x_{i} } & {2_{{}} y_{i} } & 0 & {x_{i}^{2} } & {2_{{}} x_{i} y_{i} } & {3_{{}} y_{i}^{2} } & {x_{i}^{3} } & {3_{{}} x_{i} y_{i}^{2} } \\ 0 & { - 1} & 0 & { - 2_{{}} x_{i} } & { - y_{i} } & 0 & { - 3_{{}} x_{i}^{2} } & { - 2_{{}} x_{i} y_{i} } & { - y_{i}^{2} } & 0 & { - 3_{{}} x_{i}^{2} y_{i} } & { - y_{i}^{3} } \\ 1 & {x_{j} } & {y_{j} } & {x_{j}^{2} } & {x_{j} y_{j} } & {y_{j}^{2} } & {x_{j}^{3} } & {x_{j}^{2} y_{j} } & {x_{j} y_{j}^{2} } & {y_{j}^{3} } & {x_{j}^{3} y_{j} } & {x_{j} y_{j}^{3} } \\ . & . & . & . & . & . & . & . & . & . & . & . \\ . & . & . & . & . & . & . & . & . & . & . & . \\ 0 & { - 1} & 0 & { - 2_{{}} x_{n} } & { - y_{n} } & 0 & { - 3_{{}} x_{n}^{2} } & { - 2_{{}} x_{n} y_{n} } & { - y_{n}^{2} } & 0 & { - 3_{{}} x_{n}^{2} y_{n} } & { - y_{n}^{3} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {a_{1} } \\ {a_{2} } \\ {a_{3} } \\ {a_{4} } \\ . \\ . \\ {a_{12} } \\ \end{array} } \right\}, $$

(13)

where $x_{i}$ and $y_{i}$ represent the location of the ith node. Equation (13) can be rewritten as

$$ {\mathbf{q}}_{\text{p}} = {\mathbf{Ca}}, $$

(14)

where C is the first matrix on the right-side of the Eq. (13). Finally the constant $\mathcal{a}_{1}$ through $\mathcal{a}_{12}$ are determined as follows

$$ {\mathbf{a}} = {\mathbf{C}}^{ - 1} {\mathbf{q}}_{\text{p}} . $$

(15)

The curvature–displacement relationship of the bending element is defined as follows

$$ \left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{y} } \\ {\kappa_{xy} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & { - 2} & 0 & 0 & { - 6x} & { - 2y} & 0 & 0 & { - 6xy} & 0 \\ 0 & 0 & 0 & 0 & 0 & { - 2} & 0 & 0 & { - 2x} & { - 6y} & 0 & { - 6xy} \\ 0 & 0 & 0 & 0 & { - 2} & 0 & 0 & { - 4x} & { - 4y} & 0 & { - 6x^{2} } & { - 6y^{2} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {a_{1} } \\ {a_{2} } \\ {a_{3} } \\ . \\ . \\ . \\ {a_{12} } \\ \end{array} } \right\}, $$

(16)

where $\kappa_{x} ,$$\kappa_{y}$ and $\kappa_{xy}$ are the elements of curvature vector that are equal to $\partial^{2} w/\partial x^{2}$, $\partial^{2} w/\partial y^{2}$ and $\partial^{2} w/\partial x\partial y,$ respectively. Equation (16) is summarized as

$$ {\varvec{\upkappa}} = {\mathbf{Qa}}. $$

(17)

By substituting Eq. (15) in Eq. (17) the curvature–displacement relationship of the ACM plate bending element will be as

$$ {\varvec{\upkappa}} = {\mathbf{QC}}^{ - 1} {\mathbf{q}}_{\text{p}} . $$

(18)

Finally, the bending element stiffness matrix is expressed by

$$ {\mathbf{K}}_{\text{p}} = \iint {({\mathbf{QC}}^{ - 1} )^{\text{T}} {\mathbf{D}}_{{{\text{p}}_{{}} }} {\mathbf{QC}}^{ - 1} {\text{d}}A,} $$

(19)

where ${\mathbf{D}}_{\text{p}}$ is the plate elasticity matrix. Reference [34] provides more details about the ACM plate bending element. “Appendix A” presents explicit form of the shape functions and usual form of the stiffness matrix in terms of natural coordinate system. The other advantage of the ACM bending element is its formulation that was provided in both global and natural coordinate systems.

2.2 The membrane component

The membrane element is a 12DOF unsymmetric quadrilateral element, called US-Q4θ. This element can be an appropriate choice because the accuracy and convergence of the membrane element are acceptable in membrane-dominated problems and its formulation is one of the simplest among the membrane elements. Figure 3 shows the membrane element with following degrees of freedom $u_{i}$, $v_{i}$ and $\theta_{zi}$ where $u_{i}$ and $v_{i}$ are the nodal translations along the x- and y-axes and $\theta_{zi}$ is the drilling rotation along the z-axis. The valuable advantage of the membrane element formulation is the accurate integral even for zero or negative Jacobian determinant. Moreover, the drilling vertex rotations of the US-Q4θ membrane element causes avoidance singularity problem when the element is used in a flat shell element through superposition method.

Fig. 3

The membrane element geometry and nodal degrees of freedom

The nodal displacement vector of the membrane element is

$$ {\mathbf{q}}_{\text{m}}^{\text{T}} = \{ \begin{array}{*{20}c} {u_{1} } & {v_{1} } & {\theta_{z1} } & {u_{2} } & {v_{2} } & {\theta_{z2} } & {u_{3} } & {v_{3} } & {\theta_{z3} } & {u_{4} } & {v_{4} } & {\theta_{z4} } \\ \end{array} \} . $$

(20)

The test function and trial function of the membrane element are based on the displacement field and stress field, respectively. Therefore, the membrane element stiffness matrix is expressed by

$$ {\mathbf{K}}_{\text{m}} = \int {\int {{\mathbf{B}}^{\text{T}} {\mathbf{HM}}^{ - 1}_{{}} {\mathbf{V}}t{\text{d}}A} } , $$

(21)

where t is the thickness of the membrane element, B is related to the displacement field and matrices H, M and V are deduced by the stress field. Accordingly, the strain matrix B is

$$ {\mathbf{B}} = \left[ {\begin{array}{*{20}c} \ldots & {} \\ \end{array} \begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial x}} & 0 & {\frac{{ - \partial N_{i} (y - y_{i} )}}{2\partial x}} \\ 0 & {\frac{{\partial N_{i} }}{\partial y}} & {\frac{{\partial N_{i} (x - x_{i} )}}{2\partial y}} \\ {\frac{{\partial N_{i} }}{\partial y}} & {\frac{{\partial N_{i} }}{\partial x}} & {\frac{{\partial N_{i} (x - x_{i} )}}{2\partial x} - \frac{{\partial N_{i} (y - y_{i} )}}{2\partial y}} \\ \end{array} \begin{array}{*{20}c} {} & \ldots \\ \end{array} } \right],\quad (i = 1 - 4). $$

(22)

In which x = $\sum\nolimits_{{i =_{{}} 1}}^{4} {N_{i} x_{i} }$, y = $\sum\nolimits_{{i =_{{}} 1}}^{y} {N_{i} y_{i} }$ and $N_{i}$ is the bilinear shape function of four-node isoparametric element in natural coordinates $(\xi ,\eta )$ for the ith node:

$$ N_{i} (\xi ,\eta ) = \frac{1}{4}(1 + \xi_{i} \xi )(1 + \eta_{i} \eta ),\quad (i = 1 - 4), $$

(23)

where $\xi_{i} = [\begin{array}{*{20}c} { - 1} & 1 & 1 & { - 1} \\ \end{array} ]$ and $\eta_{i} = \left[ {\begin{array}{*{20}c} { - 1} & { - 1} & 1 & 1 \\ \end{array} } \right]$, for i = 1, 2, 3, 4, are the nodal coordinates of the element in the natural coordinate system. Matrices M and V are expressed by

$$ {\mathbf{M}} = \int {\int {{\mathbf{H}}^{\text{T}} {\mathbf{D}}_{m}^{ - 1} {\mathbf{H}}t{\text{d}}A,} } $$

(24)

$$ {\mathbf{V}} = \int {\int {{\mathbf{H}}^{\text{T}} {\mathbf{B}}t{\text{d}}A} } , $$

(25)

where ${\mathbf{D}}_{m}$ is the elasticity matrix for membrane element and elements of matrix H are calculated using the airy stress function theory as follows

$$ {\mathbf{H}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 2 & 0 & 0 & {2x} & {6y} \\ 2 & 0 & 0 & {6x} & {2y} & 0 & 0 \\ 0 & { - 1} & 0 & 0 & { - 2x} & { - 2y} & 0 \\ \end{array} } \right]. $$

(26)

3 Numerical test

In this section, the performance of the proposed ACM-SQ4 shell element is evaluated using some numerical benchmark problems. As should be noted the ACM-SQ4 element is proposed for analysis of shell structures with flat geometry, in geometric nonlinear analysis of shell structures the warped geometry will happen that means the proposed element cannot be used for geometric nonlinear analysis. To assess the accuracy of the element, the obtained results are compared with other elements as listed in Table 1.

Table 1 List of considered elements in this study

3.1 The patch tests

The bending and membrane components of the proposed flat shell element passed all patch tests for membrane and plate elements; hence the developed ACM-SQ4 shell element which is a combination of them can pass all the patch tests.

3.2 Square plate problem

To evaluate the accuracy of the proposed element in bending-dominated problem, a clamped square plate subjected to a uniformly distributed load of pressure P is analyzed. Due to symmetry one-quarter of the plate (ABCD region) is modeled, as shown in Fig. 4a. The boundary conditions for the considered region are: $v = \theta_{x} = \theta_{z} = 0$ along AD, $u = \theta_{y} = \theta_{z} = 0$ along AB and $u = v = w = \theta_{x} = \theta_{y} = \theta_{z} = 0$ along CD and BC. Figure 4b shows the performance of the proposed element by the contour plot for the Von Mises stress distribution.

Fig. 4

Clamped square plate. a Geometry and material description $(a = 1,$$P = 10^{ - 5}$ thickness $t = 0.001,$ elastic modouls $E = 1.092 \times 10^{3}$ and poisson ratio $\nu = 0.3)$. b Contour plot of Von Mises stress distribution

Table 2 shows the normalized displacement $(w_{\text{A}} /w_{\text{ref}} )$ at the center of square plate problem using $N \times N$(N = 4, 8, 16) element meshes.

Table 2 Normalized deflection at center of the clamped square plate

Furthermore, the results of other shell elements are listed in Table 2 and the convergence plots are given in Fig. 5. For clamped square plate, the reference displacement at the plate center was obtained using $0.1265{\text{Pa}}^{4} /D$ where $D = Et^{3} /(12(1 - \nu^{2} ))$.

Fig. 5

Convergence of normalized deflection for the clamped square plate at point A

The results show that the proposed flat shell element has reasonable accuracy with appropriate convergence for clamped square plate as a benchmark bending-dominated problem. The percent difference between the analytical solution and numerical solution obtained for the proposed element is only 0.2%.

3.3 Cantilever beam

This is a standard problem to assess the performance of the shell elements in membrane-dominated problem. Figure 6a illustrates a cantilever beam that is subjected to a shear load at its free edge. The performance of the proposed flat shell element is shown by the contour plot for the Von Mises stress distribution in Fig. 6b.

Fig. 6

Cantilever beam subjected to tip shear load. a Geometry and material description ($E = 3 \times 10^{4} ,$$\nu = 0.25,$$t = 1,$$P = 40,$ width $w = 12$ and length $L = 48$). b Contour plot of Von Mises stress distribution

Table 3 presents the normalized results $(w_{\text{tip}} /w_{\text{ref}} )$ of the tip deflection using $N \times 4N$(N = 1, 2, 4) element meshes. The results for the proposed shell element and the other ones have been normalized using the analytical value $(w_{\text{ref}} = 0.3558)$ suggested by Timoshenko [54].

Table 3 Normalized tip deflection for the cantilever beam

As shown in Table 3, the proposed ACM-SQ4 element provides acceptable performance in comparison with other shell elements. Regarding the analytical solution, it can be seen that the error of the proposed element is less than 0.1%. Moreover, the result of ACM-SQ4 element converges to the analytical solution with less number of elements, shown in Fig. 7.

Fig. 7

Convergence of normalized tip deflection for the cantilever beam

3.4 Pinched cylinders with end diaphragms

Figure 8a shows a cylinder with end rigid diaphragms subjected to a pair of concentrated forces at cylinder mid-length. The pinched cylinder is a standard problem to evaluate the performance of the shell element in bending-dominated problem with the presence of complex membrane and in-extensible bending. Due to the symmetry conditions, the ABCD region (one-eighth of the cylinder) is analyzed. The boundary conditions are: $u = w = \theta_{y} = 0$ along AD, $u = \theta_{y} = \theta_{z} = 0$ along AB, $v = \theta_{x} = \theta_{z} = 0$ along BC, and $w = \theta_{x} = \theta_{y} = 0$ along DC. Figure 8b depicts the contour plot of analyzed model for the transverse displacement along the z direction using ACM-SQ4 element.

Fig. 8

Pinched cylinder with ends rigid diaphragm. a Geometry and material description ($E = 3 \times 10^{6} ,$$\nu = 0.3,$$t = 3,$$L = 600$ and $R = 300$). b Contour plot of transverse displacement

For all shell elements, the normalized numerical results $(w_{\text{B}} /w_{\text{ref}} )$ using $N \times N$(N = 4, 8, 16) element meshes are presented in Table 4. The numerical results are normalized by the analytical value for the deflection of load point $(w_{\text{ref}} = 1.8248 \times 10^{ - 5} )$ proposed by Flügge [55].

Table 4 Normalized displacement at point B for the pinched cylinder

The convergence plots of the normalized displacement are shown in Fig. 9; for better distinction the convergence plots are drawn for the new-version elements. It is observed that the accuracy of the ACM-SQ4 is reasonable and converges rapidly to the analytical solution. Additionally, in comparison to analytical solution the error of the proposed element is only 0.3%.

Fig. 9

Convergence of normalized displacement at point B for the pinched cylinder

3.5 Scordelis–Lo roof

The Scordelis–Lo roof is a standard test to assess the performance of the Shell elements in membrane-dominated problem with the presence of bending action. As shown in Fig. 10a, the roof structure is a part of a cylinder shell which is subjected to its self-weight and bounded by diaphragms at curved edges. Taking advantage of symmetry, the ABCD region (one-quarter of the roof) is modeled. The contour plot of the considered region for the vertical deflection using the ACM-SQ4 flat shell element is shown in Fig. 10b.

Fig. 10

Scordelis–Lo roof problem. a geometry and material description ($E = 4.32 \times 10^{8} ,$$\nu = 0.0,$$t = 0.25,$$L = 50,$ density $\rho = 360,$ acceleration of gravity $g = 1$ and $R = 25$). b Contour plot of transverse displacement

The boundary conditions for ABCD region are: $u = \theta_{y} = \theta_{z} = 0$ along the AB, $v = \theta_{x} = \theta_{z} = 0$ along the BC side, and $u = w = \theta_{y} = 0$ along AD. The vertical deflection of point C at the middle of the straight edge for the proposed element and the other ones are listed in Table 5.

Table 5 Normalized displacement at point C for the Scordelis–Lo roof

The results obtained using $N \times N$(N = 4, 8, 16) element meshes and normalized $(w_{\text{C}} /w_{\text{ref}} )$ by the reference solution $(w_{\text{ref}} = 0.3024)$ proposed by Macneal and Harder [56]. Figure 11 shows the convergence plots of normalized displacement at the middle of the straight edge for the new-version elements. It can be seen that the accuracy and convergence of the ACM-SQ4 element are reasonable. The percent difference between the analytical solution and numerical value is only 1%.

Fig. 11

Convergence of normalized displacement at point C for the Scordelis–Lo roof

3.6 Hook problem

Due to the mixed deformation pattern (bending, extension and twisting) the Hook problem is used to assess the stability of the proposed shell element. As shown in Fig. 12a, the structure consists of two different curved cylindrical shells that is clamped at one end and loaded by a uniformly distributed shear load at its tip. Figure 12b illustrates the contour plot for transverse displacement along the applied shear load, using the proposed element.

Fig. 12

Hook problem. a geometry and material description ($E = 3.3 \times 10^{3} ,$$\nu = 0.3,$$R_{1} = 14,$$\theta_{1} = 60^\circ ,$$R_{2} = 46,$$\theta_{2} = 150^\circ ,$ thickness $t = 2$ and $P = 1$). b Contour plot of transverse displacement

Table 6 shows the normalized displacement $(w_{\text{A}} /w_{\text{ref}} )$ of the free edge for the proposed shell element and the other ones using different element meshes. Moreover, the corresponding convergence plots are given in Fig. 13.

Table 6 Normalized displacement at point A for the Hook problem

Fig. 13

Convergence of normalized displacement at point A for the Hook problem

The obtained results have been normalized by the reference solution $(w_{\text{ref}} = 4.82482)$ suggested by KO et al. [57]. It is observed that the proposed flat shell element provides satisfactory accuracy with reasonable convergence. In comparison with analytical value, the error of the ACM-SQ4 element is 2.1%.

4 Conclusions

Using an appropriate element is one of the main requirements in the finite element analysis of shell structures with complex loading and boundary conditions. Moreover, the accuracy of the element should be least sensitive to the geometry of the shell structures.

In this study a rectangular flat shell element, called ACM-SQ4, is proposed by combination of US-Q4θ membrane element and well-known ACM plate bending element. The selected membrane and bending elements can be used only for membrane and bending problems, respectively. Moreover, these elements have limited degrees of freedom (i.e., in-plane loads could not be applied to ACM element). The ACM-SQ4 element can be used for membrane, bending and combined membrane-bending problems. Each node of the ACM-SQ4 element has all the six degrees of freedom that means by using this element there is not any limitation in imposed loads and boundary conditions. The formulation of the proposed shell element is simple since it is based on the superposition of the US-Q4θ membrane and ACM plate bending elements which both have simple formulation. Due to the least number of nodes (four nodes in corners without any mid-side nodes) the computational cost of the proposed element is lowest.

To evaluate the performance of the proposed shell element some numerical benchmark problems are employed. The results show that the ACM-SQ4 element for most problem provides acceptable accuracy with reasonable convergence in bending- and membrane-dominated problems with complex geometry and mixed deformations.

Some of the referenced elements like MITC4+ use 5 degrees of freedom per each node that mean these elements have lower computational cost but they did not provide appropriate accuracy. The variation of errors for the ACM-SQ4 element is 0–2.1% ensuring that when the problem changes, using the proposed shell element require minor changes in geometry, load conditions, and boundary conditions. As should be noted, the variation of errors in such a narrow domain is one of the best among the referenced shell elements in literature.

Appendix A

Natural coordinates for the plate bending element are shown in Fig. 14.

Fig. 14

Geometry of the plate bending element in Local coordinate system

The shape function of the ith degree of freedom in the natural coordinate system is

$$ \begin{aligned} N_{1} (\xi ,\eta ) = (1/8)(1 - \xi )(1 - \eta )(2 - \xi - \eta - \xi^{2} - \eta^{2} ) \hfill \\ N_{2} (\xi ,\eta ) = (b/8)(1 - \xi )(1 - \eta )( - (1 - \eta^{2} )) \hfill \\ N_{3} (\xi ,\eta ) = (a/8)(1 - \xi )(1 - \eta )(1 - \xi^{2} ) \hfill \\ N_{4} (\xi ,\eta ) = (1/8)(1 + \xi )(1 - \eta )(2 + \xi - \eta - \xi^{2} - \eta^{2} ) \hfill \\ N_{5} (\xi ,\eta ) = (b/8)(1 + \xi )(1 - \eta )( - (1 - \eta^{2} )) \hfill \\ N_{6} (\xi ,\eta ) = (a/8)(1 - \xi )(1 - \eta )( - (1 - \xi^{2} )) \hfill \\ N_{7} (\xi ,\eta ) = (1/8)(1 + \xi )(1 + \eta )(2 + \xi + \eta - \xi^{2} - \eta^{2} ) \hfill \\ N_{8} (\xi ,\eta ) = (b/8)(1 + \xi )(1 + \eta )(1 - \eta^{2} ) \hfill \\ N_{9} (\xi ,\eta ) = (a/8)(1 + \xi )(1 + \eta )( - (1 - \xi^{2} )) \hfill \\ N_{10} (\xi ,\eta ) = (1/8)(1 - \xi )(1 + \eta )(2 - \xi + \eta - \xi^{2} - \eta^{2} ) \hfill \\ N_{11} (\xi ,\eta ) = (b/8)(1 - \xi )(1 + \eta )(1 - \eta^{2} ) \hfill \\ N_{12} (\xi ,\eta ) = (a/8)(1 - \xi )(1 + \eta )(1 - \xi^{2} ). \hfill \\ \end{aligned} $$

(27)

The element stiffness matrix in the natural coordinate system is calculated by Eq. (28)

$$ {\mathbf{K}} = \int\limits_{V} {{\mathbf{B}}^{\text{T}} {\mathbf{DB}}{\text{d}}V} , $$

(28)

where ${\text{d}}V$ is the differential volume and its value in the natural coordinates of the element is equal to $abtd\xi d\eta$ and B is a $3 \times 12$ matrix shown in Eq. (29).

$$ B = \left[ {\begin{array}{*{20}c} {B_{1,1} } & {B_{1,2} } & {B_{1,3} } & {B_{1,4} } & {B_{1,5} } & {B_{1,6} } & {B_{1,7} } & {B_{1,8} } & {B_{1,9} } & {B_{1,10} } & {B_{1,11} } & {B_{1,12} } \\ {B_{2,1} } & {B_{2,2} } & {B_{2,3} } & {B_{2,4} } & {B_{2,5} } & {B_{2,6} } & {B_{2,7} } & {B_{2,8} } & {B_{2,9} } & {B_{2,10} } & {B_{2,11} } & {B_{2,12} } \\ {B_{3,1} } & {B_{3,2} } & {B_{3,3} } & {B_{3,4} } & {B_{3,5} } & {B_{3,6} } & {B_{3,7} } & {B_{3,8} } & {B_{3,9} } & {B_{3,10} } & {B_{3,11} } & {B_{3,12} } \\ \end{array} } \right]. $$

(29)

Matrix B elements in the natural coordinate system are defined as

$$ \begin{array}{*{20}c} \begin{aligned} B_{1,1} = - \frac{3}{{4a^{2} }}z\xi (1 - \eta ) \hfill \\ B_{1,2} = 0 \hfill \\ B_{1,3} = - \frac{1}{4a}z(\eta - 1)(1 - 3\xi ) \hfill \\ B_{1,4} = - \frac{3}{{4a^{2} }}z\xi (\eta - 1) \hfill \\ \end{aligned} & \begin{aligned} B_{2,1} = - \frac{3}{{4b^{2} }}z\eta (1 - \xi ) \hfill \\ B_{2,2} = \frac{1}{4b}z(\xi - 1)(1 - 3\eta ) \hfill \\ B_{2,3} = 0 \hfill \\ B_{2,4} = - \frac{3}{{4b^{2} }}z\eta (1 + \xi ) \hfill \\ \end{aligned} & \begin{aligned} B_{3,1} = \frac{2}{8ab}z(3\xi^{2} + 3\eta^{2} - 4) \hfill \\ B_{3,2} = \frac{2}{8a}z( - 3\eta^{2} + 2\eta + 1) \hfill \\ B_{3,3} = - \frac{2}{8b}z( - 3\xi^{2} + 2\xi + 1) \hfill \\ B_{3,4} = - \frac{2}{8ab}z(3\xi^{2} + 3\eta^{2} - 4) \hfill \\ \end{aligned} \\ \begin{aligned} B_{1,5} = 0 \hfill \\ B_{1,6} = - \frac{1}{4a}z(1 - \eta )(1 + 3\xi ) \hfill \\ B_{1,7} = \frac{3}{{4a^{2} }}z\xi (\eta + 1) \hfill \\ B_{1,8} = 0 \hfill \\ B_{1,9} = - \frac{1}{4a}z(1 + \eta )(1 + 3\xi ) \hfill \\ B_{1,10} = \frac{3}{{4a^{2} }}z\xi (\eta + 1) \hfill \\ B_{1,11} = 0 \hfill \\ B_{1,12} = \frac{1}{4a}z(1 + \eta )(1 - 3\xi ) \hfill \\ \end{aligned} & \begin{aligned} B_{2,5} = - \frac{1}{4b}z(\xi + 1)(1 - 3\eta ) \hfill \\ B_{2,6} = 0 \hfill \\ B_{2,7} = \frac{3}{{4b^{2} }}z\eta (1 + \xi ) \hfill \\ B_{2,8} = \frac{1}{4b}z(\xi + 1)(1 + 3\eta ) \hfill \\ B_{2,9} = 0 \hfill \\ B_{2,10} = \frac{3}{{4b^{2} }}z\eta (1 - \xi ) \hfill \\ B_{2,11} = - \frac{1}{4b}z(\xi - 1)(1 + 3\eta ) \hfill \\ B_{2,12} = 0 \hfill \\ \end{aligned} & \begin{aligned} B_{3,5} = - \frac{2}{8a}z( - 3\eta^{2} + 2\eta + 1) \hfill \\ B_{3,6} = \frac{2}{8b}z(3\xi^{2} + 2\xi - 1) \hfill \\ B_{3,7} = \frac{2}{8ab}z(3\xi^{2} + 3\eta^{2} - 4) \hfill \\ B_{3,8} = \frac{2}{8a}z(3\eta^{2} + 2\eta - 1) \hfill \\ B_{3,9} = - \frac{2}{8b}z(3\xi^{2} + 2\xi - 1) \hfill \\ B_{3,10} = - \frac{2}{8ab}z(3\xi^{2} + 3\eta^{2} - 4) \hfill \\ B_{3,11} = - \frac{2}{8a}z(3\eta^{2} + 2\eta - 1) \hfill \\ B_{3,12} = \frac{2}{8b}z( - 3\xi^{2} + 2\xi + 1). \hfill \\ \end{aligned} \\ {} & {} & {} \\ \end{array} $$

(30)