Free vibration of joined cylindrical–hemispherical FGM shells

Abstract

Free vibration response of a joined shell system including cylindrical and spherical shells is analyzed in this research. It is assumed that the system of joined shell is made from a functionally graded material (FGM). Properties of the shells are assumed to be graded through the thickness. Both shells are unified in thickness. To capture the effects of through-the-thickness shear deformations and rotary inertias, first-order shear deformation theory of shells is used. The Donnell type of kinematic assumptions is adopted to establish the general equations of motion and the associated boundary and continuity conditions with the aid of Hamilton’s principle. The resulting system of equations is discretized using the semi-analytical generalized differential quadrature method. Considering the clamped and free boundary conditions for the end of the cylindrical shell and intersection continuity conditions, an eigenvalue problem is established to examine the vibration frequencies of the joined shell. After proving the efficiency and validity of the present method for the case of thin isotropic homogeneous joined shells, some parametric studies are carried out for the system of combined moderately thick cylindrical–spherical shell system. Novel results are provided for the case of FGM joined shells to explore the influence of power-law index and geometric properties.

1 Introduction

Vibration of complicated shells has received attention in the last years [1,2,3]. A system of joined cylindrical–spherical shell structure is widely used in many industrial applications, such as pressure vessels and architectural structures. For these structures, it is well accepted that close to the joined section, localized and severe bending moments are produced when the shell is subjected to sudden loadings. Vibrations induced by such loadings may result in fatigue phenomenon. Therefore, it is of high interest and importance to understand the vibration characteristics of joined shells to establish the fundamental requirements for a safe design.

A large number of publications deal with the vibration analysis of elementary class of shells, e.g., conical, cylindrical or spherical shell elements. On such topics, therefore, wealth books are documented [4,5,6]. On the other hand, in comparison with the elementary shells, researches on vibration analysis of joined shells are limited. Hu and Raney [7] studied the joined cantilever cylindrical–conical shell in free vibration regime. Yim et al. [8] studied the free vibration analysis of the clamped–free circular cylindrical shell with a plate attached at an arbitrary axial position using the numerical method. Peterson and Body [9] developed a technique for the free vibration analysis of cylindrical shells with an inner plate at a longitudinal position. Irie et al. [10] presented a strategy to analyze the vibration of a joined cylindrical–conical shell element. The transfer matrix of the shell is expressed conveniently by the power series method and the frequency equations are derived for a given set of boundary conditions at the edges. As a special case, free vibration characteristics of an annular plate–cylindrical shell system are also analyzed. Saunders and Paslay [11] derived the analytical solution for the natural frequency of the joined conical and spherical shells by the Rayleigh–Ritz method, which shows good agreement with the modal test. Bagheri et al. [12] investigated the free vibration response of a joined shell system consisting of two conical shells. In another research, they considered the free vibration characteristics of a joined shell system containing two conical shells at the ends and a cylindrical shell at the middle [13]. The first-order shear deformation theory of shells is accompanied with the Donnell type of kinematic assumptions to establish the general equations of motion and the associated boundary and continuity conditions with the aid of Hamilton’s principle. The resulting system of equations is discretized using the semi-analytical generalized differential quadrature (GDQ) method. Bagheri et al. [14] also investigated the free vibrations of conical shells with intermediate ring support. Kerboua and Lakis [15] performed an investigation on the free vibration and aerodynamics of joined cylindrical–conical shells.

The vibration of joined spherical–cylindrical shells or cylindrical shells with different end attachments has been the subject of studies. For instance, the natural frequencies of cylindrical shells clamped at one end and closed at the other end by different types of shells of revolution (cones, hemispheres, ellipsoids, etc.) are studied by Galletly [16]. Lee et al. [17] performed an investigation on the free vibration of combined cylindrical–spherical shells. Various cases of boundary conditions are considered in this research. Rayleigh–Ritz-based solutions are developed to establish the eigenvalue problems associated with the natural frequencies and mode shapes of a thin Flügge shell system. It is shown that the vibrational behavior of the joined spherical–cylindrical shell structure is independent of the shallowness of a hemispherical shell, whereas the length of the cylindrical shell is effective in the vibrational behavior of the joined hemispherical–cylindrical shell. Wu et al. [18], using the Reissner–Naghdi–Berry’s shell theory, applied the domain decomposition method (DDM) to investigate the vibration characteristics of the combined cylindrical–spherical shell with different boundary conditions. In another study, Wu et al. [19] concentrated on the free vibration of a joined cylindrical–spherical shell with elastic support type of boundary conditions using the domain decomposition method. Using the Flügge shell theory and Rayleigh–Ritz energy method, Yosefzad et al. [20] analyzed the free vibration characteristics of the pre-stressed joined spherical–cylindrical shells with free–free boundary conditions. In the modal test, the LMS software is used to calculate the mode shapes and natural frequencies of the joined shell structure. Qu et al. [21] analyzed the free vibration of joined cylindrical–conical shell system with classical or non-classical boundary conditions. The thin shell assumptions of Reissner–Naghdi theory are used as the fundamental theoretical assumptions. The interface continuity and geometric boundary conditions are approximately enforced by means of a modified variational principle and least-squares weighted residual method. Qu and his co-authors also applied their previous method [21] to the free vibration analysis of ring-stiffened joined conical–cylindrical shell systems [22], joined conical–cylindrical–spherical shell systems [23], joined cylindrical–spherical shell with elastic-support boundary conditions [24] and spherical–cylindrical–spherical shells [25]. In a series of works, Kang[26,27,28] examined the free vibration response of cylindrical shells that are closed by various types of shell of revolution within the framework of three-dimensional elasticity theory. The total strain and kinetic energies of the joined shell system are established, and the Ritz method with the classical polynomial functions is used to establish the eigenvalue problem and extract the natural frequencies.

There are only a few works dealing with the free vibration response of joined cylindrical–spherical shells where most of them are limited to thin class of shells. Also, all investigations deal with the homogeneous class of shells and no work is yet reported on the free vibration of FGM joined cylindrical–spherical shells. The present study aims to investigate the free vibration characteristics of a joined cylindrical–spherical shell structure that is made from FGMs using the first-order shear deformable shell model suitable for moderately thick shells. The Donnell type of kinematic assumptions is used to establish the equations of motion and the associated boundary conditions. A semi-analytical procedure based on the Fourier expansion along the circumferential direction and the GDQ discretization along the tangential direction is developed to discrete the equations of motion. The GDQ method is also applied to the intersection continuity and boundary conditions. A system of homogeneous eigenvalue problems is established which may be useful to examine the frequencies of a joined cylindrical–spherical shells. After validating the proposed solution method via some comparison studies, a series of parametric studies are carried out to examine the influences of power-law index, cylindrical shell length and shell radius.

2 Material properties of FGMs

The material properties of the ceramic and metal constituents of the joined shell system are assumed to be graded in thickness direction based on the power-law function. The ceramic volume fraction $V_{\mathrm{c}}$ and metal volume fraction $V_\mathrm{m}$ are assumed to obey the following form [29,30,31,32,33,34,35,36]

$$\begin{aligned} V_{\mathrm{c}}=\left( \dfrac{1}{2}+\dfrac{z}{h}\right) ^k ,\quad V_{\mathrm{m}}=1-V_{\mathrm{c}} \end{aligned}$$

(1)

In the above equation, k is the power-law index and dictates the distribution of material properties across the thickness. It is obvious that the surface $z=+h/2$ is ceramic-rich and the surface $z=-h/2$ is metal-rich.

Following the simple rule of mixtures approach (Voigt rule), each property of the FG joined shell such as P may be written as a function of the associated properties of the constituents and volume fraction of constituents as

$$\begin{aligned} P(z)=P_{\mathrm{m}}+P_{\mathrm{cm}}\left( \dfrac{1}{2}+\dfrac{z}{h}\right) ^k , \quad P_\mathrm{cm}=P_{\mathrm{c}}-P_{\mathrm{m}} \end{aligned}$$

(2)

where $P_{\mathrm{m}}$ and $P_{\mathrm{c}}$ are the corresponding properties of the metal and ceramic constituents, respectively. In the present work, we assume that the modulus of elasticity E and mass density $\rho$ are described by Eq. (2), while Poisson’s ratio $\nu$ is considered to be constant across the thickness since it varies only in a small range.

3 Governing equations of the shell system

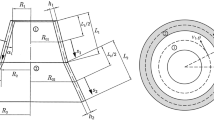
Consider a joined cylindrical–hemispherical shell made of a functionally graded material of uniform thickness h, sphere radius $r^{\mathrm{s}}=R$, cylinder radius $r^{\mathrm{c}}=R$ and cylinder length $L^{\mathrm{c}}=L$. The system is shown in Fig. 1. A $(x,\theta ,z)$ system is applied to the cylindrical shell system, whereas a $(\phi ,\theta ,z)$ system is applied to the spherical shell. The coordinate systems are also shown in Fig. 1.

Fig. 1

Geometric parameters and coordinate system sign of a joined cylindrical–spherical shell

To capture the through-the-thickness shear deformations and rotary inertia effects of the cylindrical and spherical shells, the first-order shear deformation theory (FSDT) of shells is used to formulate the governing equations of the shell. Based on the FSDT, components of the displacement on a generic point for cylindrical and spherical shells may be represented according to the mid-surface characteristics such that

$$\begin{aligned}&u^i\left( \zeta ,\theta ,z,t\right) =u_0^i\left( \zeta ,\theta ,t \right) +z\varphi _\zeta ^i\left( \zeta ,\theta ,t\right) \nonumber \\&v^i\left( \zeta ,\theta ,z,t\right) =v_0^i\left( \zeta ,\theta ,t \right) +z\varphi _\theta ^i\left( \zeta ,\theta ,t\right) \nonumber \\&w^i\left( \zeta ,\theta ,z,t\right) =w_0^i\left( \zeta ,\theta ,t \right) \end{aligned}$$

(3)

In the above equation, u, v and w are the tangential, circumferential and through-the-thickness displacements, respectively. The superscript i may be c or s associated with the cylindrical and spherical shells. Also, $\zeta$ may take $\phi$ or x for spherical and cylindrical shells, respectively. A subscript 0 indicates the characteristics of the mid-surface. Besides, $\varphi _{\zeta }$ and $\varphi _{\theta }$ are, respectively, the transverse normal rotations about the $\theta$ and $\zeta$ axes, respectively.

According to the FSDT, the components of strain field on an arbitrary point of the cylindrical or spherical shell may be obtained in terms of those belonging to the mid-surface of the shell and change of curvatures. Consequently, one may write [37]

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon _{\zeta \zeta }^i\\ \varepsilon _{\theta \theta }^i\\ \gamma _{\zeta \theta }^i\\ \gamma _{\zeta z}^i\\ \gamma _{\theta z}^i\end{array}\right\} =\left\{ \begin{array}{l} \varepsilon _{\zeta \zeta 0}^i \\ \varepsilon _{\theta \theta 0}^i\\ \gamma _{\zeta \theta 0}^i\\ \gamma _{\zeta z 0}^i\\ \gamma _{\theta z 0}^i\end{array}\right\} + z \left\{ \begin{array}{l} \kappa _{\zeta \zeta }^i \\ \kappa _{\theta \theta }^i\\ \kappa _{\zeta \theta }^i\\ \kappa _{\zeta z}^i\\ \kappa _{\theta z}^i\end{array}\right\} \end{aligned}$$

(4)

where the components of strain associated with the mid-surface of the cylindrical shell are

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon _{xx0}^{\mathrm{c}} \\ \varepsilon _{\theta \theta 0}^{\mathrm{c}}\\ \gamma _{x\theta 0}^{\mathrm{c}}\\ \gamma _{xz0}^{\mathrm{c}}\\ \gamma _{\theta z0}^{\mathrm{c}}\end{array}\right\} = \left\{ \begin{array}{l} u_{0,x}^{\mathrm{c}} \\ \dfrac{v_{0,\theta }^{\mathrm{c}}}{r^{\mathrm{c}}}+\dfrac{w_0^{\mathrm{c}}}{r^{\mathrm{c}}}\\ \dfrac{u_{0,\theta }^{\mathrm{c}}}{r^{\mathrm{c}}}+v_{0,x}^{\mathrm{c}}\\ w_{0,x}^{\mathrm{c}}+\varphi _x^{\mathrm{c}}\\ \dfrac{w_{0,\theta }^{\mathrm{c}}}{r^{\mathrm{c}}}-\dfrac{v_0^{\mathrm{c}}}{r^{\mathrm{c}}} +\varphi _\theta ^{\mathrm{c}}\end{array}\right\} \end{aligned}$$

(5)

and similarly for the spherical shell one has

$$\begin{aligned} \left\{ \begin{array}{l} \varepsilon _{\phi \phi 0}^{\mathrm{s}} \\ \varepsilon _{\theta \theta 0}^{\mathrm{s}}\\ \gamma _{\phi \theta 0}^{\mathrm{s}}\\ \gamma _{\phi z 0}^{\mathrm{s}}\\ \gamma _{\theta z 0}^{\mathrm{s}}\end{array}\right\} = \left\{ \begin{array}{l} \dfrac{u_{0,\phi }^{\mathrm{s}}}{r^{\mathrm{s}}}+\dfrac{w_{0}^{\mathrm{s}}}{r^{\mathrm{s}}} \\ \dfrac{v_{0,\theta }^{\mathrm{s}}}{r^{\mathrm{s}} \sin (\phi )}+\dfrac{u_{0}^{\mathrm{s}}}{r^{\mathrm{s}}}\cot (\phi )+\dfrac{w_0^{\mathrm{s}}}{r^{\mathrm{s}}}\\ \dfrac{v_{0,\phi }^{\mathrm{s}}}{r^{\mathrm{s}}}+\dfrac{u_{0,\theta }^{\mathrm{s}}}{r^{\mathrm{s}}\sin (\phi )}-\dfrac{v_{0}^{\mathrm{s}}}{r^{\mathrm{s}}}\cot (\phi )\\ \dfrac{w_{0,\phi }^{\mathrm{s}}}{r^{\mathrm{s}}}+\varphi _\phi ^{\mathrm{s}} -\dfrac{u_0^{\mathrm{s}}}{r^{\mathrm{s}}}\\ \dfrac{w_{0,\theta }^{\mathrm{s}}}{r^{\mathrm{s}}\sin (\phi )}-\dfrac{v_0^{\mathrm{s}}}{r^{\mathrm{s}}}+\varphi _\theta ^{\mathrm{s}}\end{array} \right\} \end{aligned}$$

(6)

The components of change of curvature in the Donnell sense compatible with the FSDT for the cylindrical shell are [37]

$$\begin{aligned} \left\{ \begin{array}{l} \kappa _{xx}^{\mathrm{c}} \\ \kappa _{\theta \theta }^{\mathrm{c}}\\ \kappa _{x\theta }^{\mathrm{c}}\\ \kappa _{xz}^{\mathrm{c}}\\ \kappa _{\theta z}^{\mathrm{c}}\end{array}\right\} = \left\{ \begin{array}{l} \varphi _{x,x}^{\mathrm{c}} \\ \dfrac{\varphi _{\theta ,\theta }^{\mathrm{c}}}{r^{\mathrm{c}}}\\ \dfrac{\varphi _{x,\theta }^{\mathrm{c}}}{r^{\mathrm{c}}}+\varphi _{\theta ,x}^{\mathrm{c}}\\ 0\\ 0\end{array}\right\} \end{aligned}$$

(7)

and for the spherical shell one may write

$$\begin{aligned} \left\{ \begin{array}{l} \kappa _{\phi \phi }^{\mathrm{s}} \\ \kappa _{\theta \theta }^{\mathrm{s}}\\ \kappa _{\phi \theta }^{\mathrm{s}}\\ \kappa _{\phi z}^{\mathrm{s}}\\ \kappa _{\theta z}^{\mathrm{s}}\end{array}\right\} = \left\{ \begin{array}{l} \dfrac{\varphi _{\phi ,\phi }^{\mathrm{s}}}{r^{\mathrm{s}}} \\ \dfrac{\varphi _{\theta ,\theta }^{\mathrm{s}}}{r^{\mathrm{s}}\sin (\phi )}+\dfrac{\varphi _{\phi }^{\mathrm{s}}}{r^{\mathrm{s}}}\cot (\phi )\\ \dfrac{\varphi _{\theta ,\phi }^{\mathrm{s}}}{r^{\mathrm{s}}}+\dfrac{\varphi _{\phi ,\theta }^{\mathrm{s}}}{r^{\mathrm{s}}\sin (\phi )}-\dfrac{1}{r^{\mathrm{s}}}\varphi _{\theta }^{\mathrm{s}}\cot (\phi )\\ 0\\ 0 \end{array} \right\} \end{aligned}$$

(8)

where in the above equations, $()_{,\phi }$$()_{,x}$ and $()_{,\theta }$ denote the derivatives with respect to $\phi , x$ and $\theta$, respectively.

For the case when material properties of the shell are linearly elastic, components of stress in terms of strains are evaluated as

$$\begin{aligned} \left\{ \begin{array}{l} \sigma _{\zeta \zeta }^i \\ \sigma _{\theta \theta }^i\\ \tau _{\zeta \theta }^i\\ \tau _{\zeta z}^i\\ \tau _{z\theta }^i\end{array}\left\lbrace = \begin{bmatrix} Q_{11}&{}\quad Q_{12}&{}\quad 0&{}\quad 0&{}\quad 0\\ Q_{12}&{}\quad Q_{22}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad Q_{44}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad Q_{55}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad Q_{66}\\ \end{bmatrix} \right\rbrace \begin{array}{l} \varepsilon _{\zeta \zeta }^i\\ \varepsilon _{\theta \theta }^i\\ \gamma _{\zeta \theta }^i\\ \gamma _{\zeta z}^i\\ \gamma _{z\theta }^i\end{array}\right\} \end{aligned}$$

(9)

where $Q_{ij}$’s $(i,j=1,2,4,5,6)$ are the reduced material stiffness coefficients and are obtained as follows

$$\begin{aligned}&Q_{11}=Q_{22}=\frac{E(z)}{1-\nu ^ 2},\;\;\; Q_{12}=\frac{\nu E(z) }{1-\nu ^ 2},\;\;\; Q_{44}=Q_{55}=Q_{66}=\frac{E(z)}{2(1+\nu )}. \end{aligned}$$

(10)

The components of stress resultants are obtained using the components of stress field as [38]

$$\begin{aligned} \nonumber&\left\{ \begin{array}{l} N_{\zeta \zeta }^i \\ N_{\theta \theta }^i\\ N_{\zeta \theta }^i\end{array}\right\} = \int _{-h/2}^{+h/2}\left\{ \begin{array}{l} \sigma _{\zeta \zeta }^i \\ \sigma _{\theta \theta }^i\\ \tau _{\zeta \theta }^i\end{array}\right\} \mathrm{d}z,\\ \nonumber&\left\{ \begin{array}{l} M_{\zeta \zeta }^i \\ M_{\theta \theta }^i\\ M_{\zeta \theta }^i\end{array}\right\} = \int _{-h/2}^{+h/2}z\left\{ \begin{array}{l} \sigma _{\zeta \zeta }^i \\ \sigma _{\theta \theta }^i\\ \tau _{\zeta \theta }^i\end{array}\right\} \mathrm{d}z,\\&\left\{ \begin{array}{l} Q_{\zeta z}^i \\ Q_{\theta z}^i\end{array}\right\} = \int _{-h/2}^{+h/2}\kappa \left\{ \begin{array}{l} \tau _{\zeta z}^i \\ \tau _{\theta z}^i\end{array}\right\} \mathrm{d}z \end{aligned}$$

(11)

In the above equation, $\kappa$ is the shear correction factor of FSDT. As known, adoption of a correction shear factor results in more accurate estimation of the natural frequencies. Since shear correction factor depends upon the boundary conditions, material properties and loading type [39], determination of its exact value is not straightforward. However, the approximate values of $\kappa =5/6$ or $\kappa =\pi ^2/12$ are used extensively. In this research, the shear correction factor is set equal to $\kappa =5/6$.

Substitution of Eq. (9) into Eq. (11) with the simultaneous aid of Eqs. (4)–(8) generates the stress resultants in terms of the mid-surface characteristics of the shell as

$$\begin{aligned} \left\{ \begin{array}{l} N_{\zeta \zeta }^i \\ N_{\theta \theta }^i\\ N_{\zeta \theta }^i\\ M_{\zeta \zeta }^i \\ M_{\theta \theta }^i\\ M_{\zeta \theta }^i\\ Q_{\theta z}^i\\ Q_{\zeta z}^i\end{array}\right\} = \begin{bmatrix} A_{11}&{}\quad A_{12}&{}\quad 0 &{}\quad B_{11}&{}\quad B_{12}&{}\quad 0&{}\quad 0&{}\quad 0\\ A_{12}&{}\quad A_{22}&{}\quad 0 &{}\quad B_{12}&{}\quad B_{11}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad A_{66} &{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ B_{11}&{}\quad B_{12}&{}\quad 0 &{}\quad D_{11}&{}\quad D_{12}&{}\quad 0&{}\quad 0&{}\quad 0\\ B_{12}&{}\quad B_{11}&{}\quad 0 &{}\quad D_{12}&{}\quad D_{22}&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad D_{66}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \kappa A_{44}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad \kappa A_{55} \end{bmatrix} \left\{ \begin{array}{l} \varepsilon _{\zeta \zeta 0}^i\\ \varepsilon _{\theta \theta 0}^i\\ \gamma _{\zeta \theta 0}^i\\ \kappa _{\zeta \zeta }^i\\ \kappa _{\theta \theta }^i\\ \kappa _{\zeta \theta }^i\\ \gamma _{\theta z 0}^i\\ \gamma _{\zeta z 0}^i\end{array}\right\} \end{aligned}$$

(12)

In the above equation, the constant coefficients $A_{ij}$, $B_{ij}$ and $D_{ij}$ indicate the well-known stretching, coupling and bending stiffnesses, respectively, which are calculated by

$$\begin{aligned} (A_{ij},B_{ij},D_{ij})=\int _{-0.5h}^{+0.5h}(Q_{ij},zQ_{ij},z^2Q_{ij})\mathrm{d}z. \end{aligned}$$

(13)

The complete set of equations of motion and boundary conditions of a joined cylindrical–hemispherical shell system may be obtained based on the generalized Hamilton principle [38]. Statement of Hamilton’s principle reads

$$\begin{aligned} \nonumber&\delta \int _{t_{1}}^{t_{2}}\left( K^i-\left( U^i+V^i\right) \right) \mathrm{d}t=0\\&{\mathrm{at}}\;\;t=t_{1},t_{2}{:}\,\delta u_{0}^i=\delta v_{0}^i=\delta w_{0}^i=\delta \varphi _{\zeta }^i=\delta \varphi _{\theta }^i=0 \end{aligned}$$

(14)

where in the above equation, $\delta K^i$ is the virtual kinetic energy of the cylindrical/spherical shell which is equal to

$$\begin{aligned} \delta K^i= \int _{V^i}\rho (z) \left( \dot{u}^i\delta \dot{u}^i+ \dot{v}^i \delta \dot{v}^i+ \dot{w}^i \delta \dot{w}^i\right) \mathrm{d}V^i \end{aligned}$$

(15)

Here, a $( \dot{\;})$ indicates the derivative with respect to time t. Besides, $\delta U^i$ is the virtual strain energy of the cylindrical/spherical shell which may be calculated as

$$\begin{aligned} \delta U^i= \int _{V^i}\left( \sigma _{\zeta \zeta }^i\delta \varepsilon _{\zeta \zeta }^i+\sigma _{\theta \theta }^i\delta \varepsilon _{\theta \theta }^i+\tau _{\zeta \theta }^i\delta \gamma _{\zeta \theta }^i+\kappa \tau _{\theta z}^i\delta \gamma _{\theta z}^i+\kappa \tau _{\zeta z}^i\delta \gamma _{\zeta z}^i\right) \mathrm{d}V^i \end{aligned}$$

(16)

And $\delta V^i$ is the virtual potential energy of the external loads which is absent for the free vibration problem. Integrating the above expressions with respect to z coordinate and performing the Green–Gauss theorem to relieve the virtual displacement gradients results in the expressions for the linear equations of motion of cylindrical and spherical shells, respectively, as

$$\begin{aligned}&N_{xx,x}^{\mathrm{c}}+\frac{N_{x\theta ,\theta }^{\mathrm{c}}}{R}=I_1 \ddot{u}_{0}^{\mathrm{c}}+I_2 \ddot{\varphi }_{x}^{\mathrm{c}} \nonumber \\&\frac{N_{\theta \theta ,\theta }^{\mathrm{c}}}{R}+N_{x\theta ,x}^{\mathrm{c}}+\frac{Q_{\theta z}^{\mathrm{c}}}{R} =I_1 \ddot{v}_{0}^{\mathrm{c}}+I_2 \ddot{\varphi }_{\theta }^{\mathrm{c}}\nonumber \\&Q_{xz,x}^{\mathrm{c}}+\frac{Q_{\theta z,\theta }^{\mathrm{c}}}{R} - \frac{N_{\theta \theta }^{\mathrm{c}}}{R}=I_1 \ddot{w}_{0}^{\mathrm{c}}\nonumber \\&M_{xx,x}^{\mathrm{c}}+\frac{M_{x\theta ,\theta }^{\mathrm{c}}}{R} -Q_{xz}^{\mathrm{c}}=I_2 \ddot{u}_{0}^{\mathrm{c}}+I_3 \ddot{\varphi }_{x}^{\mathrm{c}}\nonumber \\&M_{x\theta ,x}^{\mathrm{c}}+\frac{M_{\theta \theta ,\theta }^{\mathrm{c}}}{R}-Q_{\theta z}^{\mathrm{c}}=I_2 \ddot{v}_{0}^{\mathrm{c}}+I_3 \ddot{\varphi }_{\theta }^{\mathrm{c}} \end{aligned}$$

(17)

$$\begin{aligned}&\frac{N_{\phi \phi ,\phi }^{\mathrm{s}}}{R} +\frac{N_{\phi \theta ,\theta }^{\mathrm{s}}}{R \sin (\phi )}+\frac{N_{\phi \phi }^{\mathrm{s}}-N_{\theta \theta }^{\mathrm{s}}}{R}\cot (\phi ) +\frac{Q_{\phi }^{\mathrm{s}}}{r}=I_1 \ddot{u}_{0}^{\mathrm{s}}+I_2 \ddot{\varphi }_{\phi }^{\mathrm{s}}\nonumber \\&\frac{N_{\theta \theta ,\theta }^{\mathrm{s}}}{R \sin (\phi ) }+\frac{N_{\phi \theta ,\phi }^{\mathrm{s}}}{R}+2\frac{\cot (\phi )}{R}N_{\phi \theta }^{\mathrm{s}}+\frac{Q_{\theta }^{\mathrm{s}}}{R}=I_1 \ddot{v}_{0}^{\mathrm{s}}+I_2 \ddot{\varphi }_{\theta }^{\mathrm{s}}\nonumber \\&\frac{Q_{\phi z,\phi }^{\mathrm{s}}}{R} +\frac{1}{R \sin (\phi )}Q_{\theta ,\theta }^{\mathrm{s}}+\frac{Q_{\phi }^{\mathrm{s}}}{R}\cot (\phi ) - \frac{N_{\phi \phi }^{\mathrm{s}}+N_{\theta \theta }^{\mathrm{s}}}{R}=I_1 \ddot{w}_{0}^{\mathrm{s}}\nonumber \\&\frac{M_{\phi \phi ,\phi }^{\mathrm{s}}}{R} +\frac{M_{\phi \theta ,\theta }^{\mathrm{s}}}{R\sin (\phi )}+\frac{M_{\phi \phi }^{\mathrm{s}}-M_{\theta \theta }^{\mathrm{s}}}{R}\cot (\phi )- Q_{\phi }^{\mathrm{s}}=I_2 \ddot{u}_{0}^{\mathrm{s}}+I_3 \ddot{\varphi }_{\phi }^{\mathrm{s}}\nonumber \\&\frac{M_{\theta \theta ,\theta }^{\mathrm{s}}}{R \sin (\phi ) }+\frac{M_{\phi \theta ,\phi }^{\mathrm{s}}}{R}+2\frac{\cot (\phi )}{R}M_{\phi \theta }^{\mathrm{s}}-Q_{\theta }^{\mathrm{s}}=I_2 \ddot{v}_{0}^{\mathrm{s}}+I_3 \ddot{\varphi }_{\theta }^{\mathrm{s}} \end{aligned}$$

(18)

In Eq. (18), the notation R is used for both $r^{\mathrm{c}}$ and $r^{\mathrm{s}}$. Also, the following definitions apply

$$\begin{aligned} (I_{1},I_{2},I_{3})=\int _{-h/2}^{+h/2}\rho (1,z,z^2)\mathrm{d}z. \end{aligned}$$

(19)

4 Boundary and matching conditions

For the end of the cylindrical shell, various types of boundary conditions may be defined. The edge $x=L$ may be clamped (C) or free (F). Mathematical expression of the edge supports on the end of the cylinder takes the form

$$\begin{aligned} \nonumber&\text {C}{:}\,u_0^{\mathrm{c}}=v_0^{\mathrm{c}}= w_0^{\mathrm{c}}=\varphi _x^{\mathrm{c}} =\varphi _{\theta }^{\mathrm{c}} =0\\&\text {F}{:}\,N_{xx}^{\mathrm{c}}=N_{x\theta }^{\mathrm{c}} =Q_{xz}^{\mathrm{c}}=M_{xx}^{\mathrm{c}}=M_{x\theta }^{\mathrm{c}}=0 \end{aligned}$$

(20)

Furthermore, in view of the shell theory adopted in the present study, particular conditions (apex compatibility conditions) need to be enforced to avoid the divisions by zero arising in Eq. (6) when calculating the strain components at the pole. Following [40], imposing the finiteness of deformations at the apex, one obtains the following sets of assignments, which depend up the considered harmonic number.

$$\begin{aligned}&n\ne 1{:}\,u_0^{\mathrm{s}}=v_0^{\mathrm{s}}= Q_{\phi }^{\mathrm{s}}=\varphi _\phi ^{\mathrm{s}} =\varphi _{\theta }^{\mathrm{s}} =0\nonumber \\&n=1 {:}\,N_{\phi \phi }^{\mathrm{s}}=N_{\phi \theta }^{\mathrm{s}}= w_0^{\mathrm{s}}=\varphi _\phi ^{\mathrm{s}} +\varphi _{\theta }^{\mathrm{s}} =u_0^{\mathrm{s}}+v_0^{\mathrm{s}}=0 \end{aligned}$$

(21)

Here, n is the harmonic number through the circumferential direction.

Table 1 Non-dimensional frequency parameters, $\varOmega =\omega R\sqrt{\rho /G}$ of combined hemispherical–cylindrical shells of revolution without top opening

Table 2 First five natural frequency parameters for each circumferential mode number n in the case of completely free and clamped combined hemispherical–cylindrical shells for various power-law indices

Table 3 First five natural frequency parameters for each circumferential mode number n in the case of completely free and clamped combined hemispherical–cylindrical shells for various power-law indices

Table 4 First five natural frequency parameters for each circumferential mode number n in the case of completely free and clamped combined hemispherical–cylindrical shells for various power-law indices

At the intersection of the shell system, the continuity of displacement components as well as the force and moment resultants should be satisfied. The compatibility of the displacements at the intersection ($x=0$ and $\phi =\pi /2$) reads

$$\begin{aligned}&u_0^{\mathrm{s}}=u_0^{\mathrm{c}}\nonumber \\&w_0^{\mathrm{s}}=w_0^{\mathrm{c}}\nonumber \\&v_{0}^{\mathrm{s}}=v_{0}^{\mathrm{c}}\nonumber \\&\varphi _{\phi }^{\mathrm{s}}=\varphi _{x}^{\mathrm{c}} \nonumber \\&\varphi _{\theta }^{\mathrm{s}}=\varphi _{\theta }^{\mathrm{c}} \end{aligned}$$

(22)

and similarly, the compatibility of the stress resultants at the intersection ($x=0$ and $\phi =\pi /2$) results in

$$\begin{aligned} \nonumber&N_{\phi \phi }^{\mathrm{s}}=N_{xx}^{\mathrm{c}}\nonumber \\&Q_{\phi z}^{\mathrm{s}}=Q_{x z}^{\mathrm{c}}\nonumber \\&M_{\phi \phi }^{\mathrm{s}}=M_{xx}^{\mathrm{c}}\nonumber \\&N_{\phi \theta }^{\mathrm{s}}=N_{x\theta }^{\mathrm{c}}\nonumber \\&M_{\phi \theta }^{\mathrm{s}}=M_{x\theta }^{\mathrm{c}}. \end{aligned}$$

(23)

5 Solution procedure

Referring to the definitions of normal force and bending moment resultants from Eq. (12) and the equations of motion (17) and (18), the following separation of variables exactly satisfies the periodicity conditions of the field variables and is also compatible with the equations of motion (17) and (18) and the matching conditions (22) and (23).

$$\begin{aligned} \left\{ \begin{array}{l} u_{0}^i(\zeta ,\theta ,t) \\ v_{0}^i(\zeta ,\theta ,t)\\ w_{0}^i(\zeta ,\theta ,t) \\ \varphi _{\zeta }^i(\zeta ,\theta ,t) \\ \varphi _{\theta }^i(\zeta ,\theta ,t) \end{array}\right\} =\cos (\omega t+\psi ) \begin{bmatrix} \sin (n\theta )&{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad \cos (n\theta )&{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0 &{}\quad \sin (n\theta )&{}\quad 0 &{}\quad 0 \\ 0&{}\quad 0 &{}\quad 0&{}\quad \sin (n\theta )&{}\quad 0 \\ 0&{}\quad 0 &{}\quad 0&{}\quad 0&{}\quad \cos (n\theta ) \\ \end{bmatrix} \left\{ \begin{array}{l} U^i(\zeta ) \\ V^i(\zeta ) \\ W^i(\zeta ) \\ \Phi _{\zeta }^i(\zeta ) \\ \Phi _{\theta }^i(\zeta ) \\ \end{array} \right\} \end{aligned}$$

(24)

where in the above equation n, as mentioned , is the wave number through the circumferential direction. The time dependence of the solution (24) is chosen to overcome the periodicity condition of field variables in time domain. In this function, $\omega$ is the natural frequency of the joined shell system.

Substitution of the above equation into the equations of motion (17) and (18) results in new ten coupled ordinary differential equations in terms of the unknown through-the-meridian functions $U^i(\zeta ), V^i(\zeta ), W^i(\zeta ), \Phi _{\zeta }^i(\zeta )$ and $\Phi _{\theta }^i(\zeta )$. The transformed equations and the associated boundary conditions for the cylindrical/spherical segment are not given here and are presented in “Appendix A”.

As expected, Eqs. (A.1)–(A.10) along with a proper choice of boundary and matching conditions result in a system of homogeneous equations. To solve the system of equations as an eigenvalue problem, the GDQ method is implemented to transform the ordinary differential equations (A.1)–(A.10) into a new linear algebraic equations. The GDQ method is quite well known, and its details are not repeated herein. Meanwhile, one may refer to [41] for more details. It is worth noting that the distribution of nodal points in each segment is described by means of the Chebyshev–Gauss–Lobatto points which results in

$$\begin{aligned}&x_i=\dfrac{1}{2}L\left( 1-\cos \left( \dfrac{i-1}{N-1} \right) \right) ,\quad i=1,2,\ldots ,N\nonumber \\&\phi _i=\dfrac{1}{2}\dfrac{\pi }{2}\left( 1-\cos \left( \dfrac{i-1}{N-1} \right) \right) ,\quad i=1,2,\ldots ,N \end{aligned}$$

(25)

where N is the number of nodal points which is the same for each segment.

Four general procedures are known to apply the boundary conditions to a GDQ-based discretized system. In this study, the SBCGE technique which directly substitutes the boundary conditions into the governing equations is used to apply the boundary and matching conditions. Based on this technique, one should apply the GDQ method to both equations of motion and boundary conditions. The equations of motion after discretizing, applying the matching and boundary conditions and global assembling, take the form

$$\begin{aligned} \mathbf {K} \mathbf {\Delta }=\omega ^2 \mathbf {M} \mathbf {\Delta } \end{aligned}$$

(26)

where in the above equation M is the generalized mass matrix, K is the generalized stiffness matrix and $\mathbf {\Delta }$ is the unknown displacement vector. The natural frequencies of the structure may be obtained by solving the standard eigenvalue problem (26). In this research, the solution procedure by means of GDQ technique is implemented in a MATLAB code.

6 Numerical results and discussion

The procedure outlined in the previous sections is used herein to study the free vibration of joined cylindrical–hemispherical shell system made of a functionally graded material. In this section, at first a comparison study is conducted. Afterward, parametric studies are performed to examine the influences of involved parameters. In all the numerical results, each segmented shell is divided into 31 grid points through the $\phi$ and x directions, after the examination of convergence for the first ten natural frequencies up to four digits.

6.1 Comparison studies

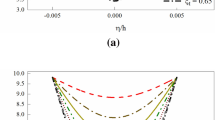
The comparison study calculates the first five frequencies of a joined cylindrical–hemispherical shell for each circumferential mode number n. Numerical results of this study are compared with the numerical results of Kang [28] which are obtained by means of the 3D elasticity theory and the Ritz method. The comparison is made in Table 1. For the results of this table, the dimensionless frequencies are defined as

$$\begin{aligned} \varOmega =\omega R\sqrt{\rho /G} \end{aligned}$$

(27)

where G is the shear modulus. For the sake of comparison, the axisymmetric frequencies of the shell (designated by $n=0$) are divided into two parts which are pure torsional (designated by a superscript T) and non-torsional (designated by A). It is seen that for both cases of boundary conditions results of our study are in close agreement with those given by Kang [28], which accepts the validity and correctness of the present formulation.

6.2 Parametric studies

After validating the present formulation and solution method, novel numerical results are given for the FGM joined cylindrical–hemispherical shells. The properties of the metal and ceramic phases are assumed as $E_\mathrm{c}=151$ GPa, $E_\mathrm{m}=70$ GPa, $\rho _\mathrm{c}=3000$ kg/m$^3$ and $\rho _\mathrm{m}=2707$ kg/m$^3$. For simplicity, Poisson’s ratio is assumed as $\nu =0.3$. Also frequencies are evaluated by

$$\begin{aligned} \varOmega =\omega R\sqrt{\rho _\mathrm{c}/G_\mathrm{c}} \end{aligned}$$

(28)

Results of this study are provided in Tables 2, 3 and 4. These three tables are associated with the three different geometric properties. In each table, two types of boundary conditions and five different values are considered for the power-law index. In each case, for each circumferential mode number the first five frequencies are tabulated. It is observed that as the power-law index of the shell increases, the frequencies of the shell decrease. This is mainly due to the higher $E/\rho$ ratio of the ceramic phase in comparison with the metal phase. Further examination of the numerical results reveals that the minimum frequency of the joined shell belongs to the higher circumferential mode numbers, which is also reported previously in [28]. It should be noted that, for the case of completely free shells, there are rigid body motion type frequencies which are designated by zero value frequencies. These frequencies are due to the incomplete constraints of the shell. Comparison of the results between Tables 2 and 3 reveals that as the length of the cylindrical shell increases, the frequencies of the combined shell decrease which is expected since the effect of edge supports becomes weaker. Also, comparison of the results between Tables 2 and 4 shows that combined shells with higher thickness have higher frequencies which is mainly due to the higher flexural rigidity of the shell.

7 Conclusion

In the current research, the free vibration response of joined cylindrical–hemispherical shell system is evaluated. Shell is assumed to be made from an FGM where properties are graded in thickness direction. A simple power-law function is used to describe the volume fraction of constituents and the simple Voigt rule of mixtures is implemented to evaluate the properties. To establish the governing equations of the shell system, the first-order shear deformation shell theory and the Donnell type of kinematic assumptions are used. Using the Hamilton principle, the complete set of governing equations and boundary conditions for the shells are obtained. With the aid of Fourier expansion through the circumferential direction and the GDQ method to the governing equations, boundary conditions and the intersection matching conditions, a complete system of algebraic equations is obtained which is solved as an eigenvalue problem. After validating the results of this study for the case of homogeneous shells, novel numerical results are obtained for the case of FGM shells. It is shown that the power-law index of the FGM, the radius-to-cylindrical shell length ratio and the length-to-radius ratio are the important factors on the frequencies of the joined shell system.

Appendix

After applying Eq. (24) to the motion equations (17) and (18), the following system of equations is extracted.

$$\begin{aligned}&A_{11}U_{,xx}^{\mathrm{c}}+\frac{A_{12}}{R}\left( -n V_{,x}^{\mathrm{c}}+ W_{,x}^{\mathrm{c}}\right) +B_{11}\Phi _{,xx}^{\mathrm{c}}-\frac{B_{12}}{R}n\Phi _{\theta ,x}^{\mathrm{c}}\nonumber \\&\quad +\,\frac{A_{66}}{R^2 } \left( -n^{2} U^{\mathrm{c}} - n RV_{,x}^{\mathrm{c}}\right) +\frac{B_{66}}{R^2}\left( -n^{2}\Phi _x^{\mathrm{c}} -n r\left( x\right) \Phi _{\theta , x}^{\mathrm{c}}\right) +\,I_1\omega ^{2}U^{\mathrm{c}}+I_2\omega ^{2}\Phi _x^{\mathrm{c}} =0\end{aligned}$$

(A.1)

$$\begin{aligned}&\frac{A_{12}n}{R }U_{,x}^{\mathrm{c}}+\frac{A_{22}}{R^2 }\left( -n^{2}V^{\mathrm{c}}+n W^{\mathrm{c}}\right) +\frac{A_{66}}{R }\left( n U_{,x}^{\mathrm{c}}+R V_{,xx}^{\mathrm{c}}\right) +\,\frac{B_{12}}{R }n\Phi _{x,x}^{\mathrm{c}}+\frac{B_{22}}{R^2}\left( -n^{2}\Phi _\theta ^{\mathrm{c}}\right) \nonumber \\&\quad +\frac{B_{66}}{R}\left( n\Phi _{x,x}^{\mathrm{c}}+R \Phi _{\theta ,xx}^{\mathrm{c}}\right) +\,\frac{\kappa A_{44} }{R^2}\left( -V^{\mathrm{c}} +R \Phi _\theta ^{\mathrm{c}} +n W^{\mathrm{c}}\right) +I_1\omega ^{2}V^{\mathrm{c}}+I_2\omega ^{2}\Phi _\theta ^{\mathrm{c}}=0\end{aligned}$$

(A.2)

$$\begin{aligned}&-\,\frac{A_{12} }{R^2}U_{,x}^{\mathrm{c}}-\frac{A_{22} }{ R^2}\left( -nV^{\mathrm{c}}+ W^{\mathrm{c}} \right) -\frac{B_{12} }{R}\Phi _{x,x}^{\mathrm{c}}+\frac{B_{22} }{R^2}n\Phi _{\theta }^{\mathrm{c}} \nonumber \\&\quad +\,\kappa A_{55}\left( \Phi _{x,x}^{\mathrm{c}}+W_{,xx}^{\mathrm{c}} \right) +\frac{\kappa A_{44}}{R^2} \left( n V^{\mathrm{c}}-n R \Phi _\theta -n^{2}W^{\mathrm{c}}\right) +I_1\omega ^{2}W^{\mathrm{c}}=0\end{aligned}$$

(A.3)

$$\begin{aligned}&B_{11}U_{,xx}^{\mathrm{c}}+\frac{B_{12}}{R }\left( -n V_{,x}^{\mathrm{c}}+ W_{,x}^{\mathrm{c}}\right) +D_{11}\Phi _{,xx}^{\mathrm{c}}-\frac{D_{12}n}{R}\Phi _{\theta ,x}^{\mathrm{c}}\nonumber \\&\quad +\,\frac{B_{66}}{R^2} \left( -n^{2} U^{\mathrm{c}} - n RV_{,x}^{\mathrm{c}}\right) +\frac{D_{66}}{R^2}\left( -n^{2}\Phi _x^{\mathrm{c}} -n R \Phi _{\theta ,x}^{\mathrm{c}}\right) \nonumber \\&\quad -\,\kappa A_{55}\left( \Phi _x^{\mathrm{c}} +W_{,x}^{\mathrm{c}}\right) +I_2\omega ^{2}U^{\mathrm{c}} +I_3\omega ^{2} \Phi _x^{\mathrm{c}} =0 \end{aligned}$$

(A.4)

$$\begin{aligned}&\frac{B_{12}}{R }nU_{,x}^{\mathrm{c}}+\frac{B_{22}}{R^2}\left( -n^{2}V^{\mathrm{c}}+n W^{\mathrm{c}}\right) +\frac{B_{66}}{R }\left( n U_{,x}^{\mathrm{c}}+RV_{,xx}^{\mathrm{c}}\right) \nonumber \\&\quad +\,\frac{D_{12}}{R}n\Phi _{x,x}^{\mathrm{c}}+\frac{D_{22}}{R^2}\left( -n^{2}\Phi _\theta ^{\mathrm{c}}\right) +\frac{D_{66}}{R}\left( n\Phi _{x,x}^{\mathrm{c}}+R \Phi _{\theta ,xx}^{\mathrm{c}}\right) \nonumber \\&\quad +\,\frac{\kappa A_{44}}{R}\left( - V^{\mathrm{c}}+R\Phi _\theta ^{\mathrm{c}} +n W^{\mathrm{c}} \right) +I_2\omega ^{2}V^{\mathrm{c}}+I_3\omega ^{2}\Phi _\theta ^{\mathrm{c}} =0\end{aligned}$$

(A.5)

$$\begin{aligned}&\frac{1}{R^2}\left\{ A_{11}U_{,\phi \phi }^{\mathrm{s}}+A_{11}\cot \left( \phi \right) U_{,\phi }^{\mathrm{s}}-\frac{A_{66}}{\sin ^2\left( \phi \right) }n^2U^{\mathrm{s}}-\left( A_{11}\cot \left( \phi \right) ^{2}+A_{12}+A_{66}\right) U^{\mathrm{s}}\right. \nonumber \\&\quad -\,\frac{\left( A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nV_{,\phi }^{\mathrm{s}}+\left( A_{11}+A_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nV^{\mathrm{s}}+\left( A_{11}+A_{12}+A_{66}\right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad +\,B_{11}\Phi _{\phi ,\phi \phi }^{\mathrm{s}}+B_{11}\cot \left( \phi \right) \Phi _{\phi ,\phi }^{\mathrm{s}}-\frac{B_{66}}{\sin ^2\left( \phi \right) }n^2 \Phi _{\phi }^{\mathrm{s}}- \left( B_{11}\cot ^2\left( \phi \right) +B_{12}-A_{66}R\right) \Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\,\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\theta ,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2U^{\mathrm{s}}+I_2\omega ^{2}\Phi _{\phi }^{\mathrm{s}}=0 \end{aligned}$$

(A.6)

$$\begin{aligned}&\frac{1}{R^2}\left\{ \frac{\left( A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nU_{,\phi }^{\mathrm{s}}+\left( A_{11}+A_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nU^{\mathrm{s}}+A_{66}V_{,\phi \phi }^{\mathrm{s}}\right. \nonumber \\&\quad +\,A_{66}\cot \left( \phi \right) V_{,\phi }^{\mathrm{s}}-\frac{A_{11}}{\sin ^2\left( \phi \right) }n^2V^{\mathrm{s}}+\left( \frac{A_{66}}{\sin ^2\left( \phi \right) }-2A_{66}\cot \left( \phi \right) ^2-A_{66}\right) V^{\mathrm{s}}\nonumber \\&\quad +\,\frac{\left( A_{11}+A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nW^{\mathrm{s}}+\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\phi ,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad +\,B_{66}\Phi _{\theta ,\phi \phi }^{\mathrm{s}}+B_{66}\cot \left( \phi \right) \Phi _{\theta ,\phi }^{\mathrm{s}}-\frac{B_{11}}{\sin ^2\left( \phi \right) }n^2\Phi _{\theta }^{\mathrm{s}}\nonumber \\&\quad \left. +\,\left( \frac{B_{66}}{\sin ^2\left( \phi \right) }-2B_{66}\cot ^2\left( \phi \right) +A_{66}R\right) \Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2V^{\mathrm{s}}+I_2{\omega }^2\Phi _{\theta }^{\mathrm{s}}=0 \end{aligned}$$

(A.7)

$$\begin{aligned}&\frac{1}{R^2}\left\{ -\left( A_{11}+A_{12}+A_{66}\right) U_{,\phi }^{\mathrm{s}}-\left( A_{11}+A_{12}+A_{66}\right) \cot \left( \phi \right) U^{\mathrm{s}}\right. \nonumber \\&\quad +\,\frac{\left( A_{11}+A_{12}+A_{66}\right) }{\sin \left( \phi \right) }nV^{\mathrm{s}}+A_{66}W_{,\phi \phi }^{\mathrm{s}}-\frac{A_{66}}{\sin \left( \phi \right) ^{2}}n^2W^{\mathrm{s}}+A_{66}\cot \left( \phi \right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad -\,2\left( A_{11}+A_{12}\right) W^{\mathrm{s}}-\left( B_{11}+B_{12}-A_{66}R\right) \Phi _{\phi .\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\,\left( B_{11}+B_{12}-A_{66}R\right) \cot \left( \phi \right) \Phi _{\phi }^{\mathrm{s}}+\frac{\left( B_{11}+B_{12}-A_{66}R\right) }{\sin \left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_1{\omega }^2W^{\mathrm{s}}=0 \end{aligned}$$

(A.8)

$$\begin{aligned}&\frac{1}{R^2}\left\{ B_{11}U_{,\phi \phi }^{\mathrm{s}}+B_{11}\cot \left( \phi \right) U_{,\phi }^{\mathrm{s}}-\frac{B_{66}}{\sin ^2\left( \phi \right) }n^2U^{\mathrm{s}}-\left( B_{11}\cot ^2\left( \phi \right) +B_{12}-A_{66}R\right) U^{\mathrm{s}}\right. \nonumber \\&\quad -\,\frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }nV_{,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nV^{\mathrm{s}}+\left( B_{11}+B_{12}-A_{66}R\right) W_{,\phi }^{\mathrm{s}}\nonumber \\&\quad +\,D_{11}\Phi _{\phi ,\phi \phi }^{\mathrm{s}}+D_{11}\cot \left( \phi \right) \Phi _{\phi ,\phi }^{\mathrm{s}}-\frac{D_{66}}{\sin ^2\left( \phi \right) }n^2 \Phi _{\phi }^{\mathrm{s}}- \left( D_{11}\cot ^2\left( \phi \right) +D_{12}+A_{66}R^{2}\right) \Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad \left. -\frac{\left( D_{12}+D_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\theta ,\phi }^{\mathrm{s}}+\left( D_{11}+D_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\theta }^{\mathrm{s}}\right\} +I_2{\omega }^2U^{\mathrm{s}}+I_3\omega ^{2}\Phi _{\phi }^{\mathrm{s}}=0 \end{aligned}$$

(A.9)

$$\begin{aligned}&\frac{1}{R^2}\left\{ \frac{\left( B_{12}+B_{66}\right) }{\sin \left( \phi \right) }nU_{,\phi }^{\mathrm{s}}+\left( B_{11}+B_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }nU^{\mathrm{s}}+B_{66}V_{,\phi \phi }^{\mathrm{s}}\right. \nonumber \\&\quad +\,B_{66}\cot \left( \phi \right) V_{,\phi }^{\mathrm{s}}-\frac{B_{11}}{\sin ^2\left( \phi \right) }n^2V^{\mathrm{s}}+\left( \frac{B_{66}}{\sin ^2\left( \phi \right) }-2B_{66}\cot ^2\left( \phi \right) +A_{66}R\right) V^{\mathrm{s}}\nonumber \\&\quad +\,\frac{\left( B_{11}+B_{12}-A_{66}R\right) }{\sin \left( \phi \right) }nW^{\mathrm{s}}+\frac{\left( D_{12}+D_{66}\right) }{\sin \left( \phi \right) }n\Phi _{\phi ,\phi }^{\mathrm{s}}+\left( D_{11}+D_{66}\right) \frac{\cos \left( \phi \right) }{\sin ^2\left( \phi \right) }n\Phi _{\phi }^{\mathrm{s}}\nonumber \\&\quad +\,D_{66}\Phi _{\theta ,\phi \phi }^{\mathrm{s}}+D_{66}\cot \left( \phi \right) \Phi _{\theta ,\phi }^{\mathrm{s}}-\frac{D_{11}}{\sin ^2\left( \phi \right) }n^2\Phi _{\theta }^{\mathrm{s}}\nonumber \\&\quad \left. +\,\left( \frac{D_{66}}{\sin ^2\left( \phi \right) }-2D_{66}\cot ^2\left( \phi \right) -A_{66}R^{2}\right) \Phi _{\theta }^{\mathrm{s}}\right\} +I_2{\omega }^2V^{\mathrm{s}}+I_3{\omega }^2\Phi _{\theta }^{\mathrm{s}}=0. \end{aligned}$$

(A.10)