1 Introduction

Nanocomposite-based shell structures are a dedicated section of structural applications in various hygrothermal conditions for many engineering applications because of their enhanced mechanical and damping properties over isotropic materials. The carbon nanotubes (CNT) discovered by Ijima [1], since then it has been used in several applications due to its large aspect ratio and lower specific weight which improves the overall elastic properties of nanocomposites (NC). The CNT reinforced with epoxy composites were tested and showed the results that CNT has a more significant impact on damping ratio than the stiffness by Rajoria and Jalili [2]. The hygrothermal effects on the conventional CFRP composites are experimentally studied by Collings and Stones [3]. The thermal and mechanical properties of MWCNT reinforced epoxy-based material are reported by Gojny et al. [4]. The authors suggested that the improved dispersion can be achieved by chemical functionalization of inclusions in the matrix phase. Results of moisture diffusion are presented for the conventional composites by David [5] and reported that CNT makes NC ideal for several engineering applications in critical hygrothermal environments and enhances its damping properties.

The strains produced due to hygrothermal conditions in the laminated beams were studied by Lee et al. [6] and presented the characterisation of the elastic and damping properties of such composites. The coefficient of thermal expansion for such a material system is assumed to be transversely isotropic. Zhang and Wang [7] presented results for the different thermal and moisture expansion of the composite material system. The strains developed in composite material under a hygrothermal environment were studied by Nanda and Pradyumna [8]. The inclusion of CNTs in nanocomposites results in a decrease in creep strains by 53% compared to epoxy matrix. The authors predicted the long-term creep behaviour of the nanocomposites by time–temperature superposition in dynamic mechanical analyser by Jia et al. [9]. The indentation tests are carried out at high temperature to determine the mechanical properties of nanocomposite-based material system and CNT has a significant impact on improving the damping properties of such composites were also presented by Teharani et al. and Saseedharan et al. [10, 11].

An experimental study carried out under the hygrothermal conditions to observe the performance of CNT reinforced epoxy materials by Jen and Huang [12]. Creep and time–temperature superposition tests were also conducted to obtain the viscoelastic properties of nanocomposites. The effect of hygrothermal treatments on mechanical properties of CFR in resin-based composites is discussed and reported by Yizhuo et al. [13]. A significant decrease was observed in the mechanical properties of such conventional composites at higher moisture exposure by Garg et al. [14].

The viscoelastic properties of short fibers reinforced composite were obtained and the creep behaviour has been analysed for glass fiber reinforced epoxy-based composites by Burgarella et al. [15] and Hagenbeek et al. [16] using dynamic mechanical analysis. Significant improvement of damping ratio was observed by the incorporation of CNT in the different composite shell structures by Khan et al. [17] and Patnaik et al. [18, 19]. In recent years, the researchers have extensively studied the free and forced vibration of different composite plate and shell structures. The effect of frequency and temperature-dependent homogenized CNT-CFRP material property on the damping of different plate/shell structures was studied by Swain and Roy [20]. The effect of CNT on damping of such CNT reinforced composite-based skew shell structures was presented by Kiani et al. [21, 22]. The author has used an oblique coordinate system to skew the structure in this research work. Mahapatra et al. [23] presented the hygro-thermo-elastic constitutive relationship-based mathematical formulation for the nonlinear free vibration study of the laminated composite shell structure. The literatures on free and forced vibration of different NC-material-based skew shell structures are limited (for example, Kandasamy and Singh [24], Shojaee et al. [25] and Biswal et al. [26]).

Parametric vibration analysis has been done for the multi-scale hybrid nanocomposites-based plate/shell structures by Ebrahimi and Dabbagh [27, 28]. The improved mathematical formulation for smart fiber-reinforced composites has been presented by Roy et al. [29]. Vibration analysis for different shell structures with improved shear deformation theory is presented by Sangtarash et al. [30] and Mallek et al. [31]. Free vibration studies of glass fiber reinforced shallow shells based on first-order shear deformation theory have been done with finite element modelling under hygrothermal conditions. The hygrothermal effect on different geometries of shell structures were presented by Sinha and Naidu [32] and, Biswal and Karimiasl and Tsai et al. [33,34,35,36]. It is also found that extensive research work has been carried out for static and bucking analysis of NC-based CNT reinforced shell structures in recent times but any possible frequency dependant NC-based materials have not been considered for several applications under hygrothermal conditions. Kundalwal and Rathi [37] developed cluster-free and uniform dispersion of multiwalled carbon nanotubes (MWCNTs) in the epoxy matrix using an innovative ultrasonic dual mixing technique. The effects of dispersion of MWCNTs on the mechanical and viscoelastic properties of MWCNT-epoxy nanocomposites were reported. Kundalwal [38] presented an extensive review on the thermomechanical properties of fiber-reinforced composites using several micromechanics models (such as the strength of the material approach, Halpin–Tsai equations, multi‐phase mechanics of materials approaches, multi‐phase Mori–Tanaka models, composite cylindrical assemblage model, Voigt–Reuss models, modified mixture rule, Cox model, effective medium approach and method of cells). Detail investigations of active constrained layer damping (ACLD) of smart laminated continuous fuzzy fiber-reinforced composite (FFRC) plate and shell structures were presented by Kundalwal and Ray [39, 40]. A finite element model was developed for such laminated structures integrated with the patches of ACLD treatment.

Nanocomposites-based structures have many applications in several engineering fields. Many literatures are available for free vibration study of the nanocomposites and nanocomposite made structures but under hygrothermal conditions, the NCs are vulnerable, due to this limitation it is very important to carry out an extensive research to study the effective volume fraction of CNT impact on the vibration and damping responses of NCs based shell structures under different hygrothermal conditions. The present research work used the dynamic mechanical analysis for the experimental viscoelastic material properties of NCs in the frequency domain. For the damping characteristics, the frequency dependant material properties cannot be directly used in the time domain so inverse fast Fourier transform (IFFT) has been employed to determine the time response of the said structure. The moisture and temperature dependant viscoelastic material properties of NCs are used to calculate effective hygrothermal stiffness of the skewed shell structure to study the damping behaviour under different hygrothemral conditions. Effect of CNTs on such CNTR viscoelastic skewed shell structure under hygrothermal environment has been done by the parametric vibration study (viz. resonant frequency, loss factor of the system etc.).

2 Mathematical modelling

Viscoelastic material properties of NCs are determined with the help of dynamic mechanical analysis. The frequency dependant properties are then used to investigate the damping behaviour of the skewed shell structure. The arbitrary coordinate system has been considered to define the skewed shell geometry which was used in finite element modelling to study the dynamic behaviour of the said structure under different hygrothermal conditions.

2.1 Creep test using dynamic mechanical analysis

Dynamic mechanical analysis machine is used to determine the CNT-based epoxy matrix material properties by making samples as per the American Society for Testing and Materials ASTM-D4065 standard. Atleast 5 samples of NCs were made with 12 h of ultrasonic sonication to minimise the agglomerations. Several tests were conducted and averaged the test data obtained for the exact prediction of creep strain behaviour. The creep strain is obtained by conducting such procedure on DMA-8000 (as shown in Fig. 1) and power law is used to calculate the prony constants. Laplace transform is used to obtain the frequency dependant viscoelastic material properties of such NCs.

Fig. 1
figure 1

a Dynamic mechanical analysis-8000 under tension support, b nanocomposite samples (i) 0% volume fraction of CNT (ii) 4% volume fraction of CNT and (iii) 8% volume fraction of CNT and c dynamic mechanical analysis connected to auxiliary humidifier setup

Full size image

The short term creep test experiments conducted on DMA-8000 for the polymer-based nanocomposites samples and obtained the creep compliance \(D\left(t\right)\) with creep strain \(\varepsilon \left(t\right)\) in time domain.

$$D\left(t\right)=\frac{\varepsilon \left(t\right)}{{\sigma }_{0}}.$$
(1)

Further, the power law is used for determining the Prony fitting constants as shown in Eq. (2)

$$\varepsilon \left(t\right)=a+b{t}^{c}.$$
(2)

Once the long term creep strain fitting has been obtained based on the power law, Prony fitting constants are determined in terms of \({E}_{i}\) and \({\tau }_{i}\). Plain epoxy (L-12-type) is tested on DMA-8000 (shown in Fig. 1a) and Prony constants are obtained from the long-term creep power law fitting at room temperature and moisture condition (mentioned in the Table 1).

Table 1 Prony constants obtained from power law fitting for neat epoxy (L12-type) with \({E}_{\infty }=\) 315,886,082.34
Full size table

The Prony constants are used to determine the relaxation modulus of such composites in the time domain. The mathematical fitting of the relaxation model originates from the Maxwell generalized model with Prony fitting constants. The Maxwell generalized model is the common linear viscoelastic model and according to the Hook’s law, the stress–strain relation for the Maxwell generalized model can be written as:

$${\sigma }_{\infty }= {\varepsilon }_{\infty }{E}_{\infty },$$
(3)

where; \({\sigma }_{\infty }\) and \({\in }_{\infty }\) are the stress and strain in the spring element which is also connected to a dashpot element.

So the relaxation modulus \(E\left(t\right)\) can be expressed as:

$$E\left(t\right)=\frac{\sigma \left(t\right)}{{\varepsilon }_{0}}={E}_{\infty }+\sum_{i=1}^{n}{E}_{i}\mathrm{exp}\left(-\frac{t}{{\tau }_{i}}\right).$$
(4)

The obtained Prony constants are not completely fitting constants but are essential parameters with physical significance in the formulation. The Prony constants are further used to determine the storage modulus \({E}^{{\prime}}\left(\omega \right)\) and loss modulus \({E}^{{\prime}{\prime}}\left(\omega \right)\) in the Laplace transform from Eq. (4) as:

$${E}^{{\prime}}\left(\omega \right)= {E}_{\infty }+ \sum_{i=1}^{n}{E}_{i}\frac{{\omega }^{2}}{{\omega }^{2}+ \frac{1}{{\tau \left(i\right)}^{2}}},$$
(5)
$${E}^{{\prime}{\prime}}\left(\omega \right)= \sum_{i=1}^{n}{E}_{i}\frac{{\omega /\tau }_{i}}{{\omega }^{2}+ \frac{1}{{\tau \left(i\right)}^{2}}}.$$
(6)

In the Eq. (5 and 6), the storage modulus \({E}^{{\prime}}\left(\omega \right)\) and loss modulus \({E}^{{\prime}{\prime}}\left(\omega \right)\) are obtained in the frequency domain with using the Laplace transform. Where, \(\omega\) is the angular frequency and \(i=\sqrt{-1}\) imaginary number and \(E\left(\omega \right)\), \({E}_{0}\), \(\omega\) are frequency-dependent modulus, instenteneous modulus, and frequency respectively. \(\tau (i)\), and \(E(i)\) are Prony constants.

2.2 Finite element modelling of CNTR skewed shell

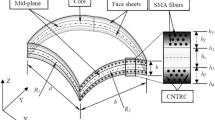
An oblique coordinate system is considered for defining the skewed shell structure geometry as shown in Fig. 2. The stress-resultant type Koiter’s shell theory is used in the finite element (FE) formulation by using the shear deformation effect according to Mindlin’s hypothesis [29].

Fig. 2
figure 2

Geometry and isoparametric mapping of skewed spherical shell

Full size image

2.2.1 Geometry of CNTR skewed shell structure

The mid-surface of the shell surface can be described in terms of position vector as

$$r(\alpha _{1} ,\alpha _{2} ) = X(\alpha _{1} ,\alpha _{2} )\mathop i\limits^{ \wedge } + Y(\alpha _{1} ,\alpha _{2} )\mathop j\limits^{ \wedge } + Z(\alpha _{1} ,\alpha _{2} )\mathop k\limits^{ \wedge } ,$$
(7)

where, \(\mathop i\limits^{ \wedge }\), \(\mathop j\limits^{ \wedge }\) and \(\mathop k\limits^{ \wedge }\) are unit vectors along the X, Y and Z axis, respectively. Normal Cartesian coordinate system (X, Y) can be written in the form of oblique coordinate system (X’, Y’) with tangent to edge [21, 22] which can be expressed as follows

$$\begin{gathered} X' = X - Y\tan (\alpha ) \hfill \\ Y' = Y\sec (\alpha ) \hfill \\ Z' = Z. \hfill \\ \end{gathered}$$
(8)

The tangent to the isoparametric curves Sα1 and Sα2 are

$$r,_{1} = \frac{\partial r}{{\partial \alpha_{1} }}{\text{and}}\;r,_{2} = \frac{\partial r}{{\partial \alpha_{2} }}.$$
(9)

The vector joining two points on the middle surface (α1, α2) and (α1 + d α1, α2 + d α2) is given as

$${\text{d}}s = (r,_{1} {\text{d}}\alpha _{1} + r,_{2} d\alpha _{2} ).$$
(10)

The scalar product of ds

$${\text{d}}s.{\text{d}}s = (r,_{1} .r,_{1} ){\text{d}}\alpha _{1} ^{2} + (r,_{2} .r,_{2} )d\alpha _{2} ^{2} .$$
(11)

Defining

$$A_{1} = \sqrt {r,_{1} .r,_{1} } \, \text{and}\,A_{2} = \sqrt {r,_{2} .r,_{2} } .$$
(12)

As the Lame’s parameters or measure numbers that are fundamentals for the understanding of curvilinear coordinates,

$${\text{d}}s^{2} = A_{1}^{2} {\text{d}}\alpha_{1}^{2} + A_{2}^{2} d\alpha_{2}^{2} .$$
(13)

Since the α1 and α2 are independent coordinates

$${\text{d}}s^{2} = {\text{d}}s_{\alpha 1}^{2} + {\text{d}}s_{\alpha 2}^{2} ,$$
(14)
$$\begin{gathered} {\text{d}}s_{\alpha 1} = A_{1} {\text{d}}\alpha_{1} \hfill \\ {\text{d}}s_{\alpha 2} = A_{2} {\text{d}}\alpha_{2} . \hfill \\ \end{gathered}$$
(15)

The unit tangent vectors to the isoparametric curve Sα1 and Sα2 can be expressed respectively as

$$\mathop {e_{1} }\limits^{ \wedge } = \frac{{r,_{1} }}{{A_{1} }}\,{\text{and}}\,\mathop {e_{2} }\limits^{ \wedge } = \frac{{r,_{2} }}{{A_{2} }}.$$
(16)

The subscripts 1 and 2 in r, 1 and r, 2 indicate the derivative with respect to α1 and α2 respectively. The unit normal vector to the tangent plane of any point on the reference surface can be expressed as

$$\mathop {e_{n} }\limits^{ \wedge } = \frac{{r_{,1} \times r_{,2} }}{{\left| {r_{,1} \times r_{,2} } \right|}}.$$
(17)

The normal curvatures of the shell midsurface can be expressed as

$$\frac{1}{{R_{1} }} = - \frac{{\mathop {e_{n} }\limits^{ \wedge } .r_{,11} }}{{A_{1}^{2} }}\,{\text{and}}\,\frac{1}{{R_{2} }} = - \frac{{\mathop {e_{n} }\limits^{ \wedge } .r_{,22} }}{{A_{2}^{2} }},$$
(18)

and the twist curvatures of the shell midsurface can be expressed as

$$\frac{1}{{R_{12} }} = - \frac{{\mathop {e_{n} }\limits^{ \wedge } .r_{,12} }}{{A_{1} .A_{2} }}.$$
(19)

2.2.2 Mapping of the isoparametric element

The shell mid-surface in the rectangular cartesian coordinate system has been mapped into the parametric space \((\alpha_{1} ,\alpha_{2} )\) and the mid-surface in the parametric space has been divided into the required number of quadrilateral elements or sub-domains. The reference coordinates \((\xi ,\eta )\) map the quadrilateral element in the curvilinear coordinates \((\alpha_{1} ,\alpha_{2} )\) into the reference coordinates that is a square as shown in Fig. 2. Any point within an element in the parametric space has been approximated by the isoparametric mapping.

Hence the curvilinear coordinates \((\alpha_{1} ,\alpha_{2} )\) of any point within an element may be expressed as

$$\begin{gathered} \alpha _{1} = \sum\limits_{{i = 1}}^{{nd}} {N_{i} \alpha _{{1i}} } \\ \alpha _{2} = \sum\limits_{{i = 1}}^{{nd}} {N_{i} \alpha _{{2i}} } . \\ \end{gathered}$$
(20)

The displacement components on the shell midsurface at any point within an element may be expressed as

$$\left\{ {\begin{array}{*{20}l} {u_{0} } \hfill \\ {v_{0} } \hfill \\ w \hfill \\ {\theta_{1} } \hfill \\ {\theta_{2} } \hfill \\ \end{array} } \right\} = \sum\limits_{i = 1}^{nd} {N_{i} } \left\{ {\begin{array}{*{20}l} {u_{0i} } \hfill \\ {v_{0i} } \hfill \\ {w_{i} } \hfill \\ {\theta_{1i} } \hfill \\ {\theta_{2i} } \hfill \\ \end{array} } \right\},$$
(21)

where, nd is the number of nodes in an element and (α1, α2) is the coordinate of midsurface at ith node in curvilinear coordinate system. u0i, v0i and w0i are the deflection of midsurface at ith node in α1, α2 and z directions respectively. θ1i is the rotation of normal at ith node about α2 axis and θ2i is the rotation of normal at ith node about α1 axis.

2.2.3 Strain–displacement relationship

Neglecting normal strain component in the thickness direction, the five strain components of a doubly curved shell may be express as

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{X^{\prime}X^{\prime}} } & {\varepsilon_{Y^{\prime}Y^{\prime}} } & {\gamma_{X^{\prime}Y^{\prime}} \begin{array}{*{20}c} { \, \gamma_{Y^{\prime}Z^{\prime}} } & {\gamma_{X^{\prime}Z^{\prime}} } \\ \end{array} } \\ \end{array} } \right]^{T} =^{{}} \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{X^{\prime}X^{\prime}}^{0} } & {\varepsilon_{Y^{\prime}Y^{\prime}}^{0} } & {\gamma_{X^{\prime}Y^{\prime}}^{0} } \\ \end{array} } & {\begin{array}{*{20}c} {\gamma_{Y^{\prime}Z^{\prime}}^{0} } & {\gamma_{X^{\prime}Z^{\prime}}^{0} } \\ \end{array} } \\ \end{array} } \right]^{T} + z\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k_{X^{\prime}X^{\prime}} } & {k_{Y^{\prime}Y^{\prime}} } & {k_{X^{\prime}Y^{\prime}} } \\ \end{array} } & {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \\ \end{array} } \right]^{T} ,$$
(22)

where, \(\varepsilon_{X^{\prime}X^{\prime}}^{0} ,\varepsilon_{Y^{\prime}Y^{\prime}}^{0} {\text{ and }}\gamma_{X^{\prime}Y^{\prime}}^{0}\) are the in-plane strains of the midsurface in the cartesian coordinate system and \(k_{X^{\prime}X^{\prime}} ,k_{Y^{\prime}Y^{\prime}} {\text{ and }}k_{X^{\prime}Y^{\prime}}\) are the bending strains (curvatures) of the midsurface in the cartesian coordinates system. After incorporating the effect of transverse stain in Koiter’s shell theory, inplane and transverse strain–displacement relations may be expressed as described in the following subsections.

2.2.4 In Plane strain displacement elements

The strain components on the midsurface of the shell element are

$$\{ \varepsilon \} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{X^{\prime}X^{\prime}}^{0} } & {\varepsilon_{Y^{\prime}Y^{\prime}}^{0} } & {\gamma_{X^{\prime}Y^{\prime}}^{0} } \\ \end{array} } & {\begin{array}{*{20}c} {k_{X^{\prime}X^{\prime}} } & {k_{Y^{\prime}Y^{\prime}} } & {k_{X^{\prime}Y^{\prime}} } \\ \end{array} } \\ \end{array} } \right]^{T} .$$
(23)

By using isoparametric 8-noded shell element, the displacement component on the shell midsurface at any point within an element can be expressed as

$$\{ \begin{array}{*{20}c} {u_{0} } & {v_{0} } & w & {\theta_{1} } & {\theta_{2} } \\ \end{array} \}^{T} = [N]\{ d^{e} \} ,$$
(24)

where, [N] is the shape functions according to Koiter’s shell theory and mentioned in the appendix.

According to Koiter’s shell theory, the midsurface strains and curvatures may be expressed in terms of field variables as

$$\varepsilon_{X^{\prime}X^{\prime}}^{0} = \frac{1}{{A_{1} }}\frac{\partial u}{{\partial \alpha_{1} }} + \frac{v}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} + \frac{w}{{R_{1} }},$$
(25)
$$\varepsilon_{Y^{\prime}Y^{\prime}}^{0} = \frac{1}{{A_{2} }}\frac{\partial v}{{\partial \alpha_{2} }} + \frac{u}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }} + \frac{w}{{R_{2} }},$$
(26)
$$\gamma_{X^{\prime}Y^{\prime}}^{0} = \frac{1}{{A_{1} }}\frac{\partial v}{{\partial \alpha_{1} }} + \frac{1}{{A_{2} }}\frac{\partial u}{{\partial \alpha_{2} }} - \frac{u}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} - \frac{v}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }} + \frac{2w}{{R_{12} }},$$
(27)
$$k_{X^{\prime}X^{\prime}} = \frac{1}{{A_{1} }}\frac{{\partial \theta_{1} }}{{\partial \alpha_{1} }} + \frac{{\theta_{2} }}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} + \frac{1}{{2R_{12} }}\left( {\frac{1}{{A_{1} }}\frac{\partial v}{{\partial \alpha_{1} }} - \frac{1}{{A_{2} }}\frac{\partial u}{{\partial \alpha_{2} }} - \frac{u}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} + \frac{v}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }}} \right),$$
(28)
$$k_{Y^{\prime}Y^{\prime}} = \frac{1}{{A_{2} }}\frac{{\partial \theta_{2} }}{{\partial \alpha_{2} }} + \frac{{\theta_{1} }}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }} - \frac{1}{{2R_{12} }}\left( {\frac{1}{{A_{1} }}\frac{\partial v}{{\partial \alpha_{1} }} - \frac{1}{{A_{2} }}\frac{\partial u}{{\partial \alpha_{2} }} - \frac{u}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} + \frac{v}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }}} \right),$$
(29)
$$k_{X^{\prime}Y^{\prime}} = \left[ \begin{gathered} \frac{1}{{A_{1} }}\frac{{\partial \theta_{2} }}{{\partial \alpha_{1} }} + \frac{1}{{A_{2} }}\frac{{\partial \theta_{1} }}{{\partial \alpha_{2} }} - \frac{{\theta_{1} }}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} - \frac{{\theta_{2} }}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }} - \\ \frac{1}{2}\left( {\frac{1}{{R_{1} }} - \frac{1}{{R_{2} }}} \right)\left( {\frac{1}{{A_{1} }}\frac{\partial v}{{\partial \alpha_{1} }} - \frac{1}{{A_{2} }}\frac{\partial u}{{\partial \alpha_{2} }} - \frac{u}{{A_{1} A_{2} }}\frac{{\partial A_{1} }}{{\partial \alpha_{2} }} + \frac{v}{{A_{1} A_{2} }}\frac{{\partial A_{2} }}{{\partial \alpha_{1} }}} \right) \\ \end{gathered} \right].$$
(30)

By using 8-noded isoparametric shape functions (mentioned in the appendix), the strain components at any point on the shell mid-surface can be expressed as

$$\left\{ \varepsilon \right\} = \left[ {B_{b}^{e} } \right]\left\{ {d^{e} } \right\}.$$
(31)

2.2.5 Transverse shear strain displacement element

According to the FOST, the transverse shear strain vector of a doubly curved shell element may be expressed as

$$\left\{ {\begin{array}{*{20}c} {\gamma_{Y^{\prime}Z^{\prime}} } \\ {\gamma_{X^{\prime}Z^{\prime}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\theta_{2} + \frac{1}{{A_{2} }}\frac{\partial w}{{\partial \alpha_{2} }} - \frac{u}{{R_{12} }} - \frac{v}{{R_{2} }}} \\ {\theta_{1} + \frac{1}{{A_{1} }}\frac{\partial w}{{\partial \alpha_{1} }} - \frac{u}{{R_{1} }} - \frac{v}{{R_{12} }}} \\ \end{array} } \right\},$$
(32)

and hence the transverse shear strain at any point on the shell mid surface can be expressed as

$$\left\{ {\begin{array}{*{20}c} {\gamma_{Y^{\prime}Z^{\prime}} } \\ {\gamma_{X^{\prime}Z^{\prime}} } \\ \end{array} } \right\} = \sum\limits_{k = 1}^{nd} {\left[ {\begin{array}{*{20}l} { - \frac{{N_{i} }}{{R_{12} }}} \hfill & { - \frac{{N_{i} }}{{R_{2} }}} \hfill & {\frac{1}{{A_{2} }}\frac{{\partial N_{i} }}{{\partial \alpha_{2} }}} \hfill & { \, 0} \hfill & {N_{i} } \hfill \\ { - \frac{{N_{i} }}{{R_{1} }}} \hfill & { - \frac{{N_{i} }}{{R_{12} }}} \hfill & {\frac{1}{{A_{1} }}\frac{{\partial N_{i} }}{{\partial \alpha_{1} }}} \hfill & {N_{i} } \hfill & { \, 0} \hfill \\ \end{array} } \right]} \left\{ {\begin{array}{*{20}l} {u_{0i} } \hfill \\ {v_{0i} } \hfill \\ {w_{i} } \hfill \\ {\theta_{1i} } \hfill \\ {\theta_{2i} } \hfill \\ \end{array} } \right\},$$
(33)
$$\left\{ {\begin{array}{*{20}c} {\gamma_{Y^{\prime}Z^{\prime}} } \\ {\gamma_{X^{\prime}Z^{\prime}} } \\ \end{array} } \right\} = \left[ {B_{s}^{e} } \right]\left\{ {d^{e} } \right\}.$$
(34)

2.2.6 Determination of elemental stiffness matrix and force vector

The A, B and D matrices can be written in the following integral forms

$$\left({A}_{ij} { B}_{ij} { D}_{ij}\right)= \left[{\int }_{-\frac{h}{2}}^\frac{h}{2}\left(1\, z\, {z}^{2}\right)\overline{{\mathcal{Q} }_{ij}}\mathrm{d}z\right], \left({A}_{ij}^{s}\right)=\left[{\int }_{-\frac{h}{2}}^\frac{h}{2}{k}_{s}\overline{{\mathcal{Q} }_{ij}}\mathrm{d}z\right].$$
(35)

The shear correction factor is taken 5/6 times in the present analysis and the elements of the A, B and D matrices are obtained as below

$$A_{{ij}} = \sum\nolimits_{{k = 1}}^{n} {(\overline{{Q_{{ij}} }} )_{k} \left( {z_{k} - z_{{k - 1}} } \right),}$$
(36)
$$B_{{ij}} = \frac{1}{2}\sum\nolimits_{{k = 1}}^{n} {(\overline{{Q_{{ij}} }} )_{k} \left( {z_{k}^{2} - z_{{k - 1}}^{2} } \right),~{\text{Here}},~i = 1,3~\;{\text{and}}~j = 1,3,}$$
(37)
$$D_{{ij}} = \frac{1}{3}\sum\nolimits_{{k = 1}}^{n} {(\overline{{Q_{{ij}} }} )_{k} \left( {z_{k}^{3} - z_{{k - 1}}^{3} } \right),}$$
(38)

where A, B and D matrices are extensional strains, coupling matrix, and bending strains respectively. The transformed stiffness matrix is denoted by \((\overline{{Q }_{ij}}{)}_{k}\) of each layer and the element in plane/bending stiffness is \([{K}_{bb}^{e}]\)

$$[K_{{bb}}^{e} ] = \int\limits_{v} {[B_{b}^{e} ]^{T} } [D_{b} ][B_{b}^{e} ]{\text{d}}V,$$
(39)
$$[K_{{bb}}^{e} ] = \int\limits_{\Omega } {[B_{b}^{e} ]^{T} } \left[ {\begin{array}{*{20}c} {[A]} & {[B]} \\ {[B]} & {[D]} \\ \end{array} } \right]_{b} [B_{b}^{e} ]{\text{d}}\Omega .$$
(40)

The transverse shear matrix is \([{K}_{bb}^{e}]\)

$$[K_{{ss}}^{e} ] = \int\limits_{v} {[B_{s}^{e} ]^{T} } [D_{s} ][B_{s}^{e} ]{\text{d}}V,$$
(41)
$$[K_{{ss}}^{e} ] = \int\limits_{\Omega } {[B_{s}^{e} ]^{T} } \left[ {\begin{array}{*{20}c} {[A]} & {[B]} \\ {[B]} & {[D]} \\ \end{array} } \right]_{s} [B_{s}^{e} ]{\text{d}}\Omega .$$
(42)

The external force vector is \({\{F}^{e}\}\)

$$\{ F^{e} \} = \int\limits_{A} {[N]^{T} } \{ f_{s}^{e} (x,y)\} {\text{d}}A.$$
(43)

2.2.7 Stiffness calculation from in-plane strains under hygrothermal condition

The in-plane strains [41] due to hygrothermal condition are written as

$$\left\{ \varepsilon \right\}^{HT} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varepsilon_{X^{\prime}X^{\prime}}^{HT0} } & {\varepsilon_{Y^{\prime}Y^{\prime}}^{HT0} } & {\gamma_{X^{\prime}Y^{\prime}}^{HT0} } \\ \end{array} } & {\begin{array}{*{20}c} {k_{X^{\prime}X^{\prime}}^{HT} } & {k_{Y^{\prime}Y^{\prime}}^{HT} } & {k_{X^{\prime}Y^{\prime}}^{HT} } \\ \end{array} } \\ \end{array} } \right]^{T} ,$$
(44)
$$({{A}_{ij} { B}_{ij} { D}_{ij})}^{HT}={\left[{\int }_{-\frac{h}{2}}^\frac{h}{2}\left(1 z {z}^{2}\right)\overline{{\mathcal{Q} }_{ij}}dz\right]}^{HT},$$
(45a)

where,

$$({\overline{{Q }_{ij})}}_{k}^{HT}=\stackrel{-}{{[\mathcal{Q}}_{ij}}{e}_{k}{]}^{HT}\, \mathrm{and}\, {e}_{k}=\{{\beta \}}_{k}^{H}\left(C-{C}_{0}\right)+ \{{{\alpha }^{o}\}}_{k}^{T}(T-{T}_{0}),$$
(45b)

In Eq. 45a, 45b, \({e}_{k}\) are the non-mechanical strains consisting coefficient of thermal expansion (α) and coefficient of moisture expansion (β). The coefficient of thermal expansion (α) and coefficient of moisture expansion (β) are calculated for the NC based on the CNT volume fraction which is mentioned in the appendix section.

$${A}_{ij}^{HT}={\sum }_{k=1}^{n}({\overline{{Q }_{ij})}}_{k}^{HT}\left({z}_{k}-{z}_{k-1}\right),$$
(46)
$${B}_{ij}^{HT}=\frac{1}{2}{\sum }_{k=1}^{n}({\overline{{Q }_{ij})}}_{k}^{HT}\left({z}_{k}^{2}-{z}_{k-1}^{2}\right), \mathrm{Here}, i=\mathrm{1,3}\, \mathrm{and}\, j=\mathrm{1,3},$$
(47)
$${D}_{ij}^{HT}=\frac{1}{3}{\sum }_{k=1}^{n}({\overline{{Q }_{ij})}}_{k}^{HT}\left({z}_{k}^{3}-{z}_{k-1}^{3}\right).$$
(48)

The transformed hygrothermal stiffness matrix is denoted by \(({\overline{{Q }_{ij})}}_{k}^{HT}\) of each layer and the element in plane/bending stiffness is \({[{K}_{bb}^{e}]}^{HT}\)

$$[K_{{bb}}^{e} ]^{{HT}} = \int\limits_{v} {([B_{b}^{e} ]^{T} )^{{HT}} } [D_{b} ]^{{HT}} [B_{b}^{e} ]^{{HT}} {\text{d}}V,$$
(49)
$$[K_{{bb}}^{e} ]^{{HT}} = \int\limits_{\Omega } {([B_{b}^{e} ]^{T} )^{{HT}} } \left[ {\begin{array}{*{20}c} {[A]} & {[B]} \\ {[B]} & {[D]} \\ \end{array} } \right]_{{_{b} }}^{{HT}} [B_{b}^{e} ]^{{HT}} {\text{d}}\Omega .$$
(50)

2.2.8 Effective elemental stiffness matrix

The effective stiffness matrix of the element under the hydrothermal conditions can be written as

$$\left[{K}_{uu}^{e}\right]=\left(\left[{K}_{bb}^{e}\right]+ \left[{K}_{ss}^{e}\right]\right)- {\left[{K}_{bb}^{e}\right]}^{HT}.$$
(51)

The elemental dynamic equation of motion can be written as

$$\left[{M}_{uu}^{e}\right]\left\{\ddot{{d}^{e}}\right\}+\left[{K}_{uu}^{e}\right]\left\{{d}^{e}\right\}=\left\{{F}^{e}\right\}.$$
(52)

The element mass matrix \(\left[{M}_{uu}^{e}\right]\) can be obtained as

$$\left[{M}_{e}\right]= {\int }_{-1}^{1}{\int }_{-1}^{1}[N{]}^{T}\left[\rho \right]\left[N\right]\left|J\right|\mathrm{d}\xi \mathrm{d}\eta ,$$
(53)

where, \(\left[N\right] and [\rho ]\) matrices are mentioned in the appendix section.

Global equation of motion after assembling the elemental mass and stiffness matrices can be written as follows

$$\left[M\right]\left\{\ddot{d}\right\}+\left[K\right]\left\{d\right\}=\left\{F\right\}.$$
(55)

The complex stiffness matrix of viscoelastic material can be written as

$$K(i\omega ) = K_{R} (\omega ) + iK_{I} (\omega ).$$
(56)

In Eq. 56, \({K}_{R}\left(\omega \right)\) and \({K}_{I}\left(\omega \right)\) are the real and imaginary parts of the complex stiffness matrix (\(K\left(i\omega \right)\)) in frequency domain.

2.3 Free vibration of the skewed shell structure

Equation of motion for free vibration analysis can be expressed as

$$\left[M\right]\left\{\ddot{d}\right\}+\left[K\right]\left\{d\right\}=\left\{0\right\}.$$
(57)

The eigenvalue problem can be further reduced as

$$\left(K\left(i\omega \right)-\lambda \left[M\right]\right)\left\{X\left(\omega \right)\right\}=\left\{0\right\}.$$
(58)

The Eigenvalue Eq. 58 is nonlinear complex equation where λ are the eigenvalues and X are the eigenvectors of the structure. Expression of complex eigenvalue can be written as

$${\lambda }_{j}={\omega }_{j}^{2}\left(1+i{\eta }_{j}\right).$$
(59)

The jth modal frequency and loss factors are ωj and ηj respectively. The modal parameters ωj, ηj and Xj are obtained from the modified model strain energy method [42,43,44]. The parameters are assumed to be converged when

$$\frac{{\omega }_{j(k)}-{\omega }_{j(k-1)}}{{\omega }_{j(k-1)}}\le {\varepsilon }_{e},$$
(60)

where, ωj(k) indicates jth model frequency evaluated at kth iteration and ɛe is a very small scaler quantity (~ 10–6).

The complex form of natural frequency can be further used for the determination of the modal loss factor of the structure/system as follows

$${\eta }_{j}=\frac{Im ({\lambda }_{j})}{Re ({\lambda }_{j})}.$$
(61)

2.4 Frequency responses of the skewed shell structure

The frequency response analysis has been done from Eq. 55, where the force vector {F} and displacement vector {d} take the form of \(\{ F_{0} \} e^{i\omega t}\) and \(\{ d_{0} \} e^{i\omega t}\) where F0, ω and d0 are the amplitude of excitation force, excitation frequency and amplitude of displacement respectively. The dynamic response of the system in the frequency domain can be obtained as

$$\left\{\left|{d}_{0}\right|\right\}= \left|[-\left[M\right]{\omega }^{2}+[K(i\omega ){]]}^{-1}\{{F}_{0}\}\right|.$$
(62)

2.5 Transient response of the skewed shell under impulse loading

The time-dependant material properties are essential to determine the transient response from the direct time integration method and mode superposition method [45] but in the present case, the material properties are determined in the frequency domain so the transient response is obtained from the frequency response analysis directly. Frequency spectra of excitation in the time domain can be expressed as

$$F\left({\omega }_{j}\right)=\mathcal{F}\left(F\left({t}_{k}\right)\right),$$
(63)

where \(\mathcal{F}()\) represents the Fourier transform of a signal in time domain. tk is a set of discrete time. The complex form dynamic response of the system in the frequency domain can be obtained by solving the equations of the linear system.

$$\left\{X({\omega }_{j})\right\}={(\left[K({\omega }_{j})\right]-{\omega }^{2}[M])}^{-1}\left\{F({\omega }_{j})\right\}.$$
(64)

The transient response d (t) in the time domain can be determined by the following equation:

$$\left\{d({t}_{k})\right\}= {\mathcal{F}}^{-1}\left(X\left({\omega }_{j}\right)\right),$$
(65)

where \({\mathcal{F}}^{-1}()\) represents the inverse Fourier transform of a signal in the frequency domain.

3 Results and discussions

A computer code has been developed based on the proposed formulation in the earlier section for analysing the CNTR viscoelastic skewed shell structure under different hydrothermal conditions. The developed mathematical model has been validated with the available results in the available literatures and using ANSYS commercial software for the spherical shell structure which are presented in Table 2. The shell structure has been discretised with 10 × 10 mesh size for the vibration study of various skewed spherical shell structures with the following SSSS boundary condition:

$$\begin{gathered} x = 0, a :u_{0} = v_{0} = w_{0} = \theta_{y} = \theta_{z} = 0 \hfill \\ y = 0, a :u_{0} = v_{0} = w_{0} = \theta_{x} = \theta_{z} = 0. \hfill \\ \end{gathered}$$
(66)
Table 2 Comparison of first fundamental frequency of 0/90 laminated spherical shell (a = b) with SSSS boundary condition for various R/a and a/h ratios
Full size table

3.1 Material properties of NCs

The NCs with different volume fractions i.e. 0%, 4% and 8% of CNT reinforcement are tested under different hygrothemal conditions on DMA-8000. The creep test is conducted to determine the time dependant storage and loss, modulus of such NCs material in different hygrothermal conditions. The required materials i.e., MWCNTs, and epoxy, are purchased from ADNANO technologies.

3.1.1 Viscoelastic properties of NCs in frequency domain

The nanocomposites samples are made with 0%, 4% and 8% CNT volume fraction (shown in Fig. 1b) as per ASTM-D4065 standard for the polymer based sample testing on the dynamic mechanical analysis (DMA-8000) with auxiliary humidifier setup as shown in Fig. 1c. The material constituents for such composites, are mentioned in Table 3. The creep test is conducted with 3 N constant static loads for the predefined constant stress on the sample under different hygrothermal conditions using the PYRIS software. The auxiliary humidity generator has been used during the test for controlled environment testing on LACERTA software. The creep strain and creep compliance are determined experimentally and calculated the Prony constants with power law fit. Further the Laplace transform has been used to calculate the storage modulus and loss modulus in frequency domain under different hygrothermal conditions. The four hygrothermal cases are considered mentioned in Table 4. The variations of storage/conservative modulus (E’) and loss factor (tan δ) with frequency for different hygrothermal conditions (such as HT 1 and HT 2 cases) are shown in Fig. 3a–d. It can be observed from the Fig. 3 that storage modulus increases with frequency whereas loss factor decreases with frequency. It can also be observed from the Fig. 3 that viscoelastic properties of the nanocomposite are significantly influenced at the higher humidity (HT 2 case). Figure 4a–d depicts the variations of storage modulus (E’) and loss factor (tan δ) with frequency for different hygrothermal conditions (such as HT 3 and HT 4 cases). It is observed that the moisture absorption through the thickness of the NCs sample induced higher strains along with thermal stresses in hygrothermal environment results in significant decrease in the viscoelastic properties.

Table 3 Basic constituents of CNTR material system [47]
Full size table
Table 4 Different hygrothermal (HT) conditions for NCs sample testing on DMA-8000
Full size table
Fig. 3
figure 3

Modulus and loss factor a storage under HT case 1, b loss factor under HT case 1, c storage under HT case 2, d loss factor under HT case 2

Full size image
Fig. 4
figure 4

Modulus and loss factor a storage under HT case 3, b loss factor under HT case 3, c storage under HT case 4, d loss factor under HT case 4

Full size image

3.2 Effects of skewing angle and CNT on spherical shell structure

The free vibration study has been carried out to observe the effect of skewing angle on the spherical shell structure (a = b and R1 = R2 = R) by considering R/a = 10 and a/h = 10 geometry. The skewing angle varies from 0° to 45° for such spherical shell with SSSS boundary condition. The case 1 of the hygrothemal condition has been considered for this analysis. The natural frequencies and modal loss factors for first mode of such structure are presented in the Table 5. It is observed from the Table 5 that the skewing angle has dominant impact on the stiffness which results in significant increase in the first fundamental frequency of such structure whereas CNT has also improved the natural frequency and modal loss factor with the increase in the CNT volume fraction. The skewing angle increases the stiffness of the structure because of the material concentration in the lesser area which leads to increase in natural frequencies. Higher skewing angle results in higher first natural frequency so, in the present study skewing angle has been taken up to 45°. The first and second mode natural frequencies and modal loss factor of the system is shown in Fig. 5a, b. It is evident from the Fig. 5 that skewing angle has higher impact on natural frequency and modal loss factor of such system. It can be observed from the Fig. 5a that stiffness of such structures can be enhanced by increasing the skewing angle.

Table 5 Natural frequency and modal loss factor of first mode for skewed spherical shell panel with R/a = 10 and a/h = 10 under HT case 1 considering SSSS boundary conditions
Full size table
Fig. 5
figure 5

Effect of skew angle on a natural frequencies, b modal loss factor of spherical shell under HT case 1

Full size image

3.3 Effects of CNT and skew angle on the frequency and time responses

The unit impulse load has been applied at the centre node to investigate the damping behaviour of the spherical shell structure with skewing angle of 45° for the HT case 1. The NCs material properties have been used in frequency domain directly to determine the frequency responses and fast Fourier transform (FFT) is employed to obtain the frequency response under HT case 1 thereafter time responses have been obtained from frequency responses using the inverse fast Fourier transform (IFFT). The different CNT volume fractions (such as 0%, 4% and 8%) have been considered for the analysis. From Fig. 6a, b, it can observed that the CNTs have significant effect on the damping properties of the spherical shell structure. Comparatively, the CNTs 8% volume fraction mitigated the vibrations quickly whereas considering the 8% CNTs, the impact of skewing angle on vibration damping of skewed spherical shell is shown in Fig. 6c, d. It is clear from Fig. 6c, d that for higher the skewing angle, the absolute amplitude in frequency and time domain decrease due to enhance of stiffness of such structures.

Fig. 6
figure 6

Various responses of thick NC skewed spherical shell under HT case 1 a frequency responses for different CNT volume fractions, b impulse responses for different CNT volume fractions 1, c frequency responses for different skewed angles, d impulse responses for different skewed angles

Full size image

3.4 Damping analysis using peaks of time responses

The transient responses are obtained for the skewed shell subjected to an impulse unit load at the centre node (transverse direction) for a duration of 10τ seconds (where τ is the time period corresponding to the first natural frequency of the system), and impulse responses of this panel have been obtained with a time step of τ seconds. Then, the transient response due to the impulse load is obtained by using FFT and IFFT. The transient responses have been obtained for different skewing angles (such as 15°, 30° and 45° under HT case 1) for the said structure and 8% CNT volume fraction is considered. The corresponding peaks of the vibration are obtained for skewed spherical shell structure under the HT case 1 which is shown in Fig. 7a–c. It is observed that vibration can quickly settle for the 8% CNT and 45° skewed angle because of enhance stiffness and damping. The present formulation can be used for thick and thin both type of skewed shells structures. Obtained results of such structures are also presented in the following sub-sections.

Fig. 7
figure 7

Peaks of impulse responses of nanocomposite spherical shell under HT case 1 with skew angles a 15°, b 30°, c 45°

Full size image

3.5 Effect of CNT on frequency and time responses of thin skewed shells

Effects of CNTs have also been observed for thin (a/h = 100) skewed shell structures under the hygrothermal case 1. The skewing angle 45° is considered for different types of thin shell structures (such as cylindrical, spherical, ellipsoidal and doubly curved) and obtained frequency and time responses of cylindrical and spherical shell structures are depicted in the Fig. 8a–d. Figure 9a–d shows the frequency and time responses of ellipsoidal and doubly curved shell structures. It is clear from the frequency response plots of Figs. 8 and 9, that CNTs may improve natural frequencies significantly. Time histories in Figs. 8 and 9 also indicate that the damping may considerably improve for such thin (a/h = 100) skewed shell structures. From the comparative studies of the different types of thin skewed shell structures (Figs. 8 and 9), it can be found that cylindrical shell is more flexible and doubly curved shell is more stiffed. All such cases vibration reduction are also possible. It is evident that CNT has significant effect on the modal parameters (such as natural frequency and modal loss factor) of such thin skewed spherical shell structures.

Fig. 8
figure 8

Responses of nanocomposite skewed shells under HT case 1 a frequency response of cylindrical shell, b time response of cylindrical shell, c frequency response of spherical shell, d time response of spherical shell

Full size image
Fig. 9
figure 9

Responses of nanocomposite skewed shells under HT case 1 a frequency response of ellipsoidal shell, b time response of ellipsoidal shell, c frequency response of doubly curved shell, d time response of doubly curved shell

Full size image

3.6 Hygrothermal effects on the modal parameters of skewed shell structures

In this study, various R/a have been considered for the NC based skewed spherical shell under different hygrothermal cases (1–4). The variations of fundamental frequency and modal loss factor with R/a for the first mode are determined and presented in Figs. 10 and 11. The ratio of R/a of the skewed shell structure is varied from deep to shallow considering a/h = 10 (thick shell) in this analysis and observed that natural frequency is decreasing with the increase in R/a value whereas the modal loss factor is slightly increasing for each hygrothermal case. The skewing angle 45° is considered for this study as the structural stiffness needed to be improved without distorting it. The CNT volume fractions of 0%, 4% and 8% have been considered for all hygrothermal cases which has significant impact on the natural frequency and damping of such shell structure. The natural frequency decreases and modal loss factor increases up-to the range of (0 < R/a > 5) but in the range of (5 < R/a > 1000), no significant changes is observed in the region from shallow shells to plate type structure due to of less influence of the twist curvature. The increase in R/a value increases the gap between curves where natural frequencies are decreased because of less impact of the CNT and this also shows that the deep shell structures are stiffer then the shallow shells/plates as shown in Fig. 10a, c. Effect of hygrothermal conditions gets severe for HT case 2–4, the stiffness of the structure reduces significantly which results in lower natural frequencies and lesser modal loss factors (as shown in Figs. 10 and 11). From Figs. 10 and 11, it can be observed that due to the hygrothermal effects, stiffness of the structures decreases whereas the modal loss factor may improve.

Fig. 10
figure 10

Variations of modal parameters of spherical shell a first natural frequency for HT case 1, b first modal loss factor for HT case 1, c first natural frequency for HT case 2, d first modal loss factor for HT case 2

Full size image
Fig. 11
figure 11

Variations of modal parameters of spherical shell a first natural frequency for HT case 3, b first modal loss factor for HT case 3, c first natural frequency for HT case 4, d first modal loss factor for HT case 4

Full size image

3.7 Modal parameters of various shell structures under different hygrothermal conditions

Various thick (a/h = 10) and thin (a/h = 100) skewed shell structures (such as cylindrical, spherical, ellipsoidal, and doubly curved) under different hygrothermal conditions are considered here to study the effects of hygrothermal on the modal parameters of first mode of such structures (as shown in Fig. 12). It can be observed from the Fig. 12 that the stiffness of such thick and thin structures decreases whereas modal loss factor increases due to the effects of hygrothermal. The moisture absorbed at HT case 4 in the polymer phase of NC is more affected which deteriorates the stiffness of such structures. It is also observed from the presented results in the above subsections that CNT and skewing angle may improve the modal parameters (such as natural frequency and modal loss factor) of thick and shell structures.

Fig. 12
figure 12

Variations of modal parameters with HT cases a first natural frequency of different thick shells, b first modal loss factor of different thick shells, c first natural frequency of different thin shells, d first modal loss factor of different thin shells

Full size image

4 Conclusions

In the presented research work, the hygrothermal dependant viscoelastic properties of NCs are obtained by the proposed combination of numerical and experimental creep methodology from DMA-8000 to study the skewed shell structures' vibration and damping characteristics numerically. The CNT is randomly mixed with 0%, 4% and 8% of volume fraction in the epoxy with the help of an ultrasonic probe sonicator. The ultrasonic sonication for mixing of CNT, is suggested at least for 12 h to have minimum agglomerations followed which the NC samples were prepared for each volume fraction as per the ASTM-D4065 standard with the required dimensional accuracy. Further creep test is conducted to observe the creep behaviour of NC in the time domain in different hygrothermal conditions on DMA-8000. It is observed that in a critical hygrothermal environment, CNT is reducing the creep strain significantly which influences the viscoelastic properties (storage modulus and loss factor) of the NC. The Prony constants were determined using the power law fit from the creep data of NC and, storage modulus and loss factor are obtained using Laplace transform in the frequency domain. The evaluated hygrothermal dependant viscoelastic properties of such NCs material system were further used for different thick (a/h = 10) and thin (a/h = 100) skewed shell structures to determine their vibration and damping characteristics in the different hygrothermal environment. An oblique coordinate system is considered to define the shell geometry with a tangent to the edge for skewing the structure. Increasing in the skewing angle causes a reduction in the surface area which leads to an increase in the material concentration, thereby resulting in an increase in the stiffness of the structure. First order shear deformation theory as per Mindlin’s hypothesis based on the stress resultant-type Koiter’s shell theory is formulated in order to study the vibration and damping behaviour of the said NC-based skewed shell structures. It is observed that the skewing angle has improved the stiffness of the structure which results in higher natural frequencies whereas the CNT content improves the stiffness and damping property of the skewed shell structures (thick and thin both type). The stresses induced due to hygrothermal conditions are incorporated into dynamic analysis by calculating the effective stiffness of such skewed shell structures. The hygrothermal dependant material properties were used for the dynamic study of the skewed shell structure which results in deteriorating the natural frequency and systems loss factor and it is also found that CNT has significantly increased the fundamental frequency and modal loss factor with respect to R/a (i.e., from deep to shallow shells) as the hygrothemral conditions gets severe. Finally, it can be concluded that the stiffness and damping property of such thick and thin skewed shell structures can be improved and controlled by the inclusion of effective volume fraction of CNT in a conventional composite which may be useful in most of the structural applications under hygrothermal environment.