1 Introduction

In the present scenario, the major concern of the high-performance engineering industries like aerospace, aeronautical, automobile, marine etc. is to reduce the weight without compromising the strength by adopting the advanced materials. The fibre-reinforced composite and sandwich components are the suitable alternative for these industries over the available monolithic metallic materials because of their variable stiffness, unmatched strength including the good damage tolerance. The sandwich structure is made of by placing the thick lightweight core (high density) in between the thin laminated facesheets. These sandwich configurations are widely acknowledged in the main stream structural engineering field due to their unparalleled stiffness and impact strength. In general, the bending load is transferred by the sandwich facesheets, whereas the core majorly helps in resisting the shear and the normal loading. All the possible design concepts generally followed in the composite laminates are often adopted for the sandwich construction. Hence, it is important to analyse the sandwich structural behaviour under the different conditions (loading and environment) without negotiating the accuracy and minimal cost. However, the design, fabrication and analysis constantly associated with some major complexities. In addition, these structures or structural members are being operated under the influences of different distinct or the combined loading and experiences variable scale of deformation due to the dynamic loading. Therefore, the mathematical modeling of these structures requires adequate precision to evaluate the transverse shear deformation effects. Therefore, the modeling and analysis steps are needed a comprehensive understanding related to the influential parameters for the accurate estimation of the desired output.

The researchers have already adopted various modeling approaches including the solution techniques (analytical, numerical, and simulation) for the evaluation of layered composite or the sandwich structural components in the past. Furthermore, the structural design associated with influential output (deflection, frequency, and transient) of the layered and sandwich structures are generally examined [1, 2] using the different types of shear deformation kinematics to mimic the mid-plane deformations via the classical laminate plate theory (CLPT), normal deformation (ND), first-order shear deformation theory (FSDT), higher order shear deformation theory (HSDT), third-order shear deformation theory (TSDT) and refined theories etc. To establish the requirements of the present analysis, a brief review of some prominent and substantial contributions in the past are discussed in the following lines what follows.

The layered composite/sandwich plate/beam like structure and corresponding responses (vibration, deflection, and transient) are examined [3,4,5,6,7,8,9] using Mindlin’s or the HSDT kinematics including von-Karman nonlinear strain for the inclusion of large deformation characteristics. Furthermore, the dynamic deflections of the skew sandwich plate structure under influence of thermomechanical combined load is investigated [10] using various kinematic theories (FSDT and HSDT). Reddy’s higher order mid-plane kinematic model including the finite-element method (FEM) are adopted [11, 12] predict the transient deflection parameter of the flat sandwich/composite structure. In addition, the FSDT and the HSDT mid-plane deformation kinematics are adopted [13] to evaluate the time-dependent responses of various structures (composite and sandwich) using the radial basis functions in a pseudo-spectral framework in conjunction with Kansa technique. The geometrically nonlinear bending and eigenvalues of the sandwich flat structure are predicted [14] using the higher order finite-element (FE) model in association with von-Karman strain. Similarly, the generalized differential quadrature (GDQ) technique in the framework of the layerwise kinematics are adopted [15] to model the sandwich plate structure for the prediction of the static and the dynamic deflections. Subsequently, Reddy’s higher order polynomial type of mid-plane deformation in conjunction with FEM steps [16, 17] utilized to investigate the effect of internal debonding between the layers on the time-dependent responses of the laminated/sandwich structure. Similarly, the layerwise theory in conjunction with Reddy’s kinematic model [18] for the free vibration frequency and transient responses of the composite and sandwich structural components. The 3D FEM steps are adopted [19] to model and predict the delamination of the Spar Wingskin Joints made up of graphite fibre-reinforced plastic (GFRP) composite under the uniformly distributed transverse loading. Furthermore, the nonuniform rational B-spline (NURBS) technique is adopted to compute the eigenvalues (frequency and critical buckling load) of the composite and the functionally graded (FG) structures [20, 21] using Reissner–Mindlin plate modeling approach. Likewise, an equivalent layerwise approach in conjunction with the local GDQ methods are adopted to model the FG sandwich/composite shell structures to predict the corresponding transverse bending and free vibration frequencies [22,23,24]. Moreover, the different kinematic theories (first-, second-, and third-order shear deformation) are undertaken to model and predict the effect of delamination on the responses of the sandwich structural components [25, 26]. The structural responses (static deflection and transient) of variable structural form, i.e., layered composite, graded carbon nanotubes, sandwich nanoplate and the hybrid smart structure are investigated [27,28,29,30,31,32,33,34,35] using the available numerical techniques (finite integral transform method, differential curvature method, differential quadrature, DQ; and harmonic differential quadrature, HDQ) and subsequent kinematic polynomials (Mindlin’s plate theory, refined zigzag theory, RZT; sinusoidal shear deformation theory, SSDT; FSDT and CLPT). Similarly, the structural responses (transverse deflection, eigenfrequency and buckling load) of the isotropic, layered composite and FG sandwich structures are computed [36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55] via different higher order and hyperbolic shear deformation polynomial kinematic theories including the mid-plane stretching effect. In addition, the deflection and stress values of the skew sandwich shell panel is investigated [56] using the higher order mid-plane kinematics including the effect of geometrical large deformations.

The inclusive review discussed in the above lines indicate the available knowledge gap in the present domain regarding the influence of the static and dynamic types of mechanical loading on the deflection values including the eigenvalues (free vibration frequency parameter) of the sandwich panel structure. Hence, a higher order polynomial kinematic theory has been adopted to model the sandwich structural panel including the different geometrical configurations (flat, single and doubly curved panel) for the computation of the related structural responses (transverse static and dynamic deflection and frequency) numerically. For the computation of relevant responses, an own home-made specialized MATLAB code is derived to predict the same using the derived model. Furthermore, the relevance of the derived numerical model for the computation of results is established with adequate comparison and convergence check. Finally, the influential parameter associated with geometry and dimension, i.e., the curvature ratios (R/a), the aspect ratios (a/b), the core-to-face thickness ratios (hc/hf), the stacking sequences and the edge support conditions on the panel (flat/curved) responses (deflection, frequency and transient) have been explored extensively via solving different kind of numerical examples.

2 Modeling

2.1 Basic assumptions

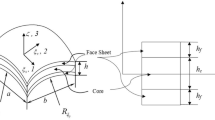
The details regarding the assumed sandwich shell panel model including the curvature (one or two) along the axes are presented in Fig. 1. In general, sandwich structural panel consisting two laminated stiff layers (facings) and a soft layer (core) in between the middle of the facings.

Fig. 1
figure 1

Geometry of the sandwich shell structure

Full size image

For the numerical analysis purpose a few relevant assumptions are considered and presented in the following points:

  • All the layers within facings (fibres and mortar) are perfectly bonded with each other to maintain as a single layer.

  • The 3D shallow shell model reduced to a 2D model by implementing the adequate plane stress/strain conditions.

  • The basic geometrical configurations are consisting of shallow curvature over a rectangular planform. Furthermore, geometrical shapes are achieved by changing the curvature parameters, i.e., the flat, cylindrical, spherical, hyperboloid and elliptical panel configurations.

  • The reference frame/global coordinate system is coinciding with the mid-plane of the shell structure.

2.2 Geometry description

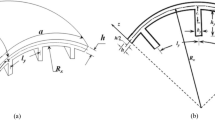
The overall thickness of the panel structure is denoted as ‘h’, which is a combination of the thickness of the top and the bottom facings hf including the core thickness ‘hc’ (refer Fig. 1). Similarly, the length and the width of the panel are denoted as ‘a’ and ‘b’, respectively. The physical sandwich model is further transformed into a mathematical form for the numerical analysis purpose using the defined geometrical dimensions. In addition, the shell configurations are achieved using the principal radii of curvatures (Rx and Ry are the radii of curvatures along the respective directions, whereas Rxy = ∞). The single/doubly curved panels are named as cylindrical panel if Rx = R and Ry = ∞, spherical panel if Rx = Ry = R, elliptical panel if Rx = R and Ry = 2R, hyperboloid panel if Rx = R and Ry = − R, and flat if Rx = Ry = ∞.

2.3 Displacement field

The displacement polynomial functions at an arbitrary point \(\left( {{x_1},{y_1},{z_1}} \right)\) of the sandwich panel structure in the reference frame can be expressed as [56]

$$\left. \begin{aligned} {u_1}\left( {{x_1},{y_1},{z_1},t} \right) & =u\left( {{x_1},{y_1}} \right)+{z_1}\theta _{1}^{*}\left( {{x_1},{y_1}} \right)+z_{1}^{2}\phi _{1}^{*}\left( {{x_1},{y_1}} \right)+z_{1}^{3}\psi _{1}^{*}\left( {{x_1},{y_1}} \right) \\ {u_2}\left( {{x_1},{y_1},{z_1},t} \right) & =v\left( {{x_1},{y_1}} \right)+{z_1}\theta _{2}^{*}\left( {{x_1},{y_1}} \right)+z_{1}^{2}\phi _{2}^{*}\left( {{x_1},{y_1}} \right)+z_{1}^{3}\psi _{2}^{*}\left( {{x_1},{y_1}} \right) \\ {u_3}\left( {{x_1},{y_1},{z_1},t} \right) & =w\left( {{x_1},{y_1}} \right)+{z_1}\theta _{3}^{*}\left( {{x_1},{y_1}} \right) \\ \end{aligned} \right\},$$
(1)

where the individual coefficients associated with the kinematic model, i.e., u, v and w defined for the sandwich structural neutral plane along their corresponding directions \(\left( {{x_1},{y_1},{z_1}} \right)\), respectively. Similarly, the rotation of normal to the mid-plane are denoted as \({\theta _1}\,{\text{and}}{\theta _2}\), respectively, with respect to the alternating axes. In addition, the higher order terms in the displacement field, i.e., \({\phi _1},{\phi _2},{\psi _1}\,{\text{and}}\,{\psi _2}\) are kept in the expression (Taylor’s series) for the order of shear stress across the thickness including the thickness stretching term as ‘\({\theta _3}\)’ and arbitrary time ‘t’.

2.4 Kinematic relations

The panel deformation is modeled using the following general form of linear strain–displacement relations including the curvature effect and expressed as

$$\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{{x_1}{x_1}}}} \\ \begin{gathered} {\varepsilon _{{y_1}{y_1}}} \hfill \\ {\varepsilon _{{z_1}{z_1}}} \hfill \\ \end{gathered} \\ {{\gamma _{{\xi _{{y_1}{z_1}}}}}} \\ {{\gamma _{{\xi _{{x_1}{z_1}}}}}} \\ {{\gamma _{{x_1}{y_1}}}} \end{array}} \right\}=\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial {u_1}}}{{\partial {x_1}}}+\frac{{{u_3}}}{{{R_{{x_1}}}}}} \\ {\frac{{\partial {u_2}}}{{\partial {y_1}}}+\frac{{{u_3}}}{{{R_{{y_1}}}}}} \\ {\frac{{\partial {u_3}}}{{\partial {z_1}}}} \\ {\frac{{\partial {u_2}}}{{\partial {z_1}}}+\frac{{\partial {u_3}}}{{\partial {y_1}}} - \frac{{{u_2}}}{{{R_{{y_1}}}}}} \\ {\frac{{\partial {u_1}}}{{\partial {z_1}}}+\frac{{\partial {u_3}}}{{\partial {x_1}}} - \frac{{{u_1}}}{{{R_{{x_1}}}}}} \\ {\frac{{\partial {u_1}}}{{\partial {y_1}}}+\frac{{\partial {u_2}}}{{\partial {x_1}}}+2\frac{{\partial {u_3}}}{{{R_{{x_1}{y_1}}}}}} \end{array}} \right\}.$$
(2)

2.5 Constitutive relations of the individual layer

Now, the general elastic constitutive relations for the layered composite sandwich structural components of any kth layer of the face sheets are mathematically expressed in the local (material) coordinate system considering the stacking sequence ‘ϴ’of the fibre as [57]

$$\left. \begin{aligned} {\left\{ {\begin{array}{*{20}{c}} {{\sigma _{{x_1}{x_1}}}} \\ \begin{gathered} {\sigma _{{y_1}{y_1}}} \hfill \\ {\sigma _{{z_1}{z_1}}} \hfill \\ \end{gathered} \\ {{\sigma _{{y_1}{z_1}}}} \\ {{\sigma _{{x_1}{z_1}}}} \\ {{\sigma _{{x_1}{y_1}}}} \end{array}} \right\}^k} & ={\left[ {\begin{array}{*{20}{c}} {{{\bar {Q}}_{11}}}&{{{\bar {Q}}_{12}}}&{{{\bar {Q}}_{13}}}&0&0&0 \\ {{{\bar {Q}}_{12}}}&{{{\bar {Q}}_{22}}}&{{{\bar {Q}}_{23}}}&0&0&0 \\ {{{\bar {Q}}_{13}}}&{{{\bar {Q}}_{23}}}&{{{\bar {Q}}_{33}}}&0&0&0 \\ 0&0&0&{{{\bar {Q}}_{44}}}&{{{\bar {Q}}_{45}}}&0 \\ 0&0&0&{{{\bar {Q}}_{54}}}&{{{\bar {Q}}_{55}}}&0 \\ 0&0&0&0&0&{{{\bar {Q}}_{66}}} \end{array}} \right]^k}{\left\{ {\begin{array}{*{20}{c}} {{\varepsilon _{{x_1}{x_1}}}} \\ \begin{gathered} {\varepsilon _{{y_1}{y_1}}} \hfill \\ {\varepsilon _{{z_1}{z_1}}} \hfill \\ \end{gathered} \\ {{\gamma _{{\xi _{{y_1}{z_1}}}}}} \\ {{\gamma _{{\xi _{{x_1}{z_1}}}}}} \\ {{\gamma _{{x_1}{y_1}}}} \end{array}} \right\}^k} \\ {\text{or}}\,\left\{ {{\sigma _{ij}}} \right\} & =\left[ {{{\overline {Q} }_{ij}}} \right]\left\{ {{\varepsilon _{ij}}} \right\} \\ \end{aligned} \right\},$$
(3)

where \(\left\{ {{\sigma _{ij}}} \right\}\), \(\left[ {{{\overline {Q} }_{ij}}} \right]\) and \(\left\{ {{\varepsilon _{ij}}} \right\}\) are the individual tensors, i.e., stress, reduced transformed stiffness and the strain, respectively.

In addition, the stress can be represented as force vector in the following form:

$$\,\left\{ F \right\}=\left[ D \right]\left\{ \varepsilon \right\}.$$
(4)

Furthermore, the individual components of the property matrix [D] can be expressed as

$$\left[ D \right]=\left[ {\begin{array}{*{20}{c}} {{A_{ij}}}&{{B_{ij}}}&{{C_{ij}}}&{{E_{ij}}} \\ {{B_{ij}}}&{{C_{ij}}}&{{E_{ij}}}&{{H_{ij}}} \\ {{C_{ij}}}&{{E_{ij}}}&{{H_{ij}}}&{{L_{ij}}} \\ {{E_{ij}}}&{{H_{ij}}}&{{L_{ij}}}&{{J_{ij}}} \end{array}} \right],$$
(5)

where \(\left[ {{A_{ij}},{B_{ij}},{C_{ij}},{E_{ij}},{H_{ij}},{J_{ij}},{L_{ij}}} \right]=\sum\nolimits_{{k=1}}^{n} {\int\nolimits_{{{z_1}_{{_{{k - 1}}}}}}^{{{z_1}_{{_{k}}}}} {{{\left( {{{\bar {Q}}_{ij}}} \right)}_k}\left( {{z_1}^{m}} \right){\text{d}}{z_1}} } \,\;{\text{for}}\,{\text{(}}i{\text{,}}\,j{\text{=1,2,}} \ldots {\text{,6)}}\;\,{\text{and}}\;\,m\,{\text{=}}\,{\text{0,1,2,}} \ldots {\text{,6.}}\)

2.6 Energy calculation

After the evaluation of stress and strain tensors of the individual layers/sandwich structural form, the strain energy (U) functional can be expressed mathematically in the following lines:

$$U=\frac{1}{2}\iint {\left\{ {\sum\limits_{{k=1}}^{N} {\int_{{{z_1}_{{k - 1}}}}^{{{z_1}_{k}}} {{{\left\{ {{\varepsilon _{ij}}} \right\}}^{\text{T}}}\left\{ {{\sigma _{ij}}} \right\}} } {\text{d}}{z_1}} \right\}{\text{d}}{x_1}{\text{d}}{y_1}}.$$
(6)

Similarly, the inertia and displacement field vectors are utilized to count the kinetic energy (V) functional for the sandwich shell structural form as

$$V=\frac{1}{2}\iint {\left\{ {\sum\limits_{{k=1}}^{N} {\int_{{{z_1}_{{k - 1}}}}^{{{z_1}_{k}}} {{\rho ^k}{{\left\{ {\dot {d}} \right\}}^{\text{T}}}\left\{ {\dot {d}} \right\}} } {\text{d}}{z_1}} \right\}{\text{d}}{x_1}{\text{d}}{y_1}},$$
(7)

where \(\rho \;{\text{and}}\;\left\{ {\dot {d}} \right\}\) are the mass density and the global velocity vector, respectively.

2.7 Work done

Now, the total work done (W) due to an externally applied mechanical load ‘F’ can be obtained using the generalized mathematical expressions as

$$W=\int {{{\left\{ d \right\}}^{\text{T}}}\left\{ F \right\}{\text{d}}A} .$$
(8)

2.8 Finite-element modeling

The FEM is an established numerical tool in the field of structural modeling and analysis for the complex geometrical and material problems with the adequate accuracy without compromising with computational cost. Hence, a nine-noded isoparametric element [58] with ten degrees of freedom per node is adopted for the current discretisation of the shell structure. The modified displacement field vector\(\left\{ \delta \right\}\) at any point in the mid-plane of the shell panel can be expressed mathematically adopting the FEM expressed as

$$\left\{ \delta \right\}=\sum\limits_{{i=1}}^{9} {\left[ {{N_i}} \right]} \left\{ {{\delta _i}} \right\},$$
(9)

where \(\left\{ \delta \right\}={\left[ {u\,\,v\,\,w\,\,\theta _{1}^{*}\,\,\theta _{2}^{*}\,\,\theta _{3}^{*}\,\,\phi _{1}^{*}\,\,\phi _{2}^{*}\,\,\psi _{1}^{*}\,\,\psi _{2}^{*}} \right]^{\text{T}}}\) is the nodal displacement vectors for the ith node and the corresponding interpolation functions (shape function) represented as \(\left[ {{N_i}} \right]\).

Now, the mid-plane strain vector can be expressed further after modifying the displacement and conceded to the following form:

$${\left\{ \varepsilon \right\}_i}=~\left[ {{B_i}} \right]\left\{ {{\delta _i}} \right\},$$
(10)

where \(\left[ {{B_i}} \right]\) is the strain–displacement relation matrix.

2.9 Governing equations and solution approach

2.9.1 Free vibration analysis

The final form of the governing equation of any free vibrated sandwich shell panel is obtained using Hamilton’s principle and expressed as

$$\delta \int\limits_{{{t_1}}}^{{{t_2}}} {(V - U){\text{d}}t=0} .$$
(11)

Now, substituting the Eqs. (6), (7) and (9) into Eq. (11), the final form of the eigenvalue equations of the sandwich panel structure can be represented as

$$\left[ M \right]\left\{ {{{\ddot {d}}_i}} \right\}+~\left[ K \right]\left\{ {{d_i}} \right\}=0,$$
(12)

where \(\left\{ {{{\ddot {d}}_i}} \right\}\) is the acceleration, \(\left\{ {{d_i}} \right\}\) is the displacement. [K] and [M] are the stiffness and mass matrices, respectively, and can be expressed as

$$\begin{gathered} \left[ K \right]=~\int_{A} {\left( {\sum\limits_{{k=1}}^{N} {\int_{{{z_1}_{{k - 1}}}}^{{{z_1}_{k}}} {{{\left[ B \right]}^{\text{T}}}\left[ D \right]\left[ B \right]} } {\text{d}}{z_1}} \right)} {\text{d}}A\;{\text{and}} \hfill \\ \left[ M \right]=~\int_{A} {\left( {\sum\limits_{{k=1}}^{N} {\int_{{{z_1}_{{k - 1}}}}^{{{z_1}_{k}}} {{{\left[ N \right]}^{\text{T}}}\left[ N \right]} } \rho {\text{d}}{z_1}} \right)} {\text{d}}A, \hfill \\ \end{gathered}$$

where \(\left[ D \right]=\sum\nolimits_{{k=1}}^{N} {\int_{{{z_1}_{{_{{k - 1}}}}}}^{{{z_1}_{{_{k}}}}} {{{\left[ T \right]}^{\text{T}}}\left[ {\bar {Q}} \right]\left[ T \right]{\text{d}}{z_1}} }\).

Furthermore, by neglecting the required matrices, the eigenvalue form of the governing equation can be defined as in Eq. (13) to obtain the natural frequency of the system and represented as

$$\left( {\left[ K \right] - {\omega ^2}\left[ M \right]} \right)\Delta =0,$$
(13)

where ω and Δ are the natural frequency and the corresponding eigenvector, respectively.

2.9.2 Static analysis

The final form of the governing equation for static analysis of any sandwich shell panel is obtained using variational principle and conceded as

$$\delta \Pi =\delta U - \delta W=0,$$
(14)

where δ is the variational symbol and \(\Pi\) is the total potential energy.

Now, the equilibrium equation under the influence of the static loading is obtained by substituting Eq. (14) for Eqs. (6), (8) and (9) as follows:

$$\left[ K \right]\left\{ d \right\}=\left\{ F \right\}.$$
(15)

2.9.3 Transient analysis

The time-dependent deflection responses are computed by solving the structural static equilibrium equation for a particular time ‘t’ including the inertia (acceleration-dependent) and damping (velocity-dependent) forces of the sandwich shell panel. The transient governing equation of equilibrium of the current system is obtained from Lagrangian equations of motion [59] and expressed as

$$\left[ M \right]\left\{ {\ddot {d}} \right\}+\left[ C \right]\left\{ {\dot {d}} \right\}+\left[ K \right]\left\{ d \right\}=\left\{ F \right\}.$$
(16)

Here, the mass, damping and stiffness matrices are denoted as [M], [C], and [K], respectively, and {F} represents the external force vector. The acceleration, velocity, and displacement vectors are represented as \(~\ddot {d},~\dot {d}\) and d, respectively.

Now, the solution is achieved by computing via the constant average acceleration technique of Newmark’s integration scheme, i.e., the transient equation of motion for the total time period of ‘T’ integrated for the small time steps (Δt). The integration parameters (α, δ, and a0–a7) associated with the governing transient equation of motion adopted from the reference [59]. Now, the effective stiffness matrix for the time step ‘t’ conceded to the following form:

$$\left[ {\hat {K}} \right]=\left[ K \right]+{a_0}\left[ M \right].$$
(17)

Similarly, the successive steps followed for each time increments, i.e., t + Δt to compute the effective load matrix and expressed as

$$^{{t+\Delta t}}\left[ {\hat {F}} \right]{=^{t+\Delta t}}\left[ F \right]+\left[ M \right]\left( {{a_0}^{t}d+{a_2}^{t}\dot {d}+{a_3}^{t}\ddot {d}} \right)+\left[ C \right]\left( {{a_1}^{t}d - {a_4}^{t}\dot {d}+{a_5}^{t}\ddot {d}} \right).$$
(18)

Now, the following sets equations are solved to compute the associated displacement, acceleration, and the velocity terms of the transient motion equation:

$$\begin{aligned} {\left[ {\hat {K}} \right]^{t+\Delta t}}d & = {^{t+\Delta t}}\left[ F \right] \\ ^{{t+\Delta t}}\ddot {d} & ={a_0}\left( {^{{t+\Delta t}}d{ - ^t}d} \right) - {a_2}^{t}\ddot {d} - {a_3}^{t}\ddot {d} \\ ^{{t+\Delta t}}\dot {d} & = {^t}\dot {d}+{a_6}^{t}\ddot {d} - {a_7}^{{t+\Delta t}}\ddot {d}. \\ \end{aligned}$$
(19)

3 Results and discussion

Now, the free vibration frequencies and the deflections (static and dynamic) are computed by solving the governing equations (eigenvalue and equilibrium) of the curved/flat sandwich shell panel. In this present analysis, the deflection and the transient responses are obtained under two different types of mechanical loading, i.e., uniformly distributed loading (UDL) and sinusoidal loading (SSL), where the load intensity of SSL follow \(q={q_0}\sin {\text{ }}\left( {\pi {x_1}/a} \right){\text{ }}sin{\text{ }}\left( {\pi {y_1}/b} \right)\). To compute the final output, i.e., the static and dynamic deflections including the free vibration frequencies a suitable compute code is prepared using the above-discussed mathematical formulation in MATLAB environment. Furthermore, the finite-element solution accuracy and the convergence criteria have been checked via solving different kind of numerical examples. The sandwich facings and the core material elastic properties are taken as same as the reference [9, 10, 14] and are provided in Table 1. In addition, the details of the edge support conditions adopted for the current analysis are shown in Fig. 2. Now, the non-dimensional parameters, i.e., the deflections and frequencies are calculated using the provided formula: \(\bar {W}=100 \times {w_{{\text{cen}}}} \times {E_2} \times {h^3}/{q_0} \times {a^4}\) and \(\varpi =\left( {\omega {b^2}/h} \right)\sqrt {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{E_2}}}} \right. \kern-0pt} {{E_2}}}} \right)}_{\text{f}}}}\), respectively, unless otherwise stated elsewhere. Similarly, the time steps are adopted for the transient analysis throughout the analysis as 5 µs.

Table 1 Elastic properties of the face and core layers
Full size table
Fig. 2
figure 2

Details of end-support conditions

Full size image

First, an example is solved to obtain the non-dimensional transverse deflection values at the centre point of the structural panel including the convergence rate. For this purpose, a simply supported (SSSS) square sandwich flat panel (0°/90°/core/90°/0°) problem is considered. The rate convergence of deflection parameters is computed for the mechanical UDL (q0 = 100 N/cm2) and is presented in Fig. 3 considering variable geometrical (a/h = 50 and 100 and, hc/hf = 2, 5 and 8) and material properties (Table 1) similar to the reference [14]. In Fig. 3, the convergence of static deflection study indicates that the deflection values are following the expected path and a (6 × 6) mesh adopted for the evaluation of new results.

Fig. 3
figure 3

Convergence study of the non-dimensional central deflection (\(\bar {W}=100w{E_{\text{c}}}{h^3}/q{a^4}\)) of SSSS square symmetric (0°/90°/core/90°/0°) sandwich flat panel under the UDL

Full size image

Now, the model has been extended to check the convergence rate for the fundamental frequency parameters using the similar configuration of the plate, i.e., square, SSSS and (0°/90°/core/0°/90°) laminated sandwich. The obtained frequency data are tabulated in Table 2 for various mesh divisions. The geometrical and the elastic material (M2) properties (Table 1) are adopted for the analysis similar to the reference [9] values including the different span-to-thickness ratios (a/h = 2, 4, 10, 20, 30, 40 and 50) and core-to-face thickness ratios (hc/hf = 10). From the tabular frequency data, it can be concluded that a (6 × 6), mesh will solve the current purpose to compute the desired eigenvalue solutions.

Table 2 Convergence study of the non-dimensional fundamental frequency (\(\varpi =\left( {\omega {b^2}/h} \right)\sqrt {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{E_2}}}} \right. \kern-0pt} {{E_2}}}} \right)}_{\text{f}}}}\)) of simply supported square symmetric (0°/90°/core/0°/90°) sandwich flat panel (hc/hf = 10)
Full size table

Furthermore, a square simply supported sandwich symmetric (0°/90°/core/90°/0°) panel problem is solved for the different mesh divisions to establish the convergence criteria for the transient case and is plotted in Fig. 4. For the computational purpose, the SSL type of loading (q0 = 100 N/cm2) is considered including the associated geometrical parameters (a/h = 100 and hc/hf = 8). The figure clearly indicates the convergence of numerical solution with respect to the mesh refinement and a (7 × 7) mesh is capable of computing the transient responses with appropriate accuracy for the subsequent computational purpose.

Fig. 4
figure 4

Convergence behaviour of transient responses of square (0°/90°/core/90°/0°) sandwich flat panel under SSL (a/h = 100, hc/hf = 8 and SSSS)

Full size image

Now, the validity of the currently derived higher order sandwich panel model has been established by comparing the results with available published deflection data. In this regard, the non-dimensional central deflections are obtained for the square SSSS symmetric (0°/90°/core/90°/0°) sandwich flat panel using M1 material properties [14]. The deflection parameters are computed under the UDL including the similar geometrical parameter as in the convergence analysis, i.e., two span-to-thickness ratios (a/h = 50 and 100) and three core-to-face thickness ratios (hc/hf = 2, 5, and 8). The comparison between the present and reference deflection values are provided in Table 3. The comparison is showing good agreement with the published deflection values computed using the different theories.

Table 3 Comparison study of the non-dimensional central deflection (\(\bar {W}=100w{E_{\text{c}}}{h^3}/q{a^4}\)) of a square SSSS symmetric (0°/90°/core/90°/0°) sandwich flat panel under the uniformly distributed loading
Full size table

Furthermore, the frequency validation has also been checked using the same problem as in the convergence test, i.e., a square SSSS anti-symmetric sandwich (0°/90°/core/0°/90°) plate structure the geometrical (a/h = 2, 4, 10, 20, 30, 40 and 50 and hc/hf = 10) and the material (M1) parameters as same as reference [9]. The results obtained using the current model and the reference frequencies are presented in Table 4. The comparison study indicates the accuracy of the derived model when compared with the frequencies computed via different mid-plane kinematic models.

Table 4 Comparison study of the non-dimensional fundamental frequency (\(\varpi =\left( {\omega {b^2}/h} \right)\sqrt {{{\left( {{\rho \mathord{\left/ {\vphantom {\rho {{E_2}}}} \right. \kern-0pt} {{E_2}}}} \right)}_{\text{f}}}}\)) of a square SSSS anti-symmetric (0°/90°/core/0°/90°) sandwich flat panel (hc/hf = 10)
Full size table

Finally, the validation of transient deflection with the published results [10] is provided in Fig. 5. The required geometrical and the material properties including dimension are considered as same as the reference [10]. The time-dependent deflections of the square sandwich flat panel problem under the influence mechanical SSL (q0 = 100 N/cm2) have been computed considering the input parameters as: SSSS, symmetric stacking sequence (0°/90°/core/90°/0°), a/h = 5 and hc/hf = 8. The figure indicates that the results are following good agreement with the reference with very small deviation [10] due to the type of kinematic theories.

Fig. 5
figure 5

Validation behaviour of transient responses of (0°/90°/core/90°/0°) a square SSSS sandwich flat panel under SSL (a/h = 5, hc/hf = 8)

Full size image

3.1 Numerical illustrations

The different convergence and the validation studies indicate that the desired responses, i.e., the free vibration, static and time-dependent deflections of the curved/flat sandwich structures can be computed via the current higher order numerical model without affecting the accuracy. Now, several numerical examples are solved to display the applicability of the current higher order FE model for the different geometries (curved/flat) and design parameters. In general, the results are computed for the square sandwich curved/flat panels using the different combinations of end conditions (Fig. 2) and given elastic properties (Table 1), unless stated otherwise. Similarly, the total time including the time steps is taken for the transient analysis as 1 ms and 5 µs, respectively, throughout the analysis.

3.1.1 Effect of the curvature ratios on the cylindrical shell panel

First, the central deflections parameters of square SSSS symmetric (0°/90°/core/90°/0°) cylindrical shell panel under two different types of mechanical loading (UDL and SSL) deflections are computed for different curvature ratios (R/a = 2, 5, 10, 20, and 50) and are presented in Table 5. The desired structural parameters are evaluated including few more geometrical parameters, i.e., a/h = 5, 20, 30, 50, 80, and 100 and hc/hf = 20. The tabulated deflection values indicate a decreasing slope for the higher span-to-thickness ratios (a/h), whereas a reverse trend for the curvature ratios (R/a). In addition, it can be noted that the deflections ate higher for the UDL type of loading in comparison to the SSL. However, the magnitude of the UDL and SSL are same at peak. This is because the load intensities throughout the structural surface area remains same under the UDL but varies sinusoidally for the SSL.

Table 5 Effect of the curvature ratios on non-dimensional central deflections of a square SSSS (0°/90°/core/90°/0°) sandwich cylindrical shell panel (hc/hf = 20)
Full size table

Now, a square symmetric (0°/90°/core/90°/0°) cylindrical shell panel (SSSS) example problem has been solved using the structural input parameters as: a/h = 5, 10, 20, 25, 30, 50, 80, and 100; R/a = 2, 5, 10, 20, 50, 80, and 100; and hc/hf = 20. Figure 6 shows the non-dimensional fundamental frequency data. The variation of the vibration frequencies is following the expected line, i.e., increasing, while the span-to-thickness ratios increase but a declining trend for the higher curvature ratios.

Fig. 6
figure 6

Effect of curvature ratios on non-dimensional frequency responses of a square SSSS (0°/90°/Core/90°/0°) sandwich cylindrical shell panel (hc/hf = 20)

Full size image

Here, another example is solved to show the effect of the curvature ratios (R/a) on the transient responses of the cylindrical shell panel under the UDL and the SSL (q0 = 100 N/cm2) type of loading and is presented in Fig. 7. To obtain the responses, a square SSSS symmetric (0°/90°/core/90°/0°) cylindrical sandwich shell panel is considered with a/h = 50 and hc/hf = 20. The results indicate that the deflection values are following an increasing trend when the curvature ratios (R/a) increase. However, the non-dimensional central deflection values \(\left( {\bar {W}} \right)\) are higher for the UDL in comparison to the SSL as discussed earlier.

Fig. 7
figure 7

Effect of curvature ratios on transient responses of a square SSSS (0°/90°/core/90°/0°) sandwich cylindrical shell panel under a UDL, b SSL(a∕h = 50, hc/hf = 20)

Full size image

3.1.2 Effect of the aspect ratios on the cylindrical shell panel

Now, the effect of the various aspect ratios on the transverse bending, frequency and transient deflections of the cylindrical panel examined in this example, similar to the earlier case. The non-dimensional transverse central point deflection parameters of a simply supported symmetric (0°/90°/core/90°/0°) cylindrical (R/a = 10) sandwich (hc/hf = 20) shell panel under two mechanical loadings (UDL and SSL) for various aspect ratios (a/b = 0.5, 1.0, 1.5, 2.0 and 3.0) are plotted in Fig. 8. In addition, the results are computed for the thick to thin structural panel considering six different span-to-thickness ratios (a/h = 5, 20, 30, 50, 80, and 100). The figure indicates the effect of both the geometrical parameters affect the deflections significantly, i.e., following a decreasing trend, while the aspect ratios and span-to-thickness ratio increase.

Fig. 8
figure 8

Effect of aspect ratios on the non-dimensional central deflection of a SSSS (0°/90°/core/90°/0°) sandwich cylindrical shell panel (R/a = 10, hc/hf = 20)

Full size image

Now, the above example is extended to compute the eigenvalues of the cylindrical sandwich panel using the similar input parameters and is plotted in Fig. 9. The responses follow the expected trend, i.e., the frequency values are decreasing, while the aspect ratios increase, whereas declining for the higher span-to-thickness ratios (a/h). In addition, the time-dependent deflections are computed for the same cylindrical sandwich shell example under the two different loadings as in the case of the deflection analysis, i.e., UDL and SDL ,and are provided Fig. 10.

Fig. 9
figure 9

Effect of aspect ratios on the non-dimensional central deflection of a SSSS (0°/90°/core/90°/0°) sandwich cylindrical shell panel (R/a = 10, hc/hf = 20)

Full size image
Fig. 10
figure 10

Effect of aspect ratios on transient responses of a SSSS (0°/90°/core/90°/0°) sandwich cylindrical shell panel under a UDL, b SSL (a∕h = 50, R/a = 20, hc/hf = 20)

Full size image

It is observed from the figure that the deflection parameter values \(\left( {\bar {W}} \right)\) follow a decreasing trend when the aspect ratios (a/b) increase. This is because of the non-dimensional formulae adopted in the current analysis. Furthermore, the similar kind of behaviour has been observed for the loading configurations (UDL and SDL) as same as the earlier case.

3.1.3 Effect of the core-to-face thickness ratios on the spherical shell panel

In this section, the effect of the core-to-face thickness ratios (hc/hf = 4, 8, 10, 15, 20, 25, and 30) are investigated on the corresponding spherical (R/a = 10) sandwich structural panel adopting the defined material and geometrical parameters. Figure 11 shows the deflection parameter of a square SSSS symmetric (0°/90°/core/90°/0°) sandwich spherical shell structure panel under the UDL and the SSL including the variable thickness ratios (a/h = 5, 20, 30, 50, 80, and 100). It can be easily understood from the figure that the deflection values are decreasing for the higher span-to-thickness ratios (a/h), whereas a reverse line followed, while the core-to-face thickness ratio increases. In addition, the present study also follows the similar type of behaviour as seen earlier for the loading condition (UDL and SSL).

Fig. 11
figure 11

Effect of core-to-face thickness ratios on the non-dimensional central deflection of a square SSSS (0°/90°/core/90°/0°) sandwich spherical shell panel (R/a = 10)

Full size image

Now, Fig. 12 shows the fundamental frequency parameter of a square symmetric (0°/90°/core/90°/0°) sandwich spherical panel for all sides simply supported. It is noticed from the provided data that the frequencies are following a declining path for the higher core-to-face thicknesses and a reverse trend when the span-to-thickness ratios (a/h) increase.

Fig. 12
figure 12

Effect of core-to-face thickness ratios on non-dimensional frequency responses of a square SSSS (0°/90°/core/90°/0°) sandwich spherical shell panel (R/a = 10)

Full size image

Furthermore, the transient responses of a square SSSS symmetric (0°/90°/core/90°/0°) sandwich spherical shell panel under two different mechanical loading (UDL and SSL) is obtained and is presented in Fig. 13. For the computational purpose, the desired structural parameters are taken as: hc/hf = 4, 10, 15, 20, and 30, a∕h = 100, and R∕a = 50. The results indicate that the transient deflection values are showing an increasing trend with an increase in the core-to-face thickness ratios (hc/hf). It is important to mention that the results follows the same trend for the UDL and the SSL case as discussed earlier, i.e., the deflection values higher for the UDL while compared with the SSL.

Fig. 13
figure 13

Effect of core-to-face thickness ratios on transient responses of a square SSSS (0°/90°/core/90°/0°) sandwich spherical shell panel under a UDL, b SSL (a∕h = 100, R∕a = 50)

Full size image

3.1.4 Effect of the lamination schemes on the hyperboloid shell panel

The effect of the face sheet laminations on the free vibration frequencies and static including the dynamic responses of the hyperboloid shell structure are discussed in this section. For the analysis purpose, the geometrical and material parameters are taken as defined earlier. The numerical deflection responses of a square SSSS sandwich (hc/hf = 20) hyperboloid shell (R/a = 10) panel under the different mechanical loading (UDL and SSL) are solved to obtain the static responses and are presented in Table 6. For the computation purpose, three different lamination schemes are considered by varying the number of facesheets [(0°/core/0°), (0°/90°/core/90°/0°), and (0°/90°/0°/90°/core/90°/0°/90°/0°)] including a/h = 5, 20, 30, 50, 80, and 100. The results are showing a declining trend for the higher span-to-thickness ratios (a/h) and the number of facesheet layers. In addition, the deflections are higher for the UDL as same as the earlier examples.

Table 6 Effect of the lamination scheme on the non-dimensional central deflection of a square SSSS sandwich hyperboloid shell panel (R/a = 10, hc/hf = 20)
Full size table

Now, the frequency responses are obtained for a square SSSS sandwich hyperboloid shell panel of different lamination schemes and are presented in Table 7. For this numerical example, the desired structural parameters are taken as, a/h = 5, 10, 20, 25, 30, 50, 80, and 100, hc/hf = 20, and R/a = 10. The results indicate that the non-dimensional eigenvalues are increasing when the span-to-thickness ratios (a/h) and the number of facesheet layers increase.

Table 7 Effect of the lamination scheme on the non-dimensional fundamental frequency of a square SSSS sandwich hyperboloid shell panel (R/a = 10, hc/hf = 20)
Full size table

Now, the effect of lamination schemes on the transient responses of the clamped sandwich (hc/hf = 10) hyperboloid shell (R∕a = 50) panel is computed under two mechanical loadings (UDL and SDL) including a∕h = 100 and is presented in Fig. 14. From the results it can be visualize that the deflection values are decreasing when the numbers of face layers’ increase. In addition, the final time-dependent deflections are following similar trend as in the earlier cases, i.e., higher for UDL while compared to the SDL.

Fig. 14
figure 14

Effect of lamination schemes on transient responses of a square CCCC sandwich hyperboloid shell panel under a UDL, b SSL (a∕h = 100, R∕a = 50, hc/hf = 10)

Full size image

3.1.5 Effect of the support conditions on the elliptical shell panel

The effect of the different edge conditions (all edges simply supported, SSSS; all edges clamped, CCCC; two opposite edges simply supported and two free, SFSF; two opposite edges clamped and two free, CFCF; and two opposite edges clamped and two free, CSCS) on the static and dynamic deflections including the eigenvalue parameters are evaluated for the elliptical sandwich shell panel.

First, the deflection values are obtained for a square symmetric (0°/90°/core/90°/0°) sandwich elliptical shell panel and are presented in Fig. 15. The results are computed for the various edge condition as mentioned above under the UDL and the SSL by considering the structural parameters as, a/h = 5, 20, 30, 50, 80, and 100, hc/hf = 20, and R/a = 10. It is noticed from the data that the responses are following the similar type of trend as seen in the earlier sections. It is also observed that the deflection values are following the decreasing trend with the change in the edge conditions from SFSF, CFCF, SSSS, CSCS, and CCCC.

Fig. 15
figure 15

Effect of support conditions on non-dimensional central deflections of a square (0°/90°/core/90°/0°) sandwich elliptical shell panel (R∕a = 10, hc/hf = 20)

Full size image

Now, the example is extended to investigate frequency parameters of the sandwich elliptical shell panel and is presented in Fig. 16. For the computational purpose, the desired structural parameters are adopted as: a/h = 5, 10, 20, 25, 30, 50, 80, and 100, hc/hf = 20, and R/a = 10. The responses indicate that the frequency values are increasing when the span-to-thickness ratios (a/h) increase. In addition, the clamped panel is showing the higher frequency parameters when compared to the other support conditions.

Fig. 16
figure 16

Effect of support conditions on non-dimensional fundamental frequency responses of a square (0°/90°/core/90°/0°) sandwich elliptical shell panel (R∕a = 10, hc/hf = 20)

Full size image

Furthermore, the effect of the predefined end conditions on the transient responses of a square sandwich elliptical shell panel is analysed under the two different type of mechanical loading, i.e., the UDL and the SSL and is presented in Fig. 17. The responses are computed using the desired structural parameters as, a∕h = 50, R∕a = 100, hc/hf = 20. It is noticed from the responses that the deflection values are following a decreasing type of trend when the support changes from, SFSF, SSSS, CFCF, CSCS, and CCCC, progressively.

Fig. 17
figure 17

Effect of support conditions on transient responses of (0°/90°/core/90°/0°) sandwich elliptical shell panel under a UDL, b SSL (a∕h = 50, R∕a = 100, hc/hf = 20)

Full size image

3.1.6 Responses of the different shell panels

Finally, the effect of the geometrical configuration on the corresponding eigenvalues and static including the dynamic deflections are investigated utilizing the predefined input geometrical and material parameters. The non-dimensional central deflection parameters of a square SSSS symmetric (0°/90°/core/90°/0°) sandwich shell panel are obtained and are tabulated in Table 8. The responses are calculated using the same material and geometrical parameters as discussed earlier under the influence of the UDL and the SSL. For the computational purpose, the necessary structural parameters are taken as, a/h = 5, 20, 30, 50, 80, and 100, hc/hf = 20, and R/a = 10. As discussed in earlier cases, the responses are following the similar type of trend, i.e., the deflection values are decreasing when the span-to-thickness ratios (a/h) increase. In addition, the deflections are higher for the UDL in comparison to the SSL as seen in the earlier examples. Furthermore, the transverse central deflection parameters are decreasing in progressive manner when the geometry changes from hyperboloid, flat, cylindrical, elliptical and spherical panel.

Table 8 Non-dimensional central deflection responses of a square SSSS symmetric (0°/90°/core/90°/0°) sandwich shell panels (R∕a = 10, hc/hf = 20)
Full size table

Table 9 reports the frequency responses for the different geometrical configurations of the square SSSS symmetric (0°/90°/core/90°/0°) sandwich panels. The structural responses are obtained by setting the geometrical parameters as: a/h = 5, 10, 20, 25, 30, 50, 80, and 100, hc/hf = 20, and R/a = 10. The frequency responses show an increasing type of trend when the span-to-thickness ratios increase as seen in the earlier examples. The frequency values are higher for and lower for the spherical and hyperboloid panel configurations.

Table 9 Non-dimensional fundamental frequency responses of a square (0°/90°/core/90°/0°) simply supported sandwich shell panels (R∕a = 10, hc/hf = 20)
Full size table

Now, the transient responses of various sandwich shell geometries (flat, cylindrical, elliptical, spherical and hyperboloid) under the influence of two loading types (UDL and SSL) computed using the current higher order model and are plotted in Fig. 18. The central deflection parameter \(\left( {\bar {W}} \right)\) of the clamped sandwich shell panels are computed using the relevant input parameters as: a∕h = 50, R∕a = 20 and hc/hf = 20. The deflections are higher for the UDL in comparison to SSL. However, the peaks are same in both the loading cases but higher deflections observed in the UDL. This is because the distribution of loading intensity throughout the panel surface area same for the UDL, whereas it varies sinusoidally for the SSL case and the deflection follows the path accordingly.

Fig. 18
figure 18

Transient responses of a square (0°/90°/core/90°/0°) clamped sandwich shell panels under a UDL, b SSL (a∕h = 50, R∕a = 20, hc/hf = 20)

Full size image

4 Conclusions

The FE solutions of structural responses, i.e., the static and the dynamic deflection including the free vibration frequencies of the layered sandwich curved structures are computed using the proposed higher order mathematical model. The results are obtained using an own home-made customized MATLAB code with the help of defined geometrical and material parameters. The solution accuracy and the corresponding consistencies of the current output are demonstrated via validating the results with that of available published data and the convergence test. The comparison of results indicate that the current higher order polynomial kinematic model is sufficient to investigate the sandwich laminated flat/curved panel structures without increasing the computational cost. In addition, the model is extended further to compute the values (deflection, frequency and time-dependent deflection) via a series of numerical examples including the variable parameters associated with geometrical dimensions and configurations. Finally, the final understanding related to the current output data displayed in a pointwise fashion in the following lines.

  • The free vibration non-dimensional frequency values are increasing, while the span-to-thickness ratios and the number of facings increase, whereas the trend follows a declined path for the aspect ratios, the curvature ratios, and the core-to-face thickness ratios

  • Similarly, the non-dimensional central transverse deflection values are increasing for the higher curvature ratios and the core-to-face thickness ratios. However, a declining trend is observed, while the span-to-thickness ratios, the aspect ratios and the number of face sheets increase.

  • Likewise, the deflection responses computed under two kinds of loading indicate that the non-dimensional central deflection values are higher under the influence of mechanical UDL instead of the SSL.

  • Finally, the significance of the support conditions are indicative for each type of analysis (static and deflection including free vibration frequencies) irrespective of geometries and geometrical parameters.