1 Introduction

Quantum information processing is a recent field that deals with exploiting the axioms of physics and computer science to explore the new possibilities offered by quantum physics. Furthermore, the primary focus of this theory is to investigate various physical systems for communicating and transferring information over long distances, without cloning the shared information between a sender and a receiver. Interestingly enough, the quantum computing aims to broaden the restricted field of classical computer science, which has been always limited to study quantum correlations and interactions between physical systems and their environments [1,2,3,4,5,6,7]. Indeed, it has been shown that finite-dimensional quantum correlations have been proven to be widely useful for developing quantum protocols with respect to their classical analogies [8]. However, from an experimental point of view, it has been shown that the effects of decoherence phenomenon resulting from the system–environment interaction have a destructive influence on studying non-classical correlations [9]. In this regards, several techniques and developed methods have been proposed to limit the interference of an open system with its surroundings during their interaction with each other [10].

In addition, many efforts have been made to highlight the dominant features in distinguishing between classical and non-classical correlations; including those carried out to quantify quantum correlations contained in quantum systems comprising at least two qubits. For example, Ollivier and Zurek showed that it is possible to quantify the non-classical correlations that originated from the discrepancy between the classical and quantum information of the studied system [11, 12]. Unfortunately, the development of quantum discord requires essentially some optimization mechanisms that still simple for X-type states, but extremely difficult for other types of states. Hence, these complexities helped Dakic et al. to improve another measure called Geometric Quantum Discord (GQD) which represents a successful measure of non-classical correlations [13].

Over the past decade, the delicate relationship between entanglement and quantum correlation has been considered as one of the most prominent subjects in quantum information theory [14,15,16]. It has been demonstrated, in particular, that quantum correlations can be generated in many-body systems while accounting for quantum phase transitions [17,18,19]. Indeed, N-body system characteristics are significantly impacted by shifts in quantum correlations. Intriguing results were found when the relationship between pairwise entanglement and quantum phase transitions in quantum spin chains was examined [20,21,22,23,24,25]. Additionally, even in the absence of entanglement, pairwise quantum discord has been evaluated to be more effective in revealing quantum phase transitions in such systems [26, 27]. These quantum particles, which were initially developed to transcend entanglement, were added because of their robustness, which is primarily to blame for this. In the recent studies, the interaction of quantum correlations and phase transitions at low temperatures has been considered (see, for instance, [28, 29]).

Quantum correlations and entanglement inherent in a quantum state that described spin systems have been extensively studied. Particularly, the works of Leonardo S. Lima demonstrated the significant impact of DM interaction and external magnetic fields on entanglement in various Heisenberg models; including one and two dimensions [30,31,32]. Precisely, He studied the impact of DM interaction and other parameters of the spin-1/2 one-dimensional Heisenberg antiferromagnetic model on the dynamics of von-Neumann entropy [30]. Interestingly enough, He investigated entanglement entropy of quantum one-dimensional integer spin Heisenberg antiferromagnetic model, demonstrating the influence of quantum phase transition on the behavior of entanglement entropy [31]. However, Werlang and Rigolin explored thermal and magnetic quantum discord in Heisenberg models. Indeed, they showed that quantum discord can increase with temperature even if the entanglement decreases, highlighting the robustness of quantum correlations against classical correlations [33].

The quantum Hellinger distance and trace distance are frequently employed to study the differences between quantum states. These two separate quantifiers are commonly utilized to avoid the more sophisticated minimization approaches found in the literature [28, 29]. However, it is critical to investigate the physical implications of Hellinger and trace distances for GQD. Indeed, the Hellinger distance quantifies the similarity of two quantum states using measurement probabilities. While the trace distance represents the structural differences between the density matrices associated with these states. Typically, both distances provide a complementary viewpoints on quantum correlations, where the Hellinger distance focusing on probabilistic similarities and the trace distance on structural differences. As a result, understanding these distances is critical for examining the dynamics of GQD in our work.

As emerges from the above paragraph, the most remarkable properties of the geometric discord are its simple computability and straightness. The main purpose of this paper is to investigate the dynamics of geometric quantum discord using trace distance (\(D_{T}\)) and Hellinger distance (\(D_{H}\)) for a two-spin Heisenberg XX chain via considering the effect of DM interaction and external magnetic field, namely B [34,35,36,37,38,39,40,41,42]. In fact, we study the influence of varying different parameters encoded in the XX-Heisenberg density operator on the behavior of GQD. Our findings show that maximizing the values of DM interactions and minimizing the values of B enhance the GQD. Moreover, we find that strong values of the temperature have a destructive effect on the behavior of GQD.

The present paper is structured as follows: in the next section, we give the necessary preliminaries used to understand the GQD. In Sect. 3, we describe the XX-Heisenberg model. Section 4 includes the numerical results and discussions. Finally, we conclude with conclusions and some future perspectives in Sect. 5.

2 Formalism of geometric quantum discord

In this section, we recall some preliminary aspects of GQD by means of trace distance and Hellinger distance. Indeed, the distance between a quantum state \(\rho \) describing a bipartite system AB and its nearest classical state is given as follows [43]:

$$ Q_{T}(\rho )=\min \left\| \rho -\chi \right\| _{1}, $$
(1)

where the minimum is taking over the set of zero-discord states \(\chi \) and the distance is the square norm in the Hilbert–Schmidt space. It is calculated as: \(\left\| \rho -\chi \right\| _{1} =Tr\sqrt{\left( \rho -\chi \right) ^{\dagger }\left( \rho -\chi \right) }\). When the measurements are taken using the subsystem A, then, the zero-discord state \(\chi \) is revealed to be [13]:

$$ \chi =\sum _{k}P_{k}\Pi _{k}^{A}\otimes \rho _{k}^{B} , $$
(2)

where \(\left\{ P_{k}\right\} \) is the probability distribution, \(\Pi _{k}^{A}\) is the orthogonal projector associated to subsystem A and \(\rho _{k}^{B}\) is the density operator of subsystem B. Based on this, the analytical expression of trace distance, namely \(D_{T}\) for any two-qubit density operator, namely \(\rho ^{X}\) is given as [44, 45]:

$$ D_{T}(\rho )=\sqrt{\frac{a\alpha _{1}^{2}-b\alpha _{2}^{2}}{a-b+\alpha _{1}^{2}-\alpha _{2}^{2}}} , $$
(3)

where \( \ \alpha _{1}=2(\rho _{23}+\rho _{14})\),\( \ \alpha _{2}=2(\rho _{23}-\rho _{14})\),\( \ \alpha _{3}=1-2(\rho _{22}+\rho _{33})\), \(x=2(\rho _{11}+\rho _{22})-1\), \(a=\max (\alpha _{3}^{2},\alpha _{2}^{2}+x^{2})\) and \(b=\min (\alpha _{3}^{2},\alpha _{1}^{2})\). On the other hand, the Hellinger distance can be considered as one of the most successful measures of GQD. In fact, it is expressed in terms of the square root of the density operator \(\rho \) as:

$$ D_{H}(\rho )=2\min \limits _{\Pi ^{A}}\left\| \sqrt{\rho }-\Pi ^{A}(\sqrt{ \rho })\right\| _{2}^{2} . $$
(4)

The minimum is taken from the complete set of the von-Neumann measurements \(\Pi ^{A}=\left\{ \Pi _{k}^{A}\right\} \), where \(\Pi ^{A}(\sqrt{\rho })=\sum \limits _{k}\Pi _{k}^{A}\sqrt{\rho }\Pi _{k}^{A}\), while \(\left\| X\right\| _{2}=\sqrt{TrX^{+}X}\) denotes the Hilbert–Schmidt distance. In general, the Hellinger distance is still difficult to be computed. Particularly, in the case of the (\(2\times n\)) system, the Hellinger distance is framed by the following expression [46]:

$$ D_{H}(\rho )=1-\alpha _{\max }\left\{ M_{AB}\right\} , $$
(5)

where \(\alpha _{\max }\) designs the minimum eigenvalue of (\(3\times 3\)) matrix \(M_{AB},\) of the following elements:

$$ \left( M_{AB}\right) _{ij}=Tr\{\sqrt{\rho }(\sigma _{A}^{i}\otimes I_{n}) \sqrt{\rho }(\sigma _{A}^{i}\otimes I_{n})\}, $$
(6)

where \(\sigma _{A}^{i}\) (\(i=x,\;y,\;z\)) being the Pauli matrices and \(I_{n}\) (\(n\times n\)) denotes the identity operator.

3 System model

3.1 XX Heisenberg model with DM interaction

In this part, we aim to investigate the interaction between two spins, namely the two-qubit Heisenberg model. Besides, we take into account the effect of Dzyaloshinskii–Moriya (DM) interaction. Indeed, the corresponding Hamiltonian of the XX-Heisenberg model with DM interaction is explicitly given as [47]:

$$ \hat{H_{S}}=J\left( \sigma _{1}^{x}\sigma _{2}^{x}+\sigma _{1}^{y}\sigma _{2}^{y}\right) +B\left( \sigma _{1}^{z}+\sigma _{2}^{z}\right) +D\left( \sigma _{1}^{x}\sigma _{2}^{y}-\sigma _{1}^{y}\sigma _{2}^{x}\right) , $$
(7)

where \(\sigma _{n}^{\alpha }\;(\alpha =x,\;y,\;z)\) denotes the Pauli operators acting in the nth spin, while J is the coupling between the two spins. Moreover, the parameters B and D describe the strengths of the magnetic field and DM interaction in z-component, respectively. However, for sake of simplicity, we suppose that \(\hbar =1\). Furthermore, one can examine the GQD by means of the trace and Hellinger distances of the above model using the thermal equilibrium state.

From the physical model described in Eq. (7), the eigenvalues and eigenvectors of \(\hat{H_{S}}\) can be derived analytically as:

$$ \lambda _{1,2}= \pm \delta , \quad \lambda _{3,4}= \pm 2 B, $$
(8)

and

$$\begin{aligned} & |\Psi _{1,2}\rangle =\frac{1}{\sqrt{2}}(\left| 10 \right\rangle \pm e^{i \theta }\left| 01 \right\rangle ), \\ & |\Psi _{3}\rangle =\left| 00 \right\rangle , \quad |\Psi _{4}\rangle =\left| 11 \right\rangle , \end{aligned}$$
(9)

where \(\delta = \sqrt{J^{2}+D^{2}}\), and \(\theta = \arctan ( D/J )\).

In our case, the proposed initial state is expressed in terms of the temperature T, as Gibbs operator of the following form:

$$ \rho (0)=Z^{-1}\sum \limits _{i=1}^{4}e^{-\beta \lambda _{i}}\left| \Psi _{i}\right\rangle \left\langle \Psi _{i}\right| , $$
(10)

with \(\beta =(k_{B}T)^{-1}\), such that \(k_{B}\) is the Boltzmann constant, while T denotes the absolute temperature of the environment. Moreover, \(\left| \Psi _{i}\right\rangle \) (\({\text {i}}=1,\ldots ,4\)) are the eigenvectors defined in Eq. (9) and \(Z=Tr(e^{-\beta \hat{H}})\) designs the partition function of the following expression :

$$ Z=2\left( \cosh (2\beta \delta ) +\cosh (2\beta B)\right) . $$
(11)

Consequently, the density matrix is obtained using in the standard basis \(\left\{ \mid 11\rangle ,\mid 10\rangle ,\mid 01\rangle ,\mid 00\rangle \right\} \) as:

$$ \rho (0)=\frac{1}{Z} \begin{pmatrix} e^{-2\beta B} & 0 & 0 & 0 \\ 0 & \cosh (2\beta \delta ) & -e^{i\theta }\sinh (2\beta \delta ) & 0 \\ 0 & -e^{-i\theta }\sinh (2\beta \delta ) & \cosh (2\beta \delta ) & 0 \\ 0 & 0 & 0 & e^{2\beta B} \end{pmatrix}. $$
(12)

3.2 Evolution of reduced density operator

In this part, we shall investigate the non-classical correlation for the joint spin–spin Heisenberg system in the presence of an external magnetic field and DM interaction. Indeed, the qubit–qubit system represents the open system of the reduced density operator \(\rho ^{S}(t)\) (see Fig. 1). Indeed, the Hamiltonian of the total system is given as:

$$ H = H_{S} + H_{R} + H_{\text {I}},$$
(13)

where \(H_{S}\) denotes the free Hamiltonian of the two-qubit system given in Eq. (7). Moreover, these two qubits (open system) are interacted with their bosonic reservoirs, namely reservoir A (\(R_{A}\)) and B (\(R_{B}\)) (environment), respectively of the following Hamiltonian:

$$\begin{aligned} \hat{H}_{R}= & \hat{H}_{R_{A}}+\hat{H}_{R_{B}} \\= & \hbar \omega _{A} b_{A^{\dagger }} b_{A}+ \hbar \omega _{B} b_{B^{\dagger }} b_{B}, \end{aligned}$$
(14)

where \(b_{j}\) and \(b_{j}^{\dagger }\) \((j=A, B)\) denote the annihilation and creation operators of the bosonic reservoirs \(R_{A}\) and \(R_{B}\) (see Fig. 1). Besides, \(\omega _{A}(\omega _{B})\) is the frequency of the electromagnetic field inside the reservoir \(R_{A} (R_{B})\). However, \(\hat{H_{I}}= \sum _{\alpha } g_{\alpha } X_{\alpha } \otimes Y_{\alpha }\) describes the interaction between the open system and the environment, where \( X_{\alpha} ^{\dagger }= X_{\alpha} \) and \( Y_{\alpha} ^{\dagger }= Y_{\alpha} \) refer to the operators describing the freedom degrees of the open system and reservoir, respectively .

Fig. 1
figure 1

Schematic illustration of the suggested model in which two qubits A and B are coupled to each other via the strength coupling J. Each qubit is coupled to its own surroundings, namely reservoir A (\(R_{A}\)) and reservoir B (\(R_{B}\)), respectively

Full size image

Now, to derive the reduced density operator \(\rho ^{S}\) of the open system (two qubits), we solve the Lindblad master equation of the following form [48]:

$$\begin{aligned} & \frac{d\rho ^{S}}{dt}=\frac{\gamma {\langle bb^{\dagger } \rangle }}{2}(2\sigma _{-}\hat{ \rho }^{S}\sigma _{+}-\sigma _{+}\sigma _{-}\hat{\rho }^{S}-\hat{\rho }^{S} \sigma _{+}\sigma _{-}) \\ & \quad +\frac{\gamma {\langle b^{\dagger }b \rangle }}{2}(2\sigma _{+}\hat{ \rho }^{S}\sigma _{-}-\sigma _{-}\sigma _{+}\hat{\rho }^{S}-\hat{\rho }^{S} \sigma _{-}\sigma _{+}), \end{aligned}$$
(15)

where \(\langle bb^{\dagger } \rangle = Tr(bb^{\dagger } \rho _{th})=\bar{n}+1\), \(\langle b^{\dagger }b \rangle =Tr(b^{\dagger }b \rho _{th})=\bar{n}\) and \(\rho _{th}=e^{-\beta H_{R}}/Tr(e^{-\beta H_{R}})\) is the thermal Gibbs state. Besides, \(\bar{n}=1/(e^{\beta \hbar \omega _{0}}-1)\) is the thermal mean photon number of the reservoir at temperature T. In addition, we suppose that \(\omega _{A}=\omega _{B}=\omega _{0}\) is the reservoir’s frequency and \(\gamma \) is the strength of damping rate. Moreover, \(\sigma ^{\pm }=\frac{1}{2}(\sigma _{x}\pm i\sigma _{y})\) are the system raising and lowering operators of the spin. Furthermore, the first and second parts of the right-hand side of Eq. (12) represent the decay rates of de-excitation and excitation of the reservoir, respectively. Mathematically, the relationship between them is given as \( \frac{\gamma _{1}}{\gamma _{2}}= e^{-\beta \omega _{0}}\) by the Kubo–Martin–Schwinger relation [44]. Finally, using the initial state in Eq. (12) of X-state form, one can straightforwardly obtain the state \(\rho ^{S}(t)\) in the standard basis \(B = \{\vert 11 \rangle ,\vert 10 \rangle ,\vert 01 \rangle ,\vert 00 \rangle \}\) of an “X” structure. In fact, the evolution of a two-qubit density can be expressed in the following form [49]:

$$ \rho ^{S} (t)= \begin{pmatrix} \rho ^{S} _{11}(t) & 0 & 0& \rho ^{S} _{14}(t) \\ 0 & \rho ^{S} _{22}(t) & \rho ^{S} _{23}(t) & 0 \\ 0 & \rho ^{S} _{32}(t) & \rho ^{S} _{33}(t) & 0 \\ \rho ^{S} _{41}(t) & 0 & 0 & \rho ^{S} _{44}(t) \end{pmatrix}. $$
(16)

The time-dependent elements of the reduced density matrix \(\rho ^{S} (t)\) of both qubits after embedding through the independent thermal reservoir are given for the initial state introduced in Eq. (12) as:

$$\begin{aligned} \rho ^{S} _{11}(t)= & u_{t}^{A}u_{t}^{B}\rho ^{S} _{11}(0)+u_{t}^{A}v_{t}^{B}(t)\rho ^{S} _{22}(0)+v_{t}^{A}u_{t}^{B}\rho ^{S} _{33}(0) \\ & \quad +v_{t}^{A}v_{t}^{B}\rho ^{S} _{44}(0), \\ \rho ^{S} _{22}(t)= & u_{t}^{A}(1-u_{t}^{B})\rho ^{S}_{11}(0)+u_{t}^{A}(1-v_{t}^{B})\rho ^{S} _{22}(0)+v_{t}^{A}(1-u_{t}^{B})\rho ^{S}_{33}(0) \\ & \quad +v_{t}^{A}(1-v_{t}^{B})\rho ^{S} _{44}(0), \\ \rho ^{S} _{33}(t)= & u_{t}^{B}(1-u_{t}^{A})\rho ^{S} _{11}(0)+v_{t}^{B}(1-u_{t}^{A})\rho ^{S} _{22}(0) \\ & \quad +u_{t}^{B}(1-v_{t}^{A})\rho ^{S} _{33}(0)+v_{t}^{B}(1-v_{t}^{A})\rho ^{S} _{44}(0), \\ \rho ^{S} _{44}(t)= & (1-u_{t}^{B})(1-u_{t}^{A})\rho ^{S}_{11}(0) \\ & \quad +(1-v_{t}^{B})(1-u_{t}^{A})\rho ^{S}_{22}(0)+(1-u_{t}^{B})(1-v_{t}^{A})\rho ^{S} _{33}(0) \\ & \quad +(1-v_{t}^{B})(1-v_{t}^{A})\rho ^{S} _{44}(0), \end{aligned}$$
(17)

while, the non-diagonal elements are:

$$\begin{aligned} & \rho ^{S} _{12}(t) =u_{t}^{A}z_{t}^{B}\rho ^{S} _{12}(0)+v_{t}^{A}z_{t}^{B}\rho ^{S} _{34}(0), \end{aligned}$$
(18)
$$\begin{aligned} & \rho ^{S} _{13}(t) =z_{t}^{A}u_{t}^{B}\rho ^{S} _{13}(0)+v_{t}^{B}z_{t}^{A}\rho ^{S} _{34}(0), \\ & \rho ^{S} _{14}(t) =z_{t}^{A}z_{t}^{B}\rho ^{S} _{14}(0),\quad \rho ^{S}_{23}(t)=z_{t}^{A}z_{t}^{B*}\rho ^{S} _{23}(0), \\ & \rho ^{S} _{24}(t) =z_{t}^{A}(1-u_{t}^{B})\rho ^{S} _{13}(0)+z_{t}^{A}(1-v_{t}^{B})\rho ^{S} _{24}(0), \\ & \rho ^{S} _{34}(t) =z_{t}^{B}(1-u_{t}^{A})\rho ^{S} _{12}(0)+z_{t}^{B}(1-v_{t}^{A})\rho ^{S} _{34}(0), \end{aligned}$$
(19)

where \(\ \rho ^{S}_{ij}(t)=\rho _{ji}^{S*}(t)\), and the analytical expressions of the functions \(u_{t}^{S},v_{t}^{S} ,z_{t}^{S},(S=A,B)\) are given by [49]:

$$\begin{aligned} u_{t}^{S}= & \frac{\bar{n}+(\bar{n}+1)\left( z_{t}^{S}\right) ^{2}}{2\bar{n}+1}, \\ v_{t}^{S}= & \frac{\bar{n}(1-\left( z_{t}^{S}\right) ^{2})}{2\bar{n}+1}, \\ z_{t}^{S}= & e^{\frac{-(2\bar{n}+1) \gamma t}{2}}. \end{aligned}$$
(20)

The quantities \(u_{t}^{S},v_{t}^{S}\) and \(z_{t}^{S}\) are time-dependent functions of the studied model. Moreover, \(S=A,B\) are related to the qubits in such a way the evolution is characterized by different values of the functions \(u_{t}^{S},v_{t}^{S}\) and \(z_{t}^{S}\).

These expressions allow us to evaluate the dynamics of the geometric quantum discord of the Heisenberg XX model with the DM interaction described by the initial state \(\rho ^{S} (0)\). Furthermore, we shall show how the GQD evolution is influenced by changing the physical parameters of the system. In fact, in the section that follows, we will plot the GQD using trace and Hellinger distances against the dimensionless parameter, \(\gamma t\), as well as the magnetic field and DM parameters B and D respectively.

3.3 Quantum correlations dynamics with DM interaction

The main subject of this part is to investigate the time-dependence of Hellinger and trace distances using the solutions given in Eqs. (17) and (18) using the results given in previous section. For sake of simplicity, we shall restrain our investigation to the case of two identical qubits locally interacting with identical environments. This means that the functions \(u_{t}^{S},v_{t}^{S},z_{t}^{S}\) \((S=A,B)\) introduced in Eq. (20) are the same for both qubits, namely \(z_{t}^{A}=\) \(z_{t}^{B}=e^{\frac{-(2\bar{n}+1) \gamma t}{2}}\), where \(\gamma _{A}=\gamma _{B}=\gamma \). Consequently, one can find that \(u_{t}^{A}=u_{t}^{B}\) and \(v_{t}^{A}=v_{t}^{B}\). Therefore, by considering these approximations, the time-dependent matrix elements of the reduced density operator, namely \(\rho ^{S} (t)\) of the Heisenberg XX model in the presence of DM interaction, as follows:

$$\begin{aligned} \rho ^{S} _{11}(t)= & \frac{1}{Z}\left[ \left( u_{t}^{A}\right) ^{2}e^{-2\beta B}+2u_{t}^{A}v_{t}^{A}(t)\cosh 2\beta \delta +\left( v_{t}^{A}\right) ^{2}e^{2\beta B}\right] , \\ \rho ^{S} _{22}(t)= & \rho ^{S} _{33}(t)=\frac{1}{Z}[u_{t}^{A}(1-u_{t}^{A})e^{-2\beta B} \\ & \quad +\left( u_{t}^{A}+v_{t}^{A}-2u_{t}^{A}v_{t}^{A}\right) \cosh 2\beta \delta +v_{t}^{A}(1-v_{t}^{A})e^{2\beta B}], \\ \rho ^{S} _{44}(t)= & \frac{1}{Z}\left[ (1-u_{t}^{A})(1-u_{t}^{A})e^{-2\beta B}+2(1-v_{t}^{A})(1-u_{t}^{A})\cosh 2\beta \delta +(1-v_{t}^{A})(1-v_{t}^{A})e^{2\beta B}\right] , \end{aligned}$$
(21)

and

$$\begin{aligned} \rho ^{S} _{12}(t)= & \rho ^{S} _{13}(t)=\rho ^{S} _{14}(t)=\rho ^{S} _{24}(t)=\rho ^{S} _{34}(t)=0, \\ \rho ^{S} _{23}(t)= & \frac{ z_{t}^{A} \ z_{t}^{B*}e^{i(\theta +\pi )}\sinh 2\beta \delta }{Z}. \end{aligned}$$
(22)

Finally, the obtained solution allows to examine the geometric non-classical correlation. First, let’s start by evaluating the dynamics of trace distance. Indeed, we have:

$$ D_{T}(\rho ^{S} )=\sqrt{\frac{a(t)\alpha _{1}^{2}(t)-b(t)\alpha _{2}^{2}(t)}{ a(t)-b(t)+\alpha _{1}(t)^{2}-\alpha _{2}(t)^{2}}}, $$
(23)

where

$$\begin{aligned} \alpha _{1}(t)= & \alpha _{2}(t)=\frac{2z_{t}^{A}(1-u_{t}^{B*})e^{i(\theta +\pi )}\sinh 2\beta \delta }{Z}, \\ \alpha _{3}(t)= & 1-\frac{4}{Z}[ u_{t}^{A}(1-u_{t}^{A})e^{-2\beta B}+\left( u_{t}^{A}+v_{t}^{A}-2u_{t}^{A}v_{t}^{A}\right) \cosh 2\beta \delta +v_{t}^{A}(1-v_{t}^{A})e^{2\beta B}], \\ x(t)= & \frac{2}{Z}\left[ u_{t}^{A}e^{-2\beta B}+\left( u_{t}^{A}+v_{t}^{A}\right) \cosh 2\beta \delta +v_{t}^{A}e^{2\beta B}\right] -1, \\ a(t)= & \max \left( \alpha _{3}(t)^{2},\alpha _{2}(t)^{2}+x\left( t\right) ^{2}\right) , \\ b(t)= & \min \left( \alpha _{3}(t)^{2},\alpha _{2}(t)^{2}\right) . \end{aligned}$$
(24)

Hence, the trace distance is obtained from the density matrix \(\rho ^{S}(t)\) of the pair qubits as the following form:

$$ D_{T}(\rho )=\frac{2e^{-(2\overline{n}+1)\gamma t}\sinh (2\beta \delta )}{Z}. $$
(25)

To give an analytical expression of Hellinger distance, we must first calculate the square root of the density operator \(\rho ^{S}(t)\). Indeed, it is computed as [50]:

$$ \sqrt{\rho ^{S} (t)}= \begin{pmatrix} \chi _{11}(t) & 0 & 0 & 0 \\ 0 & \chi _{22}(t) & \chi _{23}(t) & 0 \\ 0 & \chi _{32}(t) & \chi _{33}(t) & 0 \\ 0 & 0 & 0 & \chi _{44}(t) \end{pmatrix}, $$
(26)

where

$$\begin{aligned} \chi _{11}(t)= & \frac{\rho ^{S} _{11}(t)+\sqrt{\rho ^{S} _{11}(t)\rho ^{S} _{44}(t)}}{\sqrt{\rho ^{S} _{11}(t)+\rho ^{S} _{44}(t)+2\sqrt{\rho ^{S} _{11}(t)\rho ^{S} _{44}(t)}}}, \\ \chi _{22}(t)= & \frac{\rho ^{S} _{22}(t)+\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}{\sqrt{\rho ^{S} _{22}(t)+\rho ^{S} _{33}(t)+2\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}}, \\ \chi _{33}(t)= & \frac{\rho ^{S} _{33}(t)+\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}{\sqrt{\rho ^{S} _{22}(t)+\rho ^{S} _{33}(t)+2\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}}, \\ \chi _{44}(t)= & \frac{\rho ^{S} _{44}(t)+\sqrt{\rho ^{S} _{11}(t)\rho ^{S} _{44}(t)}}{\sqrt{\rho ^{S} _{11}(t)+\rho ^{S} _{44}(t)+2\sqrt{\rho ^{S} _{11}(t)\rho ^{S} _{44}(t)}}}, \\ \chi _{23}(t)= & \frac{\rho ^{S} _{23}(t)}{\sqrt{\rho ^{S} _{22}(t)+\rho ^{S} _{33}(t)+2\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}}, \\ \chi _{32}(t)= & \frac{\rho ^{S} _{32}(t)}{\sqrt{\rho ^{S} _{22}(t)+\rho ^{S} _{33}(t)+2\sqrt{\rho ^{S} _{22}(t)\rho ^{S} _{33}(t)-(\rho ^{S} _{32}(t))^{2}}}}. \end{aligned}$$
(27)

Hence, one can derive the Hellinger distance analytically as bellow:

$$ D_{H}(\rho )=1-\max \{W_{1},\;W_{2}\}, $$
(28)

where

$$\begin{aligned} W_{1}(t)= & 2(\chi _{11}(t)\chi _{22}(t)+\chi _{33}(t)\chi _{44}(t)), \\ W_{2}(t)= & \chi ^{2} _{11}(t)+\chi ^{2} _{22}(t)+\chi ^{2} _{33}(t)+\chi ^{2} _{44}(t)-2\chi ^{2} _{32}(t). \end{aligned}$$
(29)

In the next section, we move from the analytical results to the process of developing substantive discussions within the Heisenberg model for different parameters.

4 Numerical results and discussion

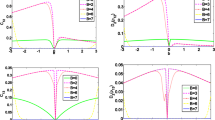
This section is dedicated to analyzing the effects of DM interaction, external magnetic fields B and reservoir temperature T on the dynamics of GQD, trace and Hellinger distances. Indeed, the quantities \(D_{T}\) and \(D_{H}\) given in Eqs. (25) and (28) are plotted versus the dimensionless parameter \(\gamma t\) for some fixed values of J, D and T. From Fig. 2, it is clear that both measures of non-classical correlation are initially maximized, that is:

$$ D_{T}(\rho )=D_{H}(\rho )=1. $$
(30)

On the other hand, the figure shows that strong external magnetic fields have a destructive effect on the nonclassical correlation of the system. Additionally, as the value of \(\gamma t\) increases significantly, both \(D_{T}\) and \(D_{H}\) are completely diminish.

Fig. 2
figure 2

Dynamics of trace distance \(D_{T}(\rho )\) (a), and Hellinger distance \(D_{H}(\rho )\) (b) versus \(\gamma t\) for different values of external magnetic field B, where \(J=D= 1\) and \({T = 0.7}\)

Full size image

In Fig. 3, we display the dynamics of non-classical correlation by means of trace and Hellinger distances against the external magnetic field parameter B for various values of \(\gamma t\). For the fixed values of J, D and T, the results show that the trace distance initially takes the maximum value, which is one, while the Hellinger distance is almost one. However, as t increases, both measures of quantum correlation decrease asymptotically until they reach minimum bounds, resulting in separability between the pair qubits.

Fig. 3
figure 3

Dynamics of a trace distance \(D_{T}(\rho )\) and b Hellinger distance \(D_{H}(\rho )\) versus external magnetic field B for different values of \(\gamma t,\) where \(J= 1\), \(D= 1.5\) and \({T = 0.7}\)

Full size image

From Figs. 2 and 3, one can conclude that it is possible to generate quantum correlation between the pair of qubits, which are proposed as an open quantum system interacting with the surrounding environment. Both figures show that the qubits are initially correlated. As, t increases, they are still coupled, but according to the decoherence phenomenon, the qubits become weakly coupled to each other. Moreover, significant values of \(\gamma t\) and B give rise to small bounds on the amounts of \(D_{T}(\rho )\) and \(D_{H}(\rho )\).

Fig. 4
figure 4

Dynamics of a trace distance \(D_{T}(\rho )\) and b Hellinger distance \(D_{H}(\rho )\) versus \(\gamma t\) for different values of D, by considering \(J = 1\), \(B = 1\) and \({T = 0.7}\)

Full size image

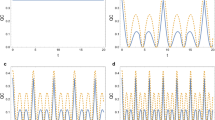
Now, consider the dynamics of non-classical correlation against \(\gamma t\) while accounting for various values of the DM parameter, namely D. Indeed, Fig. 4a and b exhibit the time-dependent trace and Hellinger distances, respectively. The plot shows that for an initial interval, namely \(\gamma t \in [0, 1]\) the qubits are correlated to each other. Furthermore, the \(D_{T}\) and \(D_{H}\) of the pair qubit reach an asymptotic regime without disappearing, indicating that \(D_{H}\) is more resistant to the thermal effect than \(D_{T}\). On the other hand, our results show that the amounts of trace and Hellinger distances are also influenced by changing the DM parameter in such a way both measures increase as the DM parameter takes strong values. Again, it is obvious that the trace distance exceeds the Hellinger distance for some regions, but they represent approximately the same behavior, which indicates that both measures represent the same information about the separability between the qubits coupled to their surrounding environment.

Fig. 5
figure 5

Dynamics of a trace distance \(D_{T}(\rho )\) and b Hellinger distance \(D_{H}(\rho )\) versus \(\gamma t\) (\(J = 1\), \(D = 1.5\) and \(B = 1.5\)), for different values of T

Full size image

We examine the GQD against the scaled parameter \(\gamma t \) by varying the temperature parameter T, where we considered the same initial settings of J and D as in Fig. 5. First, we clearly see from the plots that the trace distance is greater than the Hellinger distance for a certain region of \(\gamma t \). Second, the temperature has a clear impact on the quantification and enhancement of GQD. In fact, for small values of T, trace and Hellinger distances gradually increase to their maximum bounds, and this is for small values of \(\gamma t\). In general, the crossing-points, namely the intersection between the curves, mean that the behavior is independent of B (Fig. 2) and independent of \(\gamma t\) (Fig. 3). However, the change-points in the behaviors in Figs. 2 and 4 indicate a significant shift or transition in the dynamics of quantum correlations. This transition is due to the interactions with the environment, namely changes in the system’s environment.

Now, let us investigate the impact of varying simultaneously the parameters B and D. As illustrated in all previous figures, an asymptotic behavior is obtained again here, which indicates that the dynamics is Markovian. Indeed, the master equation in Eq. (15) indicates that the damping rate parameter is time-independent, which explains and proves the obtained results. Moreover, for all proposed cases, one can conclude that the trace distance is more robust than the Hellinger distance for certain regions, which is again proved in Fig. 6.

Fig. 6
figure 6

Dynamics of trace distance \(D_{T}(\rho )\) and Hellinger distance \(D_{H}(\rho ),\) versus B by considering \(J = 1\), \(\gamma t = 1\) , for different values of D [\(D = 0\) (a), and \(D = 1\) (b)]

Full size image

Finally, one can mention that the \(D_{T}(\rho )\) and \(D_{H}(\rho )\) may impose the same orderings of quantum states. In fact, one can see that both \(D_{T}(\rho )\) and \(D_{H}(\rho )\) decrease monotonously with respect to \(\gamma t \) and B. While, they increase monotonously versus D in the same way. For sake of comparison, one can also mention that a similar phenomenon for GQD by means of Hilbert–Schmidt distance is reported in [51, 52]. Moreover, note that a recent experimental study [53] showed that the properties of two quantum spin chain materials have been studied using various experimental techniques. Importantly, they showed that their proposed materials represent feature substantial DM interactions that are uniform within spin chain. Again, this prove as in our investigation the impact of DM on the dynamics of these kind of spin-Heisenberg systems. Roughly speaking, the DM interaction plays a significant role in the dynamics of quantum spin chains, where as in our theoretical results, the experimental observations support this result [54].

5 Conclusion

In this work, we explored the dynamics of non-classical correlation using trace and Hellinger distances, which are considered as a good metrics of geometric quantum discord. Indeed, we have examined the quantum correlations inherent in the two-spin system in its thermal equilibrium. This physical system is classified as a Heisenberg XX model, with the DM interaction induced via spin–orbit couplings. Furthermore, an external magnetic field is also involved in this study. By analyzing the dependence of the density operator on the system parameters, we found that the evolution dynamics and the external magnetic fields always degrade the trace and the Hellinger distances. However, for low values of \(\gamma t\), they measure consistently increase. Finally, we showed that for strong values of \(\gamma t \) and weak DM interaction, the quantum correlation is also enhanced in the weak magnetic field region.

The possibility to generalize our study into a system of more than two qubits still important. Indeed, it has been shown that one can generate quantum correlations for a Heisenberg system composed of four spins [55], providing a way maximize the quantum correlations via controlling temperature, Heisenberg exchange interaction, DM interaction, and decoherence parameters. Hence, another perspective can be considering through a generalization of this model for N spins.