Intrinsic decoherence effects on quantum correlations dynamics

Abstract

We investigate the influence of intrinsic decoherence on the quantum correlations in a two-qubit Heisenberg XYZ spin chain in the presence of the z-component of Dzyaloshinskii–Moriya interaction by employing logarithmic negativity and trace distance discord as reliable quantum correlation quantifiers. We highlight the dynamics behaviours of suggested quantifiers for a system initially prepared in the extended Werner-like state. For an initial separable state, it is found that the robustness and the generation of the quantum correlations depend on the physical parameters. While considering the entangled state as an initial state, the results show that despite the phase decoherence, all the correlations reach their steady state values after exhibiting some oscillations. We reveal that TDD is relatively more robust against the intrinsic decoherence compared to the logarithmic negativity and increasing the intrinsic decoherence rate leads to a drastic decrease of the quantum correlations between the two qubits.

1 Introduction

Quantum entanglement (Schrödinger 1935; Einstein et al. 1935; Nielsen and Chuang 2000; Vedral 2002; Horodecki et al. 2009; Gühne and Tóth 2009) is regarded as one of the most striking features of quantum mechanics which contributes in developing of many quantum information processing tasks, namely, quantum computing (Nielsen and Chuang 2000), quantum teleportation (Braunstein and Kimble 1998; Bouwmeester et al. 1997; Bennett et al. 1993; Ekert 1991), quantum key distribution (Ekert 1991) and many others (Nielsen and Chuang 2000). Nonetheless, several recent works showed that the quantumness of correlations that exist between a quantum systems parts is not necessarily always the entanglement type (Datta et al. 2008; Lanyon et al. 2008; Datta and Vidal 2007; Ollivier and Zurek 2001). In this respect, it has been shown that certain quantum mixed states exhibits quantum correlations despite they are separable (Lanyon et al. 2008; Datta and Vidal 2007). This type of correlation can only be captured by the so-called quantum discord that mainly aims to identify the correlations that go beyond entanglement (Henderson and Vedral 2001; Ollivier and Zurek 2001). But computing quantum discord under its entropic version is not a simple task in general. To avoid this calculation hindrance, Dakić et al. have developed a geometric variant of quantum discord by exploiting the metric in state space (Dakić et al. 2010; Paula et al. 2013). This concept serves to characterize the quantum correlations by quantifying the minimum distance between an involved quantum state and its closest classical one (Dakić et al. 2010). In this context, the trace distance discord (TDD) was recently introduced as promising geometrical approach to describe quantum correlation in terms of the Schatten 1-norm (trace norm) (Debarba et al. 2012; Montealegre et al. 2013). Owing to its easiest computability, TDD has attracted a lot of attention and proved to be a reliable measure of nonclassical correlations (Khedif and Daoud 2018, 2019; Khedif et al. 2019; Khedif and Daoud 2021). But the major challenge lies mainly in how to protect and maintain the quantified quantum correlations between the parts of open and interacted quantum systems?

In recent years, a particular interests have been devoted to the investigation of the quantum decoherence effects on the dynamics of quantum correlations (Khedif and Daoud 2018; Dehghani et al. 2020). Such unavoidable process lose the significant properties of the quantum systems due to their unwanted interaction with surrounding environments. Generally, the decoherence degrades the quantum correlations and also prevents a proper implementation of quantum information protocols based on them. Most considered environment in the literature are modeled by a thermal reservoir and the responsible on the quantum correlations degradation is the temperature (Khedif et al. 2019; Mojaveri et al. 2018, 2019; Khedif and Daoud 2021; Khedif et al. 2021). As we already mentioned, the process of decoherence hampers and delimits the optimal employ of quantum correlations. Among the decoherence phenomena, we distinguish intrinsic decoherence introduced by Milburn (Caves and Milburn 1987; Milburn 1991). This quantum mechanics concept was intensively studied by several authors (Caves and Milburn 1987; Ghirardi et al. 1986; Diosi 1989; Ghirardi et al. 1990; Ellis et al. 1989; Milburn 1991). It consists in modifying of the Schrödinger equation, characterizing the time evolution of the system, to destroy the coherence of the quantum system. The Milburn proposed model of intrinsic decoherence built on a specific modification of quantum mechanics by assuming that for a sufficiently short time steps, the system under consideration evolves continuously according to a stochastic sequence of identical unitary phase transformations rather than under to the effect of an unitary evolution. It is worth of mentioning that the effect of intrinsic decoherence in quantum systems is intensively studied in many works (He et al. 2006; Abdel-Aty 2008; Liang et al. 2008; Plenio and Knight 1997; Kuang et al. 1995; Buz̆ek and Konôpka 1998).

In the current work, we shall explore the dynamics of pairwise quantum correlations in XYZ spin—1/2 chain system with a z-component of Dzyaloshinskii–Moriya (z–DM) interaction, under the influence of the intrinsic decoherence. The Heisenberg spin systems are regarded as a potential candidate for implementing quantum communication and many other quantum information tasks. The thermal entanglement and quantum correlations which goes beyond entanglement in such systems are mainly investigated in the literature [see for instance (Rigolin 2004; Asoudeh and Karimipour 2005; Khedif et al. 2019; Habiballah et al. 2018; Mojaveri et al. 2018; Khedif et al. 2021; Khedif and Daoud 2021; Mansour and Daoud 2019; Mansour and Haddadi 2021; Sbiri et al. 2021; Khedif et al. 2021; Sbiri et al. 2022)]. In particular, we will employ the logarithmic negativity to detect thermal entanglement and TDD for describing the thermal nonclassical correlations in two-qubit Heisenberg XYZ chain that will evolve under the influence of intrinsic decoherence. In this study, we particularly calculate and compare the evolution of quantum entanglement and quantum correlation measures for a two-qubit system initially prepared in extended Werner-like (EWL) states under the interplay of z–DM interaction and the effect of the intrinsic decoherence.

We organized this paper in the following way. In Sect. 2, we review certain preliminaries about the logarithmic negativity and trace distance discord for quantifying correlations contained in a two-qubit X state. In Sect. 3, we consider an exactly solvable Hamiltonian of a two-qubit Heisenberg XYZ model with z-DM interaction, and we derive the amounts of the pairwise quantum correlations contained in the system subjected to the influence of the intrinsic decoherence. The behaviors of quantum correlations for a physical system assumed initially prepared in EWL states under the intrinsic decoherence are illustrated and discussed in Sect. 4. Finally, concluding remarks are given in the Sect. 5 to summarise our main results.

2 Quantum correlations measures

2.1 Logarithmic negativity

The logarithmic negativity (log-negativity) is regarded as an appropriate quantifier of quantum entanglement in bipartite quantum system (Vedral 2002; Plenio 2005). For an arbitrary bipartite system AB described by a density matrix $\varrho$ acting on a Hilbert space ${{\mathcal {H}}}_{AB}={{\mathcal {H}}}_{A} \otimes {{\mathcal {H}}}_{B}$, the log-negativity is given by

$$\begin{aligned} {{\mathcal {L}}_N}(\varrho )=\log _2\Vert \varrho ^{T_B}\Vert _1, \end{aligned}$$

(1)

where ${\varrho ^{T_B}}$ denotes the partial transposition of the composite density matrix $\varrho$, with respect to subsystem B (Peres 1996; Horodecki et al. 1996). The notation $\Vert .\Vert _1$ in Eq. (1) stands for the Schatten–1 norm (trace norm) which can be defined for a generic operator $\xi$ as

$$\begin{aligned} \Vert \xi \Vert _1=\mathrm{Tr}\left( \sqrt{\xi ^{\dagger }\xi }\right) . \end{aligned}$$

(2)

By construction, the log-negativity is additive and an entanglement monotone under deterministic local operations and classical communication. From (1), it follows that the log-negativity can be easily computed in terms of the absolute value of eigenvalues $\{\nu _i \}$ of the partially transposed density matrix $({\varrho })^{T_{B}}$. Indeed, it is given by

$$\begin{aligned} {\mathfrak {L}}N (\varrho )= \log _{2} \left( \sum _{i} |\nu _i| \right) . \end{aligned}$$

(3)

It is worthwhile to notice that $\mathfrak {L}N (\varrho )$ ranging between 0 for product states and 1 for the maximally entangled ones.

2.2 Trace norm measure

To quantify the discord-like quantum correlations, we employ here the TDD. It quantifies nonclassical correlations via the trace norm distance between a given state and its closest zero quantum discord one. In our study, we mainly focus on the case where the quantum system under consideration is described in the two-qubit standard computational basis $\mathcal {B}= \left\{ {\left| {00} \right\rangle ,\left| {01} \right\rangle ,\left| {10} \right\rangle ,\left| {11} \right\rangle } \right\}$ of ${{\mathcal {H}}}_{AB}$ by a X-shape density matrix given as

$$\begin{aligned} \varrho = \begin{pmatrix} a&{}\quad 0&{}\quad 0&{}\quad w \\ 0&{}\quad b&{}\quad z&{}\quad 0 \\ 0&{}\quad z^{*}&{}\quad c&{}\quad 0 \\ w^{*}&{}\quad 0&{}\quad 0&{}\quad d \end{pmatrix}. \end{aligned}$$

(4)

And let $\zeta \in {{\mathcal {H}}}_{AB}$ denotes the closest state of $\varrho$ that possesses only classical correlations between A and B (called also classical-quantum state). Phrased mathematically, the TDD between density operators $\varrho$ and $\zeta$ is defined in terms of trace norm (2) as Paula et al. (2013)

$$\begin{aligned} D_{\text {T}}(\varrho )=\min _{\zeta \in \Omega _0}\Vert \varrho -\zeta \Vert _1, \end{aligned}$$

(5)

where the optimization is performed over the set $\Omega _0$ of states with zero quantum discord. We notice that, the set of classical-quantum states $\zeta$ with respect to local measurements on subsystem A can be expressed as Luo (2008)

$$\begin{aligned} \zeta =\sum _{k=1}^{2}p_k|k\rangle \langle k|^A\otimes \varrho _{k}^{B}, \end{aligned}$$

(6)

where $\{|k\rangle ^A\}$ is an orthonormal basis of A subsystem’s Hilbert space ${{\mathcal {H}}}_A$, $\varrho _{k}^{B}$ a general reduced density operator of the subsystem B on its Hilbert space ${{\mathcal {H}}}_B$ and $\{p_k\}$ is a set of statistical probability distribution with a convex combination ($p_k \ge 0$ and $\displaystyle {\sum \nolimits _{k=1}}p_k=1$). It is worth noting that $D_{\text {T}}$ is invariant under any local unitary transformation (Ciccarello et al. 2014). Accordingly, the density matrix $\varrho$ (4) can be rewritten as

$$\begin{aligned} \varrho \Longrightarrow \tilde{\varrho }= \begin{pmatrix} a&{}\quad 0&{}\quad 0&{}\quad |w| \\ 0&{}\quad b&{}\quad |z|&{}\quad 0 \\ 0&{}\quad |z|&{}\quad c&{}\quad 0 \\ |w|&{}\quad 0&{}\quad 0&{}\quad d \end{pmatrix} \end{aligned}$$

(7)

and then the Eq. (5) becomes

$$\begin{aligned} D_{\text {T}}(\tilde{\varrho }) = \min _{\zeta \in \Omega _0}\Vert \tilde{\varrho }-\zeta \Vert _1. \end{aligned}$$

(8)

In order to evaluate TDD (8) explicitly, the state (7) should be expanded by means of the Fano–Bloch decomposition as (Bloch 1946; Fano 1983)

$$\begin{aligned} \tilde{\varrho }= \frac{1}{4}\sum _{\alpha , \beta =0 }^{3} {R_{\alpha \beta }} {\sigma _{\alpha }^{A} } \otimes {\sigma _{\beta }^{B} } \end{aligned}$$

(9)

wherein the correlation matrix elements $R_{\alpha \beta }$ are expressed in terms of 2D-Pauli matrices $\sigma _{\alpha }^{A}$ and $\sigma _{\beta }^{B}$, corresponding respectively to subsystems A and B, as $R_{\alpha \beta }=<{\sigma _{\alpha }^{A} } \otimes {\sigma _{\beta }^{B}}>$. By making use of Eqs. (7) and (9), it follows that the non zero $R_{\alpha \beta }$ are such that

$$\begin{aligned} R_{00}=1,\quad R_{11(22)}=2(|z|\pm |w|),\quad R_{33}=1-2(b+c),\quad R_{03}=2(a+c)-1,\quad R_{30}=2(a+b)-1. \end{aligned}$$

An elegant formula of the trace distance quantum discord of the state $\varrho$ (4) takes the form (Ciccarello et al. 2014)

$$\begin{aligned} D_{\mathrm{T}}(\varrho )= D_T\left( {\tilde{\varrho }} \right) =\sqrt{\frac{R_{11}^2 R_{\mathrm{max}}^2-R_{22}^2R_{\mathrm{min}}^2}{R_{\mathrm{max}}^2-R_{\mathrm{min}}^2+R_{11}^2-R_{22}^2}} \end{aligned}$$

(10)

where $R_{\mathrm{min}}^2=\min \{R_{11}^2,R_{33}^2\}$ and $R_\mathrm{max}^2=\mathrm{\max } (R_{33}^2,R_{22}^2+R_{30}^2)$.

3 The model and the initial state dynamics

3.1 Model and quantum correlations dynamics

In order to understand the behaviour of quantum correlations and then its evolution in a physical system under the intrinsic decoherence influences, we consider an interacting pair of quantum spin-1/2 particles on a one-dimensional (1D) lattice with nearest-neighbour anisotropic XYZ interaction in the presence of DM interactions. The suggested model is described by the Hamiltonian

$$\begin{aligned} \mathcal {H} =\sum _{i = x,y,z} J_i \left( \sigma _i^A \otimes \sigma _i^B\right) +\overrightarrow{D}\cdot\left( \overrightarrow{\sigma }^A\times \overrightarrow{\sigma }^B\right) \end{aligned}$$

(11)

where $J_i$’s are the strength of nearest-neighbor anisotropic spin–spin exchange interaction constant in the respective directions and $\overrightarrow{D}$ is the DM vector which we choose to be along the z-axis. In the two-qubit standard basis $\mathcal {B}$, the Hamiltonian (11) has the matrix form

$$\begin{aligned} \mathcal {H} = \begin{pmatrix} J_z &{}\quad 0 &{}\quad 0 &{}\quad \Delta \\ 0 &{}\quad -J_z &{}\quad \Sigma + 2i D &{}\quad 0 \\ 0 &{}\quad \Sigma - 2i D &{}\quad -J_z &{}\quad 0 \\ \Delta &{}\quad 0 &{}\quad 0 &{}\quad J_z \end{pmatrix} \end{aligned}$$

(12)

with $\Delta =J_x-J_y$ can be considered as an anisotropy measures of spin interaction couplings and $\Sigma =J_x+J_y$. The eigenvalues and their corresponding eigenvectors of the given Hamiltonian can be easily computed by using a simplified block Hamiltonian eigenvalue equation procedure $\mathcal {H}\vert {\phi }\rangle = E\vert {\phi }\rangle$. It follows that

$$\begin{aligned} \begin{array}{lclclclc} \displaystyle {~~~~E_{1,2}= J_z \pm \Delta , ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\vert \varphi _{1,2}\rangle =\frac{1}{\sqrt{2}}\left( |00\rangle \pm |11\rangle \right) },~~~~~~ \\ \\ \displaystyle {~~~E_{3,4}=-J_z \pm \vert \eta \vert ,~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \vert \varphi _{3,4} \rangle =\frac{1}{\sqrt{2}}\left( |01\rangle \pm \frac{\eta }{\vert \eta \vert }|10\rangle \right) } \\ \end{array} \end{aligned}$$

(13)

with $\eta =\Sigma -2iD$ and the kets $\vert 0 \rangle$ and $\vert 1 \rangle$ denote spin-up and spin-down states, respectively. In the following, we review some basics about the Milburn model of decoherence (Milburn 1991). Based on the assumption that on sufficiently short time steps, the system does not evolve continuously under unitary evolution but rather in a stochastic sequence of identical unitary transformations. In this context, Milburn has derived the master equation describing the time evolution of the quantum system as Milburn (1991)

$$\begin{aligned} \frac{d\varrho (t)}{dt} = \frac{1}{\gamma }\Bigl [\exp (-i\gamma \mathcal {H})\varrho (t) \exp (i\gamma \mathcal {H})-\varrho (t)\Bigr ], \end{aligned}$$

(14)

where $\mathcal {H}$ is the Hamiltonian of the considered system (11), $\varrho (t)$ denotes the evolved state of the system and $\gamma$ refers to the intrinsic decoherence parameter. It is interesting to notice that there is no intrinsic decoherence when $\gamma ^{-1} \rightarrow \infty$. According to this last condition, the Eq. (14) reduces to the standard von Neumann equation for the density matrix of closed quantum systems. The Milburn model of decoherence, called intrinsic decoherence, serves to modify the Schrödinger equation in such a way that the quantum coherence is automatically destroyed as the quantum system evolves. Expanding Eq. (14) to first order in $\gamma$, we obtain, after neglecting the higher order terms, the following dynamical equation

$$\begin{aligned} \frac{d\varrho (t)}{dt}=-i [\mathcal {H},\varrho (t)] -\frac{\gamma }{2}[\mathcal {H},[\mathcal {H},\varrho (t)]]. \end{aligned}$$

(15)

It is worth mentioning that the system’s non unitary evolution, under intrinsic decoherence effect, is guaranteed by the second term on the right hand side of Eq. (15). The formal solution of the above equation can be written in operator-sum representation using Kraus operators $M_l$ as Milburn (1991); Massashi et al. (2007); Bose (2003); Guo and Song (2008)

$$\begin{aligned} \varrho (t)= \sum ^{\infty }_{k=0} M_k(t) \varrho (0)M_k{}^{\dagger }(t) \end{aligned}$$

(16)

where $\varrho (0)$ is the initial density operator describing the considered quantum system and the operators $M_k(t)$ are defined as

$$\begin{aligned} M_k(t) = \sqrt{\frac{(\gamma t)^{k}}{k!}} {{\mathcal {H}}}^k \exp \left( -i{{\mathcal {H}}}t\right) \exp \left( -\frac{\gamma t}{2}\mathcal{H}^{2}\right) . \end{aligned}$$

such that

$$\begin{aligned} \sum ^{\infty }_{k=0} M_k(t) M_k{}^{\dagger }(t) =\mathbbm {1}. \end{aligned}$$

(17)

In Milburn’s model of intrinsic decoherence, the entries of the evolved state $\varrho (t)$ of the two-qubit anisotropic Heisenberg XYZ system described by the Hamiltonian (11) are expressed in the energy eigenbasis as

$$\begin{aligned} \varrho (t) = \sum _{m,n} \exp \left[ -\frac{\gamma t}{2}(E_{m}-E_{n})^{2}- i(E_{m}-E_{n})t\right] \langle \varphi _{m}\vert \varrho (0)\vert \varphi _{n}\rangle \vert \varphi _{m}\rangle \langle \varphi _{n }\vert \end{aligned}$$

(18)

where $E_{m,n}$ and $|\varphi _{m,n}\rangle$ are, respectively, the eigenvalues and the corresponding eigenvectors of Hamiltonian $\mathcal {H}$ of the system. We notice that the dynamical evolution (18) of the state $\varrho (t)$ describes an intrinsic decay of quantum coherence in the energy basis.

In what follows, we examine the intrinsic decoherence effects on quantum correlations captured by entanglement and trace distance discord. Our analysis should be focused on the correlation dynamics of mixed states ($\mathrm{Tr}(\varrho ^2)<1$). Specifically, we consider a real X-state of the form (4). The evolution of X-state (4) under the Hamiltonian Eq. (12) also retains the form of X-state. Substituting the Eqs. (13) and $\varrho (0)=\varrho$ (4) into master equation as given in Eq. (18), the exact time evolved density matrix can be straightforwardly expressed in $\mathcal {B}$ as

$$\begin{aligned} \varrho (t) = \begin{pmatrix} \varrho _{11}(t)&{}\quad 0&{}\quad 0&{}\quad \varrho _{14}(t) \\ 0&{}\quad \varrho _{22}(t)&{}\quad \varrho _{23}(t)&{}\quad 0 \\ 0&{}\quad \varrho _{23}^{*}(t)&{}\quad \varrho _{33}(t)&{}\quad 0 \\ \varrho _{14}^{*}(t)&{}\quad 0&{}\quad 0&{}\quad \varrho _{44}(t) \end{pmatrix} \end{aligned}$$

(19)

with the diagonal entries are given by

$$\begin{aligned} \varrho _{11}(t)&= \frac{a+ d}{2}+\left( \frac{a- d}{2} \cos \left( 2 \Delta t\right) -\Im (w)\sin \left( 2 \Delta t\right) \right) e^{-2 \gamma \Delta ^{2} t}\\ \varrho _{22}(t)&= \frac{b+c}{2}+ \left( \frac{b-c}{2}\cos \left( 2 \vert \eta \vert t\right) + \frac{2\Re (z)D-\Im (z)\Sigma }{\vert \eta \vert } \sin \left( 2\vert \eta \vert t\right) \right) e^{-2 \gamma \vert \eta \vert ^2 t} \\ \varrho _{33}(t)&= \frac{b+c}{2}- \left( \frac{b-c}{2}\cos \left( 2 \vert \eta \vert t\right) + \frac{2\Re (z)D-\Im (z)\Sigma }{\vert \eta \vert } \sin \left( 2\vert \eta \vert t\right) \right) e^{-2 \gamma \vert \eta \vert ^2 t} \\ \varrho _{44}(t)&=\frac{a+ d}{2}-\left( \frac{a- d}{2} \cos \left( 2 \Delta t\right) -\Im (w) \sin \left( 2 \Delta t\right) \right) e^{-2 \gamma \Delta ^{2} t} \end{aligned}$$

and off-diagonal elements are easily calculated to be

$$\begin{aligned} \varrho _{14}(t)&=\Re (w)+i\left( \frac{a- d}{2}\sin \left( 2 \Delta t\right) +\Im (w)\cos \left( 2 \Delta t\right) \right) e^{-2\gamma \Delta ^{2} t}\\ \varrho _{23}(t)&=\frac{z}{2}\left( 1+\cos \left( 2\vert \eta \vert t\right) e^{-2 \gamma \vert \eta \vert ^2 t}\right) \\&\quad +\frac{z^{*}\left( \eta ^{*}\right) ^2}{2\vert \eta \vert ^2} \left( 1-\cos \left( 2\vert \eta \vert t\right) e^{-2 \gamma \vert \eta \vert ^2t}\right) -\frac{-i\eta ^{*}}{2\vert \eta \vert }\left( c-b\right) \sin \left( 2\vert \eta \vert t\right) e^{-2 \gamma \vert \eta \vert ^2t} \end{aligned}$$

where $\Re (\Omega )$ ($\Im (\Omega )$) denotes the real (imaginary) part of $\Omega$ and $z^{*}(\eta ^{*})$ is the conjugate of $z(\eta )$.

The amount of entanglement in the evolved state $\varrho (t)$ (19) is computed by considering the logarithmic negativity $\mathfrak {L}N (\varrho _{t})$ as

$$\begin{aligned} \mathfrak {L}N (\varrho _{t})=Log_2 \left( 1+ 2(\max \{0,\nu _1\}+\max \{0,\nu _2\}) \right) , \end{aligned}$$

(20)

where the possible negative eigenvalues $\{ \nu _i, i=1,2\}$ of the transposed density matrix $(\varrho (t))^{T_2}$ are given as

$$\begin{aligned}&\nu _1=\left( -\varrho _{11}(t)-\varrho _{44}(t) + \sqrt{(\varrho _{11}(t)-\varrho _{44}(t))^{2}+4|\varrho _{23}(t)|^{2}}\right) , \\&\nu _2=\left( -\varrho _{22}(t)-\varrho _{33}(t) + \sqrt{(\varrho _{22}(t)-\varrho _{33}(t))^{2} +4|\varrho _{14}(t)|^{2}}\right) . \end{aligned}$$

On the other hand, the TDD dynamics can be guaranteed through Eq. (10) by taking into account the Fano-Bloch decomposition of the evolved state $\varrho (t)$ (19) with

$$\begin{aligned} R_{11}(t)= & {} 2\left( \vert \varrho _{23}(t)\vert +\vert \varrho _{14}(t)\vert \right) ,\\ R_{22}(t)= & {} 2\left( \vert \varrho _{23}(t)\vert - \vert \varrho _{14}(t)\vert \right) ,\\ R_{33}= & {} 1-2\left( \varrho _{22}(t)+\varrho _{33}(t)\right) ,\\ R_{03}= & {} 2\left( \varrho _{11}(t)+\varrho _{33}(t)\right) -1,\\ R_{30}= & {} 2\left( \varrho _{11}(t)+\varrho _{22}(t)\right) -1. \end{aligned}$$

3.2 Dynamics of EWL states with intrinsic decoherence

For the detailed investigations of the dynamics of quantum correlations under the intrinsic decoherence effects, we assume that the two-qubit system is initially prepared in the followig EWL

$$\begin{aligned} \varrho ^{\Phi }_p(0)= p|\Phi \rangle \langle \Phi | + \frac{1-p}{4}\mathbbm {1}_2\otimes \mathbbm {1}_2. \end{aligned}$$

(21)

In which $0 \le p \le 1$ denoting the pureness degree of the initial two-qubit states, $\mathbbm {1}_2$ is the $2\times 2$ identity operator and $|\Phi \rangle$ is the so-called pure Bell-like state given by

$$\begin{aligned} |\Phi \rangle =\cos \left( \frac{\theta }{2}\right) |01\rangle +\sin \left( \frac{\theta }{2}\right) e^{i\phi }|10\rangle \end{aligned}$$

(22)

with $0\le \theta <\pi$ and $0\le \phi <2\pi$. We note that when the above Bell-like state reduces to Bell state, those of EWL reduces to Werner state (Werner 1989). We shall note that in the two-qubit states computational basis $\mathcal {B}$, the EWL state (21) has an X structure

$$\begin{aligned} \varrho ^{\Phi }_p(0) = \begin{pmatrix} \frac{1-p}{4}&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad \frac{1-p}{4} + p \cos ^2 (\frac{\theta }{2})&{}\quad p \cos (\frac{\theta }{2}) \sin (\frac{\theta }{2})&{}\quad 0 \\ 0&{}\quad p \cos (\frac{\theta }{2}) \sin (\frac{\theta }{2})&{}\quad \frac{1-p}{4} + p \sin ^2 (\frac{\theta }{2}) &{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad \frac{1-p}{4} \end{pmatrix}. \end{aligned}$$

(23)

We notice that the X structure of the initial extended Werner-like (EWL) state (23) is preserved during its intrinsic dynamics evolution under the Hamiltonian (12). It is worthwhile to note that the EWL state $\varrho ^{\Phi }_p(0)$ is entangled for $\displaystyle p> \frac{1}{1+2\sin \theta }$.

4 Results and discussion

In what follows, our main interest focuses on the study of the intrinsic decoherence rate, along with other physical parameters, effects on the dynamical behavior of the pairwise quantum correlations captured by log-negativity and TDD. Let us first examine the bipartite EWL initial state (21) degree’s of purity p influences on the intrinsic dynamics of the quantified nonclassical correlations.

Figure 1 results display the time changes of the geometric discord and entanglement by varying the mixing parameter p.

Fig. 1

Time evolution of TDD (a) and log-negativity (b) versus the degree of purity p for EWL state (21) with initial parameters $\phi =\frac{\pi }{6}$ and $\theta =\frac{\pi }{2}$. For numerical results, we pick $\Sigma =0.5$, $D=1$ and $\gamma =0.01$. The 2D plot (c) illustrates the comparison of two nonclassical correlations quantifiers dynamics for Bell-like state (22), i.e. when $p=1$ is considered

It is clearly seen, that Fig. 1 manifests a typical difference by comparing the TDD (Fig. 1a) and entanglement measured by log-negativity (Fig.1b) during their dynamics. For initial parameters $\phi =\frac{\pi }{6}$ and $\theta =\frac{\pi }{2}$, it is shown that there is non entanglement since $p\le 1/3$. Nonetheless, a monotonic oscillating form of entanglement can occur when $p>1/3$. In contrast, the TDD is completely vanished only for maximally mixed separable state, i.e., for $p=0$. This means that discord can reveal certain nonclassicality that cannot be captured by entanglement (Khedif and Daoud 2018). That is to say, the nonclassical correlations quantified by TDD is more robust against the decoherence phenomenon than entanglement quantified by log-negativity. It is worth of mentioning that for initial entangled pure state (i.e. for $p\rightarrow 1$), the entanglement and geometric discord display an almost similar behaviours against to the intrinsic decoherence (see Fig. 1c).

Next, the effect of the parameter $\theta$ for the initial EWL state on the nonclassical correlations, including entanglement, is also demonstrated in Fig. 2.

Fig. 2

TDD (a) and log-negativity (b) as a function of $\theta$ and time for EWL state (21) with initial parameters $p={2}/{3}$ and $\phi =0$. We pick $\Sigma =1.5$, $D=1$ and $\gamma =0.01$. For the 2D plot (c), we considered $\theta =\pi /12$

As displayed in this figure, the decay of coherence can emerge also by adjusting $\theta$. We can also see that the collapse-revival of entanglement occurs only for small value of $\theta$. Near $\theta =\pi /2$, both log-negativity and TDD exhibit oscillating decays (see Fig. 2). By contrast, in the region far away from $\theta =\pi /2$ where there is little amount of initial nonclassical correlations, both log-negativity and TDD increase to their maximums at first and then decay with revivals. The difference between log-negativity and TDD is clearly visualized in Fig. 2c. From this figure results, we can observe that the log-negativity can revival after vanishing value of entanglement in the edge, while the TDD can revive immediately several times without vanishing for a period of time.

To see the DM exchange coupling effects on the quantum correlations dynamics, we examine the extreme case of an initial state given as $\varrho _p(0)= p|01\rangle \langle 01| + \frac{1-p}{4}\mathbbm {1}_2\otimes \mathbbm {1}_2$ which is a mixture of product states. Figure 3 plot illustrates the time evolution of both suggested quantum correlations versus DM parameter by considering $\Sigma =0$ and $p=2/3$.

Fig. 3

TDD (a) and log-negativity (b) as a function of DM parameter and time for $\Sigma =0$, $p=2/3$, $\theta =0$ and $\gamma =0.04$. The 2D plot (c), is given for $D=1$

It is clearly seen that, even without any initial quantum correlation between the two qubits, both quantifiers, TDD (Fig. 3a) and log-negativity (Fig. 3b), can reveal nonclassical correlations with an oscillating behaviours. It is worth of mentioning that the oscillations number increases with D, which implies that the intrinsic decoherence effect can be modulated by the spin-orbit coupling D. Besides, the difference between entanglement and nonclassical correlations captured by TDD lies in the fact that TDD can be induced immediately with both D and t while entanglement is suddenly created after certain finite time of evolution.

To go further, we explore the influence of the phase $\phi$ on the behavior of the pairwise quantum correlations in the physical system. In this respect, we visualize in Fig. 4 the dynamics of the TDD and log-negativity by changing the phase $\phi$.

Fig. 4

Time evolution of TDD (a) and log-negativity (b) in terms of the phase $\phi$ for $\Sigma =1$, $p=\frac{2}{3}$, $\theta =\frac{\pi }{2}$, $D=1$ and $\gamma =0.01$. For (c), we pick $\phi =\pi /6$

We remark that the two quantifiers TDD (Fig. 4a) and log-negativity (Fig. 4b) behave similarly and both measures can reveal quantum correlations with an oscillating behaviours. The difference between log-negativity and TDD is that the log-negativity can revival after zero entanglement in the edge, while the TDD can revive immediately several times without complectly vanishing for a period of time and for fixed value of the phase $\phi$. From Fig. 4c, we see that the TDD is more resistant against to the effects of intrinsic decoherence compared to entanglement quantified by log-negativity.

To study the influence of the coupling parameter $\Sigma =J_x+J_y$ on the pairwise quantum correlations captured by TDD and log-negativity, we depict in Fig. 5 the variations of both quantum correlations quantifiers in terms of the coupling parameter $\Sigma$ and t.

Fig. 5

TDD (a) and log–negativity (b) as a function of $\Sigma =J_x+J_y$ parameter and time for $p=\frac{2}{3}$, $\phi =\frac{\pi }{4}$, $\theta =\frac{\pi }{2}$ and $\gamma =0.04$. For the 2D plot (c), $\Sigma =2$ is considered

It is clearly seen that TDD (Fig. 5a) and log-negativity (Fig. 5b) reveal nonclassical correlations and hence they have a similar oscillating aspects. Furthermore, we also observe that both quantifiers they reach the steady state value in the asymptotic limit $t\rightarrow \infty$. It is interesting to notice that for initial separable state, the TDD is relatively more robust against to the interplay of the intrinsic decoherence and DM interaction compared to the log-negativity.

Now, we will study how TDD and log-negativity change over time t with and the intrinsic decoherence rate $\gamma$.

Fig. 6

Time evolution of TDD (a) and log–negativity (b) versus the intrinsic decoherence rate $\gamma$ for $\Sigma =2$, $D=1$, $\phi =\frac{\pi }{6}$, $\theta =\frac{\pi }{2}$ and $p=\frac{2}{3}$. For the 2D plot (c), $\gamma =0.1$ is considered

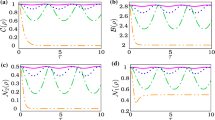
As can be seen from Fig. 6a and b, we observe a drastic decrease of TDD and log-negativity of the physical system in the presence of intrinsic decoherence. It is also seen from Fig. 6c that the local maximum values at the revival time of both quantifiers decreases gradually during the time evolution. We remark also a monotonic relationship between TDD and log-negativity and that the both quantum correlation quantifiers drop rapidly to be zero at larger time-scales as the intrinsic decoherence is introduced. Besides, Fig. 6c shows that both quantum correlation quantifiers are wiggles and reach the steady state value when the asymptotic limit $t\rightarrow \infty$ is achieved. To get more helpful insight into the intrinsic decoherence effect on the variation of quantum correlations, we plot in Fig. 7a and b the time evolution of TDD and log-negativity by considering fixed values of the intrinsic decoherence rate $\gamma$.

Fig. 7

TDD (a) and log-negativity (b) dynamics for various values of the intrinsic decoherence rate $\gamma$. We pick $\Sigma =2$, $D=1$, $\phi =\frac{\pi }{5}$, $\theta =\frac{\pi }{2}$ and $p=\frac{2}{3}$

We can see particularly form these figures that increasing values of $\gamma$ causes a rapid decay of the quantum correlation quantifiers. Furthermore, each one of them reach its own constant value in the asymptotic limit $t\rightarrow \infty$. It is also observed that log-negativity collapses faster than TDD which decreases more slowly. This implies that TDD is more resistant to the effect of the intrinsic decoherence. Finally, it was revealed that the periodic behavior of TDD and log-negativity became modest with increasing the intrinsic decohrence rate and disappear for large scale of time.

5 Concluding remarks

In this paper, we are concerned by the exploration of the quantum correlations in a physical system described by a two-qubit XYZ Heisenberg spin chain model in the presence of DM interaction along the z-axis and under the effect of intrinsic decoherence. We have used logarithmic negativity to characterise the entanglement between the two components of the system, while the existing nonclassical correlations are captured by the distance trace. We have investigated numerically the intrinsic decoherence effect on the dynamics of the two quantifiers in the presence of the DM interaction. We have showed that, in the presence of intrinsic decoherence, both TDD and log-negativity exhibit periodic behaviors and in the asymptotic limit $t\rightarrow \infty$, they saturate to their lower levels for longer time scales and increasing the intrinsic decoherence rate $\gamma$ causes rapid decay of the amount of quantum correlations exist between the two qubits.

We have restricted our study on the quantum correlations intrinsic dynamics by considering only the nearest neighbors two-qubit Heisenberg XYZ model in the presence of the spin-orbit coupling antisymmetric contribution. We believe that the quantum correlations dynamics will be efficiently adjusted by introducing the effect of Kaplan–Shekhtman–Entin–Wohlman–Aharony (KSEA) interactions Khedif et al. (2021), as a symmetric contribution of spin-orbit coupling, as well as the external inhomogeneous magnetic field. We hope to report in this issue in a forthcoming paper.