1 Introduction

As we know well, quantum correlation (QC) is one of the fundamental properties that characterize quantum systems, and by QC, the quantum realm can be distinguished from the classical realm. For the last few decades, QC has been investigated as the important resources in quantum information and quantum communication [1,2,3,4], but how to comprehend QC still remains the important task in quantum theory. Hence, many researches on QC have been actively proceeded until a recent date [5,6,7,8,9,10,11].

QC find applications in various fields, such as quantum communication, where entangled particles enable secure communication through quantum key distribution [12]. In quantum computing, correlations between qubits contribute to parallel processing and enhanced computational power [13]. Quantum correlations also play a crucial role in quantum sensing, enabling highly precise measurements with applications in fields like magnetic resonance imaging and gravitational wave detection [14].

Since qubit system is one of the essential physical systems to investigate abundant characters of QC, QC was principally discussed within Heisenberg hamiltonian models and Ising model with the magnetic field [15,16,17,18,19,20,21] and Dzyaloshinskii-Moriya (DM) interaction [22,23,24,25], and many valuable study outcomes have been accomplished. These study results indicate that the different external environments (temperature, magnetic field and DM interaction) have important influences on QC.

In recent years, many studies for spin systems have been done considering KSEA interaction. In Refs. [10, 26,27,28], the authors investigated QC considering DM and KSEA interactions in two-spin system, and also discussed the dynamics of QC considering the intrinsic decoherence [29, 30]. The obtained results indicated that DM and KSEA interactions can change QC. Besides this, various quantum correlation generation strategies have been modeled in the recent years, for example, see the Refs. [31,32,33]. All these studies show that at each configuration, the initialization, and preservation of the quantum correlations remains different. Hence, for this reason, I consider a different model such that to add up our part in the improvement of practical quantum information processing.

In my work, I address the issue of QC in a two-qubit Heisenberg spin model using the notions of thermal entanglement computed by concurrence [34]. Besides, I also intend to investigate QC beyond entanglement by geometric quantum discord (GQD) [35].

Heisenberg spin models are theoretical frameworks in quantum physics used to describe the collective behavior of spins in a magnetic system. Proposed by Werner Heisenberg, these models focus on the interaction between quantum spins without specifying their individual orientations, employing spin operators to represent the angular momentum of particles [36]. The models provide insights into the magnetic properties of materials, such as their phase transitions and magnetic ordering, and have applications in understanding phenomena like superexchange interactions in magnetic solids [37]. Therefore, it is noticeable that Heisenberg spin models are fundamental in the study of quantum magnetism.

Thus, I will devote to consider two essential QC such as TE and GQD for Heisenberg XXZ hamiltonian model with the nonuniform magnetic field and DM interaction. Here, I investigate the effect of the uniform part and nonuniform part of the magnetic field, DM interaction, exchange interaction on QC.

This paper is organized as follows. In Sect. 2, I introduce Heisenberg XXZ hamiltonian model with the external ununiform magnetic field, DM interaction, and obtain eigenvalues of hamiltonian and corresponding eigenstates. Also, I simply treat about TE and GQD and derive the reduced density matrix of considering system. Section 3 concentrate on the consideration of the controllability and robustness of TE and GQD. Finally, in Sect. 4 conclusions are found.

2 Model and quantum correlation

I discuss a \(N -\) qubit Heisenberg XXZ model under the nonuniform external magnetic field and DM interaction. The Hamiltonian is

$$H = \sum\nolimits_{{n = 1}}^{N} {\left[ {J\sigma _{n}^{x} \sigma _{{n + 1}}^{x} + J\sigma _{n}^{y} \sigma _{{n + 1}}^{y} + J_{z} \sigma _{n}^{z} \sigma _{{n + 1}}^{z} + \left( {B + b_{n} } \right)\sigma _{n}^{z} + D\left( {\sigma _{n}^{x} \sigma _{{n + 1}}^{y} - \sigma _{n}^{y} \sigma _{{n + 1}}^{x} } \right)} \right]} \,,$$
(1)

where \(\sigma_{n}^{\alpha } \left( {\alpha = x,\,y,\,z} \right)\) is the Pauli operator for qubit \(n\) and \(J,\,\,J_{z}\) indicate the real coupling constant for the interaction between the nearest two neighbor qubits in x, y, and z direction. \(D\) expresses DM interaction acting to z direction, and \(B\) is the uniform part of the magnetic field and \(b_{n}\) is nonuniform part of the magnetic fild, which acts to the z-direction. \(J,\,\,J_{z} > 0\) characterizes antiferromagnetic and \(J,\,\,J_{z} < 0\) characterizes ferromagnetic. Utilizing the periodic boundary condition, the considered Hamiltonian forms Heisenberg ring. I only investigate \(N = 3\) and \(b_{1} = b,\,\,b_{2} = 0,\,\,b_{3} = - b\). To discuss QC such as TE and GQD is necessary to obtain all eigenvalues of considering Hamiltonian and eigenstates. By slight calculation, the eigenvalues can be derived as follows

$$\begin{gathered} E_{1,8} = 3J_{z} \pm 3B, \hfill \\ E_{2,5} = - \frac{{a_{1,2} }}{3} + \sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} + \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)}} + \sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} - \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)}}, \hfill \\ E_{3,6} = - \frac{{a_{1,2} }}{3} + \frac{1}{2}\left( { - 1 + i\sqrt 3 } \right)\sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} + \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)}} + \frac{1}{2}\left( { - 1 - i\sqrt 3 } \right)\sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} - \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)\,}}, \hfill \\ E_{4,7} = - \frac{{a_{1,2} }}{3} + \frac{1}{2}\left( { - 1 - i\sqrt 3 } \right)\sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} + \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)}} + \frac{1}{2}\left( { - 1 + i\sqrt 3 } \right)\sqrt[3]{{\frac{1}{2}\left( { - g_{1,2} - \sqrt {g_{1,2}^{2} + 4f_{1,2}^{3} } } \right)}}, \hfill \\ \end{gathered}$$
(2)

where

$$\begin{gathered} f_{1,\,\,2} = \frac{{3b_{1,2} - a_{1,2}^{2} }}{9}\,,\,\,g_{1,\,\,2} = \frac{{2a_{1,2}^{3} - 9a_{1,2} b_{1,2} + 27c_{1,2} }}{27}, \hfill \\ a_{1,\,\,2} = 3J_{z} \mp 3B,\,\,\,\,b_{1,\,\,2} = 3J_{z}^{2} \mp 6BJ_{z} + 3B^{2} - 4b^{2} - 12J^{2} - 12D^{2} , \hfill \\ c_{1,\,\,2} = J_{z}^{3} + 3B^{2} J_{z} \mp 3BJ_{z}^{2} \mp B^{3} - 12J_{z} J^{2} \pm 12BJ^{2} \pm 12BD^{2} - 12\,D^{2} J_{z} - 16J^{3} + 48JD^{2} - 4b^{2} J_{z} \pm 4Bb^{2} , \hfill \\ \end{gathered}$$
(3)

where 1 and 2 correspond to the up and down sign. Note that \(g_{i}^{2} + 4f_{i}^{2} \le 0,\,\,\,i = 1,\,\,2\) and all eigenvalues are real numbers. The corresponding eigenstates are given as [11]

$$\begin{gathered} \psi_{1} = \left| {000} \right\rangle \,, \hfill \\ \psi_{i} = A_{i} \left( {a_{i2} \left| {001} \right\rangle + \left| {010} \right\rangle + a_{i5} \left| {100} \right\rangle } \right),\,\,\,\,i = 2,3,4\,, \hfill \\ \psi_{j} = B_{j} \left( {a_{j4} \left| {011} \right\rangle + a_{j6} \left| {101} \right\rangle + \left| {110} \right\rangle } \right),\,\,\,\,j = 5,6,7, \hfill \\ \psi_{8} = \left| {111} \right\rangle \,, \hfill \\ \end{gathered}$$
(4)

where

$$\begin{gathered} a_{i2} = \frac{{2J\left[ {J_{z} - B + 2b + E_{i} } \right] + 4J^{2} - 4D^{2} + 2iD\left[ {J_{z} - B + 2b + E_{i} - 4J} \right]}}{{\left( {J_{z} - B - 2b + E_{i} } \right)\left( {J_{z} - B + 2b + E_{i} } \right) - 4J^{2} - 4D^{2} }}, \hfill \\ a_{\,i5} = \frac{{2J\left[ {J_{z} - B - 2b + E_{i} } \right] + 4J^{2} - 4D^{2} + 2iD\left[ { - J_{z} + B + 2b - E_{i} + 4J} \right]}}{{\left( {J_{z} - B - 2b + E_{i} } \right)\left( {J_{z} - B + 2b + E_{i} } \right) - 4J^{2} - 4D^{2} }}, \hfill \\ a_{j4} = \frac{{2J\left( {J_{z} + B + E_{j} } \right) + 4J^{2} - 4D^{2} - 2iD\left( {J_{z} + B + E_{j} - 4J} \right)}}{{\left( {J_{z} + B - 2b + E_{j} } \right)\left[ {J_{z} + B + E_{j} } \right] - 4J^{2} - 4D^{2} }}, \hfill \\ a_{j6} = \frac{{2J\left( {J_{z} + B - 2b + E_{j} } \right) + 4J^{2} - 4D^{2} + 2iD\left( {J_{z} + B - 2b + E_{j} - 4J} \right)}}{{\left( {J_{z} + B - 2b + E_{j} } \right)\left[ {J_{z} + B + E_{j} } \right] - 4J^{2} - 4D^{2} }}, \hfill \\ \end{gathered}$$
(5)
$$\begin{gathered} A_{1i} = \left[ {2J\left( {J_{z} - B + 2b + E_{i} } \right) + 4J^{2} - 4D^{2} } \right]^{2} + 4D^{2} \left( {J_{z} - B + 2b + E_{i} - 4J} \right)^{2} \hfill \\ \,\quad \,\quad \;\;\; + \left[ {2J\left( {J_{z} - B - 2b + E_{i} } \right) + 4J^{2} - 4D^{2} } \right]^{2} + 4D^{2} \left( { - J_{z} + B + 2b - E_{i} + 4J} \right)^{2} \hfill \\ \,\quad \quad \quad + \left[ {\left( {J_{z} - B - 2b + E_{i} } \right)\left( {J_{z} - B + 2b + E_{i} } \right) - 4J^{2} - 4D^{2} } \right]^{2} \,, \hfill \\ A_{2i} = \left[ {\left( {J_{z} - B - 2b + E_{i} } \right)\left( {J_{z} - B + 2b + E_{i} } \right) - 4J^{2} - 4D^{2} } \right]\,, \hfill \\ B_{1j} = \left[ {2J\left( {J_{z} + B - 2b + E_{i} } \right) + 4J^{2} - 4D^{2} } \right]^{2} + 4D^{2} \left( {J_{z} + B - 2b + E_{i} - 4J} \right)^{2} \, \hfill \\ \,\quad \quad \quad + \left[ {2J\left( {J_{z} + B + E_{i} } \right) + 4J^{2} - 4D^{2} } \right]^{2} + 4D^{2} \left( {J_{z} + B + E_{i} - 4J} \right)^{2} \, \hfill \\ \,\quad \quad \quad + \left[ {\left( {J_{z} + B - 2b + E_{i} } \right)\left[ {J_{z} + B + E_{i} } \right] - 4J^{2} - 4D^{2} } \right]^{2} \,, \hfill \\ B_{2j} = \left( {J_{z} + B - 2b + E_{i} } \right)\left[ {J_{z} + B + E_{i} } \right] - 4J^{2} - 4D^{2} \,, \hfill \\ A_{i} = \frac{{\left| {A_{2i} } \right|}}{{\sqrt {A_{1i} } }},\,\,\,\,\,\,B_{i} = \frac{{\left| {B_{2j} } \right|}}{{\sqrt {B_{1j} } }}\,. \hfill \\ \end{gathered}$$
(6)

In this paper, I treat the two essential QC such as TE and GQD. GQD between two qubits characterized by the reduced density matrix \(\rho_{AB}\) can be taken as follows [38]

$$D_{2} \left( {\rho_{AB} } \right) = \min_{{\chi \in \Omega_{0} }} \left\| {\rho_{AB} - \chi } \right\|^{2} ,$$
(7)

where \(\left\| {\rho_{AB} - \chi } \right\|^{2} = Tr\left( {\rho_{AB} - \chi } \right)^{2}\) display the square norm in the Hilbert–Schmidt space and \(\Omega_{0}\) is the set of all possible classical states, whose form is \(\chi = \sum\nolimits_{{p_{k} }} {p_{k} \left| k \right\rangle } \left\langle k \right| \otimes \rho_{k}\). Where \(0 \le p_{k} \le 1\left( {\sum\nolimits_{k} {p_{k} = 1} } \right)\) and \(\left| k \right\rangle\) is the orthonormal basis for the subsystem. \(\rho_{k}\) is the density matrix for the subsystem. TE is indicated by concurrence, which can be got as follows [34]

$$C_{AB} = \max \left\{ {0,\,\sqrt {\lambda_{1} } - \sqrt {\lambda_{2} } - \sqrt {\lambda_{3} } - \sqrt {\lambda_{4} } } \right\},$$
(8)

where \(\lambda_{n} ,\,\,n = 1,\,2,\,3,\,4\) indicate the eigenvalues, in diminishing order of the matrix

$$R_{AB} = \rho_{AB} \left( {\sigma_{1}^{y} \otimes \sigma_{2}^{y} } \right)\rho_{AB}^{*} \left( {\sigma_{1}^{y} \otimes \sigma_{2}^{y} } \right).$$
(9)

I express the density operator of the thermal equilibrium state as

$$\rho \left( T \right) = \frac{1}{Z}\exp \left( { - \beta H} \right) = \frac{1}{Z}\sum\limits_{k = 1}^{8} {e^{{ - \beta E_{k} }} \left| {\psi_{k} } \right\rangle \left\langle {\psi_{k} } \right|} ,$$
(10)

where

$$Z = tr\left( {{\text{e}}^{ - \beta H} } \right) = \sum\limits_{k = 1}^{8} {e^{{ - \beta E_{k} }} } .$$
(11)

Here, I select Boltzmann constant \(k_{{\text{B}}} = 1\) and therefore \(\beta = 1/T\). The coupling constant \(J,\,\,J_{z}\), the temperature \(T\), DM interaction \(D\), the uniform part \(B\) and nonuniform \(b\) of the magnetic field are independent parameters. Therefore, GQD and TE are functions of \(J,\,\,J_{z} ,\,\,T,\,\,D,\,\,B,\,\,b\). In order to consider the pairwise GQD and TE, we have to discuss the reduced density matrix \(\rho_{12} = tr_{3} \left( {\rho \left( T \right)} \right)\left( {\rho_{23} = tr_{1} \left( {\rho \left( T \right)} \right),\,\,} \right.\) \(\left. {\rho_{13} = tr_{2} \left( {\rho \left( T \right)} \right)} \right)\) of sites 1 and 2 (2 and 3, 1 and 3). Thus for \(\rho_{12}\), we get the following result:

$$\rho_{12} = \frac{1}{Z}\left( {\begin{array}{*{20}c} {\beta_{1} } & 0 & 0 & 0 \\ 0 & {\beta_{2} } & {\delta^{*} } & 0 \\ 0 & \delta & {\beta_{3} } & 0 \\ 0 & 0 & 0 & {\beta_{4} } \\ \end{array} } \right),$$
(12)

where

$$\begin{gathered} \beta_{1} = e^{{ - \frac{{E_{1} }}{T}}} + \sum\nolimits_{k = 2}^{4} {A_{k}^{2} \left| {a_{k2} } \right|^{2} e^{{ - \frac{{E_{1} }}{T}}} } ,\,\,\,\,\,\beta_{2} = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} e^{{ - \frac{{E_{k} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} \left| {a_{k4} } \right|^{2} e^{{ - \frac{{E_{k} }}{T}}} } , \hfill \\ \beta_{3} = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} \left| {a_{k5} } \right|^{2} e^{{ - \frac{{E_{k} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} \left| {a_{k6} } \right|^{2} e^{{ - \frac{{E_{k} }}{T}}} } ,\,\,\,\,\beta_{4} = \sum\nolimits_{k = 5}^{7} {B_{k}^{2} e^{{ - \frac{{E_{k} }}{T}}} } + e^{{ - \frac{{E_{8} }}{T}}} , \hfill \\ \delta = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} a_{k5} e^{{ - \frac{{E_{k} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} a_{k4}^{*} a_{k6} e^{{ - \frac{{E_{k} }}{T}}} } . \hfill \\ \end{gathered}$$
(13)

While for the \(\rho_{13}\), we get

$$\begin{gathered} \beta_{1} = e^{{ - \frac{{E_{1} }}{T}}} + \sum\nolimits_{k = 2}^{4} {A_{k}^{2} e^{{ - \frac{{E_{i} }}{T}}} \,} ,\,\,\,\beta_{2} = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} \left| {a_{k2} } \right|^{2} e^{{ - \frac{{E_{i} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} \left| {a_{k4} } \right|^{2} e^{{ - \frac{{E_{k} }}{T}}} } , \hfill \\ \beta_{3} = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} \left| {a_{k5} } \right|^{2} e^{{ - \frac{{E_{i} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} e^{{ - \frac{{E_{k} }}{T}}} } \,,\,\,\,\beta_{4} = \sum\nolimits_{k = 5}^{7} {B_{k}^{2} \left| {a_{k6} } \right|^{2} e^{{ - \frac{{E_{k} }}{T}}} } + e^{{ - \frac{{E_{8} }}{T}}} , \hfill \\ \delta = \sum\nolimits_{k = 2}^{4} {A_{k}^{2} a_{k2}^{*} a_{k5} e^{{ - \frac{{E_{i} }}{T}}} } + \sum\nolimits_{k = 5}^{7} {B_{k}^{2} a_{k4}^{*} e^{{ - \frac{{E_{k} }}{T}}} } . \hfill \\ \end{gathered}$$
(14)

3 Controllability and robustness of the quantum correlation

On the basis of above consideration, I now start our consideration for the controllability and robustness of TE and GQD for the antiferromagnetic in the three-qubit Heisenberg XXZ Hamiltonian model. Here, I discuss in units where \(B,\,\,b,\,\,D,\,\,J\) and \(J_{z}\) are dimensionless.

3.1 Controllability of quantum correlation

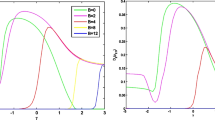
Here, I at first consider the controllability of the quantum correlation such as TE and GQD between two qubits 1 and 2 (1 and 3) for the antiferromagnetic. In Fig. 1, I indicate the figures of TE and GQD vs. b for the different uniform part of the magnetic field \(B\) with \(J = 2,\,\,J_{z} = 1,\,\,D = 0,\,\,T = 0.2\).

Fig. 1
figure 1

\(C_{12} ,\,\,D_{2} \left( {\rho_{12} } \right)\) and \(C_{13} ,\,\,D_{2} \left( {\rho_{13} } \right)\) vs.\(b\) for different uniform part of \(B\), where the parameters are selected to be \(J = 2,\,\,J_{z} = 1,\,\,D = 0,\,\,T = 0.2\)

Full size image

As illustrated in Fig. 1, \(C_{12}\) and \(D_{2} \left( {\rho_{12} } \right)\) at first increase, and next decrease with the increasing the absolute value of \(b\) for small \(B\),and for large \(B\,\,(B > 7)\) TE and GQD become zero all. \(C_{12}\) and \(D_{2} \left( {\rho_{12} } \right)\) have the largest maximum value at \(B = 2\), and \(C_{13}\) and \(D_{2} \left( {\rho_{13} } \right)\) have the largest maximum value at \(B = 3\). Also, \(D_{2} \left( {\rho_{13} } \right) - b\) curve does not change with increasing \(B\) until \(B = 3\) and then change. On the other hand, for any \(B\), \(C_{13} - b\) curve is symmetric about the inversion of nonuniform part of the magnetic field. These variations of quantum correlations can be explained as the state transition from one state to another state.

TE and GQD versus b at the different \(J\) with \(\,J_{z} = 1,\,\,D = 0,\,\,B = 0,\,\,T = 0.2\) are indicated in Fig. 2. As illustrated in Fig. 2, \(C_{12} ,\,\,D_{2} \left( {\rho_{12} } \right)\,\) and \(D_{2} \left( {\rho_{13} } \right)\) in the large absolute value of \(b\) increase and go near a straight line parallel to b axis with increasing \(J\). But \(C_{13}\) decreases with enhancing \(J\) for all absolute value of \(b\). Also, for any \(J\) all \(C_{12} - b,\,\,C_{13} - b,\,\,D_{2} \left( {\rho_{12} } \right) - b,\,\,\,D_{2} \left( {\rho_{13} } \right) - b\) curves are symmetric about the inversion of nonuniform part of the magnetic field. Also, Fig, 2 shows robustness of TE and GQD against the increasing strength of \(b\). One can see that except in the range \(- 0.2 < b < 0.2\), the state approaches to be in quantum regime in the case of \(\rho_{12}\). Besides, the similar range of \(b\) has been found not highly influential to induce TE and GQD in the case of \(\rho_{13}\). As one can see, the generation of TE shows much slower progress in \(\rho_{13}\) compared to the case of \(\rho_{12}\). On the contrary, GQD for the mentioned range of \(b\) shows the similar results both in the case of \(\rho_{12}\) and \(\rho_{13}\). Besides, the graphs show that the increasing strenth of \(J\) remains resourceful for the gneration of TE and GQD against \(b\) in XXZ Heisenberg model.

Fig. 2
figure 2

\(C_{12} ,\,\,D_{2} \left( {\rho_{12} } \right)\) and \(C_{13} ,\,\,D_{2} \left( {\rho_{13} } \right)\) vs.\(b\) for \(J\), where the parameters are selected to be \(\,J_{z} = 1,\,\,D = 0,\,\,B = 0,\,\,T = 0.2\)

Full size image

In Fig. 3 indicates the figures of TE and GQD vs. b for the different DM interaction \(D\) with \(\,J = 2,\,\,J_{z} = 1,\,\,B = 0,\,\,T = 0.2\). \(C_{12} - b,\,\,C_{13} - b,\,\,D_{2} \left( {\rho_{12} } \right) - b,\,\,\,D_{2} \left( {\rho_{13} } \right) - b\) curves are all symmetric about the inversion of nonuniform part of the magnetic field and these curves go near a straight line parallel to b axis with increasing \(D\). This shows that TE and GQD do not depend on the strength of the magnetic field for the large values of DM interaction \(D\), namely, strong DM interaction plays the essential role in the conservation of QC.

Fig. 3
figure 3

\(C_{12} ,\,\,D_{2} \left( {\rho_{12} } \right)\) and \(C_{13} ,\,\,D_{2} \left( {\rho_{13} } \right)\) vs.\(b\) for \(D\), where the parameters are selected to be \(\,J = 2,\,\,J_{z} = 1,\,\,B = 0,\,\,T = 0.2\)

Full size image

Like as Figs. 2, 3 also shows the robustness of TE and GQD against the increasing \(D\) through the total range of \(b\). One can see that the state approaches to be in quantum regime with the increasing \(D\) both in the case of \(\rho_{12}\) and \(\rho_{13}\). Moreover, the range of \(b\) has been found not widely influential to the generation of TE and GQD for large \(D\) in the case of \(\rho_{12}\) and \(\rho_{13}\).

From the above consideration, it can be seen that the quantum correlation such as GQD and TE can be either decreased or increased by the change of \(b,\,\,D,\,\,J\) and \(J_{z}\), and this shows that GQD and TE are controllable. This controllability of the quantum correlation shows that the quantum system can be translated from one state to another state by the change of the different parameters such as the magnetic field, DM interaction, exchange interaction. On one hand, QC such as TE and GQD do not depend on \(J_{z}\) in our model.

3.2 Robustness of the quantum correlation

In the previous subsection, I showed the robustness of QC against the various parameters. Here, I consider the robustness of TE and GQD against the increasing \(T\) for the total region of \(b\). In Fig. 4, I indicate the figures of TE and GQD vs. b for the different temperature \(T\) with \(\,J = 2,\,\,J_{z} = 1,\,\,D = 0,\,\,B = 0\). From Fig. 4, it can be seen that the values of GQD and TE decrease monotonously with increasing the temperature \(T\). Also, the thermal entanglement of \(\rho_{12}\) keeps zero all when the temperature \(T = 3.5\), but the thermal entanglement of \(\rho_{13}\) keeps zero all when the temperature \(T = 4.2\).

Fig. 4
figure 4

\(C_{12} ,\,\,D_{2} \left( {\rho_{12} } \right)\) and \(C_{13} ,\,\,D_{2} \left( {\rho_{13} } \right)\) vs.\(b\) for the different \(T\), where the parameters are selected to be \(\,J = 2,\,\,J_{z} = 1,\,\,D = 0,\,\,B = 0\)

Full size image

Therefore, we can see that the entanglement between the first qubit and the third(end) qubit is a little more robust for the temperature than the entanglement between the first qubit and second qubit. As one can see from Fig. 4, TE is greater than GQD for the low temperature, but GQD is greater than TE for the high temperature. Also, GQD keeps finite value at the high temperature that TE keeps zero all. Thus, GQD is more robust against temperature than TE. Also, for any \(T\), all \(C_{12} - b,\,\,C_{13} - b,\,\,D_{2} \left( {\rho_{12} } \right) - b,\,\,\,D_{2} \left( {\rho_{13} } \right) - b\) curves are symmetric for the inversion of nonuniform part of magnetic field.

4 Conclusions

In this paper, I have investigated the robustness and controllability of GQD and TE between two qubits(first qubit and second qubit, first qubit and third(end) qubit) in the three-qubit Heisenberg XXZ Hamiltonian model with the nonuniform magnetic field and DM interaction. The results obtained here show that GQD and TE are controllable and this controllability reflect the state transition. In our model, TE and GQD depend on the magnetic field, DM interaction \(D\) and exchange interaction \(J\). But the exchange interaction \(J_{z}\) does not affect the quantum correlation(TE and GQD). Also, for any \(J,\,\,D\) and \(T\), the quantum correlation such as TE and GQD always indicates exact symmetry for the inversion of \(b\). But for the inversion of \(b\), TE and GQD do not indicate symmetry for any \(J\) unlike reference [16] that consider QC of the two-qubit system. On the other hand, strong DM interaction plays the essential role in the conservation of QC in our model. From this, one can know that the required quantum correlation (TE and GQD) can be obtained by the control of parameters \(B,\,\,b,\,\,J,\,\,D\). This may provide a rational proposal to manipulate QC in the qubit systems. On the other hand, in the three-qubit Heisenberg XXZ Hamiltonian TE between the first qubit and the third(end)qubit is a little more robust against temperature than TE between the nearest neighbor qubits. But \(C_{12}\) increases monotonously and go near large finite value for the increasing of \(J\) in the large absolute value of \(b\), \(C_{13}\) decreases monotonously and go near small finite value. Also, except in the range near by \(b = 0\), results shows the robustness of TE and GQD for the increasing \(J\) against the increasing strength of \(b\), and shows the robustness of TE and GQD against the increasing \(D\) through the total range of \(b\). GQD demonstrates robustness for the temperature that TE perfectly vanish, and therefore GQD is more robust than TE against temperature, like as our previous study [11] considering the robustness of TE and GQD against the temperature versus the change of impurity parameter in Heisenberg XXZ Hamiltonian.