1 Introduction

Since the emergence of quantum entanglement as a major advance in quantum mechanics [1, 2], scientific researchers have continued to exploit and benefit from this quantum resource, which paved the way for great progress toward applications of quantum computing and quantum information devices [3, 4]. The quantum entanglement between two particles means that they form a single system, and therefore, it becomes impossible to describe each particle individually. The most complete description of individual subsystems is called entangled state and encompasses all informations about these particles.

Quantum information theory is a discipline that seeks to characterize and quantify quantum correlations, especially entanglement and therefore apply it in the manipulation, processing and transfer of information [5].

In fact, entanglement represents just a special type of quantum correlations and there are other non-classical correlations which are broader and more general than entanglement [6, 7]. In this regard, introducing other appropriate criteria is essential to go beyond entanglement. Quantum discord is introduced to characterize quantum correlations, and it is defined as the difference between quantum mutual information and classical information [8, 9]. However, to obtain an analytical expression of quantum discord is only possible for certain classes of states, and the situation is rather complicated in the general state. Indeed, the difficulty in the computation of quantum discord is due to the optimization process on all generalized local measures [10]. To remedy this difficulty, an alternative solution is to consider the geometric measure of quantum discord which is defined as the minimum distance between the given state and the zero discord state [11]. Analytically, the computation of this geometric criterion requires a simple quantum entropy discord optimization process. Despite this advantage, the geometric quantum discord is not a good measure of the quantumness of correlations [12].

To overcome these difficulties, the local quantum uncertainty (LQU) has been proposed to detect non-classical correlations [13]. In addition, this reliable quantifier fulfills all the conditions required for a quantum correlation measurement and it is easily calculable, which is not the case for other measures. LQU is based on the skew information notion induced by Wigner and Yanase [14], and is also associated with what is called the quantum Fisher information and therefore constitutes a key tool in quantum metrology protocols [15,16,17,18].

However, the exploitation of quantum correlations is limited by the phenomenon of decoherence [19], which constitutes a major obstacle in the development of quantum information processing devices [20]. When the system is coupled to its environment, correlations are created between them and the quantum aspect of the system is destroyed; it’s decoherence [21]. This is the case for open quantum systems [22, 23]. There is another kind of decoherence called “intrinsic decoherence” which involves modifying the Schrödinger equation to break the coherence of the quantum system [24]. Indeed, it was Milburn who worked on this kind of decoherence [25]. He considered that during sufficiently short time steps, the system does not evolve continuously under the unitary evolution, but instead changes in a stochastic sequence of identical unitary transformations without the usual energy dissipation associated with normal decay entirely dependent on phase [25]. This approximation is useful because it is valid for many relevant physical situations and is of great interest in the field of quantum information.

Solid state systems, such as the Heisenberg spin chains, have been the subject of intensive study in recent years and are considered to be natural candidates for the exploitation of quantum resources [26,27,28].

In this context, we study the dynamics under intrinsic decoherence of quantum correlations quantified by the concurrence (C) and LQU as a measure of entanglement and discord-like, respectively, for a two-qubit XXZ Heisenberg spin chain subjected to an inhomogeneous external magnetic field b along z-axis with Dzyaloshinskii–Moriya (DM) interaction along z-axis \(D_z\) which results from the spin-orbit coupling [29, 30]. Many recent works have shown the positive impact of the DM interaction on thermal quantum correlations [27, 31,32,33,34,35]. However, the DM interaction has a negative impact when the intrinsic decoherence is taken into account, and therefore results in the destruction of the quantum correlations of the system [36,37,38,39]. Thus, the authors in Ref. [40] have shown that the inhomogeneous magnetic field can reduce the effect of intrinsic decoherence. Our contribution is to compare the behavior of entanglement and that of LQU in three initial quantum states under intrinsic decoherence in presence of the external nonuniform magnetic field and the DM interaction. This paper is structured as follows. In Sect. 2, we give the Hamiltonian of the system under study and calculate the density matrix of the system as a function of time. We also give the analytical expressions of the quantifiers used in this work. In Sect. 3, we present and discuss the results we obtained for the different initial quantum states considered. Finally, we end the document with conclusions.

2 Theoretical model

2.1 The Heisenberg model with Dzyaloshinskii–Moriya interaction

At the onset, we present the Hamiltonian of two-qubit (spin-1/2) with Dzyaloshinskii–Moriya interaction according to z-axis (\(D_z\)) given by [27] :

$$\begin{aligned} H=-J_{x}\sigma _{1}^{x}\sigma _{2}^{x}-J_{y}\sigma _{1}^{y}\sigma _{2}^{y}-J_{z}\sigma _{1}^{z}\sigma _{2}^{z}-\frac{1}{2}D_{z}(\sigma _{1}^{x}\sigma _{2}^{y}-\sigma _{1}^{y}\sigma _{2}^{x})-b_1\sigma _{1}^{z}-b_2 \sigma _{2}^{z}, \end{aligned}$$
(1)

where \(J_i(i=x,y,z)\) denote the coupling constants; \( \sigma _j^x, \sigma _j^y \) and \(\sigma _j^z \) are the Pauli operators, \(b_j\) is the nonuniform external magnetic field acting on the qubit \(j(j=1,2)\) according to the z-axis. For simplicity, we assume that \( J_x = J_y\ne J_z \) and \(b_1 = b_2 = b \), which reduces the XYZ Heisenberg model above to the XXZ model. The eingenvalues and the corresponding eigenstates of the Hamiltonian are given by :

$$\begin{aligned} E_1&= -J_z + 2b, \qquad |\varphi _1\rangle = \cos \left( \dfrac{\theta _1}{2}\right) |00\rangle +\sin \left( \dfrac{\theta _1}{2}\right) |11\rangle ; \end{aligned}$$
(2)
$$\begin{aligned} E_2&= -J_z - 2b, \qquad |\varphi _2\rangle = \sin \left( \dfrac{\theta _1}{2}\right) |00\rangle -\cos \left( \dfrac{\theta _1}{2}\right) |11\rangle , \end{aligned}$$
(3)
$$\begin{aligned} E_3&= J_z + \chi , \qquad |\varphi _3\rangle = \cos \left( \dfrac{\theta _2}{2}\right) |01\rangle +e^{-i\varphi } \sin \left( \dfrac{\theta _2}{2}\right) |10\rangle , \end{aligned}$$
(4)
$$\begin{aligned} E_4&= J_z - \chi , \qquad |\varphi _4\rangle = \sin \left( \dfrac{\theta _2}{2}\right) |01\rangle -e^{-i\varphi } \cos \left( \dfrac{\theta _2}{2}\right) |10\rangle , \end{aligned}$$
(5)

where \( \theta _1 = k\pi / k \in \mathbb {Z}, \qquad \tan \left( \theta _2 \right) = \frac{\chi }{2 b}, \quad \tan \left( \varphi \right) = \frac{D_z}{2 J_x} \) and \( \chi = \sqrt{D_z^2 + 4 J_x^2} \).

2.2 Intrinsic decoherence

By taking into account the effect of intrinsic decoherence, the time evolution of the density matrix of the system is given by Milburn equation [25] :

$$\begin{aligned} \rho (t) = \sum \limits _{\begin{array}{c} m,n \end{array}}\exp \left[ -\dfrac{\gamma t}{2}(E_m - E_n)^2 - i(E_m - E_n)t \right] \times \langle \varphi _m |\rho (0)|\varphi _n\rangle |\varphi _m\rangle \langle \varphi _n| \end{aligned}$$
(6)

where \( E_{m,n} \) and \(\varphi _{m,n} \) are, respectively, the eigenvalues and the eigenstates of the Hamiltonian of the system, respectively, \( \gamma \) is the intrinsic decoherence rate which corresponds to \(\gamma ^{-1}\) in Milburn’s paper.

Then, we assume that the system is initially prepared in the mixed state:

$$\begin{aligned} \rho (0) = r|\psi _p\rangle \langle \psi _p| + \dfrac{1-r}{4} \mathbb {I}_1 \otimes \mathbb {I}_2 \end{aligned}$$
(7)

where \( |\psi _p\rangle =\sqrt{p}|01\rangle + \sqrt{1 - p}|10\rangle \) is a pure state with p is the degree of entanglement and \( 0 < r \leqslant 1 \) being the purity of the initial state. In the standard basis \(\lbrace |00\rangle ,|01\rangle ,|10\rangle ,|11\rangle \rbrace , \rho (0)\) can be written as :

$$\begin{aligned} \rho (0)=\left( \begin{array}{cccc} \rho _{11}(0) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \rho _{22}(0) &{}\quad \rho _{23}(0) &{}\quad 0 \\ 0 &{}\quad \rho _{32}(0) &{}\quad \rho _{33}(0) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \rho _{44}(0) \\ \end{array} \right) \end{aligned}$$
(8)

The diagonal elements of \(\rho (0)\) are :

$$\begin{aligned} \rho _{11}(0)= & {} \rho _{44}(0) = \dfrac{1 - r }{4}; \\ \rho _{22}(0)= & {} rp + \dfrac{1 - r }{4};\\ \rho _{33}(0)= & {} r(1-p) + \dfrac{1 - r }{4}; \end{aligned}$$

and the off-diagonal elements are :

$$\begin{aligned} \rho _{23}(0) = \rho _{32}(0) = r\sqrt{p(1-p)} . \end{aligned}$$

From Eq. (6), the time evolution of \(\rho (t)\) in the standard basis \(\lbrace |00\rangle ,|01\rangle ,|10\rangle ,|11\rangle \rbrace \) can be expressed as :

$$\begin{aligned} \rho (t)=\left( \begin{array}{cccc} \rho _{11}(t) &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad \rho _{22}(t) &{}\quad \rho _{23}(t) &{}\quad 0 \\ 0 &{}\quad \rho _{32}(t) &{}\quad \rho _{33}(t) &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad \rho _{44}(t) \\ \end{array} \right) \end{aligned}$$
(9)

with the diagonal elements of \(\rho (t)\) being:

$$\begin{aligned} \rho _{11}(t)= & {} \rho _{11}(0) = \rho _{44}(t)=\rho _{44}(0) = \dfrac{1-r}{4};\\ \rho _{22}(t)= & {} e^{-2\gamma \chi ^2 t} \dfrac{\sin \theta _2}{2}\\&\left[ (\rho _{22}(0)-\rho _{33}(0)) \sin (\theta _2)\cos (2\chi t)+2\rho _{23}(0)\right. \\&\left. \left( \sin ^2(\frac{\theta _2}{2})\cos (\varphi -2\chi t) - \cos ^2(\frac{\theta _2}{2})\cos (\varphi +2\chi t)\right) \right] \\&\quad + \rho _{22}(0)\left( 1 - \dfrac{\sin ^2\theta _2}{2} \right) + \rho _{33}(0)\dfrac{\sin ^2(\theta _2)}{2} + \rho _{23}(0)\dfrac{\sin (2\theta _2)}{2}\cos \varphi ;\\ \rho _{33}(t)= & {} -e^{-2\gamma \chi ^2 t} \dfrac{\sin \theta _2}{2}\\&\left[ \left( \rho _{22}(0)-\rho _{33}(0)\right) \sin (\theta _2)\cos (2\chi t)+2\rho _{23}(0)\right. \\&\left. \left( \sin ^2(\frac{\theta _2}{2})\cos (\varphi -2\chi t) - \cos ^2(\frac{\theta _2}{2})\cos (\varphi +2\chi t)\right) \right] \\&\quad + \rho _{33}(0)\left( 1 - \dfrac{\sin ^2\theta _2}{2} \right) + \rho _{22}(0)\dfrac{\sin ^2\theta _2}{2} + \rho _{23}(0)\dfrac{\sin (2\theta _2)}{2}\cos \varphi ; \end{aligned}$$

and the off-diagonal elements are :

$$\begin{aligned} \rho _{23}(t)= & {} \rho _{32}^*(t) = e^{-2\gamma \chi ^2 t} e^{i \varphi }\dfrac{\sin \theta _2}{2}\left[ (\rho _{22}(0)-\rho _{33}(0))\left( e^{2i \chi t}\sin ^2(\frac{\theta _2}{2})- e^{-2i \chi t}\cos ^2(\frac{\theta _2}{2})\right) \right. \\&\quad \left. +\rho _{23}(0)\left( e^{-i(\varphi -2\chi t)}\sin ^4(\frac{\theta _2}{2})+e^{-i(\varphi +2\chi t)}\cos ^4(\frac{\theta _2}{2})-\frac{\sin ^2\theta _2}{2}e^{i\varphi }\cos (2\chi t)\right) \right] \\&\quad + e^{i\varphi }\dfrac{\sin (2\theta _2)}{4}\left( \rho _{22}(0)-\rho _{33}(0)\right) +e^{i\varphi }\rho _{23}(0)\sin ^2\theta _2 \cos \varphi . \end{aligned}$$

2.3 Concurrence (C)

The concurrence C is used to quantify the entanglement of any mixed state of an arbitrary bipartite system. Thus, the concurrence corresponding to the density matrix \(\rho \) of Eq. (9) is defined by Wooters formula [41]:

$$\begin{aligned} C (\rho ) = \max \lbrace 0, 2\lambda _{\max } - \sum \limits _{\begin{array}{c} i=1 \end{array}}^{4} \lambda _i\rbrace \end{aligned}$$
(10)

where \(\lambda _i (i=1,2,3,4)\) are the square roots of the eigenvalues of the matrix \( R = \rho (\sigma _1^y \otimes \sigma _2^y) \rho ^*(\sigma _1^y \otimes \sigma _2^y) \). \( \rho \) is the density matrix of the bipartite system; it can be either pure or mixed. \(\rho ^*\) denotes the complex conjugation of \(\rho \) in the standard basis. C = 0 corresponds to unentangled state and C = 1 to a maximally entangled state. The time dependence of the concurrence for the density matrix of Eq. (9) is described as :

$$\begin{aligned} C (t) = 2 \ max \, \lbrace 0, |\rho _{23}(t)|-\rho _{11}(t)\rbrace \end{aligned}$$
(11)

2.4 Local quantum uncertainty (LQU)

The local quantum uncertainty quantifies the minimal quantum uncertainty in a quantum state due to a measurement of a local observable [13]. To recall, the local quantum uncertainty for a bipartite quantum state \(\rho \) is defined by:

$$\begin{aligned} LQU (\rho ) = \mathscr {U}(\rho ) \equiv \min _{K_1} \mathscr {I}(\rho , K_1 \otimes \mathbb {I}_2), \end{aligned}$$
(12)

where \(K_1\) is some local observable acting on the qubit 1, \(\mathbb {I}_2\) is the identity operator and

$$\begin{aligned} \mathscr {I}(\rho , K_1 \otimes \mathbb {I}_2)=-\frac{1}{2}\mathrm{Tr}([\sqrt{\rho }, K_1 \otimes \mathbb {I}_2]^{2}) \end{aligned}$$
(13)

is the skew information [14, 42] which represents the non-commutativity between the state and the observable \(K_1\). The analytical evaluation of the local quantum uncertainty requires a minimization procedure on the set of all observables acting on part 1 [27]. Therefore, the expression of the local quantum uncertainty for qubits (\(\frac{1}{2}\)-spin particles) is [13]:

$$\begin{aligned} LQU(\rho ) = 1 - \mathrm{max}\{ \mu _1, \mu _2, \mu _3\}, \end{aligned}$$
(14)

where \(\mu _1, \mu _2\) and \(\mu _3\) are the eigenvalues of the \(3\times 3\) matrix W defined by its matrix elements:

$$\begin{aligned} \omega _{ij} \equiv \mathrm{Tr}\{\sqrt{\rho }(\sigma _{i}\otimes \mathbb {I}_2)\sqrt{\rho }(\sigma _{j}\otimes \mathbb {I}_2)\}, \end{aligned}$$
(15)

with \(i,j = 1, 2, 3\) and \(\sigma _i\) are the usual Pauli matrices.

In this case, it is easy to check that the matrix W (Eq. 15) is diagonal. Hence, its eigenvalues are simply the diagonal elements \( \omega _{ii}\) (\( i=1,2,3\)) which are expressed as a function of time by :

$$\begin{aligned} \omega _{11}(t)&= \omega _{22}(t) = \sqrt{\frac{1-r^2}{2}+2(1-r)\sqrt{\rho _{22}(t)\left( \frac{1+r}{2}-\rho _{22}(t)\right) -|\rho _{23}(t)|^2}} . \end{aligned}$$
(16)
$$\begin{aligned} \omega _{33}(t)&= \dfrac{3-r}{4} + \sqrt{\rho _{22}(t)\left( \frac{1+r}{2}-\rho _{22}(t)\right) -|\rho _{23}(t)|^2} \nonumber \\&\quad -\dfrac{2\left[ \mathfrak {Re}^2(\rho _{32}(t)) - \mathfrak {Im}^2(\rho _{32}(t))\right] +\frac{1}{8}\left[ 4\rho _{22}(t)-(r+1)\right] ^2}{\frac{1+r}{2}+2\sqrt{\rho _{22}(t)\left( \frac{1+r}{2}-\rho _{22}(t)\right) -|\rho _{23}(t)|^2}}. \end{aligned}$$
(17)

Therefore, the time dependence of the LQU for the density matrix \(\rho \) of Eq. (9) is then given by :

$$\begin{aligned} \mathrm{LQU}(t) = 1 - \mathrm{max}\{ \omega _{11}(t), \omega _{33}(t)\}, \end{aligned}$$
(18)

Subsequently, we must consider the situations where \(\omega _{\max }\) is \(\omega _{11}\) or \(\omega _{33}\) which is analytically complicated. This question will be examined numerically in the case of the coupling constants \(J_x=J_y\) and an intrinsic decoherence rate \(\gamma \) in the presence of external nonuniform magnetic field b and taking into account the effect of DM interaction (\(D_z\)) on the quantum correlations.

3 Results and discussion

In this section, we will present our results concerning the dynamics of correlations, namely concurrence (C) and LQU, when the system is initially prepared in the mixed state, in the Werner state and in the pure state.

3.1 The system is initially in the mixed state

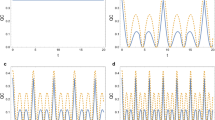
Figure 1a shows a characteristic showing aspects of the concurrence (C) and LQU as a function of the degree of entanglement p for a fixed value of r (\(r = 0.5\)) at \(t = 0\). We find that the quantum correlations increase as a function of p until the value \(p = 1/2\); then after it decreases in the same way that they have increased exhibiting symmetry in the behavior; therefore, it is sufficient to work in the range of \(p\in [0,1/2]\). The value \(p=1/2\) corresponds to the maximum of the quantum correlations in the initial system known as the Werner state which will be the object of study in the following subsection. Thus, it is quite clear that LQU prevails over C for low values of the parameter p, and as p approaches the value 1/2, the entanglement becomes strong compared to LQU. Indeed, the state \(|\psi _p\rangle \) of Eq. (7) becomes the Bell state for the value \(p=1/2\) favoring a maximum entanglement for the initial mixed state \(\rho (0)\) (Eq. 7) with respect to \(r=0.5\).

For the next figures, we show the effect of the external magnetic field (b) and of the DM interaction (\( D_z \)) on the evolution of quantum correlations (concurrence C and LQU) as a function of time for different values of the model parameters (r, p, \(\gamma \) and \(J_x=J_y\)). From Fig. 1b, when the parameters r and p are set to \(r = 0.5\) and \(p = 0.4\), respectively, and in the absence of an external magnetic field and DM interaction (\(b=0\) and \(D_z=0 \)), it is clear that the correlations are stable for a large time limit with some slow oscillations of the entanglement in a very short time region due to the rate of intrinsic decoherence (\(\gamma = 0.02\)). By introducing DM interaction (\( D_z = 0.6 \)) and in the absence of the external magnetic field b (Fig. 1c), oscillations appear for both C and LQU. Note that the time variations in LQU show more oscillations with large amplitudes, which shows that DM interaction can certainly make the effect of intrinsic decoherence more effective for LQU than C. It is also noted that correlations stabilize, at steady-state values lower than in the case where the DM interaction is zero.

When the external magnetic field becomes nonzero (Fig. 1d where \( b = 0.3 \)), the correlations are strongly affected, so that the entanglement sudden death (ESD) phenomenon appears in several time regions. That is to say, the presence of the external magnetic field b can completely destroy the correlations in certain time regions. Also, we notice in Fig. 1d that LQU is more resistant to sudden death than C. Therefore, the external magnetic field can strongly stimulate the effect of intrinsic decoherence of correlations (especially entanglement). However, Fig. 1e shows that increasing the intrinsic decoherence rate (\(\gamma =0.65\)) can prevent the ESD phenomenon from occurring and accelerate the stabilization of correlations at the same steady-states values.

Figure 1f very significantly shows the destructive effect of the external magnetic field b on the correlations in the system. At low values of b, entanglement is greater than LQU. In contrast, when b increases, entanglement collapses very quickly relative to LQU. This implies that LQU is more resistant to the effect of the magnetic field than C.

Figure 1g demonstrates the effect of the DM interaction on entanglement and on LQU. We find that, for small values of \(D_z\), entanglement appears and then suddenly disappears; this is what we called entanglement sudden revival and collapse phenomenon, while LQU keeps a larger nonzero value, but as \(D_z\) increases, LQU decreases oscillating to stabilize at a value very close to zero. Therefore, the DM interaction, even if it destroys entanglement, can be beneficial in preserving correlations in the system.

Fig. 1
figure 1

Plots of C and LQU versus p at time t = 0 and \(r=0.5\) (a) , versus time t (b–e), versus b (f) and versus \(D_z\) (g). Except (a), In all plots we set \(p = 0.4\), \(r = 0.5\) and \(J_x=J_y=0.5\): b \(D_z = 0, b = 0\) and \(\gamma = 0.02\); c \(D_z = 0.6\), \(b = 0\) and \(\gamma = 0.02\); d \(D_z = 0.6\), \(b = 0.3\) and \(\gamma = 0.02\); e \(D_z = 0.6\), \(b = 0.3\) and \(\gamma = 0.65\). f \(D_z = 0.5\), \(\gamma = 0.02\) and \(t=30\). g \(b = 0.5\), \(\gamma = 0.02\) and \(t=30\)

Full size image

3.2 The system is initially in the Werner state

By fixing the degree of entanglement at the value \(p = \dfrac{1}{2}\) in Eq. (7), the system becomes initially in the Werner state [43] :

$$\begin{aligned} \rho (0) = r|\psi \rangle \langle \psi | + \dfrac{1-r}{4} \mathbb {I}_1 \otimes \mathbb {I}_2 \end{aligned}$$
(19)

where : \(|\psi \rangle = \dfrac{1}{\sqrt{2}}(|01\rangle + |10\rangle )\) is the Bell state.

In this case, it emerges from Fig. 2a that the system is initially entangled for \(1/3 < r \le 1\), otherwise it is separable [44]. We notice that even if the system is separable (\(C = 0\) for \(0 \le r \le 1/3\)), the LQU remains nonzero. Therefore, the absence of entanglement in the system does not necessarily mean the absence of all kinds of correlations.

According to Fig. 2b, C and LQU keep stable values, i.e., the system is immune to intrinsic decoherence. When we introduce the DM interaction (\(D_z = 0.6\)) (Fig. 2c), the effect of intrinsic decoherence is clearly shown by the oscillatory behavior of the correlations as a function of time (more oscillations with large amplitudes for LQU). Once again, the effect of intrinsic decoherence is sensitive to the DM interaction.

As depicted in Fig. 2d, the presence of the magnetic field (\(b = 0.3\)) tends to destroys the correlations in the system, in particular the entanglement that undergoes the ESD phenomenon in certain time regions. Thus, the magnetic field strongly stimulates the effect of intrinsic decoherence. However, even if it takes very low values, LQU is more resistant to this effect and does not cancel out. In addition, by comparing the ESD phenomenon presented when the initial state is mixed (Fig. 1d), we find that time regions of the ESD phenomenon are shortened in this case. Thus, the correlations end at steady-state values larger than those presented in Fig. 1d. From Fig. 2e and as in the case of the mixed initial state (Fig. 1e), the ESD phenomenon can be prevented from occurring by increasing \(\gamma \) and at early time lead to the same steady-state values of the correlations depicted in Fig. 2d.

Figure 2f shows that the magnetic field b has a destructive effect on the quantum correlations. We notice that as b increases, entanglement collapses faster than LQU which decreases very slowly. This indicates that the entanglement is very sensitive to the magnetic field than LQU.

We present in Fig. 2g the effect of the DM interaction on the entanglement sudden revival and collapse phenomenon which manifests itself in increasingly weak peaks as \(D_z\) increases. Note also that LQU also exhibits peaks which decrease as \(D_z\) increases. Unlike entanglement, LQU remains nonzero and is the most resistant to the effect of the DM interaction. Therefore, one can make the DM interaction cost-effective to preserve correlations in the system.

Fig. 2
figure 2

Plots of C and LQU versus r at time t = 0 (a), versus t (b–e), versus b (f] and versus \(D_z\) (g). Except (a), in all plots we set \(p=0.5\), \(r=0.5\) and \(J_x=J_y=0.5\) : b \(D_z = 0, b = 0\) and \(\gamma = 0.02\); c \( D_z = 0.6\), \(b = 0\) and \(\gamma = 0.02\); d \( D_z = 0.6\), \(b = 0.3\) and \(\gamma = 0.02\); e \(D_z = 0.6\), \(b = 0.3\) and \(\gamma = 0.25\). f \(D_z=0.5\), \(\gamma = 0.02\) and \(t=30\). g \(b = 0.5\), \(\gamma = 0.02\) and \(t=30\)

Full size image

3.3 The system is initially in the pure state

In this subsection, we assume that the purity of the initial state is \(r = 1\). Thus, the state (Eq. 7) turns out to be the pure state :

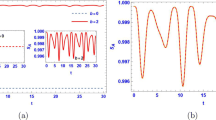
$$\begin{aligned} \rho (0) = |\psi _p\rangle \langle \psi _p|. \end{aligned}$$
(20)

In Fig. 3a, we plot the concurrence (C) and LQU as a function of the degree of entanglement p when the system is initially in the pure state (Eq. 20). The figure shows that when \(p = 0\), we have \(C = 0\) and \(LQU = 0\), i.e., the system is disentangled with absence of correlations. In this sense, speaking “disentangled” means also “uncorrelated” in terms of entanglement and LQU. Then, when the parameter p increases, the system evolves toward a maximally entangled state and presents more correlations. We notice that in all the interval \(0< p < 0.5\), the values of C remain higher than those of LQU.

Figure 3b shows the evolution over time of C and LQU, when the system is initially separable \(p = 0\) \((i.e., \rho (0) = |10\rangle \langle 10|\)) and in the absence of the external magnetic field b and the DM interaction. We note that the system generates strongly the entanglement by series of entanglement revival and collapse phenomenon over the time t; this entanglement disappears completely when t becomes very large. Under the same conditions, we find that LQU remains zero. However, if the DM interaction is introduced \((Dz = 0.8)\) (see Fig. 3c), we record a reaction from LQU presented by the same behavior as the concurrence C, but with extremely weak maxima and which disappear completely at early time t. Therefore, the DM interaction supports the appearance of LQU in the system. Moreover, we notice that the entanglement disappears in a shorter time than if \(D_z = 0\).

Figure 3d illustrates the effect of the external magnetic field b on time evolution of the concurrence (C) and the LQU in the absence of DM interaction (\(D_z=0\)). We note that the magnetic field clearly improves correlations (C and LQU) and saves them from complete destruction. It is also very clear that these correlations ultimately lead to very interesting steady-state values. Therefore, the external magnetic field b can make the system strongly correlated even though it was initially uncorrelated. Figure 3e shows the variations of C and LQU as a function of the external magnetic field b in the absence of DM interaction (\(D_z = 0\)). By increasing the intrinsic decoherence rate \(\gamma \), we note that, when the system is initially disentangled (i.e., \( p = 0\)), the magnetic field can create entanglement (as in Ref [45]) and LQU in the system and preserve theme against intrinsic decoherence, in particular entanglement which is much stronger than LQU. On the other hand, if the system is initially entangled (\(p = 1/8\), Fig. 3f), the magnetic field b has a negative effect on the correlations which fall monotonically then undergo a revival when b increases (a similar result was reported by J.L. Guo and H.S. Song in Ref.[40]). Note that LQU remains very weak compared to C.

We show in Fig. 3g how C and LQU respond to the increase of \(D_z\) when the magnetic field is zero. We note a negative effect of the DM interaction on the evolution of entanglement in the system. In fact, the entanglement tends to decrease then to disappear by oscillating when \(D_z\) increases. On the other hand, introducing \(D_z\) into a constructive domain can generate and improve LQU in the system.

Fig. 3
figure 3

Plots of C and LQU versus p at time \(t = 0\) (a), versus t (b–d), versus b (e) and (f) and versus \(D_z\) (g). Except (a), in all plots we set \(J_x=J_y=0.5\) : b \(p = 0, D_z = 0, b = 0\) and \(\gamma = 0.02\); c \(p = 0, D_z = 0.8, b = 0\) and \(\gamma = 0.02\); d \(p = 0, D_z = 0\), \(b = 0.5\) and \(\gamma = 0.02\). e \(p = 0,D_z = 0\), \(\gamma = 0.1\) and \(t=30\). f \(p = 1/8\), \( D_z = 0\), \(\gamma = 0.1\) and \(t=30\). g \(p = 0, b = 0\), \(\gamma = 0.02\) and \(t=30\)

Full size image

4 Conclusion

To conclude, we considered a two-qubit XXZ Heisenberg spin chain model in the presence of an external magnetic field b along z-axis with the DM interaction along z-axis \(D_z\). We have studied the dynamics of quantum correlations captured by the concurrence C and the local quantum uncertainty LQU under intrinsic decoherence. We have shown that the DM interaction is relevant to the appearance of intrinsic decoherence effect which breaks the coherence of the quantum system. This effect is also strongly stimulated if an external magnetic field is present so as to highlight the ESD phenomenon in certain time regions, which can lead to the complete destruction of the entanglement, whereas LQU is more robust to induced sudden death by the magnetic field. However, the ESD phenomenon can be avoided by increasing the rate of intrinsic decoherence \(\gamma \). In fact, when the initial state of the system is the Werner state, the ESD phenomenon is present in much shorter time regions than if the system is initially mixed. This is due to the degree of entanglement which is increased in the Werner state; several studies support this argument [46, 47].

Furthermore, we have shown that when the system is initially in a mixed state or in a Werner state, we can take advantage of the DM interaction to improve and preserve the correlations despite the strong negative impact of the external magnetic field.

Our most important result is that if the system is initially uncorrelated (in terms of entanglement and LQU), it is easy to generate strong entanglement, but it is difficult to generate LQU between the two qubits. Nevertheless, the presence of the DM interaction favors the generation of LQU, but it weakly reduces entanglement. Therefore, it can be said that the DM interaction promotes LQU and not entanglement. As for the external magnetic field b, it plays a capital role in maintaining these correlations during the time for very remarkable steady-state values.