1 Introduction

Quantum resource theories offer a robust framework for studying a wide range of phenomena in quantum physics. They allow us to quantify desirable quantum effects, develop novel detection protocols, and identify processes that optimize their utilization across diverse applications [1]. Within this framework, resources like quantum coherence and quantum correlations play a crucial role in quantum technologies, such as quantum information processing, quantum computation, and quantum communication [2,3,4,5,6,7,8]. One of the most fascinating forms of quantum correlation is quantum entanglement. It is essential in numerous applications in quantum computing and nanotechnology, such as quantum teleportation [9, 10], quantum sensing [11], quantum dense coding [12], quantum cryptography [13, 14], and quantum secret sharing [15]. Furthermore, several measures have been proposed to quantify entanglement, including concurrence [16] and negativity [17]. The study of entanglement has been extensively investigated in numerous research projects [18,19,20,21,22]. To quantify quantum correlation, we can use some quantum estimators, such as uncertainty induced nonlocality (UIN) and quantum uncertainty (LQU). These estimators provide a more comprehensive understanding of the quantum correlations in many systems [23,24,25,26,27].

Additionally, quantum coherence, which arises from the principle of superposition of quantum states, is a crucial quantum feature to manage and preserve. It plays a pivotal role in various fields such as quantum information processing [28], quantum thermodynamics [29], and quantum metrology. In these fields, quantum coherence has been shown to be essential for surpassing classical limitations in measurement accuracy [30]. Moreover, quantum coherence has garnered increasing attention for its involvement in biological processes, including photosynthesis [31] and bird navigation [32]. Various quantifiers, such as the \(\ell _1\) norm of coherence, the relative entropy of coherence [33], and intrinsic randomness [34], have been used to characterize quantum coherence in quantum systems.

In recent years, the study of the quantum characteristics of low-dimensional spin systems has received considerable attention in condensed matter physics [35]. These systems are considered promising options for quantum communication and information processing. In particular, the Ising-Heisenberg diamond chain is a theoretical model used to investigate the behavior of interacting spins and capture the characteristics of real magnetic materials like azurite (\(Cu_3(CO_3)_2(OH)_2\)) [36, 37]. Azurite can be considered one of the first experimental realizations of the 1D distorted diamond chain model. To study the Ising-Heisenberg diamond chain model, various mathematical methods can be used, such as the transfer matrix technique [38] and the cluster-variation approach [39]. Our research is motivated by recent studies in this field, particularly the analysis of thermal entanglement properties of both the Ising-\({\textbf {XXZ}}\) [40] and the Ising-\({\textbf {XYZ}}\) models on a diamond chain [41], the quantum correlations for the Ising-\({\textbf {XYZ}}\) diamond chain structure using quantum discord [42] and quantum Fisher information [43]. In addition, quantum teleportation via a pair of Ising-XXZ diamond chains [44,45,46] has also been highlighted in recent reports. The Ising-XYZ diamond chains serve as ideal systems to explore the effects of anisotropic spin interactions and external magnetic fields on quantum properties. Therefore, it is essential to explore quantum correlations and quantum coherence within the Ising-\({\textbf {XYZ}}\) model of a diamond chain.

The main goal of this research is to study how thermal variation affects skew information correlation and quantum coherence in the Ising-\({\textbf {XYZ}}\) diamond chain. We will examine how thermal noise, the anisotropy parameter, and the magnetic field affect quantum coherence and skew information correlations. To achieve this, we will employ two measures to assess skew information correlations in the system: uncertainty-induced nonlocality (UIN) to analyze non-classical correlations, and local quantum uncertainty (LQU) to assess uncertainty in a quantum state. Additionally, we will quantify quantum coherence using the \(\ell _1\) norm.

The document is structured as follows: Section 2 presents the explicit formulas for the three quantifiers used to describe skew information correlations and quantum coherence. In Sect. 3, we will introduce the Ising-\({\textbf {XYZ}}\) diamond chain and derive the reduced density operator using the transfer matrix approach. Section 4 discusses our results, providing an overview of the thermal dynamics of UIN, LQU, and the \(C_{\ell _1}\), and analyzing the dynamics of these three estimators. Finally, our concluding remarks can be found in Sect. 5.

2 Measures of quantum correlation and coherence

This section presents the explicit formulas for the three quantifiers used to describe skew information correlations and quantum coherence within the context of the Ising-\({\textbf {XYZ}}\) diamond chain subjected to an external magnetic field.

2.1 The \(\ell _1\) norm of coherence

The \(\ell _1\) norm of coherence introduced by Baumgratz et al. [33] is a commonly used coherence measure. It is defined as follows

$$\begin{aligned} \mathcal {C}_{\ell _{1}}(\varrho )= \min _{\eta \in \mathfrak {I}} |\varrho - \eta |, \end{aligned}$$
(1)

here, \(\mathfrak {I}\) represents a set of incoherent states, i.e., states with vanished coherence (\(\mathcal {C}_{\ell _{1}}(\eta )=0\)). Analytically, the \(\ell _1\) norm of coherence related to a quantum state \(\varrho\) can be explicitly derived in terms of the magnitudes of its non-diagonal entries (\(\varrho _{ij}\)) as

$$\begin{aligned} \mathcal {C}_{\ell _{1}}(\varrho ) = \sum _{i\ne j} |\varrho _{ij}|. \end{aligned}$$
(2)

2.2 Local quantum uncertainty

To define local quantum uncertainty (LQU), we first need to take a look at the Wigner-Yanase skew information (WYSI). This measure is mainly proposed to quantify the information content in a quantum bipartite state \(\varrho\). It is mathematically defined by [47]

$$\begin{aligned} \mathcal {I}(\varrho , K_A \otimes \mathbb {I}_B) = -\frac{1}{2}\textrm{Tr}\big ([\varrho ^{\frac{1}{2}}, K_A \otimes \mathbb {I}_B]^{2}\big ). \end{aligned}$$
(3)

Where \(K_A \otimes \mathbb {I}_B\) stands for the tensor product of the local observable \(K_A\) acting on subsystem A and the identity operator \(\mathbb {I}_B\) acting on subsystem B. The LQU related to the bipartite density matrix \(\varrho\), with respect to subsystem A, is defined as [48]

$$\begin{aligned} \mathcal {U}(\varrho )= \min _{K_A} \mathcal {I}(\varrho , K_A \otimes \mathbb {I}_B). \end{aligned}$$
(4)

Where the minimization procedure in Eq. (4) was performed over all local observables acting on qubit A. LQU, as a reliable quantum correlation measure, provides a tool to quantify discord-type correlations without requiring a complex computation procedure. For a qubit-qubit system, the LQU for subsystem A can be computed by [48]

$$\begin{aligned} \mathcal{U}\left( {{\varrho }} \right) = 1 - \mu _{\max } \left( \mathcal {W}\right) , \end{aligned}$$
(5)

where \(\mu _{max} \left( \mathcal {W}\right)\) represents the maximal eigenvalues of the symmetric matrix \(\mathcal {W}_{3\times 3}\) with entries

$$\begin{aligned} \Big (\mathcal {W}\Big )_{ij} = \textrm{Tr} \Big ( \varrho ^{1/2} \left( \tau ^i_{A}\otimes \mathbb {I}_{2}\right) \varrho ^{1/2} \left( \tau ^j_{A}\otimes \mathbb {I}_{2}\right) \Big ), \end{aligned}$$
(6)

where \(\left\{ \tau ^{i(j)}_{A}\right\} ^{i(j)=x,y,z}\) are the Pauli operators acting on part A.

2.3 Uncertainty-induced non-locality

Uncertainty-induced non-locality (UIN) serves as a genuine quantifier for the non-local quantum correlations in multipartite systems [49]. It is considered an updated version of measurement-induced quantum non locality introduced by Luo [50]. For a two-party quantum state \(\varrho\), UIN, when party A is driven by a local commuting observable \(K'_A\), is expressed in terms of the WYSI (3) as [49]

$$\begin{aligned} \mathcal {U}_c (\varrho ) = \max _{K'_A}\mathcal {I}(\varrho , K'_A \otimes \mathbb {I}_B), \end{aligned}$$
(7)

where the maximization is performed over all local maximally informative commuting observables \(K'_A\). For any bipartite \((2\otimes d)\)-dimensional quantum state, UIN can be found as follows [50]

$$\begin{aligned} \mathcal {U}_c (\varrho )=\left\{ \begin{array}{cc} 1-\mu _{\min }(\mathcal {W}), &{} \quad \pmb {v}=\pmb {0} \\ 1-\frac{1}{|\pmb {v}|^{2}}\,\pmb {v}\, \mathcal {W}\,\pmb {v}^{T}, &{} \quad \pmb {v} \ne \pmb {0}. \end{array}\right. \end{aligned}$$
(8)

\(\pmb {v}^{T}\) is the transpose of the Bloch vector \(\pmb {v}\) with norm \(\left| \pmb {v} \right|\) and \(\mu _{\min }(\mathcal {W})\) denotes the minimal eigenvalue of matrix \(\mathcal {W}_{3\times 3}\) defined in Eq. (6).

Each quantum estimator utilized in this study is based on distinct formulas and serves a specific role in characterizing quantum correlation and coherence. LQU is derived from minimal skew information and is specifically designed to assess the quantum uncertainty in nonclassical states. In contrast, UIN is determined by the maximum skew information that can be obtained from bipartite quantum states and local observables. It serves as a measure of the degree of non-locality in the state under consideration. Lastly, the \(\ell _{1}\) norm coherence (\(\mathcal {C}_{\ell {1}}\)) quantifies quantum coherence and offers insights into the superposition among constituent quantum states.

3 Model and thermalization

In this study, we deal with a system of Ising-\({\textbf {XYZ}}\) diamond chain structure subjected to an external magnetic field. We will focus on key aspects such as the Hamiltonian of the system, the energy properties, and the thermal state derived using the transfer matrix approach (TMA). Notably, prior work has already explored pairwise thermal entanglement within this framework [41]. To ensure a comprehensive understanding, we begin with an overview of the Ising-\({\textbf {XYZ}}\) diamond chain structure. This structure is governed by the Ising-\({\textbf {XYZ}}\) Hamiltonian, originally formulated in Ref. [41]. This Hamiltonian encapsulates the system’s dynamics and serves as a foundational element for our investigation.

3.1 Ising-XYZ model

As previously mentioned, we focus on the characterization of nonclassical correlations captured by the WYSI-derived quantifiers and the coherence in the Ising-\({\textbf {XYZ}}\) diamond chain exposed to an external magnetic field. The considered chain is constituted from the interstitial Heisenberg spin along with the nodal Ising spins with different types of exchange interaction. An explanatory scheme is given in Fig. 1.

Fig. 1
figure 1

Schematic illustration of Ising-\({\textbf {XYZ}}\) chain on a diamond structure. Heisenberg spins are denoted by \(\varvec{\tau }_{i,k}\) and \(\varvec{\tau }_{j,k}\), while Ising spins are represented by \(\varvec{\nu _{k}}\)

Full size image

The collective Hamiltonian describing the investigated system subject to the interplay of a longitudinal external magnetic field \(b_0\), which influences the Heisenberg spins, and a magnetic field b affecting the Ising spins, can be written as the sum of the block Hamiltonian \(\mathcal {H}_{k}\) as [51]

$$\begin{aligned} \mathcal {H}=\sum _{k=1}^{N}\mathcal {H}_{k} , \end{aligned}$$
(9)

where the \(k^{\textrm{th}}\) block Hamiltonian is expressed by [41]

$$\begin{aligned} \mathcal {H}_k=&-J\left( 1+\alpha \right) \varvec{\tau }^{x}_{i,k}\varvec{\tau }^{x}_{j,k} -J\left( 1-\alpha \right) \varvec{\tau }^{y}_{i,k}\varvec{\tau }^{y}_{j,k}\nonumber \\&-\Gamma \varvec{\tau }^{z}_{i,k}\varvec{\tau }^{z}_{j,k}-J_1\left( \varvec{\tau }^{z}_{i,k}+\varvec{\tau }^{z}_{j,k}\right) \left( \nu _{k}+\nu _{k+1}\right) \nonumber \\&-b_{0}\left( \varvec{\tau }^{z}_{i,k}+\varvec{\tau }^{z}_{j,k}\right) -\frac{b}{2}\left( \nu _{k}+\nu _{k+1}\right) . \end{aligned}$$
(10)

In the context of a spin-\(\frac{1}{2}\) system, the operators \(\varvec{\tau }_{i(j)}\) denote the Pauli spin operators acting on the interstitial sites, where \(\alpha\) represents the xy-anisotropy parameter. The interactions within the system are governed by the coupling constants J and \(\Gamma\), which describe Heisenberg-type interactions between interstitial sites. Additionally, there are Ising-type exchanges denoted by \(J_1\), corresponding to interactions between interstitial and nodal sites.

It is crucial to note that throughout our analysis, we maintain the condition \(b_0=b\). In this context, the matrix form of the block Hamiltonian \(\mathcal {H}_k\), in the computational basis \(\{|00\rangle ,|01\rangle ,|10\rangle ,|11\rangle \}\), reads as

$$\begin{aligned} \mathcal {H}_k=\left[ \begin{array}{cccc} -\left( \frac{\Gamma }{4}+\frac{b\nu }{2}\right) -\left( J_1\nu +b\right) &{} 0 &{} 0 &{}-\frac{J\alpha }{2} \\ 0 &{} \left( \frac{\Gamma }{4}-\frac{b\nu }{2}\right) &{} -\frac{J}{2} &{} 0\\ 0 &{} -\frac{J}{2} &{} \left( \frac{\Gamma }{4}-\frac{b\nu }{2}\right) &{} 0\\ -\frac{J\alpha }{2} &{} 0 &{} 0 &{} -\left( \frac{\Gamma }{4}+\frac{b\nu }{2}\right) +\left( J_1\nu +b\right) \end{array}\right] . \end{aligned}$$
(11)

By diagonalizing the above block Hamiltonian (11), we find the following eigenvalues

$$\begin{aligned} \mathcal {E}_{1,4}=&-\left( \frac{\Gamma }{4}+\frac{b\nu }{2}\right) \pm \Delta \left( \nu \right) ,\nonumber \\ \mathcal {E}_{2,3}=&-\frac{b\nu }{2}+\frac{\Gamma }{4}\mp \frac{J}{2} \end{aligned}$$
(12)

with corresponding eigenvectors

$$\begin{aligned} |\varPhi _{1}\rangle =&a_{+}\left( d_{+} |00\rangle +|11\rangle \right) , \end{aligned}$$
(13)
$$\begin{aligned} |\varPhi _{2}\rangle =&\frac{1}{\sqrt{2}}\left( |01\rangle +|10\rangle \right) , \end{aligned}$$
(14)
$$\begin{aligned} |\varPhi _{3}\rangle =&\frac{1}{\sqrt{2}}\left( |01\rangle -|10\rangle \right) , \end{aligned}$$
(15)
$$\begin{aligned} |\varPhi _{4}\rangle =&a_{-}\left( d_{-} |00\rangle +|11\rangle \right) , \end{aligned}$$
(16)

where \(\nu =\left( \nu _{k}+\nu _{k+1}\right)\), \(\Delta \left( \nu \right) =\sqrt{\left( b+J_1 \nu \right) ^2 + \frac{1}{4} J^2\alpha ^2}\), \(a_{\pm }=\frac{1}{\sqrt{1+d_{\pm }^2}}\) and \(d_{\pm }=\frac{-J\alpha }{2b+2J_{1}\nu \pm 2\Delta \left( \nu \right) }\).

3.2 Transfer matrix approach

To study the skew information correlations and coherence within the Ising-\({\textbf {XYZ}}\) diamond chain, it is necessary to derive the reduced density operator using the TMA [40]. This procedure aims to specify the system density operator depending only on the Ising spin particles \(\nu _{k}\) and \(\nu _{k+1}\). It is defined in terms of the block Hamiltonian \(\mathcal {H}_k\), which pertains to the neighboring Ising spins \(\nu _{k}\) and \(\nu _{k+1}\), as

$$\begin{aligned} \rho \left( \nu _{k},\nu _{k+1} \right) = \sum _{l=1}^{4} e^{-\beta \mathcal {H}_k}. \end{aligned}$$
(17)

In this case, the quantity \(\beta =1/(k_BT)\), where \(k_B\) represents the Boltzmann constant and T represents the absolute temperature. For later convenience, we will set \(k_B=1\). By utilizing the spectral decomposition of the block Hamiltonian \(\mathcal {H}_k\) (Eq. (11)), we can rewrite the two-qubit operator (17) as

$$\begin{aligned} \rho \left( \nu _{k},\nu _{k+1} \right) = \sum _{l=1}^{4} e^{-\beta \mathcal {E}_l} \left| \varphi _l \right\rangle \left\langle \varphi _l \right| , \end{aligned}$$
(18)

\(\mathcal {E}_l\) denotes the energy associated with the \(k^{\textrm{th}}\) state and \(\left| \varphi _l \right\rangle\) represents the corresponding eigenvector. To calculate the Boltzmann factor, denoted as \(\mathbf {\Omega }\left( \nu _k,\nu _{k+1} \right)\), we trace over the operator of the two-qubits, resulting in

$$\begin{aligned} \Omega \left( \nu _k,\nu _{k+1} \right) =\textrm{Tr}\left[ \varrho (\nu _{k},\nu _{k+1}) \right] =\sum _{l=1}^{4}e^{-\beta \mathcal {E}_l }. \end{aligned}$$
(19)

In the context of our system, the canonical partition function \(\mathcal {Z}_N\) can be formulated by considering the associated Boltzmann factors

$$\begin{aligned} \mathcal {Z}_N=\sum _{\nu }\Omega \left( \nu _1,\nu _{2} \right) ....\Omega \left( \nu _N,\nu _{1} \right) . \end{aligned}$$
(20)

Using the transfer matrix, \(\mathcal {Z}_N\), for the spin-1/2 Ising-XYZ diamond chain, is described by \(\mathcal {Z}_N = \textrm{Tr}(T^N)\), here T is formulated as follows

$$\begin{aligned} T=\left( \begin{array}{cc} \Omega \left( \frac{1}{2},\frac{1}{2}\right) &{} \Omega \left( \frac{1}{2},-\frac{1}{2}\right) \\ \Omega \left( -\frac{1}{2},\frac{1}{2}\right) &{} \Omega \left( -\frac{1}{2},-\frac{1}{2}\right) . \end{array}\right) \end{aligned}$$
(21)

Here, the elements of the matrix depend solely on the collective spin state of the two Ising spins, given by

$$\begin{aligned} \Omega (\nu )=2e^{\frac{\beta \nu b}{2}}\left[ e^{-\frac{\beta \Gamma }{4}}\cosh \left( \frac{\beta J}{2}\right) +e^{\frac{\beta \Gamma }{4}}\cosh \left( \beta \Delta \left( \nu \right) \right) \right] \end{aligned}$$
(22)

with \(\Omega (1)\equiv \Omega \left( \frac{1}{2},\frac{1}{2}\right)\), \(\Omega (0)\equiv \Omega \left( \frac{1}{2},-\frac{1}{2}\right)\), and \(\Omega (-1)\equiv \Omega \left( -\frac{1}{2},-\frac{1}{2}\right)\).

The eigenvalues of T are then given by

$$\begin{aligned} \eta _{\pm } = \frac{\Omega (1) + \Omega (-1) \pm \mathcal {A}}{2} \end{aligned}$$
(23)

with \(\mathcal {A} = \sqrt{(\Omega (1)-\Omega (-1))^2+ 4 \Omega (0)^2}\). It follows that \(\mathcal {Z}_N\) (Eq. (20)) can be rewritten as a function of the quantities \(\eta _{\pm }\) as

$$\begin{aligned} \mathcal {Z}_N = \eta _{+}^N + \eta _{-}^N \end{aligned}$$
(24)

which simplifies to \(\mathcal {Z}_N = \eta _{+}^N\) in the thermodynamic limit constrained by \(N \rightarrow \infty\). It is worth mentioning to notice that the TMA as a substantial procedure has been widely used (for more details see the references [52,53,54,55,56]).

The reduced-density operator of the diamond structure can be given as follows

$$\begin{aligned} \varrho =\left( \begin{array}{cccccccc} \varrho _{11}&{}&{}0&{}&{}0&{}&{}\varrho _{14}\\ 0&{}&{}\varrho _{22}&{}&{}\varrho _{23}&{}&{}0\\ 0&{}&{}\varrho _{23}^*&{}&{}\varrho _{33}&{}&{}0\\ \varrho _{14}^*&{}&{}0&{}&{}0&{}&{}\varrho _{44}\\ \end{array} \right) , \end{aligned}$$
(25)

which has an X form. The elements of the density matrix (25) are specified in Appendix (A).

Now we have all the necessary ingredients to compute the quantum coherence \(\mathcal {C}_{\ell _{1}}(\varrho )\) as well as the WYSI derived quantifiers LQU (\(\mathcal {U}(\varrho )\)) and UIN (\(\mathcal {U}_c(\varrho )\)). By considering the definition (2) and the density matrix (25), the quantum coherence is given by

$$\begin{aligned} \begin{array}{cc} \begin{aligned} \mathcal {C}_{\ell _{1}}(\varrho )=&{}\frac{2 e^{\frac{ \Gamma }{4T}} \alpha J}{\eta _{+}\mathcal {A}} \Big (\dfrac{e^{\frac{ b}{2T}}(-\Omega (-1)+\mathcal {A}+\Omega (1) ) \sinh (\frac{\Delta (1)}{2 T})}{\Delta (1)}\\ &{}+\frac{e^{-\frac{ b}{2T}}(\Omega (-1)+\mathcal {A}-\Omega (1))\sinh (\frac{ \Delta (-1)}{2T})}{\Delta (-1)}\\ &{}+\frac{4\Omega (0)\sinh (\frac{\Delta (0)}{2T})}{ \Delta (0)}\Big ). \end{aligned} \end{array} \end{aligned}$$
(26)

To compute LQU and UIN, it is important to specify the proper value of the matrix \(\mathcal {W}\). Regarding the reduced state (25) and Eq. (6), one finds [59]

$$\begin{aligned}&\mu _1= \left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) \left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) \nonumber \\&\quad +\frac{1}{4}\left[ \frac{\left( \xi _{11}^2-\xi _{22}^2\right) +\left( \xi _{03}^2-\xi _{30}^2\right) }{\left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) \left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) }\right] , \end{aligned}$$
(27)
$$\begin{aligned}&\mu _2= \left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) \left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) \nonumber \\&\quad +\frac{1}{4}\left[ \frac{\left( \xi _{22}^2-\xi _{11}^2\right) +\left( \xi _{03}^2-\xi _{30}^2\right) }{\left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) \left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) }\right] , \end{aligned}$$
(28)
$$\begin{aligned}&\mu _3= \frac{1}{8}\left[ \frac{\left( \xi _{03}+\xi _{30}\right) ^2-\left( \xi _{11}-\xi _{22}\right) ^2}{\left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) ^2}+\frac{\left( \xi _{03}-\xi _{30}\right) ^2-\left( \xi _{11}+\xi _{22}\right) ^2}{\left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) ^2}\right] \nonumber \\&\quad +\frac{1}{2}\left[ \left( \sqrt{\zeta _{+}}+\sqrt{\zeta _{-}}\right) ^2+\left( \sqrt{\zeta _{+}^{\prime }}+\sqrt{\zeta _{-}^{\prime }}\right) ^2\right] \end{aligned}$$
(29)

where \(\zeta _{\pm }\) and \(\zeta _{\pm }^{\prime }\) are the eigenvalues value of the reduced density matrix \(\varrho\) given by

$$\begin{aligned} \begin{array}{cc} \begin{aligned} \zeta _{ \pm }=\frac{1}{2}\left( t_1 \pm \sqrt{t_1^2-4 d_1}\right) , \quad \quad \quad \zeta _{ \pm }^{\prime }=\frac{1}{2}\left( t_2 \pm \sqrt{t_2^2-4 d_2}\right) \end{aligned} \end{array} \end{aligned}$$
(30)

with \(t_{1}=\varrho _{11}+\varrho _{44}\), \(t_{2}=\varrho _{22}+\varrho _{33}\), \(d_{1}=\varrho _{11}\varrho _{44}-\left| \varrho _{14}\right| ^{2}\) and \(d_{2}=\varrho _{22}\varrho _{33}-\left| \varrho _{23}\right| ^{2}\). In the expressions (27), (28) and (29) \(\xi _{i j}={\text {Tr}}\left( \varrho \, (\tau _i \otimes \tau _j \right) )\) with (\(i,j=0,1,2,3\)) denote the components of the correlation matrix \(\xi\) that occur when the density matrix \(\varrho\) is expanded following the Fano-Bloch decomposition [57, 58] as

$$\begin{aligned} \varrho =\frac{1}{4} \sum _{i, j=0}^3 \xi _{i j}\, \tau _i \otimes \tau _j. \end{aligned}$$
(31)

By making use of (25) and (31), one can explicitly find that [59]

$$\begin{aligned} \begin{array}{cc} \begin{aligned} \xi _{00}&{}=tr(\varrho )=1, \quad \quad \quad \quad \xi _{03}=1-2(\varrho _{22}+\varrho _{44} ), \quad \quad \\ \xi _{30}&{}=1-2(\varrho _{33}+\varrho _{44}) \\ \xi _{11}&{}=2(\left| \varrho _{14}\right| +\left| \varrho _{23}\right| ), \quad \quad \xi _{22}=2(\left| \varrho _{23}\right| -\left| \varrho _{14}\right| ),\\ \quad \quad \xi _{33}&{}=1-2(\varrho _{22}+\varrho _{33}). \end{aligned} \end{array} \end{aligned}$$
(32)

We observe that \(\xi _{11} \ge \xi _{22}\), this implies that \(\mu _{1} \ge \mu _{2}\). Therefore, the LQU and UIN take the following forms:

$$\begin{aligned} \mathcal{U}\left( {{\varrho }} \right) = 1-\max \left( \mu _{1},\mu _{3}\right) , \quad \quad \mathcal {U}_c (\varrho )=\left\{ \begin{array}{cc} 1-\min \left( \mu _{2},\mu _{3}\right) , &{} \quad \pmb {v}=\pmb {0} \\ 1-\frac{1}{|\pmb {v}|^{2}}\,\pmb {v}\, \mathcal {W}\,\pmb {v}^{T}, &{} \quad \pmb {v} \ne \pmb {0} \end{array}\right. \end{aligned}$$
(33)

Wher the Bloch vector \(\pmb {v}^{T}=\left\{ {\text {Tr}}\left( \varrho \, (\tau _1 \otimes \mathbb {I} \right) ),{\text {Tr}}\left( \varrho \, (\tau _2 \otimes \mathbb {I} \right) ),{\text {Tr}}\left( \varrho \, (\tau _3 \otimes \mathbb {I} \right) )\right\} =\left\{ 0,0,\varrho _{11} + \varrho _{22} - \varrho _{33} - \varrho _{44}\right\} {}\).

4 Results and discussion

In this section, we display the main results related to the characterization of the quantum correlations and coherence within the Ising-\({\textbf {XYZ}}\) diamond chain structure framework. Our analysis focuses on the behavior of three key quantifiers \(C_{\ell _1}(\varrho )\), UIN and LQU. For the sake of simplicity, we deal in our analysis with the dimensionless quantity T/J, \(J_1/J\), \(\Gamma /J\), and b/J by attributing to J an energy unit.

We first study how temperature and interstitial site interactions influence the quantum resource in the Ising-\({\textbf {XYZ}}\) diamond chain. In Fig. 2, we present a comprehensive analysis of the behavior of \(\ell _1\) norm coherence (\(C_{\ell _1}\)), UIN (\(U_c\left( \varrho \right)\)), and LQU (\(U\left( \varrho \right)\)) concerning variations in T/J and \(\Gamma /J\). This investigation is performed while keeping other parameters fixed at \(b/J=1\), \(\alpha =0.95\), and \(J_1/J=-0.3\). The depicted trends unveil crucial insights into the impact of temperature and anisotropy on quantum correlation and coherence within the Ising-\({\textbf {XYZ}}\) diamond chain. The observed trend indicates a decrease in quantum correlation and coherence with increasing temperature and anisotropy parameters. This suggests a detrimental effect of both temperature and anisotropy on the quantum characteristics of the system. In the first case Figs. 2d, e and f exhibit saturation behavior where all three quantifiers reach unity when \(\Gamma /J\le -1\) and \(T/J\rightarrow 0\). This implies that the system is in a bell state \(|\varphi _{2}\rangle\) (14), achieving maximal coherence, non-locality, and correlation under these specific conditions. In the second case, as \(\Gamma /J\) approaches 0, we observe that quantum coherence and correlation achieve the value around \(C_{\ell _1}=0.56\) and \(U_c\left( \varrho \right) =U\left( \varrho \right) =0.31\) at zero temperature then increase to some peak before decreasing with higher values of T/J. While for \(\Gamma /J\ge 0.5\) we observe a monotonic decay in coherence and correlation.

Additionally, a notable observation is the diminishing quantum correlation and coherence at relatively higher temperatures. This phenomenon is attributed to the presence of thermal noise, which disrupts the quantum states and reduces their coherence levels. Overall, this analysis provides valuable insights into how temperature and anisotropy parameters affect quantum correlations and coherence within the Ising-\({\textbf {XYZ}}\) diamond chain structure, shedding light on the system’s quantum behavior under varying conditions.

Fig. 2
figure 2

The variation of the \(\ell _1\) norm of coherence \(C_{\ell _1}\left( \varrho \right)\) (a, d), UIN (b, e) and LQU (c, f) in terms of temperature and \(\Gamma /J\) for \(b/J=1\), \(\alpha =0.95\) and Ising spin exchange \(J_1/J=-0.3\)

Full size image

In the next step, we will study the effect of the temperature T and the Ising spin exchange parameter \(J_1\) on the dynamics of \({C_{\ell _1}}\left( \varrho \right)\), UIN, and LQU by fixing the values of \(\alpha\), \(\Gamma /J\), and b/J. The main results are depicted in Fig. 3. These figures show that the quantum coherence and the WYSI-derived correlations behave similarly in terms of the dimensionless variables T/J and \(J_1/J\). More precisely, UIN (Fig. 3b) and LQU (Fig. 3c) capture the correlations only for small values of T/J and \(J_1/J\). Increasing one of the variables while fixing the other leads to the correlation and coherence demolition. We notice that the quantum correlation and coherence quantities are maximal when \(T\rightarrow 0\) and \(J_1 \rightarrow 0\). In Fig. 3d and e, we observe that at low temperatures, quantum coherence and non-local correlations in the Ising-\({\textbf {XYZ}}\) system increase and reach their local maximum at a \(J_1/J\)-dependent critical value of \(T_c/J\). After each local maximum, the quantum coherence and correlations decrease gradually to reach an asymptotic value without disappearing completely. This behavior indicates the presence of quantum phase transitions in the Ising-\({\textbf {XYZ}}\) system. Also, we can see that the increase in \(J_1/J\) leads to a degradation of quantum correlations and coherence.

In addition, the Fig. 3f results provide a typical behavior of the LQU for various values of \(J_1/J\) and temperature T/J. As \(J_1/J\) increases, the quantum correlation amounts decrease to achieve their peak value at a critical temperature \(T_c/J\).

Fig. 3
figure 3

The variation of \(\ell _1\) norm of coherence \(C_{\ell _1}\left( \varrho \right)\) (a, d), UIN (b, e) and LQU (c, f) in terms of temperature and Ising spin exchange \(J_1/J\) for \(\alpha =0.95\), \(b/J=0.1\), \(\Gamma /J=0.3\)

Full size image

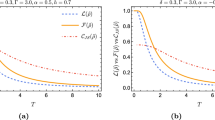
Next, Fig. 4 displays a comparison between the three studied quantifiers in terms of the temperature when the Ising spin exchange parameter is fixed at \(J_1/J=0.3\).

Fig. 4
figure 4

A comparative behavior of all considered quantifiers in terms of temperature for \(\alpha =0.95\), \(\Gamma /J=0.3\) and \(b/J=0.1\) and Ising spin exchange \(J_1/J=0.3\). The figure plots show that the quantum coherence decays more slowly in comparison with the skew-information correlation when the temperature increases relatively

Full size image

It is shown that the quantum coherence, in the chosen basis, is more robust than quantum correlation. To go further, we study in what follows the influence of the xy-anisotropy parameter \(\alpha\) on the three suggested quantifiers. To do this, we illustrate in Fig. 5 the behaviors of \(C_{\ell _1}\), UIN, and LQU in terms of \(\alpha\) for various values of the normalized magnetic field b/J.

Fig. 5
figure 5

The variation of \(\ell _1\) norm of coherence \(C_{\ell _1}\left( \varrho \right)\) (a), UIN (b) and LQU (c) as a function of xy-anisotropy parameter \(\alpha\), with varying values of b/J, while keeping other parameters such as \(T/J=0.1\), \(\Gamma /J=0.3\) and \(J_1/J=-0.3\)

Full size image

It is observed that the three quantifiers behave similarly in terms of \(\alpha\) when \(b/J\ge 0.9\). They increase from a vanished value, especially for \(b/J>0.9\), to reach a maximum value. We notice that the amounts of coherence (Fig. 5a) and correlations captured by UIN (Fig. 5b) are important when b/J is small. However, this behavior is reproduced for LQU (Fig. 5c) only when \(b/J\ge 0.9\) and refuted for \(b/J<0.9\). Besides, LQU reveals a typical behavior in terms of \(\alpha\) when \(b/J<0.9\). It decreases monotonically from a maximum value to reach a local minimum, which depends on b/J, and then increases to attain its own maximum again. We conclude from Fig. 5 that increasing \(\alpha\) generally contributes to enhancing coherence and non-local quantum correlations.

Next, we analyse the combined effect of the xy-anisotropy parameter \(\alpha\) and the temperature on the dynamics of \({C_{\ell _1}}\left( \varrho \right)\), UIN, and LQU.

Fig. 6
figure 6

The variation of \(\ell _1\) norm of coherence \(C_{\ell _1}\left( \varrho \right)\) (a), UIN (b) and LQU (c) as a function of temperature is shown for different values of \(\alpha\), with fixed parameters \(b/J=0.5\), \(\Gamma /J=0.3\) and \(J_1/J=-0.3\)

Full size image

From Fig. 6, we show plots that demonstrate that quantum coherence and WYSI-correlation are maximal for \(T/J \rightarrow 0\) and \(\alpha \le 0.25\). More precisely, it can be observed from Fig. 6a, b, that the \(\ell _1\) norm of coherence and UIN behave similarly for very small temperature values. Nevertheless, as T/J increases, quantum coherence decreases monotonically to achieve a value close to zero, while UIN disappears asymptotically. Besides, some transitions from coherent to incoherent and from non-correlated to correlated states for \(\alpha \le 0.25\) can be detected. Like the previous analysis, the LQU (Fig. 6c) shows different behavior compared to the coherence and non-local correlations captured by UIN. As Fig. 6c displays, the LQU decreases more rapidly to close to zero as T/J increases. From these obtained results, we can stress that the xy-anisotropy \(\alpha\) not only improves quantum correlations and coherence but also reduces the destructive effect of temperature.

Fig. 7
figure 7

The dynamic behavior of coherence and skew information correlations as a function of the thermal noise in the case of xy-anisotropy parameter \(\alpha <0\), with fixed parameters \(b/J=0.5\), \(\Gamma /J=0.3\) and \(J_1/J=-0.3\)

Full size image

From Fig. 7 we find that for \(\alpha <0\) or \(\alpha >0\) quantum correlation and WYSI-correlation decrease as the temperature increases. This indicates that the thermal noise degrades quantum coherence and correlations independently of the anisotropy parameter’s sign.

Finally, we study the effect of temperature on the thermal quantum coherence and correlation in the Ising-XYZ diamond chain for various external magnetic field values.

Fig. 8
figure 8

The variation of \(\ell _1\) norm of coherence \(C_{\ell _1}\left( \varrho \right)\) (a), UIN (b) and LQU (c) as a function of temperature is depicted for different values of b/J, while the other parameters are fixed at \(\alpha =0.95, \Gamma /J=0.3\) and \(J_1/J=-0.3\). In comparative behavior of all considered quantifiers in terms of temperature (d)

Full size image

To do this end, we illustrate in Fig. 8 the thermal behavior of \(C_{\ell _1}\), UIN, and LQU for some chosen values of b while keeping the other parameters \(\alpha\), \(\Gamma /J\), and \(J_1/J\) constant. It is shown that in addition to the expected destructive effect of temperature, increasing values of the external magnetic field (b/J) lead to the collapse of quantum correlation and coherence. On the other hand, as shown in Fig. 8b, c, the quantum correlation quantifiers vary in the same trend in terms of T/J. As T/J increases, WYSI-derived quantum correlations decrease rapidly and disappear for high temperatures. It should be noted that for \(b=0\) and \(T/J \rightarrow 0\), UIN is maximally correlated while LQU increases from 0.45 to reach its own maximum value and then decreases rapidly. In comparison, quantum correlations are more sensitive to magnetic field perturbations than coherence.

5 Concluding remarks

We have investigated the thermal behavior of nonclassical correlations and quantum coherence in a two-qubit Ising-\({\textbf {XYZ}}\) diamond chain structure subjected to an external uniform magnetic field. The influences of the model’s parameters on quantum correlations and the \(\ell _1\) norm of coherence are examined in detail. Our findings suggest that the Ising-\({\textbf {XYZ}}\) diamond chain structure maintains nonclassical correlations and coherence at low temperatures. However, at higher temperatures, increased thermal noise decays the existing coherence and correlations between quantum system parts. Besides, we demonstrate that when the interaction between interstitial sites (\(\Gamma /J\le -1\)) in the Ising-\({\textbf {XYZ}}\) structure chain is taken into account, the system stabilizes and, therefore, the suggested quantifiers become important. Also, our results show that increasing the xy-anisotropy parameter values reinforces quantum correlation and coherence. We also note that the UIN and \(\ell _1\) norm of coherence generally provide similar behaviors. Accordingly, in addition to characterizing non-local quantum correlations, UIN can be exploited to reveal quantum coherence in the studied system. Despite the harmful effects of temperature and high magnetic field values on quantum resources, we have shown that the amounts of quantum coherence and quantum correlations can be enhanced within these conditions by adjusting the other parameters of the investigated system.