1 Introduction

Quantum correlations are a valuable resource in many areas of quantum information (Nielsen and Chuang 2002; Adesso et al. 2016; Dillenschneider and Lutz 2009; Renou et al. 2019; Mansour and Dahbi 2020). As a result, numerous entanglement quantifiers have been developed to determine the degree of entanglement in multiparty systems (see for instance (Hu et al. 2018; Haddadi and Bohloul 2018; Mintert et al. 2004; Meyer and Wallach 2002; Brennen 2003; Scott 2004)). The problem of quantifying quantum correlations in mixed states (Horodecki and Oppenheim 2013) still relevant today. The study of entanglement in mixed states has been extensively described in many previous studies (Coffman et al. 2000; Ganczarek et al. 2012; Mansour et al. 2021, 2020; Mansour and Daoud 2019; Mansour and Hassouni 2016; Mansour and Haddadi 2021; Mansour et al. 2021; Khedif et al. 2021; Haddadi et al. 2019). However, some research has shown that separable mixed states can exhibit some quantum correlations. To solve this problem, a new quantum correlation quantifier called quantum discord was introduced in (Streltsov 2015; Ollivier and Zurek 2001; Henderson and Vedral 2001) to quantify nonclassical correlations beyond entanglement. The evaluation of this new metric requires a minimization technique that can be realized analytically for some two-qubit states (Dakić et al. 2010; Paula et al. 2013; Luo and Fu 2010; Hassan et al. 2012). The difficulty of calculating the quantum discord in general cases prompted Dakic et al. to develop a geometric version of the quantum discord (Dakić et al. 2010) based on the Hilbert–Schmidt norm. Later, based on the Wigner-Yanase skew information (Wigner and Yanase 1997; Luo 2003) which is also a useful discord-like measure of quantum correlations in bipartite and multipartite systems. Girolami et al. (Girolami et al. 2013) introduced local quantum uncertainty that is broadly used to capture nonclassical correlations and is stable under LU transformations and vanishing for classically correlated states. It also offers the advantage that it can be calculated analytically for every qubit-qudit system. The dynamics of the LQU has been extensively examined in many works (Slaoui et al. 2018; Yang et al. 2019; Chen 2005; Sbiri et al. 2021).

It is likewise interesting to be aware that local quantum uncertainty is related to quantum Fisher information (QFI) on the subject of quantum metrology. During the unitary dynamics of a given quantum state, ie., \(\rho \rightarrow \rho _\theta = U_\theta ^\dag \rho {U_\theta }\) with \({U_\theta } = {e^{i{H}\theta }}\), it has been shown in (Luo 2003, 2004) that the QFI associated with the phase parameter (\(\theta\)) bounds the skew information. As a result, in the optimal phase estimation protocol (Girolami et al. 2013), the LQU of a two-part probe state ensures a quantifiable minimum accuracy via the QFI. Using QFI, Kim et al. (Kim et al. 2018) developed the concept of local quantum Fisher information (LQFI) as a discord-like measure of nonclassical correlations. LQFI is obtained by minimizing QFI over all local operators acting on a subsystem. In addition, LQFI is a great tool to extract knowledge about the role of nonclassical correlations in improving the accuracy and overall performance of quantum metrology protocols.

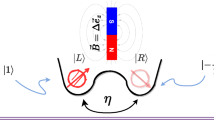
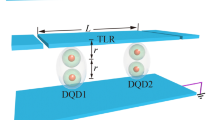
On the other hand, it has been shown that double quantum dots (DQDs) (Shinkai et al. 2009; Austing et al. 1998) provide an outstanding resource to realize quantum devices that can process quantum information (Economou et al. 2012). In fact, it has also been proposed that quantum dots can be used as charge qubits (Gorman et al. 2005) or spin qubits (Benito et al. 2017; Loss and DiVincenzo 1998; D’Anjou and Burkard 2019), or maybe both of them. Recently, it has been shown that certain quantum dot parameters can be tuned to lower the entropic uncertainty bound and improve quantum correlations (Haseli et al. 2021). Furthermore, in terms of scalability, quantum technology can benefit from the simplicity with which quantum dots can be integrated into modern electronics (Itakura and Tokura 2003; Urdampilleta et al. 2015). The regulation of tunneling in an asymmetric DQD is described and addressed in (Villas-Bôas et al. 2004). Recently, many research works have studied the dynamics of entanglement between electrons in coupled DQDs in (Oliveira and Sanz 2015; Szafran 2020) and the quantum correlations and decoherence in DQD systems in (Fanchini et al. 2010; Filgueiras et al. 2020; Qin 2016; Borges et al. 2012; Souza et al. 2019). The purpose of this work is to quantify the extent of quantum correlation in DQDs considered as isolated charge qubits. We suppose that the system remains within the strong Coulomb barrier, which permits only one electron per quantum dot. In this case, an electron occupies either the left or the right side of the charge qubit. In order to look in detail to the variation of quantum correlations in such a system, we obtained analytical expressions of the eigenvalues and related eigenstates of the thermal density matrix of the two-coupled DQDs system at equilibrium temperature.

This paper is organized as follows. In Sect. 2, we give a brief overview of LQU and LQFI used as quantifiers of quantum correlations. In Sect. 3, we present the proposed model of the two-coupled DQDs system and we derive analytically its thermal density matrix. In Sect. 4, we analyze and discuss the behavior of quantum correlations in such a physical system depending on the equilibrium temperature T, the Coulomb potential V, and the tunneling strengths \(\Delta _{1 (2)}\). We show that variations in LQU and LQFI are similar across all physical parameters. Our findings display that LQFI exhibits extra quantum correlations than LQU in all combinations examined. In the last section, we give some concluding thoughts and remarks.

2 Measures of nonclassical correlations

This section summarizes the definitions and formulas for the two main computable quantifiers used in this study, specifically LQU and LQFI.

2.1 LQU

LQU is the first quantifier of quantum correlations used in this work. Given a bipartite system with a density matrix \(\rho\) describing its state, the LQU with respect to the first subsystem is defined as (Karpat et al. 2014; Guo et al. 2015)

$$\begin{aligned} {\mathcal {U}}(\rho ) \equiv \min _{K_A} {\mathcal {I}}(\rho , K_A \otimes {\mathbb {I}}_B), \end{aligned}$$
(1)

where \(K_A\) denotes the local observable on the first subsystem, \({\mathbb {I}}_B\) is the identity operator acting on the subsystem B and

$$\begin{aligned} {\mathcal {I}}(\rho , K_A \otimes {\mathbb {I}}_B)=-\frac{1}{2}\mathrm{Tr}([\sqrt{\rho }, K_A \otimes {\mathbb {I}}_B]^{2}) \end{aligned}$$
(2)

defines the so-called Wigner–Yanase skew information (WYSI) (Wigner and Yanase 1997). If there is a local operator \(K_A\) for which \({\mathcal {I}}(\rho , K_A \otimes {\mathbb {I}}_B) =0\) then there is no quantum correlation between the two parties of the quantum system described by the state \(\rho\). The analytical computation of LQU is performed through a minimization procedure over the set of all observables acting on the first part of the composite system. In particular, for qubits, the LQU with respect to the subsystem A is given by (Girolami et al. 2013)

$$\begin{aligned} \mathcal{U}\left( {{\rho }} \right) = 1 - \max \left( {{\omega _{1}},{\omega _{2}},{\omega _{3}}} \right) \end{aligned}$$
(3)

where \(\omega _{i=1,2,3}\) are the eigenvalues of the \(3\times 3\) symmetric matrix denoted \({\mathcal {W}}\) whose entries are given by

$$\begin{aligned} \Big ({\mathcal {W}}\Big )_{ij} \equiv \mathrm{Tr} \left\{ \sqrt{\rho } \left( \sigma _{Ai}\otimes {\mathbb {I}}_{2}\right) \sqrt{\rho } \left( \sigma _{Aj}\otimes {\mathbb {I}}_{2}\right) \right\} \end{aligned}$$
(4)

with \(\sigma _{Ai} (i=x,y,z)\) denotes Pauli matrices acting on the subsystem A.

2.2 LQFI

As a second discord-type quantum correlations measure, we use the QFI based correlations quantifier. QFI is the best metric used in quantum estimation theory to characterize the accuracy in parameter estimation scenarios (see for instance (Helstrom 1969; Kay 1993; Genoni et al. 2011)). It should be emphasized that the QFI is widely linked to entanglement and quantum correlations beyond entanglement (see for instance (Chapeau-Blondeau 2017; Giovannetti et al. 2004; Huelga et al. 1997; Chapeau-Blondeau 2016)). In general, for an arbitrary quantum state \(\rho _{\theta }\) that depends on the parameter \(\theta\), we define the QFI as (Luo 2004; Ye et al. 2018; Paris 2009)

$$\begin{aligned} {\mathcal {F}}(\rho _{\theta })=\frac{1}{4}\text {Tr}[\rho _{\theta } L_{\theta }^2], \end{aligned}$$

where the symmetric logarithmic derivative \(L_{\theta }\) is defined as the solution of the equation

$$\begin{aligned} \frac{d\rho _{\theta }}{d\theta }=\frac{1}{2}( \rho _{\theta } L_{\theta }+L_{\theta }\rho _{\theta } ). \end{aligned}$$

The parametric state \(\rho _{\theta }\) can be obtained by applying an unitary operator U to an initial probe state \(\rho\) as follows \(\rho _{\theta } = U\rho U^{\dagger }\). The operator U dependent on the parameter \(\theta\) and is generated by a Hermitian operator H, i.e., \(U = \mathrm {e}^{-iH\theta }\). Then, \({\mathcal {F}}(\rho , H ) = {\mathcal {F}}(\rho _{\theta })\) can be given by

$$\begin{aligned} {\mathcal {F}}(\rho , H)=\frac{1}{2}\sum _{i,j, \lambda _i+\lambda _j>0}\frac{(\lambda _i-\lambda _j)^2}{\lambda _i+\lambda _j}|\langle \varphi _i|H |\varphi _i\rangle |^2. \end{aligned}$$
(5)

where we used the spectral decomposition of \(\rho\), i.e., \(\rho = \sum \limits _{i = 1} {{\lambda _i}| {{\varphi _i}} \rangle \langle {\varphi _i}|}\) with \({\lambda _i} \ge 0\) and \(\sum \limits _{i = 1} {{\lambda _i}} = 1\). Now we consider an \(2 \otimes d\) bipartite quantum state \({\rho }\) in the Hilbert space \(\mathcal H = H_{\mathrm{A}} \otimes H_{\mathrm{B}}\). If we assume that the dynamics of the first part of the bipartite system is controlled by the local phase shift operator \({e^{ - i\theta {H_A}}}\), with \({H_A} \equiv {H_a} \otimes {{\mathbb {I}}_B}\) which is the local Hamiltonian, one can get the following expression of the LQFI (Bera 2014)

$$\begin{aligned} {\mathcal {F}}\left( {\rho ,{H_A}} \right) = \mathrm{Tr}\left( {\rho {H_A}^2} \right) - \sum \limits _{i,j, \lambda _i+\lambda _j>0} {\frac{{2{\lambda _i}{\lambda _j}}}{{{\lambda _i} + {\lambda _j}}}{{| {\langle {{\varphi _i}} |{H_A}| {{\varphi _j}} \rangle } |}^2}}. \end{aligned}$$
(6)

The quantification of quantum correlations based on LQFI \({\mathcal {Q}}\left( \rho \right)\) is defined as the minimum QFI over all local Hamiltonian \({H_A}\) acting on the A-part of the bipartite system (Kim et al. 2018)

$$\begin{aligned} {\mathcal {Q}}(\rho )=~{\text {min}}_{H^{a}}~{\mathcal {F}}(\rho , H), \end{aligned}$$
(7)

where \(H=H^a\otimes I\). This measure is non-negative, vanishes for zero discord bipartite states, invariant under any local unitary operation and coincides with the geometric discord for pure quantum states. Choosing the local observable \(H^a=\vec {\sigma }.\vec {r}\) with \(| \vec {r}|=1\) and \(\vec {\sigma }=(\sigma _x, \sigma _y, \sigma _z)\), it can be seen that \(\mathrm{Tr}\left( {\rho {H_A}^2} \right) =1\) and the second term in the equation (6) can be expressed as

$$\begin{aligned} \sum \limits _{i,j, \lambda _i+\lambda _j>0} {\frac{{2{\lambda _i}{\lambda _j}}}{{{\lambda _i} + {\lambda _j}}}{{| {\langle {\varphi _i}|{H_A}| {{\varphi _j}} \rangle } |}^2}}&= \sum \limits _{i,j, \lambda _i+\lambda _j>0} {\sum \limits _{l,k=1}^3 {\frac{{2{\lambda _i}{\lambda _j}}}{{{\lambda _i} + {\lambda _j}}}} } \langle {\varphi _i}|{\sigma _l} \otimes {\mathbb {I}}_B| {{\varphi _j}} \rangle \langle {\varphi _j}|{\sigma _k} \otimes {\mathbb {I}}_B| {{\varphi _i}} \rangle \\\nonumber&= {{\vec r}^{\dag } }.\mathcal{M}.{\vec r} \end{aligned}$$
(8)

where the elements of the \(3 \times 3\) symmetric matrix \(\mathcal{M}\) are given by

$$\begin{aligned} {\mathcal{M}_{lk}} = \sum \limits _{i,j, \lambda _i+\lambda _j>0} {\frac{{2{\lambda _i}{\lambda _j}}}{{{\lambda _i} + {\lambda _j}}}\langle {\varphi _i}|{\sigma _l} \otimes {\mathbb {I}}_B| {{\varphi _j}} \rangle \langle {\varphi _j}|{\sigma _k} \otimes {\mathbb {I}}_B| {{\varphi _i}} \rangle }. \end{aligned}$$
(9)

To minimize \({\mathcal {F}}\left( {\rho ,{H_A}} \right)\), it is necessary to maximize the quantity \({{\vec r}^\dag }.\mathcal{M}.{\vec r}\) over all unit vectors \({\vec r}\). The closed formula of the quantum correlations quantifier based on QFI is

$$\begin{aligned} {\mathcal {Q}}(\rho )=1-\text {max}\{M_1,M_2,M_3 \}, \end{aligned}$$
(10)

where \(M_i\) are the eigenvalues of matrix \(\mathcal M\).

3 Two-coupled DQDs

The model consists of two sets of DQDs, where each double quantum dot is filled with a single electron. Each electron has two degrees of freedom, it can either be in the left quantum dot (\(|L\rangle\)) or in the right one (\(|R\rangle\)). In practice, DQDs offer a realistic physical implementation of two-level systems. An illustrated setup of the model is shown in Fig. 1. The Hamiltonian of the two-coupled DQDs system is given as follows (Fanchini et al. 2010; Filgueiras et al. 2020)

$$\begin{aligned} \begin{array}{ccc} H= & {} \Delta _{1}\sigma _{1}^{x}+\Delta _{2}\sigma _{2}^{x}+V\left( \sigma _{1}^{z}\otimes \sigma _{2}^{z}\right) \end{array} \end{aligned}$$
(11)

where \(\sigma _{1(2)}^{\alpha }(\alpha =x,z)\) denotes the so-called Pauli operators, \(\Delta _{i}\) is the strength of the tunneling coupling between the two quantum dots, and V represents the Coulomb interaction between the two electrons.

Fig. 1
figure 1

(Color online) Schematic setup of the two-coupled DQDs

Full size image

In order to make notation easier, we consider the convention \(|0\rangle \equiv |L\rangle\) and \(|1\rangle \equiv |R\rangle\) to indicate the electron occupying either the left dot (\(|L\rangle\)), or the right one (\(|R\rangle\)). The Hamiltonian (11) can be expressed in the computational basis \(\left\{ {| {00}\rangle ,| {01} \rangle ,| {10} \rangle ,| {11} \rangle } \right\}\), under its matrix form

$$\begin{aligned} H = \left( {\begin{array}{*{20}{c}} V &{} \Delta _{2} &{} \Delta _{1} &{} 0\\ \Delta _{2} &{} - V &{} 0 &{} \Delta _{1}\\ \Delta _{1} &{} 0 &{} - V &{} \Delta _{2}\\ 0 &{} \Delta _{1} &{} \Delta _{2} &{} V \end{array}} \right) , \end{aligned}$$
(12)

We can find the eigenvalues and associated eigenstates of the Hamiltonian H by a simple calculation as follows

$$\begin{aligned} E_{1}&= \sqrt{(\Delta _{-})^{2}+V^{2}},\quad |u_{1} \rangle=\Gamma _{-}\left[ \Lambda _{-}\left( -|00\rangle +|11\rangle \right) +\Delta _{-}\left( |01\rangle -|10\rangle \right) \right] \\ E_{2}&= -\sqrt{(\Delta _{-})^{2}+V^{2}},\quad |u_{2}\rangle=\Gamma _{-}\left[ \Delta _{-}\left( -|00\rangle +|11\rangle \right) +\Lambda _{-}\left( -|01\rangle +|10\rangle \right) \right]\\ E_{3}&= \sqrt{(\Delta _{+})^{2}+V^{2}},\quad |u_{3}\rangle=\Gamma _{+}\left[ \Lambda _{+}\left( |00\rangle +|11\rangle \right) +\Delta _{+}\left( |01\rangle +|10\rangle \right) \right]\\ E_{4}&= - \sqrt{(\Delta _{+})^{2}+V^{2}}, \quad |u_{4}\rangle=\Gamma _{+}\left[ \Delta _{+}\left( |00\rangle +|11\rangle \right) -\Lambda _{+}\left( |01\rangle +|10\rangle \right) \right] \end{aligned}$$
(13)

where \(\Gamma _{\pm }=\frac{1}{\sqrt{2}\sqrt{(\Delta _{\pm })^{2}+\Lambda _{\pm }^{2}}}\), \(\Lambda _{\pm }=V+\sqrt{(\Delta _{\pm })^{2}+V^{2}}\) and \(\Delta _{\pm }=\Delta _{1}\pm \Delta _{2}\). The thermal density matrix of the two-coupled DQDs system at temperature T is given by the Gibbs state

$$\begin{aligned} \rho (T) = \frac{1}{{Z}} e^{-\beta H}, \end{aligned}$$
(14)

where \(\beta =\frac{1}{k_B T}\) and Z being the partition function \(Z= tr( e^{\frac{-H}{T}}) = \sum ^{4}_{i=1} e^{\frac{-E_i}{T}}\). The Boltzmann constant \(k_B\) is set to 1 in this work. The thermal density matrix \(\rho (T)\) (14) can be analytically derived by using the spectral decomposition of the Hamiltonian (12). In the two-qubit computational basis, the bipartite state \(\rho (T)\) (14) takes the following form

$$\begin{aligned} \rho (T)=\left[ \begin{array}{cccc} \rho _{11} &{} \rho _{12} &{} \rho _{13} &{} \rho _{14}\\ \rho _{12} &{} \rho _{22} &{} \rho _{23} &{} \rho _{13}\\ \rho _{13} &{} \rho _{23} &{} \rho _{22} &{} \rho _{12}\\ \rho _{14} &{} \rho _{13} &{} \rho _{12} &{} \rho _{11} \end{array}\right] , \end{aligned}$$
(15)

where, the corresponding entries are provided by

$$\begin{aligned} \rho _{11}= & {} \frac{\Gamma _{-}^{2}\left( \Lambda _{-}^{2}e^{-\beta E_{1}}+\Delta _{-}^{2}e^{-\beta E_{2}}\right) +\Gamma _{+}^{2}\left( \Lambda _{+}^{2}e^{-\beta E_{3}}+\Delta _{+}^{2}e^{-\beta E_{4}}\right) }{Z}\\ \rho _{12}= & {} \frac{\Lambda _{-}\Delta _{-}\Gamma _{-}^{2}\left( -e^{-\beta E_{1}}+e^{-\beta E_{2}}\right) +\Lambda _{+}\Delta _{+}\Gamma _{+}^{2}\left( e^{-\beta E_{3}}-e^{-\beta E_{4}}\right) }{Z}\\ \rho _{13}= & {} \frac{\Lambda _{-}\Delta _{-}\Gamma _{-}^{2}\left( e^{-\beta E_{1}}-e^{-\beta E_{2}}\right) +\Lambda _{+}\Delta _{+}\Gamma _{+}^{2}\left( e^{-\beta E_{3}}-e^{-\beta E_{4}}\right) }{Z}\\ \rho _{14}= & {} \frac{-\Gamma _{-}^{2}\left( \Lambda _{-}^{2}e^{-\beta E_{1}}+\Delta _{-}^{2}e^{-\beta E_{2}}\right) +\Gamma _{+}^{2}\left( \Lambda _{+}^{2}e^{-\beta E_{3}}+\Delta _{+}^{2}e^{-\beta E_{4}}\right) }{Z}\\ \rho _{22}= & {} \frac{\Gamma _{-}^{2}\left( \Delta _{-}^{2}e^{-\beta E_{1}}+\Lambda _{-}^{2}e^{-\beta E_{2}}\right) +\Gamma _{+}^{2}\left( \Delta _{+}^{2}e^{-\beta E_{3}}+\Lambda _{+}^{2}e^{-\beta E_{4}}\right) }{Z}\\ \rho _{23}= & {} \frac{-\Gamma _{-}^{2}\left( \Delta _{-}^{2}e^{-\beta E_{1}}+\Lambda _{-}^{2}e^{-\beta E_{2}}\right) +\Gamma _{+}^{2}\left( \Delta _{+}^{2}e^{-\beta E_{3}}+\Lambda _{+}^{2}e^{-\beta E_{4}}\right) }{Z} \end{aligned}$$

The eigenvalues of the above thermal density \(\rho (T)\) are obtained as

$$\begin{aligned} \lambda _1= & {} \frac{2 \Gamma _{-}^2 \left( \Lambda _{-}^2+\Delta _{-}^2\right) e^{\beta E_1+\beta E_3+\beta E_4}}{e^{\beta E_1+\beta E_2+\beta E_3}+e^{\beta E_1+\beta E_2+\beta E_4}+e^{\beta E_1+\beta E_3+\beta E_4}+e^{\beta E_2+\beta E_3+\beta E_4}}\\ \lambda _2= & {} \frac{2 \Gamma _{-}^2 \left( \Lambda _{-}^2+\Delta _{-}^2\right) e^{\beta E_2+\beta E_3+\beta E_4}}{e^{\beta E_1+\beta E_2+\beta E_3}+e^{\beta E_1+\beta E_2+\beta E_4}+e^{\beta E_1+\beta E_3+\beta E_4}+e^{\beta E_2+\beta E_3+\beta E_4}}\\ \lambda _3= & {} \frac{2 \Gamma _{+}^2 \left( \Lambda _{+}^2+\Delta _{+}^2\right) e^{\beta E_1+\beta E_2+\beta E_3}}{e^{\beta E_1+\beta E_2+\beta E_3}+e^{\beta E_1+\beta E_2+\beta E_4}+e^{\beta E_1+\beta E_3+\beta E_4}+e^{\beta E_2+\beta E_3+\beta E_4}}\\ \lambda _4= & {} \frac{2 \Gamma _{+}^2 \left( \Lambda _{+}^2+\Delta _{+}^2\right) e^{\beta E_1+\beta E_2+\beta E_4}}{e^{\beta E_1+\beta E_2+\beta E_3}+e^{\beta E_1+\beta E_2+\beta E_4}+e^{\beta E_1+\beta E_3+\beta E_4}+e^{\beta E_2+\beta E_3+\beta E_4}} \end{aligned}$$

4 Results and discussions

In this section we present and discuss the main results obtained for the dynamics of quantum correlations within the two-coupled DQDs system. In our study, we use LQU and LQFI, which are theoretically measurable quantities that are crucial for the detection of quantum correlations in a quantum system with given configuration. In order to understand the influence of the system configuration, we examine the influence of each parameter, the tunneling strengths \(\Delta _{1(2)}\), the Coulomb interaction between electrons V and the temperature T as well as the cooperative effect of these parameters on the dynamics of quantum correlations within the two-coupled DQDs. We pick the values of \(\Delta _{1(2)}\), V, and T because they give more insights and excellent results for this investigation. An instructive comparison between the two measures is also presented. We start by examining the combined influence of the Coulomb potential V and temperature T on the nonclassical correlation magnitudes captured by LQU and LQFI.

Fig. 2
figure 2

Dynamics of nonclassical correlations against V and T for \(\Delta _1=15, \Delta _2=10\). a LQU, b LQFI

Full size image
Fig. 3
figure 3

Dynamics of nonclassical correlations against T for \(\Delta _1=10, \Delta _2=15\) and \(V\in [0,10,20,30,40]\). a LQU, b LQFI, c LQFI vs LQU

Full size image

In Fig. 2 we plot both LQU and LQFI as functions of T and V for \(\Delta _2=15\) and \(\Delta _1=10\). As shown in Fig. 2a, b, we observe that LQU and LQFI show a similar behavior with respect to the two parameters T and V. We notice particularly, that at \(T \rightarrow 0\), LQU and LQFI detect the same amount of quantum correlations. But as the temperature T varies, the maximum reached by LQU is slightly different from that reached by LQFI. Indeed, in the high regime \((V=40)\), LQU (LQFI) captures a maximal amount equals 0.7247 (0.7387) at \(T=1.79\) (2.71). In the weak regime (\(V < 10\)), we notice that quantum correlations are extremely overlooked even at low temperatures but could still be useful for some quantum information applications. We observe also, that quantum correlations tend to zero as the temperature increases beyond a threshold value \(T_c\). To get more insight into the role of the Coulomb potential on the evolution of quantum correlations, we plot, in Fig. 3, the thermal evolution of LQU and LQFI as functions of temperature T for selected values of V with \(\Delta _1=10\) and \(\Delta _2=15\). It can be seen from Fig. 3a, b that quantum correlations within the system are absent at zero Coulomb potential value. Then, one can conclude that the Coulomb potential V introduces the quantum correlations in two-coupled DQDs system and consequently can be used to modulate the non-classical correlations contained in such system. Also, a nice remark is that the system of two-coupled DQDs shows larger pairwise quantum correlations at low temperature values. Particularly, one can see that the two quantifiers LQU and LQFI show an increase in quantum correlations to a maximum value with increasing temperature until a critical value \(T_c\), which depends on the value of the potential V, where the quantum correlations starts decreasing to zero. In Fig. 3c we see that LQFI gives slightly better values than LQU and that the critical temperature for LQFI is higher than for LQU. The second quantifier, LQFI is thus more resistant to the effects of temperature T and reveals more nonclassical correlations than LQU in two-coupled DQDs system. The plotted results (Fig. 3c) also prove that the inequality \(\mathcal{U} (\rho _T) \le \mathcal{Q} (\rho _T) \le 2~\mathcal{U} (\rho _T)\) holds.

In the following, we explore the combined influence of the tunneling parameter \(\Delta _1\) and the temperature T on the behavior of the pairwise quantum correlations in the two coupled DQDs system. In this respect, we visualize in Fig. 4a, b, the variations of the two quantum correlation quantifiers as functions of the two parameters T and \(\Delta _1\).

Fig. 4
figure 4

Dynamics of nonclassical correlations against T and \(\Delta _1\) for \(\Delta _2=15, V=80\). a LQU, b LQFI

Full size image
Fig. 5
figure 5

Dynamics of nonclassical correlations against T for \(V=20, \Delta _2=8\) and \(\Delta _1 \in [1, 2, 3, 4]\). a LQU, b LQFI, c LQFI versus LQU

Full size image

In Fig. 4, the two quantifiers LQU and LQFI are plotted against T and \(\Delta _1\) with \(V=80\) and \(\Delta _2=15\). We mention that the blue area indicates the absence of quantum correlations, while the green-yellow area indicates their presence. At low temperatures \((T \le T_c)\), we observe that quantum correlations improve as \(\Delta _1\) gets larger. In other words, quantum correlations can withstand weak thermal noise caused by system heating when the tunneling strength \(\Delta _1\) is strong in the first DQD system. The same observation can be made when \(\Delta _1\) is swapped with \(\Delta _2\), only that the quantum correlations improve somewhat when \(\Delta _1>\Delta _2\) than when \(\Delta _1<\Delta _2\). In Fig. 5 we perform a more comprehensive investigation of the influence of \(\Delta _1\) on quantum correlations for \(V=20\) and \(\Delta _2=8\). In this case we observe that for a fixed value of \(\Delta _1\), the two quantifiers LQU and LQFI reach the maximum value at a critical value \(T_c\) of the temperature and then they began decreasing to zero with increasing of T. It is clearly seen form Fig. 5c, that the upper bounds of the LQFI are slightly larger than those of LQU and that LQFI always reveals more quantum correlations than LQU in the two-coupled DQDs. The plot (Fig. 5c) also shows that LQU is bounded by LQFI and that the inequality \(\mathcal{U} (\rho _T) \le \mathcal{Q} (\rho _T) \le 2\mathcal{U} (\rho _T)\) is fulfilled.

Next, we examine the influence of the tunneling parameter \(\Delta _1\) and the Coulomb potential V on the variation of quantum correlations in the two-coupled DQDs system and the results are visualized in Figs. 6 and 7.

Fig. 6
figure 6

Dynamics of nonclassical correlations against \(\Delta _{1}\) and V for \(\Delta _2=10, T=0.5\). a LQU, b LQFI

Full size image
Fig. 7
figure 7

Dynamics of nonclassical correlations against V for \(T=0.1\), \(\Delta _1=\Delta _2 \in [1,2,5,10]\). a LQU, b LQFI, c LQFI vs LQU

Full size image

In Fig. 6, we visualize LQU and LQFI as functions of the tunneling parameter \(\Delta _1\) and the Coulomb potential V with \(\Delta _2=10\) and \(T=0.5\). In this situation, one can observe that quantum correlations are absent when the Coulomb potential V is zero, regardless of the value of \(\Delta _1\). Figure 7 shows that quantum correlations associated with the values of V for \(T=0.1\) and \(\Delta _1=\Delta _2\). LQU and LQFI exhibit a sudden change for fixed value of \(\Delta _1\). We notice that the value of the transition point \(V_c\) increases with the increment of the value of the tunneling coupling \(\Delta _1\). Indeed, the two quantifiers display an increasing behavior until a threshold value \(V_c\), which is a \(\Delta _1\)-dependant and then start decreasing as V increases. In Fig. 7c we compare LQU and LQFI for \(T = 0.1\) and \(\Delta _1=\Delta _2 \in \{2, 5\}\). We see that LQFI captures more quantum correlations than LQU for all \(\Delta _1\) values. We also show that LQFI collapses at a slower rate compared to the LQU quantifier.

Now, we explicitly investigate the effect of the tunneling strengths \(\Delta _{1(2)}\) on the variation of the quantum correlations between the two electrons. For that end, we draw in Figs. 8 and 9 the behavior of the two quantifiers of quantum correlations as a function of the tunneling parameters \(\Delta _{1}\) and \(\Delta _{2}\) for fixed values of V and T.

Fig. 8
figure 8

Dynamics of nonclassical correlations against \(\Delta _{1}\) and \(\Delta _{2}\) for \(V=80, T=0.5\). a LQU, b LQFI

Full size image
Fig. 9
figure 9

Dynamics of nonclassical correlations against \(\Delta _{2}\) for \(V=10, T=0.1\) and \(\Delta _1\in [2,5,10,15]\). a LQU, b LQFI, c LQFI vs LQU

Full size image

In Fig. 8 we plot LQU and LQFI against the tunneling parameters \(\Delta _1\) and \(\Delta _2\) with \(V = 80\) and \(T = 0.5\). We see clearly that there is a strong dependence of both quantifiers LQU and LQFI on the strengths of tunneling parameters \(\Delta _1\) and \(\Delta _2\) , and consequently, one can control and modulate the amount of quantum correlations contained in the two-coupled DQDs system by changing the strength of the tunneling coupling between DQDs. Also observed in the figure (Fig. 8) that the LQFI has better sensitivity to the change in \(\Delta _1\) and \(\Delta _2\) than LQU. To illustrate more clearly the influence of the tunneling parameters on the variation of quantum correlations, we depict in Fig. 9 the variations of LQU and LQFI versus the strength of the tunneling parameters at \(T=0.1\) and \(V=10\). We clearly see that one can modulate quantum correlations by experimentally tuning the tunneling parameters of each DQD. Furthermore, Fig. 9a, b show obviously that LQFI and LQU exhibit similar variations versus the tunneling parameters. Both of them exhibit a sudden change behavior at a critical value of \(\Delta _1\) for fixed value of \(\Delta _2\). We see also from Fig. 9c that the amount of nonclassical correlations quantified by LQFI is larger than the LQU. This result agrees with the fact that LQFI is always greater than LQU.

5 Concluding remarks

In summary, we have considered quantum correlations within two-coupled double quantum dots with an excess electron pair using the two quantifiers, LQU and LQFI. In this model, a DQD is used as a charge qubit and is solved exactly. The thermal density operator of the two-coupled DQDs is obtained analytically and described in an exact form, which allows the investigation of the thermal quantum correlations evolution within the considered quantum system. The influence of the tunneling coupling configuration, the Coulomb interaction between two electrons and the temperature on nonclassical correlations dynamics in the two-coupled DQDs system has been detailed and analyzed. We have discovered that the Coulomb potential can be used to introduce quantum correlations into such a system. Our findings also suggest that the Coulomb potential is advantageous for maintaining nonclassical correlations at low temperatures. As a result, by experimentally manipulating the Coulomb potential and tunneling parameters of each DQD, we can regulate and modify quantum correlations that can be exploited to design quantum-controlled devices based on QDs for quantum technology. We also discovered that LQU and LQFI behave similarly and that LQU is bounded by LQFI. The analysis also showed that when T is high enough, quantum correlations vanish and thermal fluctuations take over.