The Intrinsic Decoherence Effects on Nonclassical Correlations in a Dipole-Dipole Two-Spin System with Dzyaloshinsky-Moriya Interaction

Abstract

Bipolar spin systems are expected to provide a reliable and scalable platform for advances in quantum computing and nanotechnology. Thus, the survey of the dynamics of the quantum properties of such systems is of paramount importance. This work explores the dynamics of bipartite entanglement and nonclassical correlations in a dipole-dipole two spin system with Dzyaloshinsky-Moriya (DM) interaction and under the influence of the intrinsic decoherence effects. We employ logarithmic negativity to quantify quantum entanglement. Local quantum uncertainty and quantum discord are employed to capture non-classical correlations beyond entanglement in the considered system. For this purpose, we consider that the system is initially prepared in a Werner state and we explore the effect of intrinsic decoherence rate, dipolar coupling parameters between the spins, strength of the Dzyaloshinsky-Moriya interaction and the intensities of the homogeneous magnetic fields on the dynamics of the three quantifiers of correlations within the considered system. The findings reveal that intrinsic decoherence deteriorates quantum correlations, while the dipolar coupling constant diminishes the oscillatory behavior observed but enhances the robustness of bipartite entanglement and nonclassical correlations. The negative effects of the intrinsic decoherence on the quantum correlations can be mitigated by adjusting the values of the system’s parameters as well as the Dzyaloshinsky-Moriya coupling parameter. We also show that the three studied measures behave quasi-similarly. Finally, we depict that the amounts of entanglement and nonclassical correlations within the system are closely tied to the system’s degree of purity.

1 Introduction

Quantum entanglement is a very precious resource in the implementation of numerous quantum protocols, such as teleportation protocol [1,2,3], quantum sensing [4], quantum cryptography [5], Quantum secret sharing [6] etc. However, it has been demonstrated that quantum entanglement does not fully account for quantum correlations [7, 8]. The first quantifier introduced to capture nonclassical correlations beyond entanglement was quantum discord (QD) [9, 10]. It measures the difference between total correlations and classical correlations contained in a quantum system. Considering the difficulty of the minimization procedure required for the calculation of QD, analytical expressions of this latter were only attained in a limited number of cases, e.g. two-qubit states [7, 8, 11] and bipartite quantum X-states [9, 10, 12]. To overcome the difficulty of calculation of the quantum discord, other quantifiers were proposed. Girolami et al. [13] established the notion of local quantum uncertainty (LQU), based on the Wigner-Yanase skew information [14, 15], which is another discord-like genuine measure of nonclassical correlations in composite quantum systems. Due to its stability under local unitary transformations and disappearance for classically correlated states, the LQU is a good quantifier of nonclassical correlations and it has been thoroughly explored and analyzed in various articles (see for example [16,17,18,19,20,21]).

On the other hand, the realistic quantum information processing schemes are usually affected by decoherence’s effects and as a result, quantum systems cannot be shielded against decoherence. Incorporating stable and reliable quantum technologies is complicated by this issue. Besides, decoherence can occur even in closed systems, as Milburn [22, 23] shows with intrinsic decoherence model. Several authors have examined this decoherence framework in depth [24,25,26,27]. It entails changing the Schrödinger equation, which expresses the system’s time evolution, in order to eliminate the quantum system’s coherence. The intrinsic decoherence model put forth by Milburn is based on a particular modification of quantum mechanics in which it is assumed that, for a brief enough time step, the considered system is evolving continually in accordance with a stochastic sequence of identical unitary phase transformations rather than as a result of a unitary evolution. It is important to note that numerous publications have conducted extensive research on the impact of intrinsic decoherence in quantum systems [28,29,30,31,32,33,34,35].

The dipolar spin system, which can generate a substantial number of qubits, maintain their coherence for a long period of time, and adjust their magnetic properties electronically, is one of the potential prototypes for studying a variety of quantum phenomena. These characteristics can be achieved through numerous solid-state spin systems, including quantum spin systems [36, 37], rotational-states of molecular ions, hyperfine states of atoms [38] and nitrogen vacancy-centers in diamond [39, 40]. The dipolar spin system can be manipulated to create quantum gates [41] and it may constitute a valuable quantum channel in quantum communication [42]. In addition, many other works have been carried out on the study of the spin dipolar systems [43,44,45]. In this study, we address the dynamics of logarithmic negativity, LQU and quantum discord as, respectively, bipartite entanglement and quantum correlations quantifiers in a dipolar coupled spins system under Dzyaloshinsky-Moriya interaction with the impact of intrinsic decoherence. We focus on the combined impact of intrinsic decoherence rate and the dipolar interaction coupling parameters on the evolution of bipartite entanglement and non-classical correlations within the system under consideration. We also explore the influence of the chosen initial state parameters on the evolution of quantum correlations. In the present manuscript, we opted for the well-known Werner state [46] to be our initial system density matrix. Other works studied quantum correlations in two-qubit Werner states, and more particularly the influence of the DM interaction on correlations in these states [47]. The Dzyaloshinsky-Moriya (DM) interaction was first introduced in [48, 49]. And it has been established that the DM interaction is of significant importance for the control of quantum correlations in certain quantum systems (see for instance the refs [50,51,52]. The DM interaction also has wider fields of applications, e.g. quantum metrology [53], parameter estimation [54], heat rectification [55] and quantum game theory [56].

The outline of the present manuscript is as follows. In Section 2 we present the review of the literature on the formulae for logarithmic negativity (LN), local quantum uncertainty and quantum discord quantifiers. In Section 3, we provide the Hamiltonian of the dipolar coupled-spins system with DM interaction and employ Milburn’s intrinsic decoherence model to determine its density matrix over time. In Section 4, the behaviors of logarithmic negativity, LQU, and quantum discord in the system under consideration are illustrated and analyzed. In Section 5, final remarks are provided.

2 Measures of Quantum Correlations

The definitions and explicit expressions of the three most relevant quantifiers utilized in this manuscript, namely logarithmic negativity as a quantum entanglement measure, local quantum uncertainty and quantum discord as non-classical correlations quantifiers, are summarized in this section.

2.1 Logarithmic Negativity

The LN is among the most prominent and effectively computable measures of entanglement within two-qubit systems [57, 58]. It is defined for a density matrix ϱ characterising a two-qubit system AB and operating on a Hilbert space ${\mathcal H}={\mathcal H}^{A} \otimes {\mathcal H}^{B}$ as

$$ {\mathcal L_{N}}({\varrho})=\log_{2}\|{\varrho}^{T_{2}}\|_{1}, $$

(1)

with ${{\varrho }^{T_{2}}}$ refers to the partially transposed bipartite density matrix of the operator ϱ, regarding the second party [59, 60]. The Schatten–1 norm (trace norm) of an operator symbolized by ∥.∥₁ in (1), is defined as

$$ \|\kappa\|_{1}=Tr\left( \sqrt{\kappa^{\dagger}\kappa}\right). $$

(2)

${\mathcal L_{N}}({\varrho })$ is an additive quantity and an entanglement monotone under deterministic LOCC operations [61]. Following the definition (1), it is possible to determine ${\mathcal L_{N}}({\varrho })$ based on the absolute values of eigenvalues {ν_i} of the partial transpose density operator ${{\varrho }}^{T_{2}}$ as

$$ {\mathcal L_{N}}({\varrho})= \log_{2} \left( {\sum}_{i} |\nu_{i}| \right ) $$

(3)

with $0\leq {\mathcal L_{N}}({\varrho })\leq 1$ such that ${\mathcal L_{N}}({\varrho })=0$ indicates that the state ϱ is completely separable, whereas ${\mathcal L_{N}}({\varrho })=1$ denotes a state ϱ with maximal entanglement.

2.2 Local Quantum Uncertainty

We introduce here LQU, which is one of the nonclassical correlations quantifiers used in this study. We consider a composite system represented by the density matrix ϱ, the LQU is calculated by minimizing the Wigner–Yanase skew information (WYSI) $\mathcal {I}({\varrho }, {\Lambda }_{A} \otimes \mathbb {I}_{B})$ [14] over the ensemble of all observables acting on the first subsystem as [62, 63]

$$ \mathcal{U}({\varrho}) \equiv \min_{{\Lambda}_{A}} \mathcal{I}({\varrho}, {\Lambda}_{A} \otimes \mathbb{I}_{B}), $$

(4)

with Λ_A being the local observable acting on the subsystem A, $\mathbb {I}_{B}$ is the identity matrix operating on the second subsystem B and

$$ \mathcal{I}({\varrho}, {\Lambda}_{A} \otimes \mathbb{I}_{B})=-\frac{1}{2}\text{Tr}([\sqrt{{\varrho}}, {\Lambda}_{A} \otimes \mathbb{I}_{B}]^{2}) $$

(5)

For a local observable Λ_A verifying $\mathcal {I}({\varrho }, {\Lambda }_{A}\otimes \mathbb {I}_{B})=0$, the bipartite quantum system does not contain nonclassical correlations. For bipartite systems composed of two qubits, the LQU can be explicitly expressed as follows [13]

$$ \mathcal{U}\left( {{{\varrho}}} \right) = 1 - \omega_{max}({\mathcal{W}_{AB}}) $$

(6)

where $\omega _{max}({\mathcal {W}_{AB}})$ is the maximal eigenvalue of the (3 × 3)-symmetric matrix designated by ${\mathcal {W}_{AB}}$ whose entries are provided by

$$ (\omega)_{ij} \equiv \text{Tr} \left\{\sqrt{{\varrho}} \left( \sigma_{Ai}\otimes \mathbb{I}_{2}\right)\sqrt{{\varrho}} \left( \sigma_{Aj}\otimes \mathbb{I}_{2}\right)\right\} $$

(7)

with σ_Ai(i = x,y,z) are the Pauli matrices acting on the first subsystem.

2.3 Quantum Discord

The quantum discord (QD) [7] is the third promising indicator of quantum correlations used in this work. In a two-qubit system AB, QD is given by the difference between the quantum mutual information ${\mathcal I}({\varrho }_{AB})$ and the classical correlations ${\mathcal C}({\varrho }_{AB})$ in the system

$$ {\mathcal D}({\varrho}_{AB})= -{\mathcal C}({\varrho}_{AB}) + {\mathcal I}({\varrho}_{AB}), $$

(8)

with

$$ {\mathcal I}({\varrho}_{AB})={\mathcal S}({\varrho}_{B})-{\mathcal S}({\varrho}_{AB})+ {\mathcal S}({\varrho}_{A}) $$

(9)

and

$$ {\mathcal C}({\varrho}_{AB})={\mathcal S}({\varrho}_{A})- min_{\{{\pi_{i}^{B}}\}}{\sum}_{i}p_{i}{\mathcal S}({\varrho}_{A|i}). $$

(10)

${\mathcal S}({\varrho })=-Tr({\varrho } \log _{2} {\varrho })$ is the Von-Neumann entropy [61]. ϱ_A and ϱ_B are the reduced density operators corresponding, respectively, to the subsystems A and B. $\/{\left \{ {\pi _{B}^{i}}\right \}}={|i_{B} \rangle \langle i_{B} |}$ is the complete ensemble of orthonormal projectors acting only on the second subsystem B. While ${\varrho }_{A|i}=\frac {Tr_{B}({\pi _{B}^{i}}{\varrho }_{AB} {\pi _{B}^{i}})}{p_{i}}$ is the resulting state of the first subsystem A after getting the result i on B, and $p_{i}= Tr_{AB} ({\pi _{B}^{i}} {\varrho }_{AB} {\pi _{B}^{i}})$ is the probability of having i as a result. Following the relations (9) and (10), the quantum discord (8) can be rewritten as [8]

$$ {\mathcal D}({\varrho}_{AB}) = min_{ \left\lbrace {\pi_{B}^{i}} \right\rbrace }[{\mathcal S}({\varrho}_{AB}/{\left\{ {\pi_{B}^{i}}\right\}} ]+{\mathcal S}({\varrho}_{B}) -{\mathcal S}({\varrho}_{AB}). $$

(11)

It is difficult to find analytical formulas for QD (11) within general arbitrary quantum states due to the minimization process required for the conditional entropy. Indeed, the exact analytical expressions for this latter were only obtained for a limited number of states, for instance the X-states. In this work, the state describing our considered system is actually written in the form of an X state. For X-states

$$ {\varrho}_{AB} = {\begin{bmatrix} {{{\varrho}_{11}}}&0&0&{{{\varrho}^{*}_{14}}}\\ 0&{{{\varrho}_{22}}}&{{{\varrho}^{*}_{23}}}&0\\ 0&{{\varrho}_{23}}&{{{\varrho}_{33}}}&0\\ {{\varrho}_{14}}&0&0&{{{\varrho}_{44}}} \end{bmatrix}} $$

(12)

the quantum discord is redefined by the succeeding expression [64, 65]

$$ {\mathcal D}({\varrho}_{AB})=min\{QD_{1},QD_{2}\}, $$

(13)

with

$$ QD_{i}=H({\varrho}_{11 }+{\varrho}_{33 }) +\sum\limits_{k=1}^{4} \lambda_{k} Log_{2}(\lambda_{k})+{\mathcal D}_{i}.$$

such that, ${\mathcal D}_{1}=H(\delta )$, ${\mathcal D}_{2}=-{\sum }_{n=1}^{4}{\varrho }_{nn} Log_{2}({\varrho }_{nn}) -H({\varrho }_{11 }+{\varrho }_{33})$ and $\delta =\frac {1+\sqrt {[1-2({\varrho }_{44 }+{\varrho }_{33 })]^{2}+4 (|{\varrho }_{23}|+|{\varrho }_{14}|)^{2}}}{2}$. The function H(ν) = −νLog₂(ν) − (1 − ν)Log₂(1 − ν) is the binary Shannon entropy. λ_k’s denote the eigenvalues of the density matrix ϱ_AB. Since the expressions of the three quantifiers, LN, LQU and QD are dependent on different mathematical formulae, each of them recognises a distinct type of quantum correlations. Quantum discord is based on the idea that classical information shared between two subsystems can be extracted by measuring one of them and refers to the discrepancy between mutual quantum information and classical correlations. The LQU attempts to quantify the minimal quantum uncertainty generated in a quantum state by measuring a single local observable. The logarithmic negativity is defined by the partial transposition of the density matrix of the system with respect to one of the two parts. In order to illustrate the differences and similarities in the behaviour of the three above-mentioned quantifiers, we perform here a comparative analysis between them with respect to the intrinsic decoherence rate, the dipolar coupled spins system parameters and the degree of purity of the initial Werner state.

3 Dipole–Dipole Two-Spin System

We consider a dipolar coupled-spins system with DM interaction acting in concert with external homogeneous magnetic fields. The magnetic field produced by the magnetic moment of a spin $\vec {\mu }=-\mu _{\mathcal B}g \vec {S}$ [42, 66] on the site of another spin, gives rise to the dipolar interaction. $\mu _{\mathcal B}$ stands for the magneton of Bohr and g is the gyromagnetic factor. Such system is governed by the Hamiltonian given by

$$ \hat{H} = -\frac{1}{3}{\vec{\sigma}_{1}^{T}}\cdot T\cdot{\vec{\sigma}_{2}} + D_{z}\left( {\sigma_{1}^{x}}{\sigma_{2}^{y}}-{\sigma_{1}^{y}}{\sigma_{2}^{x}}\right)+ B_{1}{\sigma_{1}^{z}} + B_{2}{\sigma_{2}^{z}}, $$

(14)

where T = diag(Δ − 3𝜖,Δ + 3𝜖,− 2Δ) is a diagonal tensor, ${\vec {\sigma }_{j}} = \{ {{\sigma _{j}^{x}}},{{\sigma _{j}^{y}}},{{\sigma _{j}^{z}}}\}$ is the Pauli operator vector, 𝜖 and Δ are the dipolar coupling parameters between the two spins. These variables affect the spin’s spatial and relative orientation [66]. Furthermore, Δ < 0 stands for spin in the x − y plane, whereas Δ > 0 stands for spin in the z-axis. According to the z-axis, B_i is the external magnetic field that is operating on the qubit i with {i = 1,2}. D_z denotes the strength of the Dzyaloshinsky-Moriya interaction along the z-axis. We notice that all parameters are dimensionless. In the computational basis {|jk〉; j,k = 0,1}, the Hamiltonian (14) can be represented as:

$$ \hat{H} = \left( \begin{array}{cccc} \frac{2}{3} {\Delta} + B_{1} + B_{2} & 0 & 0 & 2\epsilon \\ 0 & - \frac{2}{3} {\Delta} + B_{1} - B_{2} & - \frac{2}{3} {\Delta} +2iD_{z} & 0 \\ 0 & - \frac{2}{3} {\Delta} -2iD_{z} & - \frac{2}{3} {\Delta} + B_{2} - B_{1} & 0 \\ 2\epsilon & 0 & 0 & \frac{2}{3}{\Delta} -(B_{1} + B_{2}) \end{array}\right) ~, $$

(15)

Through a straightforward calculation, we can determine the Hamiltonian’s (15) eigenvalues and related eigenvectors.

$$ \begin{array}{@{}rcl@{}} \mathcal{V}_{1}&=&-\frac{2}{3} \Big({\Delta}+\sqrt{9 \big({D_{z}^{2}} + (\frac{ B_{2} - B_{1}}{2} )^{2} \big)+{\Delta}^{2}} \Big),\\ |u_{1} \rangle&=&{\varOmega}_{+}\left( \frac{\Delta-3 i D_{z}}{\frac{3}{2}(B_{1} - B_{2} )+\sqrt{9 ({D_{z}^{2}}+(\frac{ B_{2} - B_{1}}{2} )^{2})+{\Delta}^{2}}}\left| 01\right\rangle+\left| 10\right\rangle\right), \end{array} $$

(16)

$$ \begin{array}{@{}rcl@{}} \mathcal{V}_{2}&=& -\frac{2}{3} \Big({\Delta}-\sqrt{9 \big({D_{z}^{2}} + (\frac{ B_{2} - B_{1}}{2} )^{2} \big)+{\Delta}^{2}} \Big),\\ |u_{2}\rangle&=&{\varOmega}{-}\left( \frac{\Delta-3 i D_{z}}{\frac{3}{2}(B_{1} - B_{2} )-\sqrt{9 ({D_{z}^{2}}+(\frac{ B_{2} - B_{1}}{2} )^{2})+{\Delta}^{2}}}\left| 01\right\rangle+\left| 10\right\rangle\right), \end{array} $$

(17)

$$ \begin{array}{@{}rcl@{}} \mathcal{V}_{3}&=& \frac{2}{3} \Big({\Delta}-3\sqrt{\big(\frac{ B_{2} + B_{1}}{2} \big)^{2}+\epsilon^{2}} \Big), \\ |u_{3}\rangle&=&\alpha_{-}\left( \frac{\frac{ B_{2} + B_{1}}{2}-\sqrt{(\frac{ B_{2} + B_{1}}{2} )^{2}+\epsilon^{2}}}{\epsilon}\left| 00\right\rangle+\left| 11\right\rangle\right), \end{array} $$

(18)

$$ \begin{array}{@{}rcl@{}} \mathcal{V}_{4}&=& \frac{2}{3} \Big({\Delta} + 3\sqrt{\big(\frac{ B_{2} + B_{1}}{2} \big)^{2} +\epsilon^{2}} \Big),\\ |u_{4}\rangle&=&\alpha_{+}\left( \frac{\frac{ B_{2} + B_{1}}{2}+\sqrt{(\frac{ B_{2} + B_{1}}{2} )^{2}+\epsilon^{2}}}{\epsilon}\left| 00\right\rangle+ \left| 11\right\rangle \right). \end{array} $$

(19)

where ${\varOmega }_{\pm }=\frac {1}{\sqrt {1+\left |\frac {- 3 i D_{z}+ {\Delta }}{\frac {3}{2}(B_{1} - B_{2} )\pm \sqrt {9 ({D_{z}^{2}}+(\frac { B_{2} - B_{1}}{2} )^{2})+ {\Delta }^{2}}}\right |^{2}}}$, $\alpha _{\pm }=\frac {1}{\sqrt {1+\left | \frac {i(\frac { B_{2} + B_{1}}{2}\pm \sqrt {(\frac { B_{2} + B_{1}}{2} )^{2}+\epsilon ^{2}})}{i \epsilon }\right |^{2}}}$.

In order to introduce the effect of intrinsic decoherence, we use Milburn’s decoherence model [23] which supposes that quantum systems evolve continually in an arbitrary sequence of identical unitary transformations instead of a unitary evolution. The following equation (assuming $\hbar =1$) defines such evolution [23]

$$ \frac{d{\varrho}(t)}{dt} = \frac{1}{\gamma}\Bigl[e^{-i\gamma \hat{H}}{\varrho}(t) e^{i\gamma \hat{H}}-{\varrho}(t)\Bigr], $$

(20)

The time evolved operator ϱ(t) is the density matrix associated to the Hamiltonian $\hat {H}$, and γ is the intrinsic decoherence constant. Thus in the limit of $\gamma ^{-1} \rightarrow \infty$, there is no intrinsic decoherence, and (21) is reduced to the typical von Neumann equation characterising an isolated quantum system evolution. Milburn altered the Schrödinger equation to include a term that allows quantum coherence to be spontaneously destroyed throughout the evolution of the quantum system without intervention from the reservoir and without the typical energy dissipation resulting from usual decay. The ensuing main equation is obtained

$$ \frac{d{\varrho}(t)}{dt}=-\frac{\gamma}{2}[\hat{H},[\hat{H},{\varrho}(t)]]-i [\hat{H},{\varrho}(t)]. $$

(21)

where $\frac {\gamma }{2}[\hat {H},[\hat {H},{\varrho }(t)]]$ designates the nonunitary evolution under the intrinsic decoherence in our considered dipole-dipole two-spin system. A proper solution for the equation (22) is obtained using the Kraus operators $\mathcal {\hat {M}}_{l}$ [23, 67,68,69]

$$ {\varrho}(t)= \sum\limits^{\infty}_{l=0} \mathcal{\hat{M}}_{l}(t) {\varrho}(0)\mathcal{\hat{M}}^{\dagger}_{l}{}(t) $$

(22)

with ϱ(0) being the density matrix at t = 0 of the considered system and $\mathcal {\hat {M}}_{l}(t)$ are given by

$$ \begin{array}{@{}rcl@{}} \mathcal{\hat{M}}_{l}(t) = \sqrt{\frac{(t \gamma)^{l}}{l!}} { \hat{H}}^{l} \exp\left( -i{ \hat{H}}t\right) \exp\left( -\frac{\gamma t}{2}{\hat{H}}^{2}\right) \quad \text{with} \quad \sum\limits^{\infty}_{l=0} \mathcal{\hat{M}}_{l}(t) \mathcal{\hat{M}}^{\dagger}_{l}{}(t) =\mathbb{I}. \end{array} $$

The evolved matrix density ϱ(t) of the dipole-dipole two-spin system governed by $\hat {H}$ (14) and subjected to the intrinsic decoherence effects, can be obtained by

$$ {\varrho}(t) = \sum\limits_{j,k} e^{\left[-\frac{\gamma t}{2}({ \mathcal{V}}_{j}-{\mathcal{V}}_{k})^{2}- i({\mathcal{V}}_{j}-{\mathcal{V}}_{k})t\right]} \langle u_{j}\vert{\varrho}(0)\vert u_{k}\rangle \vert u_{j}\rangle\langle u_{k}\vert, $$

(23)

where ${\mathcal {V}}_{j,k}$ and |u_j,k〉 are, respectively, the eigenvalues of the Hamiltonian $\hat {H}$ (14) and their corresponding eigenstates. Equation (24) reveals how the quantum coherence is intrinsically deteriorating as the state of the system is evolving, in the basis {|u_j,k〉} corresponding to the system. Next, we study how intrinsic decoherence affects nonclassical correlations within the dipole-dipole two-spin system subjected to the DM interaction using LQU, quantum discord, and logarithmic negativity. To approximate the influence of the intrinsic decoherence on the system’s non-classical correlations, we propose that the dipole-dipole two-spin system is originally generated in the Werner state:

$$ {\varrho}^{\psi}_{p}(0)= \frac{1-p}{4}\mathbb{I}_{2}\otimes\mathbb{I}_{2} + p|{\psi}\rangle\langle{\psi}|, $$

(24)

the parameter p varies from 0 to 1 and evaluates the degree of purity of the initial state, $\mathbb {I}_{2}$ is the identity matrix, and |ψ〉 is the maximally entangled Bell-state

$$ |{\psi}\rangle =\frac{1}{\sqrt{2}}\left( |{01}\rangle+ |{10}\rangle \right), $$

(25)

In the standard basis, the initial Werner state (25) has the appropriate X-shape

$$ \begin{array}{@{}rcl@{}} {\varrho}^{\psi}_{p}(0) = \begin{pmatrix} \frac{1-p}{4}&0&0&0 \\ 0&\frac{1+p}{4} &\frac{p}{2} &0 \\ 0& \frac{p}{2} & \frac{1+p}{4} &0 \\ 0&0&0&\frac{1-p}{4} \end{pmatrix}. \end{array} $$

(26)

We recall that for $0\leq \displaystyle p \leq \frac {1}{3}$, the Werner state ${\varrho }^{\psi }_{p}(0)$ is separable. When p = 1, the initial state is maximally entangled and demonstrates quantum advantages. It is worth noting that Werner states are a very valuable family of mixed states, since they do not violate any Bell’s inequality in the range $\frac {1}{3}<p<\frac {1}{\sqrt {2}}$ although they are entangled in this interval of p values. This unequivocally established the distinction between the quantum entanglement and the nonlocality as two different quantum resources [70, 71]. Werner states also play an important role in the description of noisy quantum channels [72] and the study of entanglement purification [73], and may be useful for computation in noisy environments. Finally, the time dependant density matrix, on which different quantum measures considered in this work would be applied to assess the evolution of nonclassical correlations in the dipole-dipole two-spin system, is given as follows

$$ {\varrho}(t) = \begin{pmatrix} \hat{{\varrho}}_{11}(t)&0&0&\hat{{\varrho}}_{14}(t) \\ 0&\hat{{\varrho}}_{22}(t)&\hat{{\varrho}}_{23}(t)&0 \\ 0 & \hat{{\varrho}}_{23}^{\ast}(t) & \hat{{\varrho}}_{33}(t) & 0 \\ \hat{{\varrho}}_{14}^{\ast}(t) & 0 & 0 & \hat{{\varrho}}_{44}(t) \end{pmatrix}, $$

(27)

We point out again that, knowing the Milburn’s evolution (24) and the spectrum of the Hamiltonian $\hat {H}$ (14), the obvious expression for the time evolved state ϱ(t) can be inferred by solving the evolution equation with ϱ(0) (27) as the initial state. We note that ϱ(t) preserves the X form during its temporal evolution. The non-zero time-dependent elements of ϱ(t) are expressed as

$$ \begin{array}{@{}rcl@{}} \hat{{\varrho}}_{11}(t) &=&\frac{1-p}{4}, \end{array} $$

(28a)

$$ \begin{array}{@{}rcl@{}} \hat{{\varrho}}_{22}(t) &=& \frac{1}{64(9{D_{z}^{2}}+{\Delta}^{2})^{2}}\Big[\zeta_{-}^{2}\Big(-8p\varphi_{-}{\Delta}+(1+p)(36{D_{z}^{2}}+\varphi_{-}^{2}+4{\Delta}^{2})\Big)+\zeta_{+}^{2}\Big(-8p\varphi_{+}{\Delta}\\ &&+(1+p)(36{D_{z}^{2}}+\varphi_{+}^{2}+4{\Delta}^{2})\Big)-24e^{-\frac{2}{9}t\gamma\chi^{2}}p\zeta_{-}\zeta_{+}\Big(2(B_{1}-B_{2}){\Delta}\cos(\frac{2t\chi}{3})\\ &&-2D_{z}\chi\sin(\frac{2t\chi}{3})\Big)\Big], \end{array} $$

(28b)

$$ \begin{array}{@{}rcl@{}} \hat{{\varrho}}_{33}(t) &=& \frac{1}{16(9{D_{z}^{2}}+{\Delta}^{2})}\Big[\varphi_{-}\Big(\varphi_{-}+p(-12iD_{z}-4{\Delta}+\varphi_{-})\Big)-\frac{8p\varphi_{+}{\Delta}}{\varpi_{+}^{2}}\\ &&+(1+p)(36{D_{z}^{2}}+\varphi_{+}^{2}+4{\Delta}^{2})\\ &&+\frac{24e^{-\frac{2}{9}t\gamma\chi^{2}}p}{\varpi_{-}\varpi_{+}}\Big(2(-B_{1}+B_{2}){\Delta}\cos(\frac{2t\chi}{3})-2D_{z}\chi\sin(\frac{2t\chi}{3})\Big)\Big], \end{array} $$

(28c)

$$ \begin{array}{@{}rcl@{}} \hat{{\varrho}}_{44}(t) &=& \frac{1-p}{4}. \end{array} $$

(28d)

and the only non-zero off-diagonal entry is

$$ \begin{array}{@{}rcl@{}} \hat{{\varrho}}_{23}(t) &=&\frac{-i}{4(6D_{z}-2i{\Delta})(6D_{z}+2i{\Delta})^{2}}\Big[\frac{\zeta_{+}}{\varpi_{+}}\Big(-8p\varphi_{+}{\Delta}+(1+p)(36{D_{z}^{2}}+\varphi_{+}^{2}+4{\Delta}^{2})\Big)\\ &&+\frac{\zeta_{-}}{\varpi_{-}}\Big(\varphi_{-}(\varphi_{-}+p(-12iD_{z}+\varphi_{-}-4{\Delta}))+(6D_{z}+2i{\Delta})(6D_{z}(1+p)\\ &&-2i({\Delta}+p(-\varphi_{-}+{\Delta})))\Big)\\ &&+\frac{24e^{-\frac{2}{9}t\gamma\chi^{2}}p}{\varpi_{-}\varpi_{+}}\Big(\varphi_{+}(iD_{z}\chi-{\Delta}(B_{1}-B_{2}))(\cos(\frac{2t\chi}{3})-i\sin(\frac{2t\chi}{3}))\\ &&-\varphi_{-}(iD_{z}\chi+{\Delta}(B_{1}-B_{2}))(\cos(\frac{2t\chi}{3})+i\sin(\frac{2t\chi}{3}))\Big)\Big]. \end{array} $$

(29)

where $\chi = 2\sqrt {9 ({D_{z}^{2}}+(\frac { B_{2} - B_{1}}{2} )^{2})+ {\Delta }^{2}}$,φ_± = 3(B₁ − B₂) ± χ, $\varpi _{\pm }=1+\left |\frac {\varphi _{\pm }}{6D_{z}-2i {\Delta }}\right |^{2}$, $\zeta _{\pm }=\frac {\varphi _{\pm }}{\varpi _{\pm }}$

We emphasise that the well-known Werner states have also been the subject of other works and from many perspectives. Thus, in the paper [47], the authors studied the effect of the DM interaction on the quantum correlations exhibited by an evolved density matrix ρ(t) = U(t)ρ(0)U^‡(t) obtained by applying the unitary time evolution operator U(t) = e^−iHt to a density matrix ρ(0) initially prepared in a Werner state or a maximally-entangled mixed state (MEMS). When the initial state chosen is a Werner state (ρ(0)), it is found in [47] that the DM interaction considered in a given direction has no effect on the quantum correlations.

4 Results and Discussions

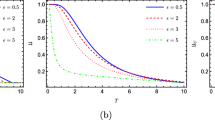
In this section, we survey the temporal evolution of quantum correlations within the dipolar coupled spins system subjected to the interplay of Dzyaloshinsky-Moriya interaction and the influence of intrinsic decoherence. In our study, logarithmic negativity (LN) is used to quantify entanglement, whilst quantum discord (QD) and LQU characterize nonclassical correlations in the given system. First of all, we note that due to the form of the initial Werner state chosen (25), the dipolar coupling constant between spins 𝜖 does not appear in the expressions of the density matrix elements (??)-(29); thus its effect can’t be studied in this section. In contemplation of the impact of the system’s configuration, we investigate the impact of each parameter and present a useful comparison between the three metrics. We start by visualizing in Fig. 1 the effect of the intrinsic decoherence on quantum correlations within the dipolar coupled spins system.

Fig. 1

$\mathcal {U}({\varrho })$ (a), QD (b) and a comparative of both (c) in terms of t and γ when Δ = 0.3,B₁ = 1.5,B₂ = 1,D_z = 0.5 and p = 0,9

Figure 1 shows that LQU and QD are both non-zero for t = 0, which means that the system is initially correlated. First, we notice that the initial amounts of quantum correlations captured by both quantifiers are not dependent on the rate of intrinsic decoherence γ, this is due to the fact that these initial amounts are fixed when the initial state is given. For γ = 0, both LQU and QD present non-damping oscillations with maximal amplitudes. This indicates that there is a strong exchange of information between the dipolar coupled spins system and the fields. Once the intrinsic decoherence is introduced, even for a very low γ rate, the oscillating nature of nonclassical correlations is reduced as a result of the damping factor $e^{-\frac {2}{9}t\gamma \chi ^{2}}$. This implies that intrinsic decoherence engenders a sort of barrier to information exchange between the dipolar coupled spins system and the fields. We notice that the frequency of the oscillations does not depend on the γ rate, but the amplitude decreases for increasing γ values. Moreover, we notice that for slightly high non-zero γ values, quantum correlations present a series of revival and collapse phenomena. However, the revival rate of quantum correlations is considerably diminished as γ takes more significant values. For γ = 1, the oscillatory behavior is disappeared, both measures decrease to reach a near-zero minimum value before reviving and reaching a negligible steady state. In Fig. 1(c), we clearly see that the two quantifiers behave similarly, even their oscillations are in phase. However, quantum discord captures a little more non classical correlations than LQU. Over time, the non-classical correlations contained in the system reach negligible steady states at nearly the same time t.

In Fig. 2, we explore the impact of the dipolar coupling constant Δ on the dynamics of LQU and QD. The other parameters characterizing the system are fixed to B₁ = 1.5,B₂ = 1,D_z = 0.5,p = 0.9 and γ = 0.01.

Fig. 2

$\mathcal {U}({\varrho })$ (a)-(d), QD (b)-(e) and a comparative of both (c)-(f) in terms of t and Δ when B₁ = 1.5,B₂ = 1,D_z = 0.5,p = 0.9 and γ = 0.01

Figure 2 depicts the effect of the dipolar coupling strength between the two spins Δ on quantum correlations, along z −axis when Δ > 0 in Fig. 2(a), (b) and (c) and in the x − y plane for Δ < 0 in Fig. 2(d), (e) and (f). All quantifiers exhibit the same oscillatory behavior (damping oscillations), although quantum discord having a slightly higher maximal bound than LQU. For Δ > 0, we notice that the amplitudes of both quantum quantifiers decrease for increasing dipolar coupling constant Δ, and the amount of quantum correlations captured is higher and more stable for high values of Δ. We remark particularly that as the values of the coupling parameter Δ increase, the oscillatory behavior quickly disappears and the quantum quantifiers reach greater frozen states. For an even stronger dipolar interaction between the two spins, the fluctuations of the quantum correlations disappear completely and they remain stable on their steady maximal value. It is worth noting that for Δ < 0 (Fig. 2(d), (e) and (f)), indicating that the spins are in the x − y plane, the same behavior of LQU and QD is displayed. The amounts of quantum correlations captured by both measures when Δ < 0 are nearly identical to those obtained for the corresponding values of Δ > 0 except that the oscillations are slightly phase-shifted in comparison with those shown for Δ > 0. However, the same frozen states are reached for different |Δ| strengths whether the dipolar coupled spins are oriented along the z-axis or in the x − y plane. Basically, increasing the strength |Δ| of the dipolar interaction attenuates the oscillatory behavior and leads quantum correlations to rapidly reach frozen states that show some robustness against the intrinsic decoherence.

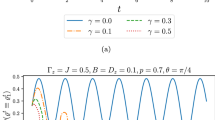
Next, we inspect the impact of the Dzyaloshinsky-Moriya interaction on nonclassical correlations contained in the dipole-dipole two-spin system. We fix the other parameters to Δ = 0.3,B₁ = 1.5,B₂ = 1,p = 0.9 and γ = 0.01.

In Fig. 3, we notice that the frequency of the oscillations is highly affected by the strength of the DM interaction. For increasing D_z values, the two measures oscillate more quickly but their oscillations are rapidly damped and vanished completely. We also see again the collapse and revival phenomena manifested by both LQU and QD. These results align with those obtained in [74]. To summarize these previous observations, we can say that despite the fact that a strong DM interaction leads to a quicker and stronger exchange of information within the system, it does not counter the negative effect of intrinsic decoherence on quantum correlations, as they are not long-preserved in the dipole-dipole coupled spin system.

Fig. 3

$\mathcal {U}({\varrho })$ (a)-(c), $\mathcal {Q}\mathcal {D}$ (b)-(d) and a comparative of both (e) in terms of t and D_z when Δ = 0.3,B₁ = 1.5,B₂ = 1,p = 0.9 and γ = 0.01

In Fig. 4, we consider the impact of the magnetic field B₂ on the LQU and QD. We note that the effects of both magnetic fields B₁ and B₂ are the same, so we choose to fix B₁ = 1,5 and vary the intensities of B₂ only.

Fig. 4

$\mathcal {U}({\varrho })$ (a) and QD (b) as functions of t and B₂ when Δ = 0.3,B₁ = 1.5,D_z = 0.5,p = 0.9 and γ = 0.01

In order to understand the impact of the external magnetic field on the dynamics of quantum correlations, we have to distinguish two cases. The first case is when B₂ = B₁ (= 1.5 in our case), for which we notice that the two quantifiers display the highest amplitudes. In fact, when the intensities of the two magnetic fields B₁ and B₂ are equal, their effect is suppressed and this can be verified in the expressions of the density matrix elements (??)-(29) where B₁ and B₂ appear in terms of the differences (B₂ − B₁) or (B₁ − B₂). For B₂ = 1.5, we observe that oscillations are indeed damped over time, due to the effect of intrinsic decoherence, but the lower bound of each quantifier does not decrease, which means that the revival phenomena is always performed starting from the same nearly zero value of the amount of quantum correlations. So in our considered system, the effect of the external magnetic field is observed in the second case where B₂≠B₁. We notice that as the difference |B₂ − B₁| increases, the oscillations of QD and LQU are quickly damped, their amplitudes decrease, and the amount of quantum correlations revives much less. For even higher values of |B₂ − B₁|, the oscillatory behavior disappears and the two quantifiers decrease abruptly to vanish completely. So large numbers of |B₂ − B₁| cancel the flow of information between the state and the fields, and we promptly reach uncorrelated frozen states.

In the following, we visualize in Fig. 5 how the purity p of the initial state affects nonclassical correlations in the dipole-dipole two spin system. We set the other parameters to Δ = 0.3,B₁ = 1.5,B₂ = 1,D_z = 0.5 and γ = 0.01.

Fig. 5

$\mathcal {U}({\varrho })$ (a) and QD (b) as functions of t and p when Δ = 0.3,B₁ = 1.5,B₂ = 1,D_z = 0.5 and γ = 0.01

We clearly see in Fig. 5 that the amount of quantum correlations increase for an increasing pureness degree p. For p = 0, both LQU and QD are null so the system does not contain discord-type quantum correlations. For sufficiently high p values, quantum correlations exhibit the typical damping oscillations behavior due to the presence of intrinsic decoherence. Once again, for relatively long time periods, we observe the occurrence of the death and revival phenomena; QD and LQU reach zero at certain times but regenerate at the exact same moment. Contrary to previous figures, where we note that the initial amounts of quantum correlations are independent of the system’s settings D_z, B, Δ and γ, the purity degree p is the only parameter affecting their initial values. Thereby, the dynamics of LQU and QD are strongly dependent on the form of the initial state, and their initial amounts are exclusively related the parameters appearing in the initial density matrix (27), in this case p.

To get an insight on the influence of the system’s configuration on entanglement captured by logarithmic negativity, we visualize the time evolution of LN for different intrinsic decoherence rates γ in Fig. 6(a), various values of the dipolar coupling constant Δ in Fig. 6(b) and different strengths of the DM interaction D_z in Fig. 6(c).

Fig. 6

${{\mathscr{L}}_{N}}({\varrho })$ as function of time t for different values of γ (a), Δ (b) and D_z (c)

We see that, for each of the three plots displayed above, previous observations related to quantum discord and local quantum uncertainty might be reiterated for logarithmic negativity, as all of the three quantifiers behave similarly. However, we clearly see that LN has larger amplitudes and a higher maximal bound compared to QD and LQU. In Fig. 6(a), we notice that in the lack of intrinsic decoherence γ = 0, oscillations are not damped so there is a perpetual back and forth between a strongly entangled state and a less entangled one. In the presence of intrinsic decoherence γ≠ 0, LN presents damping oscillations and manifests the collapse and revival phenomena. As γ increases, the oscillatory behavior is attenuated, and entanglement revives much less. However, for a given system configuration, LN reaches the same steady state (${\mathcal L_{N}}({\varrho })(t\rightarrow \infty )=0.1273$ in our case) regardless of the γ rate value. By comparing this result to the outcome in Fig. 1, we find that in the presence of external magnetic fields (B₁ = 1,5 and B₂ = 1), this system sustains more entanglement than discord-type correlations. Overall, we can state that intrinsic decoherence has deteriorating effects on both the amount and the revival rate of the entanglement within the system. It is obvious from Fig. 6(b) that large values of the dipolar coupling constant Δ minimize the oscillatory behavior but strengthen and stabilize the amount of entanglement against the effect of intrinsic decoherence, and protect it from entanglement sudden death (ESD). A strong dipolar interaction between spins enhances quantum correlations and entanglement, and helps preserving them by counteracting the intrinsic decoherence effect. Finally, we remark in Fig. 6(c) that the DM interaction has the same effect on entanglement as it does on quantum correlations captured by LQU and QD (Fig. 3). For growing D_z values, the frequency of the oscillations is increased, but they are quickly damped and entanglement is rapidly vanished.

Lastly, we plot in Fig. 7 logarithmic negativity, QD and LQU as functions of the degree of pureness p for different intrinsic decoherence rates γ.

Fig. 7

${{\mathscr{L}}_{N}}({\varrho })$ (a), $\mathcal {U}({\varrho })$ (b), QD (c) and a comparative of all in (d) as functions of p for fixed values of γ when Δ = 0.3,B₁ = 1.5,B₂ = 1,D_z = 0.5 and t = 10

It is obvious in Fig. 7 that for fixed γ rates, the degree of pureness of the system has to be increased in order to capture more quantum correlations and entanglement in the studied system. Moreover, we note that the absence of entanglement does not imply the absence of discord-type correlations, as we see that QD and LQU are non-zero even when the system is still separable for some values of the purity p. Even in the absence of intrinsic decoherence γ = 0, entanglement is not contained in the system unless a certain pureness degree is exceeded, which is quite understandable since the initial Werner state (27) is separable when $p\leq \frac {1}{3}$. In Fig. 7(d), it is clear that despite the fact that logarithmic negativity requires better purity of the system to be non-zero, we notice that for increasing values of p, LN bounds both QD and LQU. More accurately, when $p \rightarrow 1$, indicating that the initial state (25) is relatively close to the maximally entangled pure state (|ψ〉〈ψ|), the dipolar-coupled spins system exhibits more quantum entanglement than quantum correlations.

5 Conclusion

To conclude, we have surveyed the temporal evolution of logarithmic negativity, LQU and quantum discord as, respectively, entanglement and quantum correlations quantifiers within a dipole-dipole two-spin system with Dzyaloshinsky-Moriya interaction and under the intrinsic decoherence effect. We deduced that all three quantifiers behave similarly, they exhibit damping oscillations over time due to the presence of the intrinsic decoherence, and manifest the collapse and revival phenomena depending on the values of different parameters characterising the system. The dynamics of the studied measures depend strongly on the form of the initial state, we chose to work with a Werner state so the density matrix obtained is independent of the dipolar coupling constant between spins 𝜖, consequently the effect of this latter was not studied in this paper. Regarding the other parameters, we found that, as it is widely known, increasing the intrinsic decoherence parameter degrades both the amount and the revival rate of quantum correlations. While large values of the dipolar coupling constant between spins Δ attenuate the oscillatory behavior of the quantum quantifiers and allow them to be more stable and robust against the effect of the intrinsic decoherence. On the other hand, we concluded that high strengths of the DM interaction lead to a rapid damping of oscillations over time and urge the irreversible loss of quantum correlations and entanglement, but the value of D_z can be adjusted to modify the frequency of the information exchange within the dipolar coupled spins system. Lastly, we evoke that entanglement is tightly linked to the degree of pureness of the system, thus we found that the system is entangled only when a certain value of p is exceeded. Below this value, which varies depending on the other parameters too, the dipole-dipole two-spin system is separable but may contain non-classical correlations other than entanglement. The findings of this study provide a deeper knowledge of the impact of intrinsic decoherence and the initial Werner state parameters on the dynamics of entanglement and nonclassical correlations in the dipolar coupled spins system with DM interaction and can contribute to a more profound understanding of the quantum properties of such systems, which are a potential candidate for quantum technology implementation.