Dephasing effects on nonclassical correlations in two-qubit Heisenberg spin chain model with anisotropic spin–orbit interactions

Abstract

The advancement of quantum information hinges on the scalability of quantum systems to maintain non-local characteristics and improve the efficiency of quantum protocols. Strategies to enhance nonclassical correlations within quantum systems while mitigating decoherence phenomena are searing topics nowadays. Our study delves into the dynamics of nonclassical correlations within a two-qubit Heisenberg spin XXX model, utilizing Milburn’s dynamical master equation. We consider the impacts of anisotropic spin–orbit interactions, such as the Dzyaloshinskii–Moriya (DM) interaction and Kaplan–Shekhtman–Entin–Wohlman–Aharony (KSEWA) interaction, and employ three metrics, namely Bell’s inequality violation, concurrence, and local quantum uncertainty, to examine the dynamical features of nonclassical correlations under intrinsic decoherence. Our findings showcase the significance of the initial state of the two-qubit system in determining the parameters of spin–orbit interactions that influence the nonclassicality of the system. This underscores the critical role that DM and KSEWA interactions play in nonclassical correlations in solid-state quantum systems.

1 Introduction

During the past 3 decades, the field of quantum information (QI) has emerged, which focuses on manipulating single units of information called qubits. An important aspect of QI theory involves the study of quantum correlations among qubits, which provide information on quantum coherence, entanglement, and other properties of QI. Due to this, cutting-edge concepts such as quantum computers, quantum cryptography, and quantum teleportation have been developed [1, 2].

The Bell theorem is a significant milestone in quantum physics that demonstrates the limitations of locality assumptions. It reveals correlations between particles that classical physics cannot explain, emphasizing the need to properly understand these phenomena through quantum mechanics [3]. Quantum non-locality is a correlation between measurement outcomes obtained in different laboratories that cannot be explained by local hidden-variable theories [4]. Bell inequalities are utilized to assess the predictions of these theories against experimental observations [5,6,7]. The CHSH inequality, a specific violation of Bell’s inequality, establishes an upper limit on the quantum violation of certain Bell inequalities [8, 9].

Besides, an interesting aspect of quantum physics that has a significant resource in the realm of QI theory is the phenomenon of entanglement, as it highlights the non-local nature of the quantum states of two or more subsystems of a composite quantum state and emphasizes their indivisible nature, which is mathematically indicative of the non-separability [2, 10]. It is crucial, however, to grasp the distinction between quantum correlations and entanglement, as they are interrelated yet distinct. Quantum correlations refer to the statistical association between measurements of two or more quantum systems, going beyond entanglement [11]. Entanglement is a prerequisite but not a sufficient condition for quantum correlations. Quantum systems can exhibit quantum correlations without being entangled, which is the case for the Werner separable mixed states [12]. In this regard, quantum discord has been introduced to identify the genuine quantumness of correlations, revealing other quantum states correlated differently than those identified by entanglement [12, 13]. However, obtaining an analytical expression of quantum discord is only possible for certain classes of states, and the situation is rather challenging in the general state, even for a two-qubit state [14]. A new geometric formulation of quantum discord, called trace distance discord, has been introduced as a valuable tool for QI research [15, 16]. It measures the distance between a given quantum state and zero-discord classical-quantum states based on the Schatten 1-norm [17,18,19]. Local quantum uncertainty (LQU) has also been proposed as a proper metric to detect nonclassical correlations [20]. This reliable quantifier fulfills all the conditions required for a quantum correlation measurement and is easily computable, unlike other metrics. LQU is based on the skew information notion induced by Wigner and Yanase and is also associated with quantum Fisher information, which constitutes a key tool in quantum metrology protocols [21,22,23].

In the field of QI theory, it is crucial to identify potential quantum systems that can leverage quantum resources for the development of quantum technologies and information transfer protocols. The quantum correlations in solid-state systems such as spin chains are a promising emerging field. Spin chains can be used as qubits in many real physical systems, and Heisenberg spin models are the simplest spin chains in the field of condensed matter. Indeed, Heisenberg spin chains are influential models in quantum mechanics [24]. These models are utilized to investigate the ferromagnetic and antiferromagnetic properties of matter, especially in cases where the interactions between the spins could result in collective behaviors with macroscopic consequences. Ferromagnetism, for instance, is characterized by neighboring spins lining up parallel to one another, while in antiferromagnetism, neighboring spins are oriented in opposite directions. The exchange coupling is the underlying mechanism behind this spontaneous magnetization [25]. Furthermore, Heisenberg spin chains are useful approaches in quantum information applications because they hold nonclassical correlations and entanglement phenomena [26,27,28,29]. In this respect, the Heisenberg spin model is one of the natural candidates for the study and exploitation of quantum resources in experimental setups for QI processing [30]. These systems have been extensively studied in different circumstances and under different external factors such as temperature, magnetic fields, and decoherence phenomena (for instance, [31,32,33,34]). Understanding quantum correlations is essential not only for natural systems in condensed matter but also for artificially created metamaterials. This includes those created with cold atoms, ion traps, and superconducting systems [35, 36]. Having a good grasp of quantum correlations in such systems is crucial for advancing scientific and technological applications.

Besides, materials with spin–orbit coupling are particularly fascinating due to their potential to produce topological quantum states. These states play a fundamental role in various effects such as the quantum Hall effect, topological insulators, and anyonic statistics. As a result, they are a subject of great interest for researchers [37]. Antiferromagnetic crystals with tetragonal lattices, such as $\alpha -\mathrm{Fe_2O_3}$, $\mathrm{NiF_2}$, and $\mathrm{MnCO_3}$, exhibit weak ferromagnetism, a phenomenon that has been observed in the phenomenological approach developed by Dzyaloshinskii [38]. The tilting of the spins in these crystals is responsible for the weak ferromagnetism, which can be described by the term antisymmetric exchange interaction [39]. This interaction was later named the Dzyaloshinskii–Moriya (DM) interaction and is typically expressed as:

$$\begin{aligned} \hat{H}_\textrm{DM} \sim {\textbf {D}} \cdot \left( \hat{\sigma }_1 \times \hat{\sigma }_2 \right) , \end{aligned}$$

(1)

where ${\textbf {D}}=\left( D_x, D_y, D_z\right)$ denotes the DM coupling vector and $\hat{\sigma }_i^x, \hat{\sigma }_i^y$, and $\hat{\sigma }_i^z$ are the Pauli matrices associated with the two neighboring spins $(i=1,2)$. In addition, Moriya found the second-order correction term [40]:

$$\begin{aligned} \hat{H}_{\textrm{KSEWA}}=\hat{\sigma }_1 \cdot K \cdot \hat{\sigma }_2, \end{aligned}$$

(2)

where K is a symmetric traceless tensor. For a long time, this interaction was assumed to be negligible compared with the antisymmetric contribution (Eq. (1)). However, Kaplan [41] and then Shekhtman et al. [42, 43] argued the importance of the symmetric term because it can restore the O(3) invariance of the isotropic Heisenberg system, which is broken by the DM term. For this reason, the interaction of Eq. (2) began to be called the Kaplan–Shekhtman–Entin–Wohlman–Aharony (KSEWA) interaction [44].

Decoherence presents a significant challenge in the practical realization of quantum computing architectures, as it poses obstacles to the preservation and controlled manipulation of QI [45]. The scientific community has been actively engaged in efforts to combat decoherence in various quantum computing architectures, with both theoretical and experimental researchers devoting significant attention to this issue in recent years. Indeed, decoherence refers to the loss of quantum coherence in a controlled qubit system, which occurs due to the entanglement generated by unavoidable couplings to the external environment. Notably, considerable progress has been achieved in minimizing such couplings while ensuring reliable control of the quantum system [46, 47].

The present paper deals with a particular kind of decoherence that is distinct from the concept of environmental decoherence. Referred to as intrinsic decoherence, it is a mechanism whereby the coherence of a system is lost due to its intrinsic degrees of freedom. Several models have been proposed to describe intrinsic decoherence [48,49,50], one such model being the Milburn decoherence model [51].

The study of thermalization, using the Gibbs density operator at thermal equilibrium, has garnered significant interest due to the impact of temperature on all quantum systems [52, 53], leading to a reduction in the degree of quantum features. As a result, researchers have been investigating the effects of thermalization on two-qubit Heisenberg spin models [18, 27, 54, 55], particularly the isotropic two-qubit Heisenberg XXX model. This model has been thoroughly examined at thermal equilibrium in Ref. [56], shedding light on its behavior under various conditions, and the thermal state properties of the examined system were comprehensively explored. Drawing upon this foundational investigation, the principal aim of our present research is to extend these achievements by introducing the influence of the dephasing process on nonclassical correlations via the incorporation of the Milburn master equation. By doing so, we aim to enhance our understanding of the system’s behavior and the effects of the spin–orbit interactions on the quantum correlations under intrinsic decoherence, thereby contributing to a broader understanding of the subject matter.

The paper is organized as follows: Sect. 2 describes the model and the Milburn solution. In Sect. 3, we introduce quantum quantifiers that are employed in this paper. Our main results are disclosed in Sect. 4. Finally, the conclusions are presented in the last Sect. (5).

2 Description of the theoretical model and Milburn solution

In this work, we consider the bipartite system composed of a two-qubit Heisenberg XXX spin chain in the presence of DM and KSEWA spin–orbit interactions along the z-direction. The Hamiltonian is given as:

$$\begin{aligned} \hat{H}^{AB}= & {} J \sum _{i=x,y,z} \hat{\sigma }_{A}^i\hat{\sigma }_{B}^i+ D_z \left( \hat{\sigma }_A^{x} \hat{\sigma }_B^{y} - \hat{\sigma }_A^{y} \hat{\sigma }_B^{x} \right) + K_z\left( \hat{\sigma }_A^{x} \hat{\sigma }_B^{y} + \hat{\sigma }_A^{y} \hat{\sigma }_B^{x} \right) , \end{aligned}$$

(3)

where J represents the coupling exchange between the two-qubit (the chain is antiferromagnetic for $J>0$ and ferromagnetic for $J<0$), $D_z$ and $K_z$ are the DM and KSEWA spin–orbit interaction strengths in z-direction, respectively. Also, $\hat{\sigma }^i_{A(B)}$ are the usual Pauli matrices. In the following computational basis, $\mathcal {B}=\left\{ |0 \rangle =|00\rangle , |1\rangle =|01\rangle ,|2\rangle =|10\rangle , |3\rangle =|11\rangle \right\}$, the matrix form of the Hamiltonian system is given by:

$$\begin{aligned} \hat{H}^{AB}=\left( \begin{array}{cccc} J &{} 0 &{} 0 &{} -2 i K_z \\ 0 &{} -J &{} 2\eta &{} 0 \\ 0 &{} 2\eta ^* &{} -J &{} 0 \\ 2 i K_z &{} 0 &{} 0 &{} J \\ \end{array} \right) , \end{aligned}$$

(4)

where $\eta =J+i D_z$ and the asterisk ($^*$) denotes the complex conjugate. The eigenvalues of the Hamiltonian system are given by:

$$\begin{aligned} \chi _{1,2}=J\pm K_z \hspace{0.5cm} \text {and} \hspace{0.5cm} \chi _{3,4}=-J\pm 2|\eta |, \end{aligned}$$

(5)

and the corresponding eigenvectors are

$$\begin{aligned} \vert \phi _{1,2}\rangle =\frac{1}{\sqrt{2}} \left[ \pm i|0\rangle +|3\rangle \right] \hspace{0.5cm} \text {and} \hspace{0.5cm} \vert \phi _{3,4}\rangle =\frac{1}{\sqrt{2}} \left[ \pm \frac{\eta }{|\eta |}|1\rangle +|2\rangle \right] . \end{aligned}$$

(6)

To take into account the intrinsic decoherence, Milburn introduced a straightforward adjustment of conventional quantum mechanics by assuming that over sufficiently short time steps, the system does not evolve continuously under unitary evolution, but rather in a stochastic sequence of identical unitary transformations [51]. This assumption led to a modification of the Schrödinger’s equation by incorporating a term responsible for the decay of quantum coherence in the energy eigenstate basis, without any intervention of a reservoir and thus without the usual energy dissipation associated with normal decay. Milburn obtained the subsequent master equation given by:

$$\begin{aligned} \frac{\text {d} \hat{\rho }^{A B}(t)}{\text {d}t}=-i\left[ \hat{H}^{A B}, \hat{\rho }^{A B}(t)\right] -\frac{\gamma }{2}\left[ \hat{H}^{A B},\left[ \hat{H}^{A B}, \hat{\rho }^{A B}(t)\right] \right] , \end{aligned}$$

(7)

where $\hat{H}^{A B}$ is the Hamiltonian of the system, $\hat{\rho }^{A B}(t)$ denotes the state of the system, and $\gamma$ (which corresponds to $\gamma ^{-1}$ in Milburn’s paper) quantifies the phase decoherence rate. In the right part of Eq. (7), the first term generates the system’s coherent unitary time evolution, while, the second term, which does not commute with the Hamiltonian, induces the decoherence effect, which corresponds to phase damping. The formal solution of the above equation can be written in operator-sum representation using the Kraus operators $\hat{Q}^\text {k}$ as [57,58,59]:

$$\begin{aligned} \hat{\rho }^{AB}(t)=\sum _{k=0}^{\infty } \frac{(\gamma t)^{k}}{k !} \hat{Q}^\text {k}(t) \hat{\rho }^{AB}(0) (\hat{Q}^\textrm{k}(t))^\dagger , \end{aligned}$$

(8)

where $\hat{\rho }^{A B}(0)$ is the density matrix of the initial state and $\hat{Q}^\text {k}(t)$ is defined by:

$$\begin{aligned} \hat{Q}^\text {k}(t)=H^k e^{-i \hat{H}^{A B}t} e^{-\frac{t \gamma \left( \hat{H}^{A B}\right) ^2}{2}}. \end{aligned}$$

(9)

Then, the resulting state can be written as:

$$\begin{aligned} \hat{\rho }^{AB}(t)=\sum _{m,n=1}^{4}\exp \left[ -i(\chi _m-\chi _n)t-\frac{\gamma }{2}(\chi _m-\chi _n)^2t\right] \times \langle \phi _{m}| \hat{\rho }^{A B}(0) |\phi _n\rangle |\phi _m\rangle \langle \phi _n|, \end{aligned}$$

(10)

where $\chi _{m,n}$, $\vert \phi _{m,n}\rangle$ are, respectively, the eigenvalues and eigenvectors of the Hamiltonian, which govern the dynamical evolution of the system.

Next, we shall discuss the exact solution of Milburn’s master equation in two particular cases, the symmetric and non-symmetric Bell-like states.

2.1 Symmetric Bell-like state

We consider here the situation where the initial state of the system is symmetric, that is, $|\psi (0)\rangle =\cos (\theta )|0\rangle +\sin (\theta )|3\rangle$. The density matrix takes the form

$$\begin{aligned} \hat{\rho }^{AB}(t)=\sum _{i,j=1,4}\varrho _{ij} |i-1\rangle \langle j-1|, \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{aligned}&\varrho _{11}(t)=\frac{1}{2}\left[ 1+e^{-8\gamma K_z^2t}\cos [2(\theta +2K_zt)]\right] ,\\&\varrho _{44}(t)=\frac{1}{2}\left[ 1-e^{-8\gamma K_z^2t}\cos [2(\theta +2K_zt)]\right] ,\\&\varrho _{14}(t)=\frac{1}{2}e^{-8\gamma K_z^2t}\sin [2(\theta +2K_zt)]=\varrho _{41}(t).\\ \end{aligned} \end{aligned}$$

2.2 Non-symmetric Bell-like state

In this subsection, we consider that the initial state of the two qubits is non-symmetric, that is, $|\psi (0)\rangle =\cos (\theta )|1\rangle +\sin (\theta )|2\rangle$ the Milburn’s solution is

$$\begin{aligned} \hat{\rho }^{AB}(t)=\sum _{i,j=2,3}\varrho _{ij} |i-1\rangle \langle j-1|, \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned}&\varrho _{22}(t)=\frac{1}{2|\eta |}\left\{ |\eta |+e^{-8\gamma |\eta |^2t}\right. \\&\quad \left. \left[ |\eta |\cos (2\theta )\cos (4|\eta |t)+D_z\sin (2\theta )\sin (4|\eta |t)\right] \right\} ,\\&\varrho _{33}(t)=\frac{1}{2|\eta |}\left\{ |\eta |-e^{-8\gamma |\eta |^2t}\right. \\&\quad \left. \left[ |\eta |\cos (2\theta )\cos (4|\eta |t)+D_z\sin (2\theta )\sin (4|\eta |t)\right] \right\} ,\\&\varrho _{23}(t)=\varrho _{32}^*(t)=\frac{\eta }{2|\eta |^2} \left\{ J\sin (2\theta )+ie^{-8\gamma |\eta |^2t}\right. \\&\quad \left. \left[ |\eta |\cos (2\theta )\sin (4|\eta |t)-D_z\sin (2\theta )\cos (4|\eta |t)\right] \right\} . \end{aligned} \end{aligned}$$

3 Quantifiers of quantum correlations

In this section, we are interested in quantifying quantum correlations encompassed in a given two-qubit X-state, and this by introducing the mathematical expressions of three reliable quantifiers, namely Bell non-locality as a measure of the violation of Bell’s inequality, concurrence as a measure of entanglement, and local quantum uncertainty as a measure of discord-like correlation.

3.1 Bell non-locality (BL)

We utilize the maximal eigenvalues of the two-qubit Bell-CHSH function $B_\textrm{max}$ as an indicator of two-qubit non-locality [4, 60]. Indeed, Horodecki et al. discovered a necessary and sufficient condition for mixed states of two spin-$\frac{1}{2}$ particles to violate the Bell-CHSH inequality [60, 61], and the analytical expression for the two-qubit Bell-CHSH function $B_\textrm{max}$ is given by:

$$\begin{aligned} B_\textrm{max} ={2\sqrt{\xi _m+\xi _n}}, \end{aligned}$$

(13)

where $\xi _m$ and $\xi _n$ ($m,n=1,2,3$) are the largest eigenvalues of the matrix $\mathcal {A}=A^\dagger A$, and $A=[a_{ij}]$ which is derived from a two-qubit X-state, denoted by $\hat{\rho }^{AB}$. The elements of the correlation matrix A are given by [60]:

$$\begin{aligned} a_{ij} = {\text {Tr}}\{\hat{\rho }^{AB}\hat{\sigma }_i\otimes \hat{\sigma }_j\}, \end{aligned}$$

(14)

where $\hat{\sigma }_i(i=x,y,z)$, are the commonly used Pauli matrices. Furthermore, the non-locality of the two-qubit system is established when $B_\textrm{max}>2$, blue which signifies the maximum violation of the Bell-CHSH inequality. In our investigation, we quantify the Bell non-locality (BL) using the expression:

$$\begin{aligned} \text {BL} = B_\textrm{max} - 1. \end{aligned}$$

(15)

In this respect, $\text {BL}$ can be considered as a practical criterion for quantifying the degree of violation of the Bell-CHSH inequality in arbitrary two-qubit mixed states, whenever $\text {BL}>1$. (See Appendix 6.1 )

3.2 Concurrence (C)

The concurrence (C) is a bona fide quantifier of entanglement for arbitrary bipartite system AB, denoted by the state $\hat{\rho }^{AB}$. The analytical expression of the concurrence is given by Wootters formula [62]:

$$\begin{aligned} C=\max \left[ 0,2\max (\nu _k)-\sum _{k=1}^{4}\nu _k\right] , \end{aligned}$$

(16)

where $\nu _k$ are the square roots of the eigenvalues of the matrix $M=\hat{\rho }^{AB} \Gamma \hat{\rho }^{*AB} \Gamma$ and $\Gamma =\hat{\sigma }_y^A\otimes \hat{\sigma }_y^B$. Also, $\hat{\rho }^{AB}$ is the density matrix of the $2 \otimes 2$ system; it can be either pure or mixed, and $\hat{\rho }^{*AB}$ denotes its complex conjugate of $\hat{\rho }^{AB}$. $C=0$ corresponds to separable state and $C=1$ to a maximally entangled state. (See Appendix 6.2).

3.3 Local quantum uncertainty (LQU)

Local quantum uncertainty (LQU) quantifies the minimum quantum uncertainty due to a measurement of a local observable on a quantum state [20]. For a bipartite quantum state $\hat{\rho }^{AB}$, LQU is a discord-type quantifier of quantum correlations which is defined by minimizing the Wigner–Yanase skew information over all local observables $K_A$ acting on qubit $\textrm{A}$ as:

$$\begin{aligned} \text {LQU}\left( \hat{\rho }^{A B}\right) = \min _{K_A} \mathcal {I}\left( \hat{\rho }^{A B}, K_A \otimes \mathbb {I}_B\right) , \end{aligned}$$

(17)

where $\mathbb {I}_B$ is the identity operator, while the term:

$$\begin{aligned} \mathcal {I}\left( \hat{\rho }^{A B}, K_A \otimes \mathbb {I}_B\right) =-\frac{1}{2} {\text {Tr}}\{\left[ \sqrt{\hat{\rho }^{A B}}, K_A \otimes \mathbb {I}_B\right] ^2 \}, \end{aligned}$$

(18)

is the skew information [63, 64] which is an uncertainty relation introduced to provide the statistical nature of measurement errors [65]. By carrying out a minimization on the set of all observables acting on qubit $\textrm{A}$, we can derive the analytical expression of LQU for two-qubit (spin-$\frac{1}{2}$ particles) states in the following form [20]:

$$\begin{aligned} \text {LQU}\left( \hat{\rho }^{A B}\right) =1-\max \left\{ \mu _1, \mu _2, \mu _3\right\} , \end{aligned}$$

(19)

where $\mu _1, \mu _2$ and $\mu _3$ are the eigenvalues of the $3 \times 3$ matrix W defined by its matrix elements:

$$\begin{aligned} \omega _{i j} \equiv {\text {Tr}}\left\{ \sqrt{\hat{\rho }^{A B}}\left( \hat{\sigma }_i \otimes \mathbb {I}_2\right) \sqrt{\hat{\rho }^{A B}}\left( \hat{\sigma }_j \otimes \mathbb {I}_2\right) \right\} , \end{aligned}$$

(20)

with $i, j=1,2,3$ and $\hat{\sigma }_i$ are the usual Pauli matrices. (See Appendix 6.3).

4 Results and discussion

This section provides a comprehensive analysis of the quantum metrics of the system, with a specific focus on Bell non-locality (BL), concurrence (C), and local quantum uncertainty (LQU). The analysis takes into account various initial states, such as separable and maximally entangled states, and their impact under the influence of exchange coupling (J), DM interaction ($D_z$), KSEWA coupling parameter ($K_z$), and intrinsic decoherence rate ($\gamma$). The analysis is divided into two distinct scenarios. Firstly, the symmetric Bell-like initial state is considered, where the parameters $K_z$ and $\gamma$ are taken into account in the elements of the matrix $\rho (t)$ (Eq. 11). Secondly, the non-symmetric Bell-like initial state is analyzed, where the parameters J, $D_z$, and $\gamma$ are considered in the elements of the matrix $\rho (t)$ (Eq. 12).

4.1 For symmetric Bell-like initial state

The present study investigates the temporal evolution of quantum correlations in the absence of intrinsic decoherence ($\gamma =0$) and where $\theta =\pi /4$.

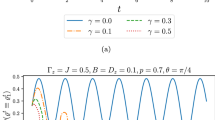
Figure 1 portrays the results of the study, where Fig. 1a demonstrates that concurrence and local quantum uncertainty are stabilized and reach their maximum values ($C=\text {LQU}=1$) when the parameter $K_z$ is equal to zero. Furthermore, the violation of Bell’s inequality is confirmed when $\text {BL}>1$. The results presented in Fig. 1b show non-damped oscillatory behavior over time where $K_z=0.5$, owing to the $\cos [2(\theta +2K_z t)]$ and $\sin [2(\theta +2K_z t)]$ terms of the matrix elements (Eq. (11)). Additionally, the measurement of local quantum uncertainty remains robust compared to the concurrence, as the region of separability ($C=0$) leaves out some correlations that are not identified as entanglement but are of the discord type (quantified here by $\text {LQU}$). Finally, Fig. 1c displays an increase in the parameter $K_z$ to a value of 1, resulting in higher periods of undamped oscillations. It is important to note that the two cases shown in Fig. 1b and c highlight the sudden death phenomenon of C and $\text {LQU}$.

Fig. 1

Temporal evolution of quantum correlations versus time t, for $\gamma = 0, \theta =\pi /4$. Where a $K_z=0$, b $K_z=0.5$ and c $K_z=1$

The following results are presented in Fig. 2, where the decoherence rate parameter is $\gamma =0.1$ and $\theta =\pi /4$. Under these conditions, Fig. 2a showcases the damping oscillations experienced by quantum correlations over time due to the term $e^{-8\gamma K_z^2 t}$ of the matrix elements $\rho$ (Eq. (11)), given a value of $K_z=0.5$. The parameter $\gamma$ accelerates the stabilization of the correlations over time, culminating in a steady state of all the quantum correlations present in the system. Moreover, $\text {LQU}$ remains robust to the effect of intrinsic decoherence by stabilizing on a nonzero steady state, while the concurrence C eventually tends toward zero. Conversely, the $\text {BL}$ measure demonstrates the non-violation of Bell’s inequality, as the effect of intrinsic decoherence explicitly manifests when this quantity tends toward 1.

Fig. 2

The same data as Fig. 1 but $\gamma = 0.1$ where a $K_z=0.5$ and b $K_z=1$

The rapid stabilization of the quantum correlations in an early time, compared to the case illustrated in Fig. 2a, and the presentation of fewer oscillations while maintaining the same steady states can be observed by increasing the parameter $K_z$ (Fig. 2b). It is important to note that the sudden death phenomenon solely concerns entanglement and not local quantum uncertainty in these two cases.

Fig. 3

The same data as Fig. 1 but for separable initial state ($\theta =\pi /2$)

The following report details of Fig. 3 demonstrate how $K_z$ affects the quantum correlations of a system under a separable initial state ($\theta =\pi /2$). The quantifiers $\text {LQU}$ and C are observed to be zero for all times when $K_z=0$, and Bell’s inequality is not violated ($\text {BL}=1$). However, when $K_z=0.5$, both quantifiers exhibit undamped oscillatory behavior as a function of time, indicating that the KSEWA coupling is the source of the oscillatory behavior. Moreover, increasing $K_z$ to 1 further increases the frequency of oscillations. These results demonstrate that the KSEWA coupling promotes the generation of quantum correlations and, in turn, the violation of Bell’s inequality ($\text {BL}>1$).

Fig. 4

The same data as Fig. 2 but for separable initial state ($\theta =\pi /2$)

In Fig. 4, we investigate the effect of the intrinsic decoherence rate, $\gamma$, on the quantifiers under the separable initial state ($\theta =\pi /2$). When $\gamma =0.1$ and $K_z=0.5$, the quantifiers exhibit damped oscillatory behavior, with $\text {LQU}$ reaching a nonzero steady state and C returning to its initial value ($C=0$). Additionally, $\text {BL}$ returns to its initial value ($\text {BL}=1$) after a few small oscillations. Setting $K_z=1$ accelerates the stabilization of the quantifiers, with fewer oscillations while retaining the same stationary states. These results demonstrate the robustness of $\text {LQU}$ compared to C. The damped oscillations observed in both figures are due to the $\cos [2(\theta +2K_z t)]$ and $\sin [2(\theta +2K_z t)]$ terms in the elements of the matrix of Eq. (11).

Fig. 5

Quantum correlations versus the KSEWA coupling parameter $K_z$ when $t=10, \gamma =0.1$ such that a $\theta =\pi /4$ and b $\theta =\pi /2$

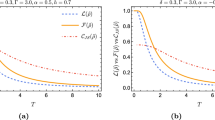
Figure 5 illustrates the quantum correlations as a function of $K_z$ under the two corresponding initial states: maximally entangled ($\theta =\pi /4$) and separable ($\theta =\pi /2$), where $\gamma =0.1$ and $t=10$. When $K_z=0$, $\text {LQU}=C=1$, indicating the optimal amount of quantum correlations in the system. In Fig. 5a, for $K_z=0$ we have $\text {LQU}=C=1$, however, as $K_z$ increases, all quantifiers oscillate and eventually return to their stationary states for large values of $K_z$. This indicates that an increase in $K_z$ has an unfavorable role in the quantum correlations in the system. The same analysis can be applied in Fig. 5b, where the initial state is separable ($\theta =\pi /2$). The quantum correlations $\text {LQU}=C=0$ when $K_z=0$. As $K_z$ increases, all quantifiers present damped oscillations as a function of time. The concurrence C returns to the value of 0, the measurement $\text {BL}$ returns to its initial state ($\text {BL}=1$), while the local quantum uncertainty $\text {LQU}$ exhibits a nonzero steady-state value.

Next, we delve into discussing the temporal evolution of the quantum quantifiers when the system is initially in a non-symmetric Bell-like state.

4.2 For non-symmetric Bell-like state

In this subsection, we undertake an analysis of the scenario in which the initial state assumes the non-symmetric Bell-like state and investigate the corresponding density matrix of Eq. (12). The elements of this matrix depend on the physical parameters J and $D_z$, which are hidden within the parameter $\eta$ under the intrinsic decoherence phenomenon.

Fig. 6

Temporal evolution of quantum correlations, where $\gamma = 0, \theta =\pi /4, D_z=0.5$ such that a $J=0$, b $J=0.5$ and c $J=1$

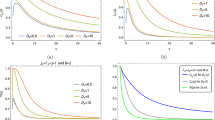
Figure 6 presents the temporal evolution of the quantities C, $\text {LQU}$, and $\text {BL}$ for the case where $\gamma =0$, $\theta =\pi /4$, and $D_z=0.5$. In Fig. 6a, we observe that when $J=0$, the quantifiers start from their maximum values and then perform undamped oscillations over time. By increasing the spin–spin exchange coupling J to 0.5 (Fig. 6b), we note that $\text {BL}$, C, and $\text {LQU}$ exhibit oscillations of small amplitudes but do not cancel out in any case. When $J=1$, Fig. 6c illustrates that the exchange coupling parameter J has a beneficial effect on the intensification of quantum correlations by approaching the quasi-stability of all quantifiers.

Fig. 7

The same data as Fig. 6 but for $\gamma =0.1$

Figure 7 examines the influence of intrinsic decoherence by fixing its rate at $\gamma =0.1$. The results illustrate the damping of the oscillatory behavior of the quantum correlations over time. In Fig. 7a, we show that C and $\text {LQU}$ start from unity ($C=\text {LQU}=1$), indicating the maximum quantum correlations for $\theta =\pi /4$. These quantities finally cancel out as t increases, highlighting the phenomena of sudden death and rebirth. Bell’s non-locality quantified by $\text {BL}$ begins with its maximum value and then exhibits a few oscillations before reaching the value 1, indicating the non-violation of Bell’s inequality. We note that even if the initial state is maximally entangled, the quantum correlations are destroyed due to the effect of intrinsic decoherence. In Fig. 7b and c, when $J=0.5$ and $J=1$, respectively. We observe that the effect of exchange coupling J is very advantageous for enhancing quantum correlations. In both cases, the quantum system becomes strongly correlated despite the effect of intrinsic decoherence supported by the parameter $\gamma$. Hence, the coupling parameter J is responsible for preserving and maintaining quantum correlations over time in the system.

Fig. 8

Temporal evolution of quantum correlations versus time t, for $\gamma = 0$, $J=0.5$, $\theta =\pi /4$. Where a $D_z =0$, b $D_z=1$ and c $Dz = 2$

Figure 8 examines the influence of the DM parameter ($D_z$) in the case where $\gamma =0$, $J=0.5$, and $\theta =\pi /4$ under different values of the $D_z$ parameter. Figure 8a shows that in the absence of the DM interaction ($D_z=0$), the quantum correlations present their maximum values and are stabilized at all times. While, in Fig. 8b for $D_z=1$, the studied quantities exhibit periodic oscillations over time. The frequency of the oscillations has multiplied by increasing the DM interaction to the value $D_z=2$ (Fig. 8c). Consequently, the DM interaction is responsible for the oscillatory behavior of the quantum correlations.

Figure 9 takes into account the effect of intrinsic decoherence by setting the parameter $\gamma$ to the value 0.1, which shows the damping oscillations of quantum correlations. By increasing the parameter $D_z$ from $D_z=1$ (Fig. 9a) to $D_z=2$ (Fig. 9b), we observe that the DM interaction has a destructive impact on the quantum correlations in the system. Therefore, the DM interaction promotes the destructive effect of intrinsic decoherence.

Fig. 9

Temporal evolution of quantum correlations versus time t, for $\gamma = 0.1$, $\theta =\pi /4$. Where a $D_z = 1$ and b $Dz = 2$

Finally, upon comparing the results of Figs. 6 and 8, we have found that when the initial state is the non-symmetric Bell-like state, the DM interaction stimulates the detrimental effect of intrinsic decoherence (See, Fig. 8). However, we also noticed that the exchange coupling parameter, denoted as J, has a positive effect on preserving and strengthening nonclassical correlations, including entanglement stability (See, Fig. 6). Therefore, it can be inferred that in solid-state systems, the exchange coupling parameter J can compensate for the negative effects caused by the DM interaction.

5 Conclusion

In summary, we have explored the effect of intrinsic decoherence on nonclassical correlations, namely, Bell non-locality, concurrence, and local quantum uncertainty in the two-qubit Heisenberg XXX spin model with anisotropic spin–orbit interactions. In particular, we have proposed a rigorous investigation of the effects of DM interaction and KSEWA interactions on different initial states. An exact solution for the Milburn equation is obtained when the two-qubit system is initially in a symmetric Bell-like state and a non-symmetric Bell-like state.

The results found in Figs. (1, 2, 3, 4, 5) demonstrate that the KSEWA coupling parameter, $K_z$, plays a crucial role in the generation and decay of quantum correlations under the influence of intrinsic decoherence. The initial state also affects this relationship. Indeed, the parameter $K_z$ is responsible for both the oscillatory behavior of the quantifiers, $\text {LQU}$, C, and $\text {BL}$.

While, in the case of the non-symmetric Bell-like state Figs. (6, 7, 8, 9), we have shown that the exchange coupling J presents a highly promising effect on enhancing quantum correlations. Despite the presence of intrinsic decoherence supported by the parameter $\gamma$, the quantum system becomes strongly correlated. Indeed, the coupling parameter J is responsible for enhancing and preserving quantum correlations over time in the system. However, we have observed that the DM interaction exerts a destructive impact on the quantum correlations in the system. As a result, the DM interaction stimulates the destructive effect of intrinsic decoherence.

It is recognized that the field of quantum information (QI) processing aims to achieve stable qubits while mitigating the destructive phenomena that affect the quantum features of the system, such as various aspects of decoherence. This is a critical aspect that determines the progress of the field. After conducting our investigation, we have determined that the KSEWA interaction and the DM interaction are the primary causes of the intrinsic decoherence appearance and decay of the nonclassical correlations that we studied. However, we found that the spin–spin exchange interaction is crucial in enhancing and preserving the nonclassical correlations. Therefore, the non-symmetric Bell-like initial state has proven to be more advantageous for practical applications in QI. Finally, it would also be interesting to probe the potential of this system as a quantum channel for quantum teleportation and quantum dense coding protocols.

Appendices

Appendices

1.1 Appendix A: Bell non-locality

Consider a two-qubit X-shape density matrix:

$$\begin{aligned} \hat{X}^{AB}=\left( \begin{array}{cccc} \rho _{11} &{} 0 &{} 0 &{} \rho _{14} \\ 0 &{} \rho _{22} &{} \rho _{23} &{} 0 \\ 0 &{} \rho _{23}^* &{} \rho _{33} &{} 0 \\ \rho _{14}^* &{} 0 &{} 0 &{} \rho _{44} \\ \end{array} \right) , \end{aligned}$$

(21)

where the elements $\rho _{ij} \ge 0 (i,j=1,2,3,4)$ fulfill the unit trace (i.e., $\sum _{i=1}^4 \rho _{ii}=1$) and positivity conditions ($\rho _{22}\rho _{33} \ge \vert \rho _{23}\vert ^2$ and $\rho _{11}\rho _{44} \ge \vert \rho _{14}\vert ^2$). The nonzero elements $a_{ij}$ of the correlation matrix A (Eq. (14)) are given by:

$$\begin{aligned} \begin{aligned}&{a}_{11}=2\mathcal {R}(\varrho _{14}+\varrho _{23}),\\&{a}_{12}=-\mathcal {J}(\varrho _{14}-\varrho _{23}),\\&{a}_{21}=-\mathcal {J}(\varrho _{14}+\varrho _{23}),\\&{a}_{22}=-\mathcal {R}(\varrho _{14}-\varrho _{23}),\\&{a}_{33}=\varrho _{11}-\varrho _{22}-\varrho _{33}+\varrho _{44}. \end{aligned} \end{aligned}$$

(22)

where $\mathcal {R}(\Omega )$ and $\mathcal {J}(\Omega )$ denote, respectively, the real and imaginary parts of a given complex number $\Omega$. So, by making use of the above nonzero elements $a_{ij}$, we straightforwardly obtain the eigenvalues of the matrix $\mathcal {A}$ as:

$$\begin{aligned} \begin{aligned}&{\xi }_1=\left( \varrho _{11}-\varrho _{22}-\varrho _{33}+\varrho _{44}\right) {}^2,\\&{\xi }_2=4 \left( |\varrho _{23}|+|\varrho _{14}|\right) {}^2,\\&{\xi }_3=4 \left( |\varrho _{23}|-|\varrho _{14}|\right) {}^2. \end{aligned} \end{aligned}$$

(23)

So, the explicit formula of Bell non-locality is:

$$\begin{aligned} BL=2\sqrt{4 \left( |\varrho _{23}|+|\varrho _{14}|\right) {}^2+\max \left[ 4 \left( |\varrho _{23}|-|\varrho _{14}|\right) {}^2,\left( \varrho _{11}-\varrho _{22}-\varrho _{33}+\varrho _{44}\right) {}^2\right] }-1. \end{aligned}$$

(24)

1.2 Appendix B: Concurrence

The analytical expression of the concurrence for a two-qubit X-shape state (21) is obtained by making use of the following matrix:

$$\begin{aligned} \begin{aligned} M=&\hat{{X}}^{AB} (\hat{\sigma }_y^A\otimes \hat{\sigma }_y^B) \hat{ {X}}^{*AB} (\hat{\sigma }_y^A\otimes \hat{\sigma }_y^B)\\ =&\left( \begin{array}{cccc} |\varrho _{14}|^2+\varrho _{11} \varrho _{44} &{} 0 &{} 0 &{} 2 \varrho _{11} \varrho _{14} \\ 0 &{} |\varrho _{23}|^2+\varrho _{22} \varrho _{33} &{} 2 \varrho _{22} \varrho _{23} &{} 0 \\ 0 &{} 2 \varrho _{33} \varrho _{23}^* &{} |\varrho _{23}|^2+\varrho _{22} \varrho _{33} &{} 0 \\ 2 \varrho _{44} \varrho _{14}^*&{} 0 &{} 0 &{} |\varrho _{14}|^2+\varrho _{11} \varrho _{44} \\ \end{array} \right) . \end{aligned} \end{aligned}$$

(25)

Hence, the expression of the concurrence is given as:

$$\begin{aligned} C=2 \max [0,|\varrho _{23}|-\sqrt{\varrho _{11}\varrho _{44}},|\varrho _{14}|-\sqrt{\varrho _{22}\varrho _{33}}]. \end{aligned}$$

(26)

1.3 Appendix C: Local quantum uncertainty

The square root of a given two-qubit X-shape density matrix (Eq. (21)) is given by:

$$\begin{aligned} \sqrt{\hat{X}^{AB}}=\left( \begin{array}{cccc} b_{11} &{} 0 &{} 0 &{} b_{14} \\ 0 &{} b_{22} &{} b _{23} &{} 0 \\ 0 &{} b_{32} &{} b_{33} &{} 0 \\ b_{41} &{} 0 &{} 0 &{} b_{44} \\ \end{array} \right) , \end{aligned}$$

(27)

where

$$\begin{aligned} \begin{aligned}&b_{11}=\\&\frac{1}{2\sqrt{2} \sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\\&\quad \bigg [\left( \varrho _{11}-\varrho _{44}+\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}\right) \sqrt{\varrho _{11}+\varrho _{44}+\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\\&- \left( \varrho _{11}-\varrho _{44}-\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}\right) \sqrt{\varrho _{11}+\varrho _{44}-\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\bigg ]\\&b_{14}=b_{41}^{*}=\frac{\varrho _{14} \left( \sqrt{\varrho _{11}+\varrho _{44}+\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4|\varrho _{14}|^2}}-\sqrt{\varrho _{11}+\varrho _{44}-\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\right) }{\sqrt{2} \sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\\&b_{22}=\\&\frac{1}{2 \sqrt{2} \sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\\&\quad \bigg [\left( \varrho _{22}-\varrho _{33}+\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}\right) \sqrt{\varrho _{22}+\varrho _{33}+\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\\&-\left( \varrho _{22}-\varrho _{33}-\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}\right) \sqrt{\varrho _{22}+\varrho _{33}-\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4|\varrho _{23}|^2}}\bigg ]\\&b_{23}=b_{32}^{*}=\frac{\varrho _{23} \left( \sqrt{\varrho _{22}+\varrho _{33}+\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4|\varrho _{23}|^2}}-\sqrt{\varrho _{22}+\varrho _{33}-\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\right) }{\sqrt{2} \sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\\&b_{33}=\\&\frac{1}{2 \sqrt{2} \sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\\&\quad \bigg [\left( \varrho _{22}-\varrho _{33}+\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}\right) \sqrt{\varrho _{22}+\varrho _{33}-\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}}\\&-\left( \varrho _{22}-\varrho _{33}-\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4 |\varrho _{23}|^2}\right) \sqrt{\varrho _{22}+\varrho _{33}+\sqrt{\left( \varrho _{22}-\varrho _{33}\right) ^2+4|\varrho _{23}|^2}}\bigg ]\\&b_{44}=\frac{1}{2\sqrt{2}\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2 +4 |\varrho _{14}|^2}} \\&\quad \bigg [\left( \varrho _{11}-\varrho _{44}-\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}\right) \sqrt{\varrho _{11}+\varrho _{44}+\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}}\\&- \left( \varrho _{11}-\varrho _{44}-\sqrt{\left( \varrho _{11} -\varrho _{44}\right) ^2+4 |\varrho _{14}|^2}\right) \sqrt{\varrho _{11} +\varrho _{44}+\sqrt{\left( \varrho _{11}-\varrho _{44}\right) ^2+4 |\varrho _{14} |^2}}\bigg ].\\ \end{aligned} \end{aligned}$$

Then, by working out Eq. (20), we can get the correlation matrix W (3 $\times$ 3) as the following:

$$\begin{aligned} \begin{aligned}&W=\\&\left( \begin{array}{ccc} 2 \left( b_{11} b_{33}+b_{22} b_{44}+2\mathcal {R}(b_{14} b_{23})\right) &{} 4 i b_{14} \mathcal {I}(b_{23}) &{} 0 \\ 4 i b_{14}^* \mathcal {I}(b_{23}) &{} 2 \left( b_{11} b_{33}+b_{22} b_{44}-2\mathcal {R}(b_{14} b_{23})\right) &{} 0 \\ 0 &{} 0 &{} b_{11}^2+b_{22}^2+b_{33}^2+b_{44}^2-2 (|b_{23}|^2+|b_{14}|^2) \\ \end{array} \right) , \end{aligned} \end{aligned}$$

(28)

where its eigenvalues are given by:

$$\begin{aligned} \begin{aligned}&\mu _1=2 \left( b_{11} b_{33}+b_{22} b_{44}-\sqrt{(b_{14} b_{23})^2+(b_{23}^* b_{14}^*)^2-|b_{14}|^2\left( b_{23}^2-4 |b_{23}|^2+b_{23}^{*^2}\right) }\right) ,\\&\mu _2=2 \left( b_{11} b_{33}+b_{22} b_{44}+\sqrt{(b_{14} b_{23})^2+(b_{23}^* b_{14}^*)^2-|b_{14}|^2\left( b_{23}^2-4 |b_{23}|^2+b_{23}^{*^2}\right) }\right) ,\\&\mu _3=b_{11}^2+b_{22}^2+b_{33}^2+b_{44}^2-2 (|b_{23}|^2+|a_{14}|^2). \end{aligned} \end{aligned}$$

(29)