1 Introduction

Quantum properties, such as superposition and entanglement, allow quantum technologies to achieve different tasks in information theory that are impossible to accomplish using classical counterparts. Indeed, quantum information processing offers many significant advantages over classical processing, for example, high-speed computing with higher precision and accuracy. In this regard, quantum entanglement remains a fundamental and extremely valuable ingredient in the development of emerging quantum technologies including quantum teleportation [1, 2], quantum cryptography [3, 4], and quantum protocols [5, 6]. Despite all its potential, it is still clunky to measure and characterize entanglement and quantum correlations in quantum systems comprised of many parties. This led to the development of multiple ways of quantifying the degree of entanglement in multipartite quantum systems [7,8,9,10,11,12,13,14]. There also have been many studies on entanglement detection within mixed states [15,16,17,18]. However, measuring quantum correlations in mixed states continues to be a challenging task [19].

Generally, quantum entanglement measures cannot capture and quantify all non-classical correlations that can occur even in separable mixed states. To resolve this problem, a quantum correlation quantifier that can compute non-classical correlations beyond entanglement, known as quantum discord, is presented in Refs. [20,21,22]. Considering the difficulty in computing quantum discord, Dakic et al. developed a geometric version of quantum discord using the Hilbert–Schmidt norm [23]. Recently, Girolami et al. [24] had just developed a new measure of non-classical correlations known as local quantum uncertainty (LQU) that is both discord-like and genuine. Based on the idea of Skew information, the local quantum uncertainty characterizes the lowest quantum uncertainty of a bipartite quantum state through the measurement of a single local observable. Considering LQU’s invariance under local unitary transformations and disappearance for classically correlated states [24], it is a suitable quantifier of quantum correlations. It has the added advantage of being analytically computed for any qubit–qudit system. Recently, there have been extensive investigations and analyses of LQU in various works; see for example the Refs. [25,26,27,28] and references therein.

On the other hand, coherence comes from the quantum state superposition principle. It is a basic concept in quantum theory, similar to that of quantum correlations, and remains an important physical resource for nearly all the quantum mechanical protocols [29,30,31,32,33,34]. Coherence also plays an important role in a wide variety of other research fields, such as in nanoscale physics [35, 36] and quantum metrology [37, 38]. Therefore, coherence is considered in Ref. [31] as the generalized quantum uncertainties and is regarded to be a valuable and essential resource in quantum information theory; for instance, see Refs. [30, 39, 40]. A precise and operational method to identify quantum coherence was introduced by Baumgratz et al. in Ref. [39]. The connection between quantum coherence with entanglement is examined in [30], while the conversion of coherence to quantum correlations is developed in the work [41].

The characterization of quantum correlations and coherence in Heisenberg spin-chain models has attracted growing interest from researchers. Quantum correlations in such systems are mainly investigated in the literature, for example, see Refs. [42,43,44,45], particularly when considering the effect of the Dzyaloshinskii–Moriya (DM) interaction introduced in [46, 47]. The DM interaction is of great importance for the modulation of correlations dynamics in a Heisenberg spin-chain [48]. Whereas the quantum coherence measures have been studied in detecting and characterizing quantum phase transitions for several spin-chain models such as the transverse-field Ising model [49], the spin-1/2 anisotropic XY chain [50], the two-dimensional Kitaev honeycomb model [51], and the anisotropic spin-1/2 Heisenberg XYZ and XXZ chains with the DM interaction in magnetic fields [52, 53]. Here, we consider that the DM interaction is accompanied by another symmetric exchange interaction introduced by Kaplan [54], Shekhtman, Entin–Wohlman, and Aharony [55, 56], and is termed as KSEA interaction [57,58,59,60].

In the present work, we explore the dynamics of coherence and quantum correlations in a Heisenberg spin-chain under the joint interaction of DM and KSEA and subjected to an external homogeneous magnetic field. We are primarily interested in comparing the variations and preservation of bipartite quantum correlations and coherence using LQU, \(l_1\) norm of coherence, and relative entropy of coherence. We consider the two-qubit XXZ spin-1/2 chain system in equilibrium with a thermal reservoir at temperature T under the combined effects of DM and KSEA interactions when subjected to a homogeneous magnetic field. Particularly, we analyze how equilibrium temperature, DM and KSEA coupling  interactions, external magnetic field strength, and anisotropy coupling parameters influence the evolution of quantum coherence and quantum correlations in the considered system. We intend to provide a design of the system–field coupling which could be usefully used to preserve quantum correlations and coherence. Besides, the main focus of this study will be to provide optimal parameters setting which best suits the preservation of maximal quantum correlations and coherence in bipartite spin-chain. To further clarify on the achieved goals, we will draw a comparative analysis of the current study to those previously done.

The outline of this work is as follows. In Sect. 2, we provide the details of \(\ell _1\) norm of coherence, entropy coherence, and local quantum uncertainty. In Sect. 3, we discuss the physical model of the two-qubit XXZ spin-chain system coupled with an external magnetic field. The results obtained for the dynamics of bipartite quantum correlations and coherence in Sect. 4. Finally, we give concluding remarks in Sect. 5.

2 Quantum correlation quantifiers

This section introduces the two quantum coherence measures and LQU used to compute coherence and quantum correlations in a two-qubit spin-chain state.

2.1 Quantum coherence measures

We emphasize that quantum coherence is a basis dependent concept, therefore, we first need to identify which states are incoherent. For a basis of the eigenvectors \(\{|i\rangle _{i=1,..,d}\}\) of a d-dimensional Hilbert space \({\mathcal {H}}_{d}\), any diagonal density matrix in this basis \((\delta = \sum _{i=1}^{d} p_{i} |i> <i|)\) is in the set of incoherent states and a specified measure of coherence of an arbitrary quantum state will estimate the distance to the nearest incoherent state. Any proper measurement for quantum coherence should satisfy some conditions, such that: (1) \(C(\varrho )=0\) if and only if \(\varrho\) is in the set of incoherent states. (2) Monotonicity under nonselective incoherent completely positive and trace preserving (ICPTP) maps [30, 39]. Here, to encounter quantum coherence in a two-qubit state, we consider two readily computable coherence estimators, namely, the relative entropy of coherence [39] and the \(\ell _1\)norm of coherence [39]. The relative entropy of coherence is a reliable coherence measure that satisfies the conditions of coherence measurement. It is defined as [39]

$$\begin{aligned} C_r (\rho ) = \mathrm{min}_{\xi \in \mathrm {I}} S\left( \rho \Vert \xi \right) , \end{aligned}$$
(1)

where \(\xi\) is an incoherent state and \(\mathrm {I}\) denotes the set of incoherent states. \(S(\rho \Vert \xi ) = \mathrm{Tr}(\rho \log _2 (\rho ) -\mathrm{Tr}(\rho \log _2 (\xi )\) denotes the relative entropy and \(S(\rho )\) is the Von Neumann entropy given by \(S(\rho ) = - \mathrm{Tr}(\rho \log _2 (\rho )) = - \sum _{i=1}^{4} \lambda _i \log _2 (\lambda _i)\), where \(\lambda _i\) are the eigenvalues of the entire density matrix operator \(\rho\). The relative entropy of coherence \((C_r (\rho ))\) is a distance-based coherence quantifier that measures coherence using the minimal distance between the quantum state  and the set of incoherent states. Using the properties of relative entropy, one can show that the relative entropy of coherence (1) is expressed as

$$\begin{aligned} C_r (\rho ) = S\left( \rho _{diag}\right) - S(\rho ), \end{aligned}$$
(2)

where \(\rho _\mathrm{diag}\) describes the quantum incoherent state. The matrix \(\rho _\mathrm{diag}\) is obtained by eliminating all the off-diagonal elements of \(\rho\) under the reference basis \(\{|i\rangle _{i=1,\ldots ,d}\}\) of a d-dimensional Hilbert space \({\mathcal {H}}_{d}\). In this basis, \(\rho _\mathrm{diag}\) is the incoherent diagonal matrix \(\rho _\mathrm{diag}= \sum _{i}^{d} \rho _{ii}|i\rangle \langle i|\). We note that the relative entropy of coherence \(C_r\) of an incoherent state \(\xi\) must be zero. However, Baumgratz et al. have proved that the coherence of a quantum system can be calculated as [39]

$$\begin{aligned} {\mathcal {C}}_{l_{1}}(\rho )= \mathrm{min}_{\xi } |\rho -\xi |. \end{aligned}$$
(3)

The \(l_{1}\) norm-based coherence monotone of measurement \({\mathcal {C}}_{l_{1}}(\rho )\) can be quantified in the particular basis \(\{|i\rangle \}_{i=1,\ldots ,d}\), by the off-diagonal elements of the density matrix as

$$\begin{aligned} {\mathcal {C}}_{l_{1}}(\rho )=\sum _{i\ne j}\left| \rho _{i,j}\right| , \end{aligned}$$
(4)

where \(|\rho _{i,j}|\) is the absolute value of \(\rho\)’s matrix elements.

2.2 Local quantum uncertainty

LQU is reliable for quantifying non-classical correlations in bipartite systems [24]. Let \(\rho \) be the state of a bipartite system AB, and \(K_A\) denotes a local Hermitian operator acting on the subsystem A, with a non-degenerate spectrum. The LQU measure for subsystem A, optimizing over all local observables operating on A, with distinct eigenvalues, is defined as [61, 62]

$$\begin{aligned} {\mathcal {U}}(\rho) \equiv \min _{K_A} {\mathcal {I}} \left( \rho, K_A \otimes I_2 \right) , \end{aligned}$$
(5)

where \(I_2\) is the identity operator acting on the subsystem B and

$$\begin{aligned} {\mathcal {I}}(\rho, K_A \otimes I_2)=-\frac{1}{2}\mathrm{Tr}\left( \left[ \sqrt{\rho}, K_A \otimes I_2\right] ^{2}\right) , \end{aligned}$$
(6)

defines the so-called Wigner–Yanase Skew Information (WYSI) [63, 64]. Skew information plays a significant role in quantum information theory and is of paramount importance for many applications. The analytical computation of LQU is performed through a minimization procedure over the set of all observables acting on subsystem A of the composite system AB. The minimization of LQU in Eq. (5) for qubit–qubit systems leads to a closed form given by [24]

$$\begin{aligned} {{{\mathcal {U}}}}\left( {{\rho }} \right) = 1 - \max \left( {{\omega _{1}},{\omega _{2}},{\omega _{3}}} \right) , \end{aligned}$$
(7)

where \(\omega _{i=1,2,3}\) are eigenvalues of the \(3\times 3\) symmetric matrix \({\mathcal {W}}_{AB}\), whose entries are

$$\begin{aligned} \left( {\mathcal {W}}\right) _{ij} \equiv \mathrm{Tr} \left[ \sqrt{\rho }\left( \sigma ^A _{i}\otimes {I}_{B}\right) \sqrt{\rho }\left( \sigma ^A _{j}\otimes {I}_{B}\right) \right] , \end{aligned}$$
(8)

with \(\sigma ^A _{i} (i=x,y,z)\) denotes the standard 2D Pauli matrices corresponding to the subsystem A.

3 Quantum coherence and non-classical correlations in the two-qubit Heisenberg XXZ model

In our study, we deal with two nearest spin-1/2 XXZ particles subjected to an external homogeneous magnetic field under the interplay of DM and KSEA interactions subjected along the z-axis (denoted by z-DM and z-KSEA, respectively). The Hamiltonian model is given by

$$\begin{aligned} \mathbf{H }= & {} J_z \sigma _{1}^{z}\sigma _{2}^{z}+ J\left( \sigma _{1}^{x}\sigma _{2}^{x}+ \sigma _{1}^{y}\sigma _{2}^{y}\right) + D_z\left( \sigma _{1}^{x}\sigma _{2}^{y}-\sigma _{1}^{y}\sigma _{2}^{x}\right) \nonumber \\&+ \Gamma _z \left( \sigma _{1}^{x}\sigma _{2}^{y}+\sigma _{1}^{y}\sigma _{2}^{x}\right) + B \left( \sigma _1^z + \sigma _2^z\right) , \end{aligned}$$
(9)

where \(\sigma _{\alpha }^{i=x,y,z}\) \((\alpha =1,~2)\) denote the standard 2D Pauli matrices corresponding to the spin \(\alpha\). J is the interaction coupling constant and \(J_z\) is the real anisotropy coupling constant describing the symmetric exchange spin–spin interaction in z-direction. B stands for the homogeneous part of the magnetic field, and \(D_z\) and \(\Gamma _z\) parameters denote the z–axis interaction resulting to spin–orbit coupling antisymmetric and symmetric spin–orbit coupling contributions, respectively. Note that we consider all the parameters dimensionless. The Hamiltonian (9) can be expressed in the computational basis (i.e., \(\sigma ^{z} \otimes \sigma ^{z}\) eigenstates) \(\lbrace \vert 00 \rangle , \vert 01 \rangle , \vert 10 \rangle , \vert 11 \rangle \rbrace\), as

$$\begin{aligned} \mathbf{H }= \left( \begin{array}{cccc} J_z+2B&{}0&{}0&{}-2i\mathrm{\Gamma }_z\\ 0&{}-J_z &{} 2 J+2iD_z&{}0\\ 0&{}2J-2iD_z &{}-J_z&{}0\\ 2i\mathrm{\Gamma }_z&{}0&{}0&{}J_z-2B \end{array} \right) . \end{aligned}$$
(10)

The eigenvalues and the corresponding eigenvectors of the Hamiltonian \(\mathbf{H }\) are

$$\begin{aligned} E_1&= J_z+ \eta , \nonumber \\ \vert \varphi _1\rangle&=\sqrt{\frac{\eta +2B}{2\eta }}\left( |00\rangle +\frac{ 2i\mathrm{\Gamma }_z}{{\eta +2 B}}\vert 11\rangle \right) , \end{aligned}$$
(11)
$$\begin{aligned} E_2&= -J_z+ \xi , \nonumber \\ \vert \varphi _2\rangle&=\frac{1}{\sqrt{2}}\left( |01\rangle +\frac{2 J-2iD_z}{\xi } \vert 10\rangle \right) , \end{aligned}$$
(12)
$$\begin{aligned} E_3&= -J_z- \xi , \nonumber \\ \vert \varphi _3\rangle&=\frac{1}{\sqrt{2}} \left( |01\rangle -\frac{2 J-2iD_z}{\xi }\vert 10\rangle \right) , \end{aligned}$$
(13)
$$\begin{aligned} E_4&=J_z- \eta , \nonumber \\ \vert \varphi _4\rangle&=\sqrt{\frac{\eta -2B}{2\eta }}\left( |00\rangle -\frac{2i\mathrm{\Gamma }_z}{\eta -2B}\vert 11\rangle \right) , \end{aligned}$$
(14)

with \(\eta =\sqrt{4B^2+4\Gamma _{z}^{2}}\) and \(\xi =\sqrt{4J^2+4D_{z}^{2}}\). The vectors \(\vert 0 \rangle\) and \(\vert 1 \rangle\) are the eigenstates of \(\sigma ^{z}\) and denote spin-up and spin-down states, respectively.

For the thermal interaction to be introduced into the spin-chain system, the thermal state of the system kept in equilibrium with a thermal reservoir at temperature T is given by the Gibbs’s density operator as

$$\begin{aligned} \rho (T) = \frac{1}{{Z}} e^{\frac{-H}{k_\mathrm{B} T}}, \end{aligned}$$
(15)

where Z being the partition function and is defined as: \(Z= \mathrm{Tr}( e^{\frac{-H}{T}}) = \sum ^{4}_{i=1} e^{\frac{-E_i}{T}}\), for which \(k_\mathrm{B}\) is the Boltzmann’s constant and is set to 1. In the two-qubit computational basis, the thermal density matrix \({\rho }(T)\) can be represented in the form of X-structure as

$$\begin{aligned} \rho (T)=\left( \begin{array}{llll} a &{} 0 &{} 0 &{} w \\ 0 &{} b &{} z &{} 0 \\ 0 &{} z^{*} &{} c &{} 0 \\ w^{*} &{} 0 &{} 0 &{} d \end{array}\right) . \end{aligned}$$
(16)

The corresponding entries are given by

$$\begin{aligned} a= & {} \frac{e^{-\beta J_z}}{{{\mathcal {Z}}}} \left[ \cosh \left( \beta \eta \right) - \frac{2B}{\eta }\sinh \left( \beta \eta \right) \right] ,\\ d= & {} \frac{e^{-\beta J_z}}{{{\mathcal {Z}}}} \left[ \cosh \left( \beta \eta \right) + \frac{2B}{\eta }\sinh \left( \beta \eta \right) \right] ,\\ w= & {} \frac{2i\mathrm{\Gamma }_z}{\eta }\frac{ e^{-\beta J_z}}{{{\mathcal {Z}}}}\sinh \left( \beta \eta \right) , \\ b= & {} \frac{ e^{\beta J_z}}{{{\mathcal {Z}}}}\left[ \cosh \left( \beta \xi \right) \right] , \\ c= & {} \frac{ e^{\beta J_z}}{{{\mathcal {Z}}}}\left[ \cosh \left( \beta \xi \right) \right] , \\ z= & {} -\frac{2 J +2iD_z}{\xi } \frac{ e^{\beta J_z}}{{{\mathcal {Z}}}}\sinh \left( \beta \xi \right) , \end{aligned}$$

and the partition function is \({{{\mathcal {Z}}}}=2\left[ e^{-\beta J_z}\cosh \left( \beta \eta \right) +e^{\beta J_z}\cosh \left( \beta \xi \right) \right]\). The eigenvalues of the two-qubit density matrix \({\rho }(T)\) are given by

$$\begin{aligned} \begin{aligned} \mu _1&= \frac{1}{2}\left( {(b + c) + \sqrt{{{\left( {{b} - {c}} \right) }^2} + 4{{\left| {{z}} \right| }^2}} } \right) ,\\ \mu _2&= \frac{1}{2}\left( {({b} + {c}) - \sqrt{{{\left( {{b} - {c}} \right) }^2} + 4{{\left| {{z}} \right| }^2}} } \right) ,\\ \mu _3&= \frac{1}{2}\left( {({a} + {d})+ \sqrt{{{\left( {{a} - {d}} \right) }^2} + 4{{\left| {{w}} \right| }^2}} } \right) ,\\ \mu _4&= \frac{1}{2}\left( ({a} + {d}) - \sqrt{{{\left( {{a} - {d}} \right) }^2} + 4{{\left| {{w}} \right| }^2}} \right) . \end{aligned} \end{aligned}$$
(17)

In the \((\sigma ^{z} \otimes \sigma ^{z})\) eigenstates basis \(\lbrace \vert 00 \rangle , \vert 01 \rangle , \vert 10 \rangle , \vert 11 \rangle \rbrace\), the analytic expression of the relative entropy of coherence (2) can be obtained as follows:

$$\begin{aligned} C_r (\rho (T))= & {} \sum _{i=1}^{4} \mu _i \log _2 (\mu _i) - a \log _2 a - b \log _2 b \nonumber \\&-c \log _2 c-d \log _2 d. \end{aligned}$$
(18)

On the other hand, we point out that in the z-basis, the \(l_1\) norm of coherence (3) of the thermal density matrix \((\rho (T))\) is calculated by summing the off-diagonal elements of the state \((\rho (T))\) (16)

$$\begin{aligned} {\mathcal {C}}_{l_{1}}(\rho (T))= & {} 2\left| \frac{2i{\Gamma }_z}{\eta }\frac{ e^{-\beta J_z}}{{{\mathcal {Z}}}}\sinh \left( \beta \eta \right) \right| \nonumber \\&+2\left| \frac{2 J+2iD_z}{\xi } \frac{ e^{\beta J_z}}{{{\mathcal {Z}}}}\sinh \left( \beta \xi \right) \right| . \end{aligned}$$
(19)

In this work, we are restricted to computing and characterizing the coherence in the z-basis. In a future paper, we will examine the coherence measures dynamics in a two-qubit one-dimensional XXZ Heisenberg spin-\(\frac{1}{2}\) chain subjected to the combined effect of DM and KSEA interactions in both x and y basis and compare them to the results obtained in this manuscript.

The amount of quantum correlations in the two-qubit XXZ Heisenberg spin-\(\frac{1}{2}\), quantified by the  LQU measure \(U\left( {{\rho (T)}} \right)\), is obtained as

$$\begin{aligned} U\left( {{\rho (T)}} \right) = 1 - \max \left( {{\omega _{1}},{\omega _{2}},{\omega _{3}}} \right) , \end{aligned}$$
(20)

where \(\omega _{1}, \omega _2\) and \(\omega _3\) are expressed as

$$\begin{aligned} \omega _{1}&= \left( \sqrt{\mu _1} + \sqrt{\mu _4} \right) \left( \sqrt{\mu _2} + \sqrt{\mu _3} \right) \nonumber \\&\quad + \frac{1}{4}\frac{\left( R^2_{11}-R^2_{22}\right) +\left( R^2_{03} -R^2_{30}\right) }{\left( \sqrt{\mu _1} + \sqrt{\mu _4}\right) \left( \sqrt{\mu _2} + \sqrt{\mu _3} \right) }, \end{aligned}$$
(21a)
$$\begin{aligned} \omega _{2}&= \left( \sqrt{\mu _1} + \sqrt{\mu _4} \right) \left( \sqrt{\mu _2} + \sqrt{\mu _3} \right) \nonumber \\&\quad + \frac{1}{4}\frac{\left( R^2_{22}-R^2_{11}\right) +\left( R^2_{03} -R^2_{30}\right) }{\left( \sqrt{\mu _1} + \sqrt{\mu _4}\right) \left( \sqrt{\mu _2} + \sqrt{\mu _3} \right) }, \end{aligned}$$
(21b)
$$\begin{aligned} \omega _{3}&= \frac{1}{2}\left[ \left( \sqrt{\mu _{1}} +\sqrt{\mu _{4}}\right) ^{2}+\left( \sqrt{\mu _{2}}+\sqrt{\mu _{3}}\right) ^{2}\right] \nonumber \\&\quad + \frac{\left( R_{03}+R_{30}\right) ^2-\left( R_{11}-R_{22}\right) ^2}{8\left( \sqrt{\mu _1} + \sqrt{\mu _4} \right) ^2}\nonumber \\&\quad + \frac{\left( R_{03}-R_{30}\right) ^2-\left( R_{11} +R_{22}\right) ^2}{8\left( \sqrt{\mu _2}+ \sqrt{\mu _3} \right) ^2 }. \end{aligned}$$
(21c)

In Eq. (21), \(R_{\alpha \beta } = \langle \sigma _{\alpha } \otimes \sigma _{\beta }\rangle\) are the correlation matrix elements occurring in the Fano–Bloch decomposition of the matrix density \(\rho (T)\) given by

$$\begin{aligned} \rho (T)=\frac{1}{4}\sum _{\alpha , \beta =0}^{3} R_{\alpha \beta } \sigma _{\alpha } \otimes \sigma _{\beta }. \end{aligned}$$
(22)

4 Results and discussion

In this section, we discuss the results obtained from modelling the dynamics of coherence and quantum correlations in a two-qubit one-dimensional XXZ Heisenberg spin-\(\frac{1}{2}\) chain subjected to the combined effect of DM and KSEA interactions in the presence of a homogeneous magnetic field and maintained at a specific temperature. Using \(l_1\)-norm of coherence (\(C_{\ell _1}(\rho )\)), relative entropy of coherence (\(C_{r}(\rho )\)), and local quantum uncertainty (\({\mathcal {U}} (\rho )\)), we illustrate the dynamics and related features of quantum correlations and coherence under various scenarios by varying the physical parameters of the considered system (\(\rho(T)=\rho\)). We begin by investigating in Fig. 1 the dynamics of the two quantum coherence measures and LQU in terms of T for selected values of \(D_z\).

Fig. 1
figure 1

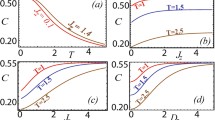
Dynamics of \(\ell _{1}\) norm coherence (a), relative entropy of coherence (b), and LQU (c) as functions of T for fixed values of \(D_{z}\) when \(\Gamma _{z}=J_{z}=J=1\) and \(B=2\). d Comparative dynamics between \(C_{\ell _{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) for \(D_{z}=2\)

Full size image

Figure  1 analyzes the dynamics of \(C_{\ell _1}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}} (\rho )\) in a two-qubit XXZ spin chain when subjected to homogeneous magnetic field characterized by DM interaction along z-axis \((D_z)\) and temperature T. The initial values of the \(C_{\ell _1}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}} (\rho )\) functions entirely depend on \(D_z\) values. We noticed that for \(D_z \ge 1\), the two-qubit state becomes maximally coherent and correlated, while, for \(D_z \le 1\), the probability of mixedness in the state increases. Besides, we observed that the three quantifiers present the same qualitative dynamics, therefore, suggesting a strong agreement between them. Besides \(D_z\), quantum correlations and coherence are greatly influenced by T. At \(T=0\) and for low values of \(D_{z}\), the \(C_{\ell _1}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}} (\rho )\) functions are not maximal however, experience a growth for smaller values of T. As T increases, the related negative effects become dominant on quantum correlations and coherence preservation, causing them to decrease. In addition, for different values of \(D_{z}\), the qualitative as well as the quantitative features of \(C_{\ell _1}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}} (\rho )\) remained different. They present a plateau, whose width is large enough for higher \(D_z\) strengths. As T grows, we observe a monotonous decay of the three quantities. In Fig. 1d, the LQU function decreases faster than the coherence quantifiers, and in comparison, \(C_{\ell _{1}}(\rho )\) remained more robust than \(C_{r}(\rho )\). It is also noticeable that quantum correlations in the current state remained suppressed as compared to the coherence. Therefore, quantum correlations were found more fragile than the related coherence.

Following, we illustrate in Fig. 2 the combined influence of the temperature and the KSEA interaction parameter \(\Gamma _{z}\) on the dynamics of \(C_{\ell _1}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}} (\rho )\) functions.

Fig. 2
figure 2

Dynamics of \(\ell _{1}\) norm coherence (a), relative coherence (b), and LQU (c) as functions of T for fixed values of \(\Gamma _{z}\) when \(D_{z}=J_{z}=J=1\) and \(B=2\). Figure 2d shows the comparative dynamics between \(C_{\ell _{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) for \(\Gamma _{z}=3\)

Full size image

Figure  2 shows that \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) present a similar pattern and exhibit three behaviors depending on the values of KSEA coupling parameter \(\Gamma _{z}\). For \(\Gamma _{z}=0.5\), we notice that at \(T=0\) the three quantifiers are at their maximal value. However, all the three functions rapidly decrease for the increasing values of T, especially \({\mathcal {U}}(\rho )\). Hence, this is important to note that quantum correlations compared to the coherence in the current two-qubit state remained more vulnerable to the negative effects of the temperature. For the range \(0.5<\Gamma _{z}\le 10\), the two-qubit state seems slightly mixed initially, rather than maximally coherent and correlated even at \(T=0\). However, for higher values of \(\Gamma _z\), the initial value of coherence and correlations increases. At the latter notes, all three functions show a smaller decline in quantum correlations and coherence for higher values of \(\Gamma _z\) against T. In addition, for the interval \(0.5<\Gamma _{z}\le 4\), the quantifiers in question do not decrease monotonically, and they spike before decreasing. We identified this important that the negative impact of temperature quickly becomes dominant over the current bipartite quantum correlations and coherence, causing them to degrade rapidly after their maximums. For \(\Gamma _{z}>4\), \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}}(\rho )\) present a plateau that is wider for larger values of \(\Gamma _{z}\) and then decrease exponentially against increasing T values. We note that \(C_{l_{1}}(\rho )\) remained more robust against high temperatures than \(C_{r}(\rho )\) as can be seen in Fig. 2d. While, \({\mathcal {U}}(\rho )\) remained more sensitive and shows an easy loss compared to the coherence measures.

In Fig. 3, we depict the dynamics of quantum correlations and coherence in a two-qubit spin-chain as function of the temperature T for various values of the external magnetic field B.

Fig. 3
figure 3

Dynamics of \(\ell _{1}\) norm coherence (a), relative coherence (b), and LQU (c) as functions of T for fixed values of B When \(D_{z}=J_{z}=\Gamma _{z}=J=1\). d Comparative dynamics between \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}}(\rho )\) for \(B=2\)

Full size image

Figure 3 shows that both temperature T and homogeneous magnetic field B have a negative effect on the initially encoded quantum correlations and coherence in the two-qubit spin-chain state. For small intensities of B, and at \(T=0\), the state remained maximally correlated, and coherent. In Fig. 3c, we noticed that \({\mathcal {U}}(\rho )\) decays rapidly as T gets enhanced. On the other hand, the \(C_{l_{1}}(\rho )\) measure as seen in Fig. 3a remained more resistant to the negative consequences of both T and B. For higher intensities of the magnetic field specifically, when \(3 \le B < 10\), the two-particle state initially remained mixed even at low-temperature values. Besides, when the state becomes mixed, \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}}(\rho )\) measures attain a maximum where \(T\ne 0\). It is also important to note that the range of maximization of the quantum correlations and coherence depends upon specific values of B and T. As seen that when B against T increases, the related maximum remains more suppressed and occurs later and vice versa. In agreement with previous results obtained in Figs. 1 and 2, quantum correlations remained more fragile to the detrimental effects of the magnetic field when compared to the coherence, as depicted in Fig. 3(d). In comparison, \(C_{l_{1}}(\rho )\) remained more robust to encounter coherence in the current two-qubit state than \(C_{r}(\rho )\). As, the coherence decay speed shown by \(C_{r}(\rho )\) is greater than that of \(C_{l_{1}}(\rho )\). Except for single maximum against high values of B, no clear revival phenomenon has been observed in all \(C_{r}(\rho )\), \(C_{\ell }(\rho )\) and \({\mathcal {U}}(\rho )\) functions.

Next, we show in Fig. 4 the dynamics of \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) measures in terms of \(\Gamma _z\) and \(D_z\) when the two-qubit state is exposed to an external homogeneous magnetic field.

Fig. 4
figure 4

Dynamics of \(\ell _{1}\) norm coherence (a), relative coherence (b), and LQU (c) as functions of \(D_{z}\) and \(\Gamma _{z}\) when \(T=J_{z}=J=1\) and \(B=2\)

Full size image

From Fig. 4, one observes that, initially, the coherence functions are zero, demonstrating that the state is initially incoherent, but in contrast, the \({\mathcal {U}}(\rho )\) measure shows that for the same values of the parameters, the state has non-zero non-classical correlations. This is interesting to find that quantum correlations withstand the detrimental effects of the magnetic field by avoiding complete loss as compared to the coherence in the state. Therefore, in certain conditions, \({\mathcal {U}}(\rho )\) function has the advantage to reveal quantum correlations not detectable by other relevant measures. We observed that coherence quantifiers have prevailed, a common qualitative dynamics. In case of the quantitative analysis, growth speed of the \(C_{l_{1}}(\rho )\) (Fig. 4a) remained higher than \(C_{r}(\rho )\) (Fig. 4b) and attains the maximum faster, relatively. As compared to the coherence measures, \({\mathcal {U}}(\rho )\) as a function of the parameters \(D_{z}\) and \(\Gamma _{z}\) shows a completely different qualitative dynamical map. As seen that coherence measures start from zero and reach their maximal; however, the \({\mathcal {U}}(\rho )\) function exhibits a continuous minimum for a specific range of \(D_{z}\) and \(\Gamma _{z}\) values and remained initially non-zero. This behavior of \({\mathcal {U}}(\rho )\) completely contradicts the dynamical map of the \(C_{l_{1}}(\rho )\) and \(C_{r}(\rho )\) measures. The efficiency of the parameters \(D_{z}\) and \(\Gamma _{z}\) to develop and preserve quantum correlations and coherence in the two-qubit spin chain is not equivalent. As compared to the \(\Gamma _z\), the \(D_z\) parameter remained more dominant to induce quantum correlations and coherence in the state. For the practical designing of quantum correlations’ retention, however, the employment of both the DM and KSEA interactions is useful and jointly avoids the related losses and failure of the quantum mechanical protocols. In agreement with previous results, the dynamical maps of quantum correlations and coherence functions do not exhibit any clear repeated revivals of coherence and quantum correlations, ensuring the absence of repeated exchange of attributes between the magnetic field and two-qubit spin-chain.

To clarify the combined effect of DM and KSEA interactions on the two-qubit spin-chain coherence and correlations, we visualize in Fig. 5 the dynamics of \(\ell _{1}\) norm coherence, relative entropy of coherence and LQU as functions of \(D_{z}\) for fixed values of \(\Gamma _{z}\) when \(T=J_{z}=J=1\) and \(B=2\).

Fig. 5
figure 5

Dynamics of \(\ell _{1}\) norm coherence (a), relative entropy of coherence (b), and LQU (c) as functions of \(D_{z}\) for fixed values of \(\Gamma _{z}\) when \(T=J_{z}=J=1\) and \(B=2\). d Comparative dynamics between \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}}(\rho )\) for \(\Gamma _{z}=1\)

Full size image

For the increasing \(D_{z}\) and fixed \(\Gamma _{z}\) values, we noticed that both coherence quantifiers increase rapidly and attain a final maximum. It is worth noting that the more incoherent the state is at first, the faster it becomes maximally coherent, and the reverse is also true. Quantum correlations, on the other hand, exhibit a different dynamical map, as shown in Fig. 5c. For the lower values of \(\Gamma _z\), the state remained highly uncorrelated initially. However, for the increasing \(D_z\) values, the non-classical correlations are induced faster. In contrast, for the increasing \(\Gamma _z\) values, especially when \(\Gamma _z \ge 0.5\), the state initially becomes more correlated, however, faces a sudden decrease and attains a minimum. Because of the efficient action of the KSEA and DM interactions, the quantum correlations again rise and reach a final maximum for higher values of \(D_z\). Note that the increase in the minimum’s depth directly depends upon the increasing values of \(\Gamma _z\). Figure 5d shows the prevalence of the coherence in the system as compared to the quantum correlations captured by \({\mathcal {U}}(\rho )\). In this regard, the \(C_{l_{1}}(\rho )\) remained more robust than \(C_{r}(\rho )\) to encounter coherence comparatively. Note that for each different set of \(D_z\) and \(\Gamma _z\) values, the coherence and quantum correlations always attain a single maximum saturation level. Besides, except for a single revival shown by \(U(\rho )\), no such oscillatory dynamical map for the case of coherence has been observed. Thus, it suggests that for a specific interval of duration depending upon the parameter setting, some parts of the field get correlated with the two-qubit system exchanging quantum correlations. However, the state regains the maximally correlated state after a small interaction time. Besides, the quantum correlations and coherence at final saturation points, both for higher and lower values of \(\Gamma _z\) are greater than that initially encoded in the state. Hence, declares the successful generation of quantum correlations and coherence in the mixed state converting it into the maximally correlated and coherent state at the final notes.

Now, we explore the combined effect of \(\Gamma _{z}\) and the anisotropy spin coupling constants J in Fig. 6 and \(J_{z}\) in Fig. 7 on the dynamics of bipartite quantum correlations and coherence under the influence of the external magnetic field.

Fig. 6
figure 6

\(\ell _{1}\) Norm coherence (a), relative entropy of coherence (b) and LQU (c) as functions of J for fixed values of \(\Gamma _{z}\). We take \(T=J_{z}=D_{z}=1\) and \(B=2\). d Comparative dynamics between \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) for \(\Gamma _{z}=2\)

Full size image

In Fig. 6, we provide the details of the dynamics of quantum correlations and coherence encoded initially in two-qubit spin-chain using \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) as functions of J when exposed to external magnetic field characterized by \(\Gamma _z\) and J. The qualitative dynamical maps of quantum correlations and coherence seem similar to those depicted in Fig. 7 but with few slight changes. For example, the initial non-classical correlations develop faster to their maximums in the current case, comparatively. Besides, the sudden decline shown by \({\mathcal {U}}(\rho )\) has lesser depth as compared to that observed in Fig. 7. Thus, ensuring that the \(\Gamma _z\) versus J relation performs better than that of \(J_z\) versus \(\Gamma _z\) relation to preserve quantum correlations and coherence. More explicitly, the coherence quantifiers increase monotonically and rapidly approach towards their maximal value against the increasing J values. In agreement with Figs. 1, 2, 3, 4, and 5, we noticed that \(C_{l_{1}}(\rho )\) captures more coherence than\(C_{r}(\rho )\). In Fig. 6c, we remarked that \({\mathcal {U}}(\rho )\) presents a different behavior than the coherence measures and can be distinguished in two regimes depending on the KSEA interaction strengths. Maximal quantum correlations at both low and higher \(\Gamma _z\) values in the first initial regions have been discovered, respectively. In the latter regions, the curves for low values of \(\Gamma _z\) achieve a constant maximal saturation level. In contrast, for the high values of \(\Gamma _z\), quantum correlations in the latter regions face a sudden decrease; however, the \({\mathcal {U}}(\rho )\) function shows a faster rise and again saturates at the final maximum values, making the state maximally correlated. Despite the different values of \(\Gamma _z\) and J, all the measures in the current case finally saturate at maximums rendering the state maximally coherent and correlated. Except for the higher values of \(\Gamma _z\), quantum correlations and coherence approach their final asymptotic values showing no repeated revivals. For all the \(\Gamma _z\) values, the initial mixed two-qubit state has been observed to be maximally correlated and coherent. Therefore, providing the evidence of the generation of extra quantum correlations and coherence.

Fig. 7
figure 7

\(\ell _{1}\) Norm coherence (a), relative entropy of coherence (b), and LQU (c) as functions of \(\Gamma _{z}\) for fixed values of \(J_{z}\). We take \(T=D_{z}=J=1\) and \(B=2\). d Comparative dynamics between \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\), and \({\mathcal {U}}(\rho )\) for \(J_{z}=1\)

Full size image

In Fig. 7, we focus on the effects of \(J_z\) versus \(\Gamma _z\) impact on the dynamics of bipartite quantum correlations and coherence in a two-qubit state placed in a magnetic field. The overall dynamical maps of the correlations functions are similar to those previously described, with quantum coherence being more prevalent in the system than quantum correlations captured by \({\mathcal {U}}(\rho )\). In addition, the \(C_{l_{1}}(\rho )\) function is encountered slightly more dominant for coherence detection than \(C_{r}(\rho )\). It is noticeable that the initial quantum correlations shown by \({\mathcal {U}}(\rho )\) are lesser against \(J_z\) than that observed for the rest of the inclusive parameters. In addition, quantum correlations drop to single minimal values and the related amplitudes inversely depend on \(J_{z}\). It is also important to note that as \(J_z\) increases, the related time span of quantum correlations and coherence in the given interval increases. As seen that the average time for the quantum correlations to attain maximum values is greater than that of its minimums (e.g., for higher values of \(J_z\)). Thus, suggesting a supporting nature of the \(J_z\) for quantum correlations and coherence in the system against the negative consequences of the applied magnetic field. In final notes, according to the \(C_{l_{1}}(\rho )\), \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) functions, the state regains the possible higher values of coherence and correlations, but does not get completely maximally correlated. In agreement with previous results, except for a single revival observed using \({\mathcal {U}}(\rho )\), no evident repeated revivals have been observed. Except \(C_{l_{1}}(\rho )\) function, we witnessed the generation of quantum correlations and coherence in the bipartite spin-chain. The statement is followed by comparing the initial and final levels of quantum correlations and coherence in \(C_{r}(\rho )\) and \({\mathcal {U}}(\rho )\) functions.

4.1 Significance of the current system–field coupling

This section delves into the significance and relevance of the current two-qubit state in relation to previous findings. Based on the current findings, we found that the current system–field coupling is more suitable for the preservation and dynamics of quantum correlations than previously studied systems. The current bipartite system is described using several parameters, such as DM, KSEA, and anisotropic coupling constants. Using the parameters listed above, the negative effects of the magnetic field on coherence and quantum correlations can be easily mitigated. Furthermore, the current parameters can be used not only for processing but also for preserving quantum information. Not only that, but we discovered that the current system is more efficient than previously designed equivalent systems. For a two-qubit state linked to external coherent fields, the quantum correlations and coherence discovered in the current set-up were higher than those found in Ref. [65]. In comparison, the current fields were also found more preserving than the classically correlated and pure local channels reported in Refs. [66,67,68]. Most of the results obtained in Refs. [69,70,71] contradict the current two-qubit state at the final notes, which can be kept maximally correlated and coherent. The most notable difference is that the current two-qubit spin chain lacks a coherence revival function, even though comparable quantum systems connected to a homogeneous magnetic field have shown significant revival features [65, 70, 71]. Therefore, the current system subjected to a magnetic field mainly avoids the backflow mechanism of information from the fields to the state and the information lost cannot be recovered. But somehow, a slight revival character for quantum correlations is observed using LQU. Thus, this also comprehends the different nature of coherence and quantum correlations. We found this intriguing that besides dynamics and preservation, the current parameters can also be practically deployed to generate quantum correlations in the current two-qubit spin-chain. Most importantly, for specific values of coupling parameters, we observed the successful generation of quantum correlations and coherence. In fact, due to the efficient design and optimal parameter settings, we have produced maximally coherent and correlated states from the initially mixed states. We believe that this system–field coupling might be a cornerstone for the practical deployment of quantum systems needing maximal coherence and correlations.

5 Concluding remarks

The critical analysis of quantum correlations and coherence is necessary to increase the efficiency of the quantum mechanical protocols. In this regard, we considered investigating a two-qubit anisotropic Heisenberg spin-chain when exposed to an external homogeneous magnetic field, further described by DM and KSEA interaction. We aimed to exploit the parameters of the current physical model for the reason to induce longer correlations and coherence preservation capacity in the two-qubit spin-chain. Using  LQU, \(\ell _1\) norm of coherence, and relative entropy of coherence, we investigate the dynamical maps of quantum correlations and coherence, respectively.

We show that the bipartite quantum correlations and coherence are vulnerable to the external magnetic field and are easily lost. To design the longer retention of the thermal quantum correlations and coherence in the current two-qubit state, one needs to include supporting material inducing preservation capacity in the state. For example, we observed that adjusting DM, KSEA, exchange coupling constants, and anisotropic properties can greatly enhance the related performance resulting in longer preservation of non-classical correlations and coherence. Besides these parameters, temperature regulation is one of the important aspects in the current study, usually, zero, as well as the non-zero low values of the temperature, remained favourable for quantum correlations and coherence preservation. However, we also found crucial that increasing values of DM and KSEA interactions can dominate the negative consequence of the magnetic fields and related temperature. In addition, the dynamics of coherence do not undergo any revival, ensuring that the state’s coherence and magnetic field do get reinforced well over each other. On the other hand, a single revival of non-classical correlations captured by LQU has been observed. For certain parameters settings, we found that the initial mixed bipartite state can be readily converted into a maximally correlated and coherent state.