1 Introduction

The normalized least-mean-square (NLMS) algorithm has been widely used in many practical fields, such as system identification, acoustic echo cancellation (AEC), channel equalization and channel estimation [7, 25, 26, 31, 33], owing to its low computational complexity and ease of implementation. However, it converges slowly for the colored input signals [7]. In order to achieve a faster convergence rate, a normalized subband adaptive filter (NSAF) algorithm has been proposed in [8]. The NSAF decomposes the colored input and desired signals into multiple subbands and then decimates these subband signals to achieve the decorrelating for the colored signal, and therefore achieves an improved convergence rate [9]. In addition, the computational complexity of the NSAF is similar to that of the NLMS, especially for the adaptive filter with a long impulsive response. Therefore, based on these properties, an important application of the NSAF is AEC. Unfortunately, similar to the NLMS algorithm, the NSAF also requires a compromise between fast convergence rate and small steady-state error, due to the use of a fixed step size.

One technique to solve the problem is to use the variable step size (VSS) instead of the constant step size in the original NSAF algorithm [1, 4, 17, 28, 29, 32, 34]. A set-membership NSAF (SM-NSAF) has been proposed in [1], which can be viewed as a variant of the VSS-type algorithms. However, we need to conduct many experiments to obtain a desired convergence performance in that the performance of the SM-NSAF is very sensitive to the choice of the error bound. In [17], the variable step size matrix NSAF (VSSM-NSAF) has been developed, whose performance is superior to that of the SM-NSAF in terms of the convergence rate, tracking capability and steady-state error. Regrettably, this algorithm still has a large steady-state error. Follow this line of thought, two variable step size NSAF algorithms have been derived in [29] and [4], by minimizing the mean square deviation (MSD) at each iteration. The difference is that the latter has the capability of tracking for non-stationary system, while the former only works well in stationary environment. As an improved version of [29], a new variable step size NSAF has been proposed in [28], which utilizes the individual step size in each subband instead of using a common step size in all subbands. Recently, a novel variable step size NSAF (NVSS-NSAF) has been proposed in [32], which derives an individual step size for each subband by minimizing the mean square of a posterior subband error. Nevertheless, these VSS algorithms presented in [1, 4, 28, 29, 32] must know the variances of the subband system noises in advance.

Another way is to use the convex combination of two adaptive filters, in which one adaptive filter provides fast convergence rate and the other one ensures small steady-state error [2, 3, 11–15, 27, 30]. In [16], the convex combination NSAF (CNSAF) algorithm has been proposed which achieves fast convergence rate and small steady-state error simultaneously without knowing the powers of the subband system noises. To further improve the transient performance of the CNSAF algorithm, an improved CNSAF (called ICNSAF) with transfer of weight has also been proposed in [16]. However, a common problem for these convex combination algorithms is a larger computational burden since two adaptive filters are run at the same time.

Benefiting from the convex combination idea, this paper derives a combined step size NSAF (CSS-NSAF) algorithm which combines a large step size and a small one via a time-varying mixing parameter, and it is indirectly obtained by minimizing the sum of squared subband errors through a modified sigmoidal function. It is worth mentioning that compared to these existing convex combination algorithms, the proposed algorithm only requires a single filter update and thus significantly reduces the computational cost.

2 Background on NSAF

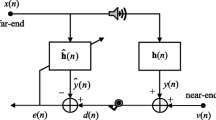
Consider the desired response d(n) originated from an unknown system

$$\begin{aligned} d(n)=\mathbf{u}^{T}(n)\mathbf{w}_o +\eta (n) \end{aligned}$$
(1)

where \(\mathbf{w}_o \) denotes an unknown \(L\times 1\) vector to be estimated, \(\mathbf{u}(n)=\left[ u\left( n \right) ,\right. \left. u(n-1),\right. \left. \ldots ,u(n-L+1) \right] ^{T}\) is the input vector, and \(\eta (n)\) stands for the white measure noise with zero mean and variance \(\sigma _\eta ^{2}\).

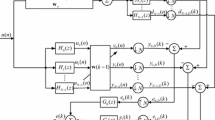
Figure 1 shows the structure of the NSAF, where the input signal u(n) and desired response d(n) are partitioned into subband signals \(u_i (n)\) and \(d_i (n)\) by using the analysis filters \(\left\{ {H_0 (z),H_1 (z),\ldots ,H_{N-1} (z)} \right\} \), respectively, and N denotes the number of subbands. The subband output signals \(y_i (n)\) are obtained by filtering \(u_i (n)\) through the adaptive filter whose weight vector is denoted as \(\mathbf{w}(k)=\hbox {[}w_0 (k),w_1 (k),\ldots ,w_{L-1} (k)]^{T}\). Then, the subband signals \(y_i (n)\) and \(d_i (n)\) are critically decimated to generate signals \(y_{i,D} (k)\) and \(d_{i,D} (k)\), respectively, where we use n and k to indicate the original sequences and the decimated sequences. The ith subband error signal is defined as \(e_{i,\mathrm{D}} (k)=d_{i,D} (k)-\mathbf{u}_i^T (k)\mathbf{w}(k)\). The weight vector of the NSAF algorithm is updated by [8]

$$\begin{aligned} \mathbf{w}(k+1)=\mathbf{w}(k)+\mu \sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k)}{\mathbf{u}_i^T (k)\mathbf{u}_i (k)+\delta }e_{i,D} (k)} \end{aligned}$$
(2)

where \(\mathbf{u}_i (k)=[\hbox {u}_i (kN),u_i (kN-1),\ldots ,u_i (kN-L+1)]^{T}\), \(\mu \) is the step size, and \(\delta \) is the regularization parameter to avoid division by zero.

Fig. 1
figure 1

Structure of the NSAF filter

Full size image

3 Proposed CSS-NSAF Algorithm

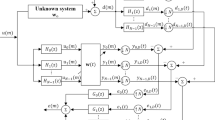
Supposing a large step size \(\mu _{1}\) and a small one \(\mu _{2}\), i.e., \(0<\mu _2 <\mu _1\), the weight vector \(\mathbf{w}(k)\) is updated to \(\mathbf{w}_1 (k+1)\) and \(\mathbf{w}_2 (k+1)\), respectively, as follows

$$\begin{aligned} \mathbf{w}_1 (k+1)= & {} \mathbf{w}(k)+\mu _1 \sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k)}{\mathbf{u}_i^T (k)\mathbf{u}_i (k)+\delta }e_{i,D} (k)} \end{aligned}$$
(3)
$$\begin{aligned} \mathbf{w}_2 (k+1)= & {} \mathbf{w}(k)+\mu _2 \sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k)}{\mathbf{u}_i^T (k)\mathbf{u}_i (k)+\delta }e_{i,D} (k)} . \end{aligned}$$
(4)

By using a variable mixing parameter \(\lambda (k)\), the updated weight vectors \(\mathbf{w}_1 (k+1)\) and \(\mathbf{w}_2 (k+1)\) can be combined as

$$\begin{aligned} \mathbf{w}(k+1)=\lambda (k)\mathbf{w}_1 (k+1)+(1-\lambda (k))\mathbf{w}_2 (k+1) \end{aligned}$$
(5)

where \(0\le \lambda (k)\le 1\). Substituting (3) and (4) into (5), we obtain the update formula of the weight vector of the proposed CSS-NSAF

$$\begin{aligned} \mathbf{w}(k+1)=\mathbf{w}(k)+\mu (k)\sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k)}{\mathbf{u}_i^T (k)\mathbf{u}_i (k)+\delta }e_{i,D} (k)} \end{aligned}$$
(6)

where \(\mu (k)=[\lambda (k)\mu _1 +(1-\lambda (k))\mu _2 ]\) denotes the combined step size and \(\mu (k)\) is expected to obtain the values of \(\mu _1\) and \(\mu _2\) when \(\lambda (k)\) is equal to 1 and 0, respectively, making the proposed CSS-NSAF algorithm obtain both fast convergence speed with the large step size \(\mu _1\) and small steady-state error with the small one \(\mu _{2}\). In order to constrain the value of \(\lambda (k)\) in the closed interval [0, 1], we introduce an auxiliary variable \(\alpha (k)\) via a modified sigmoidal activation function as follows [3]

$$\begin{aligned} \lambda (k)=\frac{C}{1+e^{-\alpha (k)}}-\left( \frac{C}{2}-\frac{1}{2}\right) \end{aligned}$$
(7)

where \(C\, (C>1)\) is a positive constant and \(\alpha (k)\) is limited as

$$\begin{aligned} \alpha (k)=\left\{ {{\begin{array}{lll} {-\ln \left( \frac{C+1}{C-1}\right) }&{} \quad {\hbox { if }\alpha (k)<-\ln \left( \frac{C+1}{C-1}\right) }&{} \\ {\ln \left( \frac{C+1}{C-1}\right) }&{} \quad \, {\hbox {if }\alpha (k)>\ln \left( \frac{C+1}{C-1}\right) }&{} \\ {\alpha (k)}&{} \qquad \quad {\hbox {otherwise}}&{} \\ \end{array} }} \right. . \end{aligned}$$
(8)
Table 1 Proposed CSS-NSAF algorithm
Full size table

It should be noted that if \(\alpha (k)\) is equal to \(-\ln (\frac{C+1}{C-1})\) and \(\ln (\frac{C+1}{C-1})\), \(\lambda (k)\) can get 0 and 1, respectively. Next, by means of the gradient descent method, we minimize the sum of squared subband errors, i.e., \(\sum _{i=0}^{N-1} {e_{_{i,\mathrm{D}} }^2 (k)} \), to recursively update \(\alpha (k)\) as follows

$$\begin{aligned} \alpha (k)= & {} \alpha (k-1)-\frac{\mu _\alpha }{2}\frac{\partial \left[ \sum \limits _{i=0}^{N-1} {e_{_{i,\mathrm{D}} }^2 (k)} \right] }{\partial \alpha (k-1)} \nonumber \\= & {} \alpha (k-1)+\mu _\alpha (\mu _1 -\mu _2 )\lambda (k-1)(1-\lambda (k-1)) \nonumber \\&\times \sum _{i=0}^{N-1} {e_{i,\mathrm{D}} (k)} \mathbf{u}_i^T (k)\sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k-1)e_{i,D} (k-1)}{\mathbf{u}_i^T (k-1)\mathbf{u}_i (k-1)+\delta }} \end{aligned}$$
(9)

where \(\mu _\alpha \) is the step size. In order to prevent the update process of \(\alpha (k)\) from stalling whenever \(\lambda (k)\) is equal to 0 or 1, we modify (9) as

$$\begin{aligned} \alpha (k)= & {} \alpha (k-1)+\mu _\alpha (\mu _1 -\mu _2 )[\lambda (k-1)(1-\lambda (k-1))+\varepsilon ] \nonumber \\&\times \sum _{i=0}^{N-1} {e_{i,\mathrm{D}} (k)} \mathbf{u}_i^T (k)\sum _{i=0}^{N-1} {\frac{\mathbf{u}_i (k-1)e_{i,D} (k-1)}{\mathbf{u}_i^T (k-1)\mathbf{u}_i (k-1)+\delta }} \end{aligned}$$
(10)

where \(\varepsilon \) is a very small positive constant. The proposed CSS–NSAF algorithm is summarized in Table 1.

Table 2 Computational complexity of the various NSAF-type algorithms
Full size table

Remark 1

It should be pointed out that the mixing parameter \(\lambda (k)\) is updated by a modified sigmoidal function, which is quite different from the common sigmoidal function of other existing convex combination algorithms [12, 13]. This modification makes the combined step size \(\mu (k)\) of the proposed CSS-NSAF get the values of large step size and small one, bringing about a significant improvement in terms of the convergence rate and steady-state error.

4 Computational Complexity

In Table 2, the computational complexity of the proposed CSS-NSAF algorithm is compared with that of the NSAF [8], NVSS-NSAF [32] and ICNSAF [16] in terms of the total number of multiplications, comparisons and additions, where K stands for the length of the analysis and synthesis filters. We can see from Table 1 that the numbers of multiplications for calculating the subband error signals and for updating the weight vector of the CSS-NSAF are \(3L+1\), and simultaneously CSS-NSAF needs 3NK multiplications to analyze and synthesize signals. Since the calculation of the accumulation in (10) does not require extra computational cost, (10) only needs 4 multiplications to update \(\alpha (k)\). Thus, a total of \(3L+3NK+5\) multiplications are required for the CSS-NSAF. Besides, the CSS-NSAF needs 2 comparisons and \(3L+3NK-3N+8\) additions as well. Since in many situation of AEC, L is typically more than one thousand and is significantly larger than the product NK, the number of multiplications could be approximated as 3L, which is apparently lower than that of the ICNSAF with about 4L. This illustrates the merit of decrease in computational burden of the proposed CSS-NSAF algorithm and the validity on the implementation issue of the AEC applications. The reason why the CSS-NSAF has a lower computation cost is that it only needs a single filter update instead of performing two filter updates simultaneously in the traditional convex combination method.

Remark 2

Here we discuss multiplications and additions of implementing the proposed CSS-NSAF algorithm in field programmable gate array (FPGA) and using chip EP4CE10F17C8N, which has at least 100 multipliers and 300 adders. Time division multiplexing (TDM) technique is used to reduce the complexity of the proposed algorithm. Supposing the length of the measured acoustic echo path is set to \(L = 1024\) and the clock cycle is \(2\times 10^{-7}s\), thus, about \(10^{5}\) multiplications and \(2.5\times 10^{5}\) additions can be performed within 1 s. Considering the actual situation, approximately \(10^{4}\) iterations can be done within 1 s based on a conservation estimate, which is feasible in practical applications.

Fig. 2
figure 2

a Measured acoustic echo path with \(L = 512\) taps, b speech signal for echo cancellation experiment

Full size image
Fig. 3
figure 3

NMSD learning curves of NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed algorithm for white Gaussian input signal with SNR = 20 dB. NVSS-NSAF: \(\lambda =4,\kappa =1\); CNSAF: \(\mu _\alpha =50\); ICNSAF: \(\mu _\alpha =50\); CSS-NSAF: \(\mu _\alpha =200\)

Full size image

5 Simulation Results

To verify the performance of the proposed CSS-NSAF, simulations are performed in the context of AEC. The unknown vector \(\mathbf{w}_o\) is illustrated in Fig. 2a with \(L = 512\) taps. To compare the tracking capability of these algorithms, the unknown vector is changed to \(-\mathbf{w}_o\) in the middle of iterations. It is assumed that adaptive filter has the same length as the unknown vector. The input signal is either a zero-mean white Gaussian signal, or an AR(1) signal generated by filtering a white Gaussian noise through a first-order autoregressive system with a pole at 0.9, or a speech input signal which is depicted in Fig. 2b. A four-band cosine-modulated filter bank is used [32]. A white Gaussian noise is added to the unknown system output as a background noise with a signal-to-noise ratio (SNR) of 20 or 30 dB. The performance is measured by the normalized MSD (NMSD), defined as \(20\log _{10} \left[ {\left\| {\mathbf{w}_o-\mathbf{w}(k)}\right\| _2^2 /\left\| {\mathbf{w}_o} \right\| _2^2}\right] \), which is used as the performance design criteria to compare the NSAF, NVSS-NSAF, CNSAF, ICNSAF and the proposed CSS-NSAF algorithms. All simulated learning curves are obtained by ensemble averaging over 50 independent trails, except for the speech input signal (one trial).

5.1 White Input

Figure 3 illustrates the NMSD learning curves of the standard NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed CSS-NSAF algorithms. In this simulation, a white Gaussian signal is used as the input signal and the SNR is 20dB. For a fair comparison, the parameters of these algorithms are chosen according to the recommended values in the literature. We can see that although the convergence speed of the proposed CSS-NSAF is slightly slower than that of the NVSS-NSAF, the CSS-NSAF still achieves a significant smaller steady-state NMSD than the NVSS-NSAF algorithm, and the proposed algorithm outperforms the NSAF, CNSAF and ICNSAF algorithms in terms of the convergence rate, tracking capability and steady-state NMSD. Here we should owe the performance improvement of the CSS-NSAF to the modified sigmoidal function, letting the proposed CSS-NSAF algorithm obtains fast convergence speed with the large step size \(\mu _1\).

In Fig. 4, the SNR is increased to 30dB and still the same input signal is used. As expected, the proposed CSS-NSAF still has an improvement in the convergence speed, steady-state NMSD as well as the tracking capability as compared to the NSAF, NVSS-NSAF, CNSAF and ICNSAF algorithms. Besides, by contrasting Fig. 4 with Fig. 3, it can be observed that the steady-state NMSD of the proposed CSS-NSAF algorithm decreases as the SNR increases.

Fig. 4
figure 4

NMSD learning curves of NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed algorithm for white Gaussian input signal with SNR = 30 dB. NVSS-NSAF: \(\lambda =4,\kappa =1\); CNSAF: \(\mu _\alpha =200\); ICNSAF: \(\mu _\alpha =200\); CSS-NSAF: \(\mu _\alpha =550\)

Full size image

5.2 AR(1) Input

Figures 5 and 6 compare the performance of the CSS-NSAF with that of the NSAF, NVSS-NSAF, CNSAF and ICNSAF algorithms for AR(1) input signal with the SNR 20dB and 30 dB, respectively. These simulation results with AR(1) input signal are similar to those with white input signal in Figs. 3 and 4, which verify the effectiveness of the proposed CSS-NSAF. The results is predictable because a modified sigmoidal function is used instead of the common sigmoidal function in other existing convex combination algorithms, which guarantees that the proposed algorithm is able to achieve faster converge rate than the NSAF, NVSS-NSAF, CNSAF and ICNSAF algorithms. Likewise, the larger the SNR value, the smaller the steady-state NMSD for AR(1) input signal.

Fig. 5
figure 5

NMSD learning curves of NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed algorithm for AR(1) input signal with SNR = 20 dB. NVSS-NSAF: \(\lambda =4,\kappa =1\); CNSAF: \(\mu _\alpha =20\); ICNSAF: \(\mu _\alpha =20\); CSS-NSAF: \(\mu _\alpha =20\)

Full size image
Fig. 6
figure 6

NMSD learning curves of NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed algorithm for AR(1) input signal with SNR = 30 dB. NVSS-NSAF: \(\lambda =4,\kappa =1\); CNSAF: \(\mu _\alpha =100\); ICNSAF: \(\mu _\alpha =100\); CSS-NSAF: \(\mu _\alpha =100\)

Full size image

5.3 Speech Input

Figure 7 shows the NMSD learning curves of the standard NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed CSS-NSAF algorithms for the speech input signal. The used speech signal is depicted in Fig. 2b, and the SNR is 30dB. Note that the regularization parameters with the speech input are set to \(15\sigma _u^2\) for all algorithms, where \(\sigma _u^2\) is the power of the input signal. With the benefit of the modified sigmoidal function, one can see that the proposed algorithm performs much better than the NSAF, NVSS-NSAF, CNSAF and ICNSAF algorithms with respect to the convergence rate and steady-state NMSD.

Fig. 7
figure 7

NMSD learning curves of NSAF [8], NVSS-NSAF [32], CNSAF [16], ICNSAF [16] and the proposed algorithm for speech input signal with SNR = 30 dB. NVSS-NSAF: \(\lambda =4,\kappa =1\); CNSAF: \(\mu _\alpha =100\); ICNSAF: \(\mu _\alpha =100\); CSS-NSAF: \(\mu _\alpha =100\)

Full size image

6 Conclusion

A novel combined step size NSAF (CSS-NSAF) algorithm has been proposed for acoustic echo cancellation (AEC) applications in this paper, which has the following advantages.

  • By minimizing the sum of squared subband errors, the mixing parameter is indirectly updated through a modified sigmoidal function, which is quite different from the common sigmoidal function of other convex combination techniques. This modification makes the combined step size achieve the values of large step size and the small one, making the proposed CSS-NSAF algorithm obtain fast convergence rate with the large step size and small steady-state error with the small one.

  • Compared with other convex combination methods, the proposed algorithm has a lower computational complexity in that it only requires a single filter update, demonstrating the efficiency on the implementation issue of the AEC applications. Simulation results in the context of AEC show that the proposed algorithm achieves better performance than other algorithms mentioned above.

  • Although the CSS-NSAF algorithm in this paper essentially belongs to linear adaptive filtering scheme for AEC applications, it also can be extended to the nonlinear model [20], fuzzy-model-based general nonlinear systems [18, 19, 21, 22], Volterra-model-based nonlinear system identification and AEC [6, 10, 23, 24] and other fields [5] in the future.

  • Filtering design of fuzzy-model-based with signal quantization is an important problem in nonlinear networked control system [21]. Therefore, it remains a future work to generalize the proposed adaptive filter algorithm for solving this practical application problem.