Adaptive Polynomial Filtering using Generalized Variable Step-Size Least Mean pth Power (LMP) Algorithm

Abstract

This correspondence presents the adaptive polynomial filtering using the generalized variable step-size least mean $p$th power (GVSS-LMP) algorithm for the nonlinear Volterra system identification, under the $\alpha$-stable impulsive noise environment. Due to the lack of finite second-order statistics of the impulse noise, we espouse the minimum error dispersion criterion as an appropriate metric for the estimation error, instead of the conventional minimum mean square error criterion. For the convergence of LMP algorithm, the adaptive weights are updated by adjusting $p\ge 1$ in the presence of impulsive noise characterized by $1<\alpha <2$. In many practical applications, the autocorrelation matrix of input signal has the larger eigenvalue spread in the case of nonlinear Volterra filter than in the case of linear finite impulse response filter. In such cases, the time-varying step-size is an appropriate option to mitigate the adverse effects of eigenvalue spread on the convergence of LMP adaptive algorithm. In this paper, the GVSS updating criterion is proposed in combination with the LMP algorithm, to identify the slowly time-varying Volterra kernels, under the non-Gaussian $\alpha$-stable impulsive noise scenario. The simulation results are presented to demonstrate that the proposed GVSS-LMP algorithm is more robust to the impulsive noise in comparison to the conventional techniques, when the input signal is correlated or uncorrelated Gaussian sequence, while keeping $1<p<\alpha <2$. It also exhibits flexible design to tackle the slowly time-varying nonlinear system identification problem.

1 Introduction

In the field of communication engineering, speech processing, image processing, and biomedical engineering, etc., many systems possess certain degrees of nonlinearity, which do not exhibit superposition property. Any such polynomial system [11] is also called Volterra system [9], which is most commonly referred /used paradigm due to its roots in the Taylor series expansion of the nonlinear functions with memory [21]. Therefore, the nonlinear system identification [16] is indispensable to establish a mathematical model for an unknown system through the input–output relationship. The researchers in the field of nonlinear system identification usually consider Volterra, Weiner [17] and Hammerstein [26] models. However, the presented research work will focus on the variable step-size adaptive nonlinear Volterra filtering [12], due to its low computational complexity compared to the variable step-size adaptive Hammerstein filtering [25].

The measurement noise is an inevitable issue in the field of nonlinear system identification, which is generally assumed to be a random process with the finite-order statistics. Under such scenario, the mean square error (MSE) appears as an appropriate metric for the estimation error. However, the impulsive noise [15] with the heavier distribution tail possesses approximately infinite second-order statistics, which connotes non-Gaussian characteristics. It leads to the need of alternate methods for the nonlinear system identification in the presence of impulse noise.

The Gaussian distribution is a special case of $\alpha$-stable processes with $\alpha =2$, which is characterized by the finite variance [20]. It is noteworthy that the $\alpha$-stable processes in the range $1<\alpha <2$ are considered to be non-Gaussian with infinite variance. In [24], Stuck has discussed that a finite variance Gaussian model is appropriate over a limited range of data, while an infinite variance model is adequate in terms of matching the observed data over a wider range. Therefore, the impulse noise occurrence may be modeled as non-Gaussian for further analysis, which favors the application of adaptive nonlinear filtering for the noise excision and nonlinear system identification [14]. Under the aforementioned conditions, the cost function based on the minimum error dispersion (MED) outperforms the conventional minimum mean square error (MMSE)-based approach [22]. Moreover, it results in the development of least mean $p$th power (LMP) adaptation algorithm, in which the cost function is convex with respect to the filter weights for the range $p\ge 1$. However, the performance of LMP algorithm supersedes the conventional LMS algorithm, only when the value of parameter $p$ is close to $\alpha$ for the range $1<p<\alpha$. But in [28], Weng and Barner have delineated that the large eigenvalue spread of the input signal autocorrelation matrix has been observed in the case of Volterra filtering, which in turn results in the slow convergence speed/rate of the LMP, as well as LMS adaptive algorithms. However, the nonlinear Volterra FSS-LMS filter can encounter divergence in case of the ill-conditioned tap input autocorrelation matrix [25].

The time-varying step-size is one of the tractable solutions to expedite the convergence process in the case of LMP algorithm. Kwong and Johnston have proposed a variable step-size LMS (KVSS-LMS) adaptive algorithm in [10] for the tracking of time-varying first-order Markovian channels, in which the step-size adjustment is controlled by the square of prediction error. Further, Aboulnasr and Mayyas have presented a variable step-size LMS (AVSS-LMS) adaptive algorithm in [1], in which the step-size of the algorithm is adjusted according to the square of time-averaged estimate of the autocorrelation of present/instantaneous estimation error $e( n)$ and the past estimation error $e( {n-1})$. In an alternate approach proposed by Ang and Farhang-Boroujeny in [2], the step-size of adaptive filter is changed according to a stochastic gradient adaptive algorithm designed to reduce the squared estimation error at each iteration, which is denoted as SVSS-LMS algorithm. All the aforementioned VSS-LMS algorithms are implemented using the linear filtering perspective.

In this paper, we propose adaptive nonlinear Volterra filtering using the generalized variable step-size least mean $p$th power (GVSS-LMP) algorithm for the slowly time-varying system identification, in the presence of $\alpha$-stable impulsive noise. This combination of GVSS and LMP algorithm enhances the convergence rate under the noisy environment. However, it reduces to the various VSS-LMP and VSS-LMS adaptive algorithms under the typical parametric conditions, which signifies its flexibility. This paper is organized as follows. In Sect. 2, we first describe the slowly time-varying nonlinear Volterra system (as shown in Fig. 1) along with the details of $\alpha$-stable impulse noise characteristics. We next introduce the adaptive nonlinear system identification method based on the MED criterion using the proposed GVSS-LMP algorithm in Sect. 3. Subsequently, the convergence and tracking mode performances of the presented algorithm are compared with KVSS-LMP [10, 28], AVSS-LMP [1, 28] and SVSS-LMS [2] adaptive algorithms in Sect. 4, to manifest its benefits and efficacy on the basis of simulation results. Finally, the concluding remarks and future scope are illustrated in Sect. 5.

Fig. 1

Nonlinear slowly time-varying system identification configuration

2 Nonlinear System Model in Noisy Environment

2.1 Slowly Time-Varying Volterra System

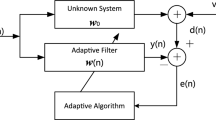
Among polynomial system models, the Volterra system [21] is the preferred paradigm because its output is nonlinear with respect to the input signals, but it is linear in terms of kernels. Therefore, the adaptive signal processing techniques may be directly extended to the Volterra filtering. In literature, there are many time-varying nonlinear wireless or underwater acoustic communication channels, which need to be tracked or estimated by the nonlinear polynomial adaptive filtering. For identification of these unknown systems, we consider the configuration shown in Fig. 1, in which the underlying system and the adaptive nonlinear Volterra filter are driven by the common input signal vector $\vec {x}( n)$. In the presence of impulse noise, the general input–output relationship of an unknown nonlinear system can be illustrated by a truncated Volterra series as

$$\begin{aligned} y( n)=h_0 +\sum \limits _{k=1}^K {\sum \limits _{m_1=0}^{M-1} \ldots } \sum \limits _{m_k=0}^{M-1} {h_k ( {n;m_1 ,\ldots ,m_k })} \prod \limits _{i=1}^k {x( {n-m_i })}+imp( n) \end{aligned}$$

(1)

Typically, the second-order Volterra series is described by the input–output relationship as

$$\begin{aligned} y(n)=h_0 +\sum \limits _{m_1 =0}^{M-1} {h_1 (n;m_1 )} x(n-m_1 )+\sum \limits _{m_1 =0}^{M-1} {\sum \limits _{m_2 =0}^{M-1} {h_2 (n;m_1 ,m_2 )} x(n-m_1 )} \nonumber \\ x(n-m_2 )+imp(n), \end{aligned}$$

(2)

where $h_{0}$ is the time-invariant zeroth-order Volterra kernel, $h_1 ,h_2$ are the first-order and the second-order Volterra kernels, respectively, $M$ is the memory length, $x( n)$ is the input signal, and $imp(n)$ is the $\alpha$-stable noise with zero-mean (inevitable disturbance). The complexity of Volterra filter is dependent upon the memory ($M)$. In the general case, the degree of nonlinearity ($K)$ of the Volterra system is usually assumed to be time-invariant [3]. As the Volterra kernels are symmetrical in nature, the value of coefficient $h_k ( {n;\,m_1 ,\,\ldots ,\,m_k })$ is kept unchanged for any of the possible k! permutations of $m_1 ,m_2 ,\ldots ,m_k$. Hence, these kernels remain time-invariant under the different permutations of its argument.

In the presented work, the values of $K$ and $M$ are considered to be known a priori. For the slowly time-varying second-order Volterra system, the input–output relationship is depicted by (1) with K = 2. Now, let us consider the $L\times 1$ dimensional expanded filter coefficients vector as

$$\begin{aligned} \begin{array}{l} \vec {h}(n)=[h_1 (n;0),h_1 (n;1),\ldots ,h_1 (n;M-1),h_2 (n;0,0),h_2 (n;0,1),\ldots \ldots , \\ \qquad \qquad \ldots \ldots ,h_2 (n;0,M-1),h_2 (n;1,1),\ldots ,h_2 (n;M-1,M-1)]^T, \\ \end{array} \end{aligned}$$

(3)

where $(.)^T$is the matrix transpose operator. The $L\times 1$ dimensional expanded input signal vector for the second-order Volterra filter with zero-mean and variance $\sigma _x^2 =1/L$ is denoted as

$$\begin{aligned} \begin{array}{l} \vec {x}(n)=[x(n),x(n-1),\ldots ,x(n-M+1),\ldots ,x^2(n),x(n)x(n-1),\ldots , \\ \qquad \qquad \ldots \ldots \;x(n)x(n-M+1),\ldots ,x^2(n-1),\ldots ,x^2(n-M+1)]^T \\ \end{array} \end{aligned}$$

(4)

Further, we can express Eq. (2) in the vector form as

$$\begin{aligned} y( n)=\vec {h}^T( n)\vec {x}( n)+imp( n) \end{aligned}$$

(5)

In the nonlinear system identification, the final goal is to identify the time-varying Volterra kernels $h_k ( {n;\,m_1 ,\,\ldots ,\,m_k })$ in Eq. (1) through measured $y( n)$ and $x( n)$, which follow the Random Walk model [1, 2, 10, 13] given by $\vec {h}( {n+1})=\vec {h}( n)+\vec {w}( {n+1})$; where $\vec {w}( n)$ is the zero-mean white Gaussian process noise vector with variance $\sigma _w^2 =0.001$ (assumed to be small for the slow time-variations). For the mathematical analysis, the adaptively estimated Volterra kernel vector may be represented by

$$\begin{aligned} \begin{array}{l} {\vec {h}}'(n)=[{h}'_1 (n;0),{h}'_1 (n;1),\,\,\ldots \,\,,{h}'_1 (n;M-1),{h}'_2 (n;0,0),{h}'_2 (n;0,1),\ldots .., \\ \ldots \ldots \ldots \ldots \ldots \ldots \ldots \ldots ..\,\,,{h}'_2 (n;0,M-1),{h}'_2 (n;1,1),\,\ldots \,,{h}'_2 (n;M-1,M-1)]^T \\ \end{array} \end{aligned}$$

(6)

Therefore, the estimated received signal is denoted by

$$\begin{aligned} {y}'( n)=\vec {{h}'}^T( n)\vec {x}( n) \end{aligned}$$

(7)

Hence, the output estimation error in the signal reception is computed by

$$\begin{aligned} e( n)=y( n)-{y}'( n) \end{aligned}$$

(8)

This error signal is fed back to the adaptive filter (self-designing filter), which begins from an initial guess based on the prior knowledge available to the system; and then it converges eventually to the optimal solution in some statistical sense through the successive iterations.

2.2 Symmetric $\alpha$-Stable Noise Model

An $\alpha$-stable process can be described by the following characteristic function [19, 22], as it exhibits no closed-form probability density function.

$$\begin{aligned} \Phi ( \Omega )=\exp \left[ {j\eta \Omega -\gamma \left| \Omega \right| ^\alpha \left\{ {1+j\beta \hbox {sgn}( \Omega )S( {\Omega ,\alpha })} \right\} } \right] \end{aligned}$$

(9)

$$\begin{aligned} \hbox {where}, S( {\Omega ,\alpha })=\left[ {\begin{array}{l} \tan ( {\frac{\alpha \pi }{2}})\,\,\,\,\hbox {for}\,\,\alpha \ne 1 \\ \frac{2}{\pi }\log \left| \Omega \right| \,\,\,\,\,\hbox {for}\,\,\alpha =1 \\ \end{array}} \right] , 0<\alpha \le 2, -\infty <\eta <+\infty , \gamma >0, \end{aligned}$$

and $-1\le \beta \le +1$. Thus, a stable distribution is completely determined by four parameters: (1) the location parameter $\eta$, (2) the index of skewness $\beta$ (the distribution is symmetric about its location parameter $\eta$, when $\beta =0$, therefore, called symmetric $\alpha$-stable distribution), (3) the scale parameter $\gamma$ is called dispersion (the parameter $\gamma ^{1/ \alpha }$ plays a role similar to the standard deviation of the Gaussian distribution), and (4) $\alpha$ is the characteristic exponent. This shape parameter is a measure of the heaviness of the tail of distribution. The processes with small values of $\alpha$ are considered to be impulsive. However, for the large values of $\alpha$, the observed values of random variable are not far from its central location. Under typical conditions, when the value of $\alpha \rightarrow 2$ and $\beta =0$, then $\Phi ( \Omega )\rightarrow \exp \left[ {j\eta \Omega -\gamma \left| \Omega \right| ^2} \right]$. This relevant stable distribution is Gaussian in nature. However in the presented work, the $\alpha$-stable random variables do not have finite variance, but these are characterized only by the finite $p$th-order moments for $p<\alpha$. It is noteworthy fact that all the moments of order less than $\alpha$ do exist and are called the fractional lower order moments (FLOM) [22], which can be derived from its dispersion and the characteristic exponent with zero location parameter as

$$\begin{aligned} \begin{array}{l} E\left| X \right| ^p=C( {p,\alpha })\gamma ^{p/ \alpha }\,\,for\,\,0<p<\alpha \\ \text{ where },\,\,C( {p,\alpha })=\frac{2^{p+1}\Gamma (({p+1}) / 2) \Gamma ( {{-p} / \alpha })}{\alpha \sqrt{\pi }\Gamma ( {{-p} / 2})} \end{array} \end{aligned}$$

(10)

which is dependent on the values of parameters $\alpha$ and $p$, not on random variable X. In the above equation, the parameter $\Gamma$ is the gamma function [19, 22].

3 GVSS-LMP Algorithm for Nonlinear System Identification

3.1 Least Mean pth Power Adaptive Algorithm

In the field of adaptive signal processing [7], the most popular approaches for the estimation/prediction schemes are based on the MMSE criterion. The corresponding cost function as per the Wiener theory is

$$\begin{aligned} J_\mathrm{MMSE} ( {\vec {{h}'}})=E\left[ {\left| {y( n)-\vec {{h}'}^T( n)\vec {x}( n)} \right| ^2} \right] , \end{aligned}$$

(11)

where $E\left[ *\right]$ is the ensembled average operator. Using the error signal $e( n)$, the non-mean square error criterion is discussed in the form of least mean forth (LMF) adaptive algorithm in [27], in which the cost function is considered to be $E\left[ {\left| {e( n)} \right| ^{2\bar{K}}} \right]$ for $\bar{K}\ge 1$ (only integer values of $\bar{K})$. In some typical cases, the LMF algorithm with $\bar{K}>1$ outperforms the conventional LMS algorithm by providing less noise in weights for the same speed of convergence. It has motivated the evolution of LMP algorithm for the noisy situations, in which $1<p<\alpha <2$. Particularly, when $\vec {{h}'}( n)\rightarrow \vec {h}( n)$ in the presence of $\alpha$-stable noise, the residual $imp(n)$ dominates in the estimation error $e( n)$ in Eq. (8). Therefore, the resulting estimation error may be assumed as approximately $\alpha$-stable process, such that the FLOM [22] is

$$\begin{aligned} E\left[ {\left| {e( n)} \right| ^{p-2}} \right] =C( {p-2,\alpha })\gamma ^{(( {p-2})/ \alpha )}=D( {p,\alpha ,\gamma }) \end{aligned}$$

(12)

Since the variance of $\alpha$-stable noise is not finite, therefore, we can utilize the MED criterion [24], i.e., the minimization of cost function

$$\begin{aligned} J_\mathrm{MED} ( {\vec {{h}'}})=E\left[ {\left| {y( n)-\vec {{h}'}^T( n)\vec {x}( n)} \right| ^p} \right] \end{aligned}$$

(13)

It is equivalent to the minimization of $p$th order FLOM. Unfortunately, this cost function $J_\mathrm{MED} ( {\vec {{h}'}})$ does not exhibit closed-form solution. Therefore, the stochastic gradient technique can be utilized as an alternative for the minimization of $J_\mathrm{MED} ( {\vec {{h}'}})$, similar to the LMS adaptive algorithm. The basic idea is to minimize the error dispersion for each successive datum or observation as much as possible. It leads to

$$\begin{aligned} \vec {{h}'}( {n+1})=\vec {{h}'}( n)-\mu ( n)\nabla _h J_{MD} ( {\vec {{h}'}}) \end{aligned}$$

(14)

Akin to the steepest descent algorithm [7],

$$\begin{aligned} \nabla _h J_\mathrm{MD} ( {\vec {{h}'}})=\frac{\delta E\left[ {\left| {y( n)-\vec {{h}'}^T( n)\vec {x}( n)} \right| { }^p} \right] }{\delta \vec {{h}'}} \end{aligned}$$

(15)

Analogous to the stochastic gradient algorithm [22],

$$\begin{aligned} \nabla _h J_\mathrm{MD} ( {\vec {{h}'}})\approx \frac{\delta \left[ {\left| {e( n)} \right| ^p} \right] }{\delta \vec {{h}'}}=p\left| {e( n)} \right| ^{p-1}\frac{\delta \left| {e( n)} \right| }{\delta \vec {{h}'}} \end{aligned}$$

(16)

$$\begin{aligned} \text{ where, } \begin{array}{lll} \quad \left| {e( n)} \right| &{}=&{} \hbox {sgn}\left\{ {e( n)} \right\} e( n)\\ &{}=&{} \hbox {sgn}\left\{ {e( n)} \right\} \left\{ {y( n)-\vec {{h}'}^T( n)\vec {x}( n)} \right\} \\ \end{array} \end{aligned}$$

(17)

$$\begin{aligned} \text{ Hence },\,\,\,\nabla _h J_{MD} ( {\vec {{h}'}})\approx -p\left| {e( n)} \right| ^{p-1}sgn\left\{ {e( n)} \right\} \vec {x}( n) \end{aligned}$$

(18)

By substituting (18) in Eq. (14), it can be shown that

$$\begin{aligned} \vec {{h}'}( {n+1})=\vec {{h}'}( n)+\left\{ {\mu ( n)p} \right\} \left| {e( n)} \right| ^{p-1}sgn\left\{ {e( n)} \right\} \vec {x}( n) \end{aligned}$$

(19)

The simplified version of LMP algorithm can be represented as

$$\begin{aligned} \vec {{h}'}( {n+1})=\vec {{h}'}( n)+{\mu }'( n)\left| {e( n)} \right| ^{p-1}sgn\left\{ {e( n)} \right\} \vec {x}( n), \end{aligned}$$

(20)

where ${\mu }'( n)=\mu ( n)p$ is the variable step-size (VSS), which plays a critical role in the convergence mode of LMP algorithm [28], for the operating range $1<p<\alpha <2$. Although the convergence analysis of LMP algorithm is a tedious problem, yet the convergence range of variable step-size ${\mu }'( n)$ in (20) can be approximated as

$$\begin{aligned} 0<{\mu }'( n)<\frac{2}{D( {p,\alpha ,\gamma })\lambda _{Max} }\,\,( {\text{ loose } \text{ bounded }, \, \left[ {\text{28 }} \right] }) \end{aligned}$$

(21)

By invoking a better approximation, it can be shown that

$$\begin{aligned} 0<{\mu }'( n)<\frac{2}{D( {p,\alpha ,\gamma })tr( {\vec {R}_{xx} })}<\frac{2}{3tr( {\vec {R}_{xx} })}\,( {\text{ tight } \text{ bounded },\,\left[ {\text{23 }, \text{28 }} \right] }), \end{aligned}$$

(22)

where $tr( {\vec {R}_{xx} })$ symbolizes the trace of autocorrelation matrix $\vec {R}_{xx}$ of the input signals. The maximum value of VSS is tightly bounded by the maximum eigenvalue $\lambda _{Max}$ of the matrix $\vec {R}_{xx} =E\left[ {\vec {x}( n)\vec {x}^T( n)} \right]$. The LMS algorithm is a special case of LMP algorithm for $p=2$ and $\alpha =2$ in Eq. (20). In the next subsection, we give details about the proposed GVSS criterion to update ${\mu }'( n)$ in the aforementioned iterative procedure.

3.2 Generalized Variable Step-Size (GVSS) Criterion

The large eigenvalue spread in the case of Volterra filtering necessitates the incorporation of variable step-size, in combination with the LMP adaptive algorithm, for the improved convergence rate. Moreover, the VSS criterion is also beneficial in the tracking of slowly time-varying channels/systems. The VSS must increase or decrease as the mean square error increases or decreases, allowing the adaptive nonlinear filter to track changes in the underlying system and to produce a small steady-state error. It should reduce the tradeoff between misadjustment and the speed of adaptation under the slowly time-varying conditions, due to its innate capability of providing both fast tracking, as well as small misadjustment. Therefore, the generalized variable step-size (GVSS) criterion is proposed to adjust the step-size under the stationary and nonstationary scenarios, which is as follows:

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }J_1 ( {n-1})+\bar{\beta }J_2 ( n) \end{aligned}$$

(23)

$$\begin{aligned} \text{ where },\,\,J_1 ( n)=\sum \limits _{\bar{p}=0}^{\bar{P}} {\lambda _1^{\bar{p}} e( n)e( {n-\bar{p}})} \,\text{ with }\,\,0\le \lambda _1 <1 \end{aligned}$$

(24)

$$\begin{aligned} J_2 ( n)=\left[ {\sum \limits _{\bar{q}=1}^{\bar{Q}} {\lambda _2^{\bar{q}} e( {n-\bar{q}})} \,\,\vec {x}^T( {n-\bar{q}})} \right] \vec {x}( n)e( n)\,\,\text{ with }\,\,0\le \lambda _2 <1 \end{aligned}$$

(25)

where $0<\bar{\alpha }\le 1$, $0\le \bar{\gamma }<1$, and $0\le \bar{\beta }<1$. The parameter $\bar{\alpha }$ induces the global exponential forgetting to the VSS, the parameter $\bar{\gamma }$ controls the convergence time, as well as the level of misadjustment [10], the parameter $\bar{\beta }$ adjusts the adaptive behavior of the step-size sequence ${\mu }'( n)$ [13]. However, $\lambda _1 \hbox {and} \lambda _2$ are the local exponential forgetting factors in Eqs. (24) and (25), respectively. For the appropriate convergence, the VSS should be bounded in the range ${\mu }'_\mathrm{Min} \le {\mu }'( n)\le {\mu }'_\mathrm{Max}$ [1]. The initial step-size is usually taken as ${\mu }'_\mathrm{Max}$, which ensures that the MED of algorithm remains bounded. However, ${\mu }'_\mathrm{Min}$ is chosen to provide the minimum level of tracking ability, which is kept close to the step-size of FSS-LMS algorithm.

Further in special case 1, if the values of parameter are $\bar{P}=0$ and $\bar{\beta }=0$ in Eq. (23), then

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }J_1 ( {n-1}) \end{aligned}$$

(26)

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }\underline{\underline{e{ }^2( {n-1})}} \end{aligned}$$

(27)

The underlined term in Eq. (27) is similar to the KVSS criterion presented in [10], (as in Eq. (33) of appendix). Next in special case 2, if the parametric values $\bar{P}=1$ and $\bar{\beta }=0$ are in Eq. (23), then

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }e{ }^2( {n-1})+\left\{ {\bar{\gamma }\lambda _1 } \right\} \underline{\underline{\left\{ {e( {n-1})e( {n-2})} \right\} }} \end{aligned}$$

(28)

The underlined term in Eq. (28) is akin to the AVSS criterion described in [1], (as in Eq. (35) of appendix). Subsequently in special case 3, if $\bar{\alpha }=1$, $\bar{Q}=1$, and $\bar{\gamma }=0$ are in Eq. (23), then

$$\begin{aligned} {\mu }'( n)={\mu }'( {n-1})+\left\{ {\bar{\beta }\lambda _2 } \right\} \left\{ {\underline{\underline{e( {n-1})\vec {x}^T( {n-1})\vec {x}( n)e( n)}} } \right\} \end{aligned}$$

(29)

The underlined term in Eq. (29) is analogous to the Mathews’ algorithm proposed in [13]. However, in special case 4, $\bar{\alpha }=1$ and $\bar{\gamma }=0$ in Eq. (23) results in

$$\begin{aligned} {\mu }'( n)\!=\!{\mu }'( {n-1})\!+\!\left\{ {\bar{\beta }\lambda _2 } \right\} \underline{\underline{\left[ {\begin{array}{l} e({n-1})\vec {x}^T({n-1})\!+\!\lambda _2 e({n-2})\vec {x}^T({n-2})\\ \!+\,\lambda _2^2 e( {n-3})\vec {x}^T( {n-3})+\ldots \ldots \\ \ldots \ldots +\lambda _2^{\bar{Q}-1} e( {n-\bar{Q}})\vec {x}^T( {n-\bar{Q}}) \\ \end{array}}\right] }} \vec {x}( n)e( n) \end{aligned}$$

(30)

The underlined term in Eq. (30) is similar to the SVSS criterion suggested in [2], (as shown in Eq. (39) of appendix). Therefore, the abovementioned GVSS criterion (23) is incorporated in Eq. (20) to formulate the proposed GVSS-LMP algorithm, which is relatively computationally complex than FSS-LMP, KVSS-LMP, AVSS-LMP, and SVSS-LMS algorithms.

4 Simulation Results

The performance evaluation of the proposed GVSS-LMP algorithm is performed by comparing it with KVSS-LMP, AVSS-LMP, and SVSS-LMS algorithm under the similar conditions, for the nonlinear system identification. The kernels of the unknown system (as shown in Fig. 1) are assumed to follow the Random Walk model for the slow time-variations in the system response (as discussed in Sect. 2.1). As in $\alpha$-stable noisy environment, the error signal variance could be infinite, therefore, the LMS algorithm based on the MMSE criterion (11) seems to be an inappropriate choice in comparison with the MED criterion $J_\mathrm{MED} ( {{h}'})$ (12). However, the value of $p$ in LMP algorithm (20) is kept close to $\alpha$ for excellent results [10] in terms of the transient and steady-state behavior, which are fixed at $\alpha =1.75\,\,and\,\,p=1.6$.

The input signal to the underlying unknown system (as shown in Fig. 1) may be correlated or uncorrelated Gaussian sequence $\vec {x}$. The white Gaussian input is quite apposite for the identification of kernels in the Volterra system because it has adequate spectral representatives and sufficient amplitude variations [6]. Moreover, the Volterra series can be expressed as G-functionals [12], which form an orthogonal set when the input is white Gaussian. However, the non-identical-independent-distributed input signals lead to the large eigenvalue spread of the autocorrelation matrix $\vec {R}_{xx}$ (particularly in the case of Volterra filters), which in turn results in the slow convergence [7]. The value of minimum step-size is ${\mu }'_\mathrm{Min} =0.0008$ and the maximum bounded value of step-size ${\mu }'_\mathrm{Max}$ is set by the Eq. (22). The signal-to-noise-ratio (SNR) is defined as the input signal variance to the dispersion of the $\alpha$-stable noise, i.e., $\mathrm{SNR}={\sigma _x^2 } /\gamma$, which is kept 15 dB for all the simulations [28]. The Volterra kernel mean square estimation error (performance appraisal factor) is calculated by the following formula

$$\begin{aligned} \hat{J}( n)=E\left[ {\left| {h( n)-{h}'( n)} \right| ^2} \right] \end{aligned}$$

(31)

As per the Monte-Carlo simulations, the performance of adaptive algorithms is compared on the basis of measured performance appraisal factor as

$$\begin{aligned} \hat{J}( n)=\sum \limits _{j=1}^{2500} {\left[ {\frac{\left| {h( {n,j})-{h}'( {n,j})} \right| ^2}{2500}} \right] } \end{aligned}$$

(32)

Example 1

We consider the second-order Volterra filter with $K=2\,\,\mathrm{and}\,\,M=3$ in the first simulation setup, with the uncorrelated Gaussian white input sequence. Similar to the methodology opted in [1], the parameter values of the adaptive algorithms are selected to produce a comparable level of misadjustment. The values of parameters are $\lambda _1 =0.8,\,\,\lambda _2 =0.5$, $\bar{\alpha }=0.97,\bar{\gamma }=15\times 10^{-5}$, $\bar{P}=\bar{Q}=2$, $\bar{\alpha }_A =0.97, \quad \bar{\alpha }_W =0.8,\,\,\bar{\rho }_W =15\times 10^{-5}$. The value of parameter $\bar{\beta }$ is varied as $\bar{\beta }=0.00003,$ GVSS-LMP1, $\bar{\beta }=0.00005,$ GVSS-LMP2, and $\bar{\beta }=0.00015,$ GVSS-LMP3. It is apparent from the simulation results depicted in Fig. 2 that the performance of GVSS-LMP algorithm improves as the value of $\bar{\beta }$ increases. The performance of $\bar{\beta }=0.00015,$ GVSS-LMP3 is approximately 7 dB better than AVSS-LMP algorithm in the tracking mode, and this proposed algorithm converges at the higher rate than other conventional algorithms.

Further, the value of $\bar{\beta }=0.00005$ is fixed under the similar conditions. However, the values of $\bar{P}\,\,and\,\,\bar{Q}$ are varied as $\bar{P}=\bar{Q}=1$, $\bar{P}=\bar{Q}=2$, $\bar{P}=\bar{Q}=3$ in the GVSS-LMP algorithm. The simulation results demonstrated in Fig. 3 evidenced that $\bar{P}=\bar{Q}=2$ is the suitable preference for GVSS-LMP algorithm, which also restricts its computational complexity.

Subsequently, the values of $\bar{\beta }=0.00005$ and $\bar{P}=\bar{Q}=2$ are fixed under the similar conditions. However, the values of $\lambda _2 =0.3,\,\,0.5,\,\,0.7$ are varied in the proposed GVSS-LMS algorithm. It may be inferred from the simulation results in Fig. 4 that the performance of presented algorithm can be improved by increasing the value of $\lambda _2$. However, for $\lambda _2 >0.75$, the observed performance advantage is marginal.

Fig. 2

Comparison of GVSS-LMP algorithm with conventional algorithms under varying value of $\bar{\beta }$ for the second-order Volterra filter

Fig. 3

Effects of the variation in the value of $\bar{P}\,\,\mathrm{and}\,\,\bar{Q}$ on GVSS-LMP algorithm

Fig. 4

Effects of variation in the value of $\lambda _2$ on GVSS-LMS algorithm.

Example 2

Now, we consider the third-order Volterra filter with $K=3$ and $M=3$ in this simulation setup with the uncorrelated Gaussian white input sequence. As the number of filter weights increases in this case [1, 7], the parameter values need to be changed to maintain the value of GVSS within limits. The values of parameters are $\lambda _1 =0.98,\,\,\lambda _2 =0.5$, $\bar{\alpha }=0.91, \quad \bar{\beta }=\bar{\gamma }=0.000025, \quad \bar{P}=\bar{Q}=2$, $\bar{\alpha }_A =0.98, \quad \bar{\alpha }_W =0.8, \quad \bar{\rho }_W =15\times 10^{-9}$. The results in Fig. 5 manifest that the performance advantage of GVSS-LMP algorithm is approximately 3 dB better than the AVSS-LMP algorithm in the tracking mode. However, the convergence rate of both algorithms is approximately same in the initial phase. But, the significant performance degradation is observed in the case of KVSS-LMP algorithm.

Fig. 5

Comparison of GVSS-LMP algorithm with conventional algorithms for the third-order Volterra filter

Example 3

Next, we consider the second-order Volterra filter with $K=2\,\,and\,\,M=3$ in this simulation setup, when the unknown system is excited by a correlated input signal as $\vec {x}( n)=0.9\vec {x}( {n-1})+\vec {v}_x ( n)$; where $\vec {v}_x ( n)$ is a zero-mean, uncorrelated Gaussian noise of unity variance. This type of input signals results in the flattened elliptical contours, which usually cause difficulties in the convergence of stochastic gradient adaptive algorithms. The values of parameters are $\lambda _1 =0.8,\,\,\,\lambda _2 =0.5$, $\bar{\alpha }=0.97,\bar{\gamma }=15\times 10^{-6}$, $\bar{P}=\bar{Q}=2$, $\bar{\alpha }_A =0.97, \quad \bar{\alpha }_W =0.8,\bar{\rho }_W =15\times 10^{-5}$. The value of parameter $\bar{\beta }$ is varied as $\bar{\beta }=15\times 10^{-6},$ GVSS-LMP1, $\bar{\beta }=15\times 10^{-7},$ GVSS-LMP2, and $\bar{\beta }=15\times 10^{-8},$ GVSS-LMP3. It is observed from the results in Fig. 6 that the performance of GVSS-LMP algorithm improves as the value of $\bar{\beta }$ increases, but the overall performance degradation is noticed for all the algorithms. We now fix the value of parameter $\bar{\beta }=15\times 10^{-6}$ for the simulation results in Fig. 7, which indicate that the proposed GVSS-LMP algorithm still outperforms the conventional algorithms. The variable step-size controls the problem of eigenvalue spread, and consequently leads to the enhanced convergence rate in the presence of impulse noise and correlated input signal.

On contrary to the case of uncorrelated input signal, it may be inferred from the results presented in Fig. 6 and Fig. 7 that the gradient-misadjustment [30] is relatively more in the case of correlated input signal. However, the convergence of GVSS-LMP algorithm is strictly dependent on the appropriate parameter tuning/setting in (23), while keeping the value of GVSS below ${\mu }'_{Max}$ (22). Akin to the VSS-LMS algorithms [4, 23], the GVSS-LMP algorithm is found to be sensitive to noise disturbances in the low signal-to-noise-ratio (SNR) environment.

Fig. 6

Effects of variation in the value of $\bar{\beta }$on GVSS-LMP algorithm for the correlated input signal

Fig. 7

Comparison of GVSS-LMP algorithm with conventional algorithms for the second-order Volterra filter with correlated input signal

5 Concluding Remarks

This paper presents a generalized variable step-size least mean $p$th power (LMP) adaptive algorithm for the $\alpha$-stable noisy environment, which is based on the MED criterion. This algorithm is implemented to identify the unknown time-varying nonlinear systems using the Volterra filtering approach. However, the MMSE criterion is found to be a special case of MED approach. The GVSS-LMP algorithm exploits the knowledge about the previous step-size, the error autocorrelation values, the value of parameter $\alpha$, the crosscorrelation between error sequence and input sequence. For excellent results, the value of parameter $p$ is kept close to $\alpha$ in the range $1<p<\alpha <2$.

It is apparent from the simulation results that the GVSS-LMP algorithm supersedes the KVSS-LMP, AVSS-LMP, and SVSS-LMS algorithms in the convergence, as well as tracking mode, when the input signal is either correlated or uncorrelated Gaussian process. The proposed algorithm also controls the adverse effects of eigenvalue spread of the input signal autocorrelation matrix, by the GVSS criterion to track the time-varying Volterra kernels. The outperforming GVSS-LMP algorithm may find applications in the systems disturbed due to the presence of non-Gaussian impulsive measurement noise, where the conventional FSS-LMS algorithm fails to perform well. Moreover, the different LMP algorithms with $p\ne 2$ and LMS algorithms with $p=2$ can be derived from the GVSS-LMP algorithm by adjusting the parameters according to the requirements. Future work includes the application of proposed adaptive nonlinear Volterra filtering technique in the emerging fields of bio-signal processing, biomedical engineering [29], nonlinearly amplified digital as well as analog communication signal processing [17] and equalization of nonlinear communication channels [18].

Appendix

The literature [8, 30] of fixed step-size LMS (FSS-LMS) algorithm reflects a tradeoff between the misadjustment and speed of adaptation, which depicts that a small step-size produces small misadjustment, but at the cost of longer convergence time. Under time-varying environment, the optimum value of the step-size in FSS-LMS algorithm strikes a balance between the amount of lag noise and gradient noise [5]. However, the optimum value of step-size can not be determined a priori due to the unknown channel parameters. Therefore, in KVSS-LMS algorithm [10], the variable step-size (VSS) is attuned using

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }\underline{\underline{e{ }^2( {n-1})}} \end{aligned}$$

(33)

In this KVSS-LMS algorithm, a large prediction error causes the step-size to increase in order to provide fast tracking, while a small prediction error leads to reduction in the step-size to yield small misadjustment. The step-size increases or decreases as the MSE increases or decreases, allowing the adaptive filter to track changes in the time-varying system, as well as to produce a small steady-state error. It also reduces sensitivity of the misadjustment to the level of nonstationarity. This approach is heuristically sound and has resulted in several ad hoc techniques, where the selection of convergence parameters is based on the magnitude of estimation error, polarity of the successive samples of the estimation error, measurement of the crosscorrelation of the estimation error with input data. However, the VSS-LMS algorithms are found to be sensitive to noise disturbances [4, 23] in the low signal-to-noise-ratio (SNR) environment because the step-size update of these algorithms are directly obtained from the instantaneous error that is contaminated by the disturbance noise.

Further in AVSS-LMS algorithm [1], the VSS is controlled using

$$\begin{aligned} {\mu }'( n)=\bar{\alpha }{\mu }'( {n-1})+\bar{\gamma }\theta ^2( {n-1}) \end{aligned}$$

(34)

$$\begin{aligned} \theta ( {n-1})=\bar{\alpha }_A \theta ( {n-2})+( {1-\bar{\alpha }_A })\underline{\underline{\left\{ {e( {n-1})e( {n-2})} \right\} }} \end{aligned}$$

(35)

Here, the error autocorrelation is usually a fine measure of the proximity to the optimum, which rejects the effect of uncorrelated noise sequence on the step-size update. In the early stages of adaptation, the error autocorrelation estimate is large, resulting in a large step-size. However, the small error autocorrelation leads to a small step-size under the optimum conditions. It results in effective adjustment of the step-size, while sustaining the immunity against independent noise disturbance, for the flexible control of misadjustment. The AVSS-LMS algorithm [1] shows substantial convergence rate improvement over the KVSS-LMS algorithm [10] and FSS-LMS algorithm [30] under the stationary environment for the low SNR, as well as the high SNR values. However, the performance of AVSS-LMS algorithm is comparable to the FSS-LMS and KVSS-LMS adaptive algorithms under the nonstationary conditions.

But in SVSS-LMS algorithm [2], the VSS is adjusted using the following recursive relation by adjusting the control parameters $\bar{\rho }_w \,\,and\,\,\bar{\alpha }_w$.

$$\begin{aligned} {\mu }'( n)={\mu }'( {n-1})+\bar{\rho }_w \vec {\psi }^T( n)\vec {x}( n)e( n) \end{aligned}$$

(36)

$$\begin{aligned} \vec {\psi }( n)=\bar{\alpha }_w \vec {\psi }( {n-1})+e( {n-1})\vec {x}( {n-1}) \end{aligned}$$

(37)

The above equation can be rewritten in the expanded form as

$$\begin{aligned} \begin{array}{l} \vec {\psi }^T\left\{ n \right\} =\bar{\alpha }_w^{\bar{Q}} \vec {\psi }^T\left\{ {n-\bar{Q}} \right\} +\bar{\alpha }_w^{\bar{Q}-1} e( {n-\bar{Q}})\vec {x}^T( {n-\bar{Q}})+\ldots \\ \qquad \qquad \qquad +\bar{\alpha }_w e( {n-2})\vec {x}^T( {n-2})+e( {n-1})\vec {x}^T( {n-1}) \\ \end{array} \end{aligned}$$

(38)

For $0\le \bar{\alpha }_w <1$ and $\bar{Q}\rightarrow high\,\,\,value$, the Eq. (38) can be approximated as

$$\begin{aligned} \begin{array}{l} \vec {\psi }^T\left\{ n \right\} \approx \underline{\underline{\bar{\alpha }_w^{\bar{Q}-1} e( {n-\bar{Q}})\vec {x}^T( {n-\bar{Q}})+}} \,\,\ldots \,\,\, \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\underline{\underline{+\,\,\bar{\alpha }_w^2 e( {n-3})\vec {x}^T( {n-3})+\bar{\alpha }_w e( {n-2})\vec {x}^T( {n-2})+e( {n-1})\vec {x}^T( {n-1})}} \\ \end{array} \end{aligned}$$

(39)

This algorithm [2] outperforms the Mathews’ algorithm [13], when both are set to track the random walk channel under the similar conditions.