1 Introduction

Adaptive filtering algorithms have been found in a wide range of practical applications such as system identification, channel equalization, beamforming, and echo cancelation [1–3]. Among these algorithms, one of the popular algorithms is the normalized least mean square (NLMS), due to its low computational complexity and robust performance. In order to obtain fast convergence rate and low steady-state misadjustment (i.e., the final weights estimation error) simultaneously, many modified NLMS methods controlling the step size have been proposed, e.g., [4–7, 25] and references therein. However, these NLMS-type algorithms suffer from slow convergence when the input signals are colored.

To solve this problem, in the recent decade, the multiband-structure of the subband adaptive filter (SAF) has been widely used [3]. This is because the SAF divides the colored input signal into multiple mutually almost exclusive subband signals, and each decimated subband input signal used in the update process of the weights is approximately white. What’s more, compared with the conventional subband structure, the multiband-structure has no band edge effects [3]. On the basis of this multiband-structure, the normalized SAF (NSAF) algorithm [8] was developed from the least perturbation principle by Lee and Gan. The NSAF exhibits faster convergence rate than the NLMS for the colored input signals, due mainly to the inherent decorrelating property of SAF [9]. Moreover, for long adaptive filter applications, the computational complexity of the NSAF is almost the same as that of the NLMS such as in echo cancelation, the echo path is long and the speech input signal is highly colored. It is worth mentioning that the NSAF will be equivalent to the NLMS when number of subbands is one. Subsequently, the theoretical models of the NSAF including the transient and steady-state behavior were provided in [10, 11]. Similar to the NLMS, the performance of the standard NSAF depends on two important parameters: the step size and the regularization parameter. The fixed step size governs a tradeoff between convergence rate and steady-state misadjustment. Specifically, for the NSAF, a large (small) step size leads to fast (slow) convergence rate but large (small) misadjustment in the steady-state. This tradeoff motivated the development of NSAF algorithm with a variable step size (VSS) [12–17]. The original purpose of the regularization parameter was to prevent the NSAF from diverging numerically when the \(l_{2}\)-norm of the input vector is very small or zero (this case is common in echo cancelation). Note that its value also reflects a compromise in the algorithm’s performance similar to the step size. Nevertheless, the only difference is that the directions of the step size and the regularization parameter controlling the algorithm’s performance are opposite. Therefore, several variable regularization (VR) NSAF algorithms have also been proposed [18–21], which in a certain degree overcome the tradeoff of fast convergence rate and low misadjustment, caused by the fixed regularization parameter. Although researchers have made some achievements in the optimization of these two parameters, many of the presented VSS-NSAF and VR-NSAF algorithms are essentially equivalent. Moreover, these algorithms are obtained based on the approach that one of the two parameters is optimized while fixing the other.

In this paper, we first analyze the convergence performance of the standard NSAF based on the first-order Markov model of the optimal weight vector. Second, a joint-optimization scheme of the step size and the regularization parameter is proposed by minimizing the mean square deviation (MSD) of the NSAF. The resulting algorithm is called the joint-optimization step size and regularization parameter NSAF (JOSR-NSAF) algorithm, which achieves improved performance.

2 Preliminary knowledge

Consider the observed data d(n) that originates from the model

$$\begin{aligned} d(n)=\mathbf{u}^{T}(n)\mathbf{w}_o +\eta (n), \end{aligned}$$
(1)

where \((\cdot )^{T}\) indicates the transpose, \(\mathbf{w}_o \) is the unknown M-dimensional vector to be estimated, \(\mathbf{u}(n)=[u(n),u(n-1),\ldots ,u(n-M+1)]^{T}\) is the input signal vector, and \(\eta (n)\) is the measurement noise which is assumed to be white Gaussian noise with zero-mean and variance \(\sigma _\eta ^2 \).

Fig. 1
figure 1

Multiband-structure diagram of the SAF

Full size image

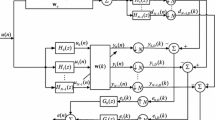
Figure 1 shows the multiband-structure diagram of the SAF, where N denotes number of subbands. The observed data d(n) and the input data u(n) are partitioned into multiple subband signals \(d_i (n)\) and \(u_i (n)\) through the analysis filter bank, namely, \(d_i (n)=d(n){*}h_i \) and \(u_i (n)=u(n){*}h_i \), where \(i=0,1,\ldots ,N-1\) and \(h_i \) is the impulse response of the ith analysis filter \(H_i (z)\), with the linear convolution \({*}\). The subband output signals \(y_i (n)\) are obtained by filtering the subband input signals \(u_i (n)\) through an adaptive filter whose weight vector is \(\mathbf{w}(k)=[w_1 (k),w_2 (k),\ldots ,w_M (k)]^{T}\). Then, the signals \(y_i (n)\) and \(d_i (n)\) are N-fold decimated [3, 8] to yield the signals \(y_{i,D} (k)\) and \(d_{i,D} (k)\) which are, respectively, formulated as \(y_{i,D} (k)=\mathbf{u}_i^T (k)\mathbf{w}(k-1)\) and \(d_{i,D} (k)=d_i (kN)\), where \(\mathbf{u}_i (k)=[u_i (kN),u_i (kN-1),\ldots , u_i (kN-M+1)]^{T}\). In this paper, we use n to indicate the original sequences and k to indicate the decimated sequences. As shown in Fig. 1, the decimated subband error signals are expressed by subtracting \(y_{i,D} (k)\) from \(d_{i,D} (k)\) as

$$\begin{aligned} e_{i,D} (k)\,=\,d_{i,D} (k)\,-\,\mathbf{u}_i^T (k)\mathbf{w}(k\,-\,1), \,i=0,1,\ldots ,N-1. \end{aligned}$$
(2)

As reported in [8], the update equation of the standard NSAF algorithm is expressed as

$$\begin{aligned} \mathbf{w}(k)=\mathbf{w}(k-1)+\mu \sum _{i=0}^{N-1} {\frac{e_{i{,\mathrm D}} (k)\mathbf{u}_i (k)}{\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}}} \end{aligned}$$
(3)

where \(\left\| \cdot \right\| \) denotes the \(l_{2}\)-norm of a vector, \(\mu \) is the step size, and \(\delta >0\) is a small regularization parameter.

3 Proposed JOSR-NSAF algorithm

In this section, the proposed JOSR-NSAF algorithm will be derived, whose inspiration comes from the joint-optimization NLMS (JO-NLMS) algorithm developed by Ciochină et al. [7].

3.1 Some insights for convergence of the NSAF

Let us assume that the unknown vector \(\mathbf{w}_o \) is time-varying and follows a simplified first-order Markov model [24], i.e.,

$$\begin{aligned} \mathbf{w}_o (k)=\mathbf{w}_o (k-1)+\mathbf{q}(k) \end{aligned}$$
(4)

where \(\mathbf{q}(k)\) is a white Gaussian noise vector with zero-mean and covariance matrix \(E\left[ {\mathbf{q}(k)\mathbf{q}^{T}(k)} \right] =\sigma _q^2 \mathbf{I}_M \) with \(\mathbf{I}_M \) being an \(M\times M\) identity matrix and \(E\left[ \cdot \right] \) denoting the mathematical expectation. Evidently, the quantity \(\sigma _q^2 \) characterizes the randomness in \(\mathbf{w}_o (k)\), and \(\mathbf{q}(k)\) is independent of \(\mathbf{w}_o (k-1)\).

Subtracting (4) from (3), we obtain

$$\begin{aligned} {\tilde{\mathbf{w}}}(k)={\tilde{\mathbf{w}}}(k-1)-\mu \sum _{i=0}^{N-1} {\frac{e_{i{,\mathrm D}} (k)\mathbf{u}_i (k)}{\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}}} +\mathbf{q}(k) \end{aligned}$$
(5)

where \({\tilde{\mathbf{w}}}(k)\buildrel \Delta \over = \mathbf{w}_o (k)-\mathbf{w}(k)\) denotes the weight error vector. Based on (1), (2) and (4), the decimated subband error signals can be rewritten as

$$\begin{aligned} e_{i,D} (k)=\mathbf{u}_i^T (k){\tilde{\mathbf{w}}}(k-1)+\mathbf{u}_i^T (k)\mathbf{q}(k)+\eta _i (k) \end{aligned}$$
(6)

where \(\eta _i (k)\) for \(i=0,1,\ldots ,N-1\) are the subband noises that can be obtained by partitioning the measurement noise \(\eta (n)\) and have zero-mean and variances \(\sigma _{\eta _i }^2 ={\sigma _\eta ^2 }/N\) [11, 22].

Taking the squared \(l_{2}\)-norm and mathematical expectation on both sides of (5), and removing the uncorrelated product of \(\mathbf{q}(k)\) and \({\tilde{\mathbf{w}}}(k-1)\), we get

$$\begin{aligned} \hbox {MSD}(k)= & {} \hbox {MSD}(k-1)+M\sigma _q^2 \nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {E\left[ {\frac{e_{i{,\mathrm D}} (k){\tilde{\mathbf{w}}}^{T}(k-1)\mathbf{u}_i (k)}{\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}}} \right] } \nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {E\left[ {\frac{e_{i{,\mathrm D}} (k)\mathbf{q}^{T}(k)\mathbf{u}_i (k)}{\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}}} \right] } \nonumber \\&+\,\mu ^{2}\sum _{i=0}^{N-1} {E\left[ {\frac{e_{i{,\mathrm D}}^2 (k)\mathbf{u}_i^T (k)\mathbf{u}_i (k)}{\left( {\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}} \right) ^{2}}} \right] } \end{aligned}$$
(7)

where \(\hbox {MSD}(k)\buildrel \Delta \over = E\left[ {\left\| {{\tilde{\mathbf{w}}}(k)} \right\| ^{2}} \right] \) denotes the MSD of the algorithm at the kth iteration. In (7), we also use the diagonal assumption, i.e., \(E\left[ {\mathbf{u}_i^T (k)\mathbf{u}_j (k)} \right] \approx 0,i\ne j\), which was made in the derivation of the standard NSAF [8]. For a long adaptive filter, it is assumed that the fluctuation of \(\left\| {\mathbf{u}_i (k)} \right\| ^{2}\) from one iteration to the next is small enough [12, 16] so that (7) becomes

$$\begin{aligned} \hbox {MSD}(k)= & {} \hbox {MSD}(k-1)+M\sigma _q^2 \nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}} (k){\tilde{\mathbf{w}}}^{T}(k-1)\mathbf{u}_i (k)} \right] }{E\left[ {\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}} \right] }}\nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}} (k)\mathbf{q}^{T}(k)\mathbf{u}_i (k)} \right] }{E\left[ {\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}} \right] }}\nonumber \\&+\,\mu ^{2}\sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}}^2 (k)\mathbf{u}_i^T (k)\mathbf{u}_i (k)} \right] }{E\left[ {\left( {\delta +\left\| {\mathbf{u}_i (k)} \right\| ^{2}} \right) ^{2}} \right] }}. \end{aligned}$$
(8)

Owing to the inherent decorrelating property of SAF, we can assume that each decimated subband input signal is close to a white signal, i.e., \(\mathbf{u}_i (k)\mathbf{u}_i^T (k)\approx \mathbf{I}_M \sigma _{u_i }^2 (k)\) and \(\mathbf{u}_i^T (k)\mathbf{u}_i (k)\approx M\sigma _{u_i }^2 (k)\) [14]. Hence, (8) is changed as

$$\begin{aligned} \hbox {MSD}(k)= & {} \hbox {MSD}(k-1)+M\sigma _q^2 \nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}} (k){\tilde{\mathbf{w}}}^{T}(k-1)\mathbf{u}_i (k)} \right] }{\delta +M\sigma _{u_i }^2 (k)}} \nonumber \\&-\,2\mu \sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}} (k)\mathbf{q}^{T}(k)\mathbf{u}_i (k)} \right] }{\delta +M\sigma _{u_i }^2 (k)}}\nonumber \\&+\,\mu ^{2}\sum _{i=0}^{N-1} {\frac{E\left[ {e_{i{,\mathrm D}}^2 (k)\mathbf{u}_i^T (k)\mathbf{u}_i (k)} \right] }{\left( {\delta +M\sigma _{u_i }^2 (k)} \right) ^{2}}}. \end{aligned}$$
(9)

To further proceed, the commonly used independence assumption [1, 7, 10, 22] that \({\tilde{\mathbf{w}}}(k-1)\), \(\mathbf{u}_i (k)\), \(\mathbf{q}(k)\) and \(\eta _i (k)\) are statistically independent is necessary. Applying this assumption and the Gaussian moment factoring theorem [1, 7], and after some manipulations, we have

$$\begin{aligned}&E\left[ {e_{i{,\mathrm D}} (k){\tilde{\mathbf{w}}}^{T}(k-1)\mathbf{u}_i (k)} \right] \approx \sigma _{u_i }^2 (k)\hbox {MSD}(k-1), \end{aligned}$$
(10)
$$\begin{aligned}&E\left[ {e_{i{,\mathrm D}} (k)\mathbf{q}^{T}(k)\mathbf{u}_i (k)} \right] \approx M\sigma _q^2 \sigma _{u_i }^2 (k), \end{aligned}$$
(11)
$$\begin{aligned}&E\left[ {e_{i{,\mathrm D}}^2 (k)\mathbf{u}_i^T (k)\mathbf{u}_i (k)} \right] \approx M\sigma _{u_i }^2 (k)\sigma _{\eta _i }^2\nonumber \\&\quad +(M+2)\sigma _{u_i }^4 (k)\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] . \end{aligned}$$
(12)

Substituting (10)–(12) into (9) yields

$$\begin{aligned} \hbox {MSD}(k)=\hbar (\mu ,\delta )\hbox {MSD}(k-1)+\varphi (\mu ,\delta ) \end{aligned}$$
(13)

where

$$\begin{aligned}&\hbar (\mu ,\delta )= \left[ 1-2\mu \sum _{i=0}^{N-1} {\frac{\sigma _{u_i }^2 (k)}{\delta \,{+}\,M\sigma _{u_i }^2 (k)}}\right. \nonumber \\&\qquad \qquad \qquad \left. +\,\mu ^{2}\sum _{i=0}^{N-1} {\frac{(M+2)\sigma _{u_i }^4 (k)}{\left( {\delta +M\sigma _{u_i }^2 (k)} \right) ^{2}}} \right] , \end{aligned}$$
(14)
$$\begin{aligned}&\varphi (\mu ,\delta )=\hbar (\mu ,\delta )M\sigma _q^2 +\mu ^{2}\sum _{i=0}^{N-1} {\frac{M\sigma _{u_i }^2 (k)\sigma _{\eta _i }^2 }{\left( {\delta +M\sigma _{u_i }^2 (k)} \right) ^{2}}} . \end{aligned}$$
(15)

The relation (13) consists of two parts \(\hbar (\mu ,\delta )\) and \(\varphi (\mu ,\delta )\), which reveal the convergence and misadjustment behavior of the NSAF, respectively.

Remark 1

The term \(\hbar (\mu ,\delta )\) controls the convergence rate of the NSAF in the mean-square sense, i.e., the convergence rate is dependent on the step size, regularization parameter, filter length, number of subbands, and subband input variances. Interestingly, the convergence rate is not influenced by the subband noise variances \(\sigma _{\eta _i }^2 \) and the model uncertainties \(\sigma _q^2 \). In addition, certain classical convergence results can be obtained by analyzing the convergence term \(\hbar (\mu ,\delta )\):

  1. 1.

    The fastest convergence rate of the NSAF is achieved when the value of \(\hbar (\mu ,\delta )\) is at its minimum. Therefore, setting the derivative of \(\hbar (\mu ,\delta )\) with respect to the step size to zero, the optimal step size for ensuring the fastest convergence rate is obtained as

    $$\begin{aligned}&\mu _{{\mathrm{opt-con}}} =\frac{\mathop {\sum }\nolimits _{i=0}^{N-1} {{\sigma _{u_i }^2 (k)\left[ {\delta +M\sigma _{u_i }^2 (k)} \right] }/{\left[ {\delta +M\sigma _{u_i }^2 (k)} \right] ^{2}}} }{\mathop {\sum }\nolimits _{i=0}^{N-1} {{(M+2)\sigma _{u_i }^4 (k)}/{\left[ {\delta +M\sigma _{u_i }^2 (k)} \right] ^{2}}} }.\nonumber \\ \end{aligned}$$
    (16)

    After neglecting the regularization parameter (i.e., \(\delta =0)\) and supposing a long filter, i.e., \(M\gg 2\), which is characteristic of echo cancelation application, e.g., \(M=512\) in the following simulation section, (16) can be approximated as \(\mu _{{\mathrm{opt-con}}} \approx 1\), which is a well-known result for the standard NSAF [3].

  2. 2.

    To ensure the mean-square stability of the NSAF, the range of the step size can be formulated by imposing \(\left| {\hbar (\mu ,\delta )} \right| <1\) as

    $$\begin{aligned} 0<\mu _{\mathrm{stability}} <2\mu _{{\mathrm{opt-con}}} . \end{aligned}$$
    (17)

    By, again, taking \(\delta =0\) and \(M\gg 2\), we obtain the stability range presented in [3, 8], i.e., \(0<\mu _{\mathrm{stability}} <2\).

Remark 2

The term \(\varphi (\mu ,\delta )\) in (13) determines the misadjustment of the NSAF. It is evident that the misadjustment depends on \(\sigma _q^2 \) and \(\sigma _{\eta _i }^2 \), which increases as these two quantities increase. It is noticeable that the smallest misadjustment of the algorithm can be obtained from the minimization of \(\varphi (\mu ,\delta )\). Thus, by setting the derivative of \(\varphi (\mu ,\delta )\) with respect to the step size to zero, the optimal step size for obtaining the smallest misadjustment is expressed as

$$\begin{aligned}&\mu _{{ \mathrm{opt-mis}}} \nonumber \\&\quad =\frac{\sigma _q^2 \mathop {\sum }\nolimits _{i=0}^{N-1} {{\sigma _{u_i }^2 (k)\left[ {\delta {+}M\sigma _{u_i }^2 (k)} \right] }/{\left[ {\delta {+}M\sigma _{u_i }^2 (k)} \right] ^{2}}} }{\mathop {\sum }\nolimits _{i=0}^{N-1} {{\left[ {(M{+}2)\sigma _q^2 \sigma _{u_i }^4 (k){+}\sigma _{u_i }^2 (k)\sigma _{\eta _i }^2 (k)} \right] }/{\left[ {\delta {+}M\sigma _{u_i }^2 (k)} \right] ^{2}}} }.\nonumber \\ \end{aligned}$$
(18)

Assuming that the unknown system is stationary, i.e., \(\sigma _q^2 \approx 0\), (18) will lead to \(\mu _{{ \mathrm{opt-mis}}} \approx 0\). This result implies that the step size should be very small (e.g., close to zero) to obtain small misadjustment.

Remark 3

From Remarks 1 and 2, it is concluded that the fixed step size determines the convergence rate and misadjustment of the NSAF in opposite directions. In other words, using a fixed step size is unrealistic to obtain an ideal NSAF performance, i.e., both fast convergence rate and small misadjustment. Hence, this conclusion motivates the VSS methods to meet these two performance considerations. In all the VSS schemes, the step size gradually decreases as the algorithm converges from the starting stage to the steady-state. Although the regularization constant in (3) is originally introduced to avoid the numerical instability of the NSAF when the \(l_{2}\)-norm of the subband input signals is very small (in the extreme case, it is zero), its value also influences the convergence rate and misadjustment of the algorithm [20]. Interestingly, the influence of the regularization constant on these two performances is opposite to that of the step size. That is to say, as the regularization constant increases, the misadjustment decreases, while slowing the convergence rate. As a result, a potential scheme is to control these two parameters simultaneously to improve the performance of the NSAF, which will be described in following subsection.

3.2 A joint-optimization scheme

Using a time-varying step size \(\mu _i (k)\) and a time-varying regularization parameter \(\delta _i (k)\) for \(i=0,1,\ldots ,N-1\). Instead of fixing their values, (13) can be rewritten as

$$\begin{aligned}&\hbox {MSD}(k)=\left\{ {1-2\sum _{i=0}^{N-1} {\frac{\mu _i (k)\sigma _{u_i }^2 (k)}{\delta _i (k)+M\sigma _{u_i }^2 (k)}} } \right. \nonumber \\&\quad \left. +\sum _{i=0}^{N-1} {\frac{\mu _i^2 (k)(M+2)\sigma _{u_i }^4 (k)}{\left[ {\delta _i (k)+M\sigma _{u_i }^2 (k)} \right] ^{2}}} \right\} \times \left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] \nonumber \\&\quad +\sum _{i=0}^{N-1} {\frac{\mu _i^2 (k)M\sigma _{u_i }^2 (k)\sigma _{\eta _i }^2 }{\left[ {\delta +M\sigma _{u_i }^2 (k)} \right] ^{2}}}. \end{aligned}$$
(19)

To minimize the MSD of the NSAF at each iteration, the following subband constraints are imposed, i.e.,

$$\begin{aligned} \frac{\partial \hbox {MSD}(k)}{\partial \mu _i (k)}=0 \hbox { and } \frac{\partial \hbox {MSD}(k)}{\partial \delta _i (k)}=0,\quad i=0,1,\ldots ,N-1.\nonumber \\ \end{aligned}$$
(20)

Applying (20), a joint-optimization strategy of \(\mu _i (k)\) and \(\delta _i (k)\) for each subband is obtained as,

$$\begin{aligned}&\frac{\mu _i (k)}{\delta _i (k)+M\sigma _{u_i }^2 (k)}\nonumber \\&\quad =\frac{\hbox {MSD}(k-1)+M\sigma _q^2 }{(M+2)\sigma _{u_i }^2 (k)\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] +M\sigma _{\eta _i }^2 }. \end{aligned}$$
(21)

Substituting (21) into (3), we obtain a new weight update expression

$$\begin{aligned}&{} \mathbf{w}(k)=\mathbf{w}(k-1) \nonumber \\&\quad +\sum _{i=0}^{N-1} {\frac{\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] e_{i{,\mathrm D}} (k)\mathbf{u}_i (k)}{(M+2)\sigma _{u_i }^2 (k)\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] +M\sigma _{\eta _i }^2 }}.\nonumber \\ \end{aligned}$$
(22)

Likewise, substituting (21) into (19), and after some simple computations, the \(\hbox {MSD}(k-1)\) in (22) is updated as

$$\begin{aligned}&\hbox {MSD}(k)=\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] \nonumber \\&\quad \times \left\{ {1-\sum _{i=0}^{N-1} {\frac{\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] \sigma _{u_i }^2 (k)}{(M+2)\sigma _{u_i }^2 (k)\left[ {\hbox {MSD}(k-1)+M\sigma _q^2 } \right] +M\sigma _{\eta _i }^2 }} } \right\} .\nonumber \\ \end{aligned}$$
(23)

3.3 Convergence of the proposed algorithm

Let us define the decimateda priori error of the ith subband as \(e_{a,i} (k)\buildrel \Delta \over = {\tilde{\mathbf{w}}}^{T}(k-1)\mathbf{u}_i (k)\), we have \(E\left[ {e_{a,i}^2 (k)} \right] =\hbox {MSD}(k-1)\sigma _{u_i }^2 (k)\), then (23) can be changed as

$$\begin{aligned} \hbox {MSD}(k)=\beta (k)\hbox {MSD}(k-1)+\beta (k)M\sigma _q^2 \end{aligned}$$
(24)

where

$$\begin{aligned}&\beta (k) \nonumber \\&\quad =1-\sum _{i=0}^{N-1} {\frac{E\left[ {e_{a,i}^2 (k)} \right] +M\sigma _q^2 \sigma _{u_i }^2 (k)}{(M+2)\left[ {E\left[ {e_{a,i}^2 (k)} \right] +M\sigma _q^2 \sigma _{u_i }^2 (k)} \right] +M\sigma _{\eta _i }^2 }}.\nonumber \\ \end{aligned}$$
(25)

By continuously iterating (24), we get

$$\begin{aligned}&\hbox {MSD}(k)=\left( {\beta (k)\cdot \cdot \cdot \beta (2)\beta (1)} \right) \hbox {MSD}(0)\nonumber \\&\quad +M\sigma _q^2 \sum _{j=1}^k {\beta (j)\cdot \cdot \cdot \beta (k)}, \end{aligned}$$
(26)

and

$$\begin{aligned}&\hbox {MSD}(k-1)=\left( {\beta (k-1)\cdot \cdot \cdot \beta (2)\beta (1)} \right) \hbox {MSD}(0) \nonumber \\&\quad +\,M\sigma _q^2 \sum _{j=1}^{k-1} {\beta (j)\cdot \cdot \cdot \beta (k-1)}. \end{aligned}$$
(27)

Combining (26) and (27) yields the following relation:

$$\begin{aligned}&\Delta \hbox {MSD(}k\hbox {)}=\hbox {MSD}(k)-\hbox {MSD}(k-1)\nonumber \\&\quad =\left( {\beta (k)-1} \right) \left( {\beta (k-1)\cdot \cdot \cdot \beta (2)\beta (1)} \right) \hbox {MSD}(0)+M\sigma _q^2 \beta (k).\nonumber \\ \end{aligned}$$
(28)

Again using the assumption of a long filter, from (25) we obtain

$$\begin{aligned} \beta (k)\approx & {} 1-\sum _{i=0}^{N-1} {\frac{E\left[ {e_{a,i}^2 (k)} \right] +M\sigma _q^2 \sigma _{u_i }^2 (k)}{M\left( {E\left[ {e_{a,i}^2 (k)} \right] +M\sigma _q^2 \sigma _{u_i }^2 (k)} \right) +M\sigma _{\eta _i }^2 }}\nonumber \\<&\left( {1-\frac{N}{M}} \right) =\beta _{\max } <1. \end{aligned}$$
(29)

To ensure the mean-square stability of the proposed algorithm, the MSD must decrease iteratively, i.e., \(\Delta \hbox {MSD}(k)<0\). Thus, the quantity \(\sigma _q^2 \) has to satisfy the inequality

$$\begin{aligned} \sigma _q^2 <\frac{\left( {1-\beta (k)} \right) }{M\beta (k)}\beta _{\max }^{k-1} \hbox {MSD}(0). \end{aligned}$$
(30)

Under the condition of (28), in the steady-state, the following relation holds

$$\begin{aligned}&\hbox {MSD}(\infty )=\mathop {\lim }\limits _{k\rightarrow \infty } \left( \beta (k)\cdot \cdot \cdot \beta (2)\beta (1)\hbox {MSD}(0)\right. \nonumber \\&\quad \left. +M\sigma _q^2 \sum _{j=1}^k {\beta (j)\cdot \cdot \cdot \beta (k)} \right) \nonumber \\&\quad <\mathop {\lim }\limits _{k\rightarrow \infty } \left( {\beta _{\max }^k \hbox {MSD}(0)+M\sigma _q^2 \frac{\beta _{\max } -\beta _{\max }^{k+1} }{1-\beta _{\max } }} \right) \nonumber \\&\quad =M\sigma _q^2 \frac{\beta _{\max } }{1-\beta _{\max } }. \end{aligned}$$
(31)

Equation (31) reveals that the convergence of the proposed JOSR-NSAF is stable in the mean-square sense.

3.4 Practical considerations

To implement the above-presented JOSR-NSAF algorithm, some practical considerations about the parameters \(\sigma _{u_i }^2 (k)\), \(\sigma _\eta ^2 \), and \(\sigma _q^2 \) are necessary which we list below.

  1. 1.

    The subband input variances \(\sigma _{u_i }^2 (k)\) for \(i=0,1,\ldots ,N-1\) can be estimated by \(\hat{{\sigma }}_{u_i }^2 (k)={\mathbf{u}_i^T (k)\mathbf{u}_i (k)}/M\) [7, 23].

  2. 2.

    The second consideration is to take the measurement noise variance \(\sigma _\eta ^2 \), which also appears in many VSS and VR versions of the NSAF, e.g., [12, 13, 15, 16, 19, 21]. Usually, in practical applications, \(\sigma _\eta ^2 \) can be easily estimated. Several different methods based on an exponential window have been developed to estimate this variance [4, 5, 12]. For example, in echo cancelation, it can be estimated during silences of the near-end talker, in a single-talk scenario [12]. Detailed discussion the performances of these estimation methods, concerning \(\sigma _\eta ^2 \), is outside the scope of this work.

  3. 3.

    The only remaining consideration is how to choose \(\sigma _q^2 \), which plays a very important role in the performance of the proposed JOSR-NSAF. For a small \(\sigma _q^2 \), the algorithm has a small steady-state misadjustment but a poor tracking capability; conversely, a large \(\sigma _q^2 \) results in good tracking performance but increases the steady-state misadjustment. To address this compromise, \(\sigma _q^2 \) is estimated as [7, 23]

    $$\begin{aligned} \hat{{\sigma }}_q^2 (k)={\left\| {\mathbf{w}(k)-\mathbf{w}(k-1)} \right\| ^{2}}/M. \end{aligned}$$
    (32)

    This relation is obtained by taking the \(l_{2}\)-norm on both sides of (4) and replacing \(\mathbf{w}_o (k)\) with its estimate \(\mathbf{w}(k)\). As can be seen, in the initial stage of adaptation or when the unknown system suddenly changes, the value of \(\hat{{\sigma }}_q^2 \) is large, thus leading to fast convergence rate and good tracking capability. Moreover, when the algorithm goes into the steady-state, the value of \(\hat{{\sigma }}_q^2 \) is small, thus obtaining low steady-state misadjustment.

Based on the above considerations, the proposed JOSR-NSAF algorithm is summarized in Table 1. Note that, the JOSR-NSAF reduces to the JO-NLMS in [7] when the number of subbands is one.

Table 1 Summary of the proposed JOSR-NSAF algorithm
Full size table

4 Simulation results

To evaluate the performance of the proposed algorithm, extensive simulations were performed in the context of acoustic echo cancelation. In our simulations, the unknown vector \(\mathbf{w}_o \) to be identified is a room acoustic echo path with \(M=512\) taps [26]. Also, to show the tracking capability of the algorithm, the unknown vector is changed abruptly from \(\mathbf{w}_o \) to \(-\mathbf{w}_o \) in the middle of the input samples. The colored input signal is either an first-order autoregression, i.e., AR(1), process with a pole at 0.95 or a speech signal. The measurement noise \(\eta (n)\) is white Gaussian with a signal-to-noise ratio (SNR) of either 30 dB or 20 dB. It is assumed that the variance of the measurement noise, \(\sigma _\eta ^2 \), is known, because it can be easily estimated similar to [4, 5, 12]. A cosine-modulated filter bank [3] is used for all the SAF algorithms. As a measure of the algorithm’s performance, the normalized MSD (NMSD), also called the misadjustment, is defined as \(10\times \log _{10} (\left\| {\mathbf{w}_o -\mathbf{w}(k)} \right\| _2^2 /\left\| {\mathbf{w}_o } \right\| _2^2 )\) (dB). All results were obtained by averaging over 30 independent runs, except for speech input (single realization).

We first compare the performance of the JO-NLMS algorithm [7] with proposed JOSR-NSAF (with \(N=2\) and 8 subbands) for an AR(1) input, as shown in Fig 2. From this figure, it can be noted that the JOSR-NSAF algorithm has faster convergence rate than the JO-NLMS (i.e., the JOSR-NSAF with \(N=1)\) algorithm for the colored input signal. Moreover, with an increased number of subbands N, the convergence rate is further improved. The reason behind this phenomenon is that each decimated subband input signal approaches a white signal as the number of subbands increases. In the following simulations, we set \(N=8\) for all the NSAF-type algorithms.

Fig. 2
figure 2

NMSD curves of the JO-NLMS and proposed JOSR-NSAF (with \(N=2\) and 8) algorithms. \(\hbox {SNR}=\hbox {30 dB}\), AR(1) input

Full size image

Figure 3 shows the NMSD performances of the standard NSAF (with \(\mu =1\) and 0.05), VSSM-NSAF [12], NVSS-NSAF [16], VRM-NSAF [19], and the proposed JOSR-NSAF algorithms using an AR(1) process as the input signal. All these VSS and VR algorithms require a priori knowledge of the measurement noise variance \(\sigma _\eta ^2 \); thus, we assume that its value is available, for a fair comparison. Also, we set the algorithms’ parameters according to the recommendations in [12, 16, 19]. As can be seen, compared with the NSAF, its VSS and VR versions improved the performance in terms of the convergence rate and steady-state misadjustment. Importantly, the improvement of the proposed JOSR-NSAF in the steady-state performance is more obvious than its counterparts. Also, it can be observed from Fig. 3 that as the SNR decreases (or the measurement noise variance \(\sigma _\eta ^2 \) increases), the steady-state misadjustment of these NSAFs increases but the convergence rate of that does not change, which is consistent with the previous analysis in Remarks 1 and 2.

Fig. 3
figure 3

NMSD curves of various NSAF-type algorithms for AR(1) input signal. a \(\hbox {SNR}=\hbox {30 dB}\); b \(\hbox {SNR}=\hbox {20 dB}\). VSSM-NSAF: \(\kappa =\hbox {6}\); NVSS-NSAF: \(\kappa =3, \lambda =4\); VRM-NSAF: \(\alpha =0.995, Q=1000\). The regularization parameter for the NSAF, VSSM-NSAF and NVSS-NSAF algorithms is chosen as \(\delta =10\sigma _{u_i }^2 \)

Full size image

Finally, Fig. 4 compares the performance of the proposed JOSR-NSAF with that of NSAF (with \(\mu =1)\), VSSM-NSAF, NVSS-NSAF, and VRM-NSAF in speech input scenario. These results are similar to those results with AR(1) input in Fig. 3, which demonstrates that the proposed algorithm also works better than the existing VSS and VR-NSAF algorithms for speech input signal. In addition, the proposed algorithm does not require any additional parameters to control its performance relative to many of its counterparts.

Fig. 4
figure 4

NMSD curves of various NSAF-type algorithms for speech input signal. The choice of the algorithms’ parameters is the same as Fig. 3. a \(\hbox {SNR}=\hbox {30 dB}\); b \(\hbox {SNR}=\hbox {20 dB}\)

Full size image

5 Conclusions

We have analyzed the convergence performance of the standard NSAF using a first-order Markov model of the optimal weight vector. Based on this model, we propose a joint-optimization NSAF algorithm by minimizing the MSD of the NSAF over both the step size and the regularization parameter, simultaneously achieving fast convergence rate and low steady-state misadjustment. Simulation results in acoustic echo cancelation application demonstrate that the proposed algorithm outperforms many existing VSS and VR extensions of the NSAF in performance.