1 Introduction

In application fields of adaptive filtering algorithms such as system identification, noise cancellation, echo cancellation, and channel estimation, the widely used algorithm is the normalized least mean square (NLMS) due to its low computational complexity [7, 9]. Compared to the conventional NLMS algorithm, the variable step size versions presented in [2, 3, 12, 16] offer the improved performance in terms of convergence rate and steady-state error. Nevertheless, these NLMS-type algorithms will suffer from slow convergence when the input signals are colored. Aiming to such input signals, the affine projection algorithm (APA) and its variants (e.g., see [13, 15] and the references therein) provide faster convergence rate than the NLMS algorithm. Because the APAs use the most recent input signal vectors to update the tap-weight vector, the NLMS uses only the current input signal vector. However, the APAs require large computational cost due to involving the matrix inversion operation in updating the tap-weight vector.

In a recent decade, in order to speed the convergence of filter for colored input signals, the subband adaptive filters (SAFs) have received great attention [4]. This is due to the fact that the SAF divides the colored input signal into almost mutually exclusive subband signals through analysis filters. Moreover, each subband input signal is approximate white. In [5], Lee and Gan proposed the normalized SAF (NSAF) algorithm based on the principle of minimum disturbance. This algorithm performs better than the NLMS in convergence rate for colored input signals, due to the inherent decorrelating property of SAF [6]. Also, the NSAF has almost the same computational complexity as the NLMS. Unfortunately, the performance of the original NSAF algorithm depends on the fixed step size that reflects a compromise between fast convergence rate and low steady-state error. To overcome this conflict, several variable step size NSAF algorithms have been proposed [1, 8, 10, 11]. In [1], a set-membership NSAF (SM–NSAF) algorithm was developed, whereas its convergence performance is sensitive to the selection of the error-bound parameter. The variable step size matrix NSAF (VSSM–NSAF) was presented in [8], which converged faster than the SM–NSAF. However, this algorithm still has large final estimation error. Following this approach, based on the same principle that minimizes the mean square deviation (MSD), two variable step size NSAF algorithms were proposed in [10] and [11], respectively. The difference is that the latter has a lower steady-state error than the former, since it uses an individual step size for each subband while the former uses a common step size for all subbands. Regrettably, both algorithms cannot track the changes in the unknown system.

In this paper, we propose a new variable step size NSAF algorithm, called NVSS–NSAF, based on the minimization of the mean square of the noise-free a posterior subband error signals with respect to the step size. The proposed algorithm assigns an individual step size for each subband and uses the noniterative shrinkage method reported in [17] to estimate the noise-free a priori subband error signals.

2 The Original NSAF Algorithm

Consider the desired signal d(n) which arises from the output end of the unknown system,

$$\begin{aligned} d(n)={\mathbf{u}}^\mathrm{T}(n){\mathbf{w}}_o +\eta (n), \end{aligned}$$
(1)

where \((\cdot )^\mathrm{T}\) denotes the transpose of a vector, \({\mathbf{w}}_o \) is the unknown M-dimensional vector that we wish to identify, \({\mathbf{u}}(n)=[u(n), u(n-1), ..., u(n-M+1)]^\mathrm{T}\) is the input signal vector, \(\eta (n)\) is the system noise with zero-mean and variance \(\sigma _\eta ^2 \) which is independent of u(n).

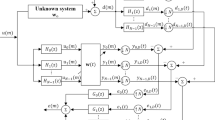
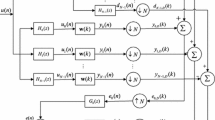
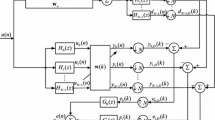
Figure 1 shows the multiband structure of SAF, where N denotes the number of subbands. The signals d(n) and u(n) are partitioned into multiple subband signals by using analysis filters \(\left\{ {H_i (z), i\in [0,N-1]} \right\} \), respectively. Then, the subband signals \(y_i (n)\) and \(d_i (n)\) for \(i\in [0, N-1]\) are critically decimated to yield \(y_{i, D} (k)\) and \(d_{i, D} (k)\), respectively. Here, n and k indicate the original sequences and the decimated sequences, respectively. The ith subband error signal \(e_{i, D} (k)\) is defined as

$$\begin{aligned} e_{i, D} (k)=d_{i, D} (k)-y_{i, D} (k)=d_{i, D} (k)-{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{w}}(k) \end{aligned}$$
(2)

where \({\mathbf{w}}(k)\) is the tap-weight vector of filter, \({\mathbf{u}}_i (k)=[u_i (kN), u_i (kN-1), ..., u_i (kN-M+1)]^\mathrm{T}\), and \(d_{i, D} (k)=d_i (kN)\).

Fig. 1
figure 1

Block diagram of multiband-structured SAF

Full size image

As introduced in [5], the original NSAF algorithm for updating the tap-weight vector is expressed as

$$\begin{aligned} {\mathbf{w}}(k+1)= {\mathbf{w}}(k)+\mu \sum _{i=0}^{N-1} {\frac{{\mathbf{u}}_i (k)e_{i, D} (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} \end{aligned}$$
(3)

where \(\mu \) is the step size.

3 Proposed Algorithm

3.1 Derivation of Algorithm

Replacing the fixed step size \(\mu \) with the time-varying individual step sizes \(\mu _i (k)\) for \(i\in [0, N-1]\), then (3) becomes

$$\begin{aligned} {\mathbf{w}}(k+1)= {\mathbf{w}}(k)+\sum _{i=0}^{N-1} {\mu _i (k)\frac{{\mathbf{u}}_i (k)e_{i, D} (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} . \end{aligned}$$
(4)

Before deriving \(\mu _i (k)\), we define the noise-free a priori subband error and noise-free a posterior subband error as follows:

$$\begin{aligned} \varepsilon _{i, a} (k)= & {} {\mathbf{u}}_i^\mathrm{T} (k)\left[ {{\mathbf{w}}_o -{\mathbf{w}}(k)} \right] ,\end{aligned}$$
(5)
$$\begin{aligned} \varepsilon _{i, p} (k)= & {} {\mathbf{u}}_i^\mathrm{T} (k)\left[ {{\mathbf{w}}_o -{\mathbf{w}}(k+1)} \right] . \end{aligned}$$
(6)

Thus, (2) can also be expressed as

$$\begin{aligned} e_{i, D} (k)=\varepsilon _{i, a} (k)+\eta _{i, D} (k) \end{aligned}$$
(7)

where \(\eta _{i, D} (k)\) is the ith subband system noise, and its variance \(\sigma _{\eta _{i, D} }^2 \) can be computed by \(\sigma _{\eta _{i, D} }^2 ={\sigma _\eta ^2 }/N\) [14].

Substituting (5)–(7) into (4), we have

$$\begin{aligned} \varepsilon _{i, p} (k)=\left[ {1-\mu _i (k)} \right] \varepsilon _{i, a} (k)-\mu _i (k)\eta _{i, D} (k)-\mathop {\mathop {\sum \limits _{j=0}}\limits _{j\ne i}}^{N-1}{\mu _j (k)\frac{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_j (k)e_{j, D} (k)}{{\mathbf{u}}_j^\mathrm{T} (k){\mathbf{u}}_j (k)}} \end{aligned}$$
(8)

Applying the diagonal assumption that has been used to derive the original NSAF, i.e., \({\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_j (k)\approx 0, i\ne j\) [5], (8) can be simplified as

$$\begin{aligned} \varepsilon _{i, p} (k)=\left[ {1-\mu _i (k)} \right] \varepsilon _{i, a} (k)-\mu _i (k)\eta _{i, D} (k) \end{aligned}$$
(9)

Taking the square and mathematical expectation of both sides of (9), we obtain

$$\begin{aligned} E\left[ {\varepsilon _{i, p}^2 (k)} \right] =\left[ {1-\mu _i (k)} \right] ^{2}E\left[ {\varepsilon _{i, a}^2 (k)} \right] +\mu _i^2 (k)\sigma _{\eta _{i, D} }^2 \end{aligned}$$
(10)

where \(E[\cdot ]\) denotes the mathematical expectation.

In order to obtain the optimum step size \(\mu _i (k)\) at each iteration, we now solve the minimization problem of \(E\left[ {\varepsilon _{i, p}^2 (k)} \right] \) with respect to \(\mu _i (k)\). Taking the derivative of \(E\left[ {\varepsilon _{i, p}^2 (k)} \right] \) with respect to \(\mu _i (k)\) and setting it to zero, the step sizes \(\mu _i (k)\) for \(i\in [0, N-1]\) are obtained as

$$\begin{aligned} \mu _i (k)=\frac{E\left[ {\varepsilon _{i, a}^2 (k)} \right] }{E\left[ {\varepsilon _{i, a}^2 (k)} \right] +\sigma _{\eta _{i, D} }^2 } \end{aligned}$$
(11)

Note that the step sizes \(\mu _i (k)\) computed by (11) always lie in the range of (0, 1). This implies that the proposed algorithm is stable, based on the fact that the range of the step size in the original NSAF for stable convergence is \(0<\mu <2\).

In practical applications, the statistical mean \(E\left[ {\varepsilon _{i, a}^2 (k)} \right] \) is generally estimated by the time average of \(\varepsilon _{i, a}^2 (k)\), i.e.,

$$\begin{aligned} \sigma _{\varepsilon _{{i, a}}}^2 (k)=\alpha \sigma _{\varepsilon _{{i, a} } }^2 (k-1)+(1-\alpha )\varepsilon _{i, a}^2 (k) \end{aligned}$$
(12)

where \(\alpha \) is the forgetting factor, which is determined by \(\alpha =1-N/{\kappa M}, \kappa \ge 1\) [8].

Now, the only thing that remains is to determine the noise-free it a priori subband error \(\varepsilon _{i, a} (k)\) in (12). Although \(\varepsilon _{i, a} (k)\) is unknown in the entire adaptive process, it can be recovered from the subband error signal \(e_{i, D} (k)\) by using the noniterative shrinkage method described in [3, 17], i.e.,

$$\begin{aligned} \varepsilon _{i, a} (k)=\hbox {sign}\left( {e_{i, D} (k)} \right) \max \left( {\left| {e_{i, D} (k)} \right| -t_i , 0} \right) \end{aligned}$$
(13)

where \(sign(\cdot )\) denotes the sign function, and \(t_i \) is the threshold parameter. The method has obtained success in image denoising applications [17]. Based on our extensive simulation results, it is found that \(t_i =\sqrt{\lambda \sigma _{\eta _{i, D} }^2 }\) with \(\lambda =3\)–5 can yield good results. Hence, the proposed NVSS–NSAF algorithm is summarized in Table 1.

Table 1 Proposed NVSS–NSAF algorithm
Full size table

3.2 Convergence of Algorithm

In this section, the convergence of the proposed algorithm is analyzed based on the mean square deviation (MSD) defined by

$$\begin{aligned} m(k)=E\left[ {\left\| {{\varvec{\theta } }(k)} \right\| ^{2}} \right] \,\buildrel \Delta \over =\, E\left[ {\left\| {{\mathbf{w}}_o -{\mathbf{w}}(k)} \right\| ^{2}} \right] \end{aligned}$$
(14)

where \(\left\| \cdot \right\| \) denotes the Euclidean norm of a vector.

Subtracting (4) from \({\mathbf{w}}_o \), taking the squared Euclidean norm of both sides, and then applying (5), we have

$$\begin{aligned} \left\| {{\varvec{\theta } }(k+1)} \right\| ^{2}=\left\| {{\varvec{\theta } }(k)} \right\| ^{2}-2\sum _{i=0}^{N-1} {\mu _i (k)\frac{\varepsilon _{i, a} (k)e_{i, D} (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} +\sum _{i=0}^{N-1} {\mu _i^2 (k)\frac{e_{i, D}^2 (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} \end{aligned}$$
(15)

where we again use the diagonal assumption [5].

From (11), one can know that \(\mu _i (k)\) for \(i\in [0, N-1]\) are deterministic in nature; thus, we can express the mathematical expectation of both sides of (15) as

$$\begin{aligned} m(k+1)=m(k)-2\sum _{i=0}^{N-1} {\mu _i (k)E\left[ {\frac{\varepsilon _{i, a} (k)e_{i, D} (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} \right] } +\sum _{i=0}^{N-1} {\mu _i^2 (k)E\left[ {\frac{e_{i, D}^2 (k)}{{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)}} \right] } . \end{aligned}$$
(16)

For a high-order adaptive filter, the fluctuation of \(\left\| {{\mathbf{u}}_i (k)} \right\| ^{2}\) from one iteration to the next can be assumed to be small enough, so that (16) becomes

$$\begin{aligned} m(k+1)-m(k)=-\sum _{i=0}^{N-1} {\mu _i (k)\frac{2E\left[ {\varepsilon _{i, a} (k)e_{i, D} (k)} \right] -\mu _i (k)E\left[ {e_{i, D}^2 (k)} \right] }{E\left[ {{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)} \right] }} . \end{aligned}$$
(17)

Substituting (7) and (11) into (17), and using the common assumption that \(\varepsilon _{i, a} (k)\) is independent of \(\eta _{i, D} (k)\) [8, 14], we get

$$\begin{aligned} m(k+1)-m(k)=-\sum _{i=0}^{N-1} {\frac{\left( {E\left[ {\varepsilon _{i, a}^2 (k)} \right] } \right) ^{2}}{\left( {E\left[ {\varepsilon _{i, a}^2 (k)} \right] +\sigma _{\eta _{i, D} }^2 } \right) E\left[ {{\mathbf{u}}_i^\mathrm{T} (k){\mathbf{u}}_i (k)} \right] }} \le 0. \end{aligned}$$
(18)

It is clear that m(k) is nonincreasing, which implies that the proposed algorithm is convergent as k increases. Also, the equality in (18) holds if and only if the algorithm has gone into the steady state, i.e., \(m(k+1)=m(k)\) as \(k\rightarrow \infty \). Hence, in this case, we obtain

$$\begin{aligned} E\left[ {\varepsilon _{i, a}^2 (\infty )} \right] =0, \quad i\in [0, N-1]. \end{aligned}$$
(19)

Based on the fact that each subband input is close to a white signal [8, 10], (19) can be simplified as \(E\left[ {\varepsilon _{i, a}^2 (\infty )} \right] \approx m(\infty )\sigma _{u_i }^2 =0\), which implies \(m(\infty )=E\left[ {\left\| {{\varvec{\theta } }(\infty )} \right\| ^{2}} \right] =0\). As a result, the proposed algorithm can theoretically converge to the optimal solution \({\mathbf{w}}_o \) in the mean square sense.

4 Simulation Results

In order to assess the algorithm performance, the Monte Carlo (MC) simulations (average of 50 independent runs) are performed in the system identification scenarios. In our simulations, the unknown vector \({\mathbf{w}}_o \) is a room acoustic impulse response with \(M=512\) taps. Also, to show the tracking capability of the algorithm, the unknown vector is changed as \(-{\mathbf{w}}_o \) at the \(8\times 10^{4}\)th input samples. The colored input signal u(n) is generated by filtering a zero-mean white Gaussian signal through a first-order system \(\phi _1(z)=1/{(1-0.9z^{-1})}\) or a second-order system \(\phi _2(z)=1/{(1-1.6z^{-1}+0.81z^{-2})}\) [10]. The background noise \(\eta (n)\) is a white Gaussian signal with a signal-to-noise ratio (SNR) of 30 dB, unless otherwise specified. Here, we assume that the variance of the system noise, \(\sigma _\eta ^2 \), is known, because it can be easily estimated online [8, 10, 11]. The cosine modulated filter bank is used in all the SAF algorithms [4]. The normalized MSD (NMSD), \(10\log _{10} \left[ {\left\| {{\mathbf{w}}_o -{\mathbf{w}}(k)} \right\| _2^2 /\left\| {{\mathbf{w}}_o } \right\| _2^2 } \right] \), is used to measure the performance of the algorithms.

This work first examines the performance of the proposed algorithm using different numbers of subbands (i.e., \(N = 2, 4\), and 8), as shown in Fig. 2. The colored input signal is generated by \(\phi _1\). As expected, the convergence rate of a large number of subbands (e.g., \(N = 8\)) is faster than that of a small one (e.g., \(N = 2\)). The reason is behind this phenomenon is that each subband input signal is closer to a white signal for a larger number of subbands. However, this phenomenon will not be obvious when the number of subbands is larger than a certain value (in this case is 4). Besides, increasing the number of subbands also means increased computational complexity. Thus, a proper selection of N relies on a trade-off between convergence rate and computational complexity. Based on this principle, the number of subbands is chosen as \(N = 4\) in the following simulations.

Fig. 2
figure 2

NMSD curves of the NVSS–NSAF with \(N = 2, 4\), and 8

Full size image

Since the proposed algorithm uses the noniterative shrinkage method to estimate \(\varepsilon _{i, a} (k)\), i.e., (13), the parameter \(\lambda \) must be selected properly. Figure 3 investigates the effect of \(\lambda \) on the performance of the proposed algorithm, where the input signal is the same as Fig.  2. As can be seen, a suitable range of \(\lambda \) is \(3\le \lambda \le 5\), because the proposed algorithm obtains a good balance between convergence rate and steady-state error.

Fig. 3
figure 3

NMSD curves of the NVSS–NSAF for different values of \(\lambda \)

Full size image

Finally, the performance of the proposed NVSS–NSAF algorithm is compared to that of the NSAF algorithm with two fixed step sizes, the VSSM–NSAF algorithm [8] and the VSS–NSAF algorithm with two values of \(\beta \) [11], as shown in Figs. 4 and 5. In Fig. 4a, b, the colored input signals are generated by \(\phi _1\) and \(\phi _2\), respectively, and SNR = 30dB. To fairly compare the algorithms, the number of subbands \(N = 4\) is used in all the algorithms, and the parameters of the algorithms in [8] and [11] are chosen according to the recommended values in the literatures. It is clear that variable step size algorithms (e.g., VSSM–NSAF, VSS–NSAF, and NVSS–NSAF) improve the performance of filter in terms of convergence rate and steady-state error, as compared to the NSAF with the fixed step size. However, among these variable step size algorithms, the VSSM–NSAF in [8] has the largest steady-state error, and the NVSS–NSAF has the lowest steady-state error. Choosing a proper value of \(\beta \), the VSS–NSAF in [11] can obtain the same convergence rate or steady-state error as the NVSS–NSAF, but it sacrifices the steady-state error or convergence rate. Besides, the VSS–NSAF in [11] has no tracking capability when the unknown system suddenly changes. Figure 5 describes the NMSD results of these SAFs for SNR = 20 dB, using the colored input signals generated by \(\phi _1\) and \(\phi _2\). As one can see, the proposed algorithm still outperforms the other algorithms in terms of convergence rate, steady-state error, and tracking capability. Moreover, one can also observe from Figs. 4 and 5 that the steady-state errors of these algorithms using the same input signal increase as the SNR decreases.

Fig. 4
figure 4

NMSD curves of various SAF algorithms with SNR = 30 dB. a The colored input is generated by \(\phi _1\). b The colored input is generated by \(\phi _2\). NSAF: \(\mu =0.7\) and \(\mu =0.2\); VSSM–NSAF: \(\kappa =6\) [8]; VSS–NSAF: \(tr\left\{ {\mathbf{P}(0)} \right\} =100\) and \(\beta =1, 2\) [11]; proposed NVSS–NSAF: \(\kappa =1, \lambda =4\) (Color figure online)

Full size image
Fig. 5
figure 5

NMSD curves of various SAF algorithms with SNR = 20 dB. a The colored input is generated by \(\phi _1\). b The colored input is generated by \(\phi _2\). The choices of the algorithms parameters are the same as Fig. 4 (Color figure online)

Full size image

5 Conclusions

In this study, we derived the NVSS–NSAF algorithm by solving the minimization problem of the mean square of the noise-free a posterior subband error with respect to the step size. The proposed algorithm uses an individual step size for each subband. In order to recover the noise-free a priori subband error from the noisy subband error signal, a noniterative shrinkage method was employed. Compared to the conventional NSAF, VSSM–NSAF in [8], and VSS–NSAF in [11] algorithms, the proposed algorithm obtains good performance in terms of the tracking capability and steady-state error.