1 Introduction

Adaptive filtering is an extremely vital technology, which is employed in a variety of fields, including echo cancellation, speech linear prediction and system identification [3, 5, 6, 21]. In the realization, the normalized least mean square (NLMS) algorithm has a wide range of applications due to the advantages of simple calculation and easy implementation [14, 21]. However, it converges slowly once the colored input signals are encountered [13]. To better handle such signals, Lee and Gan [10] proposed a normalized subband adaptive filtering (NSAF) algorithm, whose computational complexity is comparable to that of NLMS. During implementation, the colored input and desired signals are broken down into multiple uncorrelated subbands [11]. However, the original NSAF using a fixed step size cannot neutralize the contradiction between fast convergence speed and low steady-state error.

To solve the problem, one approach is to replace the NSAF’s fixed step size with a variable step size (VSS) [1, 8, 17, 29]. A set-membership NSAF (SM-NSAF) [1] has been proposed, but its convergence rate is greatly affected by the error-bound parameter. The variable step size matrix NSAF (VSSM-NSAF) algorithm [17], which outperforms SM-NSAF in terms of convergence rate, steady-state error and tracking capability, has also been designed. Unfortunately, the steady-state error of VSSM-NSAF is still relatively large. Moreover, Yu minimized the mean-square of the posteriori subband error to provide an individual step size for each subband, proposing the variable step size NSAF (VSS-NSAF) algorithm [29]. Recently, a step size converter NSAF (SSC-NSAF) algorithm [8] has been proposed, which selects the most appropriate step size for the next iteration by comparing the mean-square deviations (MSDs) for given different step sizes. Nevertheless, these VSS algorithms presented in [1, 17, 29] cannot predict how fast convergence will occur or how low steady-state error will be, so they cannot be adjusted properly to meet practical requirements.

Another method is to utilize the convex combination way of two adaptive filters, one of which uses a large step size to improve convergence speed and the other which employs a small step size to reduce steady-state error [2, 15, 16, 28]. Although these convex combination algorithms can counteract the contradiction between rapid convergence speed and small steady-state error to a certain extent, the computational complexity is greatly increased. Further, in the convergence region between the two adaptive filters, the method of weight transfer [16] or weight feedback [28] is used to accelerate the convergence speed. Applying the concept of convex combination, a combined-step-size (CSS) NSAF (CSS-NSAF) algorithm has been presented in [23], in which a large and a small step sizes are also combined. The mixing parameter in the algorithm is indirectly obtained by minimizing the sum of squares of subband errors via an improved sigmoid function. Compared with traditional convex combination algorithms, the CSS-NSAF only needs to update a single filter, thus reducing the computational complexity significantly. However, the difference value between a large step size and a small one affects the step size setting of the mixing parameter. Consequently, when designing the algorithm, there is certain restriction on the difference value between the large step size and the small one, which prevents further improvement of the convergence speed or reduction of the steady-state error.

In this paper, we propose a novel multi-combined-step-size NSAF (MCSS-NSAF) algorithm, which designs the subband mixing parameters based on the variance of the noise-free a priori subband error signals. As a consequence, our algorithm allocates an individual combined-step-size for each subband considering the difference between each subband error, where the noniterative shrinkage strategy [4, 30] is utilized to estimate the noise-free a priori subband error signal. Compared with the CSS-NSAF, it is worth noting that the subband mixing parameter is not iteratively updated, thus it is not affected by the difference value between the large step size and the small one. Additionally, we analyze the mean-square and steady-state performances of the MCSS-NSAF algorithm, and verify that the theoretical values about mean-square deviation (MSD) are in largely accord with its simulation outcomes. At last, the performances of the MCSS-NSAF algorithm, such as steady-state error, convergence speed and tracking capability, are tested through system identification experiments.

The remainder of the paper is structured as follows. The system model and NSAF-related algorithms are concisely reviewed in Sect. 2. In Sect. 3, the MCSS-NSAF algorithm is derived. Section 4 includes the performance analysis. Simulations are shown in Sect. 5, and Sect. 6 draws conclusions about the whole paper.

Notation Scalars are represented in normal font. Boldface lowercase letters denote vectors, and boldface capital letters indicate matrices. Furthermore, \((\cdot )^{T}\) represents transposition, \(E\left\{ \cdot \right\} \) is the mathematical expectation, and a vector’s Euclidean norm is indicated by \(\left\| \cdot \right\| \).

2 Background

Take into account the desired signal d(m) at time m which derives from the unknown finite impulse response (FIR) system

$$\begin{aligned} d(m)=\textbf{u} ^{T}(m)\textbf{w}_{\textrm{o}} +v(m) \end{aligned}$$
(1)

where \(\textbf{w} _{\textrm{o}}=[w_{\textrm{o},0}, w_{\textrm{o},1},..., w_{\textrm{o},L-1} ]^{T} \) denotes the tap-weight vector of the unknown system, and L is its length. \(\textbf{u}(m)=[u(m),u(m-1),...,u(m-L+1)]^{T} \) indicates the input signal vector. Moreover, v(m) represents the system noise with zero-mean and variance \(\sigma _{v}^{2}\), which is independent of \(\textbf{u}(m)\).

Fig. 1
figure 1

Framework graph of the NSAF algorithm

Full size image

2.1 Original NSAF

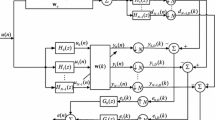
Figure 1 displays the framework graph of the NSAF algorithm, where N represents the number of subbands. The analysis filters \(\left\{ H_{i}(z), i = 0, 1, \dots , N-1 \right\} \) decompose the signal d(m) and u(m) into multiple subband forms \(d_{i}(m)\) and \(u_{i}(m)\), respectively. What is more, \(y_{i}(m)\) for \( i = 0, 1, \dots , N-1\) denote the subband output signals of the adaptive filter, and \(y_{i}(m)\) and \(d_{i}(m)\) are critically sampled to obtain \(y_{i,D}(t)\) and \(d_{i,D}(t)\), respectively. Note that m and t separately stand for the initial and sampled sequences.

Since the sampled output signal \(y_{i,D}(t)= \textbf{u} _{i}^{T}(t)\textbf{w}(t)\), the ith subband error signal \(e_{i,D}(t)\) is

$$\begin{aligned} e_{i,D}(t)=d_{i,D}(t)-\textbf{u} _{i}^{T}(t)\textbf{w}(t) \end{aligned}$$
(2)

where

$$\begin{aligned} \textbf{u} _{i}(t)=[u_{i}(tN),u_{i}(tN-1),...,u_{i}(tN-L+1)]^T \end{aligned}$$
(3)

and \(\textbf{w}(t)\) indicates the estimated value of the unknown vector \(\textbf{w} _{\textrm{o}}\) at tth iteration.

As introduced in [10], the update formula of the estimated tap-weight vector is

$$\begin{aligned} \textbf{w} (t+1)=\textbf{w} (t)+\mu \sum _{i=0}^{N-1}\frac{\textbf{u} _{i}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t) \textbf{u} _{i}(t)} \end{aligned}$$
(4)

where \(\mu \) denotes the fixed step size which must guarantee \(0<\mu <2\) for large L [31].

2.2 CSS-NSAF

In the CSS-NSAF [23], the tap-weight vector update formula is

$$\begin{aligned} \textbf{w} (t+1)=\textbf{w} (t)+\mu (t) \sum _{i=0}^{N-1}\frac{\textbf{u} _{i}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \end{aligned}$$
(5)

where

$$\begin{aligned} \mu (t)=\lambda (t)\mu _{1}+(1-\lambda (t))\mu _{2}. \end{aligned}$$
(6)

Here \(\mu (t)\) is the combined-step-size, obtained by combining a large step size \(\mu _{1}\) and a small step size \(\mu _{2}\) with a variable mixing parameter \(\lambda (t)\) \((0\le \lambda (t)\le 1)\).

The CSS-NSAF algorithm performs the quick convergence speed of \(\mu _{1}\) when \(\lambda (t) = 1\) and obtains the small steady-state error of \(\mu _{2}\) when \(\lambda (t) = 0\). By introducing an auxiliary variable \(\beta (t)\) into an improved sigmoid function [7], the value of \(\lambda (t)\) can be restricted to [0, 1] as follows

$$\begin{aligned} \lambda (t)=\left\{ \begin{array}{ll} 0 &{}\text {if } \beta (t)<-\ln \left( \frac{G+1}{G-1}\right) \\ 1 &{}\text {if } \beta (t)> \ln \left( \frac{G+1}{G-1}\right) \\ \displaystyle \frac{G }{1+e^{-\beta (t)}}-\frac{G-1}{2} &{}\text {otherwise } \end{array}\right. \end{aligned}$$
(7)

where \(G(G>1)\) denotes a positive constant. It can be seen that \(\lambda (t)\) can get 0 and 1, if \(\beta (t)\) equals \(-\ln \left( \frac{G +1}{G-1}\right) \) and \(\ln \left( \frac{G +1}{G-1}\right) \), separately. Then, minimizing the sum of squares of subband errors, i.e., \( {\textstyle \sum _{i=0}^{N-1}} e_{i,D}^{2}(t) \), obtains the update of \(\beta (t)\) as below

$$\begin{aligned} \beta (t)= & {} \beta (t-1)+\mu _{\beta }\left( \mu _{1}-\mu _{2}\right) [\lambda (t-1)(1-\lambda (t-1))+\tau ] \nonumber \\{} & {} \times \sum _{i=0}^{N-1} e_{i,D}(t) \textbf{u}_{i}^{T}(t) \sum _{i=0}^{N-1} \frac{\textbf{u}_{i}(t-1) e_{i, D}(t-1)}{\textbf{u}_{i}^{T}(t-1) \textbf{u}_{i}(t-1)} \end{aligned}$$
(8)

where \(\mu _{\beta }\) is also a step size and \(\tau \) indicates a tiny positive constant preventing the update process of \(\beta (t)\) from stalling when \(\lambda (t) = 0\) or 1.

3 Proposed MCSS-NSAF Algorithm

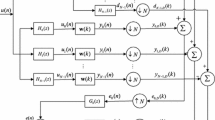
The paper focuses on the differences between each subband error \(e_{i,D}(t)\) of the NSAF algorithm. Therefore, we modify the variable mixing parameter \(\lambda (t)\) into the subband form \(\left\{ \lambda _{i}(t)\in [0,1], i = 0, 1, \dots , N-1\right\} \), and can get a new tap-weight vector update formula

$$\begin{aligned} \textbf{w} (t+1)=\textbf{w} (t)+ \sum _{i=0}^{N-1}\mu _{i}(t)\frac{\textbf{u} _{i}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \end{aligned}$$
(9)

with

$$\begin{aligned} \mu _{i}(t)=\lambda _{i}(t)\mu _{1}+(1-\lambda _{i}(t))\mu _{2} \end{aligned}$$
(10)

where \(\mu _{1}\) and \(\mu _{2}\) have the same meaning as in the CSS-NSAF algorithm.

Before introducing the update of individual subband mixing parameter \(\lambda _{i}(t)\), we define the noise-free a priori subband error

$$\begin{aligned} e_{i,p}(t)=\textbf{u} _{i}^{T}(t)[\textbf{w} _{\textrm{o}}-\textbf{w}(t)]. \end{aligned}$$
(11)

Thence, (2) can be modified as

$$\begin{aligned} e_{i,D}(t)=e_{i,p}(t)+v_{i,D}(t) \end{aligned}$$
(12)

where \(v_{i,D}(t)\) denotes the ith subband system noise, and \(\sigma _{v_{i,D}}^2\) is its variance, calculated by \(\sigma _{v_{i,D}}^2 = \sigma _{v}^2/N\) [26, 27]. In this paper, \(\sigma _{v}^2\) is assumed to be given, as it can be readily evaluated online according to Ni and Li [17], Shin et al. [24], Seo and Park [22].

In order to ensure rapid convergence speed in transient state stage and low steady-state error in steady-state stage, the subband mixing parameter \(\lambda _{i}(t)\) ought to be 1 at transient state and 0 at steady-state, respectively. Therefore, for updating the subband mixing parameters \(\lambda _{i}(t)\) for \(i = 0, 1, \dots , N-1\), the following method [32] is used

$$\begin{aligned} \lambda _{i}(t)=\frac{\sigma _{e_{i,p}}^2(t)}{\sigma _{e_{i,p}}^2(t)+\sigma _{v_{i,D}}^2} \end{aligned}$$
(13)

where \(\sigma _{e_{i,p}}^2(t)\) is the variance of the noise-free a priori subband error.

At the starting state, a large noise-free a priori subband error leads to \(\sigma _{e_{i,p}}^2(t)\gg \sigma _{v_{i,D}}^2\). Nevertheless, there maintains \(\sigma _{e_{i,p}}^2(t)\ll \sigma _{v_{i,D}}^2\) at the steady state. Hence, from (13), we have \( \lambda _{i}(t)\rightarrow 1\) at the starting state and \( \lambda _{i}(t)\rightarrow 0\) at the steady state.

In practical applications, \(\sigma _{e_{i,p}}^2(t)\) can be estimated by the following iterative method, i.e.,

$$\begin{aligned} \sigma _{e_{i,p}}^2(t)=\theta \sigma _{e_{i,p}}^2(t-1)+(1-\theta )e_{i,p}^2(t) \end{aligned}$$
(14)

where \(\theta \) \( (0\ll \theta <1)\) denotes the forgetting parameter, which is determined by \(\theta =1-N/(\kappa L),\kappa \ge 1\) [29].

Here, employ the noniterative shrinkage strategy [4, 30] to estimate \(e_{i,p}(t)\) from \(e_{i,D}(t)\)

$$\begin{aligned} \hat{e}_{i,p} (t)={\text {sign}}(e_{i,D}(t))\max (|e_{i,D}(t)|-C_{i}, 0) \end{aligned}$$
(15)

where the sign function is indicated by \({\text {sign}}(\cdot )\), and \(C_{i}\) denotes the threshold value, calculated through \(C_{i}= \sqrt{Q\sigma _{v_{i,D}}^2} \). Q is an adjustment parameter. Its influence on the proposed algorithm will be further discussed in simulations in Sect. 5. In short, the MCSS-NSAF algorithm is summarized in the Algorithm 1.

Algorithm 1
figure a

MCSS-NSAF

Full size image

4 Performance Analysis

First of all, the error of the tap-weight vector is defined as \(\textbf{w}_{\textrm{e}}(t) =\textbf{w} _{\textrm{o}}-\textbf{w}(t)\). Subtracting (9) from \(\textbf{w} _{\textrm{o}}\), the following formula is obtained

$$\begin{aligned} \textbf{w}_{\textrm{e}}(t+1)=\textbf{w}_{\textrm{e}}(t)-\sum _{i=0}^{N-1}[\lambda _{i}(t)\mu _{1}+(1-\lambda _{i}(t))\mu _{2}]\frac{\textbf{u} _{i}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)}. \end{aligned}$$
(16)

To better analyze the performance of the proposed MCSS-NSAF, a relevant assumption about the subband mixing parameter \(\lambda _{i}(t)\) is introduced [19].

Assumption 1

The subband mixing parameter \(\lambda _{i}(t)\) is independent of subband input signal \(\textbf{u} _{i}(t)\), subband error signal \(e_{i,D}(t)\) and subband system noise \(v_{i,D}(t)\).

When selecting \(0\ll \theta <1\), \(\lambda _{i}(t)\) generally changes relatively slowly compared with \(\textbf{u} _{i}(t)\) and \(e_{i,D}(t)\). Therefore, the assumption is reasonable. In the following analysis, \(\lambda _{i}(t)\) will be directly replaced by the expected value, in which \(\lambda _{i}(t)\) fluctuates around its average value. This approximation is used in [9, 32] as well.

For calculating \(E\left\{ \lambda _{i}(t) \right\} \), an approximate method is used

$$\begin{aligned} E\left\{ \lambda _{i}(t) \right\} \approx \frac{E\left\{ e_{i,p}^2(t) \right\} }{E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2},\quad i = 0, 1, \dots , N-1. \end{aligned}$$
(17)

4.1 Mean-square Performance Analysis

In this part, the convergence performance of the MCSS-NSAF algorithm is analyzed utilizing MSD defined by

$$\begin{aligned} D(t)=E\left\{ \left\| \textbf{w}_{\textrm{e}}(t) \right\| ^2 \right\} . \end{aligned}$$
(18)

For (16), by pre-multiplying \(\textbf{w}_{\textrm{e}}^T(t+1)\), taking the expectation of both sides, and then introducing (11), we get

$$\begin{aligned} D(t+1)= & {} D(t)-2\mu _{1}\sum _{i=0}^{N-1}E\left\{ \lambda _{i}(t) \right\} E\left\{ \frac{e_{i,p}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \right\} \nonumber \\{} & {} -\,2\mu _{2}\sum _{i=0}^{N-1}E\left\{ (1-\lambda _{i}(t)) \right\} E\left\{ \frac{e_{i,p}(t)e_{i,D}(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \right\} \nonumber \\{} & {} +\,\mu _{1}^2\sum _{i=0}^{N-1}E\left\{ [\lambda _{i}(t)]^2\right\} E\left\{ \frac{e_{i,D}^2(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \right\} \nonumber \\{} & {} +\,2\mu _{1}\mu _{2}\sum _{i=0}^{N-1}E\left\{ [\lambda _{i}(t)(1-\lambda _{i}(t)) ]\right\} E\left\{ \frac{e_{i,D}^2(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \right\} \nonumber \\{} & {} +\,\mu _{2}^2\sum _{i=0}^{N-1}E\left\{ [1-\lambda _{i}(t)]^2\right\} E\left\{ \frac{e_{i,D}^2(t)}{\textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)} \right\} . \end{aligned}$$
(19)

From one iteration to the next, the fluctuation of \(\left\| \textbf{u} _{i}(t) \right\| ^2\) can be presumed to be negligible as long as the adaptive filter order is sufficiently high [12, 21, 29]. So (19) can be rewritten as

$$\begin{aligned} D(t+1)&=D(t)-2\mu _{1}\sum _{i=0}^{N-1}E\left\{ \lambda _{i}(t) \right\} \frac{E\left\{ e_{i,p}(t)e_{i,D}(t)\right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)\right\} } \nonumber \\&\quad -\,2\mu _{2}\sum _{i=0}^{N-1}E\left\{ (1-\lambda _{i}(t)) \right\} \frac{E\left\{ e_{i,p}(t)e_{i,D}(t) \right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)\right\} } \nonumber \\&\quad +\,\mu _{1}^2\sum _{i=0}^{N-1}E\left\{ [\lambda _{i}(t)]^2\right\} \frac{E\left\{ e_{i,D}^2(t)\right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)\right\} } \nonumber \\&\quad +\,2\mu _{1}\mu _{2}\sum _{i=0}^{N-1}E\left\{ [\lambda _{i}(t)(1-\lambda _{i}(t)) ]\right\} \frac{E\left\{ e_{i,D}^2(t)\right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t)\right\} } \nonumber \\&\quad +\,\mu _{2}^2\sum _{i=0}^{N-1}E\left\{ [1-\lambda _{i}(t)]^2\right\} \frac{E\left\{ e_{i,D}^2(t) \right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }. \end{aligned}$$
(20)

Since \(e_{i,p}(t) \gg v_{i,D}(t)\) at initialization, \(\lambda _{i}(t)\) is close to one in (13). Moreover, applying (12) and (17) into (20), and utilizing a general assumption that \(e_{i,p}(t)\) and \(v_{i,D}(t)\) are independent of each other [27], we can obtain

$$\begin{aligned} D(t+1)-D(t) =-\mu _{1}(2-\mu _{1})\sum _{i=0}^{N-1}\frac{(E\left\{ e_{i,p}^2(t) \right\} )^2 }{(E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2)E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} } \le 0.\nonumber \\ \end{aligned}$$
(21)

It is obvious that D(t) is nonincremental when \(0\ll \mu _{1} <2\), meaning that the MCSS-NSAF algorithm converges as t increases at the initial state.

On the other side, when \(\lambda _{i}(t)\) tends to zero at the steady state, (20) will be

$$\begin{aligned} D(t+1)-D(t)=-2\mu _{2}\sum _{i=0}^{N-1}\frac{E\left\{ e_{i,p}^2(t) \right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }+\mu _{2}^2\sum _{i=0}^{N-1}\frac{E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2}{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }.\nonumber \\ \end{aligned}$$
(22)

Hence, based on (22), the MCSS-NSAF algorithm converges at the steady state, when the step size meets the following condition

$$\begin{aligned} 0<\mu _{2}\le \frac{2\sum _{i=0}^{N-1} \displaystyle \frac{E\left\{ e_{i,p}^2(t) \right\} }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} } }{\sum _{i=0}^{N-1} \displaystyle \frac{E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2}{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }} < 2. \end{aligned}$$
(23)

All in all, according to (20)–(23), we learn that the proposed MCSS-NSAF algorithm is provided with the merit of quick convergence speed as \(\mu _{1}\) at the initialization and the advantage of low steady state error as \(\mu _{2}\) at the steady-state.

When it is neither in the initialization nor steady state, substituting (10) and (12) into (20) can get

$$\begin{aligned} D(t+1)-D(t)=-\sum _{i=0}^{N-1} \mu _{i}(t) \frac{2E\left\{ e_{i,p}^2(t) \right\} -\mu _{i}(t)\left[ E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2 \right] }{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }.\nonumber \\ \end{aligned}$$
(24)

Based on (17), Eq. (24) is revised as

$$\begin{aligned}{} & {} D(t+1)-D(t) \nonumber \\{} & {} \quad = -\sum _{i=0}^{N-1} \frac{\mu _{1}E\left\{ e_{i,p}^2(t) \right\} +\mu _{2}\sigma _{v_{i,D}}^2}{ E\left\{ e_{i,p}^2(t) \right\} +\sigma _{v_{i,D}}^2}\times \frac{(2-\mu _{1}) E\left\{ e_{i,p}^2(t) \right\} -\mu _{2}\sigma _{v_{i,D}}^2}{E\left\{ \textbf{u} _{i}^{T}(t)\textbf{u} _{i}(t) \right\} }.\nonumber \\ \end{aligned}$$
(25)

From (25), \(D(t+1)\) is not greater than D(t) to guarantee convergence, when the following condition is fulfilled

$$\begin{aligned} E\left\{ e_{i,p}^2(t) \right\} \ge \frac{\mu _{2}}{2-\mu _{1}}\sigma _{v_{i,D}}^2,\quad i = 0, 1, \dots , N-1. \end{aligned}$$
(26)

Equation (26) indicates that the proposed algorithm can converge theoretically as long as the settings of the large and the small step size meet the above condition.

4.2 Steady-state Performance Analysis

When the MCSS-NSAF runs in the steady-state stage, its MSD D(t) inclines to a limited constant value. Thus, from (24) we have

$$\begin{aligned} 2\sum _{i=0}^{N-1} \mu _{i}(\infty )\frac{E\left\{ e_{i,p}^2(\infty ) \right\} }{E\left\{ \textbf{u} _{i}^{T}(\infty )\textbf{u} _{i}(\infty ) \right\} } =\sum _{i=0}^{N-1} \mu _{i}^2(\infty ) \frac{E\left\{ e_{i,p}^2(\infty ) \right\} +\sigma _{v_{i,D}}^2}{E\left\{ \textbf{u} _{i}^{T}(\infty )\textbf{u} _{i}(\infty ) \right\} }. \end{aligned}$$
(27)

Further assume that the subband signals are uncorrelated [12, 17]. Accordingly, on both sides of (27), the ith term of the summations corresponds to each other, obtaining

$$\begin{aligned}{} & {} 2\mu _{i}(\infty )\frac{E\left\{ e_{i,p}^2(\infty ) \right\} }{E\left\{ \textbf{u} _{i}^{T}(\infty )\textbf{u} _{i}(\infty ) \right\} } =\mu _{i}^2(\infty ) \frac{E\left\{ e_{i,p}^2(\infty ) \right\} +\sigma _{v_{i,D}}^2}{E\left\{ \textbf{u} _{i}^{T}(\infty )\textbf{u} _{i}(\infty ) \right\} }, \quad i = 0, 1, \dots , N-1. \nonumber \\ \end{aligned}$$
(28)

From (28), by removing the common terms, we further obtain

$$\begin{aligned} 2E\left\{ e_{i,p}^2(\infty ) \right\} =\mu _{i}(\infty )\left[ E\left\{ e_{i,p}^2(\infty ) \right\} + \sigma _{v_{i,D}}^2 \right] ,\quad i = 0, 1, \dots , N-1. \end{aligned}$$
(29)

Substituting (10) and (13) into (29), we can get

$$\begin{aligned} 2E\left\{ e_{i,p}^2(\infty ) \right\} \approx \mu _{1}E\left\{ e_{i,p}^2(\infty ) \right\} +\mu _{2}\sigma _{v_{i,D}}^2,\quad i = 0, 1,\dots , N-1. \end{aligned}$$
(30)

Simplifying (30) acquires

$$\begin{aligned} E\left\{ e_{i,p}^2(\infty ) \right\} \approx \frac{\mu _{2}}{2-\mu _{1}}\sigma _{v_{i,D}}^2,\quad i = 0, 1, \dots , N-1. \end{aligned}$$
(31)

For loss-free analysis filter groups, the variance of the output signal equals the sum of the variances of output signals from each subband [20]. Consequently, from (31), the excess mean-square error (EMSE) about the MCSS-NSAF is

$$\begin{aligned} \textrm{EMSE} (\infty ) = \sum _{i=0}^{N-1} E\left\{ e_{i,p}^2(\infty ) \right\} \approx \frac{\mu _{2}}{2-\mu _{1}}\sigma _{v}^2. \end{aligned}$$
(32)

Equation (32) indicates that the MCSS-NSAF using both smaller \(\mu _{1}\) and \(\mu _{2}\) can get a lower EMSE. However, since \(\mu _{1}\) affects the convergence rate of the algorithm, it cannot be set too small. Generally, it is recommended to be set to 1.

4.3 Computational Complexity

Table 1 summarizes the computational complexity of the NSAF [10], VSSM-NSAF [17], VSS-NSAF [29], SSC-NSAF [8], CSS-NSAF [23] and the proposed MCSS-NSAF algorithms, i.e., the number of multiplications, additions and comparisons for each iteration, where K denotes the length of the analysis filter and S stands for the number of step size used in the SSC-NSAF algorithm. As can be seen from Table 1, under the assumption that \(\sigma _{v}^2\) is known, the number of multiplications of the MCSS-NSAF algorithm is comparable to that of the traditional CSS-NSAF, and the number of additions and comparisons are slightly lower than that of the CSS-NSAF algorithm. In addition, compared with the SSC-NSAF and the VSSM-NSAF algorithms, the computational complexity of the MCSS-NSAF algorithm is lower.

Table 1 Summary of the computational complexity
Full size table

5 Simulations

To verify the performance of the MCSS-NSAF, computer simulations on system identification are implemented in this section. Figure 2 illustrates the optimal weight vector \(\textbf{w}_{\textrm{o}}\) with the length of \(L=512\). All algorithms are assessed utilizing the normalized MSD (NMSD), \(10\log _{10}{ [ \left\| \textbf{w} _{\textrm{e}}(t)\right\| _{2}^2 /\left\| \textbf{w} _{\textrm{o}} \right\| _{2}^2] }\). A white Gaussian signal with zero-mean that passes through a model system \(\Phi (z)=1/(1-0.9z^{-1})\) randomly produces the colored input signal u(m) [18, 24]. The background noise is obtained by adding the white Gaussian noise to the system output signal, and its signal-to-noise ratio (SNR) is set to 20dB or 30dB [25]. Moreover, all simulation results are collected by averaging 50 independent runs to ensure experimental accuracy.

Fig. 2
figure 2

Impulse response of the acoustic echo path with \(L = 512\)

Full size image
Fig. 3
figure 3

NMSD curves of the MCSS-NSAF for different N

Full size image
Fig. 4
figure 4

NMSD curves of the MCSS-NSAF for different Q

Full size image

5.1 Parameter Settings

Firstly, before algorithm simulations, some parameter settings need to be determined. As shown in Fig. 3, different numbers of subbands have different effects on the performance of the MCSS-NSAF. It is clear that increasing the number of subbands improves the convergence speed. The explanation for this phenomenon is that the subband input signal gets closer to the white signal as the number of subbands increases. However, this regularity is no longer be evident once N exceeds a threshold, which is 4 in this case. In addition, the computational complexity also increases as N increases. Thus, to balance the contradiction between convergence speed and computational complexity, the paper adopts \(N = 4\) in the subsequent simulations.

In the MCSS-NSAF, estimating the noise-free a priori subband error \(e_{i,p}(t)\), i.e., (15), requires a proper setting of the parameter Q. Figure 4 depicts the impact of Q on the performance of the MCSS-NSAF. It can be seen that the steady-state performance of the proposed MCSS-NSAF improves with the increase of Q. However, a large Q slows down the convergence speed. Hence, it is necessary to set a suitable Q. To obtain an excellent balance between the convergence speed and the steady-state error, we suggest that the appropriate range of Q is \(3\le Q\le 5\) based on the experiment results.

Fig. 5
figure 5

Comparison between simulation results and the theoretical values for MSD with different step size values based on (20). a \(\mu _{1}=1.00\), \(\mu _{2}=0.002\); b \(\mu _{1}=0.80\), \(\mu _{2}=0.002\); c \(\mu _{1}=1.00\), \(\mu _{2}=0.02\); d \(\mu _{1}=0.80\), \(\mu _{2}=0.02\)

Full size image

5.2 Verification of Analysis

Next, to verify the mean-square performance analysis, in Fig. 5, we compare simulation results and the theoretical values for MSD with different step size values based on (20). In Fig. 5a, the large step size \(\mu _{1}=1.00\) and the small step size \(\mu _{2}=0.002\) are adopted. As a comparison, the large step size \(\mu _{1}=0.80\) is utilized in Fig. 5b. We use \(\mu _{1}=1.00\), \(\mu _{2}=0.02\) in Fig. 5c, whereas in Fig. 5d, we employ \(\mu _{1}=0.80\), \(\mu _{2}=0.02\). From these graphs, it is evident that simulation results are essentially consistent with the theoretical values. Also, the experimental results are in accord with the expected phenomenon: the convergence speed depends on \(\mu _{1}\), while \(\mu _{2}\) affects the steady-state error.

5.3 Comparison of Algorithms

Finally, the proposed MCSS-NSAF algorithm is compared with the original NSAF [10], VSSM-NSAF [17], VSS-NSAF [29], SSC-NSAF [8] and CSS-NSAF [23] with SNR = 20dB and 30dB, respectively, and the results are shown in Fig. 6 and Fig. 7. To verify the algorithm’s adaptability to system changes, the optimal tap-weight vector is multiplied by -1 to obtain \(-\textbf{w} _{\textrm{o}}\) at the \(1.5\times 10^{5}\)th sample for testing the tracking ability of these algorithms. For experimental fairness, all the algorithms are run under the scenario of \(N = 4\), and all parameters involved are derived from the corresponding references.

Fig. 6
figure 6

NMSD learning curves of NSAF [10], VSSM-NSAF [17], VSS-NSAF [29], SSC-NSAF [8], CSS-NSAF [23] and the proposed MCSS-NSAF with SNR=20dB. NSAF: \(\mu _{1} = 1.00\) and \(\mu _{2} = 0.002\); VSSM-NSAF: \(\kappa = 6\); VSS-NSAF: \(\kappa = 1\), \(\lambda = 4\); SSC-NSAF: \(\kappa = 5\), \(q=2\), \(k=2\), \(S=3\); CSS-NSAF: \(\mu _{\beta } = 20\); the proposed MCSS-NSAF: \(\kappa = 6\), \(Q = 4 \)

Full size image

From Fig. 6, it can be seen that the algorithms with improved step sizes, whether it is VSS (e.g., VSSM-NSAF, VSS-NSAF and SSC-NSAF) or CSS (e.g., CSS-NSAF and MCSS-NSAF), demonstrate better performance than the original NSAF for steady-state error and convergence speed. However, with respect to the VSSM-NSAF, the VSS-NSAF and the SSC-NSAF, the MCSS-NSAF has the lower steady-state error and the faster tracking capability. Since the parameter \(\mu _{\beta }\) of the CSS-NSAF is affected by the difference value between \(\mu _{1}\) and \(\mu _{2}\), the CSS-NSAF with two different small step sizes, \(\mu _{2} = 0.02\) and 0.002, are tested. As can be observed, the MCSS-NSAF also outperforms the CSS-NSAF in terms of tracking ability, convergence speed and steady-state error.

Fig. 7
figure 7

NMSD learning curves of NSAF [10], VSSM-NSAF [17], VSS-NSAF [29], SSC-NSAF [8], CSS-NSAF [23] and the proposed MCSS-NSAF with SNR=30dB. NSAF: \(\mu _{1} = 1.00\) and \(\mu _{2} = 0.002\); VSSM-NSAF: \(\kappa = 6\); VSS-NSAF: \(\kappa = 1\), \(\lambda = 4\); SSC-NSAF: \(\kappa = 5\), \(q=2\), \(k=2\), \(S=3\); CSS-NSAF: \(\mu _{\beta } = 100\); the proposed MCSS-NSAF: \( \kappa = 6\), \(Q = 4 \)

Full size image

The comparisons of these NSAF-related algorithms at SNR = 30 dB are shown in Fig. 7. It can be observed that the MCSS-NSAF is still superior to the comparative algorithms in tracking capability, convergence speed and steady-state error. Furthermore, by comparing Fig. 7 with Fig. 6, one can see that the steady-state error of these algorithms decreases with increasing SNR.

6 Conclusion

In this study, we devise the MCSS-NSAF that designs an individual combined-step-size for each subband. The multi-combined-step-size is obtained by combining a large step size and a small one through a subband mixing parameter, which can be designed in view of the variance of the noise-free a priori subband error signal. In addition, by using a noniterative shrinkage strategy, the noise-free a priori subband error is recovered from the noisy subband error. Compared with the original NSAF, VSSM-NSAF, VSS-NSAF and CSS-NSAF, the MCSS-NSAF algorithm not only has quicker convergence speed and tracking capability, but also presents lower steady-state error. To further improve the performance of the MCSS-NSAF algorithm, we will investigate the effect of the sub-sampling period on the proposed algorithm in future research.