Introduction

The advancement in nanotechnology and nanoscience extended the application areas for researchers and scientists. Applications of nanofluids are encouraging in different phenomena such as the heat transfer phenomena. Advancements in technology need the proficient methods for heat transfer, and nanofluids provide the more efficient medium for heat transfer from one source to another source. In addition, numerous procedures are available in the literature which can intensifies heat transport properties in flow to improve the effectiveness of concentrating collector. Nanoliquids have higher thermo-physical properties compared with those of base liquids. Moreover, nanoliquids were employed inside absorber to serve as heat transfer liquid and, therefore, boost the performance of solar system. Sheikholeslami et al. (2014) deliberated the flow for CuO water nanofluid by considering the aspects of Lorentz forces. Khan et al. (2014) described heat sink–source characteristics for 3D non-Newtonian nanofluid. Ellahi et al. (2015) inspected the colloidal analysis for CO–H2O over inverted vertical cone. Khan and Khan (2015), (2016a) and Khan et al. (2016a) described various properties of nanoliquid by considering different non-Newtonian fluid models. Waqas et al. (2016) examined the flow of micropoler liquid due to nonlinear stretched sheet with convective condition. Khan and Khan (2016b) reported features of Burgers fluid by considering nanoparticles. Sulochana et al. (2017) studied the consequences of thin din needle with Joule heating. Hayat et al. (2017) analyzed radiative heat transfer in the presence of Lorentz’s force for nanofluid. Sheikholeslami and Shehzad (2017) reported the properties of nanofluid by considering characteristics of Lorentz force. Moreover, some recent development on nanofluid has been discussed in Sheikholeslami and Shamlooei (2017), Sheikholeslami and Rokni (2017), Irfan et al. (2018a, b, 2019a), Hayat et al. (2018), Sheikholeslami et al. (2018), Gireesha et al. (2018), Mahanthesh et al. (2018), Sheikholeslami (2018a, b), Akbar and Khan (2016), Sheikholeslami and Shehzad (2018a, b), Sheikholeslami and Sadoughi (2018), Sheikholeslami and Seyednezhad (2018), Khan et al. (2018a), Sheikholeslami and Rokni (2018), Sheikholeslami et al. (2019a, b), Sheikholeslami (2019a, b), Khan et al. (2019), Sheikholeslami and Mahian (2019), Nematpour-Keshteli and Sheikholeslami (2019).

The mass transfer phenomena is considered as an important unit of chemical process. In these phenomena, chemically reacting species (molecules) are moving from low concentrated area to high concentration. Chemical processes plays the vital role in culture and life itself. Chemical reactions are categorized in different systems due to their chemical and physical behavior, and homogeneous and heterogeneous systems are two major systems among them. Homogeneous reactions lie in the same phase space, i.e., gas, liquid, or solid spaces, while the heterogeneous reactions required more than one phase space. Khan et al. (2016b, 2017) scrutinized features chemical mechanisms for non-Newtonian fluids. Mahanthesh et al. (2017) discovered properties of vertical cone for colloidal material. Shahzad et al. (2019) reported the properties of C-matrix by employing new mathematical concept. Features of revised relation for flux and chemical processes were considered by Sohail et al. (2017). Ramesh et al. (2018) deliberated the revised conditions at boundary utilizing Maxwell nanoliquid. Irfan et al. (2018c) considered characteristics of variable conductivity and chemical processes for Carreau fluid. Tangent hyperbolic nanofluid with aspects of chemical processes and activation energy were inspected by Khan et al. (2018b). Irfan et al. (2019b) discussed the heterogeneous–homogeneous reactions for Oldroyd-B fluid.

To our knowledge, mathematical modeling for cross nanoliquid with entropy generation minimization is not yet examined. With this point of view, our concern here is to model cross nanofluid with entropy generation. Effects of viscous dissipation and thermal radiation are reported. Nanofluid modeling comprises the thermophoretic and Brownian movement aspects. Zero mass flux-type boundary condition is imposed. Idea of activation energy (AE) along with chemical reaction is also introduced. Total EG (entropy generation) rate and Bejan number are discussed for various flow variables. Numeric solutions for nonlinear systems are constructed. Nature of emerging physical is analyzed through graphs and tables.

Technical depiction and flow field equations

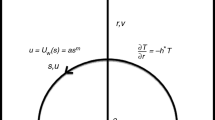
Our intention here is to formulate mixed convective cross nanomaterial flow towards moving surface. Moreover, we have considered magnetic field aspects for cross nanomaterial which acts normal to surface. Transportation of heat is analyzed by considering radiation and Joule heating aspects. The innovative relation of activation energy is introduced. Moreover, zero flux condition regarding nanofluid is imposed at boundary. Keeping in view the afforested assumptions, boundary layer approximation governs the following system of equations:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0,$$
(1)
$$\begin{aligned} u\frac{\partial u}{\partial x} + \nu \frac{\partial u}{\partial y} = & \upsilon \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] +\upsilon \frac{\partial u}{\partial y}\frac{\partial }{\partial y}\left[ {\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] \\ & - \frac{{\sigma \; \times \;B_{0}^{2} }}{{\rho_{f} }}u + g\left[ {A_{1} \left( {T - T_{\infty } } \right) + A_{2} \left( {C - C_{\infty } } \right)} \right] \\ \end{aligned}$$
(2)
$$\begin{aligned} u\frac{\partial T}{\partial x} + \nu \frac{\partial T}{\partial y} = & \frac{\nu }{{c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\frac{1}{{1 + (\varGamma \tfrac{\partial u}{\partial y})^{n} }}} \right] + \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} \\ & + \;\tau D_{B} \frac{\partial C}{\partial y}\frac{\partial T}{\partial y} - \frac{1}{{(\rho c)_{f} }}\frac{{\partial q_{r} }}{\partial y}, \\ \end{aligned}$$
(3)
$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} + w\frac{\partial C}{\partial z} = \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }} + D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} - k_{r}^{2} \left( {\frac{T}{{T_{\infty } }}} \right)^{m} \left( {C - C_{\infty } } \right)\,\exp \left( { - \frac{{E_{a} }}{KT}} \right),$$
(4)

with

$$u = U_{\text{w}} = cx{ , }v = 0,\,T = T_{\text{w}} ,\, \,\,D_{\text{B}} \frac{\partial C}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{\partial T}{\partial y} = 0\;\;\;{\text{at }}y = 0,$$
(5)
$${ }u \to 0 ,\, \, { }T \to T_{\infty } ,\, \, C \to C_{\infty } {\text{ as }}y \to \infty .$$
(6)

Here, \(\left( {\,v,\;u} \right)\) symbolizes velocity components in \(\left( {y,\;x} \right)\) direction, \(\rho_{f}\) is the density of cross liquid, \(\nu = \tfrac{\mu }{{\rho_{f} }}\) is the kinematic viscosity of fluid, \(\mu\) is the dynamic viscosity, \(\varGamma\) is the material constant, \(B_{0}\) is the uniform magnetic field strength, \(\tau = \tfrac{{\left( {\rho c} \right)_{\rho } }}{{\left( {\rho c} \right)_{\text{f}} }}\) is the ratio of heat capacity, with \(\left( {\rho c} \right)_{\text{f}}\) heat capacity of fluid and \(\left( {\rho c} \right)_{\text{p}}\) is the effective heat capacity of nanoparticles, \(\alpha = \tfrac{{k }}{{\left( {\rho c } \right)_{\text{f}} }}\) is the thermal diffusivity, \(k\) is the thermal conductivity of liquid, \(c_{\text{p}}\) is the specific heat capacity, \(\sigma^{ * }\) is the electrical conductivity, \(\left( {D_{\text{B}} ,\,D_{\text{T}} } \right)\) are the (Brownian and thermophoresis) diffusion coefficients, \(\left( {T,\,C} \right)\) are the (temperature and concentration), \(\left( {T_{\infty } ,\,C_{\infty } } \right)\)are the ambient (temperature, concentration), \(T_{\text{w}}\) is the surface temperature, \(k_{\text{r}}^{2}\) is the reaction rate, \(E_{\text{a}}\) is the activation energy, \(m\) is the fitted rate constant, \(c\) is the dimensional constant, and \(U_{\text{w}}\) is the stretching velocity.

Considering

$$\begin{aligned} \eta = & y\sqrt {\frac{c}{\nu },} \, u = cxf^{\prime } (\eta ),\, \, \nu = - \sqrt {c\nu } f(\eta ), \\ & \theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\, \, \phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{\infty } }}. \, \\ \end{aligned}$$
(7)

One has

$$\left[ {1 + \left( {1 - n} \right)\,\left( {Wef^{\prime \prime } } \right)^{n} } \right]\,f^{\prime \prime \prime } - \left[ {1 + \left( {Wef^{\prime \prime } } \right)^{n} } \right]^{2} \left[ {f^{\prime 2} + ff^{\prime \prime } + \lambda \left( {\theta + N_{r} \phi } \right)} \right] = 0,$$
(8)
$$\left( {1 + \frac{4}{3}R} \right)\,\theta^{{^{\prime \prime } }} + \mathop {Pr}\limits \left[ {f\theta^{{^{\prime } }} + Nb\theta^{{^{\prime } }} \phi^{{^{\prime } }} + Nt\theta^{{^{\prime } 2}} + \frac{{Ecf^{{^{\prime \prime } 2}} }}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right] = 0,$$
(9)
$$\phi^{{^{\prime \prime } }} + Sc\left[ {f\phi^{{^{\prime } }} + \frac{Nt}{Nb}\theta^{{^{\prime \prime } }} - \sigma \left( {1 + \delta \theta } \right)^{m} \phi \exp \left( { - \frac{E}{1 + \delta \theta }} \right)} \right] = 0,$$
(10)
$$f\left( 0 \right) = 0,\,\;f^{\prime } \left( 0 \right) = 1,\,\;f^{\prime } \left( \infty \right) \to 0,$$
(11)
$$\phi^{\prime } \left( 0 \right) = - \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\theta \left( 0 \right),\,\theta \left( \infty \right) \to 0,$$
(12)
$$\phi \left( 0 \right) = 1, \, \,\phi \left( \infty \right) \to 0,$$
(13)

where prime \(\left( {^{\prime } } \right)\) denotes differentiation with respect to \(\eta ,\) \(M = \tfrac{{\sigma B_{0}^{2} }}{{\rho_{\text{f}} c}}\) is the magnetic parameter, \(\Pr = \tfrac{\nu }{\alpha }\) is the Prandtl number, \(R = \tfrac{{4\sigma^{ * * } T_{\infty }^{3} }}{{k k^{ * } }}\) is the thermal radiation parameter, \({\text{Nb}} = \tfrac{{\tau D_{\text{B}} C_{\infty }}}{\upsilon }\) is the Brownian motion parameter, \({\text{Nt}} = \tfrac{{\tau D_{\text{T}} \left( {T_{\text{w}} - T_{\infty } } \right)}}{{\nu T_{\infty } }}\) is the thermophoresis parameter, \({\text{Ec}} = \tfrac{{c^{2} x^{2} }}{{c_{\text{p}} \left( {T_{\text{w}} - T_{\infty } } \right)}}\) is the Eckert number, \({\text{We}} = \sqrt{\tfrac{\varGamma^{2} c^{3} x^{2}}{\nu }}\) is the local Weissenberg number, \({\text{Sc}} = \tfrac{\nu }{{D_{\text{B}} }}\) is the Schmidt number, \(\sigma = \tfrac{{kr^{2} }}{c}\) is the dimensionless reaction rate, \(E = \tfrac{{E_{\text{a}} }}{{KT_{\infty } }}\) is the dimensionless activation energy, and \(\delta = \tfrac{{T_{\text{w}} - T_{\infty } }}{{T_{\infty } }}\) is the temperature difference parameter.

Quantities of physical interest

Expressions for drag force and heat transportation rate \(\left( {C_{\text{fx}} ,\;{\text{Nu}}_{\text{x}} } \right)\) in dimensional form are

$$C_{\text{fx}} = \frac{{\tau_{\text{w}} }}{{U_{\text{w}}^{2} \rho_{\text{f}} }},$$
(14)
$${\text{Nu}}_{\text{x}} = - \frac{{q_{\text{w}} x}}{{\left( {T_{\infty } - T_{\text{w}} } \right)k}},$$
(15)

in overhead expression \(\left( {q_{\text{w}} ,\tau_{\text{w}} } \right)\) characterizes the (wall heat flux, wall shear stress) which are given by

$$\tau_{\text{w}} = \mu \frac{\partial u}{\partial y}\left[ {\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right],$$
(16)
$$q_{\text{r}} = - \frac{{16\sigma^{ * * } T_{\infty }^{3} }}{{3k^{ * } }}\frac{\partial T}{\partial y}.$$
(17)

Expressions of surface drag force and local Nusselt number in dimensionless form are given by

$$C_{\text{fx}} Re_{\text{x}}^{1/2} = \left[ {\frac{1}{{1 + \left( {{\text{Wef}}^{{^{\prime \prime } }} \left( 0 \right)} \right)^{n} }}} \right]\,f^{{^{\prime \prime } }} \left( 0 \right),$$
(18)
$$Nu_{\text{x}} Re_{\text{x}}^{ - 1/2} = - \left[ {1 + \frac{4}{3}R} \right]\,\theta^{{^{\prime } }} \left( 0 \right),$$
(19)

where \(Re_{\text{x}} = \tfrac{{xU_{\text{w}} }}{\nu }\) signifies local Reynolds number.

Analysis for entropy generation

Mathematical relation of entropy generation for cross liquid in dimensional form is defined as

$$\begin{aligned} S_{\text{G}} = & \frac{{k}}{{T_{\infty }^{2} }}\left[( {1 + \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k k^{ * } }})\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \frac{\mu }{{T_{\infty } }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {\frac{1}{{1 + \left( {\varGamma \tfrac{\partial u}{\partial y}} \right)^{n} }}} \right]\, \\ & + \frac{{\sigma B_{0}^{2} u^{2} }}{{T_{\infty } }} + \frac{\text{RD}}{{C_{\infty } }}\left( {\frac{\partial C}{\partial y}} \right)^{2} + \frac{\text{RD}}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}\frac{\partial C}{\partial y}} \right). \\ \end{aligned}$$
(20)

The overhead relation in dimensionless is expressed as

$$N_{\text{G}} = \alpha_{1} \left[ {1 + \frac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + Br\left[ {\frac{1}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right]\,f^{{^{\prime \prime } 2}} + MBrf^{{^{\prime } 2}} + \frac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} ,$$
(21)

where \(N_{\text{G}} = \tfrac{{\nu T_{\infty } S_{\text{G}} }}{\kappa c\;\Delta \;T}\) depicts the entropy generation rate, \(Br = \tfrac{{\mu U_{w}^{2} }}{\kappa \;\Delta \;T}\) is the Brinkman number and \(\alpha_{2} = \tfrac{\Delta \;T}{{T_{\infty } }}\) is the dimensionless temperature ratio variable.

Mathematically, Bejan number is defined as

$$Be = \frac{{\alpha_{1} \left[ {1 + \tfrac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} }}{{\alpha_{1} \left[ {1 + \tfrac{4}{3}R} \right]\,\theta^{{^{\prime } 2}} + Br\left[ {\tfrac{1}{{1 + \left( {Wef^{{^{\prime \prime } }} } \right)^{n} }}} \right]\,f^{{^{\prime \prime } 2}} + MBrf^{{^{\prime } 2}} + \tfrac{{\alpha_{2} }}{{\alpha_{1} }}L\phi^{{^{\prime } 2}} + L\theta^{{^{\prime } }} \phi^{{^{\prime } }} }}.$$
(22)

Authentication of our outcomes

Table 1 shows prepared to authenticate the accuracy our outcomes. These tables demonstrate comparison of heat transport rate for numerous estimations of \(Pr\) with , Wang (1989), Gorla and Sidawi (1994) and Hamad (2011). It is perceived that our outcomes are in outstanding agreement.

Table 1 Comparison of our results with outcomes reported by Wang (1989), Gorla and Sidawi (1994) and Hamad (2011) for \(\left( {We\; = \;0} \right)\)
Full size table

Results

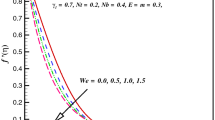
Nonlinear system subjected to conditions (11–13) is numerically tackled by employing Bvp4c scheme. Significant features of emerging physical parameters such as radiation parameter \(\left( R \right)\), magnetic parameter \(\left( M \right)\), thermophoresis parameter \(N_{\text{t}}\), local Weissenberg number \(\left( {We} \right)\), Buoyancy ratio parameter \(Nr\), Brownian motion parameter \(\left( {N_{\text{b}} } \right)\), chemical reaction parameter \(\left( \sigma \right)\), mixed convection parameter \(\left( \lambda \right)\), Prandtl parameter \((Pr)\), Eckert number \(\left( {Ec} \right)\), activation energy parameter \(\left( E \right)\), Schmidt number \(\left( {Sc} \right)\), entropy generation rate \(\left( {N_{\text{G}} } \right)\), Brinkman number \(\left( {Br} \right)\), dimensionless concentration ratio variable \(\left( {\alpha_{2} } \right)\), dimensionless temperature ratio variable \(\left( {\alpha_{1} } \right)\), and diffusive variable \(\left( L \right)\) on velocity \(f^{{^{\prime } }} \left( \eta \right)\), temperature \(\theta \left( \eta \right)\), concentration of nanomaterials \(\phi \left( \eta \right),\) Bejan number \(\left( {Br} \right)\), and entropy generation \(\left( {N_{G} } \right)\) are examined in this section. Figures 1–21 show sketched to visualize the behavior of physical parameter. Figure 1 portrays the characteristics of \({\text{We}}\) on \(f^{{^{\prime } }}\). Here, \(f^{{^{\prime } }}\) deteriorates via larger \(We\) for shear thinning liquid. Features of \(f^{{^{\prime } }}\) for varying \(Nr\) are described in Fig. 2. Larger \(Nr\) yields an augmentation in cross-nanoliquid velocity. Characteristics \(f^{{^{\prime } }}\) for varying \(\lambda\) are reported in Fig. 3. Increment in \(\lambda\) intensifies \(f^{{^{\prime } }}\). Physically, raise in \(\lambda\) yields more buoyancy forces due to which velocity of cross-liquid boosts. Impact of \(M\) against \(f^{{^{\prime } }}\) is considered in Fig. 4. Here, \(f^{{^{\prime } }}\) declines for higher estimation of \(M\). Velocity of cross nanoliquid is much higher in case of hydrodynamic when compared to hydromagnetic situation. This behavior of cross nanoliquid for hydromagnetic situation occur, because augmentation in \(M\) creates strong Lorentz force. Figure 5 demonstrates the aspects of \(Ec\) for \(\theta\). Here, \(\theta\) intensifies for larger \(Ec\). Physically, greater values of \(Ec\) produce more heat due to temperature of cross-nanoliquid enhances. Attribute of \(Pr\) on \(\theta\) is displayed in Fig. 6. Here, \(\theta\) declines for greater \(Pr\). Mathematical point of view \(Pr\) has inverse relation with thermal diffusivity. Therefore, greater \(Pr\) deteriorates significantly the temperature of cross nanoliquid. The curve of \(Nt\) for \(\theta\) is presented in Fig. 7. Clearly, larger \(Nt\) yields higher \(\theta .\) Actually, temperature difference between wall and at infinity rises due to temperature of cross-nanoliquid enhances. Nanofluid temperature upon \(R\) is illustrated through Fig. 8. An increment in \(R\) intensifies the nanoliquid temperature. Higher estimations of \(R\) produce more heat to working liquid. Figure 9 shows sketched to scrutinize the impact of \(\sigma\) on \(\phi\). Increment in \(\sigma\) deaccelerates the nanoparticles’ volume fraction \(\phi\). Figure 10 portrays the aspect of \(E\) for nanoparticles volume fraction. It is perceived from achieved data that term \(\exp \left( { - \tfrac{{E_{\text{a}} }}{\kappa T}} \right)\) deteriorates for greater values of \(E_{\text{a}}\). Significance of \({\text{Nt}}\) and \(Nb\) is emphasized in Figs. 11 and 12. For higher estimation, \(Nt\) corresponds to enhancement in \(\phi\), while opposite behavior is captured for \(Nb\). Actually, due to temperature difference between walls, nanoparticles are from higher temperature region to lower temperature region.

Fig. 1
figure 1

\(f^{{^{\prime } }}\) impact for different \(We\)

Full size image
Fig. 2
figure 2

\(f^{{^{\prime } }}\) impact for different \(Nr\)

Full size image
Fig. 3
figure 3

\(f^{{^{\prime } }}\) impact for different \(\lambda\)

Full size image
Fig. 4
figure 4

\(f^{{^{\prime } }}\) impact for different \(M\)

Full size image
Fig. 5
figure 5

\(\theta\) impact for different \(Ec\)

Full size image
Fig. 6
figure 6

\(\theta\) impact for different \(Pr\)

Full size image
Fig. 7
figure 7

\(\theta\) impact for different \(Nt\)

Full size image
Fig. 8
figure 8

\(\theta\) impact for different \(R\)

Full size image
Fig. 9
figure 9

\(\phi\) impact for different \(\sigma\)

Full size image
Fig. 10
figure 10

\(\phi\) impact for different \(E\)

Full size image
Fig. 11
figure 11

\(\phi\) impact for different \(N_{\text{t}}\)

Full size image
Fig. 12
figure 12

\(\phi\) impact for different \(N_{\text{b}}\)

Full size image

Entropy generation rate and Bejan number

Figures 13 and 14 explain significant features of \(Br\) on \(N_{\text{G}}\) and \(Be.\) It is perceived that greater \(Br\) leads to an enrichment in the rate of entropy generation. Mathematically, \(Br\) has inverse relation to \({\text{Be}}\). Consequently, \(Be\) deteriorate, while opposite trend is detected for \(N_{\text{G}}\). Behavior of \(L\) for rate of entropy generation \(N_{\text{G}}\) is disclosed through Fig. 15. This figure elaborates reduction \(N_{G}\) subjected to \(L\). Figures 16 and 17 sketch to interpret the attribute of \(M\) for \(N_{\text{G}}\) and \(Be.\) Here, \(N_{\text{G}}\) intensifies and \(Be\) deteriorates subjected to higher \(M\). Such a growth in \(N_{\text{G}}\) is perceived because resistance to motion of cross nanoliquid rises when \(M\) is enlarged. Figure 18 exhibits variation of \(\alpha_{1}\) versus \(N_{\text{G}}\). Clearly, \(N_{\text{G}}\) intensifies subjected to higher \(\alpha_{1}\). Figure 19 describes \(\alpha_{2}\) influence on \(N_{\text{G}}\). It is perceived from achieved data that \(N_{\text{G}}\) rises for larger \(\alpha_{2}\). Figures 20 and 21 sketch to demonstrate effect of \(R\) on \(N_{\text{G}}\) and \(Be.\) \(N_{\text{G}}\) and \(Be\) are augmented via larger \(R\).

Fig. 13
figure 13

\(N_{\text{G}}\) impact for different \(Br\)

Full size image
Fig. 14
figure 14

\({\text{Be}}\) impact for different \(Br\)

Full size image
Fig. 15
figure 15

\(N_{\text{G}}\) impact for different \(L\)

Full size image
Fig. 16
figure 16

\(N_{\text{G}}\) impact for different \(M\)

Full size image
Fig. 17
figure 17

\(Be\) impact for different \(M\)

Full size image
Fig. 18
figure 18

\(N_{\text{G}}\) impact for different \(\alpha_{1}\)

Full size image
Fig. 19
figure 19

\(N_{\text{G}}\) impact for different \(\alpha_{2} .\)

Full size image
Fig. 20
figure 20

\(N_{G}\) impact for different \(R\)

Full size image
Fig. 21
figure 21

\(Be\) impact for different \(R\)

Full size image

Characteristics of surface drag force and heat transfer rate

This subsection demonstrates the features of \(M\), \(\lambda\) and \(We\) on surface drag force via Table 2. We perceived that surface drag force boosts via larger \({\text{Nr}}\) for \(n < 1\). Moreover, it is scrutinized that surface drag force decline via larger \(M\), \(\lambda\), and \(We\) for both \(n < 1\) and \(n > 1\). Table 3 elaborates the influence of numerous rheological parameters on heat transfer rate. Clearly, heat transfer rate rises for increments in \(Pr\) and \(R\), while decays for higher \(Ec\) and \(N_{\text{t}}\).

Table 2 Surface drag force \(C_{\text{fx}} Re_{\text{x}}^{1/2}\) via different estimations of \(We, \, \lambda , \, Nr\) and \(M\) when \(\alpha_{1} = \sigma = \alpha_{2} = E = L = \delta = Nt = m = 0.1,\, \, Pr = 0.9, \, \,R = Ec = {\text{Br}} = 0.2,\,{\text{ Sc}} = 0.7,\,Nb = 0.4\)
Full size table
Table 3 Heat transfer rate \(Re^{ - 1/2} \;Nu_{\text{x}}\) via different estimations of \(Ec,\,Pr,\,We,\,Nt\) and \(R\) when \(Nr = 0.3,\,Nb = 0.4,\,Sc = 0.7,\,m = \sigma = E = \delta = \lambda = 0.1\)
Full size table

Conclusions

Here, mixed convective cross-nanoliquid flow containing magnetohydrodynamic (MHD) was scrutinized. Energy distribution of cross nanoliquid was investigated by considering Joule heating and radiation aspects. Significant outcomes prominent from whole analysis were as below.

  • Increment in local Weissenberg number deteriorates cross-liquid velocity.

  • Higher mixed convection parameter enriches the nanoliquid velocity.

  • Larger radiation parameter intensifies the liquid temperature.

  • Entropy generation boosts subjected to \(M\), \(Br\), \(R\), \(\alpha_{1}\), and \(\alpha_{2}\); however, it diminishes when \(L\) is increased.

  • Impact of \(M\) and \(R\) is reverse against Bejan number.