Introduction

In order to overcome rise in the energy requirements due to advancement in technological and industrial processes, the only way is to use renewable energy. That is why the scientists and researchers are devoted toward developing devices with advanced rate of cooing or heat which results in saving and storing of energy. The most appropriate, rich and easy source of such energy (renewable energy) is the solar energy. For this purpose thermal solar collectors are constructed in which ordinary fluids are used as heat transport medium. Such ordinary fluids possess very small thermal conductance and heat storing capacity due to which the performance of solar collectors is affected. Facing such issue, investigators focused toward developing materials possessing higher thermal conductance and thermal storing capacity. In this regard, pioneer work is done by Choi et al. [1, 2]. They observed better thermal conductance of the material obtained by adding nano-sized (1–100 nm) particles in the ordinary fluids. Such material is called nanofluid and the added nano-sized substances are called nanoparticles. A basic review work on hybrid nanomaterial is presented by Sarkar et al. [3]. Melting heat with chemical reactions in CNTs-nanomaterial is elaborated by Hayat et al. [4]. Hosseini et al. [5] examined entropy and MHD effects for nanomaterials flow with heat generation. Some latest investigations regarding nanomaterials flows are given in Refs. [6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

Although heat transport process is recently the core area of study but little interest has been shown toward studying heat transport via melting process. Melting heat plays a vital role in engineering, physics, technological and industrial processes. Due to applications in aforementioned fields, investigators and researchers have shown great devotion toward developing effective and sustainable technologies for energy storage. The process of storing energy involves latent heat, sensible heat and chemical heat mechanisms. Among these mechanisms, latent heat is the most efficient and economically friendly for storing energy. Melting process is directly related to the latent heat. Melting condition stores the energy in the material while this stored energy can be regained through freezing. Manufacturing of semi-conductors, soil melting, magma solidification, permafrost melting, freezing treatment of sewage, frozen ground thawing and many more are the applications of melting phenomenon. Initial analysis on melting heat by placing ice slab in stream of hot air is performed by Rebert et al. [29]. Chemical reactions, melting and MHD impacts on tangent hyperbolic material flow due to nonlinear stretching surface is expressed by Qayyum et al. [30]. Qi et al. [31] studied heat transmission during melting process of lauric acid in a cavity. Few updated analyses on melting heat can be seen in Refs. [32,33,34,35,36,37,38,39].

Literature shows that researchers have shown their attentions toward studying nanomaterials. Hybrid nanomaterials are discussed rare up to date. Further this analysis narrowed down when squeezing flow is considered in presence of Cattaneo–Christov (C–C) heat flux and Darcy–Forchheimer (D-F) porous medium. Thus, to fill up this void the hybrid nanomaterial (GO + Cu + Water) flow through Darcy–Forchheimer (D-F) porous medium bounded between two parallel walls is examined in this analysis. Lower stretching wall is subject to melting. Cattaneo–Christov (C–C) heat flux is addressed. Viscous dissipation is accounted. Related expressions of PDEs are constructed and then non-dimensionalized through suitable variables. Such non-dimensional PDEs are then solved by finite difference method. Velocities and temperature are examined under involved parameters graphically.

Mathematical modeling

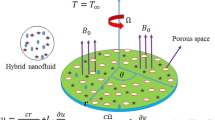
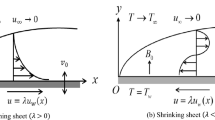
Consider 2D unsteady flow of hybrid nanomaterial confined between two infinite walls. The lower wall \(y = 0\) is fixed and stretches with velocity \(U_{\rm w} (x,t)\), while upper wall \(y = h(t)\) moves (squeezes) toward lower wall with velocity \(V_{\rm h} (t)\). Both the walls are at a distance \(h(t)\) from each other. Darcy–Forchheimer (D–C) porous medium is taken between these walls and hybrid nanomaterial flow through it. Disturbance in hybrid nanomaterial is generated by stretching the lower wall. Lower wall is also subjected to melting heat effect and Cattaneo–Christov (C–C) heat flux instead of ordinary Fourier’s heat flux (see Fig. 1). Hybrid nanomaterial is made by adding two types of nanoparticles (GO, Cu) in water-based fluid.

Fig. 1
figure 1

Physical diagram for considered problem

Full size image

Making use of above-mentioned assumptions, the flow and heat related expressions (PDEs) are [7]:

$$U_{\rm x} + V_{\rm y} = 0,$$
(1)
$$U_{{\text{t}}} + UU_{{\text{x}}} + VU_{{\text{y}}} = v_{{{\text{hnf}}}} (U_{{{\text{xx}}}} + U_{{{\text{yy}}}} ) - \frac{{v_{{{\text{hnf}}}} }}{{k_{1} }}\phi _{0} U - \frac{{c_{{\text{b}}} }}{{\sqrt {k_{1} } }}U^{2} ,$$
(2)
$$V_{{\text{t}}} + UV_{{\text{x}}} + VU_{{\text{y}}} = v_{{{\text{hnf}}}} (U_{{{\text{xx}}}} + V_{{{\text{yy}}}} ) - \frac{{v_{{{\text{hnf}}}} }}{{k_{1} }}\phi _{0} V - \frac{{c_{{\text{b}}} }}{{\sqrt {k_{1} } }}V^{2} ,$$
(3)
$$T_{{\text{t}}} + UT_{{\text{x}}} + VT_{{\text{y}}} + \tau _{0} [T_{{{\text{tt}}}} + UU_{{\text{x}}} T_{{\text{x}}} + VV_{{\text{y}}} T_{{\text{y}}} + UV_{{\text{x}}} T_{{\text{y}}} + VU_{{\text{y}}} T_{{\text{x}}} + 2UVT_{{{\text{xy}}}} + U^{2} T_{{{\text{xx}}}} + V^{2} T_{{{\text{yy}}}} + U_{{\text{t}}} T_{{\text{x}}} + 2UT_{{{\text{xt}}}} + V_{{\text{t}}} T_{{\text{y}}} + 2VT_{{{\text{ty}}}} ] = \alpha _{{{\text{hnf}}}} [T_{{{\text{xx}}}} + T_{{{\text{yy}}}} ] + \frac{{\mu _{{{\text{hnf}}}} }}{{(\rho c_{{\text{p}}} )_{{{\text{hnf}}}} }}(4(U_{{\text{x}}} )^{2} + (V_{{\text{x}}} + U_{{\text{y}}} )^{2} ),$$
(4)

with IBCs (initial and boundary conditions)

$$\begin{aligned} & U = 0,\,\,\,\,V = 0,\,\,\,\,T = T_{{\text{w}}} ,\,\,\,\,T_{{\text{t}}} = 0\,\,\,{\text{when}}\,\,{\text{ }}t = 0 \\ & U = U_{{\text{w}}} (t,x) = \frac{{U_{0} x}}{{1 - U_{1} t}},\,\,\,\,T = T_{{\text{m}}} ,\,\,\,\,k_{{{\text{hnf}}}} T_{{\text{y}}} = \rho _{{{\text{hnf}}}} (\lambda _{{\text{f}}} + C_{{\text{s}}} (T_{{\text{m}}} - T_{0} ))V\,\,\,\,{\text{when}}\,\,\,y = 0, \\ & U = 0,\,\,\,\,V = V_{{\text{h}}} (t) = h(t)_{{\text{t}}} = ,\,\,\,\,T = T_{{\text{h}}} \,\,\,\,{\text{when}}\,\,\,y = h(t). \\ \end{aligned}$$
(5)

In above equations \(U\), \(V\) and \(T\) are functions of \(x\), \(y\) and \(t\) while \(h(t) = \sqrt {\frac{{v_{\rm f} (1 - U_{1} t)}}{{U_{0} }}}\).

Consider the dimensionless quantities

$$f = \frac{L}{{v_{{\text{f}}} }}U,\,\,\,\,g = \frac{L}{{v_{{\text{f}}} }}V,\,\,\,\,t^{*} = \frac{{v_{{\text{f}}} }}{{L^{2} }}t,\,\,\,\,y^{*} = \frac{y}{L},\,\,\,\,x^{*} = \frac{x}{L},\,\,\,\,\theta = \frac{{T - T_{{\text{m}}} }}{{T_{{\text{h}}} - T_{{\text{m}}} }},\,\,\,\,\Pr = \frac{{v_{{\text{f}}} }}{{\alpha _{{\text{f}}} }},\,\,\,\,Sq = \frac{{U_{1} }}{{U_{0} }},\,\,\,\,\lambda = \frac{{L^{2} \phi _{0} }}{{\sqrt {k_{1} } }},\gamma = \frac{{\tau _{0} v_{{\text{f}}} }}{{L^{2} }},\,\,\,{\text{M}} = \frac{{U_{0} L^{2} }}{{v_{{\text{f}}} - U_{1} t^{*} L^{2} }},\,\,\,M_{1} = \frac{{(T_{{\text{h}}} - T_{{\text{m}}} )(c_{{\text{p}}} )_{{\text{f}}} }}{{\lambda _{{\text{f}}} + C_{{\text{s}}} (T_{{\text{m}}} - T_{0} )}},\,\,\,\,{\text{Fr}} = \frac{{c_{{\text{b}}} L}}{{\sqrt {k_{1} } }},\,\,\,\,Ec = \frac{{\mu _{{\text{f}}} \alpha _{{\text{f}}} }}{{L^{2} (\rho c_{{\text{p}}} )_{{\text{f}}} (T_{{\text{h}}} - T_{{\text{m}}} )}}.$$
(6)

Using these variables in Eqs. (1–5), we are left with the following dimensionless DEs and IBCs

$$f_{{{\text{x}}^{*} }} + g_{{{\text{y}}^{*} }} = 0,$$
(7)
$$f_{{{\text{t}}^{*} }} + ff_{{{\text{x}}^{*} }} + gf_{{{\text{y}}^{*} }} = A_{{11}} (f_{{{\text{x}}^{*} {\text{x}}^{*} }} - \lambda f + f_{{{\text{y}}^{*} {\text{y}}^{*} }} ) - {\text{Fr}}(f)^{2} ,$$
(8)
$$g_{{{\text{t}}^{*} }} + fg_{{{\text{x}}^{*} }} + gg_{{{\text{y}}^{*} }} = A_{{11}} (g_{{{\text{x}}^{*} {\text{x}}^{*} }} - \lambda g + g_{{{\text{y}}^{*} {\text{y}}^{*} }} ) - {\text{Fr}}(g)^{2} ,$$
(9)
$$\theta _{{{\rm t}^{*} }} + f\theta _{\rm x} + g\theta _{{{\rm y}^{*} }} + \gamma [\theta _{{{\rm t}^{*} t^{*} }} + f(t^{*} ,x^{*} ,y^{*} )f_{{{\rm x}^{*} }} \theta _{{{\rm x}^{*} }} + gg_{{{\rm y}^{*} }} \theta _{{{\rm y}^{*} }} + fg_{{{\rm x}^{*} }} \theta _{\rm y} + vf_{{{\rm y}^{*} }} \theta _{{{\rm x}^{*} }} + 2fg\theta _{{{\rm x}^{*} y^{*} }} + f^{2} \theta _{{{\rm x}^{*} x^{*} }} + g^{2} \theta _{{{\rm y}^{*} y^{*} }} + 2fg\theta _{{{\rm x}^{*} y^{*} }} + f^{2} \theta _{{{\rm x}^{*} x^{*} }} + g^{2} \theta _{{{\rm y}^{*} y^{*} }} + f_{{{\rm t}^{*} }} \theta _{{{\rm x}^{*} }} + 2f\theta _{{{\rm x}^{*} t^{*} }} + g_{{{\rm t}^{*} }} \theta _{{{\rm y}^{*} }} + 2g\theta _{{{\rm t}^{*} y^{*} }} ] = \frac{{A_{{16}} }}{{A_{{21}} }}\Pr Ec(4(f_{{{\rm x}^{*} }} )^{2} + (g_{{{\rm x}^{*} }} + f_{{{\rm y}^{*} }} )^{2} ) + \frac{{A_{{14}} }}{{A_{{15}} \Pr }}[\theta _{{{\rm x}^{*} x^{*} }} + \theta _{{{\rm y}^{*} y^{*} }} ].$$
(10)

Dimensionless IBCs are

$$\begin{aligned} f & = 0,\,\,\,\,g = 0,\,\,\,\,\theta = 1,\,\,\,\,\theta _{{{\rm t}^{*} }} = 0\,\,\,{\text{when}}\,\,{\text{ }}t^{*} = 0, \\ f & = {\text{M}}x^{*} ,\,\,\,\,\theta = 1,\,\,\,\,g = 0,\frac{{M_{1} }}{{A_{{14}} }}\theta _{{{\rm y}^{*} }} = \frac{{\Pr }}{{A_{{21}} }}g\,\,\,{\text{when}}\,\,y^{*} = 0, \\ f & = 0,\,\,\,\,g = \frac{{{\text{Sq}}}}{2}\sqrt {\text{M}} ,\,\,\,\,\theta = 0\,\,\,{\text{when}}\,\,y^{*} = 1. \\ \end{aligned}$$
(11)

Here

$$A_{{11}} = \frac{{v_{{\rm hnf}} }}{{v_{\rm f} }} = \frac{1}{{\left( {1 - \phi _{1} } \right)^{{2.5}} \left( {1 - \phi _{2} } \right)^{{2.5}} [\left( {1 - \phi _{2} } \right)\,\left( {\left( {1 - \phi _{1} } \right) + \phi _{1} \tfrac{{\rho _{{{\rm s}_{1} }} }}{{\rho _{\rm f} }}} \right) + \phi _{2} \tfrac{{\rho _{{{\rm s}_{2} }} }}{{\rho _{\rm f} }}]}}$$
(12)
$$A_{{14}} = \frac{{k_{{\rm hnf}} }}{{k_{\rm f} }},$$
(13)
$$A_{{15}} = \left( {\left( {1 - \phi _{2} } \right)\,\left( {\left( {1 - \phi _{1} } \right) + \phi _{1} \frac{{(\rho c_{\rm p} )_{{{\rm s}_{1} }} }}{{(\rho c_{\rm p} )_{\rm f} }}} \right) + \phi _{2} \frac{{(\rho c_{\rm p} )_{{{\rm s}_{2} }} }}{{(\rho c_{\rm p} )_{\rm f} }}} \right),$$
(14)
$$A_{{16}} = \frac{1}{{\left( {1 - \phi _{1} } \right)^{{2.5}} \left( {1 - \phi _{2} } \right)^{{2.5}} }}.$$
(15)

\(A_{{21}} = \frac{{\rho _{{\rm hnf}} }}{{\rho _{\rm f} }}\). (16).

In above relations \(f\), \(g\) and \(\theta\) are functions of \(t^{*}\), \(x^{*}\) and \(y^{*}\).

Hybrid nanomaterial (GO + Cu + Water) expressions via Hamilton–Crosser model

Expressions for hybrid nanomaterial (GO + Cu + Water) proposed by Hamilton–Crosser model are [7]

$$\mu _{{\rm hnf}} = \frac{{\mu _{\rm f} }}{{\left( {1 - \phi _{1} } \right)^{{2.5}} \left( {1 - \phi _{2} } \right)^{{2.5}} }},\,\;\;\upsilon _{{\rm hnf}} = \frac{{\mu _{{\rm hnf}} }}{{\rho _{{\rm hnf}} }},$$
(17)
$$(\rho c_{\rm p} )_{{\rm hnf}} = \left( {1 - \phi _{2} } \right)\,\left( {\left( {1 - \phi _{1} } \right)(\rho c_{\rm p} )_{\rm f} + \phi _{1} (\rho c_{\rm p} } \right)_{{{\rm s}_{1} }} + \phi _{2} (\rho c_{\rm p} )_{{{\rm s}_{2} }} ,$$
(18)
$$\rho _{{\rm hnf}} = \left( {1 - \phi _{2} } \right)\,\left( {\left( {1 - \phi _{1} } \right)\,\rho _{\rm f} + \phi _{1} \rho _{{{\rm s}_{1} }} } \right) + \phi _{2} \rho _{{{\rm s}_{2} }} ,$$
(19)
$$\frac{{\kappa _{{\rm hnf}} }}{{\kappa _{{\rm nf}} }} = \frac{{\kappa _{{{\rm s}_{2} }} + (n - 1)\kappa _{{\rm nf}} - (n - 1)\phi _{2} (\kappa _{{\rm nf}} - \kappa _{{{\rm s}_{2} }} )}}{{\kappa _{{{\rm s}_{2} }} + (n - 1)\kappa _{{\rm nf}} + \phi _{2} (\kappa _{{\rm nf}} - \kappa _{{{\rm s}_{2} }} )}}$$
(20)

Here \(n\) represents shape of nanoparticles (GO, Cu). We have chosen \(n = 6\;\) as we are interested in tube like or cylindrical nanoparticles.

Solutions methodology

The obtained relevant expressions (PDEs) of the problem are non-dimensionalized by choosing appropriate dimensionless variables. These PDEs are then solved numerically via FDM. This methodology is implemented on FDEs (finite difference equations). Thus, we have converted our dimensionless PDEs and IBCs into FDEs using FD forward difference approximations as below [39,40,41,42,43].

$$f_{{{\rm t}^{*} }} = \frac{{f_{{\rm i,j}}^{{{\rm n} + 1}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }},\,\,\,\,f_{{{\rm x}^{*} }} = \frac{{f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }},\,\,\,\,f_{{{\rm y}^{*} }} = \frac{{f_{{{\rm i,j} + 1}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }},\,\,\,\,g_{{{\rm t}^{*} }} = \frac{{g_{{\rm i,j}}^{{n + 1}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }},\,\,\,\,g_{{{\rm x}^{*} }} = \frac{{g_{{{\rm i} + 1,{\rm j}}}^{n} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }},\,g_{{{\rm y}^{*} }} = \frac{{g_{{{\rm i,j} + 1}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }},\,\,\,\,\,\theta _{{{\rm t}^{*} }} = \frac{{\theta _{{\rm i,j}}^{{{\rm n} + 1}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }},\,\,\,\,\theta _{{{\rm x}^{*} }} = \frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }},\,\,\,\,\theta _{{{\rm y}^{*} }} = \frac{{\theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }}.$$
(21)
$$f_{{{\rm x}^{*} x^{*} }} = \frac{{f_{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }},\,f_{{{\rm y}^{*} y^{*} }} = \frac{{f_{{{\rm i,j} + 2}}^{{\rm n}} - 2f_{{{\rm i,j} + 1}}^{{\rm n}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }},\,g_{{{\rm x}^{*} x^{*} }} = \frac{{g_{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }},\,g_{{{\rm y}^{*} y^{*} }} = \frac{{g_{{{\rm i,j} + 2}}^{{\rm n}} - 2g_{{{\rm i,j} + 1}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }},\,\theta _{{{\rm t}^{*} t^{*} }} = \frac{{\theta _{{\rm i,j}}^{{{\rm n} + 2}} - 2\theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{n} }}{{h_{\rm j}^{2} }},\,\theta _{{{\rm x}^{*} x^{*} }} = \frac{{\theta _{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }},\,\theta _{{{\rm y}^{*} y^{*} }} = \frac{{\theta _{{{\rm i,j} + 2}}^{{\rm n}} - 2\theta _{{{\rm i,j} + 1}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }},\,f_{{{\rm x}^{*} t^{*} }} = \frac{{f_{{{\rm i} + 1,{\rm j}}}^{{{\rm n} + 1}} - f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{{\rm n} + 1}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }},\,f_{{{\rm y}^{*} t^{*} }} = \frac{{f_{{{\rm i,j} + 1}}^{{{\rm n} + 1}} - f_{{{\rm i,j} + 1}}^{{\rm n}} - f_{{\rm i,j}}^{{{\rm n} + 1}} + f_{{\rm i,j}}^{n} }}{{h_{\rm i} h_{\rm n} }},\,f_{{{\rm x}^{*} y^{*} }} = \frac{{f_{{{\rm i} + 1,{\rm j} + 1}}^{{\rm n}} - f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{{\rm i,j} + 1}}^{{\rm n}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm j} }},\,g_{{{\rm x}^{*} t^{*} }} = \frac{{g_{{{\rm i} + 1,{\rm j}}}^{{{\rm n} + 1}} - g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{\rm i,j}}^{{{\rm n} + 1}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }},\,g_{{{\rm y}^{*} t^{*} }} = \frac{{g_{{{\rm i,j} + 1}}^{{{\rm n} + 1}} - g_{{{\rm i,j} + 1}}^{{\rm n}} - g_{{\rm i,j}}^{{{\rm n} + 1}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }},\,g_{{{\rm x}^{*} y^{*} }} = \frac{{g_{{{\rm i} + 1,{\rm j} + 1}}^{{\rm n}} - g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{{\rm i,j} + 1}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm j} }},\,\theta _{{{\rm x}^{*} t^{*} }} = \frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{{\rm n} + 1}} - \theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }},\,\theta _{{{\rm y}^{*} t^{*} }} = \frac{{\theta _{{{\rm i,j} + 1}}^{{{\rm n} + 1}} - \theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }},\,\theta _{{{\rm x}^{*} y^{*} }} = \frac{{\theta _{{{\rm i} + 1,{\rm j} + 1}}^{n} - \theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{{\rm i,j} + 1}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm j} }}.\,$$
(22)

Using these approximations in Eqs. (8)-(11), we get

$$\frac{{f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }}\, + \frac{{g_{{{\rm i,j} + 1}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} = 0,$$
(23)
$$\frac{{f_{{\rm i,j}}^{{{\rm n} + 1}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }} + f_{{\rm i,j}}^{{\rm n}} \frac{{f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + g_{{\rm i,j}}^{{\rm n}} \frac{{f_{{{\rm i,j} + 1}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} = - {\text{Fr(}}f_{{\rm i,j}}^{{\rm n}} )^{2} + A_{{11}} [\frac{{f_{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }} - \lambda f_{{\rm i,j}}^{{\rm n}} + \frac{{f_{{{\rm i,j} + 2}}^{{\rm n}} - 2f_{{{\rm i,j} + 1}}^{{\rm n}} + f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }}],$$
(24)
$$\frac{{g_{{\rm i,j}}^{{{\rm n} + 1}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }} + f_{{\rm i,j}}^{{\rm n}} \frac{{g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + g_{{\rm i,j}}^{{\rm n}} \frac{{g_{{{\rm i,j} + 1}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} = - {\text{Fr(g}}_{{\rm i,j}}^{{\rm n}} )^{2} + A_{{11}} [\frac{{g_{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }} - \lambda g_{{\rm i,j}}^{{\rm n}} + \frac{{g_{{{\rm i,j} + 2}}^{{\rm n}} - 2g_{{{\rm i,j} + 1}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }}],$$
(25)
$$\frac{{\theta _{{\rm i,j}}^{{{\rm n} + 1}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }} + f_{{\rm i,j}}^{{\rm n}} \frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + g_{{\rm i,j}}^{{\rm n}} \frac{{\theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} + \gamma [\frac{{\theta _{{\rm i,j}}^{{{\rm n} + 2}} - 2\theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }} + f_{{\rm i,j}}^{{\rm n}} \frac{{f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }}\frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + g_{{\rm i,j}}^{{\rm n}} \frac{{g_{{{\rm i,j} + 1}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }}\frac{{\theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} + f_{{\rm i,j}}^{{\rm n}} \frac{{g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }}\frac{{\theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }} + g_{{\rm i,j}}^{{\rm n}} \frac{{f_{{{\rm i,j} + 1}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }}\frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + 2f_{{\rm i,j}}^{{\rm n}} g_{{\rm i,j}}^{{\rm n}} \frac{{g_{{{\rm i} + 1,{\rm j} + 1}}^{{\rm n}} (t^{*} ,x^{*} ,y^{*} ) - g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{{\rm i,j} + 1}}^{{\rm n}} + g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm j} }} + f_{{\rm i,j}}^{{{\rm n}2}} \frac{{\theta _{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }} + g_{{\rm i,j}}^{{n2}} \frac{{\theta _{{{\rm i,j} + 2}}^{{\rm n}} - 2\theta _{{{\rm i,j} + 1}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }} + \frac{{f_{{\rm i,j}}^{{{\rm n} + 1}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }}\frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + 2f_{{\rm i,j}}^{{\rm n}} \frac{{\theta _{{{\rm i} + 1,{\rm j}}}^{{{\rm n} + 1}} - \theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - \theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }} + \frac{{g_{{\rm i,j}}^{{{\rm n} + 1}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm n} }}\frac{{\theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }}2g_{{\rm i,j}}^{{\rm n}} \frac{{\theta _{{{\rm i,j} + 1}}^{{{\rm n} + 1}} - \theta _{{{\rm i,j} + 1}}^{{\rm n}} - \theta _{{\rm i,j}}^{{{\rm n} + 1}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} h_{\rm n} }}] = \frac{{A_{{16}} }}{{A_{{21}} }}\Pr Ec\left( {4\left( {\frac{{f_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }}} \right)^{2} + \left( {\frac{{g_{{{\rm i} + 1,{\rm j}}}^{{\rm n}} - g_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i} }} + \frac{{f_{{{\rm i,j} + 1}}^{{\rm n}} - f_{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j} }}} \right)^{2} } \right) + \frac{{A_{{14}} }}{{A_{{15}} \Pr }}\left[ {\frac{{\theta _{{{\rm i} + 2{\rm ,j}}}^{{\rm n}} - 2\theta _{{{\rm i} + 1,{\rm j}}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm i}^{2} }} + \frac{{\theta _{{{\rm i,j} + 2}}^{{\rm n}} - 2\theta _{{{\rm i,j} + 1}}^{{\rm n}} + \theta _{{\rm i,j}}^{{\rm n}} }}{{h_{\rm j}^{2} }}} \right],$$
(26)

with IBCs

$$f_{{\rm i,j}}^{0} = 0,\,\,\,\,g_{{\rm i,j}}^{0} = 0,\,\,\,\,\theta _{{\rm i,j}}^{0} = 1,\,\,\,\,\frac{{\theta _{{\rm i,j}}^{1} - \theta _{{\rm i,j}}^{0} }}{{h_{0} }} = 0,$$
(27)
$$f_{{{\rm i},0}}^{{\rm n}} = M(x^{*} _{{{\rm i} + 1}} - x^{*} _{\rm i} ),\,\,\,\,\theta _{{{\rm i},0}}^{{\rm n}} = 1,\,\,\,\,\frac{{M_{1} }}{{A_{{14}} }}(\frac{{\theta _{{{\rm i},1}}^{{\rm n}} - \theta _{{{\rm i},0}}^{{\rm n}} }}{{h_{0} }}) = \frac{{\Pr }}{{A_{{21}} }}g_{{{\rm i},0}}^{{\rm n}} ,f_{{{\rm i},1}}^{{\rm n}} = 0,\,\,\,\,g_{{{\rm i},1}}^{{\rm n}} = \frac{{Sq}}{2}\sqrt M ,\,\,\,\,\theta _{{{\rm i},1}}^{{\rm n}} = 0.$$
(28)

Discussion

Impacts of concerned physical variables toward velocities (\(f(t^{*} ,x^{*} ,y^{*} )\), \(g(t^{*} ,x^{*} ,y^{*} )\)) and temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) are enclosed in this section. Involved parameters and expressions are listed in nomenclature (see Table 1). Table 2 comprises thermal features of nanoparticles (GO, Cu) and baseliquid (water). During analyzing impacts of concerned parameters toward \(f(t^{*} ,x^{*} ,y^{*} )\), \(g(t^{*} ,x^{*} ,y^{*} )\) and \(\theta (t^{*} ,x^{*} ,y^{*} )\), \(t^{*} = 1.0\) and \(x^{*} = 0.1\) for line graphs while in Hamilton–Crosser expressions for hybrid nanomaterial (GO + Cu + Water), \(n = 6\) is taken for cylindrical nanoparticles.

Table 1 Nomenclature
Full size table
Table 2 Features of nanoparticles (GO, Cu) and basefluid (water) [7, 25]
Full size table

Discussion for \(f(t^{*} ,x^{*} ,y^{*} )\) and \(g(t^{*} ,x^{*} ,y^{*} )\)

Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) of hybrid nanomaterial (GO + Cu + Water) due to an increase in \({\text{Sq}}\) (squeezing parameter) is captured in Fig. 2. This figure elaborates that \(f(t^{*} ,x^{*} ,y^{*} )\) increases with higher \({\text{Sq}}\) (squeezing parameter). Physically an increase in \({\text{Sq}}\) (squeezing parameter) is related with execution of more squeezing force from upper wall on the hybrid nanomaterial (GO + Cu + Water) confined between the walls. Due to this squeezing force the velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) of the hybrid nanomaterial (GO + Cu + Water) increases. Figure 3 is made for studying impact of \(\lambda\) (porosity parameter) on velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) of the hybrid nanomaterial (GO + Cu + Water). This figure shows that velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) reduces with higher \(\lambda\) (porosity parameter). Reason behind this reduction in \(f(t^{*} ,x^{*} ,y^{*} )\) is that higher \(\lambda\) (porosity parameter) relate with production of more porous space among hybrid nanomaterial (GO + Cu + Water). Such porous space resists flow of hybrid nanomaterial (GO + Cu + Water) and correspondingly \(f(t^{*} ,x^{*} ,y^{*} )\) reduces. Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) of hybrid nanomaterial (GO + Cu + Water) against variations in \({\text{Fr}}\) (Forchheimer number) is expressed in Fig. 4. This plot reveals that \(f(t^{*} ,x^{*} ,y^{*} )\) is a decreasing function of \({\text{Fr}}\) (Forchheimer number). Reason behind this decrease in \(f(t^{*} ,x^{*} ,y^{*} )\) is that higher \({\text{Fr}}\) (Forchheimer number) being associated with more resistive force (drag forces). Such force resists hybrid nanomaterial (GO + Cu + Water) flow and hence \(f(t^{*} ,x^{*} ,y^{*} )\) decreases. Figure 5 sketches impacts of \({\text{M}}\) (Reynolds number) on velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) of hybrid nanomaterial (GO + Cu + Water). Here \(f(t^{*} ,x^{*} ,y^{*} )\) intensifies with higher \({\text{M}}\) (Reynolds number). In fact an intensification in \(f(t^{*} ,x^{*} ,y^{*} )\) is that higher \({\text{M}}\) (Reynolds number) related with more turbulent flow of hybrid nanomaterial (GO + Cu + Water) and consequently \(f(t^{*} ,x^{*} ,y^{*} )\) increases. Velocity (\(g(t^{*} ,x^{*} ,y^{*} )\)) under higher estimations of \({\text{M}}\) (Reynolds number) and \({\text{Sq}}\) (squeezing parameter) is labeled in Figs. 6 and 7. These figures reveal that \(g(t^{*} ,x^{*} ,y^{*} )\) increases with higher \({\text{M}}\) (Reynolds number) and \({\text{Sq}}\) (squeezing parameter).

Fig. 2
figure 2

Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) against higher \({\text{Sq}}\)

Full size image
Fig. 3
figure 3

Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) against higher \(\lambda\)

Full size image
Fig. 4
figure 4

Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) against higher \({\text{Fr}}\)

Full size image
Fig. 5
figure 5

Velocity (\(f(t^{*} ,x^{*} ,y^{*} )\)) against higher \({\text{M}}\)

Full size image
Fig. 6
figure 6

Velocity (\(g(t^{*} ,x^{*} ,y^{*} )\)) against higher \({\text{M}}\)

Full size image
Fig. 7
figure 7

Velocity (\(g(t^{*} ,x^{*} ,y^{*} )\)) against higher \({\text{Sq}}\)

Full size image

Discussion for \(\theta (t^{*} ,x^{*} ,y^{*} )\)

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) of the hybrid nanomaterial (GO + Cu + Water) due to increment in \(M_{1}\) (melting parameter) is plotted in Fig. 8. It is examined in this figure that increase in \(M_{1}\) (melting parameter) reduces \(\theta (t^{*} ,x^{*} ,y^{*} )\). Higher \(M_{1}\) (melting parameter) is associated with more convective flow from hot hybrid nanomaterial (GO + Cu + Water) toward the cold lower wall. As a result \(\theta (t^{*} ,x^{*} ,y^{*} )\) decreases. Figure 9 sketches variations in temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) for hybrid nanomaterial (GO + Cu + Water) with rise in \(\gamma\) (thermal relaxation parameter). This figure reveals that \(\theta (t^{*} ,x^{*} ,y^{*} )\) decreases with increase in \(\gamma\) (thermal relaxation parameter). Figures 10 and 11 capture impacts of \(\phi _{1}\) (volume fraction for GO) and \(\phi _{2}\) (volume fraction for Cu). It is noted from these both figures that \(\theta (t^{*} ,x^{*} ,y^{*} )\) declines with increase in both \(\phi _{1}\) (volume fraction for GO) and \(\phi _{2}\) (volume fraction for Cu). Reason behind this reduction is the transmission of heat form heated hybrid nanomaterial (GO + Cu + Water) toward surrounding. Hence \(\theta (t^{*} ,x^{*} ,y^{*} )\) decreases. Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) due to higher \({\text{Sq}}\) (squeezing parameter) is presented in Fig. 12. It is revealed by this plot that temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) of the hybrid nanomaterial (GO + Cu + Water) increases with higher \({\text{Sq}}\) (squeezing parameter). Physically higher \({\text{Sq}}\) (squeezing parameter) is associated with insertion of more squeezing force from the upper wall on the hybrid nanomaterial (GO + Cu + Water). Thus, due to collision among the particles of the hybrid nanomaterial (GO + Cu + Water), more heat is generated and consequently \(\theta (t^{*} ,x^{*} ,y^{*} )\) boosts. Figure 13 is plotted for studying variations in temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) due to higher \({\text{Ec}}\) (Eckert number). It is observed from this plot that higher \({\text{Ec}}\) (Eckert number) is directly associated with K.E (as it is the ratio of K.E and enthalpy). Hence \(\theta (t^{*} ,x^{*} ,y^{*} )\) increases with \({\text{Ec}}\) (Eckert number).

Fig. 8
figure 8

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image
Fig. 9
figure 9

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image
Fig. 10
figure 10

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image
Fig. 11
figure 11

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image
Fig. 12
figure 12

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image
Fig. 13
figure 13

Temperature (\(\theta (t^{*} ,x^{*} ,y^{*} )\)) against higher

Full size image

Final remarks

Hybrid nanomaterial (GO + Cu + Water) bounded between infinite parallel walls is examined. Melting heat and viscous dissipation elaborate heat transmission in the considered problem. Cattaneo–Christov (C–C) heat flux model is taken into account. Worth mentioning points are that velocity () enlarges with an increase in (squeezing parameter) and (Reynolds number). Higher (porosity parameter) and (Forchheimer number) cause decay in velocity (). Velocity () is higher for (squeezing parameter) and (Reynolds number). Higher (Eckert number) and (squeezing parameter) intensify temperature () of the fluid. Fluid temperature () is controlled by choosing higher (melting parameter), (thermal relaxation time parameter), (volume fraction for GO) and (volume fraction for Cu).